华东师范大学第二附属中学校本课程 理科 四面体中的数学问题
上海华东师范大学第二附属中学必修二第一章《立体几何初步》测试题(答案解析)

一、选择题1.在空间四边形ABCD 中,AB BC =,AD DC =,则对角线AC 与BD 所成角的大小是( )A .90︒B .60︒C .45︒D .302.在三棱柱111ABC A B C -中,90BAC ∠=︒,1BC AC ,且12AC BC =,则直线11B C 与平面1ABC 所成的角的大小为( )A .30°B .45°C .60°D .90°3.在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,点E ,F 分别是棱C 1D 1,B 1C 1的中点,P 是上底面A 1B 1C 1D 1内一点,若AP ∥平面BDEF ,则线段AP 长度的取值范围是( ) A .[322,5] B .[5,22] C .[324,6] D .[6,22] 4.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .24B .30C .47D .67 5.如图正三棱柱111ABC A B C -的所有棱长均相等,O 是1AA 中点,P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC ,则直线OP 与平面ABC 所成角正弦值的最大值为( )A .22B .255C .32D .2776.下图中小正方形的边长为1,粗线画出的是某四棱锥的三视图,则该四棱锥的体积为( )A .64B .48C .32D .167.如图,在矩形ABCD 中,1AB =,3BC =,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥A BCD -正视图和俯视图如图,则三棱锥A BCD -中AC 长为( )A .32B 3C 10D .28.三个平面将空间分成n 个部分,则n 不可能是( )A .5B .6C .7D .89.一个正方体的平面展开图及该正方体的直观图如图所示,在正方体中,设BC 的中点为M ,GH 的中点为N ,下列结论正确的是( )A .//MN 平面ABEB .//MN 平面ADEC .//MN 平面BDHD .//MN 平面CDE 10.αβ是两个不重合的平面,在下列条件中,可判定平面α与β平行的是( ) A .m 、n 是α内的两条直线,且//m β,βn//B .α、β都垂直于平面γC .α内不共线三点到β的距离相D .m 、n 是两条异面直线,m α⊂,n β⊂,且//m β,//n α11.设m 、n 是两条不同的直线,α是平面,m 、n 不在α内,下列结论中错误的是( )A .m α⊥,//n α,则m n ⊥B .m α⊥,n α⊥,则//m nC .m α⊥,m n ⊥,则//n αD .m n ⊥,//n α,则m α⊥ 12.已知直线a 、b 都不在平面α内,则下列命题错误的是( )A .若//a b ,//a α,则//b αB .若//a b ,a α⊥,则b α⊥C .若a b ⊥,//a α,则b α⊥D .若a b ⊥,a α⊥,则//b α 二、填空题13.三棱锥P ABC -三条侧棱两两垂直,正四面体D ABC -与三棱锥相接且棱长为2P 与D 在面ABC 异侧,则所成多面体外接球的体积是_________.14.已知某空心圆锥的母线长为5cm ,高为4cm ,记该圆锥内半径最大的球为球O ,则球O 与圆锥侧面的交线的长为________cm .15.如图,四边形ABCD 是矩形,且有2AB BC =,沿AC 将ADC 翻折成AD C ',当二面角D AC B '--的大小为3π时,则异面直线D C '与AB 所成角余弦值是______.16.已知长方体1234ABCD A B C D -,底面是边长为4的正方形,高为2,点O 是底面ABCD 的中心,点P 在以O 为球心,半径为1的球面上,设二面角111P A B C --的平面角为θ,则tan θ的取值范围是________.17.二面角a αβ--的大小为135A AE a E α︒∈⊥,,,为垂足,,B BF a F β∈⊥,为垂足,2,31AE BF EF P ===,,是棱上动点,则AP PB +的最小值为_______. 18.如图,已知四棱锥S ABCD -的底面为等腰梯形,//AB CD ,1AD DC BC ===,2AB SA ==,且SA ⊥平面ABCD ,则四棱锥S ABCD -外接球的体积为______.19.在正三棱锥S ABC -中,23AB =,4SA =,E 、F 分别为AC 、SB 的中点,过点A 的平面α//平面SBC ,α平面=ABC l ,则异面直线l 和EF 所成角的余弦值为_________.20.将半径为3,圆心角为23π的扇形围成一个圆锥,则该圆锥内切球的体积为________. 三、解答题21.在如图所示几何体中,平面PAC ⊥平面ABC ,//PM BC ,PA PC =,1AC =,22BC PM ==,5AB =.若该几何体左视图(侧视图)的面积为34.(1)画出该几何体的主视图(正视图)并求其面积S ;(2)求出多面体PMABC 的体积V .22.如图,四棱锥P ABCD -的底面为正方形,PA ⊥底面ABCD ,E ,F ,H 分别为AB ,PC ,BC 的中点.(1)求证:DE ⊥平面PAH ;(2)若2PA AD ==,求直线PD 与平面PAH 所成线面角的正弦值.23.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,32,3,PB PD PA AD ====点,E F 分别为线段,PD BC 的中点.(1)求证://EF 平面ABP ;(2)求证:平面AEF ⊥平面PCD ;(3)求三棱锥C AEF -的体积24.如图1,在梯形ABCD 中,//BC AD ,4=AD ,1BC =,45ADC ∠=︒,梯形的高为1,M 为AD 的中点,以BM 为折痕将ABM 折起,使点A 到达点N 的位置,且平面NBM ⊥平面BCDM ,连接NC ,ND ,如图2.(1)证明:平面NMC ⊥平面NCD ;(2)求图2中平面NBM 与平面NCD 所成锐二面角的余弦值.25.将棱长为2的正方体1111ABCD A BC D -沿平面11ABCD 截去一半(如图1所示)得到如图2所示的几何体,点E ,F 分别是BC ,DC 的中点.(Ⅰ)证明:EF ⊥平面1A AC ;(Ⅱ)求三棱锥1A D EF -的体积.26.如图,四棱锥P ABCD -,底面ABCD 为矩形,PD ⊥面ABCD ,E 、F 分别为PA 、BC 的中点.(1)求证://EF 面PCD ;(2)若2AB =,1AD PD ==,求三棱锥P BEF -的体积.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】取AC 中点O ,根据条件分析AC 与平面BOD 的位置关系,由此得到异面直线AC 与BD 所成角的大小.【详解】取AC 中点O ,连接,,BO DO BD ,如图所示:因为AB BC =,AD DC =,所以,BO AC DO AC ⊥⊥,且BODO O =,所以AC ⊥平面BOD ,又BD ⊂平面BOD ,所以AC BD ⊥,所以AC 与BD 所成角为90︒,故选:A.【点睛】关键点点睛:解答问题的关键是通过找AC 中点证明线面垂直,从而确定出线线垂直关系,和常规的求解异面直线所成角的方法不同.2.A解析:A【分析】证明CBA ∠就是BC 与平面1ABC 所成的角,求出此角后,利用11//B C BC 可得结论,【详解】∵90BAC ∠=︒,12AC BC =,∴30CBA ∠=︒, ∵1BC AC ,AB AC ⊥,1BC AB B ,1,BC AB ⊂平面1ABC ,∴AC ⊥平面1ABC ,∴CBA ∠就是BC 与平面1ABC 所成的角,即BC 与平面1ABC 所成的角是30, ∵棱柱中11//B C BC ,∴11B C 与平面1ABC 所成的角的大小为30,故选:A .【点睛】思路点睛:本题考查求直线与平面所成的角,解题方法是定义法,即过直线一点作平面的垂直,得直线在平面上的射影,由直线与其射影的夹角得直线与平面所成的角,然后在直角三角形中求出此角.解题过程涉及三个步骤:一作出图形,二证明所作角是直线与平面所成的角,三是计算.3.A解析:A【分析】分别取棱A 1B 1、A 1D 1的中点M 、N ,连接MN ,可证平面AMN ∥平面BDEF ,得P 点在线段MN 上.由此可判断当P 在MN 的中点时,AP 最小;当P 与M 或N 重合时,AP 最大.然后求解直角三角形得答案.【详解】如图所示,分别取棱A 1B 1、A 1D 1的中点M 、N ,连接MN ,连接B 1D 1,∵M 、N 、E 、F 为所在棱的中点,∴MN ∥B 1D 1,EF ∥B 1D 1,∴MN ∥EF ,又MN ⊄平面BDEF ,EF ⊂平面BDEF ,∴MN ∥平面BDEF ;连接NF ,由NF ∥A 1B 1,NF =A 1B 1,A 1B 1∥AB ,A 1B 1=AB ,可得NF ∥AB ,NF =AB ,则四边形ANFB 为平行四边形,则AN ∥FB ,而AN ⊄平面BDEF ,FB ⊂平面BDEF ,则AN ∥平面BDEF .又AN ∩NM =N ,∴平面AMN ∥平面BDEF .又P 是上底面A 1B 1C 1D 1内一点,且AP ∥平面BDEF ,∴P 点在线段MN 上.在Rt △AA 1M 中,AM 222211215AA A M =+=+=同理,在Rt △AA 1N 中,求得AN 5=△AMN 为等腰三角形.当P 在MN 的中点时,AP 222322()2+ 当P 与M 或N 重合时,AP 5 ∴线段AP 长度的取值范围是3252⎡⎢⎣. 故选:A .【点睛】本题主要考查了空间中点、线、面间的距离问题,其中解答中通过构造平行平面寻找得到点P 的位置是解答的关键,意在考查空间想象能力与运算能力,属于中档试题. 4.D解析:D【分析】先找到几何体的原图,再求出几何体的高,再求几何体的体积得解.【详解】由三视图可知几何体为图中的四棱锥1P CDD E -, 由题得22437AD =-7 所以几何体的体积为11(24)676732⋅+⋅=. 故选:D【点睛】方法点睛:通过三视图找几何体原图常用的方法有:(1)直接法;(2)拼凑法;(3)模型法.本题利用的就是模型法.要根据已知条件灵活选择方法求解. 5.D解析:D【分析】先找到与平面11A BC 平行的平面OEFG ,确定点P 在直线FG 上,作出线面角,求出正弦,转化为求AP 的最小值.【详解】分别取1,,CC BC BA 的中点,连接,,,OE EF FG GO ,并延长FG ,如图,由中位线性质可知11//OE AC , 1//EF BC ,且OE EF E =, 故平面11//A BC 平面OGFE , 又P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC 则点P 在直线FG 上,OA ⊥平面ABC ,OPA ∴∠是直线OP 与平面ABC 所成角, sin OA OPA OP∴∠=, OA 为定值, ∴当OP 最小时,正弦值最大, 而22OP OA AP +所以当AP 最小时,sin OPA ∠最大, 故当AP FG ⊥时,sin OPA ∠最大, 设棱长为2, 则1212AG =⨯=,而30GAP ∠=︒, 3AP ∴=, 又1212OA =⨯=, 222sin 773()12OA OPA OP ∴∠===+故选:D【点睛】关键点点睛:由P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC ,转化为找过O 的平面与平面11A BC 平行,P 在所找平面与平面ABC 的交线上,从而容易确定出线面角,是本题解题的关键所在.6.C解析:C【分析】在长方体中还原三视图后,利用体积公式求体积.【详解】根据三视图还原后可知,该四棱锥为镶嵌在长方体中的四棱锥P -ABCD (补形法) 且该长方体的长、宽、高分别为6、4、4, 故该四棱锥的体积为1(64)4323V =⨯⨯⨯=. 故选C .【点睛】(1)根据三视图画直观图,可以按下面步骤进行:①、首先看俯视图,根据俯视图画出几何体地面的直观图 ;②、观察正视图和侧视图找到几何体前、后、左、右的高度;③、画出整体,让后再根据三视图进行调整;(2)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解. 7.C解析:C【分析】先由正视图、俯视图及题意还原三棱锥,过A 作AM ⊥BD 于点M ,连结MC ,把AC 放在直角三角形AMC 中解AC .【详解】根据三棱锥A BCD -正视图和俯视图,还原后得到三棱锥的直观图如图示,由图可知:平面ABD ⊥平面CBD ,过A 作AM ⊥BD 于点M ,连结MC ,则AM ⊥平面CBD ,∴△MCA 为直角三角形.过C 作CN ⊥BD 于点N ,在直角三角形ABD 中,AB =1,AD 3∴222BD AB AD =+= 所以∠ABD=60°,∠ADB=30°,则在直角三角形ABM 中,AB =1,∠ABM=60°,∴13,2BM AM == 同理,在直角三角形CBD 中,13,2DN CN ==. ∴MN =BD -BM -DN =112122--=, ∴222237()122CM CN MN =+=+= 在直角三角形AMC 中,22227310()22AC CM AM ⎛⎫=+=+ ⎪⎪⎝⎭故选:C【点睛】 (1)根据三视图画直观图,可以按下面步骤进行:①、首先看俯视图,根据俯视图画出几何体地面的直观图 ;②、观察正视图和侧视图找到几何体前、后、左、右的高度;③、画出整体,让后再根据三视图进行调整.(2)立体几何中求线段长度:①、把线段放在特殊三角形中,解三角形;②、用等体积法求线段.8.A解析:A【分析】三个平面不重合,先按其中平行的平面的个数分类:三个平面两两平行,两个平面平行,没有平行的平面(两两相交),对两两相交的情况,再根据三条交线互相平行,重合,交于一点,分别讨论.【详解】按照三个平面中平行的个数来分类:(1)三个平面两两平行,如图1,可将空间分成4部分;(2)两个平面平行,第三个平面与这两个平行平面相交,如图2,可将空间分成6部分;(3)三个平面中没有平行的平面:(i)三个平面两两相交且交线互相平行,如图3,可将空间分成7部分;(ii)三个平面两两相交且三条交线交于一点,如图4,可将空间分成8部分.(iii)三个平面两两相交且交线重合,如图5,可将空间分成6部分;综上,可以为4,6,7,8部分,不能为5部分,故选:A.9.C解析:C【分析】根据题意,得到正方体的直观图及其各点的标记字母,取FH 的中点O ,连接ON ,BO ,可以证明MN ‖BO ,利用BO 与平面ABE 的关系可以判定MN 与平面ABE 的关系,进而对选择支A 作出判定;根据MN 与平面BCF 的关系,利用面面平行的性质可以判定MN 与平面ADE 的关系,进而对选择支B 作出判定;利用线面平行的判定定理可以证明MN 与平面BDE 的平行关系,进而判定C ;利用M ,N 在平面CDEF 的两侧,可以判定MN 与平面CDE 的关系,进而对D 作出判定.【详解】根据题意,得到正方体的直观图及其各点的标记字母如图所示,取FH 的中点O ,连接ON ,BO ,易知ON 与BM 平行且相等,∴四边形ONMB 为平行四边形,∴MN ‖BO ,∵BO 与平面ABE (即平面ABFE )相交,故MN 与平面ABE 相交,故A 错误;∵平面ADE ‖平面BCF ,MN ∩平面BCF =M ,∴MN 与平面ADE 相交,故B 错误;∵BO ⊂平面BDHF ,即BO ‖平面BDH ,MN ‖BO ,MN ⊄平面BDHF ,∴MN ‖平面BDH ,故C 正确; 显然M ,N 在平面CDEF 的两侧,所以MN 与平面CDEF 相交,故D 错误.故选:C.【点睛】本题考查从面面平行的判定与性质,涉及正方体的性质,面面平行,线面平行的性质,属于小综合题,关键是正确将正方体的表面展开图还原,得到正方体的直观图及其各顶点的标记字母,并利用平行四边形的判定与性质找到MN 的平行线BO .10.D解析:D【分析】取a αβ⋂=,且//m a ,//n a ,利用线面平行的判定定理可判断A 选项;根据αγ⊥,βγ⊥判断平面α与β的位置关系,可判断B 选项;设AB 、AC 的中点D 、E 在平面β内,记平面ABC 为平面α,判断出A 、B 、C 三点到平面β的距离相等,可判断C 选项;过直线n 作平面γ,使得a αγ⋂=,利用线面平行、面面平行的判定定理可判断D 选项.【详解】对于A 选项,若a αβ⋂=,且//m a ,//n a ,m β⊄,n β⊄,则//m β,βn//,但α与β相交;对于B 选项,若αγ⊥,βγ⊥,则α与β平行或相交;对于C 选项,设AB 、AC 的中点D 、E 在平面β内,记平面ABC 为平面α,如下图所示:D 、E 分别为AB 、AC 的中点,则//DE BC ,DE β⊂,BC β⊄,//BC β∴,所以,点B 、C 到平面β的距离相等, 由于D 为AB 的中点,则点A 、B 到平面β的距离相等,所以,点A 、B 、C 三点到平面β的距离相等,但平面α与平面β相交; 对于D 选项,如下图所示:由于//n α,过直线n 作平面γ,使得a αγ⋂=,则//a n ,//n a ,a β⊄,n β⊂,//a β∴,//m β,m a A =,m α⊂,a α⊂,//αβ∴.故选:D.【点睛】方法点睛:证明或判断两个平面平行的方法有:①用定义,此类题目常用反证法来完成证明;②用判定定理或推论(即“线线平行”⇒“面面平行”),通过线面平行来完成证明; ③根据“垂直于同一条直线的两个平面平行”这一性质进行证明;④借助“传递性”来完成.11.D解析:D【分析】利用线面平行的性质定理和线面垂直的定义可判断A 选项的正误;由线面垂直的性质定理可判断B 选项的正误;根据已知条件判断直线n 与平面α的位置关系,可判断C 选项的正误;根据已知条件判断直线m 与平面α的位置关系,可判断D 选项的正误.【详解】对于A ,//n α,由线面平行的性质定理可知,过直线n 的平面β与平面α的交线l 平行于n , m α⊥,l α⊂,m l ∴⊥,m n ∴⊥,故A 正确;对于B ,若m α⊥,n α⊥,由直线与平面垂直的性质,可得//m n ,故B 正确; 对于C ,若m α⊥,m n ⊥,则//n α或n ⊂α,又n α⊄,//n α∴,故C 正确; 对于D ,若m n ⊥,//n α,则//m α或m 与α相交或m α⊂,而m α⊄,则//m α或m 与α相交,故D 错误.故选:D .【点睛】方法点睛:对于空间线面位置关系的组合判断题,解决的方法是“推理论证加反例推断”,即正确的结论需要根据空间线面位置关系的相关定理进行证明,错误的结论需要通过举出反例说明其错误,在解题中可以以常见的空间几何体(如正方体、正四面体等)为模型进行推理或者反驳.12.C解析:C【分析】利用线面平行的性质和判定定理可判断A 选项的正误;由线面垂直的定义可判断B 选项的正误;根据已知条件判断b 与α的位置关系,可判断C 选项的正误;根据已知条件判断b 与α的位置关系,可判断D 选项的正误.【详解】由于直线a 、b 都不在平面α内.在A 中,若//a α,过直线a 的平面β与α的交线m 与a 平行,因为//a b ,可得//b m ,b α⊄,m α⊂,所以,//b α,A 选项正确;在B 中,若a α⊥,则a 垂直于平面α内所有直线,//a b ,则b 垂直于平面α内所有直线,故b α⊥,B 选项正确;在C 中,若a b ⊥,//a α,则b 与α相交或平行,C 选项错误;在D 中,若a b ⊥,a α⊥,则//b α或b α⊂,b α⊄,//b α∴,D 选项正确.故选:C.【点睛】方法点睛:对于空间线面位置关系的组合判断题,解决的方法是“推理论证加反例推断”,即正确的结论需要根据空间线面位置关系的相关定理进行证明,错误的结论需要通过举出反例说明其错误,在解题中可以以常见的空间几何体(如正方体、正四面体等)为模型进行推理或者反驳. 二、填空题13.【分析】根据几何体的几何关系可将几何体放在正方体中多面体的外接球和正方体的外接球是同一外接球由此可求外接球的体积【详解】如图所示并且两两互相垂直所以所以正四面体与三棱锥相接且棱长为所以如图所示将此多解析:2【分析】根据几何体的几何关系,可将几何体放在正方体中,多面体的外接球和正方体的外接球是同一外接球,由此可求外接球的体积.【详解】如图所示,AB AC BC ==,并且,,PA PB PC 两两互相垂直,所以222222PA PB PA PC PB PC +=+=+,所以PA PB PC ==,正四面体D ABC -中,多面体的外接球就是此正方体的外接球,并且棱长为1,正方体外接球的半径2R R =则外接球的体积34332V R ππ==. 故答案为:3π2【点睛】关键点点睛:本题的关键点是根据多面体的几何关系可采用补体,转化为求正方体的外接球的体积,这样计算就容易了.14.【分析】由题可求出底面半径根据三角形相似关系可求出球半径再利用三角形面积关系可求出球O 与圆锥的侧面的交线的半径即可求出交线长【详解】圆锥的轴截图如图所示由题可知圆锥的高母线设的内切圆与圆锥的母线相切 解析:125π 【分析】由题可求出底面半径,根据三角形相似关系可求出球半径,再利用三角形面积关系可求出球O 与圆锥的侧面的交线的半径,即可求出交线长.【详解】圆锥的轴截图如图所示,由题可知,圆锥的高4cm AF =,母线5cm AB AC ==,设ABC 的内切圆O 与圆锥的母线相切与点E ,则OE AB ⊥,则该圆锥内半径最大的球即以O 为圆心,OE 为半径的球,在直角三角形ABF 中,2222543cm BF AB AF =-=-=,由圆的切线性质可得3cm BE BF ==,所以532cm AE AB BE =-=-=,在直角三角形AFB 和直角三角形AEO 中,因为∠∠EAO BAF =,所以△△AFB AEO ~, 所以AE OE AF BF =,则可得3cm 2OE =, 过点E 作ED AF ⊥,D 为垂足,则球O 与圆锥的侧面的交线是以DE 为半径的圆,354cm 22AO AF OF =-=-=, 因为1122△AEO S AE OE ED AO =⋅=⋅,所以6cm 5ED =, 所以球O 与圆锥的侧面的交线长为6122cm 55ππ⨯=. 故答案为:125π. 【点睛】 本题考查圆锥与球的相切问题,解题的关键是利用轴截面,用平面几何的知识解决. 15.【分析】作于于可得等于二面角的平面角从而可得然后求得而因此可得是异面直线与所成角(或补角)这样在求解可得【详解】如图作于于则连接根据二面角平面角的定义知与的夹角等于二面角的平面角所以因为所以设则在矩 解析:12. 【分析】作DM AC ⊥于M ,BN AC ⊥于N ,可得,MD NB '<>等于二面角D AC B '--的平面角,从而可得DMD '∠,然后求得DD ',而//AB CD ,因此可得D CD '∠是异面直线D C '与AB 所成角(或补角).这样在DCD '求解可得.【详解】如图,作DM AC ⊥于M ,BN AC ⊥于N ,则//DM BN ,连接,D M DD '', 根据二面角平面角的定义知MD '与NB 的夹角等于二面角D AC B '--的平面角, 所以,3MD NB π'<>=,因为//DM BN ,所以23DMD π'∠=,设1BC =,则AB ==,在矩形ABCD 中,AC =3DM ==,D M DM '==, 则22222212cos 2232DD DM D M DM D M π⎛⎫'''=+-⋅=+--= ⎪⎝⎭⎝⎭⎝⎭, 所以2DD '=,因为//AB CD ,所以D CD '∠是异面直线D C '与AB 所成角(或补角). DCD '是正三角形,3D CD π'∠=,1cos 2D CD '∠=. 所以异面直线D C '与AB 所成角余弦值是12. 故答案为:12.【点睛】关键点点睛:本题考查求异面直线所成的角,解题方法根据异面直线所成角定义作出它们所成的角,然后解三角形可得,解题关键是利用图中MD '与NB 的夹角等于二面角D AC B '--的平面角,从而求得DMD '∠,只要设1BC =,可求得DD ',从而求得结论.16.【分析】根据题意画出相应的图形结合题意找出什么情况下取最大值什么情况下取最小值利用和差角正切公式求得最值得到结果【详解】根据题意如图所示:取的中点过点作球的切线切点分别为可以判断为的最小值为的最大值解析:4747-+⎣⎦【分析】根据题意,画出相应的图形,结合题意,找出什么情况下取最大值,什么情况下取最小值,利用和差角正切公式求得最值,得到结果.【详解】根据题意,如图所示:取11A B 的中点H ,过H 点作球O 的切线,切点分别为,M N , 可以判断1O HN ∠为θ的最小值,1O HM ∠为θ的最大值, 且1112tan 12OO O HO HO ∠===, 22,1OH OM ON ===,所以7HM HN ==tan tan 7NHO OHM ∠=∠=, 1117827477tan tan()1637117O HN O HO NHO ---∠=∠-∠====+, 11171827477tan tan()7117O HM O HO OHM ++++∠=∠+∠====-, 所以tan θ的取值范围是4747-+⎣⎦, 故答案为:4747-+⎣⎦. 【点睛】方法点睛:该题考查的是有关二面角的求解问题,解题方法如下: (1)先根据题意画图;(2)结合题意,找出在什么情况下取最大值和最小值; (3)结合图形求得相应角的正切值; (4)利用和差角正切公式求得结果.17.【分析】首先将二面角展平根据两点距离线段最短求最小值【详解】如图将二面角沿棱展成平角连结根据两点之间线段最短可知就是的最小值以为邻边作矩形由可知三点共线则故答案为:【点睛】思路点睛:本题考查立体几何 解析:26【分析】首先将二面角展平,根据两点距离线段最短,求AP PB +最小值. 【详解】如图,将二面角沿棱a 展成平角,连结AB ,根据两点之间线段最短,可知AB 就是AP PB +的最小值,以,AE EF 为邻边,作矩形AEFC ,由,CF a BF a ⊥⊥可知,,C F B 三点共线, 则()222213226AB AC BC =+=++=26【点睛】思路点睛:本题考查立体几何中的折线段和的最小值,一般都是沿交线展成平面,利用折线段中,两点间距离最短求解,本题与二面角的大小无关.18.【分析】取AB 中点连接根据平行四边形性质可得为等腰梯形ABCD 的外心取SB 中点O 连接则可得O 是四棱锥的外接球球心在中求得r=OA 即可求得体积【详解】取AB 中点连接则所以四边形为平行四边形所以同理所以 82π【分析】取AB 中点1O ,连接11,OC O D ,根据平行四边形性质,可得1O 为等腰梯形ABCD 的外心,取SB 中点O ,连接1,,,OA OC OD OO ,则可得O 是四棱锥S ABCD -的外接球球心,在Rt SAB 中,求得r=OA ,即可求得体积. 【详解】取AB 中点1O ,连接11,OC O D ,则1//CD O A , 所以四边形1ADCO 为平行四边形, 所以1=1CO ,同理1=1O D ,所以1111=O A O B OC O D ==,即1O 为等腰梯形ABCD 的外心, 取SB 中点O ,连接1,,,OA OC OD OO ,则1//OO SA ,因为SA ⊥平面ABCD ,所以1OO ⊥平面ABCD ,又2AB SA ==, 所以=OA OB OC OD ==,又SA AB ⊥,所以OA OS =,即O 是四棱锥S ABCD -的外接球球心, 在Rt SAB 中,2AB SA ==, 所以122OA SB == 所以3482(2)33V ππ=⨯=, 故答案为:823π.【点睛】解决外接球的问题时,难点在于找到球心,可求得两个相交平面的外接圆圆心,自圆心做面的垂线,垂线交点即为球心,考查空间想象,数学运算的能力,属中档题.19.【分析】取中点连结根据题意得故所以为异面直线和所成角再根据几何关系求得在中故进而得答案【详解】取中点连结依题意:所以所以为异面直线和所成角在正三棱锥中是中点所以又因为平面平面所以平面所以因为分别是的 21 【分析】取AB 、BC 中点D 、G ,连结DE 、DF 、GS 、GA ,根据题意得//l BC ,//DE BC ,故//lDE ,所以DEF ∠为异面直线l 和EF 所成角,再根据几何关系求得在Rt DEF ∆中,122DF SA ==,11322DE BC AB ===,227EF DE DF =+321cos 7DE DEF EF ∠===,进而得答案. 【详解】取AB 、BC 中点D 、G ,连结DE 、DF 、GS 、GA , 依题意://l BC ,//DE BC , 所以//l DE ,所以DEF ∠为异面直线l 和EF 所成角.在正三棱锥S ABC -中,G 是BC 中点,所以SG BC ⊥,AG BC ⊥, 又因为SG AG G ⋂=,SG ⊂平面SAG ,AG ⊂平面SAG , 所以BC ⊥平面SAG ,所以BC SA ⊥. 因为F 、D 分别是SB 、AB 的中点, 所以//DF SA . 所以DEDF ⊥.Rt DEF ∆中,122DF SA ==,11322DE BC AB ===, 所以227EF DE DF +.所以321cos 7DE DEF EF ∠===. 故异面直线l 和EF 2121 【点睛】本题考查异面直线所成角的求解,考查空间思维能力与运算能力,是中档题.20.【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径设内切球半径为r ﹐圆锥高为h 结合轴截面图形计算得最后计算体积即可【详解】解:设圆锥底面半径为R 则所以设内切球半径为r ﹐圆锥高为h 则如图是圆锥轴截面三 2π 【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径1R =,设内切球半径为r ﹐圆锥高为h ,结合轴截面图形计算得2r ,最后计算体积即可. 【详解】解:设圆锥底面半径为R ,则2233R ππ=⨯,所以1R =. 设内切球半径为r ﹐圆锥高为h ,则9122h =-=, 如图,是圆锥轴截面三角形图, 所以3r Rh r =-,解得:2r , 故3442223383r V πππ==⨯=. 故答案为:23π【点睛】本题考查圆锥的侧面展开图,圆锥的内切球的体积,考查空间想象能力,是中档题.三、解答题21.(1)主视图(正视图)见解析,334S =;(2)34V =. 【分析】(1)根据侧视图计算出PAC △的边AC 上的高,进而可作出几何体PMABC 的主视图,利用梯形的面积公式可求得几何体的主视图的面积;(2)分别取AC 、PC 的中点O 、N ,连接PO 、AN ,推导出AN ⊥平面BCPM ,计算出AN 和梯形BCPM 的面积,利用锥体的体积公式可求得多面体PMABC 的体积V . 【详解】(1)在几何体PMABC 中,平面PAC ⊥平面ABC ,设PAC △的边AC 上的高为h ,则该几何体的侧视图的面积为1324AC h ⋅=,得32h =, 又因为22BC PM ==,所以,该几何体的主视图(正视图)如下图所示:由图可知,该几何体的主视图为直角梯形,其面积为()1233322S +⨯==⨯;(2)分别取AC 、PC 的中点O 、N ,连接PO 、AN ,如下图所示:PA PC =,O 为AC 的中点,所以,PO AC ⊥,由(1)可知,3PO h ==,1122AO CO AC ===,由勾股定理可得221PC PA AO PO ==+=,所以,PAC △为等边三角形,N 为PC 的中点,AN PC ∴⊥,且3sin 60AN AC ==. 1AC =,2BC =,5AB =222AC BC AB ∴+=,BC AC ∴⊥,平面PAC ⊥平面ABC ,平面PAC平面ABC AC =,BC ⊂平面ABC ,BC ∴⊥平面PAC ,AN 、PC ⊂平面PAC ,BC AN ∴⊥,BC PC ⊥, PCBC C =,AN ∴⊥平面BCPM , //PM BC ,PM PC ∴⊥,所以,梯形BCPM 的面积为()322BCPM BC PM PC S +⋅==梯形,因此,1133333224BCPM V S AN =⋅=⨯⨯=梯形.【点睛】方法点睛:求空间几何体体积的方法如下:(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.22.(1)证明见解析;(2 【分析】(1)由PA ⊥底面ABCD ,得PA DE ⊥,由Rt ABH Rt DAE ≌△△,得DE AH ⊥,可得答案.(2)由可知DE ⊥平面PAH ,连接PG ,则DPG ∠即为直线PD 与平面PAH 所成线面角,在Rt PDG △中,由sin DPG ∠可得答案. 【详解】(1)因为PA ⊥底面ABCD ,DE ⊂底面ABCD ,所以PA DE ⊥,因为E ,H 分别为正方形ABCD 的边AB ,BC 的中点,,,AB DA BH AE HBAEAD ,所以Rt ABH Rt DAE ≌△△,所以BAH ADE ∠=∠,由90AED ADE ∠+∠= 所以90BAH AED ∠+∠=,所以DE AH ⊥,因为PA ⊂平面PAH ,AH ⊂平面PAH ,PA AH A ⋂=, 所以DE ⊥平面PAH .(2)由(1)可知DE ⊥平面PAH ,设AH DE G ⋂=,如图,连接PG ,则DPG ∠即为直线PD 与平面PAH 所成线面角,因为2PA AD ==,所以PD =DE 在Rt DAE 中,由于AG DE ⊥,所以2AD DG DE =⋅,所以4DG =DG =所以在Rt PDG △中,sin DG DPG PD ∠===PD 与平面PAH 所成线面角的正弦值为5.【点睛】本题主要考查线面垂直的证明、线面角的求法,对于线面角的求法的步骤,作:作(或找)出斜线在平面上的射影,证:证明某平面角就是斜线与平面所成的角;算:通常在垂线段、斜线段和射影所组成的直角三角形中计算. 23.(1)证明见解析;(2)证明见解析;(3)98. 【分析】(1)取PA 的中点G ,连接,BG EG ,证明四边形EFBG 为平行四边形,得出//EF BG ,再由线面平行的判定定理证明即可;(2)先证明PA ⊥平面ABCD ,从而得出PA CD ⊥,再由等腰三角形的性质得出AE PD ⊥,最后由面面垂直的判定定理证明即可;(3)以AFC △为底,12PA 为高,由棱锥的体积公式得出答案. 【详解】(1)如图,取PA 的中点G ,连接,BG EG .因为点,E G 分别为,PD PA 的中点,所以1//,2EG AD EG AD =又因为F 是BC 的中点,四边形ABCD 是正方形,所以//BF EG 且BF EG = 故四边形EFBG 为平行四边形,所以//EF BG 因为BG ⊂平面,ABP EF 不在平面ABP 内, 所以//EF 平面ABP .(2)由条件知32,3PB PD PA AD AB =====, 所以PAB △和PAD △都是等腰直角三角形,,PA AB PA AD ⊥⊥ 又因为,,ABAD A AB AD =⊂平面,ABCD 所以PA ⊥平面ABCD。
2 华东师范大学第二附属中学(创新班和理科班用)数学(高中上册)-4

幂函数、指数函数、对数函数4.1幂函数一般地,函数k y x =(k 为常数,k ∈Q )叫做幂函数.下面分别研究函数11332y x y x y x y x 2====,,,的定义域、值域、奇偶性、单调性并用描点法作出它们的图像.(1)因为1123332y x x y x x y x y x ======,,,,所以这四个函数的定义域分别是:[)0,x ∈+∞,x ∈R ,x ∈R ;x ∈R .(2)它们的值域分别是:[)0x ∈+∞,,x ∈R ,[)0x ∈+∞,,x ∈R ;(3)因为函数13y x =,的定义域关于原点不对称,所以它既不是奇函数,也不是偶函数; 对于函数13y x =,它是奇函数; 对于函数2y x =,它是偶函数; 对于函数3y x =,它是奇函数;(4)对于函数12y x x ==,在区间[)0+∞,上是增函数; 同理对于函数13y x =,在()-∞+∞,上是增函数.同理对于函数2y x =,在(]0-∞,上是减函数,在[)0+∞,上是增函数. 同理对于函数3y x =,在()-∞+∞,是增函数.(5)通过列表、描点、连线等过程可以画得它们的图像如图4—1所示:y =x 13y =x 12y =x 2y =x 311yOx图4-1根据几类幂函数的图像特点,可以得到幂函数的性质:性质l 对于幂函数()k y x k =∈Q当0k >时,函数()k y x k =∈Q 的图像都经过点()()0011,,,;在第一象限内单调递增. 当0k <时,函数()k y x k =∈Q 的图像都只经过点()11,;在第一象限内单调递减. 性质2 对于幂函数()k y x k =∈Q ,设()*qk q p p=∈N ,,且p q ,互质, (1)当p 为奇数,q 为偶数时,函数q py x =分布在第一、第二象限,图像关于y 轴对称,是偶函数; (2)当p 为奇数,q 为奇数时,函数q py x =分布在第一、第三象限,图像关于原点对称,是奇函数; (3)当p 为偶数,q 为奇数时,函数q py x =分布在第一象限,图像既不关于原点对称.又不关于y 轴对称,既不是奇函数,也不是偶函数. 例1.已知函数()223n n y x n --=∈Z 的图像与两坐标轴都无公共点,且其图像关于y 轴对称,求n 的值,并画出函数的图像.解:因为图像与y 轴无公共点,故2230n n --≤,又图像关于y 轴对称,则223n n --为偶数,由2230n n --≤,得13n -≤≤,又因为n ∈Z ,所以0123n =±,,,.当0n =时,2233n n --=-不是偶数; 当1n =时,2234n n --=-为偶数; 当3n =,2230n n --=为偶数; 所以n 为1-,1或3.此时,幂函数的解析为()00y x x =≠或4y x -=,其图像如图 4—2所示.y=x 0y=x -4y=x -4O xy图4-2例2.解不等式:()()2233213a a --+<-.解:()()()()2222331112132213a a a a a <⇒+>-≠-+-,且3a ≠.化简得231080a a +->,解得4a <-或3a 2>.综上得231080a a +->,解得4a <-或23a >. 综上得()()43a ∈-∞-+∞ ,,.例3.若()()11132m m --+<-,试求实数m 的取值范围. 解:(1)10320132m m m m +>⎧⎪->⎨⎪+>-⎩,,,解得2332m <<;(2)10320132m m m m +<⎧⎪-<⎨⎪+>-⎩,,,此时无解;(3)10320m m +<⎧⎨->⎩,,解得1m <-.综上可得()23132m ⎛⎫∈-∞- ⎪⎝⎭,,.例4.已知函数()2f x x =,设函数()()()()211g x qf f x q f x =-+-+⎡⎤⎣⎦,同是否存在实数()0q q <,使得()g x 在区间(]4-∞-,上是减函数,且在区间()40-,上是增函数?若存在,请求出来;若不存在,请说明理由.解:()2f x x = ,则()()42211g x qx q x =-+-+ 假设存在实数()0q q <,使得()g x 满足题设条件, 设12x x <,则()()()()42421211222121g x g x qx q x qx q x -=-+-+-- ()()()()2212211221x x x x q x x q ⎡⎤=+-+--⎣⎦. 若(]124x x ∈-∞-,,,易知122100x x x x +<->,,要使()g x 在(]4-∞-,上是减函数,则应有()()2212210q x x q +--<恒成立.1144x x <-- ,≤,221132x x ∴+>.而0q <,()221232q x x q ∴+<.从而要使()221221q x x q +<-恒成立,则有2132q q -≥,即130q -≤.若()1240x x ∈-,,,易知()()12210x x x x +-<,要使()f x 在()40-,上是增函数,则应有()()2212210q x x q +-->恒成立.140x -<< ,240x -<<,221232x x ∴+<,而0q <,()221232q x x q +<.要使()221221q x x q +>-恒成立,则必有2132q q -≤,即130q -≥. 综上可知,存在实数130q =-,使得()g x 在(]4-∞-,上是减函数,且在()40-,上是增函数. 基础练习1.研究下列函数的性质,并作出其图像 ①16y x -=; ②43y x -=.2.设11121123232α⎧⎫∈----⎨⎬⎩⎭,,,,,,,,已知幂函数2y x =为偶函数,且在()0+∞,上递减,试确定满足条件的幂函数,并作出它们的大致图像.3.已知()()()3234110m f x m m m x x =+--≠,是幂函数,其图像分布在第一、第三象限,求()f x 的解析式.4.已知函数()()223mm f x x m -++=∈Z 为偶函数,且()()35f f <,求m 的值,并确定()f x 的解析式.5.若()()33132m m +<-,试求实数m 的取值范围. 6.若()()1122132m m +<-,试求实数m 的取值范围. 7.若()()44132m m +<-,试求实数m 的取值范围. 8.讨论函数()2221k k y k k x --=+在0x >时随着x 的增大其函数值的变化情况.9.已知幂函数()()223mm f x x m --=∈Z 为偶函数,且在区间()0+∞,上是减函数,求()f x 的解析式,并讨论函数()()()bng x a f x xf fx =-的奇偶性. 10.已知函数()()22k k f x x k -++=∈Z ,且()()23f f <.(1)求k 的值;(2)试判断是否存在正数p ,使函数()()()121g x p f x p x =-⋅+-在区间[]12-,上的值域为1748⎡⎤-⎢⎥⎣⎦,;若存在,求出这个p 的值;若不存在,说明理由. 11.设函数()bf x a x x=+(a b ,为常数),且: (1)()20f -=;(2)()f x 有两个单调递增区间.写出一个同时满足上述两个条件的有序数对()a b ,. 12.已知函数ay x x=+有如下性质:如果常数0a >,那么该函数在区间(0a ⎤⎦,上是减函数,在区间)a ⎡+∞⎣,上是增函数.(1)如果函数()20by x x x =+>的值域为[)6+∞,,求实数b 的值;(2)研究函数22cy x x=+(常数0c >)在定义域内的单调性,并说明理由;(3)对函数a y x x=+和22ay x x =+(常数0a >)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性. 4.2指数函数 一般地,函数x y a =(0a >,且1a ≠)叫做指数函数,其中x 是自变量,函数的定义域是R . 指数从有理数推广到实数后,可以证明指数的运算法则仍然成立.即()0m n m n a a a a m n +⋅=>∈R ,、()()0nm mn a a a m n =>∈R ,、()()00nn n a b a b a b n ⋅=⋅>>∈R ,,指数函数的定义:x y a =(0a >且1a ≠),函数的定义域是实数集R . 运用计算器,通过列表、描点、连线等步骤,我们可以得到如下两个函数 2xy =和12xy ⎛⎫= ⎪⎝⎭的图像和性质.列表画图(见图4-3,图4-4). y =2x321123y O x8421图4-31248y =(12)xy O x123123图4-4x… 3-2- 1- 01 2 3 … 2x y = …18 12 12 1248…12xy ⎛⎫= ⎪⎝⎭ (8)4 21121418…观察两个函数图像,你发现它们的相同点和不同点了吗?有哪些相同点?哪些不同点? 1.两个函数图像的相同点:都位于x 轴的上方,都过()01,点.2.两个函数的不同点:函数2xy =的图像是上升的;函数12xy ⎛⎫= ⎪⎝⎭的图像是下降的.3.两个函数的性质:定义域为R ,函数值都大于010212⎛⎫== ⎪⎝⎭,,函数2x y =是R 上的增函数,函数12xy ⎛⎫= ⎪⎝⎭是R 上的减函数. 指数函数的图像和性质(见下表) 指数函数 ()1x y a a =>, ()01x y a a =<<,图象y Ox1y =1y O x1y =1性质(1)定义域:R ;(2)值域:()0+∞,,即图象都在x 轴上方; (3)恒过点()01,(4)在R 上是增函数 (4)在R 上是减函数函数值分布(5)当0x >时,1y >;当0x <时01y << (5)当0x >时01y <<;当0x <时1y >(6)x y a =与x y a -=关于y 轴对称;(7)x 轴是渐近线,即图象向左、右无限延伸. 例1.已知函数x y a =(0a >,且1a ≠)在区间[]12,上的最大值比最小值大2a,求实数a 的值. 解:当1a >时,函数x y a =,在区间[1,2]内单调递增,所以()()2max 2f x f a ==, ()()min 1f x f a ==,由题意得23a a a -=,可得到43a =; 当01a <<时,函数x y a =在[]12,内单调递减,所以()()2min 2f x f a ==,()()2min 13a f x f a a a ==-=,,可得到23a =. 综上可知:43a =或23. 例2.已知定义域为R 的函数()1222x x bf x +-+=+是奇函数.(1)求b 的值;(2)判断函数()f x 的单调性;(3)若对任意的t ∈R ,不等式()()22220f t t f t k -+-<恒成立,求k 的取值范围. 解:(1)因为()f x 是奇函数,所以()00f =,即10122b b -=⇒=+. ()11222xx f x +-∴=+ (2)由(1)知()1121122221x x xf x +-==-+++, 设12x x <则()()()()21121212112221212121x x x x x x f x f x --=-=++++, 因为函数2x y =在R 上是增函数且12x x < 21220x x ∴->又()()1221210x x ++>()()120f x f x ∴->,即()()12f x f x > ()f x ∴在()-∞+∞,上为减函数.(3)因为()f x 是奇函数,从而不等式:()()22220f t t f t k -+-< 等价于()()()222222f t t f t k f k t -<--=-,因()f x 为减函数,由上式推得:2222t t k t ->-.即对一切k ∈R 有:2320t t k -->,从而判别式141203k k ∆=+<⇒<-.例3.已知函数()()211x x f x a a x -=+>+, 求证:(1)函数()f x 在()1-+∞,上为增函数; (2)方程()0f x =没有负数根. 证明:(1)设121x x -<<, 则()()121212122211x x x x f x f x a a x x ---=+--++ 1212122211x x x x a a x x --=-+-++ ()()()121212311x x x x a a x x -=-+++.121x x -<< ,121210100x x x x ∴+>+>->,,,()()()12123011x x x x -∴<++;121x x -<< ,且1a >, 12x x a a ∴<, 120x x a a ∴-<,()()120f x f x ∴-<,即()()12f x f x <,∴函数()f x 在()1-+∞,上为增函数;(2)假设0x 是方程()0f x =的负数根,且01x ≠-,则000201x x a x -+=+, 即()00000031231111x x x a x x x -+-===-+++, 当010x -<<时,01011x +<+<, 0331x ∴>+, 03121x ∴->+, 而由1a >知01x a <, ∴ ①式不成立;当01x <-时,010x +<, 0301x ∴<+, 03111x ∴-<-+, 而00x a >,∴ ①式不成立.综上所述,方程()0f x =没有负数根. 基础练习1.利用指数函数的性质,比较下列各组中两个数的大小: (1)23和 1.4143; (2)230.7-和340.7-;(3)200720082121++和200820092121++.2.若函数()12x f x m --=-的图像与x 轴有交点,则实数m 的取值范围是__________.3.设()442xx f x =+,求出12310001001100110011001f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值. 4.某工厂今年1月、2月、3月生产某产品分别为1万件、1.2件、1.3万件,为了估测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量y 与月份数x 的关系,模拟函数可以选用二次函数或函数x y ab c =+(其中a 、b 、c 为常数),已知四月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好?请说明理由.5.比较a a m m -+与b b m m -+(a b c >>,0m >且1m ≠)的大小.6.设()10101010x xx xf x ---=+.(1)证明()f x 在()-∞+∞,上是增函数; (2)求()f x 值域.7.设函数()112x x f x +--=,求使()22f x x ≥的x 取值范围. 8.(1)求函数()()14102xxf x x -⎛⎫=++ ⎪⎝⎭≥的值域;(2)如果函数()1412xxf x a -⎛⎫=-+- ⎪⎝⎭有两个不同的零点,求实数a 的取值范围.(3)()()()()217211x a x a x f x a x -+-<⎧⎪=⎨⎪⎩≥在()-∞+∞,上单调递减,求实数a 的取值范围.9.已知函数()()219xx a f x aa a--=--(0a >且1a ≠)在()-∞+∞,上是增函灵敏,求实数a 的取值范围. 能力提高10.设()()22x x x xe e e ef xg x ---+==,; (1)求证:()()()22f x f x g x =⋅且()2x 是奇函数;(2)求证:()()()()()222222121g x g x f x f x g x =-=+=+且()2g x 是偶函数. 11.设02x ≤≤,求函数1224212x xa y a -=-⋅++的最大值和最小值.12.定义在R 上的增函数()y f x =对任意x y ∈R ,都有()()()f x y f x f y +=+. (1)求()0f ;(2)求证3()f x 为奇函数;(3)若()()33920x x x f k f ⋅++-<对任意x ∈R 恒成立,求实数k 的取值范围.13.已知集合M 是满足下列性质的函数()f x 的全体:存在非零常数T ,对任竟敢x ∈R ,有()()f x T Tf x +=成立.(1)函数()f x x =是否属于集合M ?说明理由;(2)设函数()x f x a =(0a >,且1a ≠)的图像与y x =的图像有公共点,证明:()x f x a M =∈; (3)若函数()sin f x kx M =∈,求实数k 的取值范围. 14.已知函数ay x x=+有如下性质:如果常数0a >,那么该函数在(0a ⎤⎦,上减函数,在)a ⎡+∞⎣,上是增函数.(1)如果函数()20by x x x=+>在(]04,上是减函数,在[)4+∞,上是增函数,求b 的值;(2)设常数[]14c ∈,,求函数()()12cf x x x x=+≤≤的最大值和最小值;(3)当n 是正整数时,研究函数()()0n n cg x x c x=+>的单调性,并说明理由. 15.若()()121212323x p x p f x f x x p p --==⋅∈R ,,,,为常数,且()()()()()()()112212f x f x f x f x f x f x f x ⎧⎪=⎨>⎪⎩,,≤ (1)求()()1f x f x =对所有实数x 成立的充要条件(用12p p ,表示);(2)设a b ,为两实数,a b <且()12p p a b ∈,,,若()()f x f b =.求证:()f x 在区间[],a b 上的单调增区间的长度和为2b a-(闭区间[]m n ,的长度定义为n m -). 4.3 对数概念及其运和算 一般的,如果a (01a a >≠,)的b 次幂等于N ,就是b a N =,那么b 叫做以a 为底N 的对数,记作log a N b =,其中a 叫做对数的底数,N 叫做真数.例如,由239=,得到以3为底9的对数为2,记作3log 92=,由定义可知负数和零没对对数,事实上,因为0a >,所以不论b 是什么实数,都用0b a >,这就是说,不论b 是什么数,N 永远是正数,故负数和零没有对数.根据对数定义,我们可以得到3log 10a =,log 1a a =(0a >,且1a ≠)通常我们把以10为底的对数叫做常用对数,并简记作lg ,即10log lg N N =;以无理数 2.71828e = 为底的对数叫做自然对数,并简记作ln ,即log ln e N N =. 例1.将下列指数写成对数式: (1)45625=;(2)61264-=; (3)327a=;(4)1 5.733m⎛⎫= ⎪⎝⎭.解:(1)5log 6254=; (2)21log 664=-; (3)3log 27a =;(4)13log 5.73m =.例2.将下列对数式写成指数式: (1)12log 164=-;(2)2log 1287=; (3)lg 0.012=-;(4)ln10 2.303=. 解:(1)41162-⎛⎫= ⎪⎝⎭;(2)72128=; (3)2100.01-=;(4) 2.30310e =.我们学过有理数指数幂的运算性质,如m n m a a a a +⋅=(01a a >≠,,且m n ∈Q ,)利用这个性质和对数的定义,我们可以推出对数的运算性质:令1log a M b =,2log a N b ==,则根据对数的定义得:1b a M =,2b a N = 又因为1222b b b b M N a a a +⋅=⋅=,所以,()12log a b b M N +=⋅,即 ()log log log a a a M N M N ⋅=+数似的,我们可以得到对数的其他几个运算性质:log log log aa a MM N N=-(01a a >≠,;M N ,为正数); log log n a a M n M =(0a >,1a ≠;n ∈R ,M N ,为正数); log log log c a c bb a=(换底公式)(01a a >≠,;010c c b >≠>,,); 证明:设log a N x =,则x a N =.两边取以m 为底的对数:log log log log x m m m m a N x a N =⇒= 从而得:log log m m N x a = l o g l o g l o g m a mN N a ∴= 1log log a b b a=(01a a >≠,;01b b >≠,); 1log log n a a M M n =(01a a >≠,;n ∈R ,0n ≠,0M >); log a N a N =(01a a >≠,;0N >).对于一个正数的常用对数值,可以写成一个整数与一个正的纯小数(或0)之和,如: 3lg2000lg2103lg230.3010=⨯=+=+; 5lg0.00003lg3105lg350.4771-=⨯=-+=-+; lg10000lg10404==+;即正数x 的常用对数lg x 可以写成:lg x M m =+(其中M 为整数,01m <≤);那么,M 称为对数lg x 的首数,m 称为对数lg x 的尾数;如果某正数x 的常用对数lg 2.1234x =-,则将lg x 写成:lg 30.8766 3.3866x =+=,则lg x 的首数是3-,尾数是0.8766. 例3.(1)9log 27; (2)43log 81; (3)()()23log 23+-;(4)34log 5625.解:(1)3329993log 27log 3log 92===; (2)()4416433log 81log 316==;(3)()()()()12323log 23log 231-++-=+=-;(4)()3333444log 5625log 553==.例4.设a 、b 、c 为正数,且满足222a b c +=.(1)求证:22log 1log 11b c a c a b +-⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭;(2)若()482log 11log 3b c a b c a +⎛⎫+=+-= ⎪⎝⎭,,求a 、b 、c 的值.证明:(1)左边222log log log a b c a b c a b c a b c a b a b +++-+++-⎛⎫=+=⋅ ⎪⎝⎭()22222222log log a b c a ab b c abab+-++-==22222log log 21ab c c ab+-===;解:(2)由4log 11b c a +⎛⎫+= ⎪⎝⎭得14b c a ++=, 30a b c ∴-++= ①由()82log 3a b c +-=得2384a b c +-== ②由①+②得2b a -= ③ 由①得3c a b =-,代入222a b c +=得()2430a a b -=, 0a > ,430a b ∴-= ④ 由③、④解得68a b ==,,从而10c =.例5.20世纪30年代,里克特(C .F .Richter )制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,铡震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级M ,其计算公式为0lg lg M A A =-,其中,A 是被测地震的最大振幅,0A 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是0.001,计算这次地震的震级(精确到0.1); (2)5级地震给人的震感已比较明显,计算7.6的最大振幅是5级地震的最大振幅的多少倍(精确到1).解:(1)420lg20lg0.001lglg20000lg2lg10 4.30.001M =-===+≈. 因此.这是一次约为里氏4.3级的地震.(2)由0lg lg M A A =-可得000lg 1010M M A A M A A A A =⇔=⇔=⋅. 当7.6M =,地震的最大振幅为7.61010A A =⋅; 当5M =时,地震的最大振幅为51010A A =⋅;所以,两次地震的最大振幅之比是7.67.65 2.60152010101039810A A A A -⋅===≈⋅. 答:7.6级地震的最大振幅大约是5级地震的最大振幅的398倍.可以看到,虽然7.6级地震和5级地震仅相差2.6级,但7.6级地震的最大振幅却是5级地震最大振幅的398倍.所以,7.6级地震的破坏性远远大于5级地震的破坏性.例6.已知20.301029lg 0.301030<<,30.477120lg 0.477121<<,求19792000的首位数字.解:()1979lg20001979lg200019793lg2==+19796532.736391lg20006532.73837∴<<.故19792000为6533位数,由 lg51lg 2=-,lg 6lg 2lg3=+,得0.698970lg50.698971lg50.7363910.73837lg60.778149lg60.778151<<⎫⇒<<<⎬<<⎭.说明19792000的首位数字是5. 基础练习I .把下列各题的指数式写成对数式: (1)2416=;(2)031=; (3)42x =; (4)20.5x =. 2.把下列各题的对数式写成指数式: (1)5log 27x =; (2)8log 7x =;(3)4log 3x =;(4)71log 3x =.3.计算下列各题:(1)222lg 2lg 2lg5lg 2lg21⋅+⋅+-+; (2)()()231lg5lg8lg1000lg2lg lg0.066++++;(3)2662log 18log 3log 6+; (4)log 0.7lg30173⎛⎫⋅ ⎪⎝⎭;(5)1log log mm baa b⋅;(6)lg 27lg83lg 10lg1.2+-4.(1)已知5log 3a =,5log 4b =,试用a 、b 表示25log 12; (2)已知12log 27a =,求6log 16. (3)已知18log 9a =,185b =,求36log 45. 5.设()0x y z ∈+∞,,,且346x y z == (1)求证:1112x y z+=; (2)比较346x y z ,,的大小.6.用log log log a a a x y z ,,表示下列各式: (1)log axy z ; (2)23log ax yz.7.求解下列各题:(1)已知lg 2a =,103b =,试用a b ,表示24log 15; (2)已知3log 5a =,5log 7b =,试用a b ,表示75log 63;(3)已知632236a b c ==,试建立a 、b 、c 间的关系式.8.我们都处于有声世界里,不同场合,人们对音量会有不同的要求,音量大小的单位是分贝(dB ),对于一个强度为I 的声波,分贝的定义是:010lg Iy I =.这里0I 是人耳能听到的声音的最低声波强度,122010w /m I =,当0I I =时,0y =,即dB 0=.(1)如果21w /m I =,求相应的分贝值;(2)70 dB 时声音强度I 是60dB 时声音强度I '的多少倍?9.科学研究表明,宇宙射线在大气中能够产生放射性碳14.碳14的衰变极有规律,其精确性可以称为自然界的“标准时钟”.动植物在生长过程中衰变的碳14,可以通过与大气的相互作用得到补充,所以活着的动植物每克组织中的碳14含量保持不变.死亡后的动植物,停止了与外界环境的相互作用,机体中原有的碳14按确定的规律衰减,我们已经知道其“半衰期”为5730年.湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7%,试推算马王堆古墓的年代.10.设1x >,1y >,且2log 2log 30x y y x -+=,求224T x y =-的最小值.11.(1)设a ,b ,c 都是正数,且346a b c ==,求22ab bc acabc-++的值;(2)已知a ,b ,c ,且a ,b ,1c ≠,求log log log log log log b c a a a b c a b c c a a b c a b c ++---的值; (3)设()200720092008f x a x b x =⋅+⋅+,若()20207log log 2092010f =,求()20209log log 207f 的值.12.解方程组:123x y x y x yy x++⎧=⎪⎨=⎪⎩(其中x y +∈R ,). 13.对于正整数a ,b ,c ()a b c ≤≤和实数x ,y ,z ,ω,若70x y z a b c ω===,且1111x y z ω++=,求证:a b c +=.4.4 反函数一般地,对于函数()y f x =,设它的定义域为D ,值域为A .如果对A 中的任意一个值y ,在D 中总有惟一确定的x 值与它对应,且满足()x y ϕ=,这样得到的x 关于y 的函数:()()x y x D y A ϕ=∈∈,做函数()y f x =的反函数,常常将()x y ϕ=记作()()1x f y x D y A -=∈∈,.在习惯上,自变量常用x 表示,而函数用y 表示,所以把它改写为:()()1y f x x A y D -=∈∈,. 例如函数3y x =的反函数是3x y =,函数21y x =-的反函数是12x y +=.从反函数的概念可知:如果函数()y f x =有反函数()1y f x -=,那么函数()1y f x -=的反函数就是()y f x =.这就是说,函数()y f x =gn ()1y f x -=互为反函数.结论1.函数()y f x =的定义域是它的反函数()1y f x -=的值域;函数()y f x =的值域是它的反函数()1y f x -=的定义域(见下表).函数()y f x =反函数()1y f x -=定义域DA 值域 AD反函数的定义域不能由其解析式来确定,而应是原函数的值域.结论2.函数()y f x =与反函数()1y f x -=的图像在同一坐标系关于直线y x =对称; 证明:设()M a b ,是()y f x =的图像上的任意一点, 则当x a =时,()f x 有唯一的值()f a b =. ()y f x = 有反函数()1y f x -=,∴当x b =时,()1f x -有唯一的值()1f b a -=,即点()M b a ',在反函数()1y f x -=的图像上(参见图4—5).图4-5y =f 1x ()P M'My =f x ()yO x若a b =,则M ,M '是直线y x =上的同一个点,它们关于直线y x =对称.若a b ≠,在直线y x =上任意取一点()P c c ,,联结PM ,PM ',MM '由两点间的距离公式得: ()()22PM a c b c =-+-,()()22PM b c a c '=-+-,PM PM ∴='∴ 直线y x =是线段MM '的垂直平分线, ∴点M ,M '关于直线y x =对称.点M 是()y f x =的图像上的任意一点,()y f x ∴=图像上任意一点关于直线y x =的对称点都在它的反函()1y f x -=的图像上,由()y f x =与()1y f x -=互为函数可知,函数()1y f x -=图像上任意一点关于直线y x =的对称点也都在它的反函数()y f x =的图像上,∴函数()y f x =与()1y f x -=的图像关于直线y x =对称.(反之,若两个函数的图像关于直线y x =对称,则两者互为反函数,特殊地,函数()f x 的反函数是它本身()f x ⇔的图像关于直线y x =对称). 例1.求函数()2110y x x =---≤≤的反函数. 解:由21y x =-- 知()22110y x y =--≤≤, 则221x y =-,由于10x -≤≤,所以()2110x y y =---≤≤, 所以反函数为()2110y x x =---≤≤.由反函数的定义,求反函数的定义,一般应分以下步骤: (1)由已知解析式()y f x =反求出()x y Φ=; (2)交换()x y Φ=中x 、y 的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域). 例2.求函数()()20102x x y x x ⎧<⎪=⎨-⎪⎩≥的反函数.解:由2y x =,得x y =- ,即()20y x x =<的反函数为()0y x x =->;由()102y x x =-≥的反函数为()20y x x =-≤.因此原函数的反函数为()()200x x y x x ⎧-⎪=⎨->⎪⎩,.≤ 例3.函数111ax y x x ax a -⎛⎫=≠-∈⎪+⎝⎭R ,的图象关于y x = 对称,求a 的值.解:由111ax y x x ax a -⎛⎫=≠-∈ ⎪+⎝⎭R ,得()()111y x y a y -=≠+, ()()()1111xf x x a x --∴=≠-+,由题知:()()()11111x axf x f x a x ax ---==++,,1a ∴=.例4.我们知道:函数()y f x =如果存在反函数()1y f x -=,则()y f x =的图像与()1y f x -=图像关于直线y x =对称.若()y f x =的图像与()1y f x -=的图像有公共点,其公共点却不一定都在直线y x =上;例如函数()1f x x=.若函数()y f x =在其定义域上是增函数,且()y f x =的图像与其反函数()1y f x -=的图像有公共点,证明这些公共点都在直线y x =上. 证明:设点()00M x y ,是函数()y f x =的图像与其反函数()1y f x -=的图像的公共点,则有:()00y f x =,()100y f x -=,据反函数的意义有:()00x f y =.所以:()00y f x =且同时有()00x f y =.若00x y <,因为函数()y f fx =在其定义域上地增函数,所以有:()()00f x f y <, 若00y x <,与00x y <矛盾,这说明00x y <是错误的.若00x y >,因为函数()y f x =在其定义域上是增函数,所以有:()()00f x f y >, 即00y x >与00x y >矛盾,这说明00x y > 也是错误的.所以00x y =,即函数()y f x =的图像与其反函数()1y f x -=的图像有公共点在直线y x =上. 基础练习1.求下列函数的反函数: (1)53y x =-; (2)()220y x x =-≤; (3)32y x =; (4)232x y x +=-(x ∈R 且2x ≠). 2.若函数()y f x =存在反函数,则下列命题中不正确的是( ) A .函数()y f x =与函数()x f x =的图像关于直线y x =对称 B .若()y f x = 是奇函数,则()1y f x -=也是奇函数C .若()y f x =在其定义域[]a b ,上是增函数,则()1y f c -=在[]a b ,上也是增函数D .函数()y f x =与()1x f y -=的图像重合.3.函数()223f x x ax =--在区间[]12,上存在反函数的充要条件是( ) A .(]1a ∈-∞, B .[)2a ∈+∞, C .[]12a ∈,D .(][)12a ∈-∞+∞ ,, 4.已知()231x f x x +=-,函数()y g x =的图像与()11y f x -=+的图像关于直线y x =对称,则()11g =__________.5.若点124⎛⎫ ⎪⎝⎭,即在2ax b y +=的图像上,又在它的反函数图像上,则a = __________;b =__________.6.若函数()2x f x x =+的反函数是()1f x -,则112f -⎛⎫= ⎪⎝⎭__________.7.若定义在R 上的函数()1y f x =+的反函数是()11y f x -=-,且()01f =,则()2008f =__________.8.已知函数()y f x =(定义域为D ,值域为A )有反函数()1y f x -=,则方程()0f x =有解x a =,且()().f x x x D ∈的充要条件是()1y f x -=满足:__________.9.设函数()121xf x x-=+,又函数()g x 与()11y f x -=+的图像关于y x =对称,求()2g 的值. 10.若点()21,即在函数()f x mx n =+的图像上,又在它的反函数的图像上,求实数m n ,的值. 11.(1)设函数()y f x =(定义域为D ,值域为A )的反函数是()1y f x -=,且函数()y f x =在D 上单调递增,证明函数()1y f x -=在A 上也是增函数.(2)设函()y f x =是D 上的奇函数,证明函数()1y f c -=也是A 3上的奇函数. 12.已知函数()()210x f x x x +⎛⎫=> ⎪⎝⎭(1)求函数()f x 的反函数()1f x -;(2)若2x ≥时,不等式()()()11x f x a a x --⋅>-恒成立,试求实数a 的取值范围. 能量提高13.()1122f x x x -=-.(1)证明函数()f x 的反函数,并求出反函数.(2)反函数的图像是否经过()01,点?反函数的图像与y x =有无交点? (3)设反函数为()1y f x -=,求不等式()10f x -≤的解集.14.已知函数()y f x =的反函数.定义:若对给定的实数()0a a ≠,函数()y f x a =+与()1y f x a -=+互为反函数,则称()y f x =满足“a 和性质”;若函数()y f ax =与()1y f ax -=互为反函数,则称()y f x =满足“a 积性质”.(1)判断函数()()210g x x x =+>是否满足“1和性质”,并说明理由; (2)求所有满足“2和性质”的一次函数;(3)设函数()y f x =()0x >对任何0a >,满足“a 积性质”.求()y f x =的表达式. 4.5 对数函数一般地,函数log a y x =(0a >,且1a ≠)就是指数函数、x y a =(0a >,且1a ≠)的反函数.因为x y a =的值域是()0+∞,,所以,函数log a y x =的定义域是()0+∞,.函数log a y x =(0a >,且1a ≠)叫做对数函数,其中x 是自变量,定义域是()0+∞,.下面研究对数函数log a y x =(0a >,且1a ≠)的图像和性质.因为对数函数log a y x =与指数函数x y a =互为反函数,所以log a y x =的图像与指数函数x y a =的图像关于直线y x =对称.因此只要作出指数函数x y a =关于直线y x =对称的图像,就可以得到log a y x =的图像和性质.对数函数的图像和性质(见下表):1a >0a <<1图象(1,0)yO x(1,0)yO x性质(1)定义域:()0+∞, (2)值域:R(3)恒过点()10,(4)在()0+∞,上是增函数(4)在()0+∞,上是减函数函数值分布(5)当1x >时0y >;当01x <<时0y <. (5)当1x >时0y <;当01x <<时0y >.(6)log a y x =与1log ay x =关于x 轴对称; (7)y 轴是渐近线,即图像向上、下无限延伸; (8)log a y x =与x y a =互为反函数. 例1.求下列函数的定义域: (1)()2log 2y x =+; (2)3log 2x y x =+;(3)()()221ln3234f x x x x x x =-++--+;(4)()221log 43y x x =-+-.解:(1)要使函数有意义,须使()2log 20x +≥,即()22log 2log 1x +≥,因为函数2log y x =为增函数,所以21x +≥,1x ∴-≥,所以函数的定义域为{}1x x -≥.(2)因为02xx >+,即2x x ≠⎧⎨>-⎩,所以函数2log 2x y x =+的定义域是()()200-+∞ ,,.(3)y 由222320340x x x x x ≠⎧⎪-+⎨⎪--+⎩≥≥得:40x -<≤或01x <≤.又因为1x ≠,故定义域是[)()4001- ,,. (4)因为()22log 430x x -+-≠,所以22430431x x x x ⎧-+->⎪⎨-+-≠⎪⎩,所以有()()()213020x x x -⋅-<⎧⎪⎨-≠⎪⎩ 从而有函数()221log π43y x x =-+-的定义域是()()1223 ,,.例2.(1)若21a b a >>>,则log log log b b a ba b a,,从小到大依次为__________;(2)若235x y z ==,且x ,y ,z 都是正数,则2x ,3y ,5z 从小到大依次为__________. 解:(1)由21a b a >>>得b a a<,故log log 1log b b a ba b a <<<.(2)令235x y z t ===,则1t >,lg lg 2t x =,lg lg 3t y =,lg lg 5tz =, ()lg lg9lg82lg 3lg 230lg 2lg3lg 2lg3x y t t t ⋅-∴-=-=>⋅,23x y ∴>;同理可得: 250x z -<,25x z ∴<,325y x z ∴<<. 例3.已知函数()()2lg10xf x f ax b ==+,,当0x >时,恒有()1lg f x f x x ⎛⎫-= ⎪⎝⎭. (1)求()f x 的表达式;(2)设不等式()lg f x t ≤的解集为A ,且(]04A ⊆,,求实数t 的取值范围. (3)若方程()()lg 8f x x m =+的解集为∅,求实数m 的取值. 解:(1) 当0x >时,()1lg f x f x x ⎛⎫-= ⎪⎝⎭恒成立.22lglg lg x x ax b bx a ∴-=++,即()()20a b x a b x ---=恒成立, a b ∴= 又()10f =,即2a b +=,从而1a b ==,()2lg1xf x x∴=+K (2)由不等式()lg f x t ≤,即 ()22lglg 011t x t x t x x --⇒++≤≤且201xx>+ ()()()()()022020022t t t t t t t ⎧⎛⎤-∞+∞> ⎪⎥-⎝⎦⎪⎪⇒+∞=⎨⎪⎛⎤⎪<< ⎥⎪-⎝⎦⎩,,,, 由于解集(]04A ⊆,,故02t <<,所以(]0042t A t ⎛⎤=⊆ ⎥-⎝⎦,, 即8425t t t ⇒-≤≤, 又因为02t <<,所以实数t 的取值范围是805⎛⎤ ⎥⎝⎦,.(3)解法一:由()2821lg lg 82101xx m x x x m x x x⎧=+⎪⎪+=+⇒⎨+⎪>⎪+⎩()286010x m x m x x ⎧+++=⎪⇒⎨<->⎪⎩或 方程的解集为∅,故有两种情况:①方程()2860x m x m +++=无解,即0∆<,得218m <<②方程()2860x m x m +++=有解,两根均在[]10-,内,()()286g x x m x m =+++ 则()()010*******g g m ∆⎧⎪-⎪⎪⎨⎪--⎪-⎪⎩≥≥≥≤≤218610m m m ⎧⇒⎨-⎩或≤≥≤≤02m ⇒≤≤ 综合①②得实数m 的取值范围是018m <≤. 解法二:若方程有解,则由()2821lg lg 82101xx m x x x m x x x ⎧=+⎪⎪+=+⇒⎨+⎪>⎪+⎩28110x m x xx x ⎧=-⎪⇒+⎨⎪<->⎩或 由()()228108111x g x x x x x ⎡⎤=-=-++⎢⎥++⎣⎦. 当1x <-,则()()210281181g x x x +⋅+=+≥ ,当且仅当32x =-时取到18 当0x >,则()g x 是减函数,所以()()00g x g <=.即()g x 在()()10-∞-+∞ ,,上的值域为()[)018-∞+∞ ,, 故当方程无解时,m 的取值范围是[)018,.例4.设()()1011x xa f x a a a +=>≠-,(1)求()f x 的反函数()1f x -;(2)讨论()1f x -在()1+∞,上的单调性,并加以证明: (3)令()1l o g a g x x =+,当[]()()1m n m n⊂+∞<,,时,()1f x -在[]m n ,上的值域是()()g n g m ⎡⎤⎣⎦,,求a 的取值范围. 解:(1)()11log 1a x f x x --=+,(1x >或1x <-) (2)设121x x <<,()()()1212121221101111x x x x x x x x ----=<++++, 01a ∴<<时,()()1112f x f x -->,()1f x -∴在()1+∞,上是减函数; 1a >时,()()1112f x f x --<,()1f x -∴在()1+∞,上是增函数.(3)当01a <<,()1f x - 在()1+∞,上是减函数()()()()11f m g m f n g n --⎧=⎪∴⎨=⎪⎩,由1log 1log 1a a x x x -=++得11x ax x -=+,即()2110ax a x +-+=.可知方程的两个根均大于1,即()010*******f a a a⎧⎪∆>⎪⎪>⇒<<-⎨⎪-⎪>⎪⎩当1a >时,()1f x - 在()1+∞,上是增函数()()()()11111f m g n m amn ana n amn am f n g m --⎧=-=+⎧⎪∴⇒⇒=-⎨⎨-=+=⎩⎪⎩(舍去). 综上,得0322a <<-. 基础练习1.求下列函数的定义域: (1)()22log 1y x =-;(2)()212log 1y x =-;(3)1log 1axy x-=+;(4)()213log 23y x x =--;(5)24lg 1x y x -=-;(6)()()22log log 162x x y x -=+-.2.求下列函数的值域: (1)()212log 617y x x =-+;(2)()213log 45y x x =-++.3.利用对数函数的性质,比较下列各题中两个值的大小: (1)0.1log 4和0.1log π; (2)2log 3m和3log 4m ,其中0m >,1m ≠; (3)log 3a 和log 3b ,其中01a b <<<.4.函数()2log 2a y x ax =-+在[)2+∞,恒为正,求实数a 的范围.5.设()()222log 1f x x x x =+++,则对任意实数a ,b ,0a b +≥是()()0f a f b +≥的什么条件? 6.已知函数()x x x xe ef x e e ---=+的反函数是()1f x -,且()()110.80.6f k f ---=,求k 的范围.7.已知函数()11lg11xf x x x+=+-- (1)求函数()f x 的定义域,并判断它的单调性(不用证明)‘(2)若()f x 的反函数为()1f x -,证明方程()10f x -=有解,且有唯一解; (3)解关于x 的不等式()11f x x +>⎡⎤⎣⎦.8.(1)已知()log 4a y ax =-在区间[)02,上是x 的减函数,求实数a 的取值范围;(2)函数()2log a f x ax x =-,()01a a >≠,区间[]34,上是增函数,求实数a 的取值范围; (3)如果不等式2log 0a x x -<在区间102⎛⎤ ⎥⎝⎦,上恒成立,求实数a 的取值范围.9.若函数()2log 3a y x ax a =-+的值域为R ,求实数a 的取值范围. 10.已知函数()1log 1a mxf x x -=-是奇函数()01a a >≠,. (1)求出实数m 的值;(2)根据(1)的结果,判断()f x 在()1+∞,上的单调性(不必证明); (3)如果当()2x r a ∈-,时,()f x 的值域恰为()1+∞,,求a 和r 的值. 能力提高11.设函数()()()2221log log 1log 1x f x x p x x +=+-+--, (1)求函数的定义域; (2)问()f x 是否存在最大值与最小值?如果存在,请把它写出来;如果不存在,请说明理由. 12.已知()()()4log 41f x x kx k =++∈R 是偶函数. (1)求k 的值;(2)证明:对任意实数b ,函数()y f x =的图像与直线12y x b =+最多只有一个交点; (3)设()44log 23x g x a a ⎛⎫=⋅- ⎪⎝⎭,若函数()f x 与()g x 的图像有且只有一个公共点,求实数()n y g x =的取值范围.13.已知()2log f x x =,当点()M x y ,在()y f x =的图像上运动时,点()2N x ny -,在函数()n y g x =的图像上运动()n ∈N . (1)求()n y g x =的表达式.(2)求集合{A a x =于关的方程()()122g x g x a =-+有实根,}a ∈R .(3)设()()12n g x n H x ⎛⎫= ⎪⎝⎭,函数()()()11F x H x g x =-()0a x b <≤≤的值域为542222log log 22b a ⎡⎤⎢⎥++⎣⎦,,求实数a 、b 的值. 14.设()()121lgxx xn a n f x n+++-+⋅= ,,a n ∈∈R N 且2n ≥.若()f x 当()1x ∈-∞,有意义,求a 的值范围.15.已知()()2121x x a f x a -=∈+R ,是R 上的奇函数.(1)求a 的值;(2)求()f x 的反函数;(3)对任意()0k ∈+∞,解不等式()121log xf x k-+>. 16.已知()()2log 1a f x x x =++,其中1a >.(1)试求()f x 的定义域和值域;求出()f x 的反函数()1f x -; (2)求出()f x 的反函数()1f x -; (3)判断函数()1f x -;(4)若实数m 满足()()112110f m f m ---+-<,求m 的取值范围. 17.已知函数()()()2log 201a f x x x a a =+->≠, (1)求反函数()1f x -,并求出其定义域;(2)设()()12log 22a P m f n -=+,如果()()332n nP n n -+<∈N ,求a 的取值范围. 4.6指数方程和指数不等式一般的,我们把指数里含有未知数的方程叫做指数方程,求未知数x 值的过程叫做解指数方程.一般的,我们把指数里含有未知数的不等式叫做指数不等式,求未知数x 值的过程叫做解指数不等式. 例1.解下列方程: (1)943450x x -⋅-=;(2)59462x x x +=⋅(3)()993350x x x x --+-++=.解:(1)原方程可化为()2343450x x -⋅-=设()30x t t =>,得24450t t --=解得1295t t ==-,(舍去),所以有39x =,得2x =. 所以,原方程的解是2x =.(2)原方程可化为2223532220x x x x ⋅-⋅⋅+⋅= 两边各项同除以22x得233252022x⎛⎫⎛⎫⋅-+= ⎪ ⎪⎝⎭⎝⎭,令()302xt t ⎛⎫=> ⎪⎝⎭, 则方程可化为22520t t -+=,解得12122t t ==,. 所以原方程的解是132log 2x =,232log 2x =-.(3)设()332x x t t -+=≥,则2992x x t -+=-,于是,原方程可化为2430t t -+=, 解得11t =(舍去),23t =,所以有333x x -+=,化简为()233310x x -⋅+=,解方程得3532x ±=. 所以,原方程的解是1335log 2x -=,2335log 2x +=.例2.已知关于x 的方程122x a a+=-,在下列情况中分别求实数a 的取值范围: (1)方程没有实数解;(2)方程只有正实数解; (3)方程有负数解.解:(1)因为对一切x ∈R 有20x >,所以102a a+-≤,可以解得1a -≤或2a >; (2)根据指数函数的性质,当0x >时,21x >,所以112a a +>-,可以解得122a <<; (3)因为函数2x y =在()-∞+∞,上单调递增,所以,函数2x y =的图像与常数函数12a y a+=-的图像最多只有一个交点,因此,方程122x a a+=-的负数解便是唯一解, 当0x <时,021x <<,所以1012a a +<<-,即102a a +>-且112a a +<-,可以解得112a -<<.例3.解方程:3456x x x x ++=. 解:方程可化为1251236xxx⎛⎫⎛⎫⎛⎫++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.设()125236xxxf x ⎛⎫⎛⎫⎛⎫=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则()f x 在()-∞+∞,上是减函数. 因为()31f =,所以方程只有一个解3x =.例4.关于x 的不等式2223330x x a a ⋅-+-->,当01x ≤≤时恒成立,求实数a 的取值范围. 解:设解:设3x t =,则[]13t ∈,,原不等式可化为[]223213a a t t t -->-+∈,,. 等价于23a a --大于()22f t t t =-+在[]13,上的最大值.a ∴的取值范围是()()12-∞-+∞ ,,例5.设函数()112x x f x +--=,求使()22f x ≥的取值范围.解:由于2x y =是增函数,()22f x ≥等价于3112x x +--≥(1)当1x ≥时,112x x +--=,∴①式恒成立.(2)当11x -<<时,112x x x +--=,①式化为322x ≥,即314x <≤(3)当1x -≤时,112x x +--=-,①式无解 综上x 的取值范围是34⎡⎫+∞⎪⎢⎣⎭,1.解下列方程:(1)131119133x x xx -+==--,; (2)31636281x x x ⋅+=⋅;(3)()()52652610xx++-=(4)964x x x -=; (5)222114526x x x x +--+--⋅=; (6)()()222121x x x x --=-.2.解下列不等式: (1)282133x x --⎛⎫> ⎪⎝⎭;(2)114123xx>--; (3)22222233x x x x ---->-.3.已知关于x 的方程2212940x x a a ---+=有一根是2. (1)求实数a 的值;(2)若01a <<, 求不等式2212940x x a a ---+<的解集.4.设01a a >≠,,求证:关于x 的方程2x x a a a -+=的根不在区间[]01,内. 5.若(]1x ∈-∞,, 不等式()24210x x m m -++>恒成立,则实数m 的取值范围是__________.。
2 华东师范大学第二附属中学(创新班和理科班用)数学(高中上册)-7

第七章 平面向量7.1 向量的基本概念及表示现实生活中,有些量在有了测定单位之后只需用一个实数就可以表示,例如温度,时间,面积,这些只需用一个实数就可以表示的量叫作标量.还有些量不能只用一个实数表示,例如位移,力,速度等既有大小又有方向的量,这些既有大小又有方向的量叫作向量.向量既有大小又有方向,因此向量不能比较大小.数学中常用平面内带有箭头的线段来表示平面向量.以线段的长来表示向量的大小:以箭头所指的方向(即从始点到终点的方向)来表示向量的方向.一般地,以点P 为始点,点Q 为终点的向量记作PQ.为书写简便,在不强调向量的起点与终点时,向量也可以用一个小写的字母并在上面画一个小箭头来表示,如a .PQ 的大小叫作PQ 的模,记作PQ,类似地,a 的模记作a . 1.零向量:长度为0的向量叫做零向量,记作0 ;0的方向是任意的.2.单位向量:长度为1的向量叫做单位向量.3.平行向量:方向相同或相反的向量叫做平行向量(也叫共线向量). 4.相等向量:长度相等且方向相同的向量叫做相等向量.5.负向量:与a 的模相等,方向相反的向量叫作a 的负向量,记作a - .我们规定:0的相反向量仍是零向量.易知对任意向量a 有()a a --=.向量共线与表示它们的有向线段共线不同:向量共线时表示向量的有向线段可以是平行的,不一定在一条直线上;而有向线段共线则线段必须在同一条直线上.规定。
与任一向量平行.图7-1图7-1三个向量a 、b 、c 所在的直线平行,易知这三个向量平行,记作a b c∥∥,我们也可以称这三个向量共线.例l .如图7-2所示,128A A A 、是O 上的八个等分点,则在以128A A A 、及圆O 九个点中任意两点为起点与终点的向量中,模等于半径的向量有多少??A 8A 7A 6A 5A 4A 3A 2A 1图7-2解:(1)模等于半径的向量只有两类,一类是()128i OA i = 、共8个;另一类是()128iAO i =、也有8个.两类合计16个.(2)以128A A A 、为顶点的O 的内接正方形有两个,一个是正方形1257A A A A ;另一个是正方形2468A A A A .在题中所述的向量中,只有这两个正方形的边(看成有向线段,每一边对应两个向量)的√2倍的向量共有42216⨯⨯=个.注意:(1)在模等于半径的向量个数的计算中,要计算i OA 与()128iAO i = 、两类.一般地我们易想到()128i OA i = 、这8个,而易遗漏()128iAO i = 、这8个. (213A A 对应向量13A A 与31A A,因此与(1)一样,在解题过程中主要要防止漏算.认为满足条件的向量个数为8是错误的. 例2.在平面中下列各种情形中,将各向量的终点的集会分别构成什么图形? (1)把所有单位向量的起点平移到同一点O .(2)把平行于直线l 的所有单位向量的起点平移到直线l 上的p 点. (3)把平行于直线l 的所有向量的起点平移到直线l 的点p . 解:(1)以点O 为圆心,l 为半径的圆.(2)直线l 上与点p 的距离为1个长度单位的两个点.(3)直线l .例3.判断下列命题的真假:①直角坐标系中坐标轴的非负轴都是向量; ②两个向量平行是两个向量相等的必要条件;③向量AP 与CD是共线向量,则A 、B 、C 、D 必在同一直线上; ④向量a 与向量b 平行,则a 与b的方向相同或相反; ⑤四边形ABCD 是平行四边形的宽要条件是AB DC =. 解:①直角坐标系中坐标轴的非负半轴,虽有方向之别,但无大小之分,故命题是错误的.②由于两个向量相等,必知这两个向量的方向与长度均一致,故这两个向量一定平行,所以,此命题正确;③不正确.AB 与CD共线,可以有AB 与CD 平行;④不正确.如果其中有一个是零向量,则其方向就不确定;⑤正确.此命题相当于平面几何中的命题:四边形ABCD 是平行四边形的充要条件是有一组对边平行且相等.1.下列各量中是向量的有__________. (A )动能 (B )重量 (C )质量 (D )长度 (F )作用力与反作用力 (F )温度2.判断下列命题是否正确,若不正确,请简述理由.①向量AB 与CD是共线向量,则A 、B 、C 、D 四点必在一直线上; ②单位向量都相等;③任一向量与它的相反向量不相等;④共线的向量,若起点不同,则终点一定不同. 3.回答下列问题,并说明理由. (1)平行向量的方向一定相同吗? (2)共线向量一定相等吗?(3)相等向量一定共线吗?不相等的向量一定不共线吗?4.命题“a b ∥,b c ∥,则a b∥( ) A .总成立B .当0a ≠时成立 C .当0b ≠时成立D .当0c ≠时成立5.已知正六边形ABCDEF (见图7-3),在下列表达式中:①BC CD EC ++ ;②2BC DC +;③FE ED + ;④2ED FA - ;与AC相等的有__________.FC图737.2向量的加减法两个向量可以求和.一般地,对于两个互不平行的向量a 、b ,以A 为共同起点平移向量,有AB a =,AD b = ,则以AB 、AD 为邻边的平行四边形ABCD 的对角线AC c = 叫作a 和b这两个向量的和,即a b c +=.求两个向量和的运算叫做向量的加法.上述求两个向量的和的方法称为向量加法的平行四边形法则,见图7-4.平行四边形法则B图74又AD BC = A B B C A C∴+= 由此发现,当第二个向量的始点与第一个向量的终点重合时.这两个向量的和向量即为第一个向量的始点指向第二个向量终点的向量.此法则称为向量加法的三角形法则,地图7-5.三角形法则图75特殊地.求两个平行向量的和,也可以用三角形法则进行(如图7-6):(b )(a )a BA图76显然,对于任何a ,有0a a += ;()0a a +-= .对于零向量与任一向量a ,有00a a a +=+=.向量的加法具有与实数加法类似的运算性质,向量加法满足交换律与结合律:交换律:a b b a +=+结合律:()()a b c a b c ++=++与实数的减法相类似,我们把向量的减法定义为向量加法的逆运算.若向量a 与b 的和为向量c ,则向量b 叫做向量c 与a 的差,记作b c a =-.求向量差的运算叫做向量的减法.由向量加法的三角形法则以及向量减法的定义.我们可得向量减法的三角形法则,其作法:在平面内取一点O ,作OA a = ,OB b = ,则BA a b =- ,即a b - 声可以表示为从向量b的终点指向向量a的终点的向量.注意差向量的“箭头”指向被减向量,见图7-7.CB 图77此外,我们可以先做向量b 的负向量OB b =- ′,可根据向量加法的平行四边形法则得()OC a b =+-.易知向量OC BA = ,因此,()a b a b +-=-.例1.如图7-8所示,已知向量a ,b ,c ,试求作和向量a b c ++.图78分析:求作三个向量的和的问题,首先求作其中任意两个向量的和,因为这两个向量的和仍为一个向量,然后再求这个新向量与另一个向量的和.即可先作a b + ,再作()a b c ++.解:如图7-9所示,首先在平面内任取一点O ,作向量OA a = ,再作向量AB b = ,则得向量OB a b =+,然后作向量BC c = ,则向量OC a b c =++即为所求.O图79例2.化简下列各式(1)AB CA BC ++ ; (2)OE OF OD DO -+-- .解:(1)原式()0AB BC CA AB BC CA AC CA AC AC =++=++=+=-=(2)原式()()0OE OF OD DO EO OF EF =+-+=+-=例3.用向量方法证明:对角线互相平分的四边形是平行四边形.分析:要证明四边形是平行四边形只要证明某一组对边平行且相等.由相等向量的意义可知,只需证明其一组对边对应的向量是相等向量.已知:如图7-10,ABCD 是四边形,对角线AC 与BD 交于0,且AO OC =,DO OB =.ODCBA图710求证:四边形ABCD 足平行四边形.证明:由已知得AO OC = ,BO OD =,AD AO OD OC BO BO OC BC =+=+=+=,且A D B C ,,,不在同一直线上,故四边形ABCD 是平行四边形.例4.已知平面上有不共线的四点O A B C ,,,.若320OA OB OC -+=,试求AB BC 的值.解:因为23OA OC OB += ,所以()2OB OA OC OB -=-.于是有2AB BC =-.因此2AB BC= .基础练习1.若对n 个向量12n a a a,,,存在n 个不全为零的实数12n k k k ,,,,使得11220n n k a k a k a +++= 成立,则称向量12n a a a ,,,为“线性相关”,依此规定,能说明()110a =,,()211a =- ,,()322a =,“线性相关”的实数123k k k ,,依次可以取____________________(写出一组数值即可,不必考虑所有情况).2.已知矩形ABCD 中,宽为2,长为,AB a = ,BC b = ,AC c = ,试作出向量a b c ++,并求出其模的大小.3.设a ,b 为两个相互垂直的单位向量.已知OP a = ,OR ra kb =+.若PQR △为等边三角形,则k ,r 的取值为( )A.k r == B.k r == C.k r ==D.k r ==4.若A B C D 、、、是平面内任意四点,则下列四式中正确的是( )①AC BD BC AD +=+ ②AC BD DC AB -=+ ③AB AC DB DC --=④AB BC AD DC +-=A .1B .2C .3D .45.设a 表示“向东走10km ”,b 表示“5km ”,c 表示“向北走10km ”,d 表示“向南走5km ”.说明下列向量的意义.(1)a b + ;(2)b d + ;(3)d a d ++ . 6.在图7-11的正六边形ABCDEF 中,AB a = ,AF b = ,求AC ,AD ,AE .FC图7117.3 实数与向量的乘法如图7-12,已知非零向量a ,可以作出a a a ++ 和()()()a a a -+-+-.PQ MNaa a图712aOC OA AB BC a a a =++=++ ,简记3OC a = ;同理有()()()3PN PQ QM MN a a a a =++=-+-+-=- .观察得:3a 与a 方向相反相反且33a a -= .一般地,实数λ与向量a 的积是一个向量,记作:a λ.a λ的模与方向规定如下: (1)a a λλ=;(2)a λ 的方向定义为:0λ>时a λ 与a i 方向相同;0λ<时a λ 与ai 方向相反; 0λ=或0a = 时规定:0a λ=.以上规定的实数与向量求积的运算叫作实数与向量的乘法(简称向量的数乘).向量数乘的几何意义就是:把向量a 沿向量a 的方向或反方向放大或缩小,a λ 与a 是互相平行的向量.对于任意的非零向量a,与它同方向的单位向量叫做向量a 的单位向量,记作0a .易知01a a a=.向量共线定理:如果有一个实数λ,使()0b a a λ=≠ ,那么b 与a 是共线向量;反之,如果b 与()a b ≠是共线向量,那么有且只有一个实数λ,使得b a λ=.通过作图,可以验证向量数乘满足以下运算定律:当m 、n ∈R 时,有1.第一分配律()m n a ma na +=+.2.第二分配律()m a b ma mb +=+.3.结合律()()m na mn a =.例1.计算:(1)()()63292a b a b -+-+;(2)原式12711332236227a a b b a a b ⎛⎫⎛⎫=-+--++ ⎪ ⎪⎝⎭⎝⎭;(3)()()()64222a b c a b c a c -+--+--+.解:(1)原式18121893a b a b b =---+=-. (2)原式12711332236227a a b b a a b ⎛⎫⎛⎫=-+--++ ⎪ ⎪⎝⎭⎝⎭17732367a b a b ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭ 77106262b a a b =+--=. (3)原式66648442a b c a b c a c =-+-+-+-()()()64468642a a a b b c c c =-++-++--62a b =+ .例2.已知O 为原点,A ,B ,C 为平面内三点,求证A ,B ,C 三点在一条直线上的充要条件是OC OA OB αβ=+,且αβ∈R ,,1αβ+=.分析:证明三点共线可从三点构成的其中两个向量存在数乘关系.证明必要条件也是从向量共线时向量的数乘关系入手.证明:必要性.设A B C ,,三点共线,则AC 与AB 共线.于是存在实数λ,使AC AB λ=.而AC OC OA =- ,AB OB OA =- ,()OC OA OB OA λ∴-=-.()1OC OB OA λλ∴=+- .令λβ=,1λα-=,有()11αβλλ+=-+=,OC OA OB αβ∴=+,且1αβ+=. 充分性. 若OC OA OB αβ=+,且1αβ+=,则()1OC OA OB ββ=-+ ,()OC OA OB OA β=+- ,()OC OA OB OC β-=-,AC AB β∴= ,β∈R .AC ∴ 与AB 共线,而A 为AC 与AB的公共端点, A B C ∴,,三点在一条直线上.在证明必要性时,A B C ,,三点共线还可用AB kBC = ,AC kBC =表示.本题的结论还可有更一般的形式:A B C 、、三点在一条直线上的充要条件是存在实数h ,k ,l ,使0hOA kOB lOC ++=,且1h k l ++=,l k h ,,中至少有一个不为0.例3.如图7-13,设O 为ABC △内一点,PQ BC ∥,且PQt BC=,,OB b = ,OC c = ,试求OP ,OQ . 解:由平面几何知,APQ ABC ⨯△∽△,且对应边之比为t ,图713故AP AQ PQt AB AC BC===, 又A P B 、、与A Q C 、、分别共线,即知 AP t AB = ,AQ t AC = . ()()OP OA AP OA t AB OA t OB OA a t b a ∴=+=+=+-=+-,即()1OP t a tb =-+ ,()()OQ OA AQ OA t AC OA t OC OA a t c a =+=+=+-=+- ,即()1OQ t a c =-+ .例4.设两非零向量1e 和2e不共线,(1)如果12AB e e =+ ,1228BC e e =+ ,()123CD e e =-,求证A B D ,,三点共线.(2)试确定实数k ,使12ke ke +共线.(1)证明12AB e e =+ ,()121212283355BD BC CD e e e e e e AB =+=++-=+=,AB BD ∴,共线,又有公共点B A B D∴,,三点共线. (2)解12ke e + 与12e ke + 共线,∴存在λ使()1212ke e e ke λ+=+,则()()121k e k e λλ-=-,由于1e 与2e 不共线, 只能有010k k λλ-=⎧⎨-=⎩则1k =±.例5.在ABC △中,F 是BC 中点,直线l 分别交AB AF AC ,,于点D ,G ,E (见图7-14).如果AD AB λ= ,AE AC μ= ,λ,μ∈R .证明:G 为ABC △重心的充分必要条件是113λμ+=.l GF E DCB A图714解:若G 为ABC △重心,则()221332AG AF AB AC ==⋅+= 13AD AE λμ⎛⎫+ ⎪ ⎪⎝⎭. 又因点D G E ,,共线,所以,()113AD AE AG t AD t AE λμ⎛⎫=+-=+ ⎪ ⎪⎝⎭, 因AD ,AE 不共线,所以,13t λ=且113t μ=-,两式相加即得113λμ+=. 反之,若113λμ+=,则()2xAG xAF AB AC ==+ ()12x AD AE t AD t AE λμ⎛⎫=+=+- ⎪ ⎪⎝⎭, 所以,2x t λ=且12x t μ=-,相加即得23x =,即G 为ABC △重心. 基础练习1.已知向量a 、b 是两非零向量,在下列四个条件中,能使a 、b共线的条件是( ) ①234a b e -= 且23a b e +=- ;②存在相异实数λ、u ,使0a ub λ+=;③0xa yb +=(其中实数x y 、满足0x y +=); ④已知梯形ABCD 中,其中AB a = 、CD b = .A .①②B .①③C .②④D .③④2.判断下列命题的真假:(1)若AB 与CD是共线向量,则A B C D ,,,四点共线. (2)若AB BC CA ++=0,则A B C ,,三点共线.(3)λ∈R ,则a a λ>.(4)平面内任意三个向量中的每一个向量都可以用另外两个向量的线性组合表示.3.已知在ABC △中,D 是BC 上的一点,且BDDCλ=,试求证:1AB AC AD λλ+=+ . 4.已知3AD AB = ,3DE BC = .试判断AC 与AE是否共线.5.已知在四边形ABCD 中,2AB a b =+ ,4BC a b =-- ,53CD a b =--,求证:四边形ABCD 是梯形.6.已知()2cos A αα,()2cos B ββ,()10C -,是平面上三个不同的点,且满足关系式CA BC λ=,求实数λ的取值范围.7.已知梯形ABCD 中,2AB DC =,M N ,分别是DC AB 、的中点,若1AB e = ,2AD e = ,用1e ,2e表示DC BC MN 、、.8.四边形ABCD 是一个梯形,AB CD ∥且2AB CD =,M N 、分别是DC 和AB 的中点,已知AB a =,AD b = ,试用a ,b 表示BC 和MN .9.已知a b 、是不共线的非零向量,11c a b λμ=+ ,22d a b λμ=+,其中1122λμλμ、、、为常数,若c d ma nb +=+,求m n 、的值.10.设a 、b 是不共线的两个非零向量,OM ma = ,ON nb = ,OP a b αβ=+,其中m n αβ、、、均为实数,0m ≠,0n ≠,若M P N 、、三点共线,求证:1mnαβ+=.11.在ABC △中,BE 是CD 交点为P .设AB a = ,AC b = ,AP c = ,AD a λ=,(01λ<<),()01AE b μμ=<<,试用向量a ,b 表示c . 12.在平面直角坐标系中,O 为坐标原点,设向量()12OA = ,,()21OB =-,若OP xOA yOB =+ 且12x y ≤≤≤,则求出点P 所有可能的位置所构成的区域面积.7.4 向量的数量积数量积定义:一般地.如果两个非零向量a 与b 的夹角为α.我们把数量cos a b α⋅叫做a 与b 的数量积(或内积),记作:a b ⋅ ,即:cos a b a b α⋅=⋅,其中记法“a b ⋅ ”中间的“⋅”不可以省略,也不可以用“×”代替.特别地,a b ⋅ 可记作2a .规定:0与任何向量的数量积为0.非零向量夹角的范围:0≤口≤Ⅱ.投影的定义:如果两个非零向量a 与b 的夹角为α,则数量cos b θ称为向量b 在a 方向上的投影.注意:投影是一个数量.数量积的几何意义:如图7-15,我们把cos b α<叫做向量b 在a 方向上的投影,即有向线段1OB 的数量.图715当π02α<≤时,1OB 的数量等于向量1OB 的模1OB ; 当ππ2α<≤时,1OB 的数量等于向量1OB 的模-1OB ; 当π2α=时,1OB 的数量等于零. 当然,cos a α即为a 在b 方向上的投影. 综上,数量积的几何意义:a b ⋅ 等于其中一个向量a 的模a 与另一个向量b 在a 的方向上的投影cos b α的乘积.向量的数量积的运算律: ①a b b a ⋅=⋅②()()()a b b a b λλλ⋅⋅=⋅(λ为实数)③()a b c a c b c +⋅=⋅+⋅鉴于篇幅这里仅证明性质②:证明:(1)若0λ>,()cos a b a b λλθ⋅= ,()cos a b a b λλθ⋅= ,()cos a b a b λλθ⋅=,(2)若0λ<,()()()cos πcos cos a b a b a b a b λλθλθλθ⋅=-=--= ,()cos a b a b a b λλλθ⋅=⋅= ,()()()cos πcos a b a b a b λλθλθ⋅=-=--= cos a b λθ.(3)若0λ=,则()()()0a b a b a b λλλ⋅=⋅=⋅=.综合(1)、(2)、(3),即有()()()a b a b a b λλλ⋅=⋅=⋅.例1.已知4a = ,5b =,当(1)a b ∥,(2)a b ⊥ ,(3)a 与b 的夹角为30︒时,分别求a 与b 的数量积.解:(1)a b ∥,若a 与b 同向,则0θ=︒,cos04520a b a b ∴⋅=⋅︒=⨯=; 若a 与b 反向,则180θ=︒,()cos18045120a b a b ∴⋅=⋅︒⨯⨯⨯-=-. (2)当a b ⊥ 时,90θ=︒,cos900a b a b ∴⋅=⋅︒=.(3)当a 与b 的夹角为30︒时,cos3045a b a b ⋅=⋅︒=⨯= 例2.空间四点A B C D 、、、满足3AB = ,7BC = ,11CD = ,9DA =,则AC BD ⋅ 的取值有多少个?解:注意到2222311113079+==+,由于0AB BC CD DA +++=,则()()2222222DA DA AB BC CDAB BC CD AB BC BC CD CD AB ==++=+++⋅+⋅+⋅()()2222AB BC CD AB BC BC CD =-+++⋅+,即222220AC BD AD BC AB CD ⋅=+--= ,AC BD ∴⋅只有一个值0.例3.已知a b 、都是非零向量,且3a b + 与75a b - 垂直,4a b - 与72a b - 垂直,求a b、的夹角. 解:由()()223750716150a b a b a a b b +⋅-=⇒+⋅-= ①()()22472073080a b a b a a b b -⋅-=⇒-⋅+=②两式相减:22a b b ⋅= 代入①或②得:22a b = . 不妨设a b 、的夹角为θ,则221cos 22a b b a b bθ⋅=== ,又因为0πθ≤≤,60θ∴=︒.例4.在凸四边形ABCD 中,P 和Q 分别为对角线BD 和AC 的中点,求证:2222224AB BC CD DA AC BD PQ +++=++ .证明:联结BQ ,QD ,因为BP PQ BQ += ,DP PQ DQ +=, 所以()()2222BQ DQ BP PQ DP PQ +=+++222222BP DP PQ BP PQ DP PQ =+++⋅+⋅ ()22222BP DP PQ BP DP PQ =++++⋅2222BP DP PQ =++ ①又因为BQ QC BC += ,BQ QA BA +=,0QA QC += ,同理222222BA BC QA QC BQ +=++ ② 222222CD DA QA QC QD +=++ ③由①、②、③可得()()2222222224222BA BC CD QA BQ QD AC BP PQ ++=++=++=2224AC BD PQ ++.得证.例5.平面四边形ABCD 中,AB a = ,BC b = ,CD c = ,DA d = ,且a b b c c d d a ⋅=⋅=⋅=⋅,判断四边形ABCD 的形状.证明:由四边形ABCD 可知,0a b c d +++=(首尾相接)()a b c d ∴+=-+,即()()22a bc d +=+ 展开得222222a a b b c c d d +⋅+=+⋅+a b c d ⋅=⋅,222a b c d ∴+=+ ① 同理可得2222a dbc +=+ ② ①-②得2222b a ac =⇒= ,b d ∴= ,ac =,即AB CD =,BC DA =,故四边形ABCD 是平行四边形.由此a c =- ,b d =-.又a b b c ⋅=⋅ ,即()0b a c -= ()20b a ∴⋅=即a b AB BC ⊥⇒⊥ ,故四边形ABCD 是矩形.例6.已知非零向量a 和b 夹角为60︒,且()()375a b a b +⊥- ,求证:()()472a b a b -⊥-.证明:因为a 和b 夹角为60︒,所以1cos602a b a b a b ⋅=⋅⋅︒=⋅;又因为()()375a b a b +⊥- ,所以,即()()3750a b a b +⋅-=.22222217161571615781502a ab b a a b b a a b b +⋅-=+⨯⋅-=+⋅-=.()()7150a b a b ∴+⋅-= ,0a b ∴-= ,即a b =.因为()()22222214727308730871582a b a b a a b b a a b b a a b b -⋅-=-⋅+=-⨯+=-+,把a b = 代入上式消去b得()()2247271580a b a b a a a a -⋅-=-+= .所以()()472a b a b -⊥- .基础练习1.已知a b c 、、是三个非零向量,则下列命题中真命题的个数为( )①a b a b a b ⋅=⋅⇔ ∥; ②a b 、反向a b a b ⇔⋅=-⋅;③a b a b a b ⊥⇔+=- ; ④a b a c b c =⇔⋅=⋅ .A .1B .2C .3D .42.已知向量i j,为相互垂直的单位向量,28a b i j +=- ,816a b i j -=-+ ,求a b ⋅ .3.如图7-16所示,已知平行四边形ABCD ,AB a = ,AD b = ,4a = ,2b =,求:OA OB ⋅ .C图7164.设6a = ,10b =,a b -=a 和b 的夹角θ的余弦值. 5.已知a b ⊥ ,2a = ,3b = ,当()()32a b a b λ-⊥+时,求实数λ的值.6.已知不共线向量a ,b ,3a = ,2b =,且向量a b + 与2a b - 垂直.求:a 与b 的夹角θ的余弦值. 7.已知3a = ,4b =,且a 与b 不共线,k 为何值时,向量a kb + 与a kb - 互相垂直? 8.在ABC △中,已知4AB AC ⋅= ,12AB BC ⋅=-,求AB .9.在ABC △中,AB a = ,BC b = ,且0a b ⋅>,则ABC △的形状是__________.10.已知向量()24a = ,,()11b = ,.若向量()b a b λ⊥+,则实数λ的值是__________.11.如图7-17,在四边形ABCD 中,4A B B D D C++=,0AB BD BD DC ⋅=⋅= ,4AB BD BD DC ⋅+⋅= ,求()AB DC AC +⋅的值.图717D CBA能力提高12.如图7-18,在Rt ABC △中,已知BC a =,若长为2a 的线段PQ 以点A 为中点.问PQ 与BC的夹角θ为何值时,BP CQ ⋅的值最大?并求出这个最大值.PQ图71813.已知ABC △中满足()2ABAB AC BA BC CA CB =⋅+⋅+⋅,a b c 、、分别是ABC △的三边.试判断ABC △的形状并求sin sin A B +的取值范围.14.设边长为1的正ABC △的边BC 上有n 等分点,沿点B 到点C 的方向,依次为121n P P P - ,,,,若1121n n S AB AP AP AP AP AC -=⋅+⋅++⋅ ,求证:21126n n S n-=. 15.在ABC △中,AB a = ,BC c = ,CA b = ,又()()()123c b b a a c ⋅⋅⋅=∶∶∶∶,则ABC △三边长之比a b c =∶∶__________.16.在向量a b c ,,之间,该等式()()())012a b c a b b c c a ⎧++=⎪⎨⋅⋅⋅=⎪⎩∶∶成立,当1a = 时,求b 和c 的值.17.若a b c ,,中每两个向量的夹角均为60︒,且4a = ,6b = ,2c = ,求a b c ++的值. 7.5 向量的坐标表示及其运算 向量的坐标表示在平面直角坐标系中,每一个点都可用一对实数()x y ,来表示,那么,每一个向量可否也用一对实数来表示?前面的平面向量分解告诉我们,只要选定一组基底,就有唯一确定的有序实数对与之一一对应.我们分别选取与x 轴、y 轴方向相同的单位向量i ,j作为基底,由平面向量的基本定理.对于任一向量a ,存在唯一确定的实数对()x y ,使得()a xi y j x y =+∈R ,,我们称实数对()x y ,叫向量a 的坐标,记作()a x y =,.其中x 叫向量a 在x 轴上的坐标,y 叫向量a 在y 轴上的坐标,见图7-19.图719注意:(1)与a相等的向量的坐标也是()x y ,.(2)所有相等的向量坐标相同;坐标相同的向量是相等的向量. 平面向量的坐标运算(1)设()11a x y = ,,()22b x y = ,,则()1212a b x x y y +=++,.(2)设()11a x y = ,,()22b x y = ,,则()1212a b x x y y -=--,. (3)设()11A x y ,,()22B x y ,,则()2121AB OB OA x x y y =-=--,. (4)设()11a x y = ,,λ∈R ,则()a x y λλλ=,.(5)设()11a x y = ,,()22b x y = ,,则()1212a b x x y y ⋅=+. 向量平行的坐标表示设()11a x y = ,,()22b x y = ,,且0b ≠ ,则()1212a b x x y y =+∥. 向量的平行与垂直的充要条件设()11a x y = ,,()22b x y =,,且0b ≠ ,0a ≠ 则12210a b b a x y x y λ⇔=⇔-=∥. 121200a b a b x x y y ⊥⇔⋅=⇔+=. 重要的公式(1)长度公式:a =()()11a x y = ,(2)夹角公式:()())1122cos a x y b x y θ===,,,.(3)平面两点间的距离公式:()())1122A B d AB A x y B x y == ,,,,. (4)不等式:cos a b a b a b θ⋅= ≥. 例1.已知()12a a a = ,,()12b b b =,,且12210a b a b -≠,求证: (1)对平面内任一向量()12c c c ,,都可以表示为()xa yb x y +∈R,的形式;(2)若0xa yb +=,则0x y ==.证明:(1)设c xa yb =+,即()()()()1212121122c c x a a y b b a x b y a x b y =+=++,,,,, 111222.a x b y c a x b y c +=⎧∴⎨+=⎩,12210a b a b -≠ ,∴上述关于x y ,的方程组有唯一解. 1221122112211221.c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩,1221122112211221c b c b a c a c c a b a b a b a b a b --∴=+-- . (2)由(1)的结论,0c =,即120c c ==,则 122112210c b c b x a b a b -==-,122112210a c a c y a b a b -==-,0x y ∴==.小结:证明(1)的过程就是求实数x ,y 的过程,而12210a b a b -≠是上面二元一次方程组有唯一解的不可缺少的条件.另外,本题实际上是用向量的坐标形式表述平面向量基本定理.其中1x λ=,2y λ=,这里给出了一个具体的求12λλ,的计算方法.例2.向量()10OA = ,,()11OB = ,,O 为坐标原点,动点()P x y ,满足0102OP OA OP OB ⎧⋅⎪⎨⋅⎪⎩≤≤≤≤,求点()Q x y y +,构成图形的面积.解:由题意得点()P x y ,满足0102x x y ⎧⎨+⎩≤≤≤≤,令x y uy v +=⎧⎨=⎩,则点()Q u v ,满足0102u v u -⎧⎨⎩≤≤≤≤,在uOv 平面内画出点()Q u v ,构成图形如图7-20所示,∴其面积等于122⨯=.图720例3.在直角坐标系中,已知两点()11A x y ,,()22B x y ,;1x ,2x 是一元二次方程222240x ax a -+-=两个不等实根,且A B 、两点都在直线y x a =-+上.(1)求OA OB ⋅ ;(2)a 为何值时OA 与OB 夹角为π3.解:(1)12x x 、是方程222240x ax a -+-=两个不等实根,()224840a a ∴∆=-->解之a -<()212142x x a =-,12x x a += 又 A B 、两点都在直线y x a =-+上, ()()()()2212121212142y y x a x a x x a x x a a ∴=-+-+=-++=- 121224OA OB x x y y a ∴⋅=+=-(2)由题意设1x =,2x =112y x a x ∴=-+==,同理21y x =()22212121224OA OB x x x x x x ∴=+=+-=当OA 与OB 夹角为π3时,π1cos 4232OA OB OA OB ⋅==⨯=242a ∴-=解之(a =- a ∴=即为所求.例4.已知()10a = ,,()21b =,.①求3a b + ;②当k 为何实数时,ka b - 与3a b +平行,平行时它们是同向还是反向?解:①()()()31032173a b +=+=,,,,3a b ∴+= ②()()()102121ka b k k -=-=--,,,.设()3ka b a b λ-=+,即()()2173k λ--=,,,12731313k k λλλ⎧=-⎪-=⎧⎪∴⇒⎨⎨-=⎩⎪=-⎪⎩.故13k =-时,它们反向平行.例5.对于向量的集合(){}221A v x y x y ==+ ,≤中的任意两个向量12v v 、与两个非负实数αβ、;求证:向量12v v αβ+的大小不超过αβ+.证明:设()111v x y = ,,()222v x y = ,,根据已知条件有:22111x y +≤,22221x y +≤,又因为12v v αβ+=其中12121x x y y +所以12v v αβαβαβ+=+=+.基础练习1.已知()21a = ,,()34b =-,,求a b + ,a b - ,34a b + 的坐标.2.设O 点在ABC △内部,且有230OA OB OC ++=,求ABC △的面积与AOC △的面积的比.3.已知平行四边形ABCD 的三个顶点A B C ,,的坐标分别为(-2,1),(-1,3),(3,4),求顶点D 的坐标.4.已知向量i ,j 为相互垂直的单位向量,设()12a m i j =+- ,()1b i m j =+- ,()()a b a b +⊥-,求m 的值.5.已知等腰梯形ABCD ,其中AB CD ∥,且2DC AB =,三个顶点()12A ,,()21B ,,()42C ,,求D 点的坐标.6.如图7-21所示,已知()20OA =,,(1OB = ,将BA 绕着B 点逆时针方向旋转60︒,且模伸长到BA 模的2倍,得到向量BC .求四边形AOBC 的面积S .图7217.如图7-22所示,已知四边形ABCD 是梯形,AD BC ∥,2BC AD =,其中()12A ,,()31B ,,()24D ,,求C 点坐标及AC的坐标.图7228.已知向量()2334a x x x =+-- ,与AB 相等,其中()12A ,,()32B ,,求x .9.平面内有三个已知点()12A -,,()70B ,,()56C -,,求(1)AB ,AC ;(2)AB AC + ,AB AC - ;(3)122AB AC + ,3AB AC - .10.已知向量()12a = ,,()1b x =,,2u a b =+ ,2v a b =- ,且u v ∥,求x .11.已知()23a = ,,()14b =- ,,()56c = ,,求()a b c ⋅ ,和()a b c ⋅⋅ . 12.已知两个非零向量a 和b 满足()28a b +=- ,,()64a b -=--,,求a 与b 的夹角的余弦值.能力提高13.已知平面上三个向量a ,b ,c 均为单位向量,且两两的夹角均为120︒,若()1ka b c k ++>∈R,求k 的取值范围.14.已知OA ,OB 不共线,点C 分AB 所成的比为2,OC OA OB λμ=+ ,求λμ-. 7.6 线段的定比分点公式与向量的应用线段的定比分点公式设点P 是直线12P P 上异于1P 、2P 的任意一点,若存在一个实数()1λλ≠-,使12PP PP λ=,则λ叫做点P 分有向线段12PP 所成的比,P 点叫做有向线段12PP的以定比为λ的定比分点. 当P 点在线段12P P 上时0λ⇔≥;当P 点在线段12P P 的延长线上时1λ⇔<-; 当P 点在线段21P P 的延长线上时10λ⇔-<<;设()111P x y ,,()222P x y ,,()P x y ,是线段12P P 的分点,λ是实数且12PP PP λ=,则121211x x x OP y y y λλλλ+⎧=⎪⎪+⇔=⎨+⎪=⎪+⎩()12121111OP OP OP tOP t OP t λλλ+⎛⎫⇔=+-= ⎪++⎝⎭ .()1λ≠-由线段的定比分点公式得:中点坐标公式设()111P x y ,,()222P x y ,,()P x y ,为12PP的中点,(当1λ=时) 得121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩三角形的重心坐标公式ABC △三个顶点的坐标分别为()11A x y ,、()22B x y ,、()33C x y ,,则ABC △的重心的坐标是12312233x x x y y y G ++++⎛⎫ ⎪⎝⎭,. 利用向量可以解决许多与长度、距离及夹角有关的问题.向量兼具几何特性和代数特性,成为沟通代数、三角与几何的重要工具,同时在数学、物理以及实际生活中都有着广泛的应用. 三角形五“心”向量形式的充要条件设O 为ABC △所在平面上一点,角A ,B ,C 所对边长分别为a ,b ,c 则(1)O 为ABC △的外心222OA OB OC ⇔== . (2)O 为ABC △的重心0OA OB OC ⇔++= .(3)O 为ABC △的垂心OA OB OB OC OC OA ⇔⋅=⋅=⋅. (4)O 为ABC △的内心0aOA bOB cOC ⇔++=.(5)O 为ABC △的A ∠的旁心()aOA b OB cOC ⇔=+.例1.如图7-23所示,已知矩形ABCD 中,()21A ,,()54B ,,()36C ,,E 点是CD 边的中点,联结BE 与矩形的对角线AC 交于F 点,求F 点坐标.图723解: 四边形ABCD 是矩形,E 是CD 边的中点, ABF CEF ∴△∽△,且2AB CE =2AF CF ∴=即点F 分AC 所成的比2λ=.设()F x y ,.由(21)A ,,(36)C ,,根据定比分点坐标公式得 2238123x +⨯==+,12613123y +⨯==+ F ∴点坐标是81333⎛⎫⎪⎝⎭,. 例2.证明:()cos cos cos sin sin αβαβαβ-=+.证明:在单位圆O 上任取两点A ,B ,以Ox 为始边,以OA ,OB 为终边的角分别为β,α,见图7-24.β,sin β)B (cos α图724则A 点坐标为()cos sin ββ,,B 点坐标为()cos sin αα,; 则向量()cos sin OA ββ= ,,()cos sin OB αα= ,,它们的夹角为αβ-,1OA OB ==,cos cos sin sin OA OB αβαβ⋅=+ ,由向量夹角公式得:()cos cos cos sin sin OA OBOA OB αβαβαβ⋅-==+ ,从而得证.注意:用同样的方法可证明()cos cos cos sin sin αβαβαβ+=-.例3.证明柯西不等式()()()2222211221212x y x y x x y y +⋅++≥.证明:令()11a x y = ,,()22b x y =,(1)当0a = 或0b = 时,12120a b x x y y ⋅=+=,结论显然成立;(2)当当0a ≠ 且0b ≠ 时,令θ为a ,b的夹角,则[]0πθ∈,1212cos a b x x y y a b θ⋅=+=.又cos 1θ ≤,a b a b∴⋅≤(当且仅当a b ∥时等号成立).1212x x y y ∴+ ()()()2222211221212x y x y x x y y ∴+⋅++≥(当且仅当1212x x y y =时等号成立). 例4.给定ABC △,求证:G 是ABC △重心的充要条件是0GA GB GC ++=.证明:必要性 设各边中点分别为D E ,,F ,延长AD 至P ,使DP GD =,则2AG GD = GP =.又因为BC 与GP 互相平分,所以BPCG 为平行四边形,所以BG PC ∥,所以GB CP =. 所以0GA GB GC GC CP PG ++=++=.充分性 若0GA GB GC ++= ,延长AG 交BC 于D ,使GP AG =,联结CP ,则GA PG =. 因为0GC PG PC ++= ,则GB PC = ,所以GB CP ∥,所以AG 平分BC .同理BG 平分CA .所以G 为重心.例5 ABC △外心为O ,垂心为H ,重心为G .求证:O G H ,,为共线,且12OG GH =∶∶. 证明:首先()()2112333OG OA AG OA AM OA AB AC OA AO OB OC =+=+=++=+++=()13OA OB OC ++. 其次设BO 交外接圆于另一点E ,则联结CE 后得CE BC ⊥. 又AH BC ⊥,所以AH CE ∥.又EA AB ⊥,CH AB ⊥,所以AHCE 为平行四边形.所以AH EC =.所以OH OA AH OA EC OA EO OC OA OB OC =+=+=++=++ , 即3OH OG = ,所以OG 与OH共线,所以O G H ,,共线. 即12OG GH =∶∶. 注意:O G H ,,所在的直线称为欧拉线.例6.已知ABC △,AD 为中线,求证()2222122BC AD AB AC ⎛⎫=+- ⎪⎝⎭(中线长公式). 证明:以B 为坐标原点,以BC 所在的直线为x 轴建立如图7-25所示的直角坐标系,图725设()A a b ,,()0C c ,,02c D ⎛⎫⎪⎝⎭,,则()22222024c c AD a b ac a b ⎛⎫=-+-=-++ ⎪⎝⎭,()()22222222221122244BC c c AB AC a b c a b a b ac ⎛⎫⎡⎤⎪+-=++-+-=+-+⎢⎥ ⎪⎣⎦⎝⎭, 从而()2222122BC AD AB AC ⎛⎫ ⎪=+- ⎪⎝⎭,()2222122BC AD AB AC ⎛⎫=+- ⎪⎝⎭. 例7.是否存在4个两两不共线的平面向量,其中任两个向量之和均与其余两个向量之和垂直?解:如图7-26所示,在正ABC △中,O 为其内心,P 为圆周上一点,满足PA ,PB ,PC ,PO两两不共线,有POA图726()()PA PB PC PO +⋅+= ()()PO OA PO OB PO OC PO +++⋅++()()22PO OA OB PO OC =++⋅+()()22PO OC PO OC =-⋅+2240PO OC =-=有()PA PB + 与()PC PO +垂直.同理可证其他情况.从而PA ,PB ,PC ,PO满足题意、故存在这样四个平面向量.例8.已知向量1OP ,2OP ,3OP 满足条件1230OP OP OP ++= ,1231OP OP OP ===,求证:123PP P △是正三角形.解:令O 为坐标原点,可设()111cos sin P θθ,,()222cos sin P θθ,,()333cos sin P θθ,由123OP OP OP +=- ,即()()()112233cos sin cos sin cos sin θθθθθθ+=--,,, 123123cos cos cos sin sin sin θθθθθθ+=-⎧⎪⎨+=-⎪⎩①②两式平方和()1212cos 11θθ+-+=,()121cos 2θθ-=-,由此可知12θθ-的最小正角为120︒,即1OP 与2OP的夹角为120︒, 同理可得1OP 与3OP 的夹角为120︒,2OP 与3OP的夹角为120︒, 这说明123P P P ,,三点均匀分布在一个单位圆上,所以123PP P △为等腰三角形. 基础练习1.在ABC △中,若321AB BC BC CA AB CA⋅⋅⋅==,则tan A =__________. 2.已知P 为ABC △内一点,且满足3450PA PB PC ++=,那么PAB PBC PCA S S S =△△△∶∶__________.3.如图7-27,设P 为ABC △内一点,且2155AP AB AC =+,求ABP △的面积与ABC △的面积之比.PCA图7274.已知ABC △的三顶点坐标分别为()11A ,,()53B ,,()45C ,,直线l AB ∥,交AC 于D ,且直线l 平分ABC △的面积,求D 点坐标.5.已知()23A ,,()15B -,,且13AC AB = ,3AD AB =,求点C D 、的坐标.6.点O 是平面上一定点,A B C ,,是此平面上不共线的三个点,动点P 满足AC AB OP OA AB AC λ⎛⎫⎪=++ ⎪⎝⎭,[)0λ∈+∞,.则点P 的轨迹一定通过ABC △的__________心.能力提高7.设x y ∈R ,,i j 、为直角坐标系内x y 、轴正方向上的单位向量,若()2a xi y j =++,()62b xi y j =+- 且2216a b += .(1)求点()M x y ,的轨迹C 的方程;(2)过定点()03,作直线l 与曲线C 交于A B 、两点,设OP OA OB =+,是否存在直线l 使四边形OAPB 为正方形?若存在,求出l 的方程,或不存在说明理由.8.(1)已知4a = ,3b = ,()()23261a b a b -⋅+=,求a 与b 的夹角θ;(2)设()25OA = ,,()31OB = ,,()63OC =,,在OC 上是否存在点M,使MA MB ⊥ ,若存在,求出点M 的坐标,若不存在,请说明理由.9.设a b、是两个不共线的非零向量()t ∈R(1)记OA a = ,OB tb = ,()13OC a b =+,那么当实数t 为何值时,A B C 、、三点共线?(2)若1a b == 且a 与b 夹角为120︒,那么实数x 为何值时a xb -的值最小?10.设平面内的向量()17OA = ,,()51OB = ,,()21OM =,,点P 是直线OM 上的一个动点,求当PA PB ⋅ 取最小值时,OP的坐标及APB ∠的余弦值.11.已知向量()11m = ,,向量n 与向量m 夹角为3π4,且1m n ⋅=- .(1)求向量n;(2)若向量n 与向量()10q = ,的夹角为π2,向量22sin 4cos 2A p A ⎛⎫= ⎪⎝⎭ ,,求2n p + 的值.12.已知定点()01A ,,()01B -,,()10C ,.动点P 满足:2AP BP k PC ⋅= . (1)求动点P 的轨迹方程; (2)当0k =时,求2AP BP +的最大值和最小值.13.在平行四边形ABCD 中,()11A ,,()60AB =,,点M 是线段AB 的中点,线段CM 与BD 交于点P .(1)若()35AD =,,求点C 的坐标;(2)当AB AD =时,求点P 的轨迹.14.已知向量()22a = ,,向量b 与向量a 的夹角为3π4,且2a b ⋅=- ,(1)求向量b;(2)若()10t = ,且b t ⊥ ,2cos 2cos 2C c A ⎛⎫= ⎪⎝⎭ ,,其中A C 、是ABC △的内角,若三角形的三内角A B C 、、依次成等差数列,试求b c +的取值范围.。
2025届上海市华东师范大学二附中高考数学四模试卷含解析

2025届上海市华东师范大学二附中高考数学四模试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知实数,x y 满足约束条件11220220x y x y x y ≥-⎧⎪≥-⎪⎨-+≥⎪⎪--≤⎩,则23x y -的最小值是A .2-B .72-C .1D .42.空气质量指数AQI 是反映空气状况的指数,AQI 指数值趋小,表明空气质量越好,下图是某市10月1日-20日AQI指数变化趋势,下列叙述错误的是( )A .这20天中AQI 指数值的中位数略高于100B .这20天中的中度污染及以上(AQI 指数>150)的天数占14C .该市10月的前半个月的空气质量越来越好D .总体来说,该市10月上旬的空气质量比中旬的空气质量好 3.复数2(1)i i +的模为( ). A .12B .1C .2D .224.若命题:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题:在边长为4的正方形内任取一点,则的概率为,则下列命题是真命题的是( )A .B .C .D .5.5G 网络是一种先进的高频传输技术,我国的5G 技术发展迅速,已位居世界前列.华为公司2019年8月初推出了一款5G 手机,现调查得到该款5G 手机上市时间x 和市场占有率y (单位:%)的几组相关对应数据.如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月……,5代表2019年12月,根据数据得出y 关于x 的线性回归方程为0.042y x a =+.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款5G 手机市场占有率能超过0.5%(精确到月)( )A .2020年6月B .2020年7月C .2020年8月D .2020年9月6.已知抛物线C :22y px =(0p >)的焦点为F ,01,2M y ⎛⎫⎪⎝⎭为该抛物线上一点,以M 为圆心的圆与C 的准线相切于点A ,120AMF ∠=︒,则抛物线方程为( ) A .22y x =B .24y x =C .26y x =D .28y x =7.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为1F ,2F ,点P 是C 的右支上一点,连接1PF 与y 轴交于点M ,若12||FO OM =(O 为坐标原点),12PF PF ⊥,则双曲线C 的渐近线方程为( ) A .3y x =±B .3y x =C .2y x =±D .2y x =8. 若数列{}n a 满足115a =且1332n n a a +=-,则使10k k a a +⋅<的k 的值为( ) A .21B .22C .23D .249.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A .B .C .D .10.已知水平放置的△ABC 是按“斜二测画法”得到如图所示的直观图,其中B ′O ′=C ′O ′=1,A ′O ′=32,那么原△ABC 的面积是( )A 3B .2C 3D 311.已知双曲线C :22221(0,0)x y a b a b-=>>的焦点为1F ,2F ,且C 上点P 满足120PF PF ⋅=,13PF =,24PF =,则双曲线C 的离心率为 A 10B 5C .52 D .512.已知R 为实数集,{}2|10A x x =-≤,1|1B x x ⎧⎫=≥⎨⎬⎩⎭,则()A B =R( )A .{|10}x x -<≤B .{|01}x x <≤C .{|10}x x -≤≤D .{|101}x x x -≤≤=或二、填空题:本题共4小题,每小题5分,共20分。
上海市华东师范大学第二附属中学创新班和理科班用高三

6.4 反三角函数三角函数解决知道角求三角函数值的问题,例如π1sin62=,5πcos 6=这类问题称作“知角求值”问题.在科学研究和生产实践中还会遇到大量的知道三角函数值,需要求角的问题,例如知道1sin 2x =,cos x =,是什么?这类题称作“知值求角”问题.那么我们如何来解决这类问题呢?“知角求值”与“知值求角”是关系十分密切的问题,类似的情形我们在数学学习中是否遇到过呢?是什么问题呢?本质是函数与反函数的问题.那么我们如何来解决三角函数的反函数问题呢?首先回顾一下反函数的定义.若确定函数()y f x =的映射是一一映射,则()y f x =存在反函数.三角函数在定义域内是否是一一对应的呢?我们知道三角函数都是周期函数,因此定义三角函数的映射不是一一对应的,从而三角函数不存在反函数. 那么我们如何解决“知值求角”的问题呢?目前的焦点是如何摆脱不是“一一映射”的困扰.是什么因素造成了正弦函数sin y x =无法构成一一映射呢?是正弦函数的对应法则?还是函数的定义域?决定因素是定义域! 那么我们是否有可能选择自变量的取值范围,使定义在此范围上的函数sin y x =具有一一映射的特点?现在看看我们该做些什么.我们要寻找这样的集合A ,使得对于每一个正弦值(落在区间[]11-,内),在集合A 中有且只有唯一的与之对应. 我们可以先考虑寻找的集合A 具有这样的特点:对于每一个正弦值,都在集合A 存在弧度数为的角与之对应.其次是关注这样的是否唯一.若不唯一,则调整集合A ,使之满足要求. 让学生寻找集合A ,然后分析讨论.满足条件的集合是()ππππ22k k k ⎡⎤-+∈⎢⎥⎣⎦Z ,.对于每一个整数,函数ππsin ππ22y x x k k ⎛⎫⎡⎤=∈-+ ⎪⎢⎥⎣⎦⎝⎭,都有反函数. 在三角问题的研究中使用频率最高的是锐角,因此我们在确定反正弦函数时,就锁定了函数,ππsin 22y x x ⎛⎫⎡⎤=∈- ⎪⎢⎥⎣⎦⎝⎭,.定义:把函数ππsin 22y x x ⎛⎫⎡⎤=∈- ⎪⎢⎥⎣⎦⎝⎭,的反函数,叫做反正弦函数,记为[]arc sin 11y x x =∈-,,.对定义的理解:(1)arc sin x 表示一个区间ππ22⎡⎤-⎢⎥⎣⎦,内的角;(2)这个角的正弦值为.总之arc sin x 是一个落在区间ππ22⎡⎤-⎢⎥⎣⎦,内正弦值是的角.由反正弦函数的定义有()()sin arc sin 11x x x =-≤≤;()ππarc sin sin 22y y x ⎛⎫=- ⎪⎝⎭≤≤.根据前面有关反函数的知识可知:互为反函数的图像关于直线y x =对称,于是函数arc sin y x =,[]11x ∈-,的图像与函数ππsin 22y x x ⎛⎫⎡⎤=∈- ⎪⎢⎥⎣⎦⎝⎭,的图像关于直线y x =对称(见图6-17).图6-17反正弦函数的主要性质:(1)arc sin y x =的定义域是[]11-,,值域是ππ22⎡⎤-⎢⎥⎣⎦,,且在1x =-时取到最小值π2-,1x =时取到最大值π2. (2)单调性 由于正弦函数sin y x =在ππ22⎡⎤-⎢⎥⎣⎦,上单调递增,故其反函数arc sin y x =在[]11-,上也是单调递增的. (3)奇偶性 由arc sin y x =,[]11x ∈-,的图像知,它的图像关于原点对称,它是一个奇函数,且有()arc sin arc sin x x -=-.类似的,根据余弦函数、正切函数、余切函数的类似性质,我们可以定义它们的性质分别如下:定义:余弦函数cos y x =在区间[]0π,上的反函数,叫做反余弦函数,记作arc cos y x =,它的定义域是[]11-,,值域是[]0π,. 对定义的理解:(1)arc cos x 表示一个区间[]0π,内的角;(2)这个角的余弦值为.总之,arc cos x 是一个落在区间[]0π,内正弦值是的角. 由反余弦函数的定义有()()cos arc cos 11x x x =-≤≤; ()()arc cos cos 0πx x x =≤≤.反余弦函数的图像如图6-18所示.∈(0,π)图6-18反余弦函数的主要性质:(1)arc cos y x =的定义域是[]11-,,值域是[]0π,,且在1x =-时取到最大值,1x =时取到最小值0.(2)单调性 由于余弦函数cos y x =在[]0π,上单调递减,故其反函数arc cos y x =在[]11-,上也是单调递减的.(3)奇偶性 由[]arc cos 11y x x =∈-,,的图像知,它的图像既不关于原点对称,也不关于轴对称,它是一个非奇非偶函数.可以证明()arc cos πarc cos x x -=-. 反正弦函数和反余弦函数之间有个重要关系,见下述例题: 例l .求证πarc sin arc cos 2x x +=,[]11x ∈-,. 证明:()sin arc sin x x =,()πsin arc cos cos arc cos 2x x x ⎡⎤-==⎢⎥⎣⎦. 又由于ππarc sin 22x ⎡⎤∈-⎢⎥⎣⎦,,[]arc cos 0πx ∈,,πππarc cos 222x ⎡⎤-∈-⎢⎥⎣⎦,, 所以πarc sin arc cos 2x x =-,即πarc sin arc cos 2x x +=,[]11x ∈-,一般说来,要证明两个角αβ=的方法是:先证明这两个角的同一个三角函数值相等,比如sin sin αβ=;再证明这两个角在同一个单凋区间内.定义:正切函数tan y x =在区间ππ22⎛⎫- ⎪⎝⎭,内的反函数,叫做反正切函数,记作arc tan y x =,它的定义域是R ,值域是ππ22⎛⎫- ⎪⎝⎭,.对定义的理解:(1)arc tan x 表示一个区间ππ22⎛⎫- ⎪⎝⎭,内的角;(2)这个角的正切值为;总之arc tan x 是一个落在区间ππ22⎛⎫- ⎪⎝⎭,内正切值是的角,见图6-19.图6-19由反正切函数的定义()()tan arc tan x x x =-∞<<+∞; ()ππarc tan tan 22y y y ⎛⎫=-<< ⎪⎝⎭.定义:余切函数cot y x =在区间()0π,内的反函数,叫做反余切函数,记作arc cot y x =,它的定义域是R ,值域是()0π,. 对定义的理解(1)arc cot x 表示一个区间()0π,内的角; (2)这个角的余切值为;总之arc cot x 是一个落在区间()0π,内余切值是的角,见图6-20.x ,x ∈(0,π)图6-20由反正切函数的定义()()cot arc cot x x x =-∞<<+∞; ()()arc cot cot 0πy y y =<<.反正切、反余切函数的性质如下:(1)arc tan y x =的定义域是()-∞+∞,,值域是ππ22⎛⎫- ⎪⎝⎭,;arc cot y x =的定义域是()-∞+∞,,值域是()0π,.(2)单调性 arc tan y x =是()-∞+∞,上的增函数;arc cot y x =是()-∞+∞,上的减函数. (3)奇偶性 arc tan y x =是一个奇函数,对任意x ∈R 有()arc tan arc tan x x -=-;acr cot y x =是一个非奇非偶函数,且对任意x ∈R 有()arc cot πarccot x x -=-. 反正切、反余切函数之间有个重要的关系式:πarc tan arc cot 2x x x +=∈R , 例2.求下列各式的值: (1)1arc cos 2⎛⎫- ⎪⎝⎭;(2)arc sin ⎛ ⎝⎭;(3)5arc tan tan 4⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭;(4)()arc tan tan 4.解:(1)因为2π1cos32=-,且2π0π3<<,由定义知12πarc cos 23⎛⎫-=⎪⎝⎭; (2)因为πsin 3⎛⎫-= ⎪⎝⎭,且ππ22x -<<,于是由定义有πarc sin 3⎛=- ⎝⎭; (3)因为5ππtan πtan πtan 1444⎛⎫⎛⎫⎛⎫-=--=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以()5πarc tan tan arc tan 144⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭;(4)因为()tan 4tan 4π=-,且ππ4π22-<-<,所以 ()()arc tan tan4arc tan tan 4π4π=-=-⎡⎤⎣⎦.例3.求值:(1)1sin arc cos 3⎛⎫ ⎪⎝⎭;(2)14cos arc sin 25⎛⎫ ⎪⎝⎭;(3)13tan arc sin arc cos 25⎛⎫- ⎪⎝⎭.解:(1)设1arc cos 3α=,则1cos 3α=,且π02α⎛⎫∈ ⎪⎝⎭,,于是1sin arc cos sin 3α⎛⎫== ⎪⎝⎭;(2)设4arc sin5α=,则4sin 5α=,且π02α⎛⎫∈ ⎪⎝⎭,,于是3cos 5α=,所以,14cos arc sin cos 252α⎛⎫= ⎪⎝⎭;(3)设1arc sin2α=,3arc cos 5β=,则13sin cos 25αβ==,,于是cos α==,4sin 5β==,tan α=4tan 3β=.()4tan tan tan 1tan tan αβαβαβ---====+⋅. 例4.求值:(1)πarc sin sin 4⎛⎫ ⎪⎝⎭;(2)3πarc sin sin 4⎛⎫ ⎪⎝⎭.解:(1)ππarc sin sin 44⎛⎫== ⎪⎝⎭; (2)3ππarc sin sin arc sin 44⎛⎫== ⎪⎝⎭⎝⎭. 例5.比较下列各组数的大小:(1)2arc sin 3与4arc sin 7;(2)arc cot1.3与arc cot1.31;(3)2arc sin 3与2arc cot 3;(4)1arc tan 3与arc cot 2.解:(1)由于arc sin x 是一个单调递增的函数,且2437>,于是; (2)由于arc cot x 是一个单调递减的函数,1.3 1.31<,于是arc cot1.3arc cot1.31>; (3)设2arc cot3α=,则2cot 3α=,且π02α⎛⎫∈ ⎪⎝⎭,,于是1sin csc αα====,所以arc α=.又23<,故22arc sin arc cot 33<. (4)设ar cc o t2α=,则co t α=2,1tan 2α=,于是1arc cot 2arc tan 2=,故1a r ct a n a r cc o t23<.例6.已知()()πarc sin sin sin arc sin sin sin 2αβαβ++-=,求22sin sin αβ+的值. 解:()()πarc sin sin sin arc sin sin sin 2αβαβ++-=, ()arc sin sin sin αβ+与()arc sin sin sin αβ-互余.()()sin arc sin sin sin cos arc sin sin sin αβαβ+=-⎡⎤⎡⎤⎣⎦⎣⎦,sin sin αβ∴+化简,得221sin sin 2αβ+=. 例7.用反正弦函数值的形式表示下列各式中的:(1)3ππsin 522x x ⎡⎤=∈-⎢⎥⎣⎦,,; (2)[]3sin 0π5x x =∈,,;(3)3sin 5x =-,[]π2πx ∈,.解:(1)3arc sin 5x =;(2)3arc sin 5x =,或3πarc sin 5x =-;(3)3πarc sin 5x =+,或32πarc sin 5x =-.例8.比较arc sin a 与()2arc sin 1a a ≤的大小. 解:当0a =,或1a =时,22arc sin arc sin a a a a =⇒=;当[)10a ∈-,时,22arc sin arc sin a a a a <⇒<; 当()01a ∈,时22arc sin arc sin a a a a >⇒>. 基础练习1.求下列反正弦函数的值:(1)1arc sin 2;(2)arc ; (3)arc sin 0;(4)arc sin1;(5)arc sin ⎛ ⎝⎭;(6)()arc sin 1-.2.求下列函数的定义域和值域: (1)12arc cos log y x ⎛⎫= ⎪⎝⎭;(2)()12log arc cos y x =;(3)()arc cos arc sin y x =;(4)()arc sin arc cos y x =.3.求值:(1)4sin arc tan 3⎛⎫ ⎪⎝⎭;(2)12tan arc cos 13⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎦;(3)3cos 2arc tan 4⎛⎫ ⎪⎝⎭;(4)()arc sin sin 6; (5)11arc tan 2arc tan 73+;(6)4πarc tan tan 5⎛⎫ ⎪⎝⎭;(7)1arc tan arc tan x x+;(8)((arc sin arc cos -.4.求下列函数的反函数:(1)π3πsin 22y x x ⎛⎫⎡⎤=∈ ⎪⎢⎥⎣⎦⎝⎭,;(2)π02y x ⎫⎡⎤∈⎪⎢⎥⎣⎦⎭,;(3)()πlg sin 02y x x ⎛⎫⎛⎤=∈ ⎪ ⎥⎝⎦⎝⎭,;(4)()(]()lg arc sin 01y x x =∈,.5.用反正切函数值的形式表示下列各式中的:(1)4ππtan 322x x ⎛⎫=∈- ⎪⎝⎭,,;(2)123πtan π52x x ⎛⎫=∈ ⎪⎝⎭,,; (3)()24tan 2π07x x =-∈-,,. 能力提高 6.求值:(可用反三角函数表示):(1)34arc cos arc sin 45-;(2)()()arc sin sin 2arc cos cos4+;(3)315arc sin arc sin 517+.7.当[]11x ∈-,时,比较arc sin x 与arc cos x 的大小.§6.4 反三角函数 基础练习 1.(1)1πarc sin26=;(2)πarc 3=;(3)arc sin 00=; (4)πarc sin12=;(5)πarc sin 4⎛=- ⎝⎭;(6)πarc sin(1)2-=-. 2.(1)[0π]A =,;(2)12log πA ⎡⎫=+∞⎢⎪⎢⎭⎣,;(3)[0π]A =,;(4)π0lg 2A ⎡⎤=⎢⎥⎣⎦,.3.(1)45;(2)512-;(3)725;(4)62π-;(5)π4; (6)π4-;(7)π02π02x x ⎧>⎪⎪⎨⎪-<⎪⎩,,;(8)π-.4.(1)πarc sin ([11])y x x =-∈-,;(2)2arc sin ([01])y x x =∈,;(3)arc sin10((0])x y x =∈-∞,;(4)πsin102x y x ⎛⎫⎛⎤=∈-∞ ⎪ ⎥⎦⎝⎝⎭,.5.(1)4arc tan 3x =;(2)12πarc tan 5x =-;(3)24arc tan 7x =-或24arc tan π7--.能力提高 6.(1)arc -(2)3π6-;(3)84πarc sin 85-. 7.当x =时,πa r c s i n a r c c o s 4x x ==;当1x ⎡∈-⎢⎢⎭⎣时,a r c s i n a r c c o s x x <;当1x ⎤∈⎥⎦⎝时,arc sin arc cos x x >.。
华东师范大学第二附属中学(实验班用)数学习题详解-9讲诉
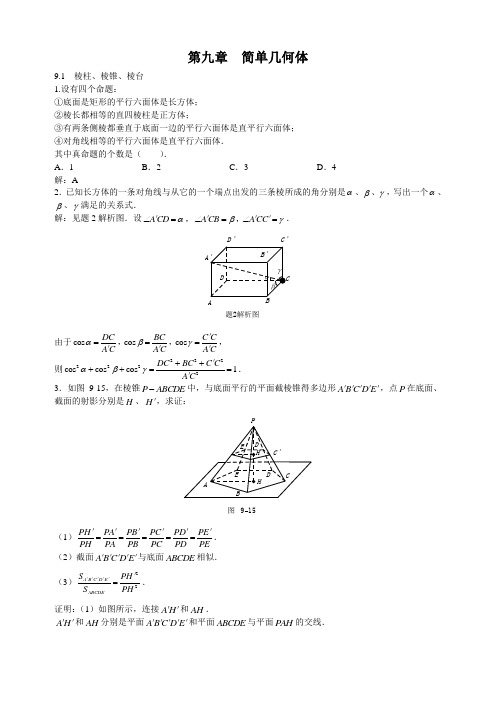
第九章 简单几何体9.1 棱柱、棱锥、棱台 1.设有四个命题:①底面是矩形的平行六面体是长方体; ②棱长都相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体; ④对角线相等的平行六面体是直平行六面体. 其中真命题的个数是( ). A .1 B .2 C .3 D .4 解:A 2.已知长方体的一条对角线与从它的一个端点出发的三条棱所成的角分别是α、β、γ,写出一个α、β、γ满足的关系式.解:见题2解析图.设A CD A CB A CC αβγ∠=∠=∠=,,′′′′.D 'C 'A题2解析图由于cos cos cos DC BC C CA C A C A Cαβγ===,,,′′′′ 则2222222cos cos cos 1DC BC C C A C αβγ++++==′′.3.如图9-15,在棱锥P ABCDE -中,与底面平行的平面截棱锥得多边形A B C D E ′′′′′,点P 在底面、截面的射影分别是H 、H ′,求证:图 915(1)PH PA PB PC PD PE PH PA PB PC PD PE =====′′′′′′. (2)截面A B C D E ′′′′′与底面ABCDE 相似. (3)22A B C D EABCDE S PH S PH =′′′′′′.证明:(1)如图所示,连接A H ′′和AH .A H ′′和AH 分别是平面ABCDE ′′′′′和平面ABCDE 与平面PAH 的交线.由于平面A B C D E ′′′′′∥平面ABCDE , 则PH PA A H AH PA H PAH PH PA =,,′′′′△′′△∥. 同理可证,PH PB PH PC PH PD PH PE PH PB PH PC PH PD PH PE====,,,′′′′′′′′. 则PH PA PB PC PD PE PH PA PB PC PD PE=====′′′′′′. (2)由于PA PB PA PB=′′,P ∠是公共角, 则PA B PAB △′′△∽,A B PA PH AB PA PH==′′′′. 同理可证,B C PH C D PH D E PH E A PH BC PH CD PH DE PH EA PH====,,,′′′′′′′′′′′′. 由于截面A B C D E ′′′′′与底ABCDE 的对应边成比例, 则截面A B C D E ′′′′′与底ABCDE 相似. (3)由(2)知,2222A B C D EABCDE S A B PH S AB PH ==′′′′′△′′′. 4.以1,l ,1? 解:3个.5.四面体OABC 中,OA ⊥面ABC ,AB AC ⊥,点P 满足OP lOA mOB nOC =++,其中l m n ,,为正数且1l m n ++=.若直线OP 是由到面OBC 、面OCA 和面OAB 的距离相等的点构成,求二面角A OBC --的余弦值(用l ,m ,n 表示). 解:1OP lOA mOB nOC m n l AP mAB nAC P =++++=⇒=+,,在面ABC 上. OA ⊥面ABC ,AB AC ⊥,则P 在面ABO 的垂足在AB 上.又ABP ABCSAP mAB nAC AB AC n S =+⊥⇒=,△△.同理ACP BCP ABC ACP ABPABC ABC ABCS S S S S m l S S S --===,△△△△△△△△.则cos ABO P ABO ABP ACO P ACO BCP S V S nA OBC S V S l--∠--====△△△△.6.如图9-16,已知正三棱柱111ABC A B C -的所有棱长都相等,E 是1A B 的中点,F 在棱1CC 上,当点F 使得1A F BF +最小时,求异面直线AE 与1A F 所成的角.图 916B 1N 1C 1A 1H GFENC BA解:如图可知F 为中点时,满足题意.由于12GH AH ==,则AG .又由于1A F =EG =AE . 则222AE EG AG +=,则90AEG ∠=︒.7.如图9-17,正四棱柱1111ABCD A B C D -中,对角线118BD BD =,与侧面11BB C C 所成角为30︒,求:D 1C 1B 1A 1DCBA图 917(1)1BD 与底面ABCD 所成角. (2)异面直线1BD 与AD 所成角. (3)正四棱柱的全面积.解:(1)在正四棱柱1A C 中,由于11D C ⊥面11BB C C , 则11D BC ∠是1D B 与侧面11BB C C 所成角,即1130D BC ∠=︒. 由于18BD =,则1114D C BC ==,, 由于1111A B C D 是正方形,则11114B C D C ==,1D D ⊥平面ABCD ,则1D BD ∠是1D B 与底面ABCD 所成角,在1Rt D DB △中,11BD B D ==18BD =,则11cos 2BD D BD BD ==,则145D BD ∠=︒, 即1BD 与底面ABCD 所成角为45︒. (2)由于11AD A D ∥,则11A D B ∠是1BD 与AD 所成角(或补角). 由于11D A ⊥平面11AA B B ,则111D A A B ⊥, 11Rt A D B △中,11148A D BD ==,,则111cos 2A D B ∠=,则1160A D B ∠=︒,即异面直线AD 与1BD ,所成角为60︒. (3)11Rt BB C △中,114B C =,1BC =则1BB =,则2(44441)S =⨯+⨯⨯=全.8.如图9-18,已知三棱锥P ABC -中,PA 、PB 、PC 与底面ABC 所成角相等,90CAB ∠=︒,AC AB PB a D ===,为BC 中点,E 点在PB 上且PC ∥截面EAD .求:图 918F EDACP(1)AE 与底面ABC 所成角. (2)PC 到平面EAD 的距离. 解:(1)证明:由于PA 、PB 、PC 与底面ABC 所成角相等, 则顶点P 在底面上的射影为底面Rt CAB △的外心. 而Rt CAB △的外心在斜边BC 的中点D 处, 即PD ⊥平面ABC , 而PD ⊆平面PBC ,则平面PBC ⊥底面ABC .由于PC ∥截面EAD ,PD ⊆平面PBC , 且平面PBC 平面EAD DE =,则PC ∥截面DE ,而D 为BC 中点, 则E 为PB 的中点. 过E 作EM PD ∥,则EM 与BC 的交点,M 为BD 的中点,连接AM , 由于PD ⊥底面ABC ,则EM ⊥底面ABC . 则EAM ∠为AE 与底面ABC 所成的角.AC AB PB a ===,则AE ,而PB PC a BC ===,,则CPB △为等腰直角三角形.在Rt AEM △中,sin EM EAM AE ∠===. 则AE 与底面ABCarc sin (2)等体积法,可得:12a .9.作出正四面体每个面的中位线,共得12条线段,在这些线段中,相互成异面直线的“线段对”有__________个. 解:24个.10.如图9-19,ABCD A B C D -′′′′为正方体.任作平面α与对角线AC ′垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l 则( ).E 'D 'C 'B 'A 'DC BA图919A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值 解:将正方体切去两个正三棱锥A A BD -′与C D B C -′′′后,得到一个以平行平面A BD ′与D B C ′′为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱A B ′′剪开,展平在一张平面上,得到一个11A B B A ′′,而多边形W 的周界展开后便成为一条与1A A ′平行的线段(如题10解析图中1E E ′),显然11E E A A =′′,故l 为定值.正确选项为B .A 1E 1B 1D 'DC BB'E'A'题10解析图11.如图9-20,长方体1111ABCD A B C D -,AB a =,BC b =,1A A c =,E 为11D C 中点,若平面11A BC 与平面ACE 所成二面角的平面角为θ,则sin θ=__________.cbaD ABC ED 1C 1B 1A 1图920解:sin θ=.12.如图9-21,已知直三棱柱111ABC A B C -的底面为直角三角形,906ACB AC ∠=︒=,,1BC CC P ==是1BC 上一动点.求1CP PA +的最小值.C 1B 1A 1PCB A图921解:将直三棱柱111ABC A B C -侧面展开可得:d =.13.设棱台的两底面积分别为S 、S ′,它的中截面的面积为0S,求证:=.证明:如题13解析图所示,因为棱台的中截面与两底面平行,所以多边形ABCDE ,00000A B C D E A B C D E ,′′′′′相似,因此2222000000S AB S A B S A B S A B ==,′′′,0000AB A BA B A B ==′′. 题13解析图D 0C 0B 0A 0E 0B'D 'C 'E'A'EDBA两式相加,又因为00A B 是梯形ABB A ′′的中位线,00000022A B AB A B A B A B +===,′′故.14.已知四棱锥P ABCD -的底面ABCD 为等腰梯形,AB DC ∥,AC BD ⊥,AC 与BD 相交于点O ,且顶点P 在底面上的射影恰为O 点,又2BO =,PO =,PB PD ⊥. (1)求异面直线PD 与BC 所成角的余弦值.(2)求二面角P AB C --的大小. (3)设点M 在棱PC 上,且PMMCλ=,问λ为何值时,PC ⊥平面BMD . 解:(1)21PO BO DO DO =⋅=,,取AB 中点E ,连DE ,故DE BC ∥,连PE ,故PDE ∠(或其补角)为异面直线PD 与BC所成角,PD =DE BC ==2PE =,则222cos 2PD DE PE PDE PD DE +-∠==⋅ (2)连OE ,PE ,可证得OE AB ⊥,PE AB ⊥,则PEO ∠为二面角P AB C --的平面角,sin PO PEO PE ∠==π4PEO ∠=. (3)222cos 2PB PC BC PB PC BC BPC PB PC +-===∠=⋅ 若PC ⊥面BMD ,则PC BM ⊥,则cos PM PB BPC MC =⋅∠==则2PMMC=.9.2 简单多面体与欧拉定理1.已知:一个简单多面体的各个顶点都有三条棱,求证:2-4V F =. 证明:由于每个定点都有三条棱,而每条棱有两个顶点,则32E V =,代入欧拉公式得322V F V +-=,即24V F =-.2.是否存在七条棱的简单多面体?解:假设存在七条棱的简单多面体,由欧拉定理可得:279F V +=+= (*)因为多面体至少四个面,至少四个顶点,即4F ,4V ,故(F ,V )只可能为(4,5)或(5,4), 我们考虑最简单的多面体——四面体。
2 华东师范大学第二附属中学(创新班和理科班用)数学(高中上册)-2
第二章 不等式Inequality§2.1不等式的性质1.两个实数a 与b 之间的大小关系 ().a b a b a b a b a b a b 1->⇔>⎧⎪2-=0⇔=⎨⎪3->0⇔<⎩();(); 若a 、b +∈R ,则()()().aa b b aa b b aa b b ⎧4>1⇔>⎪⎪⎪5=1⇔=⎨⎪⎪6<1⇔<⎪⎩;;2.不等式的性质 (1)(对称性或反身性)a b b a >⇔<; (2)(传递性)a b b c a c >>⇒>,;(3)(可加性)a b a c b c >⇒+>+,此法则又称为移项法则; (同向可相加)a b c d a c b d >>⇒+>+,; (4)(可乘性)a b c ac bc >>0⇒>,;a b >,c ac bc <0⇒<; (正数同向可相乘)a b c d ac bd >>0>>0⇒>,; (5)(乘方法则)()n n a b n a b >>0∈⇔>>0N ; (6)(开方法则)()a b o n n >>∈2⇔>0N ,≥;(7)(倒数法则)a b ab a b11>>0⇒<,. 我们证明性质(4)如果a b >,且c >0,那么ac bc >;如果a b >,且c <0,那么ac bc <. 证明:()ac bc a b c -=-. .a b a b >∴->0,根据同号相乘得正,异号相乘得负,得 当c >0时,()a b c ->0,即ac bc >; 当c <0时,()a b c -<0,即ac bc <.由性质(4),又可以得到:推论:如果a b >>0,且c d >>0,那么ac bd >.(同学们可以自己证明)很明显,这一推论可以推广到任意有限个两边都是正数的同向不等式两边分别相乘,这就是说,两个或者更多个两边都是正数的同向不等式两边分别相乘,所得不等式与原不等式同向,由此,我们还可以得到:如果a b >>0,那么()n n a b n n >∈2N ,且≥. 例1.设()f x ax bx 2=+,且()()f f 1-12214,≤≤≤≤,求()f -2的取值范围.解:因()()f a b f a b 1-1=-221=+4,,≤≤≤≤为 所以()()f f a 3-1+1=26,≤≤ 又()f a b a b a -2=4-2=2-2+2, 所以()f 5-210≤≤.例2.已知二次函数()f x ax bx c 2=++的图像过点()-10,,问是否存在常数a b c ,,,使不等式()()x f x x 21+1≤≤2对一切x ∈R 都成立? 解:假设存在常数a b c ,,,满足题意, ()f x 的图像过点()-10,, ()f a b c ∴-1=-+=0又不等式()()x f x x 211+2≤≤对一切x ∈R 都成立, ∴当x =1时,()()f 21111+12≤≤,即a b c 1++1≤≤, a b c ∴++=1由①②可得:a c b 11+==22,,()f x ax x a 211⎛⎫∴=++- ⎪22⎝⎭,由()()x f x x 211+2≤≤对一切x ∈R 都成立得:()x ax x a x 22111⎛⎫++-1+ ⎪222⎝⎭≤≤恒成立, ()ax x a a x x a 22⎧11⎛⎫-+-0 ⎪⎪22∴⎝⎭⎨⎪2-1+-20⎩≥≤的解集为R , a a a >0⎧⎪∴11⎨⎛⎫-4-0 ⎪⎪42⎝⎭⎩≤且()a a a 2-1<0⎧⎪⎨1+82-10⎪⎩≤, 即()a a 2>0⎧⎪⎨1-40⎪⎩≤且()a a 21⎧<⎪2⎨⎪1-40⎩≤, a c 11∴=∴=44,,∴存在常数a b c 111===424,,使不等式()()x f x x 211+2≤≤对一切x ∈R 都成立. 例3.已知()()f x x a x 2=+2-2+4,(1)如果对一切()x f x ∈>0R ,恒成立,求实数a 的取值范围; (2)如果对[]()x f x ∈-31>0,,恒成立,求实数a 的取值范围. 解:(1)()a a 2∆=4-2-16<0⇒0<<4;(2)()()a f ⎧--2<-3⎪⎨-3>0⎪⎩或()a ⎧-3--21⎪⎨∆<0⎪⎩≤≤或()()a f ⎧--2>1⎪⎨1>0⎪⎩,解得a ∈∅或a 1<4≤或a 1-<<12,∴a 的取值范围为1⎛⎫-4 ⎪2⎝⎭,.基础练习1.判断下列命题是否成立,并说明理由. (1)如果a b c d ><,,那么a c b d +>+; (2)如果a b c d >>,,那么a c b d -2>-2; (3)如果a b c d >>,,那么ac bd >. 2.对于实数a b c ,,中,判断下列命题的真假: ①若a b >,则ac bc 22>; ②若ac bc 22>,则a b >;③若a b <<0,则a ab b 22>>;④若a b <<0,则a b 11<;⑤若a b <<0,则b a a b>; ⑥若a b <<0,则a b >; ⑦若c a b >>>0,则a bc a c b>--; ⑧若a b a b11>>,,则a b >0<0,.3.设n >-1,且n ≠1,则n 3+1与n n 2+的大小关系是________. 4.比较下列两个数的大小:(1与2(2)2(3)从以上两小题的结论中,你能否得出更一般的结论?并加以证明. 5.已知()()()f x ax c f f 2=--41-1-125,,≤≤≤≤,求()f 3的取值范围. 能力提高6.若不等式()()a x a x 2-2+2-2-4<0对一切x ∈R 成立,求a 的取值范围. 7.若关于x 的方程x ax a 22++-1=0有一正根和一负根,求a 的取值范围.8.关于x 的方程()m x m x 2-3+3=的解为不大于2的实数,求m 的取值范围.9.已知6枝玫瑰花与3枝康乃馨的价格之和大于24元,4枝玫瑰花与5枝康乃馨的价格和小于22元,则2枝玫瑰花的价格和3枝康乃馨的价格比较结果是( ) A .2枝玫瑰花价格高; B .3枝康乃馨价格高; C .价格相同; D .不确定.§2.2一元二次不等式及其解法求不等式的解集叫做解不等式,如果两个不等式的解集相等,那么这两个不等式就叫做同解不等式,一个不等式变形为另一个不等式时,如果这两个不等式是同解不等式,那么这种变形叫做不等式的同解变形.像x x 2-5<0这样,只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式. 下面,我们来探究一元二次不等式x x 2-5<0的解集: (1)探究二次方程的根与二次函数的零点的关系: 容易知道:二次方程有两个实数根:x x 12=0=5, 二次函数有两个零点:x x 12=0=5,于是,我们得到:二次方程的根就是二次函数的零点. (2)观察图像,获得解集画出二次函数y x x 2=-5的图像,如图2-1,观察函数图像,可知:x图2-1当x <0,或x >5时,函数图像位于x 轴上方,此时,y >0,即x x 2-5>0; 当x 0<<5时,函数图像位于x 轴下方,此时,y <0,即x x 2-5<0; 所以,不等式x x 2-5<0的解集是{}|x x 0<<5. 探究一般的一元二次不筹式的解法任意的一元二次不等式,总可以化为以下两种形式: ()ax bx c a 2++>0>0,或()ax bx c a 2++<0>0,一般地,怎样确定一元二次不等式ax bx c 2++>0与ax bx c 2++<0的解集呢?从上面的例子出发,可以归纳出确定一元二次不等式的解集,关键要考虑以下两点:(1)抛物线y ax bx c 2=++与x 轴的相关位置的情况,也就是一元二次方程ax bx c 2++=0的根的情况;(2)抛物线y ax bx c 2=++的开口方向,也就是a 的符号. 总结结果:(1)抛物线()y ax bx c a 2=++>0与x 轴的相关位置,分为三种情况,这可以由一元二次方程ax bx c 2++=0的判别式b ac 2∆=-4三种取值情况(∆>0∆=0∆<0,,)来确定.因此,要分二种情况讨论;(2)a <0可以转化为a >0,分∆>0∆=0∆<0,,三种情况,得到一元二次不等式ax bx c 2++>0与ax bx c 2++<0的解集.一元二次不等式ax bx c 2++>0或()ax bx c a 2++<0≠0的解集;设相就的一元二次方程()ax bx c a 2++=0≠0的两根为x 1、x 2且x x 12≤,b ac 2∆=-4,则不等式的解不等式的解集经常用区间来表示.区间是指介于某两个实数之间的全体实数,这两个实数叫做区间的端点. a b ∀∈R ,,且a b <.{}|x a x b <<称为开区间,记为;()a b ,; {}|x a x b ≤≤称为闭区间,记为[]a b ,; {}|x a x b <≤称为左闭右开区间,记为[)a b ,;{}|x a x b <≤,称为左开右闭区间,记为(]a b ,.以上都是有限区间,以下是无限区间:[){}|a x x a +∞=,≥、(){}|a x x a +∞=>,、(]{}|a x x a -∞=,≤、(){}|b x x b -∞=<,、实数集()=-∞+∞R ,,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”.区间长度的定义:两端点间的距离(线段的长度)称为区间的长度. 例1.解不等式x x 2-+2-3>0.解:整理,得x x 2-2+3<0.因为∆<0,方程x x 2-2+3=0无实数解, 所以不等式x x 2-2+3<0的解集是∅.从而,原不等式的解集是∅. 例2.已知{}|A x x x 2=-3+20≤,(){}|B x x a x a 2=-+1+0≤, (1)若AB ,求a 的取值范围;(2)若B A ⊆,求a 的取值范围. 解:{}|A x x =12,≤≤当a >1时,{}|B x x a =1≤≤;当a =1时,{}B =1;当a <1时,{}|B x a x =1≤≤.(1)若AB ,则a a a >1⎧⇒>2⎨>2⎩;(2)若B A ⊆,当a =1时,满足题意;当a >1时,a 2≤,此时a 1<2≤;当a <1时,不合题意. 所以,a 的取值范围为[)12,.例3.已知关于x 的不等式()()kx k x 2--4-4>0,其中k ∈R .(1)当k 变化时,试求不等式的解集A ;(2)对于不等式的解集A ,若满足A Z B =(其中Z 为整数集).试探究集合B 能否为有限集?若能,求出使得集合B 中元素个数最少的k 的所有取值,并用列举法表示集合B ;若不能,请说明理由. 解:(1)当k =0时,()A =-∞4,;当k >0且k ≠2时,()A k k 4⎛⎫=-∞4++∞ ⎪⎝⎭,,;当k =2时,()()A =-∞44+∞,,;(不单独分析k =2时的情况不扣分) 当k <0时,A k k 4⎛⎫=+4 ⎪⎝⎭,.(2)由(1)知:当k ≥0时,集合B 中的元素的个数无限; 当k <0时,集合B 中的元素的个数有限,此时集合B 为有限集.因为k k4+-4≤时取等号当且仅当k =-2时取等号,所以当k =-2时,集合B 的元素个数最少. 此时()A =-44,,故集合()B =-3-2-10123,,,,,,.例4,已知a 为实数,关于x 的二次方程()()x a x a a 227-+13+--2=0有两个实根分布在()()0112,,,上,求a 的取值范围.解:令()()()f x x a x a a 22=7-+13+--2,由二次函数图像知 ()()().f f f 0>0⎧⎪1<0⎨⎪2>0⎩,,即.a a a a a 222⎧--2>0⎪-2-8<0⎨⎪-3>0⎩,, 解得a -2<<-1或a 3<<4. 所以a 范围是()()-2-134,,.基础练习1.设a b c a b c 111222,,,,,均为非零实数,不等式a x b x c 2111++>0,a x b x c 2222++>0的解集分别是集合M N ,,则a b c a b c 111222==是“M N =”的充要条件对吗? 2.已知不等式ax bx c 2++>0的解集为{}|x x 2<<4,求不等式cx bx a 2++<0的解集. 3.不等式()ax ab x b 2++1+>0的解是x 1<<2,求a b ,的值. 4.若不等式x kx 2-+-4<0的解集为R ,求实数k 的取值范围. 5.已知不等式ax x 2-3+6>4的解集为{}|x x x b <1>或. (1)求a 、b ; (2)解不等式x cax b->0-(c 为常数). 能力提高6.若关于m 的不等式()mx m x m 2-2+1+-10≥的解集为空集,求m 的取值范围. 7.已知不等式组x x a a x a 22⎧-+-<0⎨+2>1⎩的整数解恰好有两个,求a 的取值范围.8.已知()f x ax bx c 2=++在[]01,上满足()f x 1≤,试求a b c ++最大值.§2.3分式不等式像x x 16<-1-1这样,只含有一个未知数,并且分母含未知数的不等式,称为分式不等式,解分式不等式,关键是将它变为整式不等式去解,其一般特征为: 分式不等式()()f xg x >0(或0≥)或()()f xg x <0(或0≤)要正确运用以下同解原理.(1)()()f xg x ≥0(或<0)与()()f x g x ⋅>0(或<0)同解.(2)()()f x g x 0≥(或0≤)与不等式组()()()f x g x g x ⎧⋅0⎪⎨≠0⎪⎩≥()()()f x g x g x ⎛⎫⎧⋅0⎪ ⎪⎨ ⎪≠0⎪⎩⎝⎭或≤同解. 例1.解不等式x x x x 22-9+117-2+1≥.解:移项,通分得x x x x 22-6+5+40-2+1≥,()()()x x x 22+13-4∴0-1≤ 转化为()()()()x x x x 22⎧2+13-4-10⎪⎨-1≠0⎪⎩,,≤ ()()x x x ⎧2+13-40⎪∴⎨-1≠0⎪⎩,,≤ 则所求不等式的解集为x x x ⎧14⎫-<11<⎨⎬23⎩⎭或≤≤.例2.解关于x 的不等式()x a x x ax222+-1+3>1+.解:原不等式等价于x x x ax22-+3>0+.由于x x 2-+3>0对x ∈R 恒成立, ∴x ax 2+>0,即()x x a +>0当a >0时,{}|x x a x <->0或; 当a =0,{}|x x x ∈≠0R 且; 当a <0时,{}|x x x a <0>-或.例3.k 为何值时,下式恒成立:x kx kx x 322+2+<14+6+3.解:原不等式可化为:()()x k x k x x 222+6-2+3->04+6+3,而x x 24+6+3>0,∴原不等式等价于()()x k x k 22+6-2+3->0,由()()k k 2∆=6-2-4⨯2⨯3-<0得k 1<<3. 基础练习1.解下列不等式:(1)x x x x 22-3+2<0-2-3;(2)x x -30-2≥; (3)x x1>; (4)()()x x x x 232-2≥+1>0++1;(5)x x x x 2215-11+2<0-2+3+2.2.已知关于x 的不等式k x bx a x c++<0++的解集为()()-2-123,,,求关于x 的不等式kx bx ax cx -1+<0-1-1的解集. 3.若a b c >>,a 、b 、c 为常数,求关于x 的不等式()()()x a x c x b 2-->0-的解集. 4.解不等式x x x x 1111+>++4+5+6+3. 5.若不等式x ax x 2+0+4+3≥的解集为{}|x x x -3<<-12或≥,求实数a 的值.6.若m n >>0,求关于x 的不等式()()mx n x x --20-1≥解集.§2.4 高次不等式像x x x 22+3>2+6这样,只含有一个未知数,并且未知数的次数高于两次的不等式称为高次不等式. 我们研究()()()()x x x x -1+1-2-3<0的解,此不等式的左端是关于x 的高次不等式,已不能用一元二次不等式解法求解,首先解方程()()()()x x x x -1+1-2-3=0得x 的四个解分别为1,-1,2,3.然后将x 的取值分成5段,使得四个因式x x x x -1+1-2-3,,,的积为负的范围就是所求的解集. 列表:借助于数轴并根据积的符号法则表示为图2-2.图2-2由图可知:原不等式的解集为()()23-11,,. 此方法为“数轴标根法”也可以叫“串线法”,高次不等式常常用“数轴标根法”来解,其步骤是: ①等价变形后的不等式一边是零,一边是各因式的积.(未知数系数一定为正数) ②把各因式的根标在数轴上. ③用曲线穿根,(奇次根穿透,偶次根不穿透)看图像写出解集. 例1.解不等式x x x 32+3>2+6.解:原不等式化为()(x x x +3>0∴原不等式的解为x x -3<<例2.解不等式:()()()()x x x x x 2+1-20-3-5≤.解:原不等式等价于()()()x x x x -20-3-5≤或x =-1.标根(见图2-3);图2-3解集为[](){}0235-1,,.基础练习1.解不等式x x x 32+3>2+6.2.解不等式()()x x x x 22-4-5++2<0. 3.解不等式()()()()x x x x 23+2-1+1-2<0. 能力提高4.对于一切x 1⎡⎤∈-2⎢⎥2⎣⎦,,不等式ax x x 32-++10≥恒成立,求实数a 的取值范围.5.设P x x x x 432=+6+11+3+31,求使P 为完全平方数的整数x 的值.6.已知x y a x y b c >0>0=+==,,,,问是否存在正数m 使得对于任意正数x y ,可使a b c ,,为三角形的三边构成三角形,如果存在,求出m 的值,如果不存在,请说明理由. 7.已知函数()()x k k x f x x x 42242++2-4+4=+2+4的最小值是0,求非零实数k 的值.§2.5无理不等式像x 3-不等式,关键是把它同解变形为有理不等式组.无理不等式一般有如下几种形式:>()()()()f xg x f x g x ⎧0⎫⎪⇒⎪⎬⎪⇔0⎨⎪⎭⎪>⎪⎩定义域≥≥例1>0. 解:根式有意义∴必须有:x x x 3-40⎧⇒3⎨-30⎩≥≥≥又有x -3 x -3解之:x 1>2∴{}{}|x x x x x x ⎧1⎫>3>=>3⎨⎬2⎩⎭>()()()()f x g x f x g x 2⎧0⎪⎪⇔0⎨⎪>⎡⎤⎪⎣⎦⎩≥≥或()()fx g x ⎧0⎪⎨<0⎪⎩≥ 例2x >4-3.解:原不等式等价于下列两个不等式组得解集的并集: Ⅰ:()x x x x x x 222⎧4-30⎪⎪-+3-20⎨⎪-+3-2>4-3⎪⎩≥≥ Ⅱ:x x x 2⎧-+3-20⎨4-3<0⎩≥解Ⅰ:x x x x 4⎧⎪3⎪64⎪12⇒<⎨53⎪⎪63<<⎪52⎩≤≤≤≤ 解Ⅱ:x 4<23≤∴原不等式的解集为xx ⎧6⎫<2⎨⎬5⎩⎭≤.()()()()()f x g x g x f x g x 2⎧0⎪⎪⇔>0⎨⎪<⎡⎤⎪⎣⎦⎩型≥例3x +2. 解:原不等式等价于()x x x x x x 222⎧2-6+4⎪⎪+2>0⎨⎪2-6+4<+2⎪⎩≥0x x x x 21⎧⎪⇒>-2⎨⎪0<<10⎩或≥≤{}|x x x ⇒2<100<1或≤≤ 例4>.解:要使不等式有意义必须:x x x x x 1⎧2+10-⎧1⎪⇒⇒-2⎨⎨+102⎩⎪-1⎩≥≥≥≥≥.>)22∴>,即()x >-+1.x +10≥,∴不等式的解为x 2+10≥ 即x 1≥-2.基础练习1.解下列不等式:(1(2)x x 3-3+3 (3(4)(x -10. 2>3. 3>. 4>1.5.满足x 3-x 的集合为A ;满足()x a x a 2-+1+0≤的x 的集合为B . (1)若A B ⊂,求a 的取值范围; (2)若A B ⊇,求a 的取值范围;(3)若A B 为仅含一个元素的集合,求a 的值. 6.求不等式()x x 224<2+9的解集.7.求使关于x k 有解的实数k 的最大值. §2.6 绝对值不等式1.含有绝对值不等式有以下两种基本形式:(1)()x a a a x a <>0⇔-≤≤(()x a a a x a >0⇔-≤≤≤), (2)()x a a x a x a >>0⇔><-或(()x a a x a x a >0⇔-或≥≥≤). 2.解绝对值不等式的关键在于去掉绝对值的符号,一般有以下方法: (1)定义法;(2)零点分段法:通常适用于含有两个及两个以上的绝对值符号的不等式; (3)平方法:通常适用于两端均为非负实数时(比如()()f x g x <); (4)图像法或数形结合法. 例1.解不等式x x 2-5+5<1.解法一:利用不等式()x a a <>0的解集是{}|x a x a -<<和整体的思想()()f x f x <1⇔-1<<1,因此,这个不等式可化为x x x x 22⎧-5+5<1⎪⎨-5+5>-1⎪⎩ ①②解不等式①得解集{}|x x 1<<4 解不等式②得解集{}|x x x <2>3或∴原不等式的解集是不等式①和不等式②的解集的交集,即解集为{}|x x x 1<<23<<4或解法二:平方去绝对值.原不等式可化为:()()xx x x 22-5+6-5+4<0,即()()()()x x x x -2-3-4-1<0 利用“数轴标根法”(见图2-4),图2-4∴原不等式的解集是{}|x x x 1<<23<<4或.例2.解关于x 的不等式()x m m 2-1<2-1∈R .解:若m 2-10≤,即m 12≤,则x m 2-1<2-1恒不成立,此时原不等式无解;若m 2-1>0,即m 1>2,则()m x m -2-1<2-1<2-1,所以m x m 1-<<. 综上,当m 12≤时,原不等式的解集为∅;当m 1>2时,原不等式解集为{}|x m x m 1-<<. 例3.解下列不等式: (1)x 4<2-37≤; (2)x x -2<+1; (3)x x 2+1+-2>4.解:(1)原不等式可化为x 4<2-3≤7或x 2-3<-4-7≤,∴原不等式解集为17⎡⎫⎛⎤-2-5⎪ ⎢⎥22⎣⎭⎝⎦,,.(2)原不等式可化为()()x x 22-2<+1,即x 1>2, ∴原不等式解集为1⎛⎫+∞ ⎪2⎝⎭,.(3)当x 1-2≤时,原不等式可化为x x -2-1+2->4,x ∴<-1,此时x ∴<-1;当x 1-<<22时,原不等式可化为x x 2+1+2->4,∴x >1,此时x 1<<2;当x 2≥时,原不等式可化为x x 2+1+-2>4, ∴x 5>3,此时x 2≥. 综上可得:原不等式的解集为()()-∞-11+∞,,.例4.某段城铁线路上依次有A 、B 、C 三站,km AB =5,km BC =3,在列车运行时刻表上,规定列车8时整从A 站发车,8时07分到达B 站并停车1分钟,8时12分到达C 站,在实际运行中,假设列车从A 站正点发车,在B 站停留1分钟,并在行驶时以同一速度km/h v 匀速行驶,列车从A 站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差. (1)分别写出列车在B 、C 两站的运行误差;(2)若要求列车在B 、C 两站的运行误差之和不超过2分钟,求v 的取值范围. 解:(1)列车在B 、C 两站的运行误差(单位:分钟)分别是 v 300-7和v 480-11 (2)由于列车在B 、C 两站的运行误差之和不超过2分钟,所以 v v 300480-7+-112≤ 当v 3000<7≤时,①式变形为v v300480-7+-112≤,解得v 300397≤≤. 当v 300480<711≤时,①式变形为v v 3004807-+-112≤,解得v 300480<711≤. 当v 480>11时,①式变形为v v3004807-+11-2≤, 解得v 480195<114≤. 综上所述,v 的取值范围是195⎡⎤39⎢⎥4⎣⎦,.基础练习1.解不等式x x x 2-1<++1.2.已知{}|A x x a =2-3<,{}|B x x =10≤,且A B ,求实数a 的取值范围.3.求不等式x x 3+14+2>5的解集. 4.求不等式x x -1+-5<7的解集.5.(1)对任意实数x x x a +1+-2>,恒成立,求a 的取值范围. (2)对任意实数x x x a -1-+3<,恒成立,求a 的取值范围.能力提高6.在一条公路上,每隔km 100有个仓库(如图2-5),共有5个仓库,一号仓库存有10t 货物,二号仓库存20t ,五号仓库存40t ,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输1km 需要0.5元运输费,那么最少要多少运费才行?五四三二一图2-57.若关于x 的不等式x x a -4++3<的解集不是空集,求a 的范围.§2.7绝对值的不等式的性质 定理:a b a b a b -++≤≤证明:()a a a a b a b a b b b b ⎫-⎪⇒-+++⎬-⎪⎭≤≤≤≤≤≤a b a b ⇒++≤ ①又a a b b =+- b b -=由①a a b b a b b =+-++-≤ 即 a b a b -+≤ ② 综合①②:a b a b a b -++≤≤.注意:1︒左边可以“加强”同样成立,即a b a b a b -++≤≤.2︒这个不等式俗称“三角不等式”——三角形中两边之和大于第三边,两边之差小于第三边.3︒a b ,同号时右边取“=”,a b ,异号时左边取“=”. 推论1.n n a a a a a a 1212++++++……≤. 推论2.a b a b a b --+≤≤. 证明:在定理中以b -代b 得:()()a b a b a b a b --+-+-+-≤≤≤,即a b a b a b --+≤≤.例1.设a b <1<1,,求证a b a b ++-<2.证明:当a b +与a b -同号时,a b a b a b a b a ++-=++-=2<2; 当a b +与a b -异号时,()a b a b a b a b b ++-=+--=2<2. a b a b ∴++-<2.例2.已知()f x a b ≠时,求证:()()f a f b a b -<-. 证明:()()f a f b -===()()a b a b a b a b a ba b+-+-=++≤a b =-.基础练习1.ab >0,则①a b a +> ②a b b +< ③a b a b +<- ④a b a b +>-四个式中正确的是( ) A.①②B.②③C.①④D.②④2.x 为实数,且x x m -5+-3<有解,则m 的取值范围是( )A.m >1B.m 1≥C.m >2D.m 2≥ 3.不等式a b a b+1+≤成立的充要条件是( )A.ab ≠0B.a b 22+≠0C.ab >0D.ab <04.已知a b ≠,a b a b m n a ba b-+==-+,,那么m 、n 之间的大小关系为( )A.m n >B.m n <C.m n =D.m n ≤能力提高5.已知()()f x x ax b a b 2=++∈R ,,求证:()()()f f f 1+22+32≥. 6.实数x 1、x 2、…、x 2007∈R ,满足x x x x x x 213220072008-+-++-=2007…,设kk x x x y k12+++=…,k =123,,…,2007.求y y y y y y 213220072006-+-++-…的最大值.§2.8 含字母系数的不等式像()ax a x 2-+1+1<0这样,只含有两个或两个以上的未知数的不等式,称为含字母系数的不等式.解不等式时,对字母的取值要进行恰当的分类,分类时要不重、不漏,然后根据分类进行求解. 例1.解关于x 的不等式()ax a x 2-+1+1<0其中a >0 解:由一元二次方程()ax a x 2-+1+1<0的根为x x a121-1=,知 (1)当a1>1,即a 0<<1时二次函数()y ax a x 2=-+1+1的草图为图2-6: 故原不等式的解为a 1⎛⎫1 ⎪⎝⎭,.图2-6(2)a10<<1,即a >1时二次函数()y ax a x 2=-+1+1的草图为图2-7:图2-7故原不等式的解为a 1⎛⎫1 ⎪⎝⎭,. (3)a1=1,即a =1时二次函数()y ax a x 2=-+1+1的草图为图2-8:故原不等式的解为∅.图2-8综上,当a 0<<1时原不等式的解集为a 1⎛⎫1 ⎪⎝⎭,;当a >1时原不等式解集为a 1⎛⎫1 ⎪⎝⎭,;当a =1时原不等式解集∅.例2.解关于x 的不等式()x x a a 2---1>0. 解:原不等式可以化为:()()x a x a +-1->0. 若()a a >--1即a 1>2,则x a >或x a <1-. 若()a a =--1即a 1=2,则x x x 211⎛⎫->0⇒≠∈ ⎪22⎝⎭R ,.若()a a <--1即a 1<2,则x a <或x a >1-. 例3.关于x 的不等式()ax a x a 2+-1+-1<0对于x ∈R 恒成立,求a 的取值范围. 解:当a >0时不合题意,a =0也不合题意,必有:()()a a a a a a a 22<0⎧<0⎧⎪⇒⎨⎨3-2-1>0∆=-1-4-1<0⎪⎩⎩()()a a a a <0⎧1⎪⇒⇒<-⎨3+1-1>03⎪⎩.例4.解不等式:aa x >1--2. 解:原不等式可化为:()()a x a x -1+2->0-2,即()()()a x a x -1+2--2>0⎡⎤⎣⎦.当a >1时,原不等式与()a x x a -2⎛⎫--2>0 ⎪-1⎝⎭同解.若a a -22-1≥,即a 0<1≤时,原不等式无解:若a a -2<2-1,即a <0或a >1, 于是a >1时,原不等式的解为()a a -2⎛⎫-∞2+∞ ⎪-1⎝⎭,,.当a <1时,若a <0,解集为a a -2⎛⎫2 ⎪-1⎝⎭,;若a 0<<1,解集为a a -2⎛⎫2 ⎪-1⎝⎭,. 综上所述:当a >1时,解集为()a a -2⎛⎫-∞2+∞ ⎪-1⎝⎭,,;当a 0<<1时,解集为a a -2⎛⎫2 ⎪-1⎝⎭,; 当a =0时,解集为∅;当a <0时,解集为a a -2⎛⎫2 ⎪-1⎝⎭,.基础练习1.设a b >0>0,,解关于x 的不等式ax bx -2≥.2.解关于x 的不等式:()()x a x x x 22-+1+1>1-1(其中a >1).3.解关于x 的不等式:()m x x 2+1-4+10≤()m ∈R . 4.解关于x 的不等式:ax x x 2-1>0--2.5.关于x 的不等式()()()m x m x m 2+1-2-1+3-1<0的解是一切实数,求实数m 的取值范围. 能力提高6.设m m ∈≠0R ,,解关于x 的不等式x m x m m m 211⎛⎫-++-<0 ⎪⎝⎭.7.设不等式()()x m x 22-1>-1对满足m 2≤的一切实数m 的值都成立,求x 的取值范围. 8.若关于x 的不等式ax +2<6的解休是()-12,,求不等式xax 1+2≤的解集. 9.设不等式x ax a 2-2++20≤的解集为M ,如果[]M ⊆14,,求实数a 的取值范围. 10.已知不等式xy ax y 22+2≤对于[][]x y ∈12∈23,,,恒成立,求a 的取值范围. §2.9基本不等式及其应用图2-9是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客,你能在这个图案中找出一些相等关系或不等关系吗?图2-9将图中的“风车”抽象成如图2-10,在正方形ABCD 中有个全等的直角三角形.设直角三角形的两条直角边长为a b ,.这样,4个直角三角形的面积的和是ab 2,正方形的面积为a b 22+.由于4个直角三角形的面积小于正方形的面积,我们就得到了一个不等式:a b ab 22+2≥.当直角三角形变为等腰直角三角形,即a b =时,正方形EFGH 缩为一个点,这时有a b ab 22+=2. 定理1(基本不等式1):C图2-10一般的,如果a b ∈R ,,那么a b ab 22+2≥(当且仅当a b =时取“=”号) 证明:因为()a b ab a b 222+-2=-当a b ≠时,()a b 2->0,当a b =时,()a b 2-=0, 所以,()a b 2-0≥,即a b ab 22+2≥.特别的,如果a b >0>0,,我们用分别代替a 、b,可得a b +≥()a ba b +>0>02, 通常我们称a b+2为a 、ba 、b 的几何平均数. 例1.已知x 、y 都是正数,求证: (1)y xx y+2≥; (2)()()()x y x y xy x y 223333+++8≥.证明:x y ,都是正数x yx y x y y x2233∴>0>0>0>0>0>0,,,,, (1)x y y x +=2≥即x yy x+2≥. (2)x y x y x y 2233+0+0+0,,≥≥≥()()()x y x y x y x y 223333∴+++=8≥ 即()()()x y x y xy x y 223333+++8≥.说明:在运用定理:a b+2时,注意条件a 、b 均为正数,结合不等式的性质(把握好每条性质成立的条件),进行变形. 例2.(1)用篱笆围成一个面积为2m 100的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短,最短的篱笆是多少?(2)段长为m 36的篱笆围成一个一边靠墙的矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?解:(1)设矩形菜园的长为m x ,宽为m y ,则xy =100,篱笆的长为()m x y 2+.由x y+2x y +≥()x y 2+40≥.等号当且仅当x y =时成立,此时x y ==10.因此,这个矩形的长、宽都为m 10时,所用的篱笆最短,最短的篱笆是40m .(2)设矩形菜园的宽为m x ,则长为()m x 36-2,其中0x <<18, 其面积()()x x S x x x x 22112+36-236⎛⎫=36-2=⋅236-2=⎪2228⎝⎭≤ 当且仅当x x 2=36-2,即x =9时菜园面积最大,即菜园长m 18,宽为9m 时菜园面积最大为2162m . 归纳:1.两个正数的和为定值时,它们的积有最大值,即若a b +∈R ,,且a b M +=,M 为定值,则M ab 24≤,等号当且仅当a b =时成立.2.两个正数的积为定值时,它们的和有最小值,即若a b +∈R ,,且ab P =,P 为定值,则a b +≥,等号当且仅当a b =时成立.定理2(基本不等式2):如果a b c +∈R ,,,那么a b c abc 333++3≥(当且仅当a b c ==时取“=”)证明: ()a b c abc a b c a b ab abc 3333322++-3=++-3-3-3 ()()()()a b c a b a b c c ab a b c 22⎡⎤=+++-++-3++⎣⎦()a b c a ab b ac bc c ab 222⎡⎤=+++2+--+-3⎣⎦()()a b c a b c ab bc ca 222=++++---()()()()a b c a b b c c a 2221⎡⎤=++-+-+-⎣⎦2. a b c ∈+R ,,, ∴上式0≥.从而a b c abc 333++3≥.推论:如果a b c ∈+R ,,,那么a b c ++3a b c ==时取“=”)证明:a b c 333++++≥≥a b c++⇒3由此推出:a b c abc 3++⎛⎫⎪3⎝⎭≥.例3.求证:(1)()a b c a b c 111⎛⎫++++ ⎪⎝⎭≥9;(2)a b c b c a b c a a b c ⎛⎫⎛⎫++++9 ⎪⎪⎝⎭⎝⎭≥.证明:(1) a b c ,,都是正数a b c a b c ++111∴>0++>03,≥ ()a b c a b c 111⎛⎫∴++++=9 ⎪⎝⎭≥.(2)a b c ,,都是正数a b c b c a ∴++=3≥,b c a a b c ++3≥. a b c b c a b c a a b c ⎛⎫⎛⎫∴++++9 ⎪⎪⎝⎭⎝⎭≥. 例4.一根水平放置的长方体形枕木的安全负荷与它的宽度a 成正比,与它的厚度d 的平正比,与它的长度l 的平方成反比,见图2-11.lda图2-11(1)将此枕木翻转90︒(即宽度变为了厚度),枕木的安全负荷变大吗?为什么?(2)现有一根横断面为半圆(半圆的半径为R )的木材,用它来成长方体形的枕木,木材长度即为枕木规定的长度,问如何截取,可使安全负荷最大?解:(1)由题可设安全负荷ad y k l 212=⋅(k 为正常数),则翻转90︒后,安全负荷da y k l 222=⋅.因为y dy a 12=,所以,当d a 0<<时,y y 12<,安全负荷变大;当a d 0<<时,y y 12>,安全负荷变小.(2)如图2-12,设截取的枕木宽为a ,高为d ,则图2-12a d R 222⎛⎫+= ⎪2⎝⎭即a d R 222+4=4 枕木长度不变,u ad 2∴=最大时,安全负荷最大.u d d ∴====当且仅当d R d 222=-2,即取d a ===,时,u 最大,即安全负荷最大. 定理3(基本不等式3) *ni a a a n a R i n n+12+++∈∈1N …,,≤≤.这个结论最终可用数学归纳法,二项式定理证明(这里从略).这里涉及到“平均数”的概念.如果n a a a n +12∈>1R ,,…,,且n +∈N ,则na a a n12+++…叫做这n 做这n 个正数的几何平均数.定理3的语言表述为:n 个正数的算术平均数不小于它们的几何平均数. 基础练习1.已知a 、b 、c 都是正数,求证:()()()a b b c c a abc +++8≥. 2.设a b c +∈R ,,,且ab bc ca ++=108,求ab bc cac a b++的最小值. 3.(1)若x >0,求()f x x x9=4+的最小值; (2)若x <0,求()f x x x9=4+的最大值. 4.(1)若x ≠0,求x x1+的取值范围; (2)若ab =1,求a b +的取值范围; (3)若x 5<4,求x x 14-2+4-5的最大值;(4)若x >2,求x x x 2-3+3-2的最小值;(5)若x y >0,,且x y 19+=1,求x y +的最小值;(6)若x y >0,,x y +=1,求x y41+的最小值;(7)求y 2=y 2=(8)若a b >0,,且ab a b =++3,求ab 的取值范围.5.某工厂要建造一个长方体无盖贮水池,其容积为3m 4800,深为m 3,如果池底每21m 的造价为150元,池壁每2m 1的造价为120元,问怎样设计水池能使总造价最低,最低总造价是多少元?6.某房屋开发公司用100万元购得一块土地,该地可以建造每层m 21000的楼房,楼房的总建筑面积(即各层面积之和)每平方米平均建筑费用与建筑高度有关,楼房每升高一层,整幢楼房每平方米建筑费用提高%5.已知建筑5层楼房时,每平方米建筑费用为400元,公司打算造一幢高于5层的楼房,为了使该楼房每平方米的平均综合费用最低(综合费用是建筑费用与购地费用之和),公司应把楼层建成几层? 能力提高7.用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次....的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药量的12,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上,设用x 单位量的水清冼一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数()f x . (1)试规定()f 0的值,并解释其实际意义;(2)试根据假定写出函数()f x 应该满足的条件和具有的性质;(3)设()f x x 21=1+,现有()a a >0单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.8.设a a a a 11211>-1≠=1+1+,.(1a a 12,之间; (2)a a 12,;(3.9.设常数a b +∈R ,,试探求不等式()ax a b b 2=+-1+>0对任意x >1成立的充要条件. 10.已知集合(){}|D x x x x x x k 121212=>0>0+=,,,(其中k 为正常数). (1)设u x x 12=,求u 的取值范围;(2)求证:当k 1≥时,不等式k x x x x k 22212⎛⎫⎛⎫112⎛⎫--- ⎪⎪ ⎪2⎝⎭⎝⎭⎝⎭≤对任意()x x D 12∈,恒成立;(3)求使不等式k x x x x k 22212⎛⎫⎛⎫112⎛⎫--- ⎪⎪ ⎪2⎝⎭⎝⎭⎝⎭≥对任意()x x D 12∈,恒成立誓k 2的范围.11.已知a b c +∈R ,,,且满足()()kabc a b a b c a b c22++++4++≥,求k 的最小值.§2.10 不等式的证明证明不等式不但用到不等式的性质,不等式证明的技能、技巧,还要注意到横向结合内容方方面面.如与数列、三角函数、函数等相结合,解答时需要综合运用这些知识.不等式的证明,由于题型多变,技巧性强加上无固定程序可循,因此常有一定的难度,解决个困难的出路在于深刻理解不等式证明中应用的数学思维方法和数学思想方法,熟练掌握等式的性质和一些基本不等式.不等式的证明常用方法有:比较法、分析法、综合性、反证法. 1,比较法比较法是证明不等式的常用方法,它有两种基本形式: ①求差比较法,步骤是:作差——变形——判断.变形方向:变为一个常数;或变为平方和形式;或变为因式之积的形式. 这种比较法是普遍适用的,是无条件的.它的理论依据是实数大小关系:a b a b a b a b a b a b ->0⇔>⎧⎪-=0⇔=⎨⎪-<0⇔<⎩应用范围:常用于指(对)数式的比较.这种比较法是有条件的,这个条件就是“除式”的符号一定. 例1.若a b n >0>1,,,则n n n n a b a b ab -1-1++≥ 证明:()()()()n n n n n n a b a b ab a a b b a b -1-1-1-1++=---()()n n a b a b A -1-1=--=.若a b >,则n n a b -1-1>,则A >0; 若a b <,则n n a b -1-1<,则A <0; 若a b =,则A =0. ∴原不等式成立.②求商比较法,步骤是:作商——变形——判断. 做商法是依据当b >0,且ab>1时,则a b >,反之则亦然. 例2.设a b c ,,为正数,证明()a b c a n ca b c abc ++3≥.证明:易知上式是轮换的,不妨设a b c ≥≥. 上式即()a b ca b c a b c abc ++333≥a bb ca ca b c b c a c a b a b c a b a a b c b c c ---222+++⎛⎫⎛⎫⎛⎫=1 ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭≥.∴原不等式成立.比较法是证明不等式最基本,也是最常用的方法之一,它主要有作差或作商,变形,判断三个步骤. 基础练习1.(1)若x >1,求证:x x x31>+-1; (2)若a b ∈R ,,求证:a b ab a b 22+++-1≥;(3)若a b <<0,求证:a b a b a b a b2222++<--;(4)若a b >0>0,,求证:a b b a a b a b ≥. 2.若x y z a b c +∈∈R R ,,,,,,则()b c c a a b x y z xy yz zx a b c222+++++2++≥. 3.若a b c ,,为不全相等的正数,则a b ab b c a c ac abc 22222++++>6. 4.已知ab R +∈,且a b ≠,求证:()()()a b a ab b a b 222222--+<-.2.分析法证明不等式时,有时可以从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题,如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立,这种方法通常叫做分析法,分析法也称逆推法.例3(22>即12+>16+2+即35>19+,即4,即15<16(22>即12+>16+35>19+即35>19+,即4,即15<16例4.已知n ∈N ,求证:n n n n 111111111⎛⎫⎛⎫1++++++++ ⎪ ⎪+1352-12462⎝⎭⎝⎭……≥① 证明:要证明不等式(1),只须证()n n n n 1111111⎛⎫⎛⎫1+++++1++++ ⎪ ⎪352-12462⎝⎭⎝⎭……≥②②式左边即n n n n 111⎛⎫+++++ ⎪22352-1⎝⎭…③ ②式右边即n n n 11111111⎛⎫⎛⎫+++++++++ ⎪ ⎪24622462⎝⎭⎝⎭……④n n n n 1111111⎛⎫⎛⎫=+++++++++ ⎪ ⎪22462462⎝⎭⎝⎭…… 比较③和④可知要证②式成立,只须证明 n n 1111⎛⎫++++ ⎪22462⎝⎭…≥⑤ n n111111++++++352-1462……≥⑥ ⑤,⑥两式显然成立,故不等式①成立.用分析法证明不等式时,应注意每一步推理都要保证能够反推回来.分析法的优点就是比较符合探索题解的思路,缺点就是叙述往往比较冗长,因此,思路一旦打通,可改用综合法解答,它适用于条件简单而求证复杂或从条件无从下手的题. 基础练习1<2.设,x y >0>0,证明不等式:()()x yxy11223323+>+.3.已知,,a b c 分别为一个三角形的三边之长,求证c a b a b b c c a++<2+++. 4.若,,x y z +∈R ,且x y z xyz ++=,证明不等式y z z x x yx y z x y z 2⎛⎫+++111++2++ ⎪⎝⎭≥.5,已知,,x y z ∈+R ,且x y z 222++=1,求证:x y z x y z 222++1-1-1-6.已知,,a b c 01≤≤,求证:a b cbc ca ab ++2+1+1+1≤. 3.综合法综合法是“由因导果”,即从已知条件出发,依据不等式性质,函数性质或熟知的基本不等式,逐步推导出要证明的不等式.例5.已知△的三边长为,,a b c ,且a b c s ++=2,求证:()()()abcs a s b s c ---8≤. 证明:由条件得:,,s a s b s c ->0->0->0 ()()()s a s b c s a s c s a b 222-+-1⎛⎫∴--=2--= ⎪244⎝⎭≤.同理:()()()(),a b s b s c s c s a 22----44≤≤.三式相乘再开方得()()()abcs a s b s c ---8≤.在实际应用中,常常用分析法寻找思路,用综合法表述,即所谓的综合分析法,这样使得叙述不会太过于冗长,请看下例:例6.设,,,a b x y R ∈,且,a b x y 2222+=1+=1,试证:ax by +1≤. 证法1:用分析法。
2 华东师范大学第二附属中学(创新班和理科班用)数学(高中上册)-9
第九章简单几何体9.1棱柱、棱锥、棱台1.棱柱有两个面平行,其余各面都是四边形,且任意相邻的两个四边形的公共边都互相平行的多面体叫做棱柱(prism).棱柱的互相平行的两个面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻两个侧面的公共边叫做棱柱的侧棱,底面多边形的顶点叫做棱柱的顶点,不在同一个面上的两个顶点的连线叫做棱柱的对角线.两个底面间的距离叫做棱柱的高.侧棱和底面不垂直的棱柱叫做斜棱柱,侧棱和底面垂直的棱柱叫做直棱柱,底面是正多边形的直棱柱叫做正棱柱(参见图9-1).AA'D'F'直五棱柱斜五棱柱图91棱柱的性质:(1)棱柱的侧面都是平行四边形;(2)棱柱的底面及平行于底面的截面是全等的多边形.直棱柱的性质:(1)直棱柱的侧面都是矩形;(2)直棱柱的侧棱与高相等;(3)正棱柱的侧面都是全等的矩形.底面是n边形的棱柱叫做n棱柱,底面是平行四边形的棱柱叫做平行六面体,底面是矩形的直棱柱叫做长方体,所有棱长都相等的长方体叫做正方体(参见图9-2).CBACBAC'C'B'B'B'A'A'A'DD'D'DD'C'DCBA正方体长方体平行六面体图92例1.如图9-3,长方体1111ABCD A B C D-中,AB a=,BC b=,1BB c=,并且0a b c>>>.求沿着长方体的表面自A到1C的最短线路的长.c a bDCAD'A'B'C'图93解:将长方体相邻两个展开有下列三种可能,如图9-4.b aa cA 1C 1B 1B 1cca b B AAB CC B AC 1D 1A 1C 1B 1A 1(c )(b )(a )图94一个图形中1AC 的长分别为:,0a b c >>> ,0ab ac bc ∴>>>.例2.如图9-5,ABCD A B C D -′′′′为正方体.任作平面α与对角线AC ′垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l .则( )图9-5D'C'B'A'D C BAA .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值解:将正方体切去两个正三棱锥A A BD -′与C D B C -′′′后,得到一个以平行平面A BD ′与D B C ′′为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱A B ′′剪开,展平在一张平面上,得到一个平行四边形11A B B A ′′,而多边形W 的周界展开后便成为一条与1A A ′平行的线段(如图9-6中1E E ′),显然11E E A A =′′,故l 为定值.B'E'A'B 1E 1A 1D C BD'图9-6例3.直三棱柱111A B C ABC -中,平面1A BC ⊥平面11ABB A,且1AC ,则AC 与平面1A BC 所成的角θ的取值范围是__________.解:030θ︒<<︒ 作1AD A B ⊥于D ,易证AD ⊥平面1A BC ,所以ACD θ∠=.设1AA a =,AB x =,则sin AD θ==⋅,故22223sin 13sin a x θθ=-.易证BC ⊥平面11A ABB , 故90CBA ∠=︒,从而AB AC <,即x <,于是22223sin 0313sin a a θθ<-≤,1sin 2θ<,又090θ︒<<︒,得030θ︒<<︒. 2.棱锥有一个面是多边形,其余各面都是有一个公共顶点的三角形的多面体叫做棱锥(pyramid ).棱锥的多边形面叫做棱锥的底面,其余各三角形叫做棱锥的侧面,相邻侧面的公共边叫做棱锥的侧棱,各侧面的公共顶点叫做棱锥的顶点,顶点到底面的距离叫做棱锥的高(参见图9-7).POFEDCB图9-7底面是正多边形,顶点在底面的射影是底面中心的棱锥叫做正棱锥.例4.正四棱锥S ABCD -中,45ASB ∠=︒,二面角A SB C --为θ且cos m θ=m n ,为整数),则m n +=__________.解:因各侧面为全等的等腰三角形.在SAB △内作高AE ,则CE 也是SBC △的高,故AEC θ∠=.设1SA =则AE CE ==,452sin 2AB BC ︒==,2222458sin 2AC AB BC ︒=+==()41cos45-︒=4-222cos 32AE CE AC AE CEθ+-==-⋅得385m n +=-+=. 棱锥的性质:若棱锥被平行于底面的平面所截,则(1)侧棱和高被这个平面分成比例线段; (2)截面与底面是相似多边形;(3)截面面积与底面面积之比,等于顶点到截面与顶点到底面的距离的平方比. 正棱锥的性质:(1)侧棱都相等,侧面都是全等的等腰三角形; (2)对角面都是等腰三角形;(3)高、侧棱、外接圆半径构成直角三角形; (4)高、斜高、内切圆半径构成直角三角形;(5)侧棱、斜高、底面边长的一半构成直角三角形;(6)外接圆半径、内切圆半径、底面边长的一半构成直角三角形. 例5.正六棱锥的底面周长为24,侧面与底面所成角为60︒,求:(1)棱锥的高;(2)斜高;(3)侧棱长;(4)侧棱与底面所成角.分析:本题涉及了正棱锥的若干基本量,可以把基本量放置到直角三角形中,由已知量求未知量. 解:正六棱锥的底面周长为24,见图9-8.图9-8E DPSCB AHO∴正六棱锥的底面边长为4. 在正棱锥S ABCDEF -中,取BC 中点H ,连SH ,SH BC ⊥, O 是正六边形ABCDEF 的中心. 连SO ,则SO ⊥底面ABCDEF OH BC ∴⊥.SHO ∴∠是侧面与底面所成二面角的平面角,即么60SHO ∠=︒.(1)在Rt SOH △中,OH ==60SHO ∠=︒, tan 606SO OH ∴=︒=.(2)同样在SOH △中,斜高2SH OH == (3)Rt SOH △中,6SO =,4OB BC ==.SB ∴(4)SO ⊥ 底面ABCDEF ,SBO ∴∠是侧棱与底面所成角,同样在SOB △中,3tan 2SO SBO BO ∠==,3arctan 2SBO ∴∠=. 例6.如图9-9所示,正四棱锥P ABCD -棱长均为13,M ,N 分别是PA ,BD 上的点,且58PM MA BN ND ==∶∶∶.图9-9P MENODCB(1)求证:直线MN ∥平面PBC ;(2)求直线MN 与底面ABCD 所成角的正弦. 分析:(1)要证明MN ∥平面PBC ,只需证明MN 与平面PBC 内某一条直线平行.为此连AN 并延长交BC 于E ,连PE .可考虑证明MN PE ∥.(2)若能证明MN PE ∥,则PEO ∠即为直线MN 与底面所成的角. 解:(1)连AN 并延长交BC 于E ,再连PE . BE AD ∥,EN AN BN ND ∴=∶∶, 又BN ND PM MA =∶∶,EN AN PM MA ∴=∶∶,PE MN ∴∥,又PE ⊂平面PBC ,MN ⊄平面PBC ,MN ∴∥平面PBC .(2)设O 为底面中心,连PO ,EO ,则PO ⊥上平面ABCD .又MN PE ∥,则PEO ∠为直线MN 与平ABC 所成的角.由58BE AD BN ND ==∶∶∶及13AD =,得658BE =,在PBE △中,60PBE ∠=︒,13PB =,658BE =,由余弦定理,得918PE =.在Rt POE △中,PO =,918PE =,则sin PO PEO PE ∠==例7.在正三棱锥P ABC -中,2AB a PA a ==,,过A 作平面分别交平面PBC 于DE .当截面ADE△的周长最小时,ADE S =△__________,P 到截面ADF 的距离为__________. 解:将三棱锥的侧棱PA 剪开,当ADE △的周长最小时,其展开图如图9-10.A'a2aEDPCB A图9-10ADE △的周长即是展开图中线段AA ′的长.易证ABD PAB △△∽,又22PA AB a ==,故2AD AB BD a ===,3324PD PD PB BD a DE BC a PB =-==⋅=,.ADE △中,DE上的高AH .于是212ADE S AH DE =⨯⨯=△; 从P 向底面作高PO .则PO =.于是2313P ABC V -=. 又22916PDE PBC S PD S PB ==△△,得33991616A PDE A PBCV V --===. 设P 到截面的距离为d,则313A PDE P ADE ADE V V d S --==⋅=△,于是d . 拓展 已知正四棱锥-S ABCD 的侧面与底面所成二面角的平面角是1θ,相邻两侧面所成二面角的平面角是2θ,试用1θ表示2θ,参见图9-11.ODCBF ES图9-11解:设正四棱锥S ABCD -的底面边长是a ,斜高是h ′,1cos 2ah θ=′(见图9-12). h baF EBAS图9-12过点A 作AE SB ⊥,E 是垂足,联结2CE AEC θ∠=,. 设AE b =,F 是AB中点,SF h SA ==,′ AB SA ABE SAF AE SF ∴= ,△△∽,即a b =222222122cos 1cos 2b b a ab b bθθ+-==-=-⋅⋅ ,221πarccos(cos )θθ∴=-.3.棱台用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台,参见图9-13.原棱锥的底面和截面分别叫做棱台的下底面和上底面,其他各面叫做棱台的侧面,参见图9-13.相邻两个侧面的公共边叫做侧棱,上下底面之间的距离叫做棱台的高.由n 棱锥所截得的棱台叫做n 棱台,由正棱锥所截得的棱台叫做正棱台.D'E C A(b )(a )图9-13正棱台的性质:(1)上下底面以及平行于底面的截面是边数相同的正多边形;(2)侧棱都相等,侧面都是全等的等腰梯形,此等腰梯形的高叫做正棱台的斜高; (3)对角面都是等腰梯形;(4)高、上下底面的外接圆半径、侧棱构成直角梯形; (5)高、上下底面的内切圆半径、斜高构成直角梯形; (6)斜高、侧棱、上下底面边的一半构成直角梯形.例8.如图9-14,已知正四棱台中,41624S S S ===上下,,侧.O G FEDC B AG'O'D'E'B'A'图9-14(1)求侧面与下底面所成二面角的平面角; (2)求相邻两个侧面所成二面角的平面角; (3)求对角面的面积S 对.解:(1)设E 、F ′分别是BC 、B C ′′的中点,点F 是点E ′在底面的射影,F EF ∠′是侧面与下底面所成二面角的平面角.41624S S S === 上下,,侧, 422AB A B EE ∴===,,′′′.21160OE O E EF E EF ==∴=∠=︒ ,,,′′′.(2)过点A 作AG B B ⊥′,G 为垂足,联结CG ,H 是点B ′在AB 上的射影,AGC ∠相邻两个侧面所成二面角的平面角.在等腰梯形A ABB ′′中,12()12B H HB AB A B BB ==-==,,′′′′,sin 4AG AB ABG ∴=⋅∠==.6464321cos 4AGC +-∠==- , ∴相邻两个侧面所成二面角的平面角是1πarccos 4-.(3) 在等腰梯形A ACC ′′中,A C AC O O ===′′′,12S ∴==对基础练习1.设有四个命题:①底面是矩形的平行六面体是长方体; ②棱长都相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体; ④对角线相等的平行六面体是直平行六面体. 其中真命题的个数是( ) A .1 B .2 C .3 D .42.已知长方体的一条对角线与从它的一个端点出发的三条棱所成的角分别是αβγ、、,写出一个αβγ、、满足的关系式.3.如图9-15,在棱锥P ABCDE -中,与底面平行的平面截棱锥得多边形A B C D E ′′′′′,点P 在底面、截面的射影分别是H 、H ′,求证:图9-15(1)PH PA PB PC PD PE PH PA PB PC PD PE=====′′′′′′; (2)截面A B C D E ′′′′′与底面ABCDE 相似; (3)22A B C D EABCDE S PH S PH=′′′′′′.4.以1,1,1?5.四面体OABC 中,OA ⊥面ABC ,AB AC ⊥,点P 满足OP lOA mOB nOC =++,其中l m n ,,为正数且1l m n ++=.若直线OP 是由到面OBC 、面OCA 和面OAB 的距离相等的点构成,求二面角A OBC --的余弦值(用l m n ,,表示). 6.如图9-16,已知正三棱柱111ABC A B C -的所有棱长都相等,E 是1A B 的中点,F 在棱1CC 上,当点F 使得1A F BF +最小时,求异面直线AE 与1A F 所成的角.B AE GC H N 1FB 1A 1图9-167.如图9-17,正四棱柱1111ABCD A B C D -中,对角线18BD =,1BD 与侧面11BB C C 所成角为30︒,求:D C B AD 1C 1B 1A 1图9-17(1)1BD 与底面ABCD 所成角; (2)异面直线1BD 与AD 所成角;(3)正四棱柱的全面积.8.如图9-18,已知三棱锥-P ABC 中,P A P B P C 、、与底面ABC 所成角相等,90CAB AC AB PB a D ∠=︒===,,为BC 中点,E 点在PB 上且PC ∥截面EAD .求:AFBCEP图9-18(1)AE 与底面ABC 所成角; (2)PC 到平面EAD 的距离.9.作出正四面体每个面的中位线,共得12条线段,在这此线段中,相互成异面直线的“线段对”有__________个.10.如图9-19,-ABCD A B C D ′′′′为正方体.任作平面α与对角线AC ′垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l .则( )D'C'B'A'D CBA图9-19A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值11.如图9-20,长方体1111ABCD A B C D -,1AB a BC b A A c ===,,,E 为11D C 中点,若平面11A BC 与平面ACE 所成二面角的平面角为θ.则sin θ=__________.EB'A'D'C'cba DC图9-2012.如图9-21,已知直三棱柱111-ABC A B C 的底面为直角三角形,1906ACB AC BC CC ∠=︒===,,P 是BC 上一动点.求1CP PA +的最小值.C 1B 1A 1PCB A图9-2113.设棱台的两底面积分别为S S ,′.它的中截面的面积为0S,求证:14.已知四棱锥P ABCD-的底面ABCD为等腰梯形,AB DC∥,AC BD⊥,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又2BO PO PB PD==⊥,.(I)求异面直线PD与BC所成角的余弦值;(Ⅱ)求二面角P AB C--的大小;(Ⅲ)设点M在棱PC上,且PMMCλ=,问λ为何值时,PC⊥平面BMD.9.2简单多面体与欧拉定理多面体的概念在自然界和日常生活中,我们会看到各种形状各异的物体,有些物体可以看成是某些简单几何体的复合体.现在我们就从一些简单的几何体入手,开始对空间物体的认识和研究.由若干个多边形围成的封闭立体叫做多面体(polyhedron).构成多面体的各平面多边形叫做多面体的面(face of polyhedron),相邻多边形的公共边叫做多面体的棱(edge of polyhedron),棱与棱的交点叫做多面体的顶点(vertex),联结不在同一平面内的两个顶点的线段,叫做多面体的对角线.若把多面体的任意一个平面伸展成平面,而此多面体的所有其他各面都在这个平面的同旁.则这样的多面体叫做凸多面体.图9-22中(a)是凸多面体,而(b)不是凸多面体.(b)(a)图9-22多面体的面数至少是四.多面体按照其面数分别叫做四面体、五面体等等.图9-22(a)的几何体叫做二十面体.1.正多面体正多面体是一种特殊的凸多面体,它包括两个特征:①每个面都是有相同边数的正多边形;②每个顶点都有相同数目的棱数.正多面体只有5种(如图9-23),其顶点数V、面数F、棱数E如下表.正十二面体正十二面体正八面体正六面体正四面体图9-23V著名数学家欧拉对正多面体进行了研究,发现了多面体的顶点数、面数、棱数间的关系.欧拉(Euler ,L.,1707~1783)瑞士数学家,大部分时间在俄围和法国度过.他16岁获硕士学位,早年在数学天才丹尼尔·伯努利(Bernoulli ,Danicl ,1700~1784)赏识下开始学习数学,并毕生研究数学,是数学史上最“高产”的数学家,在世发表700多篇论文.他的研究论著几乎涉及到所有数学分支,有许多公式、定理、解法、函数、方程、常数等是以欧拉名字命名的.欧拉还是数学符号发明者,如用()f x 表示函数、∑表示连加、i 表示虚数单位、π、e 等.在多面体研究中首先发现并证明了欧拉公式,今天我们沿着他的足迹探索这个公式. 2.多面体拓扑变形与简单多面体的概念考虑一个多面体,例如止六面体,假定它的面是用橡胶薄膜做成的,如果充以气体.那么它会连续(不破裂)变形,最后可变成一个球面.像这样,表面经过连续变形可变为球面的多面体,叫做简单多面体.有关多面体的关系.参见图9-24.图9-24正多面体正四面 体 正方体棱锥棱柱简单多面体凸多面体3.欧拉定理定理 简单多面体的顶点数V 、棱数E 及面数F 间有关系2V F E +-=.公式描述了简单多面体中顶点数、面数、棱数之间特有的规律. 定理的证明分析:以四面体ABCD 为例.将它的一个面BCD 去掉,再使它变为平面图形(见图9-25),四面体的顶点数V 、棱数E 与剩下的面数1F 变形后都没有变(这里11F F =-).因此,要研究V E 、和F 的关系,只要去掉一个面,将它变形为平面图形即可.ABCDDCA B图9-25只需平面图形证明:11V F E +-=.(1)去掉一条棱,就减少一个面,1V F E +-的值不变.例如去掉BC ,就减少一个面ABC .同理,去掉棱CD BD 、,也就各减少一个面ACD ABD 、(见图9-26),由于V 、1F E -的值都不变,因此1V F E +-的值不变.BA CDD CBA 图9-26(2)再从剩下的树枝形中,去掉一条棱,就减少一个顶点,1V F E +-的值不变.例如去掉CA ,就减少一个顶点C .同理去掉AD 就减少一个顶点D ,最后剩下AB (见图9-27).DBA A BD CBA图9-27在以上变化过程中,1V F E +-的值不变,12011V F E +-=--=,所以 112V F E V F E +-=+-+=.对任意的简单多面体,运用这样的方法,都是只剩下一条线段.公式对任意简单多面体都是正确的. 定理的意义(几点说明)(1)数学规律 公式描述了简单多面体中顶点数、面数、棱数之间特有的规律.(2)思想方法创新提高 在定理的发现及征明过程中,在观念上,假设它的表面是橡皮薄膜制成的,可随意拉伸;在方法上将底面剪掉,然后其余各面拉开铺平,化为平面图形(立体图→平面图). (3)引入拓扑新学科 “托开图”与以前的展开图是不同的,从立体图到拉开图,各面的形状,以及长度、距离、面积、全等等与度量有关的量发生了变化,而顶点数、面数、棱数等不变.事实上.定理在引导大家进入一个新几何学领域:拓扑学.我们用一种可随意变形但不得撕破或粘连的材料(如橡皮泥)做成的图形,拓扑学就是研究图形在这种变形过程中的不变的性质. (4)给出多面体分类方法在欧拉公式中,令()f p V F E =+-()f x 叫做欧拉示性数,定理告诉我们,简单多面体的欧拉示性数()2f p =.除简单多面体外,还有不是简单多面体的多面体.例如,将长方体挖去一个洞,联结底面相应顶点得到的多面体.它的表面不能经过连续变形变为一个球面,而能变为一个环面,它的欧拉示性数为()1616320f p =+-=,所以带一个洞的多面体的欧拉示性数等于零. (5)利用欧拉定理可解决实际问题. 例1.一个简单多面体的棱数可能是6吗?解:设有简单多面体棱数6E =,由欧拉公式2V F E +-=得8V F +=. 又4V ≥,4F ≥.所以8V F +≥.所以4V =、4F =,即有4个顶点、4个面.由于四面体有且只有4个顶点,从而有且只有4个面. 所以符合条件的多面体只有一种类型:四面体即三棱锥.例2.有一个各面都是三角形的正多面体,设顶点数V 、面数F 、棱数E ,(1)求证:3222FE F V ==+,.(2)如果过各顶点的棱数都相等,则此多面体是几面体?(1)证明:因为此正多面体有F 个面,每个面有3条边,所以F 个面总共有3F 条边,但由于各棱是两个面的交线且被计算过两次,所以实际棱数为32E F =;由欧拉公式2V F E +-=得322222FV E F F F =-+=-+=+.(2)解:设各顶点处有m 条棱,则2mV E =,又3222F E F V ==+,,代入上式得66m E m =-. 故60m ->,所以6m <,从而35m ≤≤,所以345m =、、,从而4820F =、、. 由此可知,此多面体分别为四面体、八面体和二十面体.例3.运用欧拉公式,求解足球问题.解:设足球表面有正五边形x 块,正六边形y 块,则由上面总结可知:多面体的顶点个数就是正五边形顶点个数之和,所以5V x =,又由于每条棱都是两个多边形的公共边,故562x yE +=. 而正五边形和正六边形块数之和就是整个多边形的块数:F x y =+,代入V F E +-=2,得744x y -=, ① 球体表面每个顶点处有3个正多边形,由此发现563x y V +=,②联立解得1220x y ==,,此时32F x y =+=,即共有32个面.另外,也可以计算出共有60个顶点. 基础练习1.已知:一个简单多面体的各个顶点都有三条棱.求证:24V F =-. 2.是否存在七条棱的简单多面体?3.1996年的诺贝尔化学奖授予对发现60C 有重大贡献的三位科学家.60C 是由60个原子组成的分子,它的结构为简单多面体的结构(见图9-28).这个多面体有60个顶点,从每个顶点都引出3条棱,各面的形状分为五边形或六边形两种,计算60C 分子中形状为五边形和六边形的面各有多少.图9-289.3 旋转体的概念平面上一条封闭曲线所围成的区域绕着它所在平面上的一条定直线旋转而形成的几何体叫做旋转体.定直线叫做旋转体的轴.1.圆柱将矩形ABCD绕一条边AB所在直线旋转一周形成的几何体叫做圆柱(见图9-29).AB所在直线叫做圆柱的轴,线段AD、BC旋转而成的圆面叫做圆柱的底面.线段CD旋转而成的曲面叫做圆柱的侧面,CD叫做圆柱侧面的一条母线,圆柱底面间的距离叫做圆柱的高.D图9-29圆柱的性质:(1)圆柱的两个底面是相等的圆,它们所在的平面平行;(2)圆柱的轴经过两个底面的圆心,且垂直于两个底面,联结两个底面的圆心的线段长等于圆柱的高.通过圆柱轴的截面,叫做圆柱的轴截面.圆柱的轴截面是矩形.若圆柱的轴截面是正方形,则这个圆柱叫做等边圆柱.例1.已知圆柱的底面圆半径是r,用一个乎行于轴的平面截圆柱,所得的截面面积是轴截面面积的一半,求圆柱的轴到截面的距离.解:如图9-30所示,设圆柱的高是h,平行于轴的平面截面是A ACC AC a=,′′,截面A ACC′′和轴截面A ABB′′的面积分别是S截和S轴.BABAB'A'图9-30S截=ah,S轴2rh=,S截∶S轴=12∶,a r ∴=.过底面圆圆心O 作AC 的垂线,垂足是D OD ,是圆柱的轴到截面的距离. OAC △是边长是r的正三角形,OD ∴=. 2.圆锥将直角三角形ABC 绕其一条直角边AB 所在直线旋转一周形成的几何体叫做圆锥(见图9-31).C图9-31AB 所在直线叫做圆锥的轴,点A 叫做圆锥的顶点,直角边BC 旋转而成的圆面叫做圆锥的底面,斜边AC 旋转而成的曲面叫做圆锥的侧面,斜边AC 叫做圆锥侧面的一条母线,圆锥的顶点到底面间的距离叫做圆锥的高. 圆锥的性质:(1)圆锥的底面是圆,它们所在的平面垂直圆锥的轴;(2)圆锥的轴经过顶点和底面的圆心,联结顶点和底面的圆心的线段长等于圆锥的高; (3)圆锥的母线都经过顶点且相等,各条母线和轴的夹角相等.通过圆锥轴的截面,叫做圆锥的轴截面.圆锥的轴截面是等腰三角形.若圆锥的轴截面是正三角形,则这个圆锥叫做等边圆锥.例2.在等边圆锥(圆锥的轴截面为等边三角形)中,底面半径为R ,AB 为底面直径,60ABC ∠=︒,,求异面直线PA BC ,的距离.解:在PA 上任取一点M ,过M 作ML ⊥底面圆O ,垂足为L (如图9-32).图9-32轴截面PAB ⊥底面圆O ,L ∴在直径AB 上. 再过L 作LN BC ⊥,垂足为N .由三垂线逆定理,可知MN BC ⊥.设60cot 60ML x PAB AL ML =∠=︒∴=⋅︒= ,,. 2BL AB AL R x ∴=-=,又60ABC ∠=︒, ∴直角三角形BNL中,1sin 6022N BL R x x ⎛∠=⋅︒==- ⎝⎭.∴直角三角形MLN中,MN==.当且仅当x=时等号成立.MN的最短距离即异面直线PA BC,之间的距离故异面直线PA BC,.3.圆台将直角梯形ABCD绕其垂直底面的腰AB所在直线旋转一周形成的几何体叫做圆台(见图9-33).AB所在直线叫做圆台的轴,梯形的两条底边AC BD、旋转而成的两个互相平行的圆面叫做圆台的底面,梯形另一条腰CD旋转而成的曲面叫做圆台的侧面,腰CD叫做圆台侧面的一条母线,两个底面间的距离叫做圆台的高.C图9-33圆台的性质:(1)圆台的两个底面是圆,它们所在的平面平行;(2)圆锥的轴经过两个底面的圆心,并且与底面垂直,联结两个底面的圆心的线段长等于圆台的高;(3)圆台的母线都相等,各条母线的延长线相交于一点.通过圆台轴的截面,叫做圆台的轴截面.圆台的轴截面是等腰梯形.例3.已知圆台的母线长为l,母线与下底面所成的角为θ,圆台的高是上、下底面圆半径的等差中项,求圆台的高和上、下底面圆半径.解:如图9-34所示,设圆台的高为h,上、下底面圆半径分别是r R、.rlhR B AO'A'O图9-34cos22sinR r l R r h lθθ-=+==,,11sin sin cos sin cos22h l R l r lθθθθθ⎛⎫⎛⎫∴==+=-⎪ ⎪⎝⎭⎝⎭,,.4.球将圆心为O的半圆绕其直径AB所在的直线旋转一周形成的几何体叫做球.半圆的圆弧所形成的曲面叫做球面,点O叫做球心,原半圆的半径和直径是球的半径和直径.在半圆旋转形成球的过程中,半圆上的点C′绕着它在直径上的射影O′旋转形成一个圆心为O′、半径为1r O C =′′的圆.当O ′位于球心O 时,圆O ′叫做球O 的大圆;当O ′异于球心O 时,圆O ′叫做球O 的小圆.C图9-35球的性质:(1)同一个球的半径都相等;(2)用任意平面截球所得的截面都是圆,球心与球截面圆心的连线与截面垂直;(3)若用R 和r 分别表示球的半径和截面圆的半径,用d 表示球心到截面网的距离,则d(4)同一个球的大圆互相平分.在平面上,两点间的距离是联结两点的直线段的长度.在球面上,联结两点的最短路径叫做两点的球面距离.可以证明两点的球面距离是过这两点的球的大圆的劣弧的长度.例4.已知地球的半径为R ,球面上A B ,两点都在北纬45︒圈上,它们的球面距离为π3R ,A 点在东经30︒上,求B 点的位置及A B ,两点所在其纬线圈上所对应的劣弧的长度. 解:如图9-36,设球心为O ,北纬45︒圈的中心为1O ,图9-36由A B ,两点的球面距离为π3R ,所以π3AOB ∠=, OAB ∴△为等边三角形.于是ABR =.由11cos 45O A O B R ==⋅︒=, 22211O A O B AB ∴+=.即1π2AO B ∠=. 又A 点在东经30︒上,故B 的位置在东经120︒,北纬45︒或者西经60︒,北纬45︒. ∴AB ,两点在其纬线圈上所对应的劣弧1π2O A R ⋅=.例5.如图9-37所示,在棱长为l 的正方体内有两个球相外切且又分别与正方体内切.DCBA图9-37(1)求两球半径之和;(2)球的半径为多少时,两球体积之和最小.解:(1)如图9-38,球心1O 和2O 在AC 上,过1O ,2O 分别作AD ,BC 的垂线交于E ,F .O 2O 1F E DCBA图9-38则由1AB AC ==,12AO CO ,.)r R r R ∴+++=,R r ∴+==(2)设两球体积之和为V ,则332244π()π()(-)33V R r r R R Rr r =+=++24()33R r rR ⎤=+-⎦24π33R R ⎤⎫⎥=--⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦22433R ⎤⎥=-+⎥⎝⎭⎣⎦.当R =时,V 有最小值. ∴当R r ==时,体积之和有最小值. 例6.空间四个球,它们的半径分别是2、2、3、3.每个球都与其他三个球外切.另一个小球与这四个球都相切,求这个小球的半径.解:设半径为3的球心为A B 、,半径为2的球心为C D 、(见图9-39).则易知6AB =,4CD =,5AC AD BC BD ====.设小球中心为O ,半径为r ,则O 在四面体ABCD 内且3AO BO r ==+,2CO DO r ==+.取AB 中点E ,联结CE ,DE ,则CE AB ⊥,DE AB ⊥,故平面CDE 为线段AB 的垂直平分面α,所以O 在平面CDE 内,又由2OC OD r ==+知O 在CD 的垂直平分面β内,故O 在等腰CED △底边CD 上的高EF 上(F 为CD 中点),易算出4ED EC =,得ECD △为等边三角形.于是EF ==.而OF.OE 代入OE OF EF +==611r =. OFEDCB A 图9-39基础练习1.已知等边圆锥的轴截面面积是 2.求正四面体的内切球和外接球的半径之比.3.由曲线2244x y x y ==-,,4x =,4x =-围成的图形绕y 轴旋转一周所得的几何体的体积为1V ;满足2216x y +≤,22(2)4x y +-≥,22(2)4x y ++≥的点()x y ,组成的图形绕y 轴旋转一周所得的几何体的体积为2V ,求21V V ∶. 4.三个圆柱侧面两两相切,且它们的轴也两两相互垂直,如果每个圆柱底面半径都是1,求这三个圆柱侧面都相切的最小球的半径.5.已知SN 是联结南北两极的球直径,O ′是线段SN 三等分点,求过点O ′且垂直SN 的平面截球所得的截面圆面积与球的大圆面积的比值.6.四面体A BCD -中,5AB CD AC BD AD BC ====,A BCD -的外接球半径.7.已知A B 、两点在半径为R 的球面上,点A 位于东经x ︒,北纬y ︒,点B 位于东经u ︒,北纬v ︒.(1)当1575x u y v ===,,时,求A B 、两点的球面距离; (2)当451575y v x u ====,,时,求A B 、两点的球面距离. 8.如图9-40,在三棱锥S A B C -的棱S A S B S ,,上分别有点111A B C ,,,且11S A S A S B S BS C S C ⋅=⋅=⋅.求证:A B C ,,111A B C ,,在同一球面上.B图9-409.4 几何体的直观图和三视图在阳光的照射下,物体会在地面上留下影子.根据这种简单的自然现象,进行抽象研究,人们形成了一套将三维空间的物体在二维平面上表示的投影理论和投影方法.画家利用投影法在二维画布上描绘三维空间的自然景物.设计师利用投影法在二维图纸上设计绘制物体的图样.将空间一点S 作为投影中心,平面H 作为投影面,由投影中心S 引出的线称为投影线.在这个投影体系中,过投影中心S 向空间点A 引投射线与投影面H 相交,其交点a 就是空间点A 在投影面H 上的投影.由于投射线交于投射中心,我们把这样的投影叫做中心投影法,参见图9-41(a ).H F EA DSf de b aB (a )(b )图9-41将投影中心S 移至与投影面的无穷远点,此时全部投影线互相平行,这种投影法叫做平行投影法. 在平行投影法中,根据投射线与投影面是否垂直又分为正投影法和斜投影法两种. 正投影——投射线与投影而垂直,如图9-42(a )所示. 斜投影——投射线与投影面不垂直,如图9-42(b )所示.(b )斜投影法(a )正投影法图9-42单面投影图是指将空间形体向单一投影面投射得到的投影网,参见图9-41(b );多面正投影是指将空间形体向两个或两个以上互相垂直的投影面投射得到的投影图.利用平行投影法,将物体连同其直角坐标系投射在单一投影面上所得到的具有立体感的图形叫做轴测投影图,简称轴测图.坐标轴Ox Oy Oz 、、叫做轴测投影轴,简称轴测轴.轴测图立体感强,常被用作在图纸上进行空间构思和表达零部件结构形状、装配关系的效果图,是机械工业常用的辅助图样.。
上海市华东师范大学第二附属中学实验班用2018届高三数
第九章 简单几何体9.1 棱柱、棱锥、棱台 1.设有四个命题:①底面是矩形的平行六面体是长方体; ②棱长都相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体; ④对角线相等的平行六面体是直平行六面体. 其中真命题的个数是( ). A .1 B .2 C .3 D .4 解:A2.已知长方体的一条对角线与从它的一个端点出发的三条棱所成的角分别是α、β、γ,写出一个α、β、γ满足的关系式. 解:见题2解析图.设A CD A CB A CC αβγ∠=∠=∠=,,′′′′.γβαD 'C 'B'A'D C BA题2解析图由于cos cos cos DC BC C CA C A C A Cαβγ===,,,′′′′ 则2222222cos cos cos 1DC BC C C A C αβγ++++==′′.3.如图9-15,在棱锥P ABCDE -中,与底面平行的平面截棱锥得多边形A B C D E ′′′′′,点P 在底面、截面的射影分别是H 、H ′,求证:图 915C 'D 'E'H 'DHECBAP(1)PH PA PB PC PD PE PH PA PB PC PD PE =====′′′′′′. (2)截面A B C D E ′′′′′与底面ABCDE 相似. (3)22A B C D EABCDE S PH S PH =′′′′′′.证明:(1)如图所示,连接A H ′′和AH .A H ′′和AH 分别是平面ABCDE ′′′′′和平面ABCDE 与平面PAH 的交线. 由于平面A B C D E ′′′′′∥平面ABCDE , 则PH PA A H AH PA H PAH PH PA=,,′′′′△′′△∥. 同理可证,PH PB PH PC PH PD PH PE PH PB PH PC PH PD PH PE====,,,′′′′′′′′. 则PH PA PB PC PD PE PH PA PB PC PD PE=====′′′′′′. (2)由于PA PB PA PB=′′,P ∠是公共角, 则PA B PAB △′′△∽,A B PA PH AB PA PH==′′′′. 同理可证,B C PH C D PH D E PH E A PH BC PH CD PH DE PH EA PH====,,,′′′′′′′′′′′′. 由于截面A B C D E ′′′′′与底ABCDE 的对应边成比例, 则截面A B C D E ′′′′′与底ABCDE 相似. (3)由(2)知,2222A B C D EABCDE S A B PH S AB PH ==′′′′′△′′′. 4.以1,l ,1? 解:3个.5.四面体OABC 中,OA ⊥面ABC ,AB AC ⊥,点P 满足OP lOA mOB nOC =++,其中l m n ,,为正数且1l m n ++=.若直线OP 是由到面OBC 、面OCA 和面OAB 的距离相等的点构成,求二面角A OB C --的余弦值(用l ,m ,n 表示). 解:1OP lOA mOB nOC m n l AP mAB nAC P =++++=⇒=+,,在面ABC 上. OA ⊥面ABC ,AB AC ⊥,则P 在面ABO 的垂足在AB 上.又ABP ABCSAP mAB nAC AB AC n S =+⊥⇒=,△△.同理ACP BCP ABC ACP ABPABC ABC ABCS S S S S m l S S S --===,△△△△△△△△.则cos ABO P ABO ABP ACO P ACO BCP S V S nA OBC S V S l--∠--====△△△△.6.如图9-16,已知正三棱柱111ABC A B C -的所有棱长都相等,E 是1A B 的中点,F 在棱1CC 上,当点F 使得1A F BF +最小时,求异面直线AE 与1A F 所成的角.图 916B 1N 1C 1A 1H GFENC BA解:如图可知F 为中点时,满足题意.由于12GH AH ==,则AG .又由于1A F =EG =AE =. 则222AE EG AG +=,则90AEG ∠=︒.7.如图9-17,正四棱柱1111ABCD A B C D -中,对角线118BD BD =,与侧面11BB C C 所成角为30︒,求:D 1C 1B 1A 1DCBA图 917(1)1BD 与底面ABCD 所成角. (2)异面直线1BD 与AD 所成角. (3)正四棱柱的全面积.解:(1)在正四棱柱1A C 中,由于11D C ⊥面11BB C C , 则11D BC ∠是1D B 与侧面11BB C C 所成角,即1130D BC ∠=︒. 由于18BD =,则1114D C BC ==,, 由于1111A B C D 是正方形,则11114B C D C ==,1D D ⊥平面ABCD ,则1D BD ∠是1D B 与底面ABCD 所成角,在1Rt D DB △中,11BD B D ==18BD =,则11cos BD D BD BD =则145D BD ∠=︒, 即1BD 与底面ABCD 所成角为45︒. (2)由于11AD A D ∥,则11A D B ∠是1BD 与AD 所成角(或补角). 由于11D A ⊥平面11AA B B ,则111D A A B ⊥, 11Rt A D B △中,11148A D BD ==,,则111cos 2A DB ∠=,则1160A D B ∠=︒, 即异面直线AD 与1BD ,所成角为60︒. (3)11Rt BB C △中,114B C =,1BC =则1BB =则2(44441)S =⨯+⨯⨯=全.8.如图9-18,已知三棱锥P ABC -中,PA 、PB 、PC 与底面ABC 所成角相等,90CAB ∠=︒,AC AB PB a D ===,为BC 中点,E 点在PB 上且PC ∥截面EAD .求:图 918BF EDACP(1)AE 与底面ABC 所成角. (2)PC 到平面EAD 的距离. 解:(1)证明:由于PA 、PB 、PC 与底面ABC 所成角相等, 则顶点P 在底面上的射影为底面Rt CAB △的外心. 而Rt CAB △的外心在斜边BC 的中点D 处, 即PD ⊥平面ABC , 而PD ⊆平面PBC ,则平面PBC ⊥底面ABC .由于PC ∥截面EAD ,PD ⊆平面PBC , 且平面PBC 平面EAD DE =,则PC ∥截面DE ,而D 为BC 中点, 则E 为PB 的中点. 过E 作EM PD ∥,则EM 与BC 的交点,M 为BD 的中点,连接AM , 由于PD ⊥底面ABC ,则EM ⊥底面ABC . 则EAM ∠为AE 与底面ABC 所成的角.AC AB PB a ===,则AE ,而PB PC a BC ===,,则CPB △为等腰直角三角形.在Rt AEM △中,sin EM EAM AE ∠===. 则AE 与底面ABC,所以成角为arc sin (2)等体积法,可得:12a .9.作出正四面体每个面的中位线,共得12条线段,在这些线段中,相互成异面直线的“线段对”有__________个. 解:24个.10.如图9-19,ABCD A B C D -′′′′为正方体.任作平面α与对角线AC ′垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l 则( ).E 'D 'C 'B 'A 'DC BA图919A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值 解:将正方体切去两个正三棱锥A A BD -′与C D B C -′′′后,得到一个以平行平面A BD ′与D B C ′′为上、下底面的几何体V ,V 的每个侧面都是等腰直角三角形,截面多边形W 的每一条边分别与V 的底面上的一条边平行,将V 的侧面沿棱A B ′′剪开,展平在一张平面上,得到一个11A B B A ′′,而多边形W 的周界展开后便成为一条与1A A ′平行的线段(如题10解析图中1E E ′),显然11E E A A =′′,故l 为定值.正确选项为B .A 1E 1B 1D 'DC BB'E'A'题10解析图11.如图9-20,长方体1111ABCD A B C D -,AB a =,BC b =,1A A c =,E 为11D C 中点,若平面11A BC 与平面ACE 所成二面角的平面角为θ,则sin θ=__________.cbaD ABC ED 1C 1B 1A 1图920解:sin θ=.12.如图9-21,已知直三棱柱111ABC A B C -的底面为直角三角形,906ACB AC ∠=︒=,,1BC CC P ==是1BC 上一动点.求1CP PA +的最小值.C 1B 1A 1PCB A图921解:将直三棱柱111ABC A B C -侧面展开可得:d =13.设棱台的两底面积分别为S 、S ′,它的中截面的面积为0S,求证:=. 证明:如题13解析图所示,因为棱台的中截面与两底面平行,所以多边形ABCDE ,00000A B C D E A B C D E ,′′′′′相似,因此2222000000S AB S A B S A B S A B ==,′′′,0000AB A BA B A B ==′′. 题13解析图D 0C 0B 0A 0E 0B'D 'C 'E'A'EDBA两式相加,又因为00A B 是梯形ABB A ′′的中位线,00000022A B AB A B A B A B +===,′′故=.14.已知四棱锥P ABCD -的底面ABCD 为等腰梯形,AB DC ∥,AC BD ⊥,AC 与BD 相交于点O ,且顶点P 在底面上的射影恰为O 点,又2BO =,PO =PB PD ⊥. (1)求异面直线PD 与BC 所成角的余弦值.(2)求二面角P AB C --的大小. (3)设点M 在棱PC 上,且PMMCλ=,问λ为何值时,PC ⊥平面BMD . 解:(1)21PO BO DO DO =⋅=,,取AB 中点E ,连DE ,故DE BC ∥,连PE ,故PDE ∠(或其补角)为异面直线PD 与BC所成角,PDDE BC ==2PE =,则222cos 2PD DE PE PDE PD DE +-∠==⋅ (2)连OE ,PE ,可证得OE AB ⊥,PE AB ⊥,则PEO ∠为二面角P AB C --的平面角,sin PO PEO PE ∠==π4PEO ∠=. (3)222cos 2PB PC BC PB PC BC BPC PB PC +-=∠=⋅ 若PC ⊥面BMD ,则PC BM ⊥,则cos PM PB BPC MC =⋅∠==则2PMMC=. 9.2 简单多面体与欧拉定理1.已知:一个简单多面体的各个顶点都有三条棱,求证:2-4V F =. 证明:由于每个定点都有三条棱,而每条棱有两个顶点, 则32E V =,代入欧拉公式得322V F V +-=,即24V F =-.2.是否存在七条棱的简单多面体?解:假设存在七条棱的简单多面体,由欧拉定理可得:279F V +=+= (*)因为多面体至少四个面,至少四个顶点,即4F ,4V ,故(F ,V )只可能为(4,5)或(5,4),我们考虑最简单的多面体——四面体。
上海华东师范大学第二附属中学平面向量及其应用专题(有答案)百度文库
由正弦定理及三角形性质判断A,由余弦定理判断B,由正弦函数性质判断C,由三角形面积公式,余弦定理及正弦定理判断D.
【详解】
中, ,由 得 ,A正确;
锐角三角形 中, ,∴ ,B正确;
中,若 ,则 或 ,即 或 , 为等腰三角形或直角三角形,C错;
中,若 , ,三角形面积 , , ,∴ , ,
对于选项B中:因为,且,所以角有两
解析:BC
【分析】
根据题设条件和三角形解的个数的判定方法,逐项判定,即可求解,得到答案.
【详解】
对于选项A中:由 ,所以 ,即三角形的三个角是确定的值,故只有一解;
对于选项B中:因为 ,且 ,所以角 有两解;
对于选项C中:因为 ,且 ,所以角 有两解;
对于选项D中:因为 ,且 ,所以角 仅有一解.
【详解】
∵ ,
整理可得: ,
可得 ,
∵A为三角形内角, ,
∴ ,故A正确,B错误,
∵ ,
∴ ,
∵ ,且 ,
∴ ,
解得 ,
由余弦定理得 ,
解得 ,故C错误,D正确.
故选:AD.
【点睛】
本题主要考查正弦定理,余弦定理以及两角和与差的三角函数的应用,还考查了运算求解的能力,属于中档题.
4.ABD
【分析】
根据题目可知,利用正弦定理与三角恒等变换逐个分析即可判断每个选项的正误.
故选:BC.
【点睛】
本题主要考查了三角形解得个数的判定,其中解答中熟记三角形解得个数的判定方法是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
9.AC
【分析】
根据平面向量基本定理判断A;由数量积的性质可判断;由向量的中点表示和三角形的重心性质可判断,由数量积及平面向量共线定理判断D.
