高中数学思维导图
高中数学思维导图:复数,推理证明,算法初步
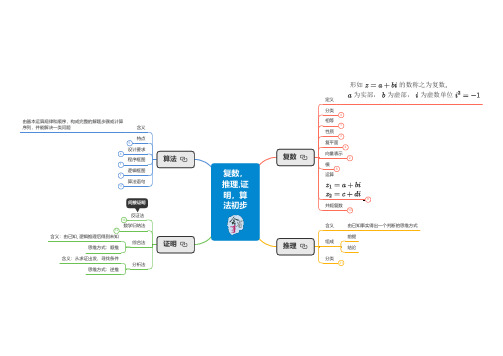
定理逆定理
与已知矛盾
常见矛盾
与假设矛盾 与定义,定理,公理矛盾
自相矛盾
数学归纳法
适用题型 适用范围
证明恒等式
证明整除与几何问题
证明不等式
证明数列有问题
证明立体几何问题
仅限与正整数有关的问题
:验证
时命题成立
: 假设
时,命题成立,
步骤
Байду номын сангаас
证明
时,命题也成立
:命题对从 开始的所有正整数 都成立
综合法
含义:由已知, 逻辑推理后得到未知 思维方式:顺推
由基本运算规律和顺序,构成完整的解题步骤或计算 序列,并能解决一类问题
含义
特点
5
设计要求
4
程序框图
1
逻辑框图
1
算法语句
17
间接证明
反证法
14
数学归纳法
12
含义:由已知, 逻辑推理后得到未知 思维方式:顺推
综合法
含义:从求证出发,寻找条件 思维方式:逆推
分析法
算法 证明
复数, 推理,证 明,算 法初步
含义
证明命题都使用演绎推理,合情推理不能用做证明 从一般性原理出发,推出某个特殊情况下的结论
一般 特殊
特点
三段论:
而
则
内容
一般原理:大前提,M是P
表示形式
特殊情况:小前提,S是M 结论:S是P
证明
间接证明
反证法
含义
假设求证不成立,推理,找出矛盾
反设 归谬 结论
步骤
由已知推出的结论很少
适用范围
存在性命题 结论中含有:否定,唯一,无限,至多,至少
高中数学思维导图:不等式
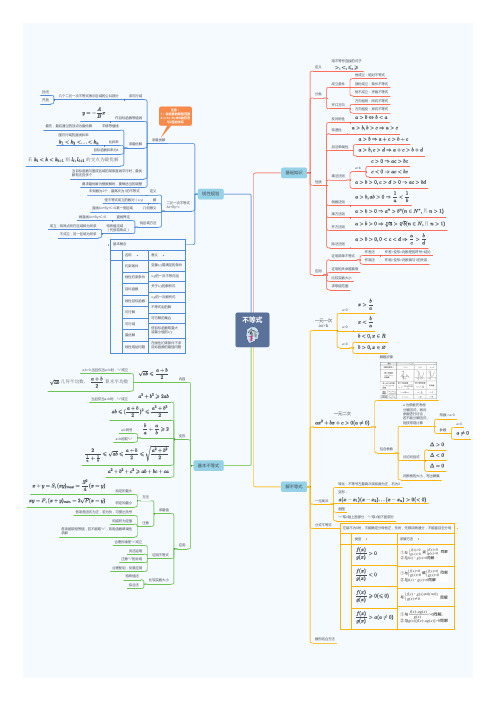
名称
意义
约束条件
变量x,y需满足的条件
线性约束条件 x,y的一次不等式组
目标函数 线性目标函数 可行解 可行域 最优解 线性规划问题
关于x,y的解析式
x,y的一次解析式
不等式组的解
可行解的集合
使目标函数取最大 或最小值的x,y
在线性约束条件下求 目标函数的最值问题
线性规划
a,b>0,当且仅当a=b时,“=”成立
特殊值法 综合法
比较实数大小
应用
不等式
定义 分类
用不等号连接的式子
成立条件
开口方向 反对称性 传递性
恒成立:绝对不等式 部份成立:条件不等式 恒不成立:矛盾不等式 方向相同:同向不等式 方向相反:异向不等式
加法单调性
基础知识
a>b
性质
乘法法则
倒数法则
且
乘方法则
且
开方法则
应用
除法法则 证明简单不等式
证明相关命题真假 比较实数大小 求取值范围
内容
几何平均数,
算术平均数
当且仅当a=b时,“=”成立
a,b同号 a=b时取“=”
变形
基本不等式
和定积最大
积定和最小 各项各因式为正,若为负,可提出负号
方法
求最值
和或积为定值
各项能取相等值,若不能取“=”,改用函数单调性 求解
注意
合理拆凑使“=”成立
灵活运用 注意“1”的妙用
证明不等式
合理配组,反复应用
封闭 开放
几个二元一次不等式表示区域的公共部分
求可行域
最先,最后通过的顶点为最优解
作目标函数等值线 平移等值线
注意: 1:自变量的取值范围 2:z=Ax+By中B的符号
人教A版高中数学必修1第三章《函数的应用》思维导图

人教A版高中数学必修1第三章《函数
的应用》思维导图
用思维导图复习,一天顶一个月。
高中数学必修和选修课本共计13本,通常两年内学完,平均一年6本,每学期3本。
每本平均三到四章,每学期5个月,大约半月学完一章。
而高考总复习的时间则更为宝贵,如果高考一轮复习的时候,在基础知识模块,大家还需要消耗大量时间去翻看教材显然得不偿失。
当然,我们并不是说教材不重要,相反,教材非常重要。
而是希望大家在平时的学习过程中,养成总结梳理的习惯,尤其是在高一高二的时候。
只要大家学会使用思维导图梳理,这样在高三的时候就可以快人一步,将更多的宝贵时间拿来突破自己的弱项,争取取得更好的成绩。
已经进入高三的同学,也不用担心,后续我们会持续更新,大家关注我们的文章即可,我们会帮大家梳理好,大家可以通过文章末尾留言免费获取。
本文,我们主要梳理了人教版A版高中数学必修1(也就是高一数学)第三章《函数的应用》。
主要内容大纲如下:
其中重点在于零点问题、函数模型及函数的应用。
下面我们逐一展开回忆下。
一、函数与方程
二、函数模型及其应用
到本文为止,有关人教版A版高中数学必修一(也就是高一数学必修1)的内容,我们就在前面三篇文章给大家梳理完了,至于第一章《集合与函数的概念》及第二章《基本初等函数(I)》,请大家查阅我们前面两天的文章即可。
大家如果觉得这种方式好,可以自己下载思维导图软件尝试下。
时间紧迫,需要x mind 思维导图原图进行复习的同学,可以在评论区联系我们获取。
001 高中数学 集合 思维导图 横版 A3打印

A与B的交集 性质 Ø
或
性质 Ø
若给定全集 ,有
,则
(
)
(
) Ø 性质
A与B的并集 补集
四、集合的基本运算
, 结合律 , 分配律
, 德.摩根律
, 交换律
集合运算律
整数集合 正整数集合 有理数集合 自然数集合
实数集
三、常用数集及记法
集合
一、集合的概念与表示
某些指定的对象在一起就构成一个集 合。集合中的每一个对象叫集合的元 定义 素。
全集 空集
不含有任何元素,符号表示: Ø
二、集合的关系
子集
:若
则
真子集 集合相等
若
则
且
,若
可能
元素与集合的关系
属于∈ 不属于∉
列表法
把集合中的元素一一列举出来
表示方法 描述法
集合中的元素公共属性描述出来
图示法 用封闭的曲线表示
有限集合 集合元素有限
分类 无限集合 集合元素无限
空集 不含有任何元素的集合Biblioteka 确定性 给定集合,元素是确定的
元素特性 互异性 集合中不允许有相同元素出现
无序性 集合里元素的构成顺序随意
高中数学思维导图大全

国
`截式: y =妇干 b
',两点式:� V-VI-=-X-— X1 芍( :¢:X动 五) y?-P1 芬寸
!截距式: :+责= l (吐 0,b#o)
注意(1)截距百 :,可负,也可
1彝为o. (2)方程
各种形式的变化 和适用范围
宜 线
一般式:Ax+By+ C = O(AB-:f:. o)
的
两直线 行
序性
组合的分类
^集 卜巳渠合的表示一 口
列举法,特征性质描述法、Veen图法 性质
(2)A云小(3)则A�B则A.::B或4=, 凡 (4)若A�B, B竺C,则AGC; (5)含有11. '个元素的集合有2“ 个子无宇 有2片-i 个真丁采:
(6)E心;的区别�E表示元素与集合关系
已表示集合与集合关系; (7)屿{叶区别· 一 般地,a表示元压 {叶表示只有 一 个元素tr的菜合:
咖
(
5 l, 万
L1 5 ` 为方向向泣}
la•司 lal• 2直线与平面的夹角6cosO=
恒|
(a 为直线方向向址,行为平面法向盘}
I· 杭I 面角0:cos_0·=� 匠.开介 1 枫
飞,h,.为两平面 向优).
倾斜角与斜卒
倾斜伽「包18OO)和斜率K气na的变化
!点斜式:,V - y0 =沁-X。)
,p) +b
描点法(五点作阻法— ) I 斗几何作图法
对称轴.(正切函数 除外)经过函数图 象的蚊扁氓t低)
点且垂直x轴的直线
对称中心是正余弦函
_佟]象的零点,正切 函数的对称中心为 (一 .k.2it ,.0) (kGZ)
碑象可由正千玄曲线经过平移、伸缩得到,但耍注意先平移后伸缩与先伸缩后平移不同:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学思维导图
高中数学思维导图
一、基础数学思维
1. 数学思想的基础:公理与定义
2. 数学的证明方法:归纳法、反证法、直接证明法等
3. 数学符号的运用:数学符号的含义、符号的运算法则等
4. 数学运算:四则运算、幂运算、根号运算等
5. 基础数学工具:比例、百分数、坐标系、三角函数等
二、代数思维
1. 代数基础:代数式、方程、函数等
2. 函数的性质:奇偶性、周期性、单调性等
3. 多项式函数:求极限、图像、导数、零点等
4. 三角函数:定义、性质、公式、图像等
5. 指数与对数:定义、性质、公式、应用等
三、几何思维
1. 几何基础:点、线、面、角等基本概念
2. 几何证明:直线、三角形、四边形等几何图形的证明方法
3. 圆与圆周角:圆的性质、圆心角、圆周角等
4. 圆锥曲线:椭圆、双曲线、抛物线等
5. 空间几何:立体图形、体积、表面积等
四、数据思维
1. 统计学基础:数据的收集、整理、描述等
2. 统计学方法:中心极限定理、样本误差、置信区间等
3. 概率学基础:试验、随机事件、概率等
4. 概率学应用:概率分布、期望、方差等
5. 统计学计算:统计量、协方差、相关系数等
五、应用思维
1. 数学建模:基础模型、优化模型、决策模型等
2. 实际应用:金融、物流、航空、生物等实际问题的数学分析
3. 数学思维应用:思维方法的应用于科学、技术、文化、艺术等领域
4. 跨学科思维:数学与其他学科的融合,如数理化、数理生等交叉学科
5. 数学思维与未来:数学思维在新时代的重要性和应用前景
六、总结与展望
1. 数学思维的学习方法
2. 数学思维的培养和提升
3. 数学思维在求学与职场中的应用
4. 数学思维的发展趋势和未来展望
5. 数学思维对人类文明进步的贡献。
