人教版高中数学必修一章节思维导图全套
高中数学必修全思维导图

调性不同,则 y f [g(x)] 是减函数。
4、奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反。 5、常用函数的单调性解答:比较大小、求值域、求最值、解不等式、证不等式、作 函数图象。 六、函数奇偶性的常用结论:
1、如果一个奇函数在 x 0 处有定义,则 f (0) 0 ,如果一个函数 y f (x) 既是
高一数学必修 1 知识网络
集合
( 1)元素与集合的关系:属于()和不属于()
集合与元素
( 2)集合中元素的特性:确定性、互异性、无序性 ( 3)集合的分类:按集合中元素的个数多少分为:有限集、无限集、空集 ( 4)集合的表示方法:列举法、描述法(自然语言描述、特征性质描述)、图示法、区间法
C.
4、空集是任何集合的(真)子集。
集合
真子集:若A
B且A
B(即至少存在x0
B但x0
A),则A是B的真子集。
集合与集合
运算集并交合集集Ca相r定定性性d等(义义质质A:::::ABAAAA)BBBC且AAaArdAAxx,(,A//BxAxA) CAAa或且rAdxx(AB,B,)BB-AACarBdB(ABBBA)A,,AABBAA,, AABB
定义
按照某个对应关系f , y都有唯一确定的值和它对应。那么y就是x的函数。记作y f ( x ).
近代定义:函数是从一个数集到另一个数集的映射。
定义域 函数及其表示 函数的三要素 值域 对应法则
解析法
函数的表示方法 列表法
函数
几类不同的增长函数模型 函数模型及其应用 用已知函数模型解决问题 建立实际问题的函数模型
高中数学思维导图知识图谱(全高清版)
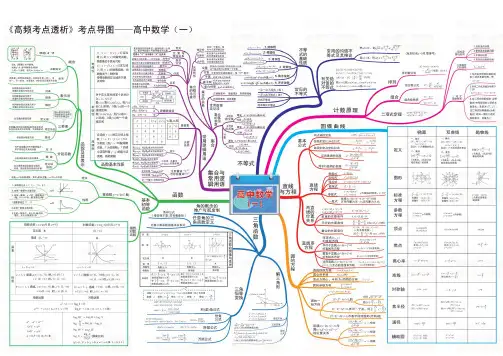
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
新人教版A版高中高一数学必修一知识点思维导图

一般地我们把研究对象统称为元素,把一些元素组成的总体叫同向可加性我们把只含有一个未知数,并且未知求出相应的一元二次方程的根利用二次函数的图像与X轴的交点确定一元二次不等式的解集如果积xy等于定值P,那么当x=y时,和x+y有最小值如果积xy等于定值S,那么当x=y时,积xy有最大值积定和最小,和定积最大设A、B是非空的实数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,是幂函数的底数,幂函数的系数是1, 比如2不是幂函数一次函数:二次函数:反比例函数:第五章 三角函数角的定义平面内一条射线绕着它的端点旋转所成的图形叫做角角的分类按照旋转方向正角负角零角按照终边位置第一象限角第二象限角第三象限角第四象限角度量角的两种制度角度制弧度制诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等sin(2kπ+α)=sinα k∈zcos(2kπ+α)=cosα k∈ztan(2kπ+α)=tanα k∈z 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系sin(π+α)=-sinα k∈zcos(π+α)=-cosα k∈ztan(π+α)=tanα k∈z 公式三:任意角α与 -α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα弧长与角的换算1°=π/180°,1rad=180°/π弧长公式L=n× π× r/180,L=α× r扇形面积公式S=LR/2三角函数的定义域、值域y=sinαy=cosαy=tanα三角函数的单调性正弦函数余弦函数一周是360度,也是2π弧度,即360°=2π.(n是圆心角度数,r是半径,L是圆心角弧长,α是圆心角度数)(R是扇形半径,L是扇形对应的弧长)定义域是R,值域[-1,1]定义域是R,值域[-1,1]定义域是α≠kπ+π/2区间是(kπ-π/2,kπ+π/2)值域是Ry=sinx在[2kπ-π/2,2kπ+π/2],k∈Z,上是增函数;在[2kπ+π/2,2kπ+3π/2],k∈Z,上是减函数;三角函数y=sin x,它的定义域为全体实数,值域为[-1,1]y=cosx在[2kπ,2kπ+π],k∈Z,上是减函数;在[2kπ+π,2kπ+2π],k∈Z,上是增函数;余弦函数的定义域是整个实数集,值域是[-1,1];余弦函数是周期函数,其最小正周期为2π。
人教版高中数学必修一章节思维导图全套
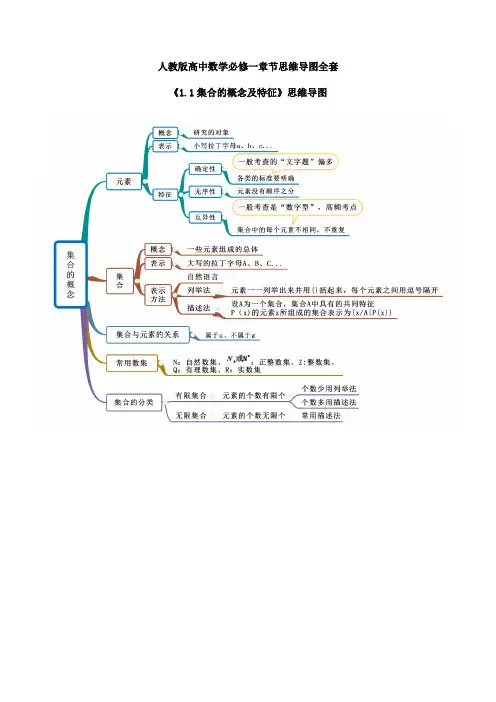
《3.2 函数的性质》思维导图
《3.3 幂函数》思维导图
《4.1 指数的运算》思维导图
《4.2指数函数》思维导图
《4.3 对数的运算》思维导图
《4.4 对数函数》思维导图
《4.5 函数的应用(二)》思维导图
《5.1 任意角和弧度制》思维导图
《5.2 三角函数的概念》思维导图
人教版高中数学必修一章节思维导图全套
《1.1集合的概念及特征》思维导图
《1.2 集合间的关系》思维导图
《1.3 集合的基本运算》思维导图
《1.4 充分、必要条件》思维导图
《1.5 全称量词与存在量词》思维导图
《2.1 等式与不等式的性质元二次方程、不等式》思维导图
《5.3 诱导公式》思维导图
《5.4 三角函数的图象与性质》思维导图
《5.5 三角恒等变换》思维导图
《5.6 函数 》思维导图
《5.7 三角函数的应用》思维导图
人教版高中数学知识框架思维导图(04)-按章节整理(含目录高清版)
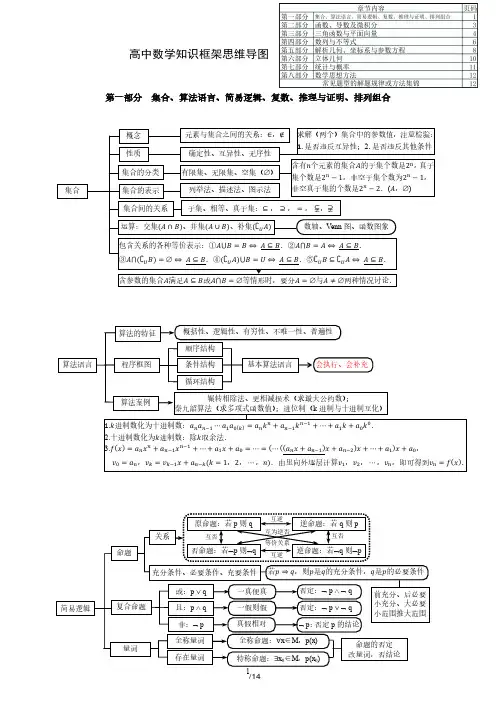
几何意义
归纳
合情推理
猜想
类比
推理
演绎推理
推理与证明
三段论
大前提、小前提、结论
综合法
由因导果
分析法
执果索因
直接证明
证明
间接证明
1.验证 = 0 (初始值)命题成立;
2.若 = ( ≥ 0 )时命题成立,证明 = + 1时命题也成立.
数学归纳法
两个原理
反设、归谬、结论
反证法
分类加法计算原理和分步乘法计算原理
1.f (a+x)=f (b-x),对称轴为 =
对称性
2.f (a+x)+f (b-x)=c,对称中心为(
2
+
2
, )
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
最值
一次、二次函数、反比例函数、双勾函数
基本初等函数
指数函数、对数函数、幂函数、三角函数
分段函数
利用对称性求函数
对称变换: = () → = −(), = () → = (−), = () → = −(−)
函数图象
及其变换
翻折变换: = () → = |()|, = () → = (||)
伸缩变换: = () → = (), = () → = ()
②减法:( + i)-( + i)=(-c)+(b-d)i;
③乘法:( + i)·( + i)=(c-bd)+(d+bc)i;
运算
④除法:
+i
+i
=
(+i)(−i)
(+i)(−i)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《3.3 幂函数》思维导图
《4.1 指数的运算》思维导图
《4.2指数函数》思维导图
《4.3 对数的运算》思维导图
《4.4 对数函数》思维导图
《4.5 函数的应用(二)》思维导图
《5.1 任意角和弧度制》思维导图
《5.2 三角函数的概念》思维导图
《5.3 诱导公式》思维导图
《5.4 三角函数的图象与性质》思维导图
《5.5 三角恒等变换》思维导图
《5.6 函数 》思维导图
《5.7 三角函数的应用》思维导图
人教版高中数学必修一章节思维导图全套11集合的概念及特征思维导图12集合间的关系思维导图13集合的基本运算思维导图14充分必要条件思维导图15全称量词与存在量词思维导图21等式与不等式的性质思维导图22基本不等式思维导图23二次函数与一元二次方程不等式思维导图31函数的概念思维导图32函数的性质思维导图33幂函数思维导图41指数的运算思维导图42指数函数思维导图43对数的运算思维导图44对数函数思维导图45函数的应用二思维导图51任意角和弧度制思维导图52三角函数的概念思维导图53诱导公式思维导图54三角函数的图象与性质思维导图55三角恒等变换思维导图56函数思维导图57三角函数的应用思维导图
人教版高中数学必修一章节思维导图全套
《1.1集合的概念及特征》思维导图
《1.2 集合间的关系》思维导图
《1.3 集合的基本运算》思维导图
《1.4 充分、必要条件》思维导图
《1.5 全称量词与存在量词》思维导图
《2.1 等式与不等式的性质》思维导图
《2.2 基本不等式》思维导图
《2.3 二次函数与一元二次方程、不等式》思维导图
