平面体系的机动分析
平面体系的机动分析测试题
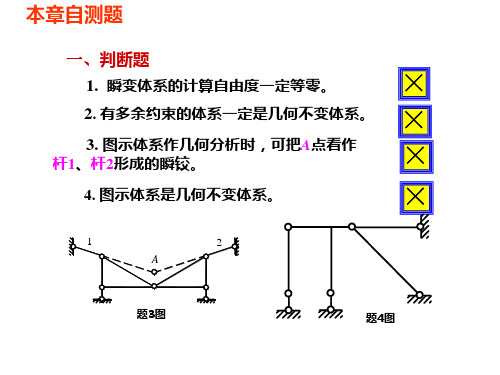
2. 三个刚片每两个刚片之间由一个铰相连接构成的体
系是
D。
A.几何可变体系 B. 无多余约束的几何不变体系
C.瞬变体系 D.体系的组成不确定
3. 图示结构为了受力需要一共设置了五个支座链杆,
对于保持其几何不变来说有 个多2余约束,其中第 个
链杆是1 必要约束,不能由其他约束来代替。
B.有无多余约束的几何不变体系 D.常变体系
提示:体系用不交于一点的三根链杆与基础相连,只需分析 体系本身。选择刚片示于图中,根据三刚片规律。
I
4m
II
B
C
h
III
A
题4图
6m
3m 3m
6m
题5图
5.图示体系A 铰可在竖直线上移动以改变等长杆AB、
AC的长度,而其余结点位置不变。当图示尺寸为哪种情况
4
1
2
3
5
5'
6
8
7
9
解:先去掉二元体35、55',刚片2367仅需3个链杆即可 构成无多余约束的几何不变体系,原体系有一个多余约束,
所以答案选择 。 D
本章自测题
2.图示体系的几何组成为:
A.常变体系 B.无多余约束的几何不变体系
C.瞬变体系 D.有多余约束 的几何不变体系
解:刚片124与基础用铰1相连,刚片356与基础用铰
(a)
(b)
(c)
(d)
本章自测题
6.图a 属几何
A体系。
A.不变,无多余约束 C.可变,无多余约束
(a)
B.不变,有多余约束 D.可变,有多余约束
(b)
图b属几何 B 体系。 1.2.10
平面体系机动分析.

合理,当发生微小位移后,约束的布 置变得合理,就成为几何不变体系;
瞬变体系
2) 在发生微小位移之前,体系具有自由度,因此瞬变体系至 少有一个多余约束。
瞬变体系是绝对不能用来作为结构使用的。 返 回
几何可变体系分:瞬变体系 和 常变体系;
常 变 体 系 ——可以发生大位移的几何可变体系。
几何不变体系( 体系
几何可变体系(
可作为结构)有 无多 多余 余约 约束 束- -超静静定定结结构构 不能作为结构)瞬 常变 变变 变体 体
不变体系
常变体系
返回
小结
以上介绍了几何不变体系的三条简单 组成规则,而它们实质上只是一条规则
,即三刚片规则(或三角形规则)。按
这些规则组成的几何不变体系W=0(体系 本身W=3),因此都是没有多余联系的几何 不变体系。
刚片:几何形状不能变化(几何不变)的平面物体
y B
xA
y
o
x
独立变化的几何参数为:x、y、。 返回
2.约束:
减少自由度的装置(又称为联系)。凡是减少一个 自由度的装置称为一个约束。
3.约束的种类:
⑴ 链杆: 一根链杆相当一个约束。
y
B
x A
y
o
y
xo
B
A 2
1
x
返回
⑵ 单连铰结:两个刚片的铰称为单铰 y
例如:
.
O
F
D B
A
C
E
刚片Ⅰ
基础为刚片Ⅰ,杆BCE为 刚片Ⅱ,用链杆AB、 EF 、 CD 相联,为几何不变 体系。
Ⅱ
ⅠLeabharlann 返回2. 基本的三刚片规则(三角形规则):
李廉锟第四版《结构力学》第2章平面体系的机动分析习题+参考答案
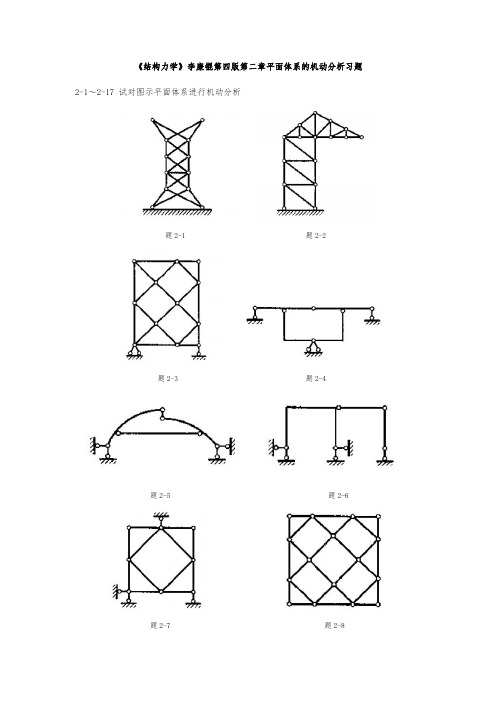
《结构力学》李廉锟第四版第二章平面体系的机动分析习题2-1~2-17试对图示平面体系进行机动分析题2-1题2-2题2-3题2-4题2-5题2-6题2-7题2-8题2-9(a、b处非结点)题2-10(k处非结点)题2-11题2-12题2-13题2-14题2-15(k处非结点)题2-16题2-172-18、2-19添加最少数目的链杆和支承链杆,使体系成为几何不变,而且无多余约束。
题2-18题2-19《结构力学》李廉锟第四版第二章平面体系的机动分析参考答案题2-1说明:自上往下依次拆除二元体,或者自下往上依次添加二元体,故体系为有一个多余约束的几何不变体系(多余约束:中间的横杆或者也可以看成支座上多了一根水平杆)。
题2-2说明:如图所示取刚片1和刚片2,采用二刚片规则(两刚片用一个铰和一根不通过此铰的链杆相联),为几何不变体系,而且没有多余联系。
刚片1由二元体组成,刚片2从大地向上组装二元体组成。
题2-3说明:先不考虑支座的三根链杆,考虑上部几何构造,去掉二元体简化分析,取如上图所示刚片1、刚片2和刚片3。
刚片1和刚片2通过一个实铰联结;刚片1和刚片3通过两根平行链杆联结,交于无穷远处;刚片2和刚片3通过两根平行链杆联结,交于无穷远处;三铰不共线,故上部无多余约束且几何不变。
最后上部与大地通过一个铰和一根不通过此铰的链杆相联,故整个体系为无多余约束的几何不变体系。
题2-4说明:如上图所示取刚片1、刚片2和刚片3,刚片1和刚片2交于铰12O ,刚片1和刚片3交于铰13O ,刚片2和刚片3交于铰23O ,三铰不共线,故原体系为无多余约束的几何不变体系。
题2-5说明:将大地等效成一根链杆,取如图所示刚片1和刚片2,显然两刚片通过三根链杆相联,且三根链杆既不相互平行也不相交于一点,故原体系为无多余约束的几何不变体系。
题2-6说明:先拆除二元体以简化分析,可知右部分为常变部分;左部分为有一个多余约束的几何不变体系,故体系为几何常变体系。
第二章:平面体系的机动分析(结构力学 李廉锟 第五版 配套)

y A' B' D Dy B Dx
x
A 0
自由度: 描述几何体系运动时,所需独立坐标的数目。 几何体系运动时,可以独立改变的坐标的数目。 几何可变体系自由度大于0 几何不变体系自由度等于0 平面内的点自由度为2 平面内的刚体自由度为3
联系(约束)
如果体系有了自由度,必须消除,消除的办法是增加约束。
W=3×7-(2×9)-3=0
平面杆件体系的自由度
若每个节点均为自由,则有2j个自由度,但连接节点的每根杆 件都起一个约束作用,则体系的计算自由度为
W=2j-b -r
j---刚片数; b---杆件数; r ---支座链杆数。
算例
j=4
b=4 r=3
j=8
b=12
r=4
W=2×4-4-3=1
W=2×8-12-4=0
在运动中改变位置。
虚铰特例 2杆平行等长,刚片位置改变,链杆仍平行但改变方 向,虚铰转到另一无穷远点(常变体系)
2杆平行不等长,刚片位置改变,链杆不再平行, 虚铰转到有限远点(瞬变体系)
基本组成规则
基本规则的应用
利用组成规律可以两种方式构造一般的结构:
(1)从基础出发构造
(2)从内部刚片出发构造
2.5 机动分析
1,3
.
.1,2
2,3
.
.
无多余约束的几何不变体系
几何瞬变体系
1,2
. .
1,3 2,3
. 2,3
几何瞬变体系
1,2 1,3
F
D C E
F
D C B E
A
A
B
F
D
C A
E
D
E
C
平面体系的机动分析PPT双语71页

平面体系的机动分析
(Geometric Construction Analysis of Plane Systems)
§2-1 引 言 Introduction
结构:由杆件、结点和支座组成的杆件体系 Structure consists of members, joints and supports.
If the deformation of materials is neglected, then framed systems can be classified into two categories: 几何不变体系 ( geometrically stable system )
几何可变体系( geometrically unstable system )
几何可变体系( geometrically unstable system )
在一般荷载作用下,几何形状及位置将发生改变机构
的体系。(不考虑材料的变形) Under the action of any loads, the system will change its shape and its location if the deformations of the members are neglected.
几何不变体系 ( geometrically stable system )
在任意荷载作用下,几何形状及位置均 保持不变的体系。(不考虑材料的变形)
结构
Under the action of any loads, the system still maintain its shape and remains its location if the deformations of the members are neglected.
第二章-平面体系几何组成分析

2-3 几何不变体系的基本组成规律 基本规则
2-4 瞬变体系
FNAB =FNAC =FN
2FN sina=FP
δ
FN =FP /(2 sina )
l2 2 l 2
2l
2-5 几何组成分析示例 几何组成分析目的
体系
几何不变 几何可变
无多余约束的几何不变体系 有多余约束的几何不变体系
瞬变体系 常变体系
2-2 平面体系的计算自由度 约束/联系
复刚结点
连接n个刚片的复刚结点, 相当于(n -1)个单刚结点, 能减少3(n -1)个自由度, 故相当于3(n -1)个约束。
2-2 平面体系的计算自由度 必要约束/多余约束
必要约束
多余约束
多余约束
必要约束
结论:只有必要约束才能对体系自由度有影响。
2-2 平面体系的计算自由度
2-5 几何组成分析示例 例题 I
B
A
C
DE
B
AⅠ
ⅡC
DE
Ⅲ
2-5 几何组成分析示例 例题 II
2-5 几何组成分析示例 例题 III
利用虚铰
等效链杆
2-5 几何组成分析示例 例题 VI
将刚片画成直杆
将
画成
2-5 几何组成分析示例 例题 V
主从结构
2-5 几何组成分析示例 例题 VI
C B A
第二章
平面体系的机动分析
Geometric Construction Analysis of Planar Systems
2-1 概述 机动分析前提假设
结构可变性分为: 物理可变形;几何可变性。
机动分析前提假设: 不考虑材料变形。
2-1 概述 体系的分类
平面体系的机动分析—习题课

结构的几何构造分析
5、在一个平面体系上增加二元体不会改变体系的计算自由度。(√)
(√) 6、若平面体系的计算自由度W<0,则体系不可能是静定结构。 7、若平面体系的计算自由度W=0,则体系为无多余约束的 几何不变体系或瞬变体系,而不可能是常变体系。 (×)
二、选择题
A 1、W≤0是保证体系为几何不变的———条件。 (A)必要条件 (C)非必要条件 (B)充分条件 (D)必要和充分条件 D 2、在土木工程不能作为建筑工程应用的是———— (A)几何不变体系,无多余约束 (C)几何不变体系,有多余约束
而不要成为几何可变体系或瞬变体系,以避免发生严重 的工程事故。尤其新型结构,更应注意结构的几何构造 分析。 2 从几何构造分析的观点看,结构体系可分类如下:
几何体系
几何不变体系 几何可变体系
常变体系 瞬变体系
17
结构的几何构造分析
3 在结构几何构造分析中,可先计算体系的自由度 W (V ) 。
若体系的
5
结构的几何构造分析
2、二个虚铰在无穷远处:
若组成两无穷远处虚铰的两对平行链杆互不平行,则体系 为几何不变体系;若两虚铰的四根链杆互相平行但不等长, 则为体系为瞬变体系;若两虚铰的四根链杆平行且等长,则 体系为常变体系。
3、三个虚铰在无穷远处: 若三刚片用三对平行但不等长的链杆相联,则体系为瞬变 体系;若三刚片用三对平行且等长的链杆相联,则为体系为 常变体系。 注:这里指每对链杆都是从每一个刚片的同侧方向联结另一 个刚片;若两链杆是从刚片的异侧方向联结另一个刚片,则 6 体系为瞬变体系。
W (V ) 0
,则体系为几何可变体系;若体系的
W (V ) 0 ,则应对体系进行几何构造分析。若对几何构造分
2011 第二章 平面体系的机动分析9.8

链杆 体系
链杆
A D
刚片1 刚片
B
§2-3 几何不变体系的基本组成规则
任何体系增减二元体,其机动性质不变。 注: 任何体系增减二元体,其机动性质不变。
Ⅰ
减二元体简化分析 加二元体组成结构
§2-3 几何不变体系的基本组成规则
例:分析图示铰结体系
以铰结三角形123为基础,增加一个二元体得结点4, 为基础,增加一个二元体得结点 , 以铰结三角形 为基础 1234为几何不变体系;如此依次增加二元体,最后的体系 为几何不变体系; 为几何不变体系 如此依次增加二元体, 为几何不变体系,没有多余联系。 为几何不变体系,没有多余联系。 或:从结点10开始拆除二元体,依次拆除结点9,8, 从结点 开始拆除二元体,依次拆除结点 , , 开始拆除二元体 7…,最后剩下铰结三角形 ,最后剩下铰结三角形123,它是几何不变的,故原体 ,它是几何不变的, 系为几何不变体系,没有多余联系。 系为几何不变体系,没有多余联系。
§2-2 平面体系的计算自由度
四、平面体系的计算自由度 体系中各构件间无任何约束时的总自由度数与 总约束数之差称计算自由度 计算自由度( ) 总约束数之差称计算自由度(W)。 算法1 算法1 W = 3m-(2h+r) 算法2 算法2
m ---- 体系刚片数 体系刚片数 h ---- 单铰结点数 r ---- 支座链杆数 支座链杆数
相交在∞点 相交在∞点
A
Ⅱ Ⅰ
A
A’
Ⅱ Ⅰ
图 2 虚铰
Ⅱ
图 1实铰 实铰
Ⅰ
§2-2 平面体系的计算自由度
3、刚结点 1个单刚结点=3个联系 个单刚结点=3个联系 =3
复刚结点
一个连接 n个刚片的复刚相 个刚片的复刚相 当于(n-1)个单刚结点,相当于 当于 个 刚结点, 3(n-1)个约束。 个约束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使得体系减少自由度的联结装置称约束或联系。在刚片间加入某些联结装置,它们的
自由度将减少,减少一个自由度的装置就称为一个约束,减少n个自由度的装置就称为个约束。
n
2.1.1不同联结装置对体系的约束作用
1.链杆的作用
图2-4(a)表示用一根链杆BC联结的两个刚片Ⅰ和Ⅱ。未联结以前,这两个刚片在平面
(2)自由度。
图2-2所示为平面内一点A的运动情况。一点在平面内可以沿水平方向(x轴方向)移
动,又可以沿竖直方向(y轴方向)移动。当给定x、y坐标值后,A点的位置确定。换句话
说,平面内一点有两种独立运动方式(两个坐标x、y可以独立地改变),即确定平面内一点
的位置需要两个独立的几何参数
(x、y坐标值
),因此我们说一点在平面内有两个自由度。
后的自由度总数为五个(6- 1=5)。由此可见,一根链杆使体系减少了一个自由度,也就是说,
一根链杆相当于一个联系或一个约束。
2.单铰的作用
图2-4(b)表示用一个铰B联结的两个刚片Ⅰ和Ⅱ。在未联结以前, 两个刚片在平面内共
有六个自由度。在用铰B联结以后,刚片Ⅰ仍有三个自由度,而刚片Ⅱ则只能绕铰B作相
EF来看,E点的运E点的这种运动不可能
发生,也就是链杆
EF阻止了刚片Ⅰ和刚片Ⅱ的相对转动。因此,这样组成的体系是几何不
变体系。
图2-7两刚片组成规则
如果在刚片Ⅰ和刚片Ⅱ之间再增加一根链杆,如图2-7(c)所示,显然体系仍是几何不变
的,但从保证几何不变性来看它是多余的。这种可以去掉而不影响体系几何不变性的约束
对转动,即再用一个独立参数(夹角)就可确定它的位置,所以减少了两个自由度。因此,
两个刚片用一个铰联结后的自由度总数为四个(6- 2=4),我们把联结两个刚片的铰称为单铰。
由此可见,一个单铰相当于两个联系,或两个约束,也相当于两根链杆的作用;反之,两
根链杆也相当于一个单铰的作用。
我们将地基看作是不动的,这样,如果在体系上加一个可动铰支座,就使体系减少一
显然,可动铰支座即链杆支承只能阻止刚片沿链杆方向的运动,使刚片减少了一个自由度,相当于一个约束;铰支座阻止刚片上下、左右的移动,使刚片减少两个自由度,相当于两个约束;固定支座阻止刚片上下、左右的移动,也阻止其转动,所以相当于三个约束。
图2-4
链杆、单铰、复铰、刚性联结相当的约束数目示意图
5.虚铰的作用
BC的圆弧上运动。 由于
AB和
BC
是在
C点用铰
联结在一起的,
C点不可能同时在两个不同的圆弧上运动,
因此刚片之间不可能发生相对运
动,所以这样组成的体系是几何不变的。
图2-8三刚片组成规则
因为两根链杆的作用相当于一个单铰的作用,则将图2-8(a)中的任一单铰换为两根链杆
所构成的虚铰,如图2-8(b)中的a、c,此时,三刚片用三个铰(两个虚铰和一个实铰)联结,
2.2.1两刚片之间的联结
图2-7(a)表示用两根不平行的链杆相联结的刚片Ⅰ和刚片Ⅱ。设刚片Ⅱ固定不动,则刚
片Ⅰ的运动方式只能是绕AB与CD杆延长线的交点即相对转动瞬心而转动。当刚片Ⅰ运动
时,其上的A点将沿与链杆AB垂直的方向运动,而C点将沿与链杆CD垂直的方向运动。
因为这种转动只是瞬时的,在不同瞬时,
与两根链杆相应的虚铰位置也跟着改变。
图2-5
虚铰
2.1.2体系自由度的计算公式
我们已经研究了不同约束对体系自由度的影响,下面给出平面刚片系统计算体系自由度的公式:
W 3m 2n c c0
(2-1)
式中,m表示体系中的刚片数
(地基不计入);n为联结刚片的单铰数;
c为联结刚片的链杆
数;c0为体系与地基联结的支座链杆数,且将三类支座均用相应的链杆约束代替,即可动
图2-2平面内一点的自由度示意图图2-3平面内一刚片的自由度示意图
综上所述,可以说,某个体系的自由度,就是该体系运动时可以独立变化的几何参数
的数目,或者说,就是用来确定该体系的位置所需独立坐标的数目。一般来说,如果一个
体系有n个独立的运动方式,我们就说这个体系有n个自由度。凡是自由度大于零的体系
都是几何可变体系。
的两根连杆称为二元体。二元体的特征是两链杆用铰相连,而另一端分别用铰与刚片或体
系相联。根据二元体的ຫໍສະໝຸດ 成特征可得出以下规则。规则三 :在一个刚片上增加一个二元体,仍为几何不变体系。
由规则三不难得出以下推论:在一个体系上依次加入二元体,不会改变原体系的计算
自由度,也不影响原体系的几何不变性和可变性。反之,若在已知体系上依次排除二元体,
能承受荷载而维持平衡。通过体系的几何组成,可以确定结构是静定的还是超静定的,以
便在结构计算中选择相应的计算方法。
为了分析平面体系的几何组成,首先介绍几个基本概念。
(1)刚片。
一个在平面内可以看作刚体的物体,它的几何形状和尺寸都是不变的。因此,在平面
体系中,当不考虑材料的应变时,就可以把一根梁、一根链杆或者体系中已经确定为几何不变的某一部分看作一个刚片,结构的基础也可以看作刚片。
也不会改变原体系的计算自由度、几何不变性或可变性。
例如分析图2-10所示桁架时,由规则二可知,任选一铰结三角形都是几何不变体系,
并以此为新的刚片,采用增加二元体的方式分析。例如取新刚片AHC,增加一个二元体得
结点Ⅰ,从而得到几何不变体系
AHIC,再以其为基础,增加一个二元体得结点
D,⋯,如
此依次增添二元体而最后组成该桁架,故知它是一个几何不变体系,且无多余约束。
铰支座的c0=1,固定铰支座的
c0=2,定向支座的c0=2,固定支座的c0
=3。显然,几何不变
体系的自由度必然是等于零或小于零,即由式(2-1)计算出的W≤0。
图2-6(a)所示为一简支梁,其刚片数m=1,单铰数n=0,链杆数c=0,支座链杆数c0=3,
则自由度W=0。而图2-6(b)所示的体系刚片数m=9,单铰数n=12,链杆数c=0,支座链
内共有六个自由度。用链杆
BC
联结以后, 对刚片Ⅰ而言, 其位置需用刚片上
A点的坐标
x、
y和AB连线的倾角来确定,因此它有三个自由度。但是对刚片Ⅱ而言,由于与刚片Ⅰ已
用链杆BC联结,它只能沿着B为圆心、BC为半径的圆弧运动和绕C点转动,再用两个独
立参数和即可确定它的位置,所以减少了一个自由度。因此,两个刚片用一根链杆联结
为几何不变体系。如图2-1(a)所示的体系就是一个几何不变体系,因为在所示荷载作用下,
只要不发生破坏,它的形状和位置是不会改变的。在任意荷载作用下,不考虑材料的应变,
体系的形状和位置可以改变,则称这样的体系为几何可变体系。图2-1(b)所示的体系,在所
示荷载P的作用下,即使P的值非常小,它也不能维持平衡,这是由于体系缺少必要的杆件或杆件布置不合理而导致的。一般工程结构都必须是几何不变体系,而不能采用几何可
变体系,否则将不能承受任意荷载而维持平衡。因此,在设计结构和选取计算简图时,首
先必须判别它是否几何不变,从而决定能否采用,这一工作就称为体系的机动分析或几何
组成分析。此外,以后会看到,机动分析还将有助于结构的内力分析。
图2-1体系几何性质
对体系进行机动分析的目的就是确定该体系是否几何不变,从而决定它能否作为结构。确定体系是否为几何不变体系,需要研究几何不变体系的组成规律,以保证所设计的结构
且三个铰不在一条直线上,这样组成的体系同样为几何不变的,而且无多余约束。
由以上分析可得出以下规则。
规则二 :三个刚片用不在同一条直线上的三个铰两两铰联,组成的体系是几何不变的,
并且没有多余约束。
2.2.3二元体的概念
图2-9所示体系中Ⅰ为一刚片,从刚片上的
、
1、
A B两点出发,用不共线的两根链杆
链杆2在结点C相连。 将链杆1、链杆2均视为刚片, 则由规则二可知, 该体系是几何不变的。由于实际结构的几何组成中这种联结方式应用很多,为了便于分析,我们将这样联结
称为多余约束。
由以上分析可得以下规则。
规则一 :两个刚片用不交于一点也不互相平行的三根链杆相联结,则所组成的体系是
几何不变的,并且没有多余约束。
如果两根链杆AB和CD相交成为实铰,如图
2-7(d)所示,显然,它也是一个几何不变
体系,故规则一也可以表述为:两个刚片用一个铰和轴线不通过这个铰的一根链杆相联结,则所组成的体系也是几何不变体系。
了四个自由度。我们把联结两个以上刚片的铰称为复铰。由上述可见,一个联结三个刚片
的复铰相当于两个单铰的作用。一般情况下,如果n个刚片用一个复铰联结,则这个复铰
相当于n-1个单铰的作用。
4.刚性联结的作用
图2-4(d)所示为两根杆件AB和BC在B点连接成一个整体,其中的结点B为刚结点。
原来的两根杆件在平面内共有六个自由度,刚性连接成整体,形成一个刚片,只有三个自由度,所以一个刚性联结相当于三个约束。
个自由度;加一个固定铰支座,就使体系减少两个自由度;加一个固定支座,就使体系减少三个自由度。
3.复铰的作用
图2-4(c)表示用一个铰C联结的三个刚片Ⅰ、Ⅱ和Ⅲ。 在未联结以前, 三个刚片在平面
内共有九个自由度。在用铰C联结以后,刚片Ⅰ仍有三个自由度,而刚片Ⅱ和刚片Ⅲ则都
只能绕铰C作相对转动,即再用两个独立参数(夹角、)就可确定它们的位置,因此减少
2.2.2三刚片相互联结
将三个刚片Ⅰ、Ⅱ和Ⅲ用不在同一直线上的三个铰两两相联,即得三角形ABC,如
图2-8(a)所示。从几何上看,它的几何形状是不会改变的。从运动上看,如将刚片Ⅰ固定不
动,则刚片Ⅱ只能绕
A点转动,其上的
C点必在半径为
AC
的圆弧上运动;而刚片Ⅲ则只
