同样签订“广场协议”,货币大幅升值100%以上,为什么只有日本败了,这个国家却安然无恙
安徽省县中联盟2023-2024学年高二上学期10月联考数学试卷及答案

函蜘郎长芒邻茶栩2023"-'2024学年安徽县中联盟高二10月联考数学试题考生注意:l.满分150分,考试时间120分钟。
2.考生作答时,请将答案答在答题卡上。
选择题每小题选出答案后,用2B铅笔把答超卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
3.本卷命题范困:人教版必修第一册、第二册,选择性必修笫一册2.2结束。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.L已知i是虚数单位,-a+bi=2b-i,a,bER,则la一如=A.我B.戎 C.22.已知直线l的一个方向向批为(烈,-3),则直线l的倾斜角a=A. 30•B. so· c. 120° o. 1so03.在棱长为2的正方体ABCD-A心C1D1中,E、F,G、H分别为AIBl、B心、A1D1、BB1的中.盲盲点,则IGF+GH+2EGI=A../6B.2屈D../5C.月D.2我l4.已知直线l1y=-工+1与y轴交千点P,将l绕点P逆时针旋转45°后与工轴交千点Q,要使2直线l平移后经过点Q,则应将直线l1A.向左平移一个单位长度 16B.向右平移一个单位长度65C.向左平移一个单位长度 53 D.向右平移一个单位长度3一酝• 盲• • 5.巳知向批OA=(0,1,2),0B=(一1,0,l),0C=(2,1,入),若O,A,B,C共而,则0C在OB上的投影向址的桢为A.q B.我c.孚过6.光线通过点A(2,3),在直线l,工+y+l=O上反射,反射光线经过点B(2,2),则反射光线所.(f: ·1'[线方程为A. 6:r-5y-2=0C. 5:r-6y+2=0认6.1·+Sy-22=0D.釭+6y-22=0[抖二J O丿l联打·数学卷第1页(共4页)RJ】4048B7.已知向俅a=(2,1),b= (0,2),c=(一1,1),集合A={,m m=a+入b},B={nl n=b+入2c},其中入1山ER,则A.AnB=0B.An B={2,0}C.若d EAn B,则(a,心为钝角D.若dEA nB,则l b=d2&已知a=/1了一』了,b=6斗,c=logs3-¾log克则9A.a<b<cB. b<c<aC. b<a<cD. c<a<b二、选择题:本题共4小题,每小题5分,共20分。
冀教版七年级英语上册Lesson8 课件

一、单项选择
1.—___A_____people travel every year?
—Perhaps when we are talking about it, more than
100 planes have taken off around the world.
8.How many c_l_a__s_s_e_s_(class) do you have at school? 9.I buy crayontso________(paint). 10.How about _mp_ia_xi_in_nt_g__(mix) these colours?
本节课主要学习了以下重点内容: (1)重点单词:want, paint, make, look等。 (2)重点短语:mix…and…, in the sky等。 (3)重点句式:I don’t like red. How about…?
3.MiHxowbltuoemaankde ygerleleonw?.
I am a rainbow. Look at me.
How many colors do you see?
I am red, orange and blue.
I am green, yellow and purple, too.
want之后加动词不 the park
定式to do表示想 tomorrow.我想明
做某事。
天去公园。
want sb. to do I want Jenny to
sth.想让某人做某 go with me.我想
事。
让詹妮和我一起
苏科版七年级数学下册7.1直线平行的条件和探索例题和同步练习(含练习答案)

苏科版七年级数学下册直线平行的条件和探索【直线平行的条件和性质】【学习目标】1.同位角、内错角、同旁内角的识别;2.会判定两条直线平行;3.平行线的性质.【基础知识梳理】1.如图,同位角的是;内错角的是;同旁内角的是.2.直线平行的条件:(1)基本事实:,两直线平行;(2)定理:,两直线平行;(3)定理:,两直线平行.3.平行线的性质:(1)基本事实:两直线平行,;(2)定理:两直线平行,;(3)定理:两直线平行,.【典型例题】一、三线八角模型例1:如图所示,同位角一共有对,分别是;内错角一共有对,分别是;同旁内角一共有对,分别是.【变式】已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上.例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1一同旁内角→∠9一内错角→∠3.路径2:∠1一内错角→∠12一内错角→∠6一同位角→∠10一同旁内角→∠3.试一试:(1)从起始∠1跳到终点角∠8;(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?二、平行线的判定例2:如图,点E在AC的延长线上,给出四个条件:①∠1=∠2;②∠3=∠4:③∠A=∠DCE;④∠D+∠ABD=180°.其中能判断AB∥CD的有.(填写所有满足条件的序号)三、平行线的性质例3:如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,求图2中∠AEF的度数.【变式】如图,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,求∠F的度数.四、综合运用例4:填空并完成以下证明:已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.证明:FH⊥AB(已知)∴∠BHF=.∵∠1=∠ACB(已知)∴DE∥BC()∴∠2=.()∵∠2=∠3(已知)∴∠3=.()∴CD∥FH()∴∠BDC=∠BHF=.°()∴CD⊥AB.例5:(1)如图(1),若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由;(2)如图(2),要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的数量关系,试说明理由.【变式】问题情境:如图1,AB∥CD,∠P AB=130°,∠PCD=120°.求∠APC度数.小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.问题迁移:(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.【拓展应用】例6:如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.【能力提升】1.如图所示,下列结论中不正确的是()A.∠1和∠2是同位角B.∠2和∠3是同旁内角C.∠1和∠4是同位角D.∠2和∠4是内错角2.在同一个平面内,不相邻的两个直角,如果它们有一条边共线,那么另一边互相()A.平行B.垂直C.共线D.平行或共线3.如图,F A⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是()A.由∠CAB=∠NCD,得AB∥CD B.由∠DCG=∠BAC,得AB∥CDC.由∠MAE=∠ACG,∠DCG=∠BAE,得AB∥CD D.由∠MAB=∠ACD,得AB∥CD4.如图,在△ABC中,以点C为顶点,在△ABC外画∠ACD=∠A,且点A与D在直线BC的同一侧,再延长BC至点E,在所作的图形中,∠A与是内错角;∠B与是同位角;∠ACB与是同旁内角.5.如图,已知∠1=(3x +24)°,∠2=(5x +20)°,要使m ∥n ,那么∠1= (度).6.如图,BE ∥CF ,则∠A +∠B +∠C +∠D = 度.7.如图,直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交,若∠1=30°,求∠2的度数.8.(1)如图①,若∠B +∠D =∠BED ,试猜想AB 与CD 的位置关系,并说明理由;(2)如图②,要想得到AB ∥CD ,则∠1、∠2、∠3之间应满足怎样的数量关系,试说明理由.9.如图,AD ∥BC ,∠DAC =120°,∠ACF =20°,∠EFC =140°.求证:EF ∥AD .10.【探究】如图①,∠AFH 和∠CHF 的平分线交于点O ,EG 经过点O 且平行于FH ,分别与AB 、CD 交于点E 、C .(1)若∠AFH =60°,∠CHF =50°,则∠EOF = 度,∠FOH = 度.(2)若∠AFH +∠CHF =100°,求∠FOH 的度数.【拓展】如图②,∠AFH 和∠CHI 的平分线交于点O ,EG 经过点O 且平行于FH ,分别与AB 、CD 交于点E 、G .若∠AFH +∠CHF =α,直接写出∠FOH 的度数.(用含α的代数式表示)【能力提升】答案第1题 第3题 第4题 第5题 第6题1.如图所示,下列结论中不正确的是()A.∠1和∠2是同位角B.∠2和∠3是同旁内角C.∠1和∠4是同位角D.∠2和∠4是内错角解:A、∠1和∠2是同旁内角,故本选项错误,符合题意;B、∠2和∠3是同旁内角,故本选项正确,不符合题意;C、∠1和∠4是同位角,故本选项正确,不符合题意;D、∠3和∠4是内错角,故本选项正确,不符合题意;故选:A.2.在同一个平面内,不相邻的两个直角,如果它们有一条边共线,那么另一边互相()A.平行B.垂直C.共线D.平行或共线解:如图所示:不相邻的两个直角,如果它们有一条边共线,内错角相等,或同旁内角互补,那么另一边互相平行或共线.故选:D.3.如图,F A⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是()A.由∠CAB=∠NCD,得AB∥CDB.由∠DCG=∠BAC,得AB∥CDC.由∠MAE=∠ACG,∠DCG=∠BAE,得AB∥CDD.由∠MAB=∠ACD,得AB∥CD解:A、正确,同位角∠CAB=∠NCD,故AB∥CD;B、错误,∠DCN=∠BAC不是同位角,所以B不对;C、正确,∠MAE=∠ACG,∠DCG=∠BAE,可得同位角∠BAN=∠DCN,故AB∥CD;D、正确,同位角∠MAB=∠ACD,故AB∥CD.故选:B.4.如图,在△ABC中,以点C为顶点,在△ABC外画∠ACD=∠A,且点A与D在直线BC的同一侧,再延长BC至点E,在作的图形中,∠A与是内错角;∠B与是同位角;∠ACB与是同旁内角.解:如图所示,∠A与∠ACD、∠ACE是内错角;∠B与∠DCE、∠ACE是同位角;∠ACB与∠A、∠B是同旁内角.5.如图,已知∠1=(3x+24)°,∠2=(5x+20)°,要使m∥n,那么∠1=75(度).解:如图所示:∠1+∠3=180°,∵m∥n,∴∠2=∠3,∴∠1+∠2=180°,∴3x+24+5x+20=180°,解得:x=17,则∠1=(3x+24)°=75°.6.如图,BE∥CF,则∠A+∠B+∠C+∠D=180度.解:如图所示,由图知∠A+∠B=∠BPD,∵BE∥CF,∴∠CQD=∠BPD=∠A+∠B,又∵∠CQD+∠C+∠D=180°,∴∠A+∠B+∠C+∠D=180°.7.如图,直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交,若∠1=30°,求∠2的度数.解:如图,∵∠ACB=90°∴∠1+∠3=90°,∵∠1=30°,∴∠3=60°,∵a∥b,∴∠2=∠3=60°.8.(1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由;(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的数量关系,试说明理由.解:(1)AB∥CD,理由:如图(1),延长BE交CD于F.∵∠BED=∠B+∠D,∠BED=∠EFD+∠D,∴∠B=∠EFD,∴AB∥CD;(2)∠1=∠2+∠3.理由如下:如图(2),延长BA交CE于F,∵AB∥CD(已知),∴∠3=∠EF A(两直线平行,同位角相等),∵∠1=∠2+∠EF A,∴∠1=∠2+∠3.9.如图,AD∥BC,∠DAC=120°,∠ACF=20°,∠EFC=140°.求证:EF∥AD.证明:∵AD∥BC,∴∠DAC+∠ACB=180°,∵∠DAC=120°,∴∠ACB=60°,又∵∠ACF=20°,∴∠BCF=∠ACB-∠ACF=40°,又∵∠EFC=140°,∴∠BCF+∠EFC=180°,∴EF∥BC,∵AD∥BC,∴EF∥AD.10. 【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.(1)若∠AFH=60°,∠CHF=50°,则∠EOF=度,∠FOH=度.(2)若∠AFH+∠CHF=100°,求∠FOH的度数.【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF =α,直接写出∠FOH的度数.(用含α的代数式表示)解:【探究】(1)∵∠AFH=60°,OF平分∠AFH,∴∠OFH=30°,又∵EG∥FH,∴∠EOF=∠OFH=30°;∵∠CHF=50°,OH平分∠CHF,∴∠FHO=25°,∴△FOH中,∠FOH=180°-∠OFH-∠OHF=125°;故答案为:30,125;(2)∵FO 平分∠AFH ,HO 平分∠CHF ,∴∠OFH =12 ∠AFH ,∠OHF =12∠CHF . ∵∠AFH +∠CHF =100°,∴∠OFH +∠OHF =12 (∠AFH +∠CHF )=12×100°=50°. ∵EG ∥FH ,∴∠EOF =∠OFH ,∠GOH =∠OHF .∴∠EOF +∠GOH =∠OFH +∠OHF =50°.∵∠EOF +∠GOH +∠FOH =180°,∴∠FOH =180°-(∠EOF +∠GOH )=180°-50°=130°.【拓展】∵∠AFH 和∠CHI 的平分线交于点O ,∴∠OFH =12 ∠AFH ,∠OHI =12∠CHI , ∴∠FOH =∠OHI -∠OFH=12(∠CHI -∠AFH ) =12(180°-∠CHF -∠AFH ) =12(180°-α) =90°-12α.。
淮南市(二模)2023届高三第二次模拟考试数学试卷及答案

淮南市2023届高三第二次模拟考试学试题数本试卷分为第I卷(选择题〉和第E卷〈非选择题〉两部分.考试时间120分钟.第I卷,....... 3、N··一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,有且只有一项符合题目要求.1己知全集U=R ,集合A=�eRly=�},则CuA=<D . {x i x 三-1}C .{x lx 豆-1}B .{x lx <O }A .{x lx <-1}2己知复数z 满足(2-i)·z = i2023,(i 是虚数单位),则复数z 在复平面内所对应的点位于〉A.第一象限B.第二象限c.第三象限 D.第四象限3.四位同学各自在“五一”劳动节五天假期中任选一天参加公益活动,则甲在5月1日、乙不在5D .-25c 土25月1日参加公益活动的概率为(4 B. -54己知函数f(x )=A s 叫ω+的,[A >阳〉喇〈立的相邻两个对称中心距离为2且图\2)象经过Ml 乏,A i ,若将f(x )图象上的所有点向右平移至个单位长度得到函数g(x )的图象,飞。
)6则函数g(x )的单调递减区间是〈 B.[k π中π刽k eZ[叶,kπ叶ke ZA.D.[k 什叶十εZC.[k 7r,ktr +f J.k eZ〉〉汩。
A ..!_52,r5.在A ABC中,己知LACB=一-,BC=4,AC=3,D是边AB的中点,点E满足3一-3一-1一一一一一『A E=-AB+-AC,则CD·DE=()4 4A.-三B.l c ..!.8 2 86.我国古代数学在宋元时期达到繁荣的顶点,涌现了一大批卓有成就的数学家,其中朱世杰与秦九韶、杨辉、李冶被誉为我国“宋元数学四大家”朱世杰著有《四元玉鉴》和《算学启蒙》等,在《算学启蒙》中,最为引人入胜的问题莫过于堆垛问题,其中记载有以下问题:“今有三角、四角果子垛各一所,共积六百八十五个,只云三角底子一面不及四角底子一面七个,问二垛底子一面几何?”其中“积”是和的意思,“三角果子垛”是每层都是正三角形的果子垛,自上至下依次有I,3, 6, 10, 15, ...,个果子,“四角果子垛”是每层都是正方形的果子垛,自上至下依次有L4, 9, 16, ...,个果子,“底子一面”指每垛最底层每条边”根据题意,可知该三角、四角果子垛最底层每条边上的果子数是〈(参考公式:川山·+n2=巾+俨1))A.4,11B.5,12 c.6,137.如圈,αiβ,αnβ=l,Aeα,Beβ,点A,B在棱l上的射影分别是码,B i,若AA1=BB1 =2, AB=4,则异面直线AB1与A1B所成角的余弦值为D.7,14A.主B.I第7题图5521c.一D.一338.定义在R上的函数f(x)满足f(-x)+f(x)+2cosx=0,当x�O时,J'(x)>sinx,则不等式f(x)+2cosx>f(π-x)的解集为A.(J, +co)B.(斗) c.(-咒) D.(一∞,π)二、多项选择踵I;I 尔踵共4,J、踵,每小题5分,共20分.在每小踵给出的选项中,有多项符合匾目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.己知单位向盘a,b ,则下列命题正确的是(A. (;i+b )土(;i -b )B剖=(-手,J.b -(coC若|二-bl 川,记向盘二,5的夹角为θ,则θ的最小值为子’--‘’霄『-.-D 若(a.b) =二,则向盘b栩如上的投影向盘是γ飞’I 3IO.己知圆M 的方程为:x 2+y 2+ax +咿-2a-4=o,(a εR ),点P(l,l ),给出以下结论其中正确的有(A.过点P 的任意直线与圆M都相交B若因l M 与直线川+川无交点则ae (÷棉)C.四M 面积最小时的圆与圆Q:x 2+ y 2 +6x-10y+16=0有三条公切线D.无论。
0到100分设计测试用例

0到100分设计测试用例摘要:一、测试用例设计的重要性1.软件测试的基本概念2.测试用例的作用3.测试用例设计的原则二、0到100分设计测试用例的方法1.等价类划分法2.边界值分析法3.错误推测法4.场景法5.因果图法6.判定表驱动法7.功能图法三、测试用例设计的实践与优化1.确定测试目标2.分析需求和功能3.选择合适的测试用例设计方法4.制定测试计划5.执行测试用例6.分析测试结果7.优化测试用例设计四、总结1.测试用例设计在软件测试中的重要性2.不同测试用例设计方法的优缺点3.如何提高测试用例设计的质量和效率正文:一、测试用例设计的重要性软件测试是保证软件质量的关键环节,而测试用例设计则是软件测试的核心。
测试用例是测试人员进行测试的依据,通过对软件的各种输入和操作进行验证,以发现潜在的缺陷和问题。
一个好的测试用例设计可以有效提高软件的质量和稳定性,减少开发和维护成本,提升用户体验和满意度。
二、0到100分设计测试用例的方法1.等价类划分法:将可能的输入数据分为相似的组,每组中的数据都能使被测程序产生相同的输出。
等价类划分法可以有效减少测试用例数量,提高测试效率。
2.边界值分析法:针对程序的边界条件进行测试,边界值分析法有助于发现程序在边界情况下的逻辑错误和异常行为。
3.错误推测法:基于程序员的经验和直觉,推测程序中可能存在的错误,设计测试用例进行验证。
4.场景法:根据实际场景和用户需求,模拟用户操作和程序运行过程,设计测试用例。
5.因果图法:通过分析程序输入与输出之间的因果关系,设计测试用例。
6.判定表驱动法:根据程序的逻辑判断条件,设计测试用例,用于验证程序的分支和循环逻辑。
7.功能图法:通过绘制程序功能图,分析各功能模块之间的接口和调用关系,设计测试用例。
三、测试用例设计的实践与优化1.确定测试目标:明确测试的目的和范围,为测试用例设计提供依据。
2.分析需求和功能:深入了解软件需求和功能,找出潜在的测试需求和风险点。
解放J6锡柴电装系统故障码大揭密
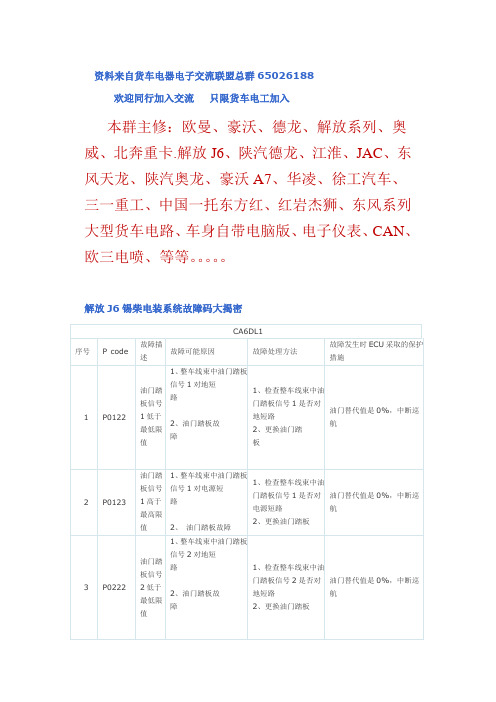
资料来自货车电器电子交流联盟总群65026188
欢迎同行加入交流只限货车电工加入
本群主修:欧曼、豪沃、德龙、解放系列、奥威、北奔重卡.解放J6、陕汽德龙、江淮、JAC、东风天龙、陕汽奥龙、豪沃A7、华凌、徐工汽车、三一重工、中国一托东方红、红岩杰狮、东风系列大型货车电路、车身自带电脑版、电子仪表、CAN、欧三电喷、等等。
解放J6锡柴电装系统故障码大揭密
资料来自货车电器电子交流联盟总群65026188
欢迎同行加入交流只限货车电工加入
本群主修:欧曼、豪沃、德龙、解放系列、奥威、北奔重卡.解放J6、陕汽德龙、江淮、JAC、东风天龙、陕汽奥龙、豪沃A7、华凌、徐工汽车、三一重工、中国一托东方红、红岩杰狮、东风系列大型货车电路、车身自带电脑版、电子仪表、CAN、欧三电喷、等等。
小学五年级数学思维专题训练—等积变形(含答案解析)
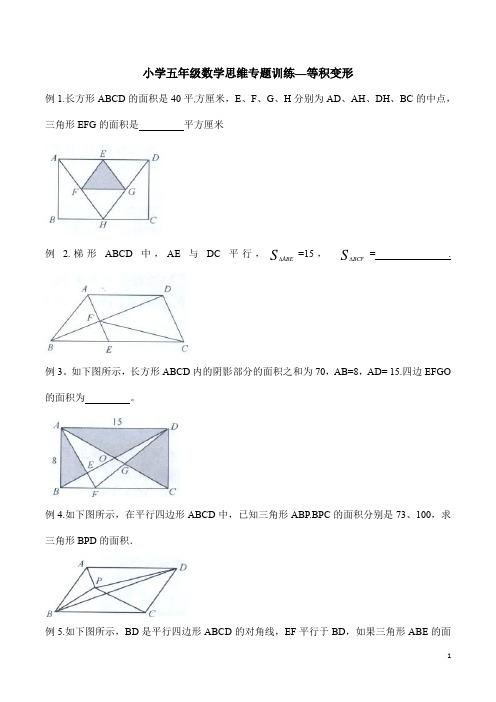
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
外研版英语七年级上册Module 5 Unit1 I love history课件

like作动词时,意为“喜欢”;作介词时,意为“像”,可 与be或look连用。 eg:It is like a bird.
它像一只鸟。
5 difficult/'dɪfɪklt/ adj.困难的
辨析difficult和hard difficult与hard用作形容词时,均可表示“困难的”,其 反义词为easy。一般情况下能互换,但两者之间也有区别:
介词 用法
in
表示“月、季节、年、世纪”或泛指“上午、下午、晚 上”。eg:in May在五月,in the evening在晚上
表示“在具体的某一天”或“(在具体的某一天的)早上、
on
下午、晚上”等,“在星期几”或“在星期几的早上、下 午、晚上”等,“在某一节日”。eg: on Sunday morning
2:45读作:a quarter to three 表示“在某一时刻”,即“在某时间点”,应该用介词at。 eg:at three o'clock在3点钟
对时刻提问时,一般用what time。 eg:—What time is it now?现在几点了?
—It's half past seven.七点半。
3 maths/mæθs/n.数学
eg:Do you like maths?你喜欢数学吗? maths是mathematics的缩写形式,英国英语中常用maths,美国英 语中常用math。 中学常见学科如下:Chinese语文 maths数学 English英语 physics 物理 chemistry化学 science科学 biology生物 politics政治 history历 史 geography地理 art美术 music音乐 PE (physical education)体育
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同样签订“广场协议”,货币大幅升值100%以上,为什么只有日本败了,这个国家却安然无恙!
今天,想讲一段历史,一段货币战争的历史。
很多人都听说过它,却只知其一,未知其二,只见树木,未见森林。
他可谓人类史上最臭名昭著的一次货币战争,以美国的大获全胜而结束。
没错,它就是“广场协议”。
很多人不明白,日本为何竟如此愚蠢,自己把自己放在火上烤,还烤熟了。
很多人也不知道,签订广场协议的并不仅仅只有日本,还有另外一个国家,而它不仅却惊险涉水,挺了过去,甚至还越走越稳了。
1 广场协议事情还得从七八十年代说起。
那些年,美国财政赤字日益扩大,贸易逆差更是前所未有的高,到1984年甚至达到了惊人的1600亿美元,占到了美国当年GDP的3.6%。
迫不得已之下,美国不得不提高国内基准利率,吸引国际投资,发展经济。
但这样一来,又造成大量国际热钱流入,美元不断升值,导致出口下降,更加扩大了贸易逆差,得不偿失。
1978年底,又爆发第二次石油危机,能源价格大幅上升,物
价齐涨,令美国国内通货膨胀严重。
当时的美联储不得不三次提高利率,收紧货币政策,市场利率一度达到了惊人的20%。
如此高利率,推升美元从1979年到1984年5年间升值近60%,出口困难,贸易逆差更加严重,令美国国内一片恐慌,而与此相反,日本经济却一路狂飙,每年增速高达10%,甚至超越美国成为全球最大债权国,令全球惊呼,日本的时代来了。
卧榻之下岂容他人鼾睡!
作为全球霸主,美国怎么可能允许别人比自己强,哪怕是自己的小弟,哪怕只是一点点可能,也必欲除之而后快。
所以,当时的美国工商学界,纷纷游说,强烈要求政府干预汇率市场,最终,美国对日本挥起了大刀。
这可谓是一场美国版的“鸿门宴”。
1985年9月,在美国的精心策划下,拉上日本、德国、法国、英国四国财长,联合在美国纽约广场饭店开会。
会上,美国大获全胜,最终签订了一份协议,史称“广场协议”。
协议要求五国必须联合干预汇率市场,令美元贬值,从而遏制美国的巨额贸易逆差。
从此拉开了日元大幅升值的序幕,也拉开了日本失去二十年的序幕。
2 日本被迫签订广场协议很多人感到不可思议,
难道日本财长是李鸿章,为什么要签这种丧权辱国的协议?实际上,要怪就怪日本当时心肠太软了,不知道美国当时背后藏着刀。
会议一开始,美国财长就开始大哭起来,抱怨美国财政赤字越来越大,贸易逆差越来越大,央求各国一起救美国。
注意,是求,这在以往是绝对不可能的。
要知道,以前每次开会,美国都是老大,扮演着训话的角色,各国只有听的份。
这次美国却完全像个受伤的羔羊,哭哭啼啼,几乎令人怜悯。
吃人家的嘴软,拿人家的手短,二战之后,日本、欧洲等国都受到美国的援助,经济复苏才如此之快,现在美国求帮忙,他们哪里好意思拒绝,而且这里是在人家的地盘上。
人在屋檐下,哪有不低头。
无奈之下,日本财长只好松话了,愿意升值20%,帮助美国度过难关。
其他国家财长也只好纷纷答应了。
按说,以当时日本的经济强势程度,日元升值20%,也不算什么。
但谁知,这仅仅只是一场大戏的开始,精彩的还在后面。
3 愈演愈烈,日本难挽败局协议一经生效,日本还未回过头来,美国财长就接受了一项新的工作,工作内容是每天不停向媒体大倒苦水,一个劲的抱怨,美元还是偏高,还有下跌空间。
金融市场最重要的是什么,是预期。
全球对美元贬值的预期开始疯狂升温。
日本根本没有喘息的机会,从1985年到1988年,不到4年,日元便升值了100%以上。
上山容易下山难,之后几年更是备受国际炒家追捧,一路狂飙,全球炒家对日元升值的预期挡都挡不住。
面对局面的失控,出口的不断下滑,日本国内一片惊慌。
为了控制日元汇率,日本政府不断下调利率,甚至降到了历史最低点,达到2.5%,并维持这种低利率长达两年零三个月,但始终无法扭转这种说不清道不明的“预期”。
低利率不仅未能稳住日元汇率,还令市场资金大量流动性过剩,出口下降,制造业不景气,大量资金开始疯狂流入股市和楼市。
而股价的节节攀升,令许多上市公司不愿再向银行贷款,而是到股市上融资,很多企业甚至把在股市圈到的钱,用来归还银行贷款,导致银行贷款规模急剧下降。
无奈之下,银行只好把贷不出去的钱投入到急需资金的楼市,形成恶性循环。
眼看着泡沫越来越大,日本政府只好转过头来开始提高市场利率,抑制通货膨胀,谁知竟对房地产市场形成抽水效应,刺穿了泡沫,大量银行坏账浮出水面,银行倒闭如风吹。
到1991年,日本股市、楼市全面崩盘,遭遇了前所未有大危机,之后更是长达20年深陷泥潭,一蹶不振。
曾经有一位美国经济学家不无骄傲的表示,美国就是要“让日本自己拿自己的锅煮自己”,而这个“锅”就是“低利率、升值预期和资产泡沫”。
听罢令人不寒而栗,美国不仅要阉割日本,还想要它的命,完全不顾昔日主仆的情谊。
美国财长一小哭,日本长哭二十年,个中滋味,或许只有日本人自己才能体味。
4 相同处境,德国走了另一条路这一场货币战争,美国可谓大获全胜,而日本警钟长响。
无数人看到了货币战争的残酷,更看清了美国的嘴脸。
中国更是时刻警惕着日本的覆辙,一直强调独立自主的货币政策。
但很多人却忽略了,签订广场协议的并不仅仅只有日本,还有德国、英国和法国。
尤其是德国马克,从1960到1990年,累计升值了2.79倍,甚至超过了日元。
同样处境,只有日本失去了二十年,德国却挺了过来,而且愈发强劲了。
令无数人倍感不解,难道德国人都是神仙,对美国的子弹可以免疫吗?
当然不是,之所以避开了日本覆辙,是因为德国走了和日本完全不同的路。
在经济学中,“独立货币政策、资本自由流动、固定汇率”三者只能选其二,一个国家不能同时兼具三个。
与日本神经紧张,疯狂盯着汇率不同,德国选择了前两个,
放弃了对汇率的干预,重点关注国内物价和生产稳定,其次才考虑汇率稳定。
与日本疯狂的降准降息,企图扭转汇率不同,德国降低了贴现率和抵押贷款利率,却把存款利率提高到了5.5%以上。
与日本央妈乖乖听从美国货币政策调度,m2增速从8%上升到12不同,德国的m2增速却不断温和下降。
借着这一系列不同,德国成功避开了险滩,不仅没有出现大规模的资产泡沫,经济和出口甚至也完全未受汇率的大幅波动影响。
在签订广场协议之后几年,汇率虽然不断高涨,经济增长却仍然高达2.3%,到1986年甚至还取代美国成为全球最大的贸易出口国。
虽然德国位居欧洲,欧洲一体化为德国分担了很多风险,但无疑政策的差异才是德国走出困难的关键。
5 结语未来,第三次世界大战或许永远不会发生,但货币战争却每天都在上演。
当我们看着貌似平静的世界,千万别天真的以为,国与国之间真的有什么岁月静好!
在如今的美国,不停地加息、缩表、减税,美元贬值等,一套套组合拳打得天花乱坠,眼花缭乱之际。
千万别迷失了方向,更别忘了广场协议的教训。
我们虽然不会去签订广场协议2,但这场协议之后日本、德国不同的选择、不同的结局,无疑能给带来了深刻的教训和
借鉴。
任凭外面如何强横,如何风起云涌。
我们都要立足自己,立足国内,尤其是资产价格是否存在泡沫,制造业是否健康,金融杠杆是否合理。
在当今,我们不断的强调金融去杠杆,控制房地产泡沫,降低m2增速,发展实体经济,无疑是最正确的选择。
另外,希望大家借这篇文章了解,广场协议究竟是怎么回事,而不再云里雾里。
新年快到了,提前给大家拜年,祝大家新年快乐!
参考资料:人民币不高兴
欢迎小伙伴们转发、点赞、发表神评!。
