第三章 量子力学中的力学量 第六讲 电子在库仑场中的运动 ppt 量子力学教学课件
量子力学 电子在库仑场中的运动

94§3.3 电子在库仑场中的运动重点:电子在库仑场中运动的结果的理解 难点:电子在库仑场中运动的求解过程一、粒子在辏力场(中心对称或球形对称场)中的运动:特点:)r (U )r (U =r与ϕθ,无关,中心对称。
辏力场在经典物理及量子力学中都是一类重要问题。
原子中电子在核电场中的运动,核中单个核子在其余核子产生的平均场中运动都属于这类问题。
定态dinger o Schr &&方程为:Ψ=ΨE H ˆ (1) 其中:)r (U 2Hˆ22+∇μ−=h ,Ψ=ΨE H ˆ在球坐标系中的可以表示为: Ψ=Ψ+Ψϕ∂∂θ+θ∂∂θθ∂∂θ+∂∂∂∂μ−E )r (U ]sin 1)(sin sin 1)r r (r[r 2222222h 即:Ψ=Ψ++⊥E )]r (U T ˆT ˆ[r 其中:μ=∂∂∂∂−μ=2p ˆ)]r r (rr [21T ˆ2r 222rh 为径向动能算符 (2) )r r ˆp ˆp ˆr r ˆ(21pˆr r r r r ⋅+⋅= (3)(这样才能保证其厄米性)=⊥T ˆ2222222r 2L ˆ]sin 1)(sin sin 1[r 2μ=ϕ∂∂θ+θ∂∂θθ∂∂θμ−h95μ=μ×=⊥2p ˆr2)pˆr (222r r 为横向(角)动能算符 (4) 于是方程可以写为:Ψ=Ψ+μ+E )]r (U r 2L ˆT ˆ[22r (5) 采用分离变量法,设),(Y )r (R ),,r (ϕθ=ϕθΨ,代入上式后两边同除以2r2RYμ,得 22r 2L Y LˆY1R ]E )r (U T ˆ[R r 2−=−=−+μ 于是:0R ]E )r (U r2L T ˆ[22r =−+μ+(径向dinger o Schr &&方程) (6) Y L Y Lˆ22=(角向方程) (7) 而角向方程Y L Y Lˆ22=的解与辏力场的具体形式无关,即: 22)1(L h l l += ,),(Y Y m ϕθ=l所以径向dinger o Schr &&方程可以表述为: 0R ]E r 2)1()r (U T ˆ[22r=−μ+++h l l (8) 即:)r (ER )r (R ]r 2)1()r (U )r r (r r 2[22222=μ+++∂∂∂∂μ−h l l h二、电子在库仑场中的运动(辏力场的一种形式) 1.定态方程:质量为μ,带电e −的电子受核电荷为Ze 的吸引势能,即体系势能:96rZe)r (U 2s −=其中1Z =,为氢原子;1Z >,为类氢原子, 如+He 、++Li 和+++Be 等。
量子力学QMChap3

x
I. 求解
(r ) ( x ) 采用分离变量法,令: p ( y ) ( z )
F ( x)
n 0 F ( n ) (0) n!
xn
则可定义算符 Û 的函数 F(Û)为:
ˆ) F (U
n 0
F ( n ) (0) n!
n ˆ U
例如:
e
i ˆ Ht
n 0
1 n!
n ˆ [ Ht ] i
(6)算符的本征值方程
ˆ x x F
力学量由算符描述。 需要什么样的算符来描述,如何描述,正是本章的内容。
主要内容
• • • • • • • §3.1 表示力学量的算符 §3.2 动量算符和角动量算符 §3.3 电子在库仑场中的运动 §3.4 氢原子 §3.5 厄密算符的本征函数的正交性 §3.6 算符与力学量的关系 §3.7 算符的对易关系 两力学量同时有确定值的 条件 测不准关系 • §3.8 力学量平均值随时间的变化 守恒定律
(3)算符之和
定义: 若两个算符 Ô、Û ,对体系的任何波函数ψ 有: ( Ô + Û) ψ= Ôψ+ Ûψ= Êψ 则Ô + Û = Ê 称为算符之和。
例如:
表明 ˆ 等于 H a m ilto n 算符H ˆ和 体系动能算符T ˆ之和。 势能算符V
ˆ T ˆ V ˆ H
显然,算符求和满足交换率和结合率。
库仑定律-ppt课件

时,绳与竖直方向的夹角α=45°,g取 10 m/s2,k=9.0×109 N·m2/C2,且A、B两
小球均可视为点电荷,求:
(1)A、B两球间的静电力的大小;
(2)A球的质量。
【答案】(1)0.02 N
作者编号:43999
问题3:r1、r2与B、C的电量关系?
C qc
中间电荷
靠近两侧
电荷量较
小的那个
r1
FCA
Aq
A
A
r2
FCA FBA
B q
B
FBA
结论3:近小远大
k
qC q A
qB q A
k
2
2
r1
r2
2
qC
r
12
qB
r2
r1 r2时,qC q B
r2 r1时,q B qC
三个自由电荷平衡的规律:三点共线、两同夹异、两大夹小、近小远大。
新知学习
2.理想化的模型,实际上是不存在的。
3.均匀带电的球体,由于球所具有对称性,即使它们之间的距离不是
很大,一般也可以当作点电荷来处理---电荷集中在球心的点电荷。
两个带电体之间存在相互作用力,这种相互
作用力的大小与哪些因素有关呢?
作者编号:43999
新知学习
02 影响静电力的因素
如图所示,用摩擦起电的方法分别让球形导体 A 和通草球 B 带同种电荷,并使
(2)2×10-3 kg
作者编号:43999
课堂练习
1.下列关于点电荷的说法正确的是( C )
A.只有体积很小的带电体才能看成点电荷
库仑定律ppt课件

A.
5
F
9
4
B. F
9
5
C. 4 F
D)
9
D. 5 F
例3.真空中有三个点电荷,它们固定在边长50cm的等
边三角形的三个顶点上,每个点电荷都是+2×10-6C,
求它们各自所受的库仑力。
三个点电荷的受力情况都相同,以q3为例
q1
q3受到大小相同的库仑力F1和F2
q2
)
A.电荷量关系:qa=qb
B.质量关系:ma>mb
C.比荷关系: <
D.定量关系:ma sin α=mb sin β
在光滑绝缘的水平面上,有一个绝缘的弹簧,弹簧的两端
分别与金属小球A、B相连,如图所示,若A、B带上等量
同种电荷,弹簧的伸长量为x1,若让A、B的带电量都增
为原来的两倍,弹簧的伸长量为x2,则( C)
2
库仑定律
【复习回顾】
同种电荷相互
排斥
异种电荷相互
吸引
【思考】
电荷之间相互作用力的大小与哪些因素有关?
电荷间的作用力,随电荷电量的增大而增大,
随距离的增大而减小
定量的关系是什么呢?
一、库仑的实验
(一) 法国物理学家库仑利用扭秤研究出
了电荷间相互作用力的大小跟电量和距
离的关系。
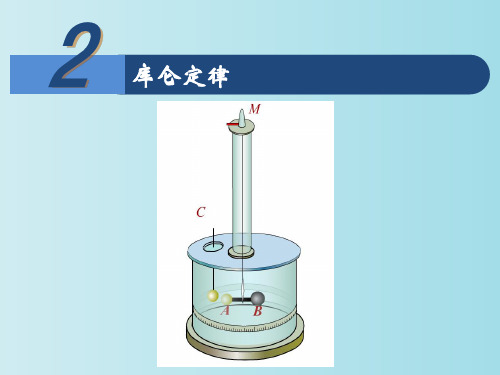
1、实验装置:库仑扭秤
录每次悬丝扭转的角度,便可
找出F与r的关系
细银丝
平衡小球B
带电小球C
带电小球A
探究F与q的关系:
改变A和C的电量q1、q2,记录每次悬丝
扭转的角度,便可找出F与q1、q2的关系
库仑定律ppt课件

在国际单位制中,电荷量的单位是库仑(C),力的单位是牛顿(N),
距离的单位是米(m)。k的数值是
• 静电力计算
根据库仑定律,两个电荷量为1C的点电荷在真空中相距1m时,相
互作用力是 9.0×109N。差不多相当于一百万吨的物体所受的重力!可
见,库仑是一个非常大的电荷量单位,我们几乎不可能做到使相距1m
起当年一些研究者的注意,英国科学家卡文迪什和普里斯特利等人
都确信“平方反比”规律适用于电荷间的力。不过,最终解决这一
问题的是法国科学家库仑。他设计了一个十分精妙的实验(扭秤实
验),对电荷之间的作用力开展研究。最后确认:真空中两个静止
点电荷之间的相互作用力,与它们的电荷量的乘积成正比,与它们
的距离的二次方成反比,作用力的方向在它们的连线上。这个规律
叫作库仑定律(Coulomb’s law)。这种电荷之间的相互作用力叫作
静电力(electrostatic force)或库仑力。
➢ 类比在库仑定律的建立过程中发挥了
重要作用。类比会引起人们的联想,
产生创新。但是类比不是严格的推理,
不一定正确,由类比而提出的猜想是
否正确需要实践的检验。
那么,什么是点电荷呢?
和C之间的作用力使A远离。扭转悬丝,使A回到初始位
置并静止,通过悬丝扭转的角度可以比较力的大小。改
变A和C之间的距离r,记录每次悬丝扭转的角度,就可
以找到力F与距离r的关系,结果是力F与距离r的二次方
成反比,即
在库仑那个年代,还不知道怎样测量物体所带的电荷量,甚至
连电荷量的单位都没有。不过两个相同的金属小球,一个带电、一
q1和q2的乘积成正比,即
① 库仑最初的实验是用带电木髓小球进行的,并非金属小球。这个
库仑定律 教学PPT课件
B.弹簧伸长量为Mgsin α k0
C.A 球受到的库仑力大小为 2Mg
D.相邻两小球间距为 q0
3k 7Mg
金版学案第8题:
8.(多选)如图所示,两根绝缘丝线挂着两个质量相同
的小球A、B,此时上、下丝线的受力分别为TA和TB. 如果使A带正电,使B带负电,上、下丝线的受力分
别为TA′和TB′,则下列关于TA′和TB′的关系判断正确 的是( AD )
从例题可以看
出:微观粒子间的 万有引力远小于库 仑力,因此在研究 微观粒子的相互作 用时,可以把万有 引力忽略.
多个库仑力作用时的矢量和:
例2、真空中有三个点电荷,它们固定在边长50cm的 等边三角形的三个顶点上,每个点电荷都是+2×10−6C , 求它们各自所受的库仑力。
课堂练习:
2、(多选)两个相同的金属小球,带电荷量之比为 1:7,当二者间距为L且L远大于小球的半径时,相 互间的库仑力为F,将两小球接触后又放回原处后, 相互作用力的大小变为( BD) A.4/7F B.16/7F C.3/7F D.9/7F
(A )
A.ta n3α =q2 q1
B.ta n2α=q2 q1
C .ta n3α =q1 q2
D.ta n2α=q1 q2
将两个气球充气后挂起来,让他们碰在一起(图a). 用毛皮分别摩擦两个气球相接触的部分(图b). ①放开气球后,你观察到什么现象? ②如果摩擦得越厉害,现象又有什么不同?为什么?
①两个气球和毛皮相互摩擦后带同种电荷,同种电荷 相互排斥,观察到两个气球相互排斥 ②摩擦得越厉害,排斥的越远
课堂小结:
1、内容:真空中两个点电荷之间的相互作用力,跟它
们的电荷量的乘积成正比,跟它们的距离的二次方成
《库仑定律》PPT教学课件
例1 对于库仑定律,下列说法正确的是 q1q2
A.凡计算真空中两个点电荷间的相互作用力,就可以使用公式F=k r2
B.两个带电小球即使相距非常近,也能用库仑定律
√C.相互作用的两个点电荷,不论它们的电荷量是否相同,它们之间的库
仑力大小一定相等
D.当两个半径为r的带电金属球中心相距4r时,对于它们之间的静电作用
就Байду номын сангаас大.( √ )
(5)若点电荷q1的电荷量大于q2的电荷量,则q1对q2的静电力大于q2对q1的
静电力.( × )
2.(2020·十堰市高二期末)真空中有两个静止点电荷,它们之间的库仑力
的大小为F.若将它们的距离减小为原来的 12,同时将它们的电荷量均增大
为原来的2倍,则它们之间的库仑力将变为
A. F
图3
例3 如图4所示,分别在A、B两点放置点电荷 Q1=+2×10-14 C和Q2=-2×10-14 C.在AB的垂 直平分线上有一点C,且AB=AC=BC=6×10-2
m.如果有一电子静止放在C点处,静电力常量k=
9.0×109 N·m2/C2,则它所受的静电力的大小为 _8_×__1_0_-_2_1 _ N,方向__平__行__于__A_B_连__线__向__左___.
针对训练 如图5所示,有三个点电荷A、B、C位于一个等边三角形的三个 顶点上,已知三角形的边长为1 cm,B、C所带电荷量为qB=qC=+1×10-6 C,A所带电荷量为qA=-2×10-6 C,静电力常量k=9.0×109 N·m2/C2,A所受 B、C两个电荷的静电力的合力F的大小和方向为
知识梳理 重点探究 随堂演练 课时对点练
知识梳理 一、电荷之间的作用力 1.实验探究:利用如图1所示的装置探究影响电荷之间相互作用力的因素. 实验结论:电荷之间的作用力随着电荷量的增大而增大 ,随着距离的增 大而 减小 .
库仑定律课件ppt
电磁波产生机理
01
02
03
电磁感应
变化的磁场会在空间中激 发电场,从而产生电磁波 。
振荡电流
振荡电流在导线中产生交 变磁场,进而激发电磁波 。
天线辐射
天线上的交变电流产生电 磁场,以电磁波形式向外 辐射。
电磁波传播特性
电磁波传播速度
在真空中,电磁波传播速度等于光速。
电磁波频谱
根据频率和波长的不同,电磁波可分为无线电波、微波、 红外线、可见光、紫外线、X射线和伽马射线等。
库仑定律在电子显微镜成像中的应用
库仑定律可以解释电子在电磁透镜中的聚焦和成像过程,有助于优化电 子显微镜的成像效果和提高分辨率。
03
库仑定律在电子衍射中的应用
电子衍射是电子显微镜技术的重要组成部分,库仑定律为电子衍射现象
提供了理论解释,有助于分析样品的晶体结构和化学成分。
等离子体物理和核聚变研究
等离子体物理基础
VS
电势差与电场强度关系
电势差与电场强度之间存在一定的关系, 通过电势差可以计算电场强度的大小和方 向。
电荷分布与相互作用
电荷分布对电场影响
分析不同电荷分布对电场强度和电势差的影 响,如均匀带电球体、无限大带电平面等。
电荷间相互作用力
根据库仑定律,计算两个点电荷之间的相互 作用力,包括大小、方向和作用点。
库仑定律在天线设计中的应用
天线是无线通信的关键部分,其性能直接影响到通信质量。库仑定律为天线设计提供了指 导,如天线长度、形状等参数的选择。
电子显微镜技术
01 02
电子显微镜原理
电子显微镜利用电子束代替光束进行成像,具有更高的分辨率。库仑定 律描述了电子在电磁场中的运动规律,为电子显微镜技术的发展提供了 理论支持。
量子力学讲义 第三章 3.5、3.6、3.7、3.8
ˆ |2 d | F
0
可把常数记为Fn,把状态 记为ψn,于是得:
(2)力学量的本征方程
若体系处于一种特殊状态, 在此状态下测量F所得结果 是唯一确定的,即:
(F) 0
2
则称这种 状态为力 学量 F 的 本征态。
ˆ F ) (F 0 或 ˆ 常 数 F
ˆ n Fn n F
m m m
m
ˆm )*nd Fm m *nd (F
二式相 减 得:
(Fm Fn ) m *nd 0
若Fm≠Fn, 则必有:
ˆm )*nd m * F (F ˆnd Fn m *nd
(2)分立谱、连续谱正交归一表示式
1. 分立谱正 交归一条 件分别为: 3. 正交归一系
Ylm ( ,) Nlm Pl (cos ) eim
m
构成正交归 一函数系
0
2
0
* Ylm ( ,)Ylm ( ,)sindd ll
ˆ 的本征函数 (4)氢原子能量算符H
nlm (r, ,) Rnl (r)Ylm (,) 组成正交归一函数系
i 1
方程的归一化条件有 f 个,正交条 件有f(f-1)/2 个,所以共有独立方 程数为二者之和等于 f(f+1)/2 。
Fn A jini
i 1
nj
* nj ji A j i ni * ni d jj
构成正交归一系
m(x) n(x)dx mn
ˆ z 的本征函数 (2)角动量分量算符 L
1 i m m() e (m 0, 1, 2, ) 2
物理库仑定律ppt课件
电场线的指向
电场线的指向表示电场强 度的方向,即正电荷受力 的方向。
电场强度与电势的关系
电势差与电场强度
在匀强电场中,电势差与 电场强度成正比,即 U=E*d。
电势与电场强度
在非匀强电场中,电势与 电场强度没有直接关系, 但沿电场线方向,电势逐 渐降低。
等势面
等势面是电势相等的点所 构成的曲面,在等势面上 移动电荷时,电场力不做 功。
电荷。
点电荷的场强
点电荷在空间中产生的电场强度与 该电荷的电量成正比,与距离的平 方成反比。
电场线
电场线是用来描述电场分布的假想 曲线,其方向与电场强度方向相同 。
电场线的概念
01
02
03
电场线的性质
电场线始于正电荷,终止 于负电荷,且不闭合。在 均匀电场中,电场线是等 距的直线。
电场线的疏密
电场线的疏密程度表示电 场强度的大小,越密集的 地方电场强度越大。
详细描述
在实验中,通过给定两个带电金属球的电量,测量电场力的大小,并观察电场力与电量之间的关系是否符合库仑 定律中的正比关系。
库仑定律的验证
库仑定律可以通过实验进行验证 。
著名的卡文迪许扭秤实验是验证 库仑定律的重要实验之一。
通过测量不同点电荷之间的相互 作用力,可以验证库仑定律的正
确性。
03 库仑定律的应用
电场强度的计算
总结词定律计算 电场中任意一点的电场强度。
物理库仑定律ppt课件
目录
Contents
• 库仑定律的概述 • 库仑定律的推导过程 • 库仑定律的应用 • 库仑定律的拓展 • 库仑定律的实验验证
01 库仑定律的概述
库仑定律的定义
总结词
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S(s-1)- l(l 1)=0 求 s 得: s1=l+1,s2=-l ,s 为负时有极点心舍去
s=(l 1),代入(15)式得: nr snr l1=n
nr L 1 n
nr 是径向的量子数,n 是总量子数(主量子数)n=1、
2、3、4…………..
将
n 代入(9)得: n
0
0
0
0
变化 s2 , s1
将上式第一、四项求和括号内抽出 =0 的项,将剩下的项
写成 → +1,与其它合并。b0[S(s-1)- l(l 1)] ρs-2
+ {b1 [(s+ +1)(s+ )-l(l 1)]-b (s+ - )} S1=0 v0
若满足方程,令ρ的系数为“0”
b0[s(s-1)- l(l 1)]=0 (13)
±1,±2,±3,…±L,有 2L+1 个Y lm
因此对于一个 n
个值,有
n1
(2l
1)
n2
,
n2
个(r,
,)
l0
所以:电子第 n 个能级是n2 度简并
如:n=2 时有 4 个(r,,)
n=3 时有 9 个(r,,)
(3)几个简单的径向函数
2
n=1,L=0
:
R1,0
(r
)
(
z a0
)
3
2
exp
(
zr a0
第三章 量子力学中的力学量
第六讲 电子在库仑场中的运动
重点:理解所得出结论
难点:推导过程
一、 推导电子在库仑场中的 Ψ(r, θ,φ)
一个电子在带正电荷所产生的场中运动,电子的质量μ,
-e(电荷),核的电荷 ze:z=1 氢原子,z>1, 类氢原子,
取核为坐标原点:
则电子所受吸引力的势能
U
ze
2 s
的有限性相矛盾,则μ的形式如下:
μ(ρ)= e 2 f(ρ)(11)
代入(10)式得:
d2 f
d 2
df
d
[
l
(l
2
1)
]
f
0
(12)
令(12)解 f(ρ)= 0b sv,(b0≠0) (13)
S>1,保证在
r=0
时,(
R
u r
)Ψ
有限,代入(12)式并展
开得:
b (s )(s 1) s2 b (s ) s1) b s1 b l(l 1) s2 0,
=(-1)
n 1(2l
l 1 2)
b0
b = = (-1) = l L 1 n 2 2(2l 3) b1
l L 1n 2(2l 3)
n 1(2l
l 1 2)
b0
(n l 1)(n 2!(2l 2)(2l
l 2) 3)
b0
b3
(n l 1)(n l 3!(zl 2)(2l
na0
(n l 1)!
2n[(nl)!]3
1
}2
讨论
(1)由
En
z2e4s
22n2
E n 只与 n 有关,且与
1 成正比,利用此公式可推导出原子的跃迁公式
n2
(2)(r,,)RnlY cm(,) 由 对于一个 n 值有一
个 En , l : 0,1,2 n 1 ,n 个 Rnl ,对每一个 L, m=0,
r
1
es= (4 0 ) 2 (问电子绕核作什么运动?)
E>0 时,E=T+V>0 ,r=∞,
T>-V=
ze
2 s
r
T>0, 对 E 的任何值电子可以运动到无限远。
Ψ≠0,系统是连续态(E),(3)存在满足波函数解。
E<0
时,由
E=T+V(r)=T-
ze
2 s
r
<0,
r→∞时,T<0
Ψ=0 是束缚态→E 一般不连续。
2)(n l 3) 3)(2l 4)
b0
………………………………………
b nl 1
将 b b 用 b 表示可得: 0 、 1。。。。。。。。。。。。 bnl1
0
[ b f () 0
l1 1 n l 1 (n l 1)(n l 2) 1!(2l 2) 2!(2l 2)(2l 3)
讨论:E0 时:令
R(r)=
(r) r
,
a=
8 | E (
2
|)
1 2
,
2zes2
a2
2es2
(
2
|E
|
)
1 2
(9)
作ρ=ar 的变换代入(6)得:
d 2 d 2
[
1 4
l
(l
2
1)
]
0
(10)
当ρ→∞时,(10)变为:
d 2 d 2
1 4
0
此式解:
μ(ρ)= e 2 , 特解。
e
2
与
Ψ
)
3
n=2,L=0,1:
R2,0
(r)
(
z 2a
0
2
)
(2
zr
a0
)
exp(
zr
2 a0
)
3
R2,1
(r
)
(
z 2a0
2
)
4zr
1
a0 (3)2
exp
(
ar
3 a0
)
n=3,L=0,1,2
R R R , ,
3,0
3,1
3,2
例 1:求 R10
b
1
(s
s 1)(s
)
l(l
1)
b
(14)
由(14)式可知
b 1
→∞时, b
1
而级数 e
1
1!
2 2!
3 3!
.....
!
......
相邻两项之比
1
,而e 随ρ→∞而趋于∞
所以 f ()在ρ→∞而趋于∞
若使 有限, f ()应为有限项。
设 nr , b1 0 则由(14)得 nr s (15)
2
+….]
(2l 1)(n l 1)
=-b0 [(n1)!]2
L l1 2l1 ( ) n1
(17)
式中
n L 1
L (1) [(nl)!] 2l1() n 1 0
2 1
(n l 1 )!(2l 1 )!!
(18)
a=
e 2z 2 s n 2
2z
n a0
2
a0 2
es
2sindrdd 1
r0 0 0
(r,
,
)
R nl
Y
cm
(
,
)
代入
上式得
:
R (r)r Y Y 2
r0 nl
2 2
dr
* ( ,)
(,)dd 1
0 0 lm
lm
R r 由于Y lm 是归一化的
, 所以 r0
2 (r) 2 dr 1
nl
将 (19)式 代入 上式得
N
nl
{(
2z 3 )
氢原子玻轨道半径
ar 2z r
n a0
,
由可得径向波函数:
R(r)=
(r r
)
பைடு நூலகம்
μ(ρ)= e 2 f(ρ)
由此可得径向波函数:
Rnl
(r)
N
nl
zr
e na0
(
2z na0
l
r)
L ( 2l1 nl
2zr )
n a0
(L=0,1,2,…….n-1) (19)
r
2
*
(r, ,)(r, ,)
ze
2 s
(
2
|z
|
)
1 2
,导出:
E=﹣
z
2
e
2 s
22 n 2
n=1、2、3……..(16)
将 n, s l 1代入(14)得
b b L 1 n
1 ( 1)( 2l 2)
将 b b 用 b 表示可得: 0 、 1。。。。。。。。。。。。 bnl1
0
b0=b0
b = b L 1 n 1 1(2l 2) 0
