六年级下册平面图形的认识练习题
小学六年级-阴影部分面积及答案完整

创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)创作编号:GB8878185555334563BT9125XW创作者:凤呜大王* 13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*。
2022年精品解析人教版(五四制)六年级数学下册第九章几何图形初步同步训练试卷(精选含答案)

六年级数学下册第九章几何图形初步同步训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、下列立体图形中,各面不都是...平面图形的是( ) A . B . C . D .2、如图,已知线段a ,b .按如下步骤完成尺规作图,则AC 的长是( )①作射线AM ;②在射线AM 上截取2AB a =;③在线段AB 上截取BC b =.A .a b +B .b a -C .2a b +D .2a b -3、如图,将一副直角三角尺按不同方式摆放,则图中α∠与β∠互余的是( )A.B.C.D.4、如图,一副三角尺按不同的位置摆放,其中符合∠α=∠β的图形共有()A.4个B.3个C.2个D.1个5、如图,在一密闭的圆柱形玻璃杯中装一半的水,水平放置时,水面的形状是()A.圆B.平行四边形C.椭圆D.长方形6、如图是一个几何体的侧面展开图,则该几何体是()A.三棱柱B.三棱锥C.五棱柱D.五棱锥7、如图,用剪刀沿虚线将一个长方形纸片剪掉一个三角形,发现剩下纸片的周长比原纸片的周长小,能正确解释这一现象的数学知识是( )A .两点之间,线段最短B .经过一点有无数条直线C .两点确定一条直线D .垂线段最短8、如图所示,从左面看该几何体得到的平面图形是( )A .B .C .D .9、下列立体图形如图放置,其中同一几何体的左视图与主视图不同的是() A . B . C . D .10、如图,将一副直角三角尺按不同方式摆放,则图中α∠与β∠互余的是()A.B.C.D.第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、三棱柱有______个面,______条棱.2、用一个平面去截一个几何体,若截面是长方形,则该几何体可能是______(写三个).3、要在墙上订牢一根木条,至少需要2颗钉子,其理由是______.4、若∠α=53°18′,则∠α的余角的度数为 _____.5、已知一个角的度数为25°,则它的余角度数等于______.三、解答题(5小题,每小题10分,共计50分)AB=,点C是AB的中点,点D是BC的中点,E是AD的中点,求线段AE的1、如图,线段6cm长.︒÷-︒.2、计算21655'18''33357'20''3、如图,已知线段AB,按要求完成下列作图和计算.(1)延长线段AB到C,使BC=2AB;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的条件下,延长线段BA到D,使AD:AC=5:3,点M是BD的中点,若AM=4,求AB的长度.4、如图1,∠BOC和∠AOB都是锐角,射线OB在∠AOC内部,∠AOB=α,∠BOC=β.(本题所涉及的角都是小于180°的角)(1)如图2,OM平分∠BOC,ON平分∠AOC,当α=40°,β=70°时,求∠MON的大小;解:因为OM平分∠BOC,∠BOC=β=70°,所以∠COM=12∠BOC=12×70°=35°,因为∠AOB=α=40°,∠BOC=β=70°,所以∠AOC=∠AOB+∠BOC=40°+70°=110°,因为ON平分∠AOC,∠AOC=110°,所以∠CON=12=°,所以∠MON=∠CON﹣∠COM=°﹣35°=°.(2)如图3,P为∠AOB内任意一点,直线PQ过点O,点Q在∠AOB外部,类比(1)的做法,完成下列两题:①当OM平分∠POB,ON平分∠POA,∠MON的度数为(用含有α或β的代数式表示);②当OM平分∠QOB,ON平分∠QOA,∠MON的度数为(用含有α或β的代数式表示).5、如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.(1)①若m=50,则射线OC的方向是;②图中与∠BOE互余的角有,与∠BOE互补的角有.(2)若射线OA是∠BON的平分线,则∠AOC=°.(用含n的代数式表示)-参考答案-一、单选题1、B【解析】【分析】根据立体图形的基本性质即可求解.【详解】解:A.四棱锥是由平面围成,B. 圆锥是由2个面围成,底面是平面,侧面是曲面,不都是由平面图形围成,C. 六棱柱是由平面围成,D. 三棱柱是由平面围成,故选:B.【点睛】本题考查了立体图形的基本性质,逐个判断即可得出答案.2、D【解析】【分析】根据题意作出图形,根据线段的和差进行求解即可【详解】解:如图,根据作图可知,AC AB BC =-2a b =-故选D【点睛】本题考查了尺规作图作线段,线段和差的计算,数形结合是解题的关键.3、A【解析】【分析】A 项根据平角的意义即可判断;B 根据同角的余角相等即可判断;C 根据等角的补角相等即可判断;D 根据角度的关系求出两角的角度再进一步判断即可.【详解】解:A 、图中∠α+∠β=180︒-90︒=90︒,∠α与∠β互余,故本选项符合题意;B 、图中∠α=∠β,不一定互余,故本选项不符合题意;C、图中∠α=∠β=135︒,不是互余关系,故本选不符合题意;D、图中∠α=45︒,∠β=60︒,不是互余关系,故本选不符合题意;故选:A.【点睛】本题考查了余角和补角,是基础题,熟记余角的概念是解题的关键.4、B【解析】【分析】根据直角三角板可得第一个图形∠β=45°,进而可得∠α=45°;根据余角和补角的性质可得第二个图形、第三个图形中∠α=∠β,第四个图形∠α和∠β互补.【详解】解:根据角的和差关系可得第一个图形∠α=∠β=45°,根据同角的余角相等可得第二个图形∠α=∠β,根据等角的补角相等可得第三个图形∠α=∠β,因此∠α=∠β的图形个数共有3个,故选:B.【点睛】此题主要考查了余角和补角,关键是掌握余角和补角的性质:等角的补角相等.等角的余角相等.5、D【解析】【分析】根据圆柱的横截面即可得出答案.【详解】解:根据图形可得,水面的形状为:长方形,故选:D.【点睛】本题考查了认识立体图形,关键是要知道垂直于圆柱底面的截面是长方形,平行圆柱底面的截面是圆形.6、D【解析】【分析】由题意可知,该几何体侧面为5个三角形,底面是五边形,从而得到该几何体为五棱锥,即可求解.【详解】解:由题意可知,该几何体侧面为5个三角形,底面是五边形,所以该几何体为五棱锥.故选:D【点睛】本题主要考查了几何体的展开图,熟练掌握棱锥的展开图是解答本题的关键.7、A【解析】【分析】根据题意,可根据两点之间,线段最短解释.【详解】解:∵剩下纸片的周长比原纸片的周长小,∴能正确解释这一现象的数学知识是两点之间,线段最短.故选A【点睛】本题考查了两点之间线段最短,掌握线段的性质是解题的关键.8、D【解析】【分析】细心观察图中几何体中正方体摆放的位置,从左面看图形即可判定.【详解】解:从左面看,是一列两个小正方形.故选:D.【点睛】本题考查从不同方向看几何体,解题关键是掌握空间想象力.9、B【解析】【分析】结合题意,根据立体图形左视图和主视图的性质,对各个选项逐个分析,即可得到答案.【详解】的左视图和主视图是均为正方形,故选项A不符合题意;的左视图和主视图均为三角形,故选项C不符合题意;的左视图和主视图均为圆形,故选项D不符合题意;的主视图为长方形,左视图为圆形,即左视图和主视图不同故选:B.【点睛】本题考查了立体图形视图的知识;解题的关键是熟练掌握左视图和主视图的性质,从而完成求解.10、A【解析】【分析】A项根据平角的意义即可判断;B根据同角的余角相等即可判断;C根据等角的补角相等即可判断;D 根据角度的关系求出两角的角度再进一步判断即可.【详解】解:A、图中∠α+∠β=180︒-90︒=90︒,∠α与∠β互余,故本选项符合题意;B、图中∠α=∠β,不一定互余,故本选项不符合题意;C、图中∠α=∠β=135︒,不是互余关系,故本选不符合题意;D、图中∠α=45︒,∠β=60︒,不是互余关系,故本选不符合题意;故选:A.【点睛】本题考查了余角和补角,是基础题,熟记余角的概念是解题的关键.二、填空题1、 5 9【解析】【分析】根据三棱柱的特征即可解答.【详解】解:三棱柱有5个面,9条棱,故答案为:5,9.【点睛】本题考查了认识立体图形,熟练掌握三棱柱的特征是解题的关键.2、长方体、正方体、圆柱(答案不唯一)【解析】【分析】截面的形状是长方形,说明从不同的方向看到的立体图形的形状必有长方形或正方形,由此得出长方体、正方体、圆柱用一个平面去截一个几何体,可以得到截面的形状是长方形.【详解】解:用一个平面去截一个几何体,如果截面的形状是长方形,原来的几何体可能是长方体、正方体、圆柱.故答案为:长方体、正方体、圆柱(答案不唯一).【点睛】此题考查用平面截几何体,解题的关键是掌握截面的形状既与被截的几何体有关,还与截面的角度和方向有关.3、两点确定一条直线【解析】【分析】根据两点确定一条直线解答即可.【详解】解:要在墙上订牢一根木条,至少需要2颗钉子,其理由是:两点确定一条直线故答案为:两点确定一条直线.【点睛】本题考查了直线的性质,熟练掌握两点确定一条直线是解答本题的关键.︒4、3642'【解析】【分析】相加为90°的两个角互为余角,根据定义解答.【详解】︒,解:90°-∠α=90°-53°18′=3642'︒.故答案为:3642'【点睛】此题考查了余角的定义,熟记定义并正确运算是解题的关键.5、65︒##65度【解析】【分析】根据余角的定义以及性质求出余角的度数即可.【详解】︒-︒=︒解:它的余角度数等于902565故答案为:65︒.【点睛】此题考查了求余角度数的问题,解题的关键是掌握余角的定义以及性质.三、解答题1、线段AE的长为2.25cm【解析】【分析】由点C是AB的中点可得AC=BC=3cm,由点D是BC的中点可得BD=CD=1.5cm,从而求出AD的长,再由E是AD的中点求解即可.【详解】解:∵点C是AB的中点,∴AC=BC=3cm,又∵点D是BC的中点,∴BD=CD=1.5cm,∴AD=AB-BD=6-1.5=4.5cm,∵E是AD的中点,AD=2.25cm.∴AE=12【点睛】本题考查了两点间的距离以及线段中点的定义,利用线段的和差是解题关键.2、38°21'6''【解析】【分析】根据角度的四则运算方法及变换进率计算即可得.【详解】︒÷-︒,解:21655'18''33357'20''=︒-︒,7218'26''3357'20''=︒.3821'6''【点睛】题目主要考查角度各单位的变换进率及角度的四则运算,熟练掌握各个单位之间的换算进率是解题关键.3、 (1)见解析(2)2【解析】【分析】(1)根据要求作出图形即可;(2)设AB=k,BC=2k,则AC=3k.构建方程求出k,即可解决问题.(1)解:如图,线段BC即为所求;(2)解:设AB=k,BC=2k,则AC=3k.∵AD:AC=5:3,∴AD=5k,BD=6k,∵DM=BM=3K,∴AM=2k=4,∴k=2,∴AB=2.【点睛】本题考查作图﹣复杂作图,线段的和差定义等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.4、(1)∠AOC;55;55;20(2)①12α;②180°-12α【解析】【分析】(1)依据题干中的思路,利用角平分线的定义和用角的和差表示角的大小即可得出结论;(2)①利用角平分线的定义,类比(1)的做法解答即可;②设∠BOP=x,则∠AOP=α-x,利用角平分线的定义,类比(1)的做法解答即可,(1)∵OM平分∠BOC,∠BOC=β=70°∴∠COM=12∠BOC=12×70°=35°,∵∠AOB=α=40°,∠BOC=β=70°∴∠AOC=∠AOB+∠BOC=40°+70°=110°∵ON平分∠AOC,∠AOC=110°∴∠CON=12∠AOC=55°,∴∠MON=∠CON-∠COM=55°-35°=20°.故答案为:∠AOC;55;55;20;(2)①根据题意画出图形,如下图,∵OM平分∠POB,ON平分∠POA,∴∠MOP=12∠BOP,∠NOP=12∠AOP.∴∠MON=∠MOP+∠NOP=1 2∠BOP+12∠AOP=12(∠AOP+∠BOP)=12∠AOB=12α.故答案为:12α;②根据题意画出图形,如下图,设∠BOP=x,则∠AOP=α-x.∴∠QOB =180°-∠BOP =180°-x ,∠AOQ =180°-∠AOP =180°-α+x .∵OM 平分∠QOB ,∴∠QOM =12∠QOB =90°-12x .∵ON 平分∠QOA ,∴∠QON =12∠QOA =90°-12α+12x .∴∠MON =∠QOM +∠QON=90°-12x +90°-12α+12x=180°-12α.故答案为:180°-12α.【点睛】本题主要考查了角的计算,角的概念,角平分线的定义(把一个角分成两个相等的角的射线),利用图形准确用角的和差表示角的大小是解题的关键.5、 (1)①北偏东40︒;②COE ∠和BOS ∠,AOS ∠和BOW ∠. (2)12m . 【解析】【分析】(1)①根据题意即可求出n 的值,即可得出答案;②由90CON BOS ∠+∠=︒,得出90BOE COE ∠+∠=︒,即COE ∠与∠BOE 互余.由90BOE BOS ∠+∠=︒,可得出BOS ∠与∠BOE 互余;根据90CON COE ∠+∠=︒,90BOE COE ∠+∠=︒,即可推出CON BOE ∠=∠.再由180CON COS ∠+∠=︒,180BOE BOW ∠+∠=︒,即可得出与∠BOE 互补的角有AOS ∠和BOW ∠;(2)根据角平分线定义可知12NOA BOA BON ∠=∠=∠.再根据180BON BOS ∠=︒-∠,即可求出1902NOA BOS ∠=︒-∠.结合题意,即可根据AOC NOA NOC ∠=∠-∠,求出AOC ∠的大小. (1)①∵50m =,且m °的角与n °的角互余,∴905040n =-=,∴射线OC 的方向是北偏东40︒;故答案为:北偏东40︒,②∵m °的角与n °的角互余,即90CON BOS ∠+∠=︒,∴90BOC BOE COE ∠=︒=∠+∠.∵90BOE BOS ∠+∠=︒,∴与∠BOE 互余的角有COE ∠和BOS ∠;∵90CON COE ∠+∠=︒,90BOE COE ∠+∠=︒,∴CON BOE ∠=∠.∵180CON COS ∠+∠=︒,180BOE BOW ∠+∠=︒,∴与∠BOE 互补的角有COS ∠和BOW ∠.故答案为:COE ∠和BOS ∠,COS ∠和BOW ∠;(2)∵射线OA 是∠BON 的角平分线, ∴12NOA BOA BON ∠=∠=∠. ∵180BON BOS ∠=︒-∠ ,∴1902NOA BOS ∠=︒-∠. ∵90NOC BOS ∠=︒-∠, ∴1190(90)22AOC NOA NOC BOS BOS BOS ∠=∠-∠=︒-∠-︒-∠=∠. ∴12AOC m ∠=︒. 故答案为:12m 【点睛】本题综合考查了方位角,角度的互余和互补,结合角平分线考查了角在几何图形中的和差运算,理解这些基本定义是解题的关键.。
2020-2021学年人教版六年级下册小升初总复习《长方形和正方形》专项训练卷2
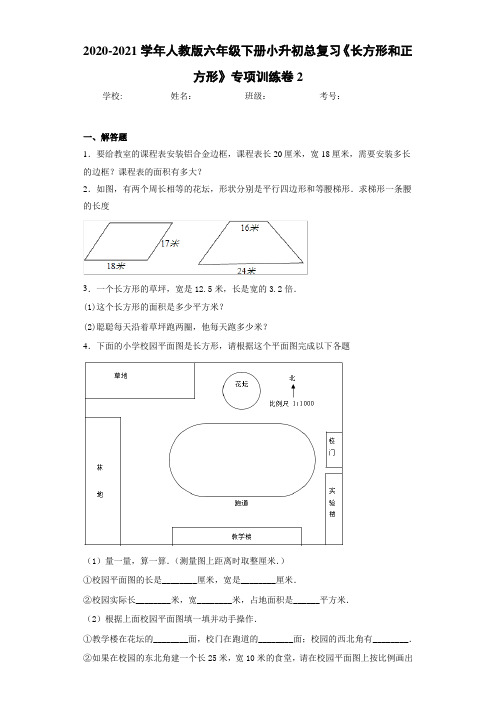
2020-2021学年人教版六年级下册小升初总复习《长方形和正方形》专项训练卷2学校:___________姓名:___________班级:___________考号:___________一、解答题1.要给教室的课程表安装铝合金边框,课程表长20厘米,宽18厘米,需要安装多长的边框?课程表的面积有多大?2.如图,有两个周长相等的花坛,形状分别是平行四边形和等腰梯形.求梯形一条腰的长度3.一个长方形的草坪,宽是12.5米,长是宽的3.2倍.(1)这个长方形的面积是多少平方米?(2)聪聪每天沿着草坪跑两圈,他每天跑多少米?4.下面的小学校园平面图是长方形,请根据这个平面图完成以下各题(1)量一量,算一算.(测量图上距离时取整厘米.)①校园平面图的长是________厘米,宽是________厘米.②校园实际长________米,宽________米,占地面积是______平方米.(2)根据上面校园平面图填一填并动手操作.①教学楼在花坛的________面,校门在跑道的________面;校园的西北角有________.②如果在校园的东北角建一个长25米,宽10米的食堂,请在校园平面图上按比例画出食堂的位置.(3)校园的林地里一共有李子树、杏树和桃树64棵,它们的棵数之比依次是1:3:4校园里有李子树、杏树和桃树各多少棵?5.有一块长方形果园,它的长是80米,宽比长短35米,整个果园占地面积是多少?6.一块长方形菜地,长6米,宽5米,四周围上篱笆,其中有一面靠墙,篱笆至少长多少米?7.请你画出已学过的2种不同图形,使它们的面积相等,并计算出它们的面积。
8.如图所示,张叔叔靠墙围了一个长方形花圃,长5米,宽2米,三面围上篱笆,篱笆长多少米?9.在一块长90米、宽40米的长方形地里栽苹果树,每棵苹果树的株距是4米,行距是5米,这块地可以栽苹果树多少棵?二、连线题10.用下列物体的面可以画出哪些图形?连一连。
小学六年级数学_阴影部分面积例题(含答案)

阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.(2012•长泰县)求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)薃考点艿组合图形的面积;梯形的面积;圆、圆环的面积.莈分析莇阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.薄解答蚂解:(4+6)×4÷2÷2﹣3.14×÷2,袇=10﹣3.14×4÷2,膇=10﹣6.28,莂=3.72(平方厘米);螀答:阴影部分的面积是3.72平方厘米.芇点评袈组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)蒄考点芁组合图形的面积.莀分析肅根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).节解答荿解:扇形的半径是:蝿10÷2,袅=5(厘米);莃10×10﹣3.14×5×5,蚂100﹣78.5,芈=21.5(平方厘米);薅答:阴影部分的面积为21.5平方厘米.蒅点评螀解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)肆考点芃组合图形的面积.芁分析螀分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.袆解答莅解:10÷2=5(厘米),荿长方形的面积=长×宽=10×5=50(平方厘米),膀半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),薇阴影部分的面积=长方形的面积﹣半圆的面积,膂=50﹣39.25,螁=10.75(平方厘米);虿答:阴影部分的面积是10.75.莇点评膃这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.芅考点节组合图形的面积.蒈专题螈平面图形的认识与计算.肂分析莁由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.羇解答芄解:8×4﹣3.14×42÷2,肄=32﹣25.12,葿=6.88(平方厘米);莇答:阴影部分的面积是6.88平方厘米.肅点评膅解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)葿考点蒅圆、圆环的面积.肄分析莂由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.衿解芆解:S=πr2答肅=3.14×(4÷2)2蒀=12.56(平方厘米);莈阴影部分的面积=2个圆的面积,羆=2×12.56,袂=25.12(平方厘米);袃答:阴影部分的面积是25.12平方厘米.螈点评螇解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)肀考点袀长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.芇分析螃图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.蒂解答芀解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);羈图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);袄答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.薀点蝿此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面评积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.肁组合图形的面积.蚃考点薈分由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,析羅利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.腿解:圆的半径:15×20÷2×2÷25,螄解答羇=300÷25,蚅=12(厘米);袅阴影部分的面积:2,薂×3.14×12蒇=×3.14×144,蒆=0.785×144,蚃=113.04(平方厘米);蚀答:阴影部分的面积是113.04平方厘米.膀点评膆此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.罿考点蚇组合图形的面积;三角形的周长和面积;圆、圆环的面积.薃分析艿(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;莈(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.莇解答薄解:(1)阴影部分面积:蚂3.14×﹣3.14×,袇=28.26﹣3.14,膇=25.12(平方厘米);莂(2)阴影部分的面积:螀3.14×32﹣×(3+3)×3,芇=28.26﹣9,袈=19.26(平方厘米);蒃答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.肃点评羀此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)肅考点节组合图形的面积;圆、圆环的面积.荿专题蝿平面图形的认识与计算.袅分析莃观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.蚂解答芈解:周长:3.14×(10+3),薅=3.14×13,蒅=40.82(厘米);螀蚈面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,莆=×3.14×(42.25﹣25﹣2.25),节=×3.14×15,膂=23.55(平方厘米);肇答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.肆点评芃此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
赢课堂六年级下册数学答案人教版

赢课堂六年级下册数学答案人教版赢课堂六年级下册数学答案人教版第一单元有理数的认识1.1 有理数概念- 有理数定义:有理数是可以表示为两个整数比值(分母不为零)的数字。
- 分类:正有理数、负有理数、零。
- 相反数和绝对值的概念和性质。
1.2 有理数的比较- 有理数比较的方法:同分母比大小、通分比大小。
- 有理数大小关系:同号比大小、异号比大小。
1.3 有理数的加减法- 有理数加法的概念和性质:正数加正数、负数加负数、正数加负数、零的加法。
- 有理数减法的概念和性质:正数减正数、负数减负数、正数减负数、零的减法。
- 有理数加减混合运算。
第二单元整式的认识2.1 整式的概念- 整式定义:由若干个数及它们的积和商组成的表达式。
- 常数项、一次项、二次项等概念。
2.2 整式的加减法和合并同类项- 整式加减法的概念和性质:同类项加减法、异类项加减法。
- 合并同类项的方法。
2.3 整式的乘法- 整式的乘法公式。
- 应用整式乘法计算多项式的乘积。
2.4 一元二次方程的认识- 一元二次方程的定义和性质。
- 解方程的三种方法:代数法、因式分解法、配方法。
第三单元平面图形的认识3.1 平面图形的认识- 图形分类:点、线段、直线、角、多边形等。
- 图形性质:相似、全等、平行等。
3.2 直角三角形的认识- 直角三角形的定义和性质。
- 勾股定理和勾股定理的应用。
3.3 三角形的认识- 三角形的分类:等边三角形、等腰三角形等。
- 三角形的周长和面积计算。
3.4 四边形的认识- 四边形的分类:平行四边形、矩形、正方形等。
- 四边形的周长和面积计算。
第四单元空间图形的认识4.1 空间图形的认识- 图形分类:点、线、面、体等。
- 图形性质:相似、全等等。
4.2 立体图形的认识- 立体图形的分类:正方体、长方体、正方体台等。
- 立体图形的表面积和体积计算。
4.3 视图的认识- 正视图、侧视图和俯视图的概念和性质。
- 画出平行于坐标面的立体图形的视图。
数学六年级下人教新课标阴影部分面积专项练习(含答案)
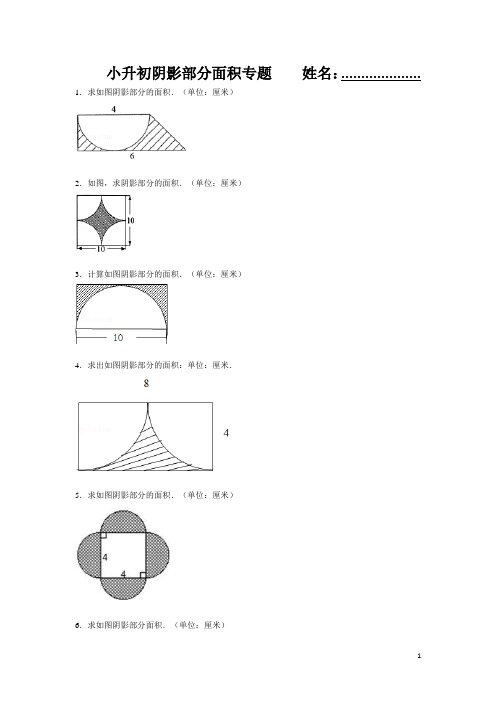
小升初阴影部分面积专题姓名:.................... 1.求如图阴影部分的面积.(单位:厘米)2.如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点:组合图形的面积;梯形的面积;圆、圆环的面积.分析:阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答:解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析:根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答:解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评:解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析:分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答:解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评:这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点:组合图形的面积.专题:平面图形的认识与计算.分析:由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答:解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评:解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点:圆、圆环的面积.分析:由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答:解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评:解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点:长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析:图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答:解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评:此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点:组合图形的面积.分析:由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答:解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评:此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点:组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析:(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答:解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评:此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点:组合图形的面积;圆、圆环的面积.专题:平面图形的认识与计算.分析:观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答:解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评:此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点:圆、圆环的面积.分析:先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答:解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评:此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析:先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答:解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评:考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点:组合图形的面积.分析:求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答:解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评:解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点:组合图形的面积.专题:平面图形的认识与计算.分析:如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答:解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评:解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点:梯形的面积.分析:如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答:解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评:此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点:组合图形的面积.分析:根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答:解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评:考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点:组合图形的面积.分析:由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答:解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评:解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.求阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析:由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答:解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评:考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
平面图形的认识(一)综合测试卷(word含答案)
一、初一数学几何模型部分解答题压轴题精选(难)1.如图下图所示,已知AB//CD, ∠B=30°,∠D=120°;(1)若∠E=60°,则∠F=________;(2)请探索∠E与∠F之间满足的数量关系?说明理由.(3)如下图所示,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数;【答案】(1)90°(2)解:如图,分别过点E,F作EM∥AB,FN∥AB∴EM∥AB∥FN∴∠B=∠BEM=30°,∠MEF=∠EFN又∵AB∥CD,AB∥FN∴CD∥FN∴∠D+∠DFN=180°又∵∠D =120°∴∠DFN=60°∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°∴∠EFD=∠MEF +60°∴∠EFD=∠BEF+30°(3)解:如图,过点F作FH∥EP由(2)知,∠EFD=∠BEF+30°设∠BEF=2x°,则∠EFD=(2x+30)°∵EP平分∠BEF,GF平分∠EFD∴∠PEF= ∠BEF=x°,∠EFG= ∠EFD=(x+15)°∵FH∥EP∴∠PEF=∠EFH=x°,∠P=∠HFG ∵∠HFG=∠EFG-∠EFH=15°∴∠P=15°【解析】【解答】解:(1)分别过点E、F作EM∥AB,FN∥AB,则有AB∥EM∥FN∥CD.∴∠B=∠BEM=30°,∠MEF=∠EFN,∠DFN=180°-∠CDF=60°,∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,∴∠EFD=∠BEF+30°=90°.【分析】(1)分别过点E、F作AB的平行线,根据平行线的性质即可求解;(2)根据平行线的性质可得∠DFN=60°,∠BEM=30°,∠MEF=∠NFE,即可得到结论;(3)过点F作FH∥EP,设∠BEF=2x°,根据(2)中结论即可表示出∠BFD,根据角平分线的定义可得∠PEF=x°,∠EFG=(x+15)°,再根据平行线的性质即可得到结论.2.如图,在平面直角坐标系中,已知点A(0,4),B(3,0),线段AB平移后对应的线段为CD,点C在x轴的负半轴上,B、C两点之间的距离为8.(1)求点D的坐标;(2)如图(1),求△ACD的面积;(3)如图(2),∠OAB与∠OCD的角平分线相交于点M,探求∠AMC的度数并证明你的结论.【答案】(1)解:∵B(3,0),∴OB=3,∵BC=8,∴OC=5,∴C(﹣5,0),∵AB∥CD,AB=CD,∴D(﹣2,﹣4)(2)解:如图(1),连接OD,∴S△ACD=S△ACO+S△DCO﹣S△AOD=﹣=16(3)解:∠M=45°,理由是:如图(2),连接AC,∵AB∥CD,∴∠DCB=∠ABO,∵∠AOB=90°,∴∠OAB+∠ABO=90°,∴∠OAB+∠DCB=90°,∵∠OAB与∠OCD的角平分线相交于点M,∴∠MCB=,∠OAM=,∴∠MCB+∠OAM==45°,△ACO中,∠AOC=∠ACO+∠OAC=90°,△ACM中,∠M+∠ACM+∠CAM=180°,∴∠M+∠MCB+∠ACO+∠OAC+∠OAM=180°,∴∠M=180°﹣90°﹣45°=45°.【解析】【分析】(1)利用B的坐标,可得OB=3,从而求出OC=5,利用平移的性质了求出点D的坐标.(2)如图(1),连接OD,由S△ACD=S△ACO+S△DCO+S△AOD,利用三角形的面积公式计算即得.(3)连接AC,利用平行线的性质及直角三角形两锐角互余可得∠OAB+∠DCB=90°,利用角平分线的定义可得∠MCB+∠OAM==45°,根据三角形的内角和等于180°,即可求出∠M的度数.3.如图1,∠AOB=120°,∠COE=60°,OF平分∠AOE(1)若∠COF=20°,则∠BOE=________°(2)将∠COE绕点O旋转至如图2位置,求∠BOE和∠COF的数量关系(3)在(2)的条件下,在∠BOE内部是否存在射线OD,使∠DOF=3∠DOE,且∠BOD=70°?若存在,求的值,若不存在,请说明理由.【答案】(1)40(2)解:∵∴∴(3)解:存在.理由如下:∵设∴∵∴∴∴∴【解析】【解答】⑴∴∵OF平分∠AOE,∴∴∴故答案为:40。
小学六年级-阴影部分面积-专题-复习-经典例题(含答案)
小升初阴影部分面积专题姓名:.................... 1.求如图阴影部分的面积.(单位:厘米)2.如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.(2012•长泰县)求阴影部分的面积.(单位:厘米)参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点:组合图形的面积;梯形的面积;圆、圆环的面积.分析:阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答:解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析:根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答:解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评:解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.考点:组合图形的面积.分析:分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答:解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评:这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点:组合图形的面积.专题:平面图形的认识与计算.分析:由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答:解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评:解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.考点:圆、圆环的面积.分析:由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答:解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评:解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点:长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析:图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答:解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评:此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.考点:组合图形的面积.分析:由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答:解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评:此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点:组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析:(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答:解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评: 此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点:组合图形的面积;圆、圆环的面积.专题:平面图形的认识与计算.分析:观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答: 解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评: 此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr ,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点: 圆、圆环的面积.分析: 先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可. 解答: 解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评: 此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点: 组合图形的面积.分析: 先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答: 解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评: 考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点:组合图形的面积.分析:求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答:解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评:解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点:组合图形的面积.专题:平面图形的认识与计算.分析:如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答:解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评:解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点:梯形的面积.分析:如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答:解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评:此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点:组合图形的面积.分析:根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答:解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评:考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点:组合图形的面积.分析:由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答:解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评:解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点:组合图形的面积.分析:由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答:解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评:考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
2019-2020学年度苏教版六年级数学下册期末图形几何复习题
六年级数学下册期末图形几何一、仔细审题,正确填空。
1、70公顷=( )平方千米 5003升=( )立方厘米 0.45米=( )分米 32立方分米=( )立方米2、如果把圆分成32等份.拼成近似的长方形,这个长方形的长是6. 28厘米,那么圆的周长是( )厘米,面积是( )。
3、通过纸上的一点能画( )条直线,通过纸上的两点能画( )条直线。
纸上有十个点,任意三个点都不在一条直线上,通过两点画直线,可画( )条。
4、在钟面上,9点30时,分针和时针所夹的角是( )度。
5、已知图A 、图B 中小方格的大小相等,则图A 和图B 周长的比是( ),面积的比是( )。
6、一个圆柱的底面直径扩大到原来的4倍,高不变,侧面积扩大到原来的( )倍,体积扩大到原来的( )倍。
7、一个等腰三角形的周长是24分米,其中两条边长度的比是2 : 1,则这个等腰三角形的底为( )分米,腰长( )分米。
8、如图,把一个底面半径为5厘米、髙10厘米的圆柱体切拼成 一个近似的长方体,表面积比原来增加了( )立方厘米。
9、把一个表面积为12平方分米的正方体木块放在桌面上,木块在桌面上所占的面积( )平方分米。
若把两个这样的正方体拼成一个长方体,则表面积减少了( )平方分米。
10、把一根长2米的圆柱体木料锯成三段,表面积增加了4平方分米,这根木料的体积是( )立方分米。
二、认真分析,判断是非。
1.等边三角形和等腰三角形都不一定是锐角三角形。
( )2.用同一根绳子围成长方形、正方形或圆,它们的面积都相等。
( )3.圆的周长和它的半径成正比例。
( )4.8个小正方体一定能拼成一个较大的正方体。
( )5.将圆锥沿着它的高平均切成两半,它的截面是个等腰三角形()三、反复比较,慎重选择。
1、—个长方形的长和宽各增加5厘米,增加的面积()25平方厘米。
A.等于B.大于C.小于2、3时30分,钟面上时针和分针成()。
A.直角B.锐角C.钝角3、用一副三角板可以拼成()的角。
六年级下册小升初数学知识点精讲课件(平面图形的认识)课件人教版(19张PPT)
重点1 01
重点透视
03
02
1
2
3
三角形
三角形三边的关系 4
5
重点2
由三条线段首尾顺次相接 围成的图形叫作三角形。
三角形的各部分的名称:
顶点
边
高边
顶点
边底
顶点
三角形的分类:
按
角
钝角三角形
分
按 边
分
三角形三边的关系:
三角形任意两边之和大于第三边, 任意两边之差小于第三边。
三角形内角和: 教师:同学们,欢迎来到数学乐园,你们的入场券就是课前合作完成的思维导图。先有请在班级空间上获赞最多的小组来分享一下你
就变为180°÷2=90°。
三角形任意两边之和 01 大于第三边,任意两 边之差小于第三边。
03 正方形是特殊的长方 形,长方形和正方形 是特殊的平行四边形。
归纳总结
平面图形 的认识
02 三角形的内角是180°。
04 同一个圆中 d=2r,r=d÷2
谢谢
∠ADB=180°-72°=108°
?
∠BAD=180°-50°-108°=22°
72°
答:∠BAD的度数是22°。 B D
50° C
题2 填一填
4.5
10.2 15
4
7.2 200
12
d=2r r=d÷2
题3 下列每组数表示三根小木棒的长度,三根小棒能摆
成三角形的一组是
A.1 cm,2 cm,3 cm C.2 cm,3 cm,5 cm
重点3
由四条线段首尾顺次相接 围成的图形叫作四边形。
四边形的分类:
平行四边形 长方形 正方形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级下册平面图形的认识练习题
1.一个直角三角形的三条边长度分别是6厘米、8厘米、10厘米.最长边上的高是()厘米.
2.一张正方形纸边长是5厘米.至少用这样的正方形纸()张.才能拼成一个大一些的正方形.拼成的正方形周长是().面积是().
3.将一个圆沿半径分成若干等份.拼成一个近似长方形.这个近似长方形的长是宽的()倍.
4.一个直角梯形上、下底之和是15厘米.两条腰分别长4厘米、5厘米.这个梯形的面积是().
5.半圆形纸片的周长是10.28分米.它的半径是().
6.将一个圆平均分成若干份.拼成一近似长方形.长方形的面积与圆的面积().长方形的宽是圆的().长方形的长是圆的().
7.心决定圆的().半径决定圆的().
8.一个时钟的时针长10厘米.一昼夜这时针走了()厘米.
9.一圆形水池.直径为30米.沿着池边每隔5米栽一棵树.最多能栽()棵. 10.把一平行四边形的框架拉成一长方形.面积().周长().把一平行四边形通过剪、移、拼的方法拼成一长方形.面积().周长().
二.判断
1.半径是2厘米的圆.周长和面积相等. ()
2.两端都在圆上的线段中.直径最长. ()
3.大圆的圆周率大于小圆的圆周率. ()
4.边长是4米的正方形.它的周长和面积是相等的. ()
5.三角形的面积是平行四边形的面积的一半. ()
6把一个平行四边形活动框架(四根木条钉成的)拉成一个长方形.那么原来平行四边形与现在长方形相比周长不变、面积变了 . ()
三.选择
(1)用一根长2米的绳子将一只羊拴在一根木桩上.这只羊最多能吃到()平方米的草.
A 12.56
B 6.28
C 50.24
D 25.12
(2)一个平行四边形和一个三角形等底等高.已知平行四边形的面积是30平方厘米.那么三角形面积是()平方厘米.
A 15
B 30 C60
( 3)一个平行四边形和一个三角形等底等高.已知平行四边形比三角形的面积大7平方厘米.三角形的面积是()平方厘米.平行四边形的面积是()平方
分米.
四.解决问题
1.在一个直径为20厘米的圆内剪一个最大的正方形.正方形的面积占圆面积的几分之几?
2.从一张长3厘米、宽2.5厘米的长方形纸片上剪下一个最大的正方形.求这个正方形的周长.
3.在一个半径5米的圆形花坛周围修一条宽2米的走道.走道的面积是多少平方米?
4.巴依老爷让阿凡提用12.56米长的篱笆围一个羊圈.这个羊圈所围的羊皮的只数就是他一年的工钱.如果阿凡提想得到的羊尽可能的多.你能帮他设计出一个最佳方案吗?
5.一块三角形菜地的面积是0.25公顷.菜地的底为125米.高是多少米?
6.卧室里的挂钟的底板是从一块长1.2米.宽0.6米的长方形簿片中剪下的一个最大的圆.你知道这个圆有多大吗?
14、教室里有一面墙的形状如右图.粉刷这面墙.每平方米需要800克涂料.一共需要多少千克涂料?。
