5.1 平行关系的判定
平行关系、垂直关系

有关垂直关系的证明方法:
2、线面垂直
(1)利用线面垂直的判定定理
(2)利用面面垂直的性质定理
(3)利用向量法
有关垂直关系的证明方法:
3、面面垂直 (1)利用面面垂直的定义
(2)利用面面垂直的判定定理
1、空间四面体ABCD中,若AB=BC, AD=CD,E为AC的中点,则有( 4 )
A E D B C
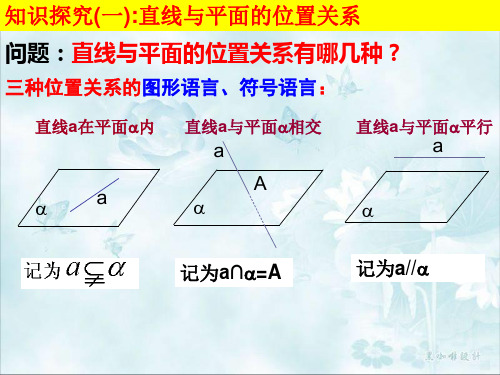
空间两条直线的位置关系有三种:
位置关系 相交直线 平行直线 共面情况 在同一平面内 在同一平面内 公共点个数 有且只有一个 没 有 没 有
异面直线 不同在任何一平面内
证明三点共线通常采用以下方法: (1)首先找出两个平面,然后证明这三点都是这两个平面 的公共点,根据基本性质2,这些点都在交线上. (2)由其中任意两点确定一条直线,再证另一点在这条直 线上.
D F G
A
B
C
E
练习
1.已知:ABCD为正方形,SD⊥平面AC,
问:图中所示的7个平面中,共有多少个平面互相垂直?
1.平面SAD⊥平面ABCD S
2.平面SBD⊥平面ABCD
3.平面SCD⊥平面ABCD 4.平面SAD⊥平面SCD 5.平面SBC⊥平面SCD 6.平面SAB⊥平面SAD
D A O
AD ⊥面BCD
AD ⊥BC DE
④
线面垂直
② ③
线线垂直
例 2、已知在正方体ABCD—A ′B ′C ′D ′中,E 为CC′中点,F为AC和BD的交点,
求证:A′F
⊥平面BED
D′ B′ D F A B P C′ E
(方法一)转化为平面几何 (方法二)三垂线定理
一. 平行直线 1. 平行直线的定义:同一平面内不相交的 两条直线叫做平行线. 2. 平行性质:过直线外一点有且只有一条 直线和这条直线平行. 3. 公理4:平行于同一直线的两条直线互相 平行,此性质又叫做空间平行线的传递性.
平行关系的判定1

汝南双语学校:赵保刚
小结
1、直线和平面平行的定义 2、直线和平面平行的判定
定理:若平面外一条直线与此平面内的一条直线 平行,则该直线与此平面平行。
简记为:
作用:判断或证明线面平行 关键:在平面内找(或作)一条直线与 面外的直线平行
汝南双语学校:赵保刚
课本P41 1,2. 每课一练P26
D1 C1
平面BC1、平面A1C1
A1 D
B1 C
汝南双语学校:赵保刚
2.已知直线a,b和平面α ,下列 命题正确的是( D )
A.若a//α ,b α ,则a//b; B.若a//α, b //α,则a//b;
∩ ∩
C.若a//b, b α,则a//α;
D.若a//b, a//α ,则b //α或b α.
直线和平面平行:一条直线与一个平 面没有公共点,叫做直线与平面平行。
a
直线a平行于平面 α,记作 a∥α.
α
α
画图时通常把表示直线的线段画在 表示平面的平行四边形的外面,并且 使它与平行四边形的一边平行或与平 行四边形内的一条线段平行。
命题:若平面外一条直线与此平 面内的一条直线平行,则该直线 与此平面平行。
AB、AD的中点. 求证:EF//平面BCD.
E
A F
分析:EF在面BCD外,要 D 证明EF∥面BCD,只要证明 B C EF和面BCD内一条直线平行即 可。EF和面BCD哪一条直线平 行呢?连结BD立刻就清楚了。 汝南双语学校:赵保刚
1.如图:长方体 ABCD-A1B1C1D1中,则: (1)与AB平行的平面是 平面A1C1、平面DC1 (2)与AA1平行的平面是 平面BC1、平面DC1 (3)与直线AD平行的平面是
直线与平面平行的判定定理教学设计(教案)

直线与平面平行的判定定理教学设计(教案)第一章:直线与平面平行的概念引入1.1 教学目标让学生了解直线与平面平行的概念。
学生能够通过实例判断直线与平面是否平行。
1.2 教学内容直线与平面平行的定义。
直线与平面平行的判定方法。
1.3 教学步骤1. 引入直线与平面平行的概念,展示实例图片,引导学生观察并描述直线与平面的关系。
2. 给出直线与平面平行的定义,解释其含义。
3. 引导学生通过实例判断直线与平面是否平行,引导学生运用定义进行判断。
1.4 教学评估通过课堂提问,检查学生对直线与平面平行概念的理解。
通过实例判断练习,检查学生能否运用定义判断直线与平面是否平行。
第二章:直线与平面平行的判定定理2.1 教学目标让学生了解直线与平面平行的判定定理。
学生能够运用判定定理判断直线与平面是否平行。
2.2 教学内容直线与平面平行的判定定理。
判定定理的证明。
2.3 教学步骤1. 引入直线与平面平行的判定定理,展示实例图片,引导学生观察并描述直线与平面的关系。
2. 给出判定定理,解释其含义。
3. 进行判定定理的证明,解释证明过程。
4. 引导学生通过实例判断直线与平面是否平行,引导学生运用判定定理进行判断。
2.4 教学评估通过课堂提问,检查学生对直线与平面平行判定定理的理解。
通过实例判断练习,检查学生能否运用判定定理判断直线与平面是否平行。
第三章:直线与平面平行的判定定理的应用3.1 教学目标让学生能够运用直线与平面平行的判定定理解决实际问题。
3.2 教学内容直线与平面平行的判定定理在实际问题中的应用。
3.3 教学步骤1. 引入实际问题,展示实例图片,引导学生观察并描述直线与平面的关系。
2. 引导学生运用判定定理解决实际问题,解释解题过程。
3. 提供练习题,让学生独立解决实际问题,并提供解答。
3.4 教学评估通过课堂提问,检查学生对直线与平面平行判定定理在实际问题中的应用的理解。
通过练习题,检查学生能否独立解决实际问题。
空间中的平行关系

(1)试确定F的位置;
(2)求三棱锥A-CDF的体积.
解 (1)连接BE交AD于点O,连接OF,因为CE∥平面ADF,CE⊂平面BEC,平面
ADF∩平面BEC=OF,
所以CE∥OF.
因为O是BE的中点,所以F是BC的中点.
(2)因为 BC 与平面 ABD 所成角为 30°,BC=AB=1,
D.既不充分也不必要条件
答案 B
解析 因为直线a,b,平面α,β,a⊂α,b⊂α,由a∥β,b∥β,得α,β平行或相交;
由α∥β,得a∥β,b∥β,
所以a∥β,b∥β是α∥β的必要不充分条件.故选B.
3.(多选)在正方体ABCD-A1B1C1D1中,下列结论正确的是有(
A.AD1∥BC1
B.平面AB1D1∥平面BDC1
所以 C 到平面 ABD 的距离为 h=BC·
sin
1
30°= .
2
因为 AE=2,F 是 BC 的中点,
所以
1
1
1
VA-CDF=VF-ACD= VB-ACD= VC-ABD=
2
2
2
1
3
× ×
1
1
×1×2×
2
2
=
1
.
12
解题心得在应用线面平行的性质定理进行平行转化时,一定注意定理成立
的条件,通常应严格按照定理成立的条件规范书写步骤,如:把线面平行转
α,β相交于点A,B,C,D,若PA=4,PB=5,PC=3,则
PD=
答案
.
15
4
解析 由题意,平面 α∥平面 β,则
Hale Waihona Puke 所以·PD=
=
3×5
线面位置关系的八大定理
l m β
α
线面位置关系的八大定理(平行关系)
一、直线与平面平行的判定定理:
文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行 图形语言:
符号语言:
//a b a b αα⊄⎫⎪⊂⎬⎪⎭
⇒//a α
作用:线线平行⇒线面平行
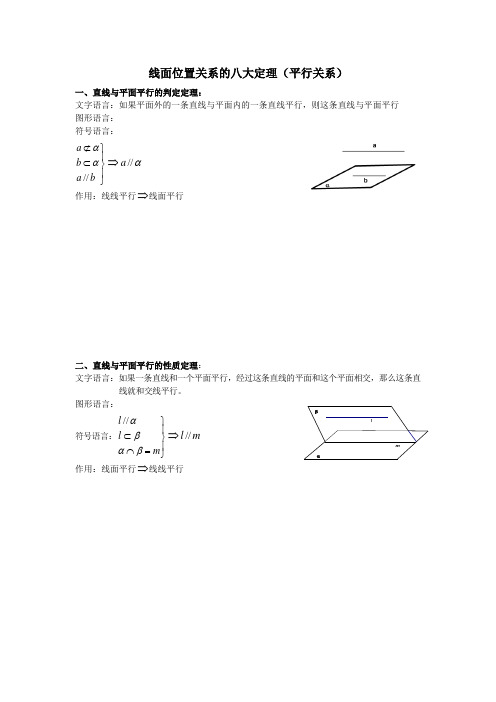
二、直线与平面平行的性质定理:
文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直
线就和交线平行。
图形语言:
符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭
⇒//l m
作用:线面平行⇒线线平行
三、平面与平面平行的判定定理
文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言:
符号语言:
//a b a b A a b α
α
αββ
β⊂⎫⎪⊂⎪⎪=
⇒⎬⎪⎪⎪⎭
∥∥ 作用:线面平行⇒ 面面平行
推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平
面平行。
四、平面与平面平行的性质定理:
文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行 图形语言:
符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭
作用: 面面平行⇒线线平行
性质:当两平面平行时,其中一个平面内的任一条直线平行与另一平面。
推论:两条直线被三个平行平面所截,截得的对应线段成比例。
线面平行的判定定理ppt课件
三个条件缺一不可,缺少其中任何一条,则 结论就不一定成立了.
2、简记:线线平行,则线面平行。
3、定理告诉我们:
直线间平行关系
直线与平面平行关系
空间问题
平面问题
理论迁移
例1.空间四边形ABCD中,E,F分别为AB,AD的
中点,试判断EF与平面BCD的位置关系,并予
以证明.P29例1.
A
解:EF∥平面BCD。
求证:AB1//平面DBC1
A1
C1
B1
P
D
A
C
B
2、如图,在正方体 ABCD——A1B1C1D1中, O是底面ABCD对角线的交点. 求证:C1O//平面AD1B1.
A1 C1
B1
E
A D C
B
4、如图 ,正方体AC1中,点N是BD中点,点M是B1C中 点.
求证: MN // 平面AA1B1B .
件是要满足六个字,
b
“面外、面内、平行”. b//a
a //
反思3:运用定理的关键是找平行线,找平行线又经常会 用到三角形中位线定理.
理论迁移
例2. 如图,四面体ABCD中,E,F,G,H分别 是AB,BC,CD,AD的中点.
(1)E、F、G、H四点是否共面?
(2)试判断AC与平面EFGH的位置关系;A
根据定义,判定直线与平面是否平行,只需 判定直线与平面有没有公共点.但是,直线无限 延长,平面无限延展,用定义这种方法来判定直 线与平面是否平行是很困难的.
那么,是否有简单的方法来判定直线与平面 平行呢?
知识探究(三):直线与平面平行的判断定理 1、直观感知
三.线面平行判定定理的探究
动手操作—确认定理
必修二立体几何初步第三讲---平行关系.

专题平行关系本讲义主要内容:第一部分:【知识回顾】1.直线与平面平行的判定(1直线与平面平行的定义:如果一条直线与一个平面没有公共点,我们就说这条直线与这个平面平行.(2直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.符号表示为:.注意:这个定理是证明直线与平面平行最常用的一个定理,也就是说欲证明一条直线与一个平面平行,一是说明这条直线不在这个平面内,二是要证明已知平面内有一条直线与已知直线平行.2.两个平面平行的判定(1两个平面平行的定义:两个平面没有公共点,则两个平面平行.(2平面与平面的平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.符号表示为:.注意:这个定理的另外一种表达方式为“如果一个平面内有两条相交直线和另一个平面内的两条相交直线分别平行,那么这两个平面平行”.(3平行于同一平面的两个平面互相平行.即.3.直线与平面平行的性质(1 直线与平面平行的性质定理:一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.符号表示为:.注意:如果一条直线和一个平面平行,那么这条直线和平面内的无数条直线平行,但不能误解为“如果一条直线与一个平面平行,那么这条直线就和平面内的任意一条直线平行”.实际上,如果一条直线和一个平面平行,这条直线和平面内的直线平行或异面,有两种位置关系.(2直线与平面平行的性质:过平面内一点的直线与该平面平行的一条直线平行,则这条直线在这个平面内.符号表示为:若,点,且,则.4.平面与平面平行的性质(1如果两个平面平行,那么其中一个平面内的任意直线均平行与另一个平面.此结论可以作为定理用,可用来判定线面平行.(2两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.(3夹在两个平行平面间的平行线段相等.第二部分:【经典例题】例1 下面说法正确的是()A. 直线平行于平面内的无数条直线,则∥;B. 若直线在平面外,则∥;C. 若直线∥,直线,则∥;D. 与两条异面直线都平行的平面有无穷多个例2 下列说法中正确的是()①若一个平面内有两条直线都与另一个平面平行,则这两个平面平行;②若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;④若一个平面内的两条内的两条相交直线分别平行于另一个平面,则这两个平面平行。
高中数学必修课件第一章平行关系的性质

思路梳理
首先,根据平行面的定义和性质 ,明确平行面被第三个平面截得 的交线也是平行的。然后,利用 这一性质来证明题目中的结论。
实际应用场景举例
01
建筑学
在建筑设计中,平行面的概念被广泛应用于墙体、地面和天花板的布局
。通过确保这些平面相互平行,可以创造出稳定、和谐的视觉效果。
02 03
机械工程
在机械设计中,平行面被用于确保机器部件的精确配合。例如,轴承和 轴之间的配合就需要保证它们各自的平面相互平行,以确保机器的正常 运转。
答案
根据已知条件和三角函数公式,证明了两直线所成的同 角三角函数值相等,因此两直线平行。
拓展:其他函数在平行关系中应用
要点一
指数函数和对数函数
要点二
三角函数与其他函数的复合应用
在平行线问题中,有时可以利用指数函数和对数函数的性 质和公式进行求解。
在解决平行线问题时,可以将三角函数与其他函数进行复 合应用,如三角函数与二次函数、三角函数与反三角函数 等,从而得到更复杂的数学模型和更精确的求解结果。
探讨平行关系在代数、几何、三角函数等领域的 应用。
解题方法技巧归纳
判定平行线的方法
01
通过同位角、内错角、同旁内角等角度关系判定两直线是否平
行。
利用平行线性质解题
02
运用平行线的性质定理和推论解决相关问题,如角度计算、线
段比例等。
平行平面问题的求解策略
03
掌握平行平面在空间几何中的判定和性质,运用空间想象和逻
误区提示
在判断两直线是否平行时,要注意同位角、内错角和同旁内角的概念及性质,避免出现混淆或误判的情况。同时 ,在求解角度问题时,也要注意对顶角和邻补角的概念及性质。
