晶胞计算习题
晶胞计算习题

1.回答下列问题(1)金属铜晶胞为面心立方最密堆积, 边长为acm。
又知铜的密度为ρ g·cm-3, 阿伏加德罗常数为_______。
(2)下图是CaF2晶体的晶胞示意图, 回答下列问题:①Ca2+的配位数是______, F-的配位数是_______。
②该晶胞中含有的Ca2+数目是____, F-数目是_____, ③CaF2晶体的密度为ag·cm-3, 则晶胞的体积是_______(只要求列出算式)。
2.某些金属晶体(Cu、Ag、Au)的原子按面心立方的形式紧密堆积, 即在晶体结构中可以划出一块正立方体的结构单元, 金属原子处于正立方体的八个顶点和六个侧面上, 试计算这类金属晶体中原子的空间利用率。
(2)(3)3、单晶硅的晶体结构与金刚石一种晶体结构相似, 都属立方晶系晶胞, 如图:(1)将键联的原子看成是紧靠着的球体, 试计算晶体硅的空间利用率(计算结果保留三位有效数字, 下同)。
(2)已知Si—Si键的键长为234 pm, 试计算单晶硅的密度是多少g/cm3。
4、金晶体的最小重复单元(也称晶胞)是面心立方体, 如图所示, 即在立方体的8个顶点各有一个金原子, 各个面的中心有一个金原子, 每个金原子被相邻的晶胞所共有。
金原子的直径为d, 用NA表示阿伏加德罗常数, M表示金的摩尔质量。
请回答下列问题:(1)金属晶体每个晶胞中含有________个金原子。
(2)欲计算一个晶胞的体积, 除假定金原子是刚性小球外, 还应假定_______________。
(3)一个晶胞的体积是____________。
(4)金晶体的密度是____________。
5.1986年, 在瑞士苏黎世工作的两位科学家发现一种性能良好的金属氧化物超导体, 使超导工作取得突破性进展, 为此两位科学家获得了1987年的诺贝尔物理学奖, 实验测定表明, 其晶胞结构如图所示。
(4)(5)(6)(1)根据所示晶胞结构, 推算晶体中Y、Cu、Ba和O的原子个数比, 确定其化学式。
高中化学晶胞的相关计算专项训练知识点及练习题及答案

高中化学晶胞的相关计算专项训练知识点及练习题及答案一、晶胞的相关计算1.铁(Fe)、铜(Cu)、银(Ag)是常见的金属元素,它们的单质及其化合物在生活中有广泛应用。
(1)Ag 与 Cu 在同一族,则 Ag 在周期表中________ (填“s”、“p”、“d”或“ds”)区;[Ag(NH3)2]+中Ag+空的 5s 轨道和 5p 轨道以sp 杂化成键,则该配离子的空间构型是________。
(2)基态 Cu+的简化电子排布式为________。
(3)表中是 Fe 和 Cu 的部分电离能数据:请解释 I2(Cu)大于 I2(Fe)的主要原因:________。
元素Fe Cu第一电离能 I1/kJ·mol-1759746第二电离能 I2/kJ·mol-115611958(4)亚铁氰化钾是食盐中常用的抗结剂,其化学式为 K4[Fe(CN)6]。
①CN-的电子式是________;1mol 该配离子中含σ 键数目为________。
②该配合物中存在的作用力类型有________ (填字母)。
A.金属键 B.离子键 C.共价键 D.配位键 E.氢键 F.范德华力(5)氧化亚铁晶体的晶胞结构如图所示。
已知:氧化亚铁晶体的密度为ρg•cm﹣3,N A代表阿伏加德罗常数的值。
在该晶胞中,与 Fe2+紧邻且等距离的 Fe2+数目为________,Fe2+与O2﹣最短核间距为________pm。
2.国庆70周年阅兵式展示了我国研制的各种导弹。
导弹之所以有神奇的命中率,与材料息息相关,镓(Ga)、锗(Ge)、硅(Si)、硒(Se)的单质及某些化合物(如砷化镓、磷化镓等)都是常用的半导体材料。
回答下列问题:(1)硒常用作光敏材料,基态硒原子的核外电子排布式为[Ar]__。
(2)根据元素周期律,原子半径Ga__As,第一电离能Ga__As。
(填“大于”或“小于”)(3)水晶的主要成分是二氧化硅,在水晶中硅原子的配位数是__。
习题和思考题

《无机材料科学基础》习题和思考题第一章晶体1.球体按立方最紧密堆积方式堆积,取出立方晶胞,画出立方晶胞中的四面体空隙和八面体空隙的位置分布图。
2.用鲍林规则分析氧化镁晶体结构。
已知镁离子半径为0.65Å,氧离子半径为1.40Å。
(1)确定晶胞中质点的位置坐标;(2)计算每个晶胞中含氧化镁“分子”数,(3)已知晶胞常数a=4.20 Å,求氧化镁堆积系数和密度,(4)氧化镁晶体中最邻近的两个镁离子中心距为多少?次邻近的两个镁离子中心距为多少?最邻近和次邻近的两个氧离子中心距为多少?(5)画出氧化镁晶胞的(111)、(110)、(100)面的质点分布图并在图上标出氧离子的密排方向,求个面的面密度。
3.已知纤锌矿结构中存在两套硫离子和两套锌离子的六方底心格子,并已知锌离子填充在硫离子最紧密堆积体的四面体空隙中,现以一套硫离子的等同点为基准取六方晶胞,画出晶胞中的质点分布图,计算晶胞中所含式量分子数。
4.完成下表5. 六方最紧密堆积与四方最紧密堆积的堆积密度相同,为什么许多氧化物是以氧离子的立方最紧密堆积为基础,而较少以六方最紧密堆积为基础?6. 用鲍林规则分析镁橄榄石的结构:P48 图2-18(1)标记为50的Mg2+与哪几个氧离子配位形成[MgO6]八面体?写出O2+的标高;(2)标记为25的两个O2+与哪几个镁离子配位?写出Mg2+离子的标高;(3)标记为75的O2+离子与哪几个镁离子配位?写出Mg2+离子的标高;(4)标记为0和50的两个Mg2+的[MgO6] 八面体共用几个顶点?写出O2+的标高;(5)[SiO4] 和 [MgO6] 之间、[MgO6]和[MgO6] 八面体之间有那些连接方式?(6)镁橄榄石的晶胞是什么形状?计算晶胞中含有的式量分子数。
第二章晶体缺陷1.氧化镁为氯化钠型结构,氧化锂为反萤石型结构,在两种结构中氧离子都作立方最紧密堆积,为什么在氧化镁中主要的热缺陷是肖特基型,而在氧化锂中却是弗伦克尔型?萤石型结构的氧化物晶体中常见的热缺陷估计主要是什么类型?为什么?2.已知氯化钠晶体中肖特基缺陷形成焓为2.2ev,而氧化镁晶体中肖特基缺陷形成焓为6ev,试分别计算400℃时氯化纳晶体与氧化镁晶体中肖特基缺陷的浓度。
《结晶学基础》第十章习题答案9501第一步:计算出金刚石的晶胞参数a...

《结晶学基础》第十章习题答案9501第一步: 计算出金刚石的晶胞参数a 。
d =3A/a N ZM a = (30231051.3)1002.6/()00.128(-⨯⨯⨯)1/3pm = 356.8 pm 第二步: 根据C 原子的坐标参数, 计算键长。
其中,相邻两个C 原子的坐标: (0,0,0); (1/4,1/4,1/4);它们之间的距离即键长是晶 胞对角线长的1/4,晶胞对角线长为3ad c —c = 43a = 48.3563⨯pm = 154 pm9502(B)950334.01%9504(1)硅晶体晶胞中有8个Si 原子, d =23310023.606.288⨯⨯⨯a , a = 543pm (2) r Si —Si =(1/4)3a = 235 pm 9505 a = 31178⨯pm = 540 pm9506 (1)60sin 21642A c a N )(+=866.01037.752.41002.618424223⨯⨯⨯⨯⨯⨯-g ·cm -3=0.917 g ·cm -3(2) O —H …O 氢键存在于各邻近的O …O 之间, 氢键键长为0.375×737 pm=276 pm 。
9506 (1)60sin 21642A c a N )(+=866.01037.752.41002.618424223⨯⨯⨯⨯⨯⨯-g ·cm -3=0.917 g ·cm -3(2) O —H …O 氢键存在于各邻近的O …O 之间, 氢键键长为0.375×737 pm=276 pm 。
9508含有2个B------B 三中心二电子桥键。
9509参看周公度编著,《结构化学基础》,北京大学出版社,1989, p.444 。
4个B------B 三中心二电子硼氢桥键 1个 五中心六电子硼键。
9510(1) 参看周公度编著, 《结构化学基础》,北京大学出版社,1989, p.444 。
【化学奥赛】晶体结构习题new!
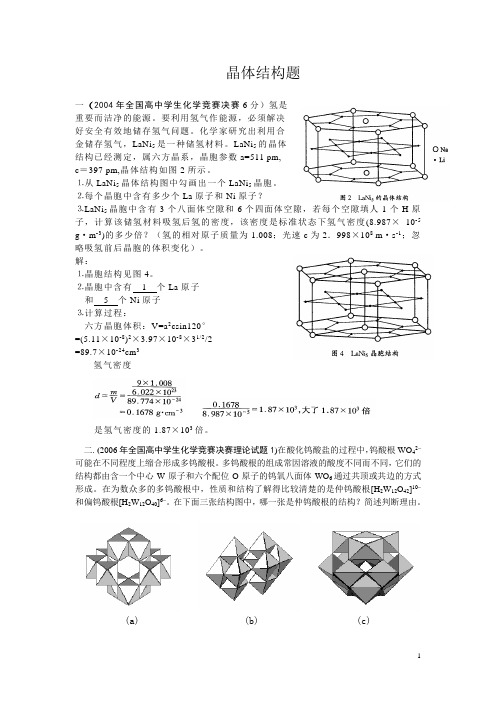
晶体结构题一(2004年全国高中学生化学竞赛决赛6分)氢是重要而洁净的能源。
要利用氢气作能源,必须解决好安全有效地储存氢气问题。
化学家研究出利用合金储存氢气,LaNi5是一种储氢材料。
LaNi5的晶体结构已经测定,属六方晶系,晶胞参数a=511 pm,c=397 pm,晶体结构如图2所示。
⒈从LaNi5晶体结构图中勾画出一个LaNi5晶胞。
⒉每个晶胞中含有多少个La原子和Ni原子?⒊LaNi5晶胞中含有3个八面体空隙和6个四面体空隙,若每个空隙填人1个H原子,计算该储氢材料吸氢后氢的密度,该密度是标准状态下氢气密度(8.987×10-5 g·m-3)的多少倍?(氢的相对原子质量为1.008;光速c为2.998×108 m·s-1;忽略吸氢前后晶胞的体积变化)。
解:⒈晶胞结构见图4。
⒉晶胞中含有1个La原子和5个Ni原子⒊计算过程:六方晶胞体积:V=a2csin120°=(5.11×10-8)2×3.97×10-8×31/2/2=89.7×10-24cm3氢气密度是氢气密度的1.87×103倍。
二. (2006年全国高中学生化学竞赛决赛理论试题1)在酸化钨酸盐的过程中,钨酸根WO42-可能在不同程度上缩合形成多钨酸根。
多钨酸根的组成常因溶液的酸度不同而不同,它们的结构都由含一个中心W原子和六个配位O原子的钨氧八面体WO6通过共顶或共边的方式形成。
在为数众多的多钨酸根中,性质和结构了解得比较清楚的是仲钨酸根[H2W12O42]10-和偏钨酸根[H2W12O40]6-。
在下面三张结构图中,哪一张是仲钨酸根的结构?简述判断理由。
(a) (b) (c)解:提示:考察八面体的投影图,可以得到更清楚地认识。
三.(2006年全国高中学生化学竞赛决赛理论试题4)轻质碳酸镁是广泛应用于橡胶、塑料、食品和医药工业的化工产品,它的生产以白云石(主要成分是碳酸镁钙)为原料。
黄昆固体物理习题-第一章 晶体结构

第一章习题参考解答解答:设立方晶格的边长为a,一个晶胞中的原子数为n,原子球半径为R,晶胞体积为V,则致密度(或叫填充率)K为:V Rn K3 34π•= ch1.1 题略3343===0.52(2)6R K R ππ(1) 简单立方,晶胞内含有一个原子n=1,原子球半径为R ,立方晶格的顶点原子球相切,立方边长a=2R ,体积为(2R)3,所以VR n K 334π•=(2)体心立方晶胞内有2个原子,n=2,原子球半径为R ,晶胞边长为a ,立方晶格的体对角线原子球相切,体对角线长为4个原子半径,所以ππ83)34(342,3433=⨯=R R K R =0.68ππ83)34(342,3433=⨯==R R K R a(3)面心立方晶胞内有4个原子,晶胞的面对角线原子球相切,面对角线长度为4个原子半径,立方体边长为a ,ππ62)24(34433=⨯=R RK =0.74,24R a =(4)六角密排原胞内中含2个原子,正四面体四个顶点处的原子球相切,边长为a ,六角柱高h =0.74ππ62322]321)2[(34223=•⨯⨯⨯=a R R K hs 斜边2R=a[(2R)2-[(2Rsin60)х2/3]2=(h/2)2底边竖直边ππ16383433=⨯=a R K =0.34(5)金刚石在单位晶格中含有8个原子,碳原子最近邻长度2R 为体对角线1/4长,体对角线为,38a R =证明1:设六角层内最近邻原子间距为a ,相邻两层间的最近邻为d ,则633.13/8,])2()3[(,])2()3[(21222122≈=+==+=a c c a a a d c a d 由此解出此时有构,时构成理想的密堆积结当ch1.2 题略a d证明2:设六角层内最近邻原子间距为a,相邻两层间的最近邻为d,则a dch1.3 题略解:对于体心立方,原胞基矢为:对于体心立方原胞体积为:1.3)(21k j a a +=)(22i k a a +=)(23j i a a +=对于面心立方,原胞基矢为:根据倒格子基矢定义,并将体心原胞基矢代入计算之,可得:将计算所得到的倒格子基矢与面心立方原胞基矢相同,可知体心立方的倒格子是面心立方。
(3.7)--第3章部分习题解答
转变为一个 fcc 晶胞。故
rCu = 0.3611ᄡ 2 / 4 nm = 0.1277 nm
(2)从附录查出 Au 的相对原子量为 196.97,故得 xAu=40%的 Cu-Au 固溶体中每个原子的平
均重量 A
A
=
63.55
ᄡ0.6 + 196.97 6.0238 ᄡ1023
ᄡ 0.4
g
=
1.941 ᄡ10-22
g
求每个晶胞的原子数 n
3-12.纯铁在 912 °C 由 bcc 结构转变为 fcc 结构,体积减少 1.06%,根据 fcc 结构的原子半径
计算 bcc 结构的原子半径。它们的相对变化为多少?如果假定转变前后原子半径不变,计算
转变后的体积变化。这些结果说明了什么?
解:设 bcc 结构的点阵常数为 ab,fcc 结构的点阵常数为 af,由 bcc 结构转变为 fcc 结构时体 积减少 1.06%,因为每个 bcc 单胞包含 2 个原子,FCC 单胞 4 个原子,所以 2 个 BCC 晶胞
解:(1)从附录查出铜的相对原子质量为 63.55,阿佛加得罗常数是 6.02381023,每个 Cu 原
子的质量 ACu 为
ACu
=
63.55 6.0238 ᄡ1023
g
= 10.55 ᄡ10-23g
Cu 属 fcc 结构,每个晶胞含 4 个原子,设 Cu 晶胞的点阵常数为 a,一个晶胞的质量是 4 个
三条边共有
3/2
个原子),所以面密度
rp
=
4 a2
3
=
43 3a 2
。
图 x3-1
图 x3-2 所示为体心立方结构(100)、(110)、(111)晶面(部分)的原子排列情况。图 x3-2 所 示(100)面的面积为 a2,而在这面积中含一个原子(四个顶角共有一个原子),所以面密度 P=1/a2。 图 x3-2 所示(110)面的面积为 2a2 ,而在这面积中含两个原子(四个顶角共有一个原子, 中心有一个原子),所以面密度 r p = 2 / a2 。 图 x3-2 所示(111)面的面积是等边三角形,面积等于 a2 3 / 2 ,而在这面积中含 1/2 个原子
晶体学习题与答案
一、 名词解释(1)阵点;(2)(空间)点阵;(3)晶体结构;(4)晶胞;(5)晶带轴;二、填空(1)晶体中共有 种空间点阵,属于立方晶系的空间点阵有 三种。
(2)对于立方晶系,晶面间距的计算公式为 。
(3){110}晶面族包括 等晶面。
(4){h 1k 1l 1}和{h 2k 2l 2}两晶面的晶带轴指数[u v w]为 。
(5)(110)和(11-0)晶面的交线是 ;包括有[112]和[123]晶向的晶面是 。
三、计算及简答(1)原子间的结合键共有几种?各自有何特点?(2)在立方晶系的晶胞中,画出(111)、(112)、(011)、(123)晶面和[111]、[101]、[111-]晶向。
(3)列出六方晶系{101-2} 晶面族中所有晶面的密勒指数,并绘出(101-0)、(112-0)晶面和〔112-0〕晶向。
(4)试证明立方晶系的〔111〕晶向垂直于(111)晶面。
(5)绘图指出面心立方和体心立方晶体的(100)、(110)、及(111)晶面,并求其面间距;试分别指出两种晶体中,哪一种晶面的面间距最大?(6)在立方晶系中,(1-10)、(3-11)、(1-3-2)晶面是否属于同一晶带?如果是,请指出其晶带轴;并指出属于该晶带的任一其他晶面。
(7)写出立方晶系的{111}、{123}晶面族和<112>晶向族中的全部等价晶面和晶向的具体指数。
(8)计算立方晶系中(111)和〔111-〕两晶面间的夹角。
(9)若采用四轴坐标系标定六方晶体的晶向指数,应该有什么约束条件?为什么?答 案二、填空(1)14 简单、体心、面心(2)222hkl d h k l =++(3) (110)、(101)、(011)、(1-10)、(1-01) 、(01-1) (4)1122k l u k l =;1122l h v l h =;1122h k w h k = (5)〔001〕 (111-)三、简答及计算(1)略(2)(3){101-2}晶面的密勒指数为(101-2)、(1-012)、(01-12)、(011-2)、(1-102)、(11-02)。
晶胞计算习题问题详解
1、【答案】(1)mol-1(2)①8 4 ②48③【解析】(1)铜晶胞为面心立方最密堆积,1个晶胞能分摊到4个Cu原子;1个晶胞的体积为a3cm3;一个晶胞的质量为a3ρ g;由=a3ρ g,得N A=mol-1。
(2) ①每个Ca2+周围吸引8个F-,每个F-周围吸收4个Ca2+,所以Ca2+的配位数为8,F-的配位数为4。
②F-位于晶胞部,所以每个晶胞中含有F-8个。
含有Ca2+为×8+×6=4个。
③ρ===a g·cm-3,V=。
2、【解析】试题分析:本考查学生对知识综合利用能力,要求对晶胞知识能够融会贯通。
依题意画出侧面图,设正立方体边长为a,则体积为a3。
,AC=4r,故原子半径,根据均摊法得,每个正立方体包括金属原子8×1/8+6×1/2=4(个),球体体积共4×空间利用率为:.考点:均摊法计算点评:本题考查相对综合,是学生能力提升的较好选择。
3、(1)34.0% (2)2.36 g/cm3【解析】(1)该晶胞中Si原子个数=4+8×1/8+6×1/2=8,设Si原子半径为xcm,该晶胞中硅原子总体积=,根据硬球接触模型可知,体对角线四分之一处的原子与顶点上的原子紧贴,设晶胞边长为a,所以,解得a=,晶胞体积=()3,因此空间利用率=×100%=34.0%。
(2)根据以上分析可知边长=,所以密度==2.36g/cm3。
4、【答案】(1)4(2)金属原子间相接触,即相切(3)2d3(4)【解析】利用均摊法解题,8个顶点上每个金原子有属于该晶胞,6个面上每个金原子有属于该晶胞,故每个晶胞中金原子个数=8×+6×=4。
假设金原子间相接触,则有正方形的对角线为2d。
正方形边长为d。
所以V晶=(d)3=2d3,V m=N A=d3N A,所以ρ==。
5、【答案】(1)YBa2Cu3O7(2)价n(Cu2+)∶n(Cu3+)=2∶1【解析】(1)由题图所示晶胞可知:一个晶胞中有1个Y3+,2个Ba2+。
第一章晶格结构习题
第一章晶体结构习题1、晶体结构的堆积比率 在sc, bcc 和fcc 结构中,fcc 是原子排列最密积的,sc 是最稀疏的,它们的配位数分别是fcc-12;bcc-8;sc-6;而金刚石结构比简单立方结构还要稀疏,配位数是4。
如果把同样的硬球放置在这些结构原子所在的位置上,球的体积取得尽可能大,以使最近邻的球正好接触,但彼此并不重迭。
我们把一个晶胞中被硬球占据的体积和晶胞体积之比定义为结构的堆积比率(又叫最大空间利用率)。
试证明以上四种结构的堆积比率是fcc :74.062=π bcc :68.083=π sc :52.061=π 金刚石:34.0163=π 2、点阵常数的计算 已知氯化钠是立方晶体,其分子量为58.46,在室温下的密度是2.167×103 kg·m -3,试计算氯化钠结构的点阵常数。
3、立方晶系的晶面和晶向 证明立方晶系中方向[hkl ]垂直于平面(hkl )。
4、六角密堆积结构 (a) 证明理想的六角密堆积结构(hcp)的轴比c /a 是 (8/3)1/2=1.633。
(b) 钠在23K 附近从bcc 结构转变为hcp 结构(马氏体相变),假如在此相变过程中保持密度不变,求hcp 相的点阵常数a 。
已知bcc 相的点阵常数是4.23Å,且hcp 相的c /a 比值与理想值相同。
5、面间距 考虑晶体中一组互相平行的点阵平面 (hkl ),(a) 证明倒易点阵矢量G (hkl )=h b 1+k b 2+l b 3垂直于这组平面(hkl );(b) 证明两个相邻的点阵平面间的距离d (hkl )为:)(2)(hkl G hkl d π= (c) 证明对初基矢量a 1、a 2、a 3互相正交的晶体点阵,有 232221)/()/()/(1)(a l a k a h hkl d ++=(d) 证明对简单立方点阵有 )()()()(222l k h ahkl d ++=6、一个单胞的尺寸为a 1=4 Å ,a 2=6 Å ,a 3=8 Å ,α=β=90°,γ=120°,试求:(a) 倒易点阵单胞基矢;(b)倒易点阵单胞体积;(c) (210)平面的面间距。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*1、回答下列问题(1)金属铜晶胞为面心立方最密堆积,边长为a cm。
又知铜的密度为ρ g·cm-3,阿伏加德罗常数为_______。
(2)下图是CaF2晶体的晶胞示意图,回答下列问题:①Ca2+的配位数是______,F-的配位数是_______。
②该晶胞中含有的Ca2+数目是____,F-数目是_____,③CaF2晶体的密度为a g·cm-3,则晶胞的体积是_______(只要求列出算式)。
2、某些金属晶体(Cu、Ag、Au)的原子按面心立方的形式紧密堆积,即在晶体结构中可以划出一块正立方体的结构单元,金属原子处于正立方体的八个顶点和六个侧面上,试计算这类金属晶体中原子的空间利用率。
(2)(3)3、单晶硅的晶体结构与金刚石一种晶体结构相似,都属立方晶系晶胞,如图:(1)将键联的原子看成是紧靠着的球体,试计算晶体硅的空间利用率(计算结果保留三位有效数字,下同)。
(2)已知Si—Si键的键长为234 pm,试计算单晶硅的密度是多少g/cm3。
4、金晶体的最小重复单元(也称晶胞)是面心立方体,如图所示,即在立方体的8个顶点各有一个金原子,各个面的中心有一个金原子,每个金原子被相邻的晶胞所共有。
金原子的直径为d,用N A表示阿伏加德罗常数,M表示金的摩尔质量。
请回答下列问题:(1)金属晶体每个晶胞中含有________个金原子。
(2)欲计算一个晶胞的体积,除假定金原子是刚性小球外,还应假定_______________。
(3)一个晶胞的体积是____________。
(4)金晶体的密度是____________。
5、1986年,在瑞士苏黎世工作的两位科学家发现一种性能良好的金属氧化物超导体,使超导工作取得突破性进展,为此两位科学家获得了1987年的诺贝尔物理学奖,实验测定表明,其晶胞结构如图所示。
(4)(5)(6)(1)根据所示晶胞结构,推算晶体中Y、Cu、Ba和O的原子个数比,确定其化学式。
(2)根据(1)所推出的化合物的组成,计算其中Cu原子的平均化合价(该化合物中各元素的化合价为、、和)。
试计算化合物中两种价态的Cu原子个数比。
6、(1)NiO(氧化镍)晶体的结构与NaCl相同,Ni2+与最邻近O2-的核间距离为×10-8cm,计算NiO晶体的密度(已知NiO的摩尔质量为74.7 g·mol-1)。
(2)天然的和绝大部分人工制备的晶体都存在各种缺陷,例如在某种NiO晶体中就存在如下图所示的缺陷:一个Ni2+空缺,另有两个Ni2+被两个Ni3+所取代。
结果晶体仍呈电中性,但化合物中Ni和O的比值却发生了变化。
某氧化镍样品组成为Ni0.97O,试计算该晶体中Ni3+与Ni2+的离子数之比。
7、下图是金属钨晶体中的一个晶胞的结构示意图,它是一种体心立方结构。
实验测得金属钨的密度为19.30 g·cm-3,钨的相对原子质量是183.9。
假设金属钨原子为等径刚性球,试完成下列问题:(7)(8)(1)每一个晶胞中均摊到________个钨原子。
(2)计算晶胞的边长a。
(3)计算钨的原子半径r(提示:只有体对角线上的各个球才是彼此接触的)。
8、铁、钴、镍为第四周期第Ⅷ族元素,它们的性质非常相似,也称为铁系元素.(1)铁、钴、镍都是很好的配位化合物形成体.①[Co(H2O)6]2+在过量氨水中易转化为[Co(NH3)6]2+.写出Co2+的价层电子排布图.[Co(H2O)6]2+中Co2+的配位数为:NH3分子的中心原子杂化方式为.H2O 分子的立体构型为.②铁、镍易与一氧化碳作用形成羰基配合物,如:Fe(CO)5,Ni(CO)4等.CO与N2属于等电子体,则CO分子中σ键和π键数目比为,写出与CO互为等电子体的一种阴离子的离子符号.(2)+2价和+3价是Fe、Co、Ni等元素常见化合价.NiO、FeO的晶体结构类型均与氯化钠的相同,Ni2+和F22+的离子半径分别为69pm和78pm,则熔点NiO FeO(选填“<”“>”“=”);某种天然Nio晶体存在如图所示缺陷:一个Niz+空缺,另有两个Ni2+被两个Ni3+所取代.其结果晶体仍呈屯中性.某氧化镍样品组成为Ni0.97O.该晶体中Ni3+与Ni2+的离子数之比为.9、CaO与NaCl的晶胞同为面心立方结构,已知CaO晶体密度为a g·cm-3,N A表示阿伏加德罗常数,则CaO晶胞体积为________cm3。
10、原子序数依次递增且都小于36的X、Y、Z、Q、W四种元素,其中X是原子半径最小的元素,Y原子基态时最外层电子数是其内层电子数的2倍,Q原子基态时2p原子轨道上有2个未成对的电子,W元素的原子结构中3d能级有4个未成对电子。
回答下列问题:(1)Y2X2分子中Y原子轨道的杂化类型为,Y2X2分子中σ键和π键个数比为。
(2)化合物ZX3的沸点比化合物YX4的高,其主要原因是。
(3)元素Y的一种氧化物与元素Z的一种氧化物互为等电子体,元素Z的这种氧化物的分子式是。
(4)元素W能形成多种配合物,如:W(CO)5等。
①基态W3+的M层电子排布式为。
②W(CO)5常温下呈液态,熔点为—20.5℃,沸点为103℃,易溶于非极性溶剂,据此可判断W(CO)x晶体属于(填晶体类型),该晶体中W的化合价为。
(5)下列有关的说法正确的是。
A.分子晶体中,共价键键能越大,该分子晶体的熔沸点越高B.电负性顺序:X<Y<Z<QC.因为晶格能CaO比KCl高,所以KCl比CaO熔点低D.H2YO3的分子结构中含有一个非羟基氧,故其为中强酸(6)Q和Na形成的一种只含有离子键的离子化合物的晶胞结构如图,距一个阴离子周围最近的所有阳离子为顶点构成的几何体为。
已知该晶胞密度为ρ g/cm3,阿伏加德罗常数为N A,求晶胞边长a= cm。
(用含ρ、N A的计算式表示)11、由原子序数由小到大的A、B、C、D、E五种元素构成某配位化合物X,其原子个数比为14:4:5:1:1。
其中C、D元素同主族且原子序数D为C的二倍,E元素的外围电子排布为(n-l)d n+61Ns1,回答下列问题。
(1)该配位化合物X的化学式为。
(2)元素B、C、D的第一电离能的由小到大排列顺序为。
(用元素符号表示)(3)D元素原子的最外层电子轨道表示式为________ 。
(4)C元素可与A元素形成两种常见的化合物,其原子个数比分别为1:1和l:2,两种化合物可任意比互溶,解释其主要原因为。
(5)碳铂是一种含BA3分子的具有抗癌活性的金属配合物,碳铂的结构如下图:其中碳原子的杂化方式有____ 。
碳铂中含有的作用力有(填字母)。
A.共价键 B.配位键 C.金属键 D.键 E.键(6)A元素与E元素可形成一种红色离子化合物Y,其原子个数比为1:1,该化合物Y可与稀硝酸反应,生成一种蓝色溶液和两种无色气体(其中一种为A元素的单质),写出该反应的化学方程式。
单质E的晶胞如图所示,若设该晶胞的边长为acm,阿伏加德罗常数为N A,单质E的摩尔质量为Mg/mol,则表示该晶胞密度的计算式为p= g/cm3。
(11)(12)(13)12、晶体具有规则的几何外形,晶体中最基本的重复单元被称为晶胞。
NaCl晶体结构如图所示。
已知Fe x O晶体晶胞结构为NaCl型,由于晶体缺陷,x值小于1。
测知Fe x O晶体密度为5.71 g/cm3,晶胞边长为4.28×10-10 m。
创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*(1)Fe x O中x值(精确至0.01)为____。
(2)晶体中的Fe以Fe2+和Fe3+的形式存在,在Fe2+和Fe3+的总数中,Fe2+的占有率(用小数表示,精确至0.001)为___。
(3)与某个Fe2+(或Fe3+)距离最近且等距离的O2-的个数为___。
(4)在晶体中,铁元素的离子间最短距离为______m。
13、金属钨晶体晶胞的结构模型如下图所示。
实验测得金属钨的密度为19.30已知钨的相对原子质量为183.8。
回答下列问题:(1)在钨晶体中每个晶胞占有的钨原子数为__________个。
(2)钨晶体晶胞的边长为__________。
(3)钨原子的半径为__________。
14、1986年,在瑞士苏黎世工作的两位科学家发现一种性能良好的金属氧化物超导体,使超导工作取得突破性进展,为此两位科学家获得了1987年的诺贝尔物理学奖,实验测定表明,其晶胞结构如图所示。
(14)(17)(1)根据所示晶胞结构,推算晶体中Y、Cu、Ba和O的原子个数比,确定其化学式。
(2)根据(1)所推出的化合物的组成,计算其中Cu原子的平均化合价(该化合物中各元素的化合价为、、和)。
试计算化合物中两种价态的Cu原子个数比。
15、用X射线研究某金属晶体,测得在边长为360 pm的立方晶胞中含有4个金属原子,此时金属的密度为9.0 g/cm3。
试回答下列问题:(1)此金属晶胞属于哪一种类型?(2)求每个晶胞的质量。
(3)求此金属的相对原子质量。
(4)求此金属原子的原子半径(pm)。
16、NaCl晶体中Na+与Cl-都是等距离交错排列,若食盐的密度是2.2 g·cm-3,阿伏加德罗常数为6.02×1023mol-1,食盐的摩尔质量为58.5 g·mol-1。
则食盐晶体中两个距离最近的钠离子中心间的距离是多少?17、(9分)(2018·全国卷Ⅲ)锌在工业中有重要作用,也是人体必需的微量元素。
回答下列问题:世纪金榜导学号36092152(1)Zn原子核外电子排布式为______________________________。
(2)黄铜是人类最早使用的合金之一,主要由Zn和Cu组成。
第一电离能I1(Zn)_______I1(Cu)(填“大于”或“小于”)。
原因是_________________。
(3)ZnF2具有较高的熔点(872 ℃),其化学键类型是_______;ZnF2不溶于有机溶剂而ZnCl2、ZnBr2、ZnI2能够溶于乙醇、乙醚等有机溶剂,原因是_______。
(4)《中华本草》等中医典籍中,记载了炉甘石(ZnCO3)入药,可用于治疗皮肤炎症或表面创伤。
ZnCO3中,阴离子空间构型为_______,C原子的杂化形式为_______。
(5)金属Zn晶体中的原子堆积方式如图所示,这种堆积方式称为。
六棱柱底边边长为a cm,高为_______c cm,阿伏加德罗常数的值为N A,Zn的密度为_______g·cm-3(列出计算式)。
18、砷的一些化合物常用作半导体、除草剂、杀鼠药等。
