小升初奥数—平面图形计算练习题
小升初数学真题分项汇编专题05平面图形答案及解析

加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!小升初数学真题分项汇编专题05平面图形一、选择题1.图中圆的面积是28.26cm2,平行四边形的面积是()。
A.24cm2B.30cm2C.12cm2D.15cm2 2.把一根长10cm的铁丝剪成三段,下面剪法中能围成三角形的是()。
A.2cm、3cm、5cm B.2cm、2cm、6cmC.1cm、3cm、6cm D.4cm、2cm、4cm3.一个平行四边形两条邻边的长分别是10cm和7cm,其中一条边上的高是8cm,这个平行四边形的面积是()。
A.63cm2B.80cm2C.56cm24.用三根同样长的绳子,分别围成一个长方形、正方形和圆形,面积最大的是()。
小升初专项复习《平面图形》(一)练习及答案

小升初专项复习《平面图形》一、填空题1.若等腰三角形的两边长分别为2和6,则它的周长为。
2.一个等腰三角形的两边长分别是 米和 米,这个三角形的周长是米。
3.长方形的面积是24平方厘米,长和面积的比是1:4,则长方形的宽是厘米。
4.用一根10.28米长的铁丝围成一个半圆,这个半圆的面积是平方米。
5.如图,把圆分成若干等份,剪拼成一个近似的长方形,已知长方形的宽为5cm,则长是cm,长方形的面积是cm2。
6.同一个圆中圆的与的比值叫做圆周率。
7.圆的位置与有关系,圆大小的与有关系。
8.晶晶画了一个平行四边形,它的高是 dm,底是高的 。
这个平行四边形的面积是dm2。
9.如图,零件厂要加工一批环形铁片,每个铁片的面积是平方厘米。
10.一个平行四边形的底是8厘米,面积是48.8平方厘米,高是厘米,与它等底等高的三角形的面积是平方厘米。
11.等腰三角形的一个底角是40°,它的顶角是°,这是一个角三角形。
12.一个梯形的上底是5厘米,下底是10厘米,高是5厘米(如图)。
这个梯形的一个钝角是°,这个梯形的面积是平方厘米。
13.一个长方形的长:宽=7:5,长比宽多6厘米,这个长方形的周长是,面积是。
14.在一个长8cm,宽3cm的长方形中剪出一个最大的半圆,这个半圆的周长是cm,面积是cm2。
15.如图,平行四边形的面积是20平方厘米,图中甲乙丙三个三角形的面积比是。
二、单选题16.两个正方形的边长的比是5:3,它们的面积的比是()A.3:5B.1:3C.5:1D.25:917.在一个长1.25米,宽0.8米的长方形里,最多能剪()个半径为20厘米的圆。
A.5B.7C.6D.2418.自行车的前轮半径为30厘米,后轮半径为20厘米。
如下图,当前轮向前行驶了5圈回到E点的位置时,后轮F点的位置是下图中的()。
A.B.C.D.19.如图,把正方形桌子面的四边撑起,就成了一张圆面桌子,经过测量圆面桌子的面积为π平方米,那么这张桌子的正方形桌面的面积为()平方米。
奥数——平面图形的面积一

平面图形的面积(一)——图形的等分例1 有一个三角形花坛,要把它平均分成两个相等的三角形,可以怎样分?练习将任一三角形分成面积相等的六个三角形,应怎么分?例2 三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
练习已知AE=3AB,BD=2BC,三角形ABC的面积是6,求三角形BDE的面积。
练习如图所示,找出梯形ABCD中有几组面积相等的三角形。
例3 已知三角形ABC的面积是12平方厘米,并且BE=2EC,F是CD的中点。
求阴影部分面积。
练习AC是CD的3倍,E是BC的中点,三角形CDE的面积为2平方厘米。
求三角形ABC的面积。
练习如图,正方形ABCD的边长是4厘米,CG=3厘米,长方形EFGD的长是5厘米,DE长几厘米?例4 在一块长方形的地里有一口长方形的水井,试画一条线把除井处的这块地平分成两块。
练习下图为5个面积为1的正方形拼成的。
试用一直线将此图形划分为面积相等的两块。
例5 将下图分成4个形状、大小完全相同的图形,且每个部分中都有一个小黑圈。
练习将下图分成4个形状相同、面积相等的小块。
作业1、三角形的面积公式:________________。
同底等高的三角形面积___________。
平行线间的距离处处___________。
2、甲、乙两个三角形的高相等,若甲的底是乙的底的5倍,则甲的面积就是乙面积的_____倍。
3、甲、乙两个三角形的底相等,若甲的高是乙的高的4倍,则甲的面积就是乙面积的______倍。
4、把一个等边三角形分成面积相等的三个三角形,有________种不同的方法。
5、如图1,该图是一个直角梯形,面积相等的三角形有_________组,请分别写出________________ __________________________________。
6、如图2,AD与BC平行,AD=5,BC=10,三角形ADC面积为10,则三角形ABC的面积是_______________。
人教版六年级下册数学小升初专题训练:平面图形(含答案)

人教版六年级下册数学小升初专题训练:平面图形一、单选题1.用一块长12米、宽8米的长方形铁皮剪成半径是1.5米的小圆(不能剪拼),至多能做( )个。
A.11B.8C.10D.132.如果要搭成一个从正面、左面、上面看到的图形都是如图的几何体,需要( )个小正方体。
A.3B.4C.5D.63.下图是由一个圆分成若干等分后,拼成的一个近似长方形,这个圆的周长与长方形的周长相差约4厘米,这个圆的周长约是( )厘米。
A.6.28B.9.42C.12.56D.无法计算4.从12时到13时,钟的时针与分针可成直角的机会有( )A.1次B.2次C.3次D.4次5.下列时刻中,钟表中时针与分针不成直角的是( )。
A.3:00B.21:00C.9:00D.12:206.一个半径是5cm的半圆,它的周长是( )cm。
A.31.4B.15.7C.25.7D.20.7二、填空题7.已知一个等腰三角形的两条边分别是5厘米、10厘米,那么它的周长是 厘米。
8.一个花坛的直径是6m,花坛周围有一条宽1m的环形小路,小路的面积是 m2。
9.一个挂钟的时针长5厘米,一昼夜这根时针的尖端走了 厘米,针尖扫的面积是 平方厘米。
10.把一个长、宽分别是15厘米和10厘米的长方形,拉成一个一条高为12厘米的平行四边形,它的面积是 平方厘米。
11.李大伯用5π米长的篱笆靠墙围了一个半圆形养鸡场,养鸡场的面积是 平方米。
12.如图。
∠1=30°,∠2= ,∠3= ,∠4= 。
13.从9:00到9:15,分针旋转了 度,若分针长6厘米,这根分针针尖走过的长度是 厘米,扫过的面积是 平方厘米。
14.一个三角形内角度数的比是2:3:5,其中最大的内角是 度,这是个 角三角形。
15.如图中正方形的面积是40cm2,那么涂色部分的面积是 cm2。
16.一辆自行车车轮直径是0.5米,脚踏板齿轮有48个齿,后齿轮有16个齿,脚踏一圈,自行车前进 米.17.把两个正方形拼成一个长方形,拼成的长方形周长是30厘米,这个长方形的面积是 平方厘米。
小升初奥数课课练-平面几何-通用版
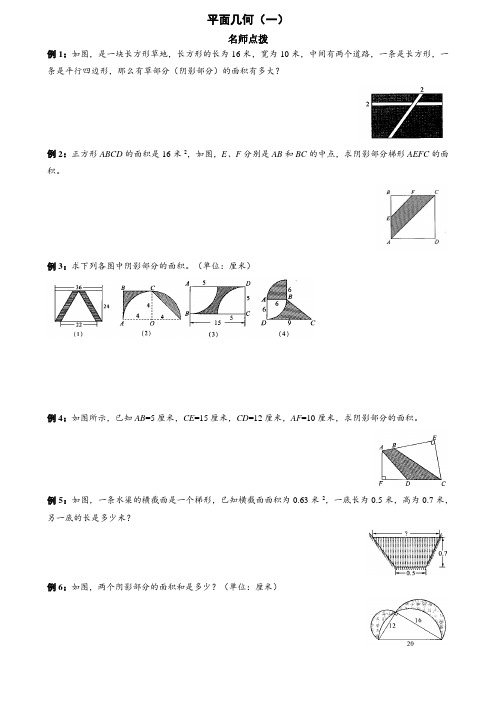
平面几何(一)名师点拨例1:如图,是一块长方形草地,长方形的长为16米,宽为10米,中间有两个道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大?例2:正方形ABCD的面积是16米2,如图,E、F分别是AB和BC的中点,求阴影部分梯形AEFC的面积。
例3:求下列各图中阴影部分的面积。
(单位:厘米)例4:如图所示,已知AB=5厘米,CE=15厘米,CD=12厘米,AF=10厘米,求阴影部分的面积。
例5:如图,一条水渠的横截面是一个梯形,已知横截面面积为0.63米2,一底长为0.5米,高为0.7米,另一底的长是多少米?例6:如图,两个阴影部分的面积和是多少?(单位:厘米)名校真题1. 在面积相等的下列平面图形中,周长最小的是( ) A. 正方形 B. 等边三角形 C. 长方形 D. 圆形2. 一个三角形的三个角的度数都是质数,这个三角形是( )A. 钝角三角形B. 直角三角形C. 等腰三角形D. 不能确定3. 三角形中最大的一个角一定( )A. 不小于600B. 大于900C. 小于900D. 大于600而小于9004. 一个半圆形零件的周长是17.99厘米,这个半圆的直径是___________厘米。
5. 如图,图形的半径为20厘米,它的周长是___________厘米。
6. 把7个长4厘米、宽3厘米的小长方形,不重叠地拼成一个大长方形,这样拼成的大长方形中最小周长是____________厘米。
名校集训 A 级1. 5127.155123.83.22+⨯+⨯ 2. ⎪⎭⎫ ⎝⎛+⨯⨯913193B 级1. 如图所示,正方形的边长是20厘米,阴影部分的面积是多少平方厘米?2. 如图,四边形ABCD是正方形,ABHE是梯形,ACHE是平行四边形,ECGF是长方形,已知AE=7厘米,BH=12厘米,求阴影部分的面积。
3. 三角形ABC是直角三角形,EG垂直于AC,EG等于3厘米,AB、BC、AC的长度分别是30厘米、40厘米、50厘米,求正方形BDEF的面积。
六年级奥数《平面图形》练习题

第十一讲平面图形(必做与选做)1.在一张长12厘米、宽6厘米的长方形纸上剪下一个最大的半圆,这个半圆的周长是多少厘米?A. 24.84B. 30.84C. 43.68D. 49.68解析:最大的半圆以长方形长为直径,宽为半径。
这个半圆的周长C=3.14×6+12=30.84(厘米)。
所以选B。
2.在一张长12厘米、宽5厘米的长方形纸上剪下一个最大的半圆,这个半圆的周长是多少厘米?A. 20.7B. 25.7C. 27.5D. 41.4解析:最大的半圆以长方形的宽为半径,宽的两倍为直径。
这个半圆的周长C=3.14×5+5×2=25.7(厘米)。
所以选B。
3.在一张长12厘米、宽7厘米的长方形纸上剪下一个最大的半圆,剩下纸的周长是多少厘米?A. 32.84B. 30.84C. 44.84D. 63.68解析:最大的半圆是以长方形的长为直径,长的一半为半径。
剩下的纸的周长C=12+7×2+3.14×(12÷2)=44.84(厘米)。
所以选C。
4.有2根直径都是3分米的圆柱形木头,现用绳子分别在两处把它们捆在一起,至少需要绳子多少分米?(接头处不计)A. 15.42B. 24.84C. 30.84D. 49.68解析:需计算两部分的长度,一部分是两条线段的长度,都是直径的长度;另一部分是两段圆弧的长度,一共是一个圆的周长。
因此一共需要绳子:(3.14×3+3×2)×2=30.84(分米)。
所以选C。
5.有3根直径都是5分米的圆柱体木头,现用绳子分别在三处把它们捆在一起,至少需要绳子多少分米?(接头处不计)A. 30.7B. 61.4C. 77.1D. 92.1解析:需计算两部分的长度,一部分是三条线段的长度,都是直径的长度;另一部分是三段圆弧的长度,一共是一个圆的周长。
因此一共需要绳子:(3.14×5+5×3)×3=92.1(分米)。
小升初平面图形计算专题练习
湄洲湾妈祖品牌策划方案1. 简介湄洲湾妈祖是中国福建省的一个著名的宗教文化品牌,以妈祖文化为核心,涵盖了宗教、文化、旅游等领域。
本文档将详细介绍湄洲湾妈祖品牌的策划方案,以提升品牌知名度和影响力,进一步推动区域发展。
2. 目标本品牌策划的目标是提升湄洲湾妈祖品牌的知名度和影响力,吸引更多的游客和信徒前往湄洲湾朝拜并体验当地的文化,促进区域的旅游和经济发展。
3. 目标受众•国内外游客:通过品牌策划,吸引更多的国内外游客来到湄洲湾朝拜和旅游。
•信徒和宗教界人士:提高妈祖信仰的认知度和参与度,吸引更多的信徒前来朝拜。
4. 品牌定位湄洲湾妈祖品牌定位为“传承妈祖文化,引领宗教旅游潮流”,旨在将湄洲湾打造成世界一流的宗教旅游目的地,进一步推动当地旅游和经济发展。
5. 策略与措施5.1 提升品牌知名度•加强媒体宣传:与知名媒体合作,通过新闻报道、广告等方式扩大品牌的知名度。
•社交媒体推广:通过社交媒体平台,发布有关湄洲湾妈祖品牌的内容,吸引用户关注和分享,扩大品牌影响力。
•参加宗教文化展会:积极参加国内外的宗教文化展会,展示湄洲湾妈祖文化,吸引更多的观众。
5.2 提高游客体验•丰富的旅游项目:开发多样化的旅游项目,如宗教朝拜、文化表演、民俗体验等,满足不同游客的需求。
•改善基础设施:投资改善湄洲湾的基础设施,包括交通、餐饮、住宿等,提升游客的出行和居住体验。
•妈祖文化教育:开展妈祖文化教育活动,让游客了解和体验湄洲湾的妈祖文化,增加游客的参与度和忠诚度。
5.3 打造特色品牌•文化创意产品:开发具有湄洲湾特色的文化创意产品,如纪念品、手工艺品等,增加游客的购物需求,推动当地经济发展。
•品牌合作:与其他知名品牌合作,如旅行社、酒店等,共同打造湄洲湾妈祖品牌形象,提升品牌竞争力。
•慈善公益活动:开展相关的慈善公益活动,提高品牌的社会形象,增加公众对品牌的认可度和支持度。
6. 落地计划•第一阶段(1-3年):加强媒体宣传,提高品牌知名度;改善基础设施,提高游客体验。
小升初数学《平面图形》综合试题及答案
小升初数学《平面图形》综合试题一、填空题1.同一平面内的两条直线的位置关系有两种情况:________和________.2.下面各组直线中,哪两条直线互相垂直?在下面的括号里画“√”。
( ) ( ) ( )3.在两点之间的所有连线中,(____)最短.4.用一个能放大3倍的放大镜看一个15°的角,这个角的度数是(____)。
按度数从小到大,可以把角分为(____)、(____)、(____)、(____)和(____)。
5.一个平行四边形的面积是32m2,与它等底等高的三角形的面积是(____)m2。
6.一个三角形最小的角是60°,那么这个三角形按边分是(_____)三角形。
7.一个等腰梯形的上底是6cm,下底是8cm,一条腰长是7cm,围成这个等腰梯形至少需要(____)cm长的铁丝.8.两个完全一样的三角形可以拼成一个(_____)形。
如果拼成的图形的面积是126cm2,那么一个三角形的面积是(____)cm2。
如果每个三角形的面积是15dm2,那么拼成的图形的面积是(____)dm29.照图操作画出的圆的周长是(____)cm,圆的面积是(____)cm2.10.画圆时,圆规两脚间的距离是2.5cm,则半径是(____)cm,直径是(____)cm。
11.一个边长是20cm的正方形,里面有一个最大的圆,这个圆的半径是(____)cm,面积是(____)cm2。
12.如图,一个平行四边形被分成了甲、乙、丙三部分,已知甲的面积比丙的面积大6cm2,那么丙的面积是(____)cm2。
13.如图,已知大正方形的边长是5cm,小正方形的边长是3cm,那么阴影部分的面积是(____)cm2。
14.一个三角形,其中两个角分别是35°和45°,那么另一个角是(____)°。
按角来分,这是一个(____)三角形。
15.一个直角三角形三条边的长度分别是6cm、8cm、10cm,斜边上的高是(____)cm。
小学奥数 几何类 几何图形周长和面积的基本计算 基本图形的面积计算.题库版
小学数学平面图形计算公式:1 、正方形:周长=边长×4;面积=边长×边长2 、正方体:表面积=棱长×棱长×6;体积=棱长×棱长×棱长3 、长方形:周长=(长+宽)×2;面积=长×宽4 、长方体:表面积(长×宽+长×高+宽×高)×2;体积=长×宽×高 5、 三角形:面积=底×高÷2 6 平行四边形:面积=底×高 7 梯形:面积=(上底+下底)×高÷2模块一、基本公式的应用【例 1】 如图,两个正方形边长分别是5厘米和4厘米,图中阴影部分为重叠部分。
则两个正方形的空白部分的面积相差多少平方厘米?【考点】基本图形的面积计算 【难度】2星 【题型】解答 【关键词】2007年,第12届,华杯赛,五年级,决赛,第9题,10分【解析】 5×5-4×4=9(平方厘米),两个正方形的空白部分的面积相差9平方厘米。
【答案】9平方厘米【巩固】 如图12,边长为4cm 的正方形将边长为3cm 的正方形遮住了一部分,则空白部分的面积的差等于 2cm 。
【考点】基本图形的面积计算 【难度】2星 【题型】填空 【关键词】2009年,第7届,希望杯,4年级,初赛,19题【解析】 空白部分的面积差等于两个正方形的面积差,即⨯-⨯=44337(平方厘米)。
【答案】7平方厘米【例 2】 在一个正方形水池的四周,环绕着一条宽2米的路(如图),这条路的面积是120平方米,那么水池的面积是______ 平方米。
例题精讲知识点拨4-2-1.基本图形的面积计算水池【考点】基本图形的面积计算【难度】2星【题型】填空【关键词】2003年,第1届,希望杯,4年级,初赛,19题【解析】四个边角的面积和为2×2×4=16,则水池的边长为:104÷2÷4=13,所以水池的面积是:13×13=169平方米。
小升初奥数—平面图形计算
小升初奥数—平面图形计算一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可。
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了。
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C 重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初奥数一平面图形计算(一)一、填空题1. 如下图,把三角形ABC的一条边AB延长1倍到D ,把它的另一边AC延长2倍到E,得到一个较大的三角形2. 如下图,在三角形ABC中,BC=8厘米,AD =6厘米,E、F分别为AB和AC的中点•那么三角形EBF的面积是 _______ 平方厘米.1 13.如下图,BE 3BC,CD舟AC,那么,三角形AED的面积是三角形ABC面积的______________3 44. ________________ 下图中,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的长的2倍,那么三角形CDE的面积是平方厘米.5. ______________________________________________________________________________________ 现有一个5X 5的方格表(如下图)每个小方格的边长都是1,那么图中阴影部分的面积总和等于_______________6. _____________ 下图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是平方厘米.7. ___________________________ 如图所示,一个矩形被分成A、B、C、D四个矩形.现知A的面积是2cmf, B的面积是4cn i, C的面积是6cm.那么原矩形的面积是平方厘米.A BC LND8 ----------8. 有一个等腰梯形,底角为45°,上底为8厘米,下底为12厘米,这个梯形的面积应是_________ 平方厘米•9. 已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,那么阴影部分的面积是____________ 平方厘米•10. 下图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是二、解答题11. 已知正方形的面积是50平方厘米,三角形ABC两条直角边中,长边是短边的2.5倍,求三角形ABC的面积.12. 如图,长方形ABCD中,AB=24cm,BC=26cm,E是BC的中点,F、G分别是AB、CD的四等分点,H为AD上任意一点,求阴影部分面积.13. 有两张正方形纸,它们的边长都是整厘米数,大的一张的面积比小的一张多44平方厘米.大、小正方形纸的边长分别是多少?14. 用面积为1,2,3,4的四张长方形纸片拼成如图所示的一个长方形.问:图中阴影部分面积是多少?所以,AED 的面积是 ABC 的1.24. 5.因为D 是BC 的中点,所以三角形ADC 和三角形ABD 面积相等(等底、等高的三角形等积),从而三 角形ADC 的面积等于三角形ABC 面积的一半,即30十2=15(平方厘米).在 CDE 与 ADC1 1 1 中,DE -DA ,高相等,所以CDE 的面积是 ADC 面积的-.即CDE 的面积是一 15 5(平方厘3 3 3米)5. 10三个阴影三角形的高分别为3,2,2,底依次为2,4,3,所以阴影部分面积总和等于10.6. 60设正方形ABCD 的面积为a ,长方形EFGH 的面积为b ,重叠部分EFNM 的面积为c ,则阴影部分的面积差是:(a c ) (b c ) a b .即阴影部分的面积差与重叠部分的面积大小无关 应等于正方形ABCD 的面积与长方形EFGH 的面积之差.所求答案:10 x 10-8 x 5=60(平方厘米).7. 24图中的四个矩形是大矩形被两条直线分割后得到的 ,矩形的面积等于一组邻边的乘积.从横的方向看, 两个相邻矩形的倍比关系是一致的,B 是A 的2倍,那么D 也应是C 的2倍,所以D 的面积是2x 6=12cm 2, 从而原矩形的面积是2+4+6+12=24cm 2 .8. 20如下图,从上底的两个端点分别作底边的垂线 ,则BCFE 是矩形,AB CD米).因为 A 45°,所以ABE 是等腰直角三角形,则BE AB 2(厘米).根据梯形的 求积公式得:S 梯形8丁 220(平方厘米).9. 14由已知条件,平行四边形DEFC 的面积是:56十2=28(平方厘米)如下图,连接1EC , EC 为平行四行形DEFC 的对角线,由平行四边形的性质如,S DEC S DEFC2 28 14(平方厘米).在 AED 与 CED 中,ED 为公共底边,DE 平行于AC ,从而平面图形计算(一)习题答案1. 6.如下图,连接BE ,因为CE 2AC ,所以,S BCE 2SAB BD ,所以,S ABE S BDE ,这样以来,S ADE 6S AB c •2. 6.已知E 、F 分别是AB 和AC 的中点,因此 ABF 的面积是 的寸,EBF 的面积又是 ABF 的面积的1.又因为S A BC 2 BCABC ,即 SABC 的面积1 AD 1 82(平方厘米),所以S EBF11 3.-.由 BE BC ,CD 3 1 124 6(平方厘米).2 21 2 AC ,可知 EC 2BC ,AD4 3ABC 与AEC 是同一个顶点底边在同一条线段,所以这两个三角形等高 则三角形面积与底边成正比例关系 ,因此S AEC ABC理可知S AED33S .这样以来,AED 的面积是4AEC3 1 ABC 的-的-,即是 ABC 的面积的-.3 42(12 8) 2 2(厘33 /8相等,所以,S AED S CED 14(平方厘米).10.97因为长方形的面积等于 ABC 与ECD 的面积和,所以 ABC 与ECD 重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,即49 35 13阴影11. 画两条辅助线如下图,根据条件可知,正方形面积是长方形 ABCD 面积的2.5倍.从而ABCD 的面积是50- 2.5=20(平方厘米).所以 ABC 的面积是20十2=10(平方厘米).12. 连结BH , BEH 的面积为1 (36 2) 24 2个三角形的底 BF 、DG 相等,且都等于长方形宽的4,它们的高AH 与DH 之和正好是长方形的长,所以这两个角形的面积之和1 BF AH 1 DG DH2 21BF (AH2DH )2BF AD24 36 108 (cm 2).于是,图中阴影部分的面积为216+108=324(cm 2).13.把两张正方形纸重叠在一起,且把右边多出的一块拼到上面,成为一个长方形,如图: 这个长方形的面积是44平方厘米,它的长正好是两个正方形的边长的和,它的宽正好是 两个正方形的边长的差.因为两个整数的和与它们的差是同奇或同偶 44=1 X 44=2X 22=4X 11.所以,两个正方形的边长的厘米数的和与差只能是 是(22+2) - 2=12(厘米),12-2=10(厘米).,而44又只能分解成下面的三种形式:22与2.于是,两个正方形的边长14.如图大长方形面积为1+2+3+4=10.延长RA 交底边于Q ,延长SB 交底边于P .矩形ABPR 面 积是上部阴影三角形面积的2倍.矩形ABSQ 是下部阴影三角形面积的2倍.所以矩形RQSP 的面积是阴影部分面积的两倍.知CA 1 CD32此矩形RQSP 的面积是大矩形面积的3 3 1 2 CB CD AB CB CA CD CD CD 因77 3211 1 10,阴影部分面积是大矩形面积的.阴影部分面积=—X 10=.216(cm 2).把BHF 和DHG 结合起来考虑 ,这两21 21 21 21小升初奥数一平面图形计算(二)DE 是 ______ 厘米.一、填空题 1. 下图是由16个同样大小的正方形组成的 ,如果这个图形的面积是400平方厘米,那么它的周长是______ 厘米.2. 第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是那么7,2,1三个数字所占的面积之和是 __________ . 3.下图中每一小方格的面积都是 1平方厘米,那么用粗线围成的图形面积是 ________ 平方厘米•4. _____________________________________________________________________ 下图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是 __________________________________ 平方厘米.5.在 ABC 中,BD 2DC ,AE BE ,已知 ABC 的面积是18平方厘米,则四边形AEDC 的面积等7. 如图正方形 ABCD 的边长是4厘米,CG 是3厘米,长方形DEFG 的长DG 是5厘米,那么它的宽1.于 ______ 平方厘米.6.下图是边长为4厘米的正方形,AE =5厘米、OB 是厘米.BF8. 如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是2520303616129. _____________________________________________________________________ 如下图,正方形ABCD 的边长为12, P是边AB上的任意一点,M、N、丨、H分别是边BC、AD 上的三等分点,E、F、G是边CD 上的四等分点,图中阴影部分的面积是____________________________________________ .10. 下图中的长方形的长和宽分别是面积是______ 平方厘米•、解答题11.图中正六边形ABCDEF的面积是54. AP 2PF,CQ 2BQ,求阴影四边形CEPQ的面积.13. 一个周长是56厘米的大长方形,按下图中(1)与⑵ 所示意那样,划分为四个小长方形•在(1)中小长方形面积的比是:A:B 1:2, B:C 1:2.而在⑵中相应的比例是A :B 1:3, B :C 1:3.又知,长方形D的宽减去D的宽所得到的差,与D的长减去在D的长所得到的差之比为1:3.求大长方形的面积.6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的12.如图,涂阴影部分的小正六角星形面积是16平方厘米•问:大正六角星形面积是多少平方厘米£)a nacC D11 / 814.如图,已知CD 5, DE 7, EF 15, FG 6.直线AB 将图形分成两部分,左边部分面积是 38, 右边部分面积是65.那么三角形 ADG 面积是 _________________________ .'“平面图形计算(二)习题答案1. 170.每个小正方形的面积为 400十16=25平方厘米,所以每个小正方形的边长为 5cm,因此它的周长是34 X 5=170 厘米.2. 25. 7,2,1 所占面积分别为 7.5,10和7.5 .3. 6.5.直接计算粗线围成的面积是困难的 ,我们通过扣除周围的正方形和直角三角形来计算 .周围有正方形3个,面积为1的三角形5个,面积为1.5的三角形一个,因此围成面积是 4X 4-3-5-1.5=6.5( 平方厘 米).4. 24仿上题,大、小两个正方形面积之和减去两只空白三角形的面积和 ,所得的差就是阴影部分的面A25 20 30D36B 16C12积.4282[8 8 4 (4 8)][2 c ] =16+64-(32+24)=80-56=24( 平方厘米)5. 12 如下图,连接AD ,因为BD 2DC ,所以S ABD2SADC ;又 S ABD S ADC S ABC 18, SAEDC 6. 3.27. SABDSABC SABE3.2 DEFG 12因为 AE BE ,所以SBDE186 12(平方厘米).图,连接BE ,贝y S ABE5 OB ,于是1 5 OB 8.2OB如下图,连接AG ,则 AGD 的面积是正方形SBDE2 441SADE S ABD 6;因此* --------- c l8 (平方厘米).从另一角度2 5=3.2(厘米)ABCD面积的2,也是长方形的面积的2,于是长方形DEFG 的面积等于正方形 ABCD 的面积4 X 4=16(平方DE 16 5 3.2(厘米).厘米).243我们用A , B , C , D 分别表示待计算的小矩形面积上、下两个矩形,长是相同的. 8. 9. 因此它们的面积之比,就是宽之比,反之,宽之比,就是面积之比.这样就有:20:16= A :36,20 3616 25c 16 3045;20:16=25: B , B20 ;20:16=30: C , C24; 20:16= D :12,16 20 20 20 1215.因此,大矩形的面积是:45+36+25+20+20+16+30+24+15+12=243 1660 如下图,连接PD ,则阴影部分就是由四个三角形PGD 和PEF 的底都有3,高为12,所以S PGDPEFPDH , PGD , 12 PEF 和PMN 组成. 12 18.PDH 和 PMN 的底都是4,两条高分别为PA 和PB 则:S pDH S pMNPA4 PB=2( PA +PB )=2 X 12=24所以,阴影部分的面积是: S PGDSPEF SPDHS PMN =18+18+24=6012 / 8AED 的面积是(65-38 X 5) - (3- 5)=10.三角形 ADG 面积是 10X (3+1)=40.44110. 4长方形EFGH 的面积是6X 4=24(平方厘米)s SS ,uAEFAHG 2 EFGH SEBA SADH SAEF SAHG S阴影总面积=12-1°=2(平方厘米)1 1又S ECH S EFGH 24 6(平方厘米)所以,四边形ABCD 的面积等于:4 4)=6-2=4(平方厘米)11. 如图,将正六边形 ABCDEF 等分为54个小正三角形.根据平行四边形对角线平分平行四边形面积 采用数小三角形的办法来计算面积• PEF 面积=3; CDE 面积=9;四边形ABQP 面积=11.上述三块面积之和为3+9+11=23,因此,阴影四边形CEPQ 面积为54-23=31. 12.如图,涂阴影部分小正六角星形可分成12个与三角形OPN 全等(能完全重叠地放在一起)的小三角16 4形.三形OPN 的面积是平方厘米.正三角形OPM 面积是由三个与三角形12 34成.所以正三角形OPM 的面积等于-3 4(平方厘米).由于大正方六角星形由3OPM 全等的三角形组成,所以大正六角星形的面积是 OPN 全等的三角形组12个与正三角形13.设大长方形的宽为X ,则长为28- X .因为,D 宽 92810曰 28 7x 是 ,x 10 20 4 X 12=48(平方厘米)23—x, D 宽一X ,所以,D 宽3 宽4宽丄28 x .由题设可知, 10x 12x — .1221 :3或10 D 长 4 28 x , D 长528 x x 104米.14.三角形AEG 面积是三角形 AED 面积的(15+6)十7=3(倍),三角形BEF 面积是三角形 BEC 面积的15十(5+7)= 5 (倍).所以65-38 X 5等于三角形 AEG 面积与三角形 AED 面积的5之差,因此三角形4 4 4&大长方形的长=28-8=20,从而大长方形的面积为8X 20=160平方厘12(平方厘米)Ju。
