【高考推荐】2019-2020高考数学专题八平面向量精准培优专练文
2020届高三精准培优专练八 平面向量(文) 文科版

2020届高三好教育精准培优专练例1的圆两两外切(M ,N ,P 为圆心),且等边ABC △的每一边都与其中的两个圆相切,则AP AN ⋅= .例2:已知对任意平面向量(,)AB x y =,把AB 绕其起点沿逆时针方向旋转θ角得到向量(cos sin ,sin cos )AP x y x y θθθθ=-+,叫做把点B 绕点A 逆时针旋转θ角得到点P .若平面内点A ,点(0,1)B ,把点B 绕点A 顺时针方向旋转4π3后得到点P ,则点P 的坐标为( ) A .2)-B .(0,2)-C .D .例3:如图在矩形ABCD 中,AB =4BC =,点E 为BC 的中点,点F 在CD 上,若3AB AF ⋅=,则AE BF ⋅的值是( )三、平面向量数量积二、平面向量的坐标运算一、平面向量的线性运算培优点八 平面向量A.5-- B.5C.4+D.5例4:在ABC △中,6AC =,7BC =,1cos 5A =,O 是ABC △的内心,若OP xOA yOB =+, 其中01x ≤≤,12y ≤≤,动点P 的轨迹所覆盖的面积为( )A B .C .103D .203例5:在矩形ABCD 中,1AB =,2AD =,动点P 在以点C 为圆心且与BD 相切的圆上, 若AP AB AD λμ=+,则λμ+的最大值为( ) A .3 B .C D .2一、选择题1.梯形ABCD 中,AB CD ∥且AB AD BC λμ=+,则λμ+=( )对点增分集训五、平面向量和平面几何的综合四、平面向量和三角形函数,解三角形的综合A .1B .1-C .0D .不能确定2.在ABC △中,M 是AB 边所在直线上任意一点,若2CM CA CB λ=-+,则λ=( ) A .1B .2C .3D .43.已知两点(1,0)M -,(1,0)N ,若直线340x y m -+=上存在点P 满足0PM PN ⋅=,则实数m 的 取值范围是( ) A .(,5][5,)-∞-+∞ B .(,25][25,)-∞-+∞ C .[5,5]-D .[25,25]-4.已知2==a b ,且0⋅=a b ,1()2=+c a b ,-=d c ,则d 的取值范围是( )A .[0,B .[0,2]C .D .[0,1]5.若O 为ABC △所在平面内任意一点,且满足()(2)0OB OC OB OC OA -⋅+-=,则ABC △的 形状为( ) A .等腰三角形 B .直角三角形 C .正三角形D .等腰直角三角形6.长度都为2的向量OA ,OB 的夹角为π3,点C 在以O 为圆心的圆弧AB (劣弧)上,OC mOA nOB =+,则m n +的最大值是( )A .B .3C D .7.过点(1,1)P -作圆22()(2)1()C x t y t t -+-+=∈R 的切线,切点分别为A ,B ,则PA PB ⋅的最小值为( )A .103B .403C .214D .38.如图,四边形OABC 是边长为1的正方形,3OD =,点P 为BCD △内(含边界)的动点,设OP OC OD αβ=+(α,β∈R ),则54αβ+的最大值是( )A .14B .920C .34D .17609.如图,在ABC △中,π3BAC ∠=,2AD DB =,P 为CD 上一点,且满足12AP mAC AB =+,若ABC △的面积为AP 的最小值为( )ABC .3D .4310.已知AB AC ⊥,1AB t =,AC t =,1[,4]4t ∈;若P 是ABC △所在平面内一点,且4AB AC AP ABAC=+,则PB PC ⋅的取值范围是( )A .[13,17]B .[12,13]C .3[,12]4D .3[,13]411.在平面内,定点A ,B ,C ,D 满足DA DB DC==,2DA DB DB DC DC DA ⋅=⋅=⋅=-,动点P ,M 满足1AP =,PM MC =,则2BM 的最大值是( )A .434B .494C .374+ D .374+ 12.如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==.若点E 为边CD 上的动点,则AE BE ⋅的最小值为( )A .2116B .32C .2516D .3二、填空题13.已知G 为ABC △的重心,过点G 的直线与边AB ,AC 分别相交于点P ,Q . 若AP AB λ=,则当ABC △与APQ △的面积之比为20:9时,实数λ的值为 .14.已知腰长为2的等腰直角三角形ABC 中,M 为斜边AB 的中点,点P 为ABC △所在平面内一动点,若2PC =,则()()PA PB PC PM ⋅⋅⋅的最小值是 .15.在ABC △中,0GA GB GC ++=,且0GA GB ⋅=,若tan tan tan tan tan A B mA B C+=,则实数m 的值是 .16.如图,等边ABC △的边长为2,顶点B ,C 分别在x 轴的非负半轴,y 轴的非负半轴上移动,M 为AB 的中点,则OA OM ⋅的最大值为 .例1:【答案】18+【解析】由题意易得23AM=()()AP AN AM MP AM MN⋅=+⋅+2AM AM MN MP AM MP MN=+⋅+⋅+⋅22cos302cos601812=+⨯︒+︒=+.例2:【答案】A【解析】(AB=,顺时针旋转4π3时,4π3θ=-,代入得4π4πcos()1sin()033x'=--⨯-=,4π4π)cos()233y'=-+-=-,即(0,2)AP=-,∵A,∴2)P-,故选A.例3:【答案】B【解析】选基向量AB和BC,由题意得0AB BC⋅=,3AB=,4BC=,∴AF AD DF BC DF=+=+,∴()3AB AF AB BC DF AB BC AB DF⋅=⋅+=⋅+⋅=,即cos0AB DF=1DF=,∵点E为BC的中点,1DF=,∴12AE AB BC=+,3BF BC CF BC AB-=+=-,∴221331()()522AE BF AB BC BC AB AB BC--⋅=+⋅-=-+=故选B.例4:【答案】A【解析】如图,根据题意知,P点在以BD,BF为邻边的平行四边形内部,培优点八平面向量答案∴动点P 的轨迹所覆盖图形的面积为2AOB S △, 在ABC △中,1cos 5BAC ∠=,6AC =,7BC =, ∴由余弦定理得,213649526AB AB +-=⋅,解得5AB =或135AB =-(舍去),又O 为ABC △的内心,所以内切圆半径2ABCS r a b c=++△,又12AOB S r AB =⋅⋅△,∴5512556sin 56718263OB ABC S S BAC =⋅=⨯⨯⨯⨯∠==++△△,∴动点P 的轨迹所覆盖图形的面积为3A . 例5:【答案】A 【解析】如图,以A 为原点,以AB ,AD 所在的直线为x ,y 轴建立如图所示的坐标系,则(0,0)A ,(1,0)B ,(0,2)D ,(1,2)C ,∵动点P 在以点C 为圆心且与BD 相切的圆上,设圆的半径为r ,∵2BC =,1CD =,∴BD ==1122BC CD BD r ⋅=⋅,∴5r =, ∴圆的方程为224(1)(2)5x y -+-=,设点P 的坐标为(1,2)55θθ++,∵AP AB AD λμ=+,所以2)(1,0)(0,2)(,2)θθλμλμ++=+=,1θλ+=22θμ+=,∴2sin()2λμθθθϕ+=++=++,其中tan 2ϕ=, ∵1sin()1θϕ-≤+≤,13λμ≤+≤,故λμ+的最大值为3,故选A .一、选择题 1.【答案】C【解析】由梯形ABCD 易得:0AB BC CD DA +++=,所以AB DC AD CB -=+, 又AB AD BC λμ=+,所以(1)(1)DC AD BC λμ=-++, 由于AB CD ∥,所以(1)(1)λμμλ-=+,可得0λμ+=.故选C . 2.【答案】C【解析】∵ABC △中,M 是AB 边所在直线上任意一点, ∴存在实数μ,使得AM MB μ=,即()CM CA CB CM μ-=-, 化简得111CM CA CB μμμ=+++,∵2CM CA CB λ=-+,∴结合平面向量基本定理,得1211μμλμ⎧=-⎪+⎪⎨⎪=⎪+⎩,解之得3λ=,32μ=-.故选C . 3.【答案】C【解析】设(,)P x y ,则(1,)PM x y =---,(1,)PN x y =--,由PM PN ⊥,得221x y +=,∴点P 的轨迹为一个以原点为圆心,1为半径的圆,因P 在直线340x y m -+=上,故圆心到直线的距离1d =≤,故[5,5]m ∈-,故选C .4.【答案】A【解析】如图所示,OA =a ,OB =b ,且OA OB ⊥,又1()2=+c a b ,取AB 中点为C ,可得OC =c ,∵-d c ,∴d 的终点D 在以C为半径的圆上运动, 当D 点在O 点处,d 的最小值为0;当D 点在OC 的延长线时,d的最大值为,∴d的取值范围是,故选A . 5.【答案】A【解析】()(2)0OB OC OB OC OA -⋅+-=,即()0CB AB AC ⋅+=, ∵AB AC CB -=,∴()()0AB AC AB AC -⋅+=,即AB AC=,∴ABC △是等腰三角形,故选A . 6.【答案】B【解析】∵OC mOA nOB =+,∴22()OC mOA nOB =+,∴224442m n mn OA OB =++⋅⋅,即22π444222cos 3m n mn =++⨯⨯⨯, 即221m n mn ++=,故22()()14m n m n mn ++-=≤,(当且仅当m n =时,等号成立);故24()3m n +≤,故m n +3=. 7.【答案】C【解析】由已知得圆心坐标(,)x y 满足2x ty t =⎧⎨=-⎩,即2y x =-,可知圆心C 在直线2y x =-上运动,则1PC -≥=.设CPA θ∠=,则22cos 2(12sin )PA PB PA PB PA θθ⋅=⋅=-222222(1)(1)3PC PC PCPC=--=+-,易知函数23y x x =+-在[8,)+∞上为增函数,所以2218384PA PB ⋅≥+-=.故选C . 8.【答案】D【解析】以O 为坐标原点,以OD ,OC 所在的直线分别为x ,y 轴建立平面直角坐标系,如图所示,则(0,0)O ,(1,0)A ,(0,1)C ,设(,)P x y . 因为OP OC OD αβ=+,所以3OP OC OA αβ=+,即(3,)P βα,所以3x y βα=⎧⎨=⎩,所以3yx αβ=⎧⎪⎨=⎪⎩,则54125x y αβ+=+.由题意知动点(,)P x y 的运动区域为BCD △内(含边界), 因此平行于直线0125x y +=的直线经过点(1,1)B 时,125x y+取得最大值, 即max max 1117()()5412512560x y αβ+=+=+=,故选D . 9.【答案】B【解析】设3AB a =,AC b =,则三角形ABC的面积为1π3sin 23ab ⨯=,解得83ab =, 由1324AP mAC AB mAC AD =+=+,且C ,P ,D 三点共线,可知314m +=,14m =, 故1344AP AC AD =+. 以A 点为坐标原点,以AB 所在直线为x 轴,过A 点作AB 的垂线为y 轴,建立如图所示坐标系,则(0,0)A ,(2,0)D a ,(3,0)B a,1()2C b,则1()2AC b =,(2,0)AD a =,13()82AP b a =+,则2222222213193319()()1828644864164AP b a b a ab b b a =++=+++=++31134ab ≥=+=(当且仅当2219164b a =,即6b a =时取“=”).故AP 的最小值为B . 10.【答案】D【解析】由题意建立如图所示的坐标系,可得(0,0)A ,1(,0)B t,(0,)C t ,∵4(1,0)(0,4)(1,4)AB AC AP ABAC=+=+=,∴(1,4)P ,∴1(1,4)PB t=--,(1,4)PC t =--,∴11(1)4(4)17(4)1713PB PC t t t t ⋅=----=-+≤-=, 当且仅当14t t =,即11[,4]24t =∈时,取等号, 由4t =可得13=17(16)44PB PC ⋅-+=,由14t =可得17(14)12PB PC ⋅=-+=, ∴PB PC ⋅的最大值为13,最小值为34.则PB PC ⋅的范围是3[,13]4.故选D . 11.【答案】B 【解析】由题意,DA DB DC==,∴D到A,B,C三点的距离相等,D是ABC△的外心,2DA DB DB DC DC DA⋅=⋅=⋅=-()0DA DB DB DC DB DA DC DB CA⇒⋅-⋅=⋅-=⋅=,∴DB AC⊥,同理可得,DA BC⊥,DC AB⊥,从而D是ABC△的垂心,∴ABC△的外心与垂心重合,因此ABC△是正三角形,且D是ABC△的中心,1cos()222DA DB DA DB ADB DA DB DA⋅=⋅∠=⨯-=-⇒=,∴正三角形ABC的边长为∴以A为原点建立直角坐标系,B,C,D三点坐标分别为(3,B,C,(2,0)D,由1AP=,设P点的坐标为(cos,sin)θθ,其中[0,2π)θ∈,而PM MC=,即M是PC的中点,可以写出M的坐标为3cos(2Mθ+,则222π3712sin()cos33712496()2444BMθθ+--+=+=≤=,当2π3θ=时,2BM取得最大值494.故选B.12.【答案】A【解析】以A为坐标原点,AB所在直线为x轴,建立如图所示的平面直角坐标系,因为在平面四边形ABCD 中,1AB AD ==,120BAD ∠=︒, 所以(0,0)A ,(1,0)B ,1(,)22D -, 设(1,)C m ,(,)E x y,所以3(,22DC m =-,1(22AD =-, 因为AD CD ⊥,所以31(,)(,02222m -⋅-=,即31()022m ⨯-+=,解得m =C , 因为E 在CD上,所以2y ≤≤, 由CECD k k =,得21112y x =-+,即2x =-, 因为(,)AE x y =,(1,)BE x y =-,所以(,)(1,)AE BE x y x y ⋅=⋅-222222)246x x y y y =-+=--++=-+.因为函数2()46f y y =-+在上单调递减,在上单调递增,所以2min 21()4616f y =⨯-+=. 所以AE BE ⋅的最小值为2116,故选A .二、填空题 13.【答案】34或35【解析】设AQ AC μ=,则由AP AB λ=,209ABC APQS S =△△,可得1sin 20219sin 2AB AC A AB AC AB AC AP AQ A λμ⋅⋅==⋅⋅,所以920λμ=.① 又G 为ABC △的重心,所以111111()()3333AG AB AC AP AQ AP AQ λμλμ=+=+=+. 结合P ,G ,Q 三点共线,得11133λμ+=.② 联立①②消去μ,得2202790λλ-+=,解得34λ=或35. 14.【答案】32-【解析】如图,以C 为原点,CB ,CA 的方向分别为x 轴,y 轴的正方向建立平面直角坐标系,则(0,0)C ,(2,0)B ,(0,2)A ,(1,1)M ,(2cos ,2sin )P θθ,(2cos ,22sin )PA θθ=--,(22cos ,2sin )PB θθ=--,∴44(cos sin )PA PB θθ⋅=-+,(2cos ,2sin )PC θθ=--,(12cos ,12sin )PM θθ=--,∴42(cos sin )PC PM θθ⋅=-+,故()()[44(cos sin )][42(cos sin )]PA PB PC PM θθθθ⋅⋅⋅=-+⋅-+, 设cos sin t θθ+=,[t ∈,则2()()(44)(42)8(32)PA PB PC PM t t t t ⋅⋅⋅=-⋅-=-+,当t =时,()()PA PB PC PM ⋅⋅⋅取得最小值,其最小值为32-15.【答案】12【解析】设在ABC △中,三个内角BAC ∠,ABC ∠,ACB ∠的对边分别是a ,b ,c , ∵0GA GB GC ++=,则G 为ABC △的重心, 又∵0GA GB ⋅=,则AG BG ⊥,如图,作ABC △的中线AF ,BE ,CD ,∴12AD BD GD GC ===.由余弦定理得2222cos AC AD CD AD CD ADC =+-⋅∠,2222cos(π)BC BD CD BD CD ADC =+-⋅-∠,∴222222220AC BC AD CD BD CD AD +=+++=,即2225a b c +=, 由正弦定理得222sin sin 5sin A B C +=,再由余弦定理得2222244sin cos 222sin sin a b c c CC ab ab A B+-===,∴2sin sin cos 2sin A B C C =,∴sin sin cos 2sin cos cos sin cos cos A B C CA B C A B=,∴tan tan 2sin()2(tan tan )tan cos cos A B A B A B C A B +==+,∴1tan tan 2tan tan tan A BA B C+=,∴12m =.16.【答案】52+【解析】设OBC θ∠=,因为2BC =,所以(2cos ,0)B θ,(0,2sin )C θ,则(2cos ,2sin )BC θθ=-, 设(,)BA x y =,因为ABC △是边长为2的等边三角形,所以2242cos 2sin 2x y x y θθ⎧+=⎨-+=⎩,解得cos sin x y θθθθ⎧=-⎪⎨=+⎪⎩,即(3cos sin )BA θθθθ=-+,则(3cos sin )OA OB BA θθθθ=+=++, 因为M 为AB 的中点, 所以1331(cos ,sin )22222OM OB BA θθθθ=+=++, 所以2311522cos 2cos22222OA OM θθθθθ⋅=+++=++5)2θϕ=++(其中cosϕ=,sin ϕ=),所以OA OB ⋅的最大值为52+。
2019届高考数学专题八平面向量精准培优专练理

培优点八 平面向量1.代数法例1:已知向量a,b 满足=3a ,b ()⊥+a a b ,则b 在a 方向上的投影为( ) A.3 B .3- C. D 【答案】C【解析】考虑b 在a 上的投影为⋅a bb,所以只需求出a ,b 即可. 由()⊥+a a b 可得:()20⋅+=+⋅=a a b a a b ,所以9⋅=-a b.进而⋅==a b b .故选C . 2.几何法例2:设a ,b 是两个非零向量,且2==+=a b a b,则=-a b _______. 【答案】【解析】可知a ,b ,+a b 为平行四边形的一组邻边和一条对角线, 由2==+=a b a b可知满足条件的只能是底角为60o ,边长2a=的菱形, =. 3.建立直角坐标系例3:在边长为1的正三角形ABC 中,设2BC BD =uu u v uu u v ,3CA CE =uu v uu u v ,则AD BE ⋅=u u u v u u u v__________.【答案】14AD BE ⋅=-uuu v uu uv【解析】上周是用合适的基底表示所求向量,从而解决问题,本周仍以此题为例,从另一个角度解题, 观察到本题图形为等边三角形,所以考虑利用建系解决数量积问题, 如图建系:A ⎛ ⎝⎭,1,02B ⎛⎫- ⎪⎝⎭,1,02C ⎛⎫ ⎪⎝⎭, 下面求E 坐标:令(),E x y ,∴1,2CE x y ⎛⎫=-⎪⎝⎭uu u v ,12CA ⎛=- ⎝⎭uu v ,由3CA CE =uu v uu u v可得:11132233x x y y ⎧⎛⎫⎧-=-= ⎪⎪⎪⎪⎪⎝⎭⇒⎨⎨⎪⎪==⎪⎪⎩⎩13E ⎛ ⎝⎭,∴0,AD ⎛= ⎝⎭uuu v,56BE ⎛= ⎝⎭uu u v ,∴14AD BE ⋅=-uuu v uu u v .一、单选题1.已知向量a ,b 满足1=a ,2=b ,且向量a ,b 的夹角为4π,若λ-a b 与b 垂直,则实数λ的值为( ) A .12-B .12C. D【答案】D【解析】因为12cos4π⨯⨯=⋅=a b ()40λλλ-⋅=⋅=⇒=a b b ,故选D . 2.已知向量a ,b 满足1=a ,2=b,+=a b ⋅=a b ( ) A .1 BCD .2【答案】A【解析】由题意可得:22221427+=++⋅=++⋅=a b a b a b a b ,则1⋅=a b .故选A . 3.如图,平行四边形ABCD 中,2AB =,1AD =,60A ∠=o ,点M 在AB 边上,且13AM AB =, 则DM DB ⋅=uuu u v uu u v( )A .1-B .1 C. D【答案】B【解析】因为13AM AB =,所以DB AB AD =-uu u v uu u v uuu v ,13DM AM AD AB AD =-=-uuuu v uuu v uuu v uu u v uuu v ,则()22114333DB BM AB AD AB AD AB AB AD AD ⎛⎫⋅=-⋅-=-⋅+ ⎪⎝⎭uu u v uuu v uu u v uuu v uu u v uuu v uu u v uu u v uuu v uuu v14142111332=⨯-⨯⨯⨯+=.故选B . 4.如图,在ABC △中,BE 是边AC 的中线,O 是BE 边的中点,若AB =uu u v a ,AC =u u u v b ,则AO =u u u v( )A .1122+a bB .1124+a bC .1142+a bD .1144+a b【答案】B【解析】由题意,在ABC △中,BE 是边AC 的中线,所以1AE AC =uu u v uuu v,对点增分集训又因为O 是BE 边的中点,所以()12AO AB AE =+uuu v uu u v uu u v,所以()1111122224AO AB AE AB AE =+=+=+u u u v u u u v u u u v u u u v u u u v a b ,故选B . 5.在梯形ABCD 中,AB CD ∥,1CD =,2AB BC ==,120BCD ∠=o ,动点P 和Q 分别在线段BC 和CD 上,且BP BC λ=uu v uu u v ,18DQ DC λ=uuuv uuu v ,则AP BQ ⋅uu u v uu u v 的最大值为( ) A .2- B .32-C .34 D .98【答案】D【解析】因为AB CD ∥,1CD =,2AB BC ==,120BCD ∠=o ,所以ABCD 是直角梯形,且CM =30BCM ∠=︒,以AB 所在直线为x 轴,以AD 所在直线为y 轴,建立如图所示的平面直角坐标系:因为BP BC λ=uu v uu u v ,18DQ DC λ=uuuv uuu v ,动点P 和Q 分别在线段BC 和CD 上,则(]01λ∈,,()20B ,,()2P λ-,18Q λ⎛ ⎝,所以()1112254848AP BQ λλλλ⎛⋅=-⋅-=+-- ⎝uu u v uu u v , 令()115448f λλλ=+--且(]01λ∈,, 由基本不等式可知,当1λ=时可取得最大值, 则()()max 119154488f f λ==+--=.故选D . 6.已知ABC △中,2AB =,4AC =,60BAC ∠=︒,P 为线段AC 上任意一点,则PB PC ⋅uu v uu u v的范围是( )A .[]14,B .[]04,C .944⎡⎤-⎢⎥⎣⎦, D .[]24-,【答案】C【解析】根据题意,ABC △中,2AB =,4AC =,60BAC ∠=︒,则根据余弦定理可得2416224cos6012BC =+-⨯⨯⨯︒=,即BC =.∴ABC △为直角三角形以B 为原点,BC 为x 轴,BA 为y 轴建立坐标系,则()02A ,,()C ,则线段AC 12y+=,(0x ≤≤.设(),P x y ,则()()222443PB PC x y x y x y x ⋅=---=+-=-+uu v uu u v ,,.∵0x ≤≤944PB PC -≤⋅≤uu v uu uv .故选C .7.已知非零向量a ,b ,满足=a b 且()()320+⋅-=a b a b ,则a 与b 的夹角为( )A .4π B .2π C .34π D .π【答案】A【解析】非零向量a ,b ,满足=a b 且()()320+⋅-=a b a b ,则()()320+⋅-=a b a b , ∴22320+⋅-=a a b b ,∴223cos 20θ+⨯⨯-=a a b b ,∴2213cos 202θ⨯⨯⨯-=b b b ,∴cos θ=,4θπ=,∴a 与b 的夹角为4π,故选A .8.在Rt ABC △中斜边BC a =,以A 为中点的线段2PQ a =,则BP CQ ⋅uuv uu u v的最大值为( )A .2-B .0C .2D .【答案】B【解析】∵在Rt ABC △中斜边BC a =,∴BA CA ⊥, ∵A 为线段PQ 中点,且2PQ a =,∴原式()22222cos a BA AQ AQ CA a AQ BA CA a AQ CB a a θ=-+⋅-⋅=-+-=-+⋅=-+u u v u u u v u u u v u u v u u u v u u v u u v u u u v u u v , 当cos 1θ=时,有最大值,0BP CQ ⋅=uu v uu u v .故选B .9.设向量a ,b ,c ,满足1==a b ,12⋅=-a b ,6,0--=oa b c c ,则c 的最大值等于( )A .1BCD .2【答案】D【解析】设OA =uu v a ,OB =uu u v b ,OC =uuu v c ,因为12⋅=-a b ,6,0--=oa b c c ,所以120AOB ∠=︒,60ACB ∠=︒,所以O ,A ,B ,C 四点共圆,因为AB =-uu u v b a ,()222223AB =-=+-⋅=uu u v b a b a a b ,所以AB =由正弦定理知22sin120ABR ==︒,即过O ,A ,B ,C 四点的圆的直径为2,所以c 的最大值等于直径2,故选D .10.已知a 与b 为单位向量,且⊥a b ,向量c 满足2--=c a b ,则c 的取值范围为( )A .1,1⎡+⎣B .2⎡⎣C .D .3⎡-+⎣【答案】B【解析】由a ,b 是单位向量,0⋅=a b ,可设()1,0=a ,()0,1=b ,(),x y =c , 由向量c 满足2--=c a b ,∴()1,12x y --=,2=,即()()22141x y +-=-,其圆心()1,1C ,半径2r =,∴OC =22c B .11.平行四边形ABCD 中,AC uuu v ,BD uu u v 在AB uu u v 上投影的数量分别为3,1-,则BD uu u v 在BC uu uv 上的投影的取值范围是( ) A .()1,-+∞ B .()1,3- C .()0,+∞ D .()0,3【答案】A【解析】建立如图所示的直角坐标系:设(),0B a , 则()3,C b ,()1,D a b -,则()31a a --=,解得2a =.所以()1,D b ,()3,C b .BD uu u v 在BC uu u v 上的摄影cos BM BD θθ==uu u v ,当0b →时,cos 1→-,得到:1BM →-,当b →+∞时,0θ→,BM →+∞,故选A .12.如图,在等腰直角三角形ABC 中,AB AC ==D ,E 是线段BC 上的点,且13DE BC =,则AD AE ⋅u u u v u u u v的取值范围是( ) A .84,93⎡⎤⎢⎥⎣⎦B .48,33⎡⎤⎢⎥⎣⎦C .88,93⎡⎤⎢⎥⎣⎦D .4,3⎡⎫+∞⎪⎢⎣⎭【答案】A【解析】如图所示,以BC 所在直线为x 轴,以BC 的中垂线为y 轴建立平面直角坐标系, 则()0,1A ,()1,0B -,()1,0C ,设(),0D x ,则2,03E x ⎛⎫+ ⎪⎝⎭,113x ⎛⎫-≤≤ ⎪⎝⎭.据此有(),1AD x =-uuu v ,2,13AE x ⎛⎫=+- ⎪⎝⎭uu u v ,则222181339AD AE x x x ⎛⎫⋅=++=++ ⎪⎝⎭uuu v uu u v .据此可知,当13x =-时,AD AE ⋅uuu v uu u v取得最小值89;当1x =-或13x =时,AD AE ⋅uuu v uu u v取得最大值43; AD AE ⋅uuu v uu u v 的取值范围是84,93⎡⎤⎢⎥⎣⎦.故选A .二、填空题13.已知向量()1,2=a ,()2,2=-b ,()1,λ=c ,若()2+∥c a b ,则λ=________. 【答案】1.【解析】因为()1,2=a ,()2,2=-b ,所以()24,2+=a b , 又()1,λ=c ,且()2+∥c a b ,则42λ=,即12λ=.14.若向量a ,b 满足1=a ,=b ()⊥+a a b ,则a 与b 的夹角为__________.【答案】34π【解析】由()⊥+a a b 得,()0⋅+=a a b ,即20+⋅=a a b ,据此可得2cos ,⋅=⋅⋅=-a b a b a b a ,∴cos ,==a b , 又a 与b 的夹角的取值范围为[]0,π,故a 与b 的夹角为34π.15.已知正方形ABCD 的边长为2,E 是CD 上的一个动点,则求AE BD ⋅uu u v uu u v的最大值为________.【答案】4【解析】设DE DC AB λλ==uu u v uuu v uu u v ,则AE AD DE AD AB λ=+=+u u u v u u u v u u u v u u u v u u u v,又BD AD AB =-uu u v uuu v uu u v ,∴()()()22144AE BD AD AB AD AB AD AB AB AD λλλλ⋅=+⋅-=-+-⋅=-uu u v uu u v uuu v uu u v uuu v uu u v uuu v uu u v uu u v uuu v,∵01λ≤<,∴当0λ=时,AE BD ⋅uu u v uu u v取得最大值4,故答案为4.16.在ABC △中,90C ∠=︒,30B ∠=︒,2AC =,P 为线段AB 上一点,则PB PC +uu v uu u v的取值范围为____.【答案】【解析】以C 为坐标原点,CB ,CA 所在直线为x ,y 轴建立直角坐标系,可得()0,0C ,()0,2A ,()B ,则直线AB 12y+=,设(),P x y ,则2y =,0x ≤≤(),PB x y =-uu v ,(),PC x y =--uu u v ,则|()()22222PB PC x y +=+uu v uu u v22161628333x x ⎛=-+=+ ⎝⎭,由x ⎡=⎣,可得PB PC +u u v u u u v 的最小值为 ,时,则PB PC +uu v uu u v的最大值为即PB PC +uu v uu u v的取值范围为.故答案为.。
2019年高考数学一轮复习 第八单元 平面向量单元B卷 文

第八单元 平面向量注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知向量(3,2)=a ,(1,2)=-b ,(4,1)=c ,若()()2k +-∥a c b a ,()k ∈R , 则k =( )A .43B .1922-C .1613-D .1316-2.已知平面直角坐标系中,O 为原点,点(3,1)A ,(1,3)B -,若点C 满足OC mOA nOB =+,其中m ,n ∈R ,1m n +=,则点C 的轨迹方程为( ) A .22(1)(2)5x y -+-= B .32110x y +-= C .20x y -=D .250x y +-=3.若向量()3,1AB =-,()1,2=n ,且7AC ⋅=n ,那么BC ⋅n 的值为( ) A .6-B .0C .6D .6-或64.如果向量a 与b 的夹角为θ,那么我们称⨯a b 为向量的“向量积”,⨯a b 的大小为sin θ⨯=⋅a b a b ,如果5=a ,1=b ,3⋅=-a b ,则⨯=a b ( )A .3B .4-C .4D .55.已知向量(1,2)=a ,(1,1)=b ,若a 与λ+a b 的夹角为锐角,则实数λ的取值范围是( ) A .5(,)3-+∞B .5(,0)(0,)3-+∞ C .5(,)3-∞-D .5(,)3-∞6.已知向量a ,b 满足:29=a ,12⋅=-a b ,则b 的取值范围是( )A .4[,)3+∞B .(0,4]C .(4,)+∞D .[4,)+∞7.已知点(0,0)O ,(3,0)B,(C 向量DC OB =,E 为线段DC 上的一点,且四边形OBED 为等腰梯形,则向量OE 等于( )A.B.5(2或 C.5(2D.或8.已知i 为x 轴上的单位向量,坐标平面内的点(2,1)A -,(1,3)B ,(2,1)C -,若向量AB mBC +(m 为实数)与2AC +i 垂直,则实数m =( ) A .1-B .1C .2-D .29.设点P 是ABC △所在平面内一点,且PA PB P B PC P C P A ⋅=⋅=⋅,则点P 是ABC △的( ) A .内心B .外心C .重心·D .垂心10.已知20=≠a b ,且关于x 的方程20x x ++⋅=a a b 有实根,则a 与b 的夹角的取值范围是( ) A .0,6π⎡⎤⎢⎥⎣⎦B .,3π⎡⎤π⎢⎥⎣⎦C .2,33ππ⎡⎤⎢⎥⎣⎦D .,6π⎡⎤π⎢⎥⎣⎦11.已知向量≠a e ,1=e ,对任意t ∈R ,恒有t -≥-a e a e ,则( ) A .⊥a e B .()⊥-a a e C .()⊥-e a eD .(()()+⊥-a e a e12.已知A 、B 、C 是平面上不共线的三点,O 为平面ABC 内任一点,动点P 满足等式()()()111123OP OA OB OC λλλ⎡⎤=-+-++⎣⎦,(0)λλ∈≠R 且,则P 的轨迹一定通过 ABC △的( )A .内心B .垂心C .重心D .AB 边的中点二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上)13.已知点)2,1(A ,)4,3(B ,)2,2(-C ,)5,3(-D ,则向量AB 在向量CD 上的投影为 . 14.已知向量(cos ,sin )αα=a ,(cos ,sin )ββ=b,5-=a b ,则cos()αβ-= . 15.已知正方形ABCD 的边长为1,点E 是边AB 上的动点,则DE DC ⋅的最大值为 . 16.在ABC △中,角A ,B ,C 对应的边分别为a ,b ,c ,1AB AC BA BC ⋅=⋅=, 那么c = .三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)设a,b,满足1==a b,及32-=a b(1)求a与b的夹角;(2)求3+a b的值.18.(12分)已知向量a、b两个单位向量,且k k+=-a b b,其中0>k.(1)向量a、b能垂直吗?证明你的结论;(2)若a与b的夹角为60,求k的值.2319.(12分)已知点(0,3)P -,点A 在x 轴上,点B 在y 轴的正半轴上,点M 满足:0PA AM ⋅=,32AM MB =-,当点A 在x 轴上移动时,求动点M 的轨迹方程.20.(12分)在四边形ABCD 中,已知(6,1)AB =,(,)BC x y =,(2,3)CD =--,BC DA ∥; (1)试求x 与y 满足的关系式;(2)若AC BD ⊥,求x 、y 的值及四边形ABCD 的面积.421.(12分)已知A 、B 、C 的坐标分别为)0,3(A ,)3,0(B ,)sin ,(cos ααC ,3,22αππ⎛⎫∈ ⎪⎝⎭.(1)若AC BC =,求角α的值;(2)若1AC BC ⋅=-,求22sin sin 21tan ααα++的值.22.(12分)在直角坐标系中,已知一个圆心在坐标原点,半径为2的圆,从这个圆上任意一点P 向y 轴作垂线段'PP ,'P ′为垂足.(1)求线段'PP 中点M 的轨迹C 的方程;(2)过点)0,2(-Q 作直线l 与曲线C 交于A ,B 两点,设N 是直线4017x +=上一动点,满足ON OA OB =+(O 为坐标原点),问是否存在这样的直线l ,使得四边形OANB 为矩形?若存在,求出直线l 的方程;若不存在,说明理由.单元训练金卷▪高三▪数学卷答案(B )第八单元 平面向量一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.【答案】C【解析】∵(3,2)=a ,(1,2)=-b ,(4,1)=c ,∴(34,2)k k k +=++a c ,2(5,2)-=-b a , 又()()2k +-∥a c b a ,∴2(34)5(2)k k +=-+,解得1613k =-,故选C . 2.【答案】D【解析】由平面向量基本定理知,当OC mOA nOB =+且1m n +=时,点A ,B ,C 共线,∴点C 的轨迹为直线AB ,设(),C x y ,由两点式的直线方程得,133113y x --=---, 化简为250x y +-=,故选D . 3.【答案】C【解析】()7(3,1)(1,2)6BC AC AB AC AB ⋅=⋅-=⋅-⋅=--⋅=n n n n ,故选C . 4.【答案】C【解析】∵cos 3θ⋅=⋅=-a b a b ,3cos 5θ=-,又θ为a 与b 的夹角,∴4sin 5θ=, ∴4sin 5145θ⨯=⋅=⨯⨯=a b a b ,故选C . 5.【答案】B【解析】∵a 与λ+a b 均不是零向量,且夹角为锐角,∴()0λ⋅+>a a b , 即(1,2)[(1,2)(1,1)]0λ⋅+>,∴530λ+>,则53λ>-,但当0λ=时,a 与λ+a b 共线且同向, 不满足题设,∴0λ≠,综上知,53λ>-且0λ≠,故选B . 6.【答案】D【解析】∵29=a ,∴3=a ,又∵12⋅=-a b ,∴12⋅=a b ,∵cos θ⋅=⋅a b a b ≤⋅a b ,∴123≤b ,则4≥b ,即b 的取值范围是[4,)+∞,故选D . 7.【答案】A【解析】∵(3,0)DC OB ==,)3,4(C ,∴)3,1(D .如图所示,E 为线段DC 上的一点,设E 点坐标为)3,(x ,由2==OD BE 解得2=x 或4x =舍去,∴OE )3,2(=,故选A . 8.【答案】A【解析】由题设知,(3,2)AB =,(4,2)AC =-,(1,4)BC =-,(3,2)(1,4)AB mBC m +=+⋅-(3,24)m m =+-,∵i 为x 轴上的单位向量,∴(1,0)=i ,则2(4,2)2(1,0)(6,2)AC +=-+=-i ,∵向量AB mBC +与2AC +i 垂直,∴()(2)0AB mBC AC +⋅+=i ,即(3,24)(6,2)0m m +-⋅-=,化简得,14140m +=,解得1m =-.故选A . 9.【答案】D【解析】∵PA PB PB PC ⋅=⋅,∴0PB PC PA PB ⋅-⋅=,即0PB AC ⋅=同理,由PB PC PC PA ⋅=⋅可得0PC AB ⋅=,所以P 是ABC △的垂心,故选D . 10.【答案】B 【解析】20x x ++⋅=a a b 有实根,∴240∆-⋅≥=a a b ,∴214⋅≤a b a ,设a 与b 的夹角为θ,∵20=≠a b ,∴22114cos 122θ⋅=≤=⋅aa b a b a ,又0θ≤≤π,∴,3θπ⎡⎤∈π⎢⎥⎣⎦,故选B . 11.【答案】C【解析】∵t -≥-a e a e ,∴22||||t -≥-a e a e , ∴2222222t t -⋅+≥-⋅+a a e e a a e e ,由1=e 得,22210t t -⋅⋅+⋅-≥a e a e 对任意t ∈R 恒成立,∴224()4(21)0(1)0∆=⋅-⋅-≤⇒⋅-≤a e a e a e ,则1⋅=a e ,∴()2110⋅-=⋅-=-=e a e e a e ,因此,()⊥-e a e ,故选C .12.【答案】C【解析】取AB 的中点D ,则2OA OB OD +=,∴2(1)1233OP OD OC λλ-+=+,∴D C P 、、三点共线,∴点P 轨迹一定通过ABC △的重心,故选C .二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】5102 【解析】(2,2)AB =,(1,3)CD =-,设AB 和CD 的夹角为α,则向量AB 在向量CD 上的投影为2cos AB CD AB CDα⋅==. 14.【答案】35【解析】∵1=a ,1=b ,∴2222222(cos cos αβ-=-⋅+=+-a b a a b b a bsin sin )112cos()αβαβ+=+--,又-=a b ,∴245-=a b , 故112cos()αβ+--45=,即3cos()5αβ-=.15.【答案】1.【解析】过点E 向CD 作垂线,垂足为F ,则2cos 1DE DC DC DE CDE DC DF DC ⋅=⋅∠=⋅≤=, 当且仅当点E 与点B 重合时,DE DC ⋅取到最大值1. 16.【解析】由1AB AC BA BC ⋅=⋅=得,cos cos 1bc A ac B ==,∴cos cos b A a B =,由正弦定理得到,sin cos sin cos B A A B =,∴s i n c o s c o s s i n0A B A B -=,sin()0A B -=,∴A B k -=π,()k ∈Z ,又∵A B -π<-<π,∴A B =,则a b =.又1cos =A bc,22212b c a bc bc+-∴⨯=,∴22c =,c =三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【答案】(1),3π〈〉=a b ;(2 【解析】(1)32-=a b 2291247-⋅+=a a b b,1,23π∴⋅=⇒〈〉=a b a b . (2)3+=a b. 18.【答案】(1)不能,见解析;(2)1=k .【解析】(1)∵k k +=-a b b ,∴22()3()k k +=-a b a b , 即2222(3)(13)80k k k -+-+⋅=a b a b , 由1==a b 得,214k k+⋅=a b .∵012>+k ,∴0⋅≠a b .∴向量a 与b 不能垂直. 1cos602=.19.【答案】4(0)x y y =>.【解析】设(,)M x y ,(,0)A a ,(0,)(0)B b b >,由题设知,(,3)PA a =,(,)AM x a y =-,(,)MB x b y =--; ∵0PA AM ⋅=,∴(,3)(,)()30PA AM a x a y a x a y ⋅=⋅-=-+=①∵32AM MB =-,∴3(,)(,)2x a y x b y -=---; 即323()2x a x y b y ⎧-=⎪⎨⎪=--⎩,解得23x a yb ⎧=-⎪⎨⎪=⎩; 代入①式得,11()3022x x x y -++=,即24x y =. ∵03>=b y ,∴动点M 的轨迹方程为24(0)x y y =>.20.【答案】(1)20x y +=;(2)63x y =-⎧⎨=⎩,16ABCD S =,21x y =⎧⎨=-⎩,16ABCD S =.【解析】(1)(,)BC x y =,()(4,2)DA AD AB BC CD x y =-=-++=---+,BC DA ∥,则有(2)(4)0x y y x ⋅-+-⋅--=,化简得,20x y +=;(2)(6,1)AC AB BC x y =+=++,(2,3)BD BC CD x y =+=--;又AC BD ⊥,则(6)(2)(1)(3)0x x y y +-++-=,即2242150x y x y ++--=;联立222042150x y x y x y +=⎧⎨++--=⎩,解得63x y =-⎧⎨=⎩或21x y =⎧⎨=-⎩; 由BC DA ∥,AC BD ⊥知,四边形ABCD 为对角线互相垂直的梯形,当63x y =-⎧⎨=⎩时,(0,4)AC =,(8,0)BD =-,1162ABCD S AC BD ==,当21x y =⎧⎨=-⎩时,(8,0)AC =,(0,4)BD =-,1162ABCD S AC BD ==.21.【答案】(1)54απ∈;(2)59-.【解析】(1)()cos 3,sin AC αα=-,()cos ,sin 3BC αα=-,(cosAC =cos BC =.由AC BC =得sin cos αα=.又3,22αππ⎛⎫∈ ⎪⎝⎭,54απ∴∈.(2)由1AC BC ⋅=-,得()()cos 3cos sin sin 31αααα-+-=-,2sin cos 3αα∴+=① 又222sin sin 22sin 2sin cos 2sin cos sin 1tan 1cos αααααααααα++==++,由①式两分平方得412sin cos 9αα+=,52sin cos 9αα∴=-, 22sin sin 251tan 9ααα+∴=-+.22.【答案】(1)2214y x +=;(2)存在,()122y x =±+. 【解析】(1)设),(y x M 是所求曲线上的任意一点,),(11y x P 是方程422=+y x 的圆上的任意一点,则),0(1'y P ,则有11122x x y y y ⎧=⎪⎪⎨+⎪=⎪⎩,即112x x y y =⎧⎨=⎩,代入224x y +=,化简得2214y x +=,所以线段'PP 中点M 的轨迹C 的方程2214y x +=.(2)当直线l 的斜率不存在时,与椭圆无交点.所以设直线l 的方程为)2(+=x k y ,与椭圆交于),(11y x A 、),(22y x B 两点,N 点所在直线方程为4017x +=, 由()22142y x y k x ⎧+=⎪⎨⎪=+⎩得()222244440k x k x k +++-=, 由()()4221644440kk k ∆=-+-≥,243k ∴≤, 即k ≤≤212244k x x k-+=+,()2122414k x x k -=+, ON OA OB =+,即AN OB =,∴四边形OANB 为平行四边形. 假设存在矩形OANB ,则0OA OB ⋅=,即12120x x y y +=.即()()22212121240k x x k x x k ++++=,于是有2216404k k -=+,得12k =±, 设()00,N x y ,由ON OA OB =+,得2012244174k x x x k=+=-=-+, 即点N 在直线417x =-上.∴存在直线l 使四边形OANB 为矩形,直线l 的方程为()122y x =±+.。
2020年高考数学(文科)二轮复习押题特训专题08 平面向量(含答案解析)

2020年高考数学(文科)二轮复习押题特训专题08 平面向量1.在△ABC中,“△ABC为直角三角形”是的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件【解析】选B若△ABC为直角三角形,角B不一定为直角,即不一定等于0;若,则AB⊥BC,故角B为直角,即△ABC为直角三角形,故“△ABC为直角三角形”是的必要不充分条件.2.已知点M(-3,0),N(3,0).动点P(x,y)满足则点P的轨迹的曲线类型为()A.双曲线B.抛物线C.圆D.椭圆【解析】B3.已知非零向量a,b,满足a⊥b,则函数f(x)=(a x+b)2(x∈R)是()A.既是奇函数又是偶函数B.非奇非偶函数C.偶函数D.奇函数【解析】选C因为a⊥b,所以a·b=0,所以f(x)=(a x+b)2=|a|2x2+2a·b x+|b|2=|a|2x2+|b|2,所以函数f(x)=(a x+b)2为偶函数.4.若非零向量且则△ABC为()A.三边均不相等的三角形B .直角三角形C .等边三角形D .等腰非等边三角形【解析】选C知,角A 的平分线与BC 垂直,∴||=||;由知,cos A =12,∴A =60°.∴△ABC 为等边三角形.5.在△ABC 中,满足||=||,(-3)⊥,则角C 的大小为( )A.π3B.π6C.2π3D.5π6 【解析】C6.设O 是△ABC 的外心(三角形外接圆的圆心).若=13+13,则∠BAC 的度数等于( )A .30°B .45°C .60°D .90°【解析】选C 取BC 的中点D ,连接AD ,则+=2.由题意得3=2,∴AD 为BC 的中线且O 为重心.又O 为外心,∴△ABC 为正三角形,∴∠BAC =60°. 7.若函数f (x )=2sin ⎝ ⎛⎭⎪⎫π6x +π3(-2<x <10)的图象与x 轴交于点A ,过点A 的直线l 与函数的图象交于B ,C 两点,则(+)·=( )A .-32B .-16C .16D .32【解析】选D 函数f (x )=2sin ⎝ ⎛⎭⎪⎫π6x +π3(-2<x <10)的图象如图所示.由f (x )=0,解得x =4,即A (4,0),过点A 的直线l 与函数的图象交于B ,C 两点,根据对称性可知,A 是B ,C 的中点,所以+=2,所以(+)·=2·=2||2=2×42=32.8.已知A 、B 、C 是圆x 2+y 2=1上的三点,且+=,其中O 为坐标原点,则的面积等于________.【答案】32【解析】如图所示,由||=||=||=1知,▱OACB 是边长为1的菱形, 且∠AOB =120°∴S ▱OACB =||||sin 120°=1×1×32=32.9.已知△ABC 的三个内角A ,B ,C 的对边分别为a ,b ,c ,向量m =⎝ ⎛⎭⎪⎫cos C 2,sin C 2,n=⎝ ⎛⎭⎪⎫cos C 2,-sin C 2,且m 与n 的夹角为π3. (1)求角C ;(2)已知c =72,S △ABC =332,求a +b 的值.即12=a +b 2-2ab -c 22ab =a +b2-12-⎝ ⎛⎭⎪⎫72212,解得a +b =112.10.在△ABC 中,若·=·=2,则边AB 的长等于________.【答案】2【解析】由题意知·+·=4,即·(+)=4,即·=4,∴||=2.11.已知|a |=2|b |,|b |≠0,且关于x 的方程x 2+|a |x -a ·b =0有两相等实根,则向量a 与b的夹角是________.【答案】2π3【解析】由已知可得Δ=|a |2+4a ·b =0,即4|b |2+4×2|b |2cos θ=0, ∴cos θ=-12,又∵0≤θ≤π,∴θ=2π3.12.设向量a =(2cos α,2sin α),b =(cos β,sin β),其中0<α<β<π,若以向量a +b 与a -2b 为邻边所作的平行四边形是菱形,则cos(β-α)=________.【答案】14【解析】由题意知,|a +b |=|a -2b |,所以a 2+2a ·b +b 2=a 2-4a ·b +4b 2,所以2a ·b =b 2,即4cos (β-α)=1,所以cos(β-α)=14.13.已知在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且2S △ABC =3·.(1)求角B 的大小;(2)若b =2,求a +c 的取值范围.取等号),解得0<a +c ≤4.又a +c >b ,∴2<a +c ≤4,∴a +c 的取值范围是(2,4].法二:由正弦定理得a =43sin A ,c =43sin C , 又A +C =2π3,∴a +c =43(sin A +sin C )=43[sin A +sin(A +B )]=43⎝⎛⎭⎪⎫sin A +12sin A +32cos A =4⎝ ⎛⎭⎪⎫32sin A +12cos A =4sin ⎝ ⎛⎭⎪⎫A +π6. ∵0<A <2π3,∴π6<A +π6<5π6,∴12<sin ⎝ ⎛⎭⎪⎫A +π6≤1,∴a +c 的取值范围是(2,4].14.已知向量a =⎝ ⎛⎭⎪⎫sin x ,32,b =(cos x ,-1).(1)当a ∥b 时,求tan 2x 的值;(2)求函数f (x )=(a +b )·b 在⎣⎢⎡⎦⎥⎤-π2,0上的值域.。
2019高考数学文科总复习第8单元【平面向量】测试A卷及答案解析

sin x 2cos x 0 , tanx 2 ,
2
sin
x
4
2 sin x cos x
2 tan x 1
2 2 1 3 2 ,故答案为 3 2 .
sin x cos x sin x cos x
tan x 1
2 1
据此可知: 2m n 62 82 10 .
15.【答案】
3 5
,
4 5
【解析】 AB
1,5 4,1
3,4 ,
AB
5
,
与向量
AB
方向相同的单位向量为
3 5
,
4 5
.
16.【答案】 8, 15
A.平行四边形
B.菱形
C.矩形
D.正方形
11.已知向量 a ,b 的夹角为120 ,且 a 2 , b 3 ,则向量 2a 3b 在向量 2a b 方向上的投影为( )
A.
83 13
B.
6 13 13
C. 5 6 6
D.
19 13 13
12.在锐角 △ABC
中, B 60 ,
【解析】a a b ,所以, a a b 0 ,即 a a a b | a |2 a b cos a, b 0 ,
所以 cos
a,b
| a |2 ab
2 2
,又
a, b
0,
,故
a
与
b
的夹角为
3 4
,故选
C.
7.【答案】A
2019衡水名师原创文科数学高考专题卷专题八《平面向量》
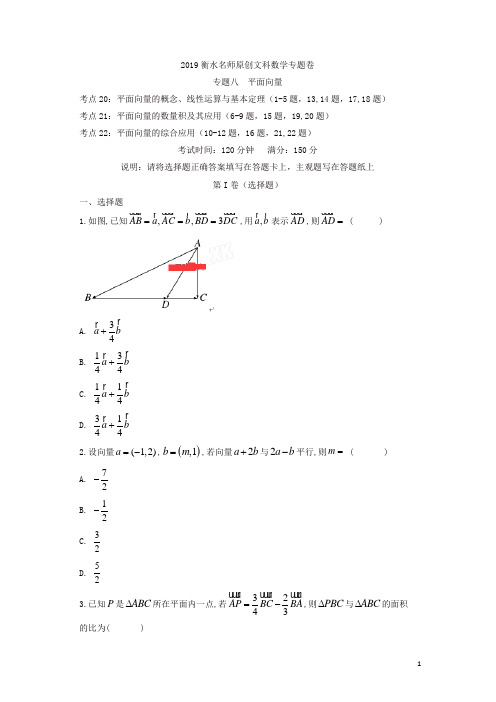
2019衡水名师原创文科数学专题卷专题八 平面向量考点20:平面向量的概念、线性运算与基本定理(1-5题,13,14题,17,18题) 考点21:平面向量的数量积及其应用(6-9题,15题,19,20题) 考点22:平面向量的综合应用(10-12题,16题,21,22题)考试时间:120分钟 满分:150分说明:请将选择题正确答案填写在答题卡上,主观题写在答题纸上第I 卷(选择题)一、选择题1.如图,已知,,3AB a AC b BD DC ===,用,a b 表示AD ,则AD = ( )A. 34a b + B.1344a b + C.1144a b + D.3144a b + 2.设向量(1,2)a =-,(),1b m =,若向量2a b +与2a b -平行,则m = ( ) A. 72- B. 12- C.32 D.523.已知P 是ABC ∆所在平面内一点,若3243AP BC BA =-,则PBC ∆与ABC ∆的面积的比为( )A.13 B.12 C.23D.344.在矩形ABCD 中, 1,2AB AD ==,动点P 在以点 C 为圆心且与BD 相切的圆上.若AP AB AD λμ=+,则λμ+的最大值为( )A. 3?B.D. 25.在矩形ABCD 中, 1AB =,2AD =,动点P 在以点C 为圆心且与BD 相切的圆上.若AP AB AD λμ=+,则λμ+的最大值为( )A. 3B.D. 2 6设,为非零向量,则“存在负数,使得”是“”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.已知6a =,3b =,12a b ⋅=-,则向量a 在向量b 方向上的投影是( ) A. 4- B. 4 C. 2- D. 28.已知圆 O 的半径为2,圆 O 的一条弦AB 的长是3,P 是圆 O 上的任意一点,则AB AP ⋅的最大值为( ) A. 9 B. 10 C.212D.2329.向量 ,a b 的夹角为120,1a b ==,2c =,则a b c ++的最大值为( ) A. 1 B. 2 C. 3 D. 410.已知ABC ∆的外接圆半径为1,圆心为点O ,且3450OA OB OC ++=,则ABC ∆的面积为( ) A.85B.75 C.65D.4511.已知向量,,a b c 满足2a =,3b a b =⋅=,若()22?03c a c b ⎛⎫--= ⎪⎝⎭,则b c -的最小值是( )A. 2B. 2+C. 1D. 212.已知AB AC ⊥,1AB t=,AC t =,若点P 是ABC ∆所在平面内的一点,且4AB AC AP ABAC=+,则PB PC ⋅的最大值等于( )A.13B.15C.19D.21 二、填空题13.若点M 是ABC ∆所在平面内的一点,且满足53AM AB AC =+,则ABM ∆与ABC ∆的面积比为__________.14.如图,正方形ABCD 中, M 、N 分别是BC 、CD 的中点,若AC AM BN λμ=+,则λμ+=__________.15.已知向量||1,||2||a a b a b =+=-,则b 的取值范围是__________.16.在等腰直角ABC ∆中, 90ABC ∠=,2AB BC ==,,M N 为AC 边上两个动点,且满足MN =则BM BN ⋅的取值范围为__________.三、解答题17.已知向量(cos ,1sin ),(cos ,sin )()m n R ααααα=-=-∈ 1.若m n ⊥,求角α的值 2.若||3m n -=,求2cos α的值18.在直角坐标系xOy 中,已知点(1,1),(2,3),(3,2)A B C ,点(,)P x y 在ABC ∆中三边围成的区域(含边界)上,且(,)OP AB AC R λμλμ=+∈. 1.若23λμ==,求OP ; 2.用,x y 表示λμ-并求λμ-的最大值.19.已知向量(cos ,1)a x =-,13sin ,2b x ⎛⎫=- ⎪⎭,函数()()2f x a b a =+⋅- 1.求函数f ()x 的最小正周期及单调递增区间 2.当0,2x π⎡⎤∈⎢⎥⎣⎦时,求f ()x 的值域20.如图,在平面直角坐标系 xOy 中,点A 在 x 轴的正半轴上,直线AB 的倾斜角为34π,2OB =,设AOB θ∠=,3,24πθπ⎛⎫∈ ⎪⎝⎭.1.用θ表示点B 的坐标及OA ;2.若4tan 3θ=-,求OA OB ⋅的值.21.已知向量(2cos ,sin )a x x =,向量sin ,2cos 33b x x ⎛ππ⎫⎛⎫⎛⎫=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,()1f x a b =⋅-,求:1. ()f x 的最小正周期及单调区间2.是否存在ABC ∆,使角,A B 是方程()0?f x =的两不等实根?若存在求内角C 的大小,若不存在说明理由.22.已知动点(),S x y 到直线:l x =)T .1.求动点S 的轨迹 C 的方程;2.设轨迹 C 上一动点P 满足: 2OP OM ON λμ=+,其中,M N 是轨迹 C 上的点,直线OM 与ON 的斜率之积为12-,若(,)Q λμ为一动点, 1E ⎛⎫⎪ ⎪⎝⎭,2E ⎫⎪⎪⎝⎭为两定点,求12QE QE +的值.参考答案一、选择题 1.答案:B解析:,,3AB a AC b BD DC ===,用,a b 表示AD ,则1344AD a b =+,选B. 2.答案:B解析:()212,4a b m +=-+,2(2,3)a b m -=--,因为向量2a b +与2a b -平行,所以(12)34(2)m m -+⨯=⨯--, 解之得12m =-,故选B. 3.答案:A解析:在线段AB 上取D 使23AD AB =,则23AD BA =-, 过A 作直线l 使//l BC ,在l 上取点E 使34AE BC =,过D 作l 的平行线, 过E 作AB 的平行线,设交点为P , 则由平行四边形法则可得3243AP BC BA =-, 设PBC ∆的高线为h ,ABC ∆的高线k, 由三角形相似可得:1:3h k =, ∵PBC ∆与ABC ∆有公共的底边BC , ∴PBC ∆与ABC ∆的面积的比为13,故选:A.4.答案:A 解析:5.答案:A解析:如图所示,建立平面直角坐标系:设()0,1A ,()0,0B ,()2,0C ,()2,1D ,(),P x y ,根据等面积公式可得圆的半径r =,即圆C 的方程是()22425x y -+=,(,1)AP x y =-,()0,1AB =-,(2,0)AD =,若满足AP AB AD λμ=+,即2{1x y μλ=-=-,2xμ=,1y λ=-,所以12xy λμ+=-+, 设12x z y =-+,即102xy z -+-=, 点(),P x y 在圆()22425x y -+=上,所以圆心到直线的距离d r ≤,≤,解得13z ≤≤, 所以z 的最大值是3,即λμ+的最大值是3,故选A. 答案: A 解析: 由于,是非零向量,“存在负数,使得.”根据向量共线基本定理可知与共线,由于,所以与方向相反,从而有,所以是充分条件。
2020届高三精准培优专练八平面向量(理)学生版
2020届高三好教育精准培优专练培优点八平面向量一、平面向量的建系坐标化应用例1:在A4BC中,BC = 6, 8C边上的高为2,则丽•衣的最小值为二、平面向量中三点共线间]例2:设。
,〃是两个不共线的单位向量.若。
满足。
=(3-2㈤, + (24 —2)〃,且|c| = g,则当|〃一4 最小时,在。
与方的夹角的余弦值为.三、平面向量与三角形的四心问题例3:已知A, B,。
是平面内不共线三点,。
是AABC的外心,动点尸满足OP = -[(l-2)OA + (l-2)OB + (l + 22)OC](2eR),则P的轨迹一定通过AABC的()A.内心B.垂心C.外心D.重心四、平面向量与三角函数结合例4:已知向量a = (cosox-sin0K,sin5), b = (-cos cox - sin cox, 25/3 cos cox),设函数(1 A/(x)=a・〃 + 4(/leR)的图象关于直线工=兀对称,其中尤为常数,且Ge -J .I,/(1)求函数/(X)的最小正周期;(2) y = /。
)的图象经过点]:,0),求函数/(外在区间]。
,5]上的取值范围.对点增分集训一、选择题1.已知向量” = (cos6-2,sine),其中8eR,则lai的最小值为()A. 1B. 2C. >/5D. 32.在ZXABC中,G为AABC的重心,过G作直线分别交直线A8 , AC于点M , N,设丽=x丽,德=沃,则上=()x+ yA. 3B. -C. 2D.-3 33.若。
为△ABC所在平面内一点,且满足1。
4一。
1=1。
3 +。
-2。
41,则AABC的形状为()A.等腰直角三角形B.直角三角形C.等腰三角形D.等边三角形4.已知向量”=(cos25。
,sin 25°), = (sin200,cos 20°),若/是实数,且〃 =。
+必,则1〃1 的最小值B. 1・•・•I•已知非零向量而与衣满足•抚=。
【新】2019年高考数学一轮复习第八单元平面向量单元A卷文
第八单元 平面向量注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设平面向量()3,5=a ,()2,1=-b ,则2-=a b ( ) A .()7,3B .()7,7C .()1,7D .()1,32.在ABC △中,点D 为边AB 的中点,则向量CD =( )A 1BA BC - B 2BA BC - C BA BC +D BA BC +3.已知向量()4,2=-a ,(),1x =b .若a ,b 共线,则x 的值是( ) A .1-B .2-C .1D .24.已知平面向量()1,3=a ,(),3x =-b ,且∥a b,则 ) A .10B C .5D5.已知向量()3,1=a ,()21,k k =-b ,且()+⊥a b a ,则k 的值是( ) A .1-B.37C .35-D .356.若向量a 、b 满足1=a 、=b ()⊥+a a b ,则a 与b 的夹角为( ) A.2π B .23π C .34π D .56π7.单位圆O 中一条弦AB ,则·ABOB =( )A.1B C .2 D .无法确定8.已知向量a 与b 反向,则下列等式中成立的是( ) ABCD 9.在ABC △中,2BD DC =,AD mAB nAC =+,则mn的值为( ) A .12B .13C .2D .310.四边形ABCD 中,AB DC =,且AD AB AD AB-=+,则四边形ABCD 是( ) A .平行四边形B .菱形C .矩形D .正方形11.已知向量a ,b 的夹角为120︒,则向量23+a b 在向量2+a b 方向上的投影为( ) AB C D 12.在锐角ABC △中,60B =︒,2AB AC -=则AB AC ⋅的取值范围为( ) A .()0,12 B .1,124⎡⎫-⎪⎢⎣⎭C .(]0,4D .(]0,2二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上)13.已知向量()sin ,2x =a ,()cos ,1x =b ,满足∥a b ,则. 14.已知向量()12,=-m ,(),4x =n ,若⊥m n ,则2+=m n __________. 15.已知点()4,1A ,()1,5B ,则与向量AB 方向相同的单位向量为________. 16.已知()2,3A ,()4,3B -,点P 在线段AB 3AP PB =,则点P 的坐标是____________.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(10分)已知向量()1,3=a ,()2,2=-b , (1)设2=+c a b ,求()⋅b a c ; (2)求向量a 在b 方向上的投影.18.(12分)已知向量()3,2=a ,()1,2=-b . (1)求2a +b 的值;(2)若()m ⊥+a b b ,求m 的值.19.(12,()sin ,cos x x =n , (1)若⊥m n ,求tan x 的值; (2)若向量m ,n20.(12分)已知平面上三点A B C 、、满足,()23BC k =-,,()24AC =,, (1)若三点A B C 、、不能构成三角形,求实数k 满足的条件; (2)ABC △是不以C ∠为直角的Rt △,求实数k 的值.21.(12分)如图,在OAB △中,点P 为直线AB 上的一个动点,且满足AP AB λ=.(1)若13λ=,用向量OA ,OB 表示OP ;(2)若4OA =,3OB =,且60AOB ∠=︒,请问λ取何值时使得OP AB⊥?22.(12分)在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,向量()sin ,A b c =+p , (),sin sin q a c C B =--,满足+=-p q p q .(1)求角B 的大小;(2)设1sin ,32C ⎛π⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭m ,()()2,cos20k A k =≠n ,⋅m n 有最大值为32,求k 的值.单元训练金卷▪高三▪数学卷答案(A )第八单元 平面向量一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.【答案】A【解析】∵()3,5=a ,()2,1=-b ,∴()()()()23,522,134,527,3-=--=+-=a b , 故选A . 2.【答案】A【解析】由题意结合平面向量的运算法则可得:11CD CB BD BC BA BA BC =+=-+=-.本题选择A 选项. 3.【答案】B【解析】∵()4,2=-a ,(),1x =b ,且a ,b 共线,∴24x -=,解得2x =-.故选B . 4.【答案】D【解析】由题意得,()1,3=a ,(),3x =-b ,且()11,3x ⇒=-⇒=--∥a b b , 则()21,3+=--a b ,即D . 5.【答案】A【解析】因为向量()3,1=a ,()21,k k =-b ,所以()22,1k k +=++a b ,又因为()+⊥a b a ,所以()770k +⋅=+=a b a ,1k =-,故选A . 6.【答案】C【解析】()⊥+a a b ,所以,()0⋅+=a a b ,即2||cos ,0⋅+⋅=+⋅=a a a b a a ba b ,所以2||cos ,=-=⋅a a b a b ,又[],0,∈π a b ,故a 与b 的夹角为34π,故选C . 7.【答案】A【解析】单位圆O 中一条弦AB ,则222+OA OB AB =,OAB △是等腰直角三角形,所以AB 与OB ,·2112AB OB =⨯⨯=,故选A .8.【答案】C【解析】向量a 与bC . 9.【答案】A 【解析】如图,()22123333AD AB BD AB BC AB AC AB AB AC =+=+=+-=+, 又AD mAB nAC =+23n =,故12m n =.故选A .10.【答案】C【解析】由于AB DC =,故四边形是平行四边形,根据向量加法和减法的几何意义可知,该平行四边形的对角线相等,故为矩形,故选C. 11.【答案】D【解析】向量a ,b 的夹角为120︒所以2222341261+=+⋅=a b a a b +9b ,23+a b 22224413+=+⋅+=a b a a b b ,所以2+a b()()232cos 23,2232++++=++a b a b a b a b a b a b,所以向量23+a b在向量2+a b 方向上的投影为23cos 23,2+++==a b a b a b D . 12.【答案】A【解析】以B 为原点,BA 所在直线为x 轴建立坐标系,∵60B =︒2AB AC -=,∴(C ,设(),0A x ,∵ABC △是锐角三角形, ∴120A C +=︒,∴3090A ︒<<︒,即A 在如图的线段DE 上(不与D ,E 重合),∴14x <<,则2AB AC x ⋅=-,所以AB AC ⋅的取值范围为()0,12,故选A .二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】【解析】因为向量()sin ,2x =a ,()cos ,1x =b ,∥a b ,sin 2cos 0x x ∴-=,tan 2x =,14.【答案】10【解析】由题意可得:240x ⋅=-+⨯=m n ,8x ∴=,即()1,2=-m ,()8,4=n ,则()()()22,48,46,8+=-+=m n ,据此可知:210+=m n . 15.【答案】34,55⎛⎫- ⎪⎝⎭【解析】()()()154134AB =-=-,,,,5AB =,∴与向量AB 方向相同的单位向量为34,55⎛⎫- ⎪⎝⎭.16.【答案】()8,15-【解析】因为P 在AB 的延长线上,故AP ,PB 共线反向,故3AP PB =-,设(),P x y , ,解得815x y ==-⎧⎨⎩,P 的坐标为()8,15-,故填()8,15-.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【答案】(1)()16,16--;(2) 【解析】(1)()()()2,62,24,4=+-=c ,()()26416,16⋅=-=-⇒⋅=--b a b a c .(2)向量a 在b方向的投影18.【答案】(1(2)15-.【解析】(1)由已知得()21,6=a +b ,所以2=a +b (2)依题意得()3,22m m m +=-+a b ,又()m ⊥ +a b b ,()·0m ∴= +a b b ,即()()132220m m --++=,解得15m =-. 19.【答案】(1)tan 1x =;(2)12. 【解析】(1)由⊥m n 可得0⋅=m n ,即0xx =, 化简可得sincos x x =,则tan 1x =.(2而由m ,n)1sin cos 22x x -=, 20.【答案】(1)12k =;(2)2-,1-,3. 【解析】(1)A B C ,,三点不能构成三角形,∴三点A B C ,,共线;∴存在实数λ,使BC AC λ=;22 34k λλ-=⎧∴⎨=⎩,解得12k =.k ∴满足的条件是12k =.(2)()()()23241AB CB CA k k =-=-----=,,,ABC △为直角三角形;∴若A ∠是直角,则AB AC ⊥,2402AB AC k k ∴⋅=+=∴=-,; 若B ∠是直角,则AB BC ⊥,2230AB BC k k ∴⋅=-++=,解得1k =-,或3;综上可得k 的值为:2-,1-,3.)2133OP OA OB =+;13)由题意得1AP AB =,∴()1OP OA OB OA -=-,∴21OP OA OB =+.(2)由题意知43cos606OA OB ⋅=⨯⨯︒=.∵AP AB λ=, ∴()OP OA OB OA λ-=-,∴()1OP OA OB λλ=-+. ∵OP AB ⊥,∴()()10OP AB OAOB OB OA λλ⎡⎤⋅=-+⋅-=⎣⎦,∴()()()()2212161216190OA OB OA OB λλλλλλ+-⋅--=---+=, 22.【答案】(1)3B π=;(2)1k =或2k =. 【解析】(1)由条件+=-p q p q ,两边平方得0⋅=p q ,又()sin ,A b c =+p ,(),sin sin --a c C B =q ,代入得()()()sin sin sin 0a c A b c C B -++-=, 根据正弦定理,可化为()()()0-a a c b c c b -++=,即222a c b ac +-=,又由余弦定理2222cos =a c b a B +-,所以1cos 2B =,3B π=.(2)1sin ,32C ⎛π⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭m ,()2,cos2n k A =,()0k ≠,()2112sin cos 22sin cos 22sin cos 3222k C k A C B k A A k A π⎛⎫⋅=++=++=+-⎪⎝⎭m n 2211sin 2sin sin 22k k k A A k A k k ⎛⎫=-++=--++ ⎪⎝⎭,而203A <<π,(]sin 0,1A ∈,①01k <≤时,sin 1A =取最大值为3222k -=,1k =. ②1k >时,当1sin A k =时取得最大值,1322k k +=解得1k =或2k =, 1k =(舍去)2k ∴=.③0k <时,开口向上,对称轴小于0当sin 1A =取最大值3222k -=,1k =(舍去), 综上所述,1k =或2k =.。
2019高考数学练习题--平面向量-45页word资料
2019年高考数学------平面向量一、选择题1 .(2019辽宁文)已知向量a = (1,—1),b = (2,x).若a ·b = 1,则x =( )A .—1B .—12C .12D .12 .(2019辽宁理)已知两个非零向量a ,b 满足|a +b |=|a -b |,则下面结论正确的是 ( )A .a ∥bB .a ⊥bC .{0,1,3}D .a +b =a -b3 .(2019天津文)在ABC ∆中,90A ∠=︒,1AB =,设点,P Q 满足,(1),A P A B A Q A C R λλλ==-∈.若2BQ CP ⋅=-,则λ=A .13B .23C .43D .24 .(2019重庆文)设x R ∈ ,向量(,1),(1,2),a x b ==-且a b ⊥ ,则||a b += ( )A B C .D .105 .(2019重庆理)设,x y ∈R,向量()()()4,2,,1,1,-===y x ,且//,⊥,则_______=( )A B C .D .106 .(2019浙江文)设a,b 是两个非零向量. ( )A .若|a+b|=|a|-|b|,则a ⊥bB .若a ⊥b,则|a+b|=|a|-|b|C .若|a+b|=|a|-|b|,则存在实数λ,使得b=λaD .若存在实数λ,使得b=λa,则|a+b|=|a|-|b|7 .(2019浙江理)设a ,b 是两个非零向量.( )A .若|a +b |=|a |-|b |,则a ⊥bB .若a ⊥b ,则|a +b |=|a |-|b |C .若|a +b |=|a |-|b |,则存在实数λ,使得a =λbD .若存在实数λ,使得a =λb ,则|a +b |=|a |-|b |8 .(2019天津理)已知△ABC 为等边三角形,=2AB ,设点P,Q 满足=A P A Bλ,=(1)AQ AC λ-,R λ∈,若3=2BQ CP ⋅-,则=λ ( )A .12B .12C .12D .32-±9 .(2019广东文)(向量、创新)对任意两个非零的平面向量α和β,定义⋅⋅=⋅αβαβββ,若平面向量a 、b 满足0≥>a b ,a 与b 的夹角0,4πθ⎛⎫∈ ⎪⎝⎭,且a b 和b a 都在集合2n n Z ⎧⎫∈⎨⎬⎩⎭中,则=a b ( )A .12 B .1C .32D .5210 .(2019广东文)(向量)若向量()1,2AB =,()3,4BC =,则AC =( )A .()4,6B .()4,6--C .()2,2--D .()2,211 .(2019福建文)已知向量(1,2),(2,1)a x b =-=,则a b ⊥的充要条件是( )A .12x =-B .1x =-C .5x =D .0x =12.(2019大纲文)ABC ∆中,AB 边的高为CD ,若CB a =,CA b =,0a b ⋅=,||1a =,||2b =,则AD =( )A .1133a b -B .2233a b - C .3355a b - D .4455a b -13 .(2019湖南理)在△ABC 中,AB=2,AC=3,AB BC = 1则___BC =.( )A B C . D 14 .(2019广东理)对任意两个非零的平面向量α和β,定义⋅⋅=⋅αβαβββ,若平面向量a 、b 满足0≥>a b ,a 与b 的夹角0,4πθ⎛⎫∈ ⎪⎝⎭,且a b 和b a 都在集合2n n Z ⎧⎫∈⎨⎬⎩⎭中,则=a b( )A .12B .1C .32D .5215 .(2019广东理)(向量)若向量()2,3BA =,()4,7CA =,则BC =( )A .()2,4--B .()2,4C .()6,10D .()6,10--16 .(2019大纲理)ABC ∆中,AB 边上的高为CD ,若,,0,||1,||2CB a CA b a b a b ==⋅===,则AD = ( )A .1133a b -B .2233a b - C .3355a b - D .4455a b -17.(2019安徽理)在平面直角坐标系中,(0,0),(6,8)O P ,将向量OP 按逆时针旋转34π后,得向量OQ 则点Q 的坐标是 ( )A .(-B .(-C .(2)--D .(2)-二、填空题10.(2019浙江文)在△ABC 中,M 是BC 的中点,AM=3,BC=10,则AB AC ⋅=________.11.(2019上海文)在知形ABCD 中,边AB 、AD 的长分别为2、1. 若M 、N 分别是边BC 、CD 上的点,||||CD CN BC BM =,则AN AM ⋅的取值范围是_________ .12.(2019课标文)已知向量a ,b 夹角为045,且|a |=1,|2-a b 则|b |=_______. 13.(2019江西文)设单位向量(,),(2m x y b ==-。
12-20全国卷高考真题分类汇编(文科)平面向量专项练习(解析)
12-20全国卷高考真题分类汇编(文科)平面向量专项练习(解析)1.(2020年高考数学课标Ⅲ卷文科)在平面内,A .B 是两个定点,C 是动点,若=1AC BC ⋅,则点C 的轨迹为 ( ) A .圆 B .椭圆C .抛物线D .直线【答案】A【解析】设()20AB a a =>,以AB 中点为坐标原点建立如图所示的平面直角坐标系,则:()(),0,,0A a B a -,设(),C x y ,可得:()(),,,AC x a y BC x a y →→=+=-, 从而:()()2AC BC x a x a y →→⋅=+-+,结合题意可得:()()21x a x a y +-+=,整理可得:2221x y a +=+,即点C 的轨迹是以AB 故选:A .【点睛】本题主要考查平面向量及其数量积的坐标运算,轨迹方程的求解等知识,意在考查学生的转化能力和计算求解能力.2.(2019年高考数学课标Ⅱ卷文科)已知向量()()2,3,3,2a b ==,则a b -= ( )A B .2C .D .50【答案】【答案】A【解析】由已知,(2,3)(3,2)(1,1)a b -=-=-,所以||(1)a b -=-= A【点评】本题主要考查平面向量模长的计算,容易题,注重了基础知识、基本计算能力的考查.3.(2019年高考数学课标Ⅰ卷文科)已知非零向量a ,b 满足||2||a b =,且()a b b -⊥,则a 与b 的夹角为() ( )A .6π B .3π C .23π D .56π【答案】【答案】B【解析】 ||2||b a =,且b b a ⊥-)(,∴0)(=⋅-b b a ,有0||2=-⋅b b a ,设a 与b 的夹角为θ,则有0||cos ||||2=-⋅b b aθ,即0||cos ||222=-b b θ,0)1cos 2(||2=-θb , 0||≠b ,∴21cos =θ,3πθ=,故a 与b的夹角为3π.4.(2019年高考数学课标Ⅰ卷文科)古希腊时期,人们认为最美人体的头顶至肚脐的长0.618≈,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之105cm ,头顶至脖子下端的长度为26cm ,则其身高可能是()( )A .165cmB .175cmC .185cmD .190cm【答案】【答案】B 【解析】 方法一:设头顶处为点A ,咽喉处为点B ,脖子下端处为点C ,肚脐处为点D ,腿根处为点E ,足底处为F ,t BD =,λ=-215,根据题意可知λ=BD AB ,故t AB λ=;又t BD AB AD )1(+=+=λ,λ=DFAD,故t DF λλ1+=;所以身高t DF AD h λλ2)1(+=+=,将618.0215≈-=λ代入可得t h 24.4≈.根据腿长为cm 105,头顶至脖子下端的长度为cm 26可得AC AB <,EF DF >;即26<t λ,1051>+t λλ,将618.0215≈-=λ代入可得4240<<t ,所以08.1786.169<<h . 方法二:由于头顶至咽喉的长度与头顶至脖子下端的长度极为接近,故头顶至脖子下端的长度cm 26可估值为头顶至咽喉的长度;根据人体的头顶至咽喉的长度与咽喉至肚脐的长度之比是215-(618.0215≈-称为黄金分割比例)可计算出咽喉至肚脐的长度约为cm 42;将人体的头顶至咽喉的长度与咽喉至肚脐的长度相加可得头顶至肚脐的长度为cm 68,头顶至肚脐的长度与肚脐至足底的长度之比是215-可计算出肚脐至足底的长度约为110;将头顶至肚脐的长度与肚脐至足底的长度相加即可得到身高约为cm 178,与答案cm 175更为接近.5.(2018年高考数学课标Ⅱ卷文科)已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b( )A .4B .3C .2D .0【答案】B解析:向量,a b 满足1,1a a b =⋅=-,则2(22213a a b a a b ⋅-=-⋅=+=),故选B . 6.(2018年高考数学课标Ⅰ卷文科)在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB =( )A .3144AB AC - B .1344AB AC -C .3144AB AC +D .1344AB AC +【答案】A解析:如图所示EB ED DB =+,11()24ED AD AC AB ==+,11()22DB CB AB AC ==-,111131442244EB AC AB AB AC AB AC ∴=++-=-.7.(2017年高考数学课标Ⅱ卷文科)设非零向量满足则 ( )A .B .C .D .ABCDE,a b a b a b +=- a b ⊥a b = a b //a b >【答案】 A【解析】方法一:本题考查平面向量的运算.由题意得.,所以:,即.故选A .方法二:由平面向量加减法的几何意义知:分别是以和为邻边所作平行四边形的两对角线,,所以该平行四边形为矩形,邻边垂直,即.【考点】向量的数量积【点评】应用平面几何性质以及向量的平行四边形法则可得:非零向量.8.(2016年高考数学课标Ⅲ卷文科)已知向量1=2BA ⎛ ⎝⎭,31=2BC ⎛⎫ ⎪ ⎪⎝⎭,则ABC ∠= ( ) A .30︒ B .45︒ C .60︒ D .120︒【答案】A 【解析】由题意,易知1122BA BC ⋅==, 112BA ⎛== ,1BA ⎛== ∴32cos 112BA BC ABC BA BC ⋅∠===⨯,所以30ABC ∠=︒,故选A .9.(2015年高考数学课标Ⅱ卷文科)已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a ( ) A .1- B .0 C .1 D .2 【答案】C分析:由题意可得2112=+=a ,123,⋅=--=-a b 所以()222431+⋅=+⋅=-=a b a a a b .故选C .考点:本题主要考查向量数量积的坐标运算. 10.(2015年高考数学课标Ⅰ卷文科)已知点(0,1),(3,2)A B ,向量(4,3)AC =--,则向量BC =( )A .(7,4)--B .(7,4)C .(1,4)-D .(1,4)【答案】A分析:∵=(3,1),∴=(-7,-4),故选A . 考点:向量运算11.(2014年高考数学课标Ⅱ卷文科)设向量a ,b 满足||=10a b +,||=6a b -,则a b ⋅=( )()()22a b a b a ba b +=-⇒+=-222222a b a b a b a b ++⋅=+-⋅0a b ⋅=a b ⊥,a b a b +-a b a b a b +=-a b ⊥,a b a b a b +=-a b ⇔⊥AB OB OA =-BC =AC AB -A.1B.2C.3D.5 【答案】A解析:∵||10||=6a b a b ⎧+=⎪⎨-⎪⎩,∴2222210 12= 6 2a b a b a b a b ⎧++⋅=⎪⎨+-⋅⎪⎩◯◯.∴①﹣②:1a b ⋅=.∴选A .考点:(1)向量的模的公式的应用;(2)向量的数量积运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
培优点八 平面向量1.代数法例1:已知向量a ,b 满足=3a,b ()⊥+a a b ,则b 在a 方向上的投影为( ) A .3 B .3-C.D【答案】C【解析】考虑b 在a 上的投影为⋅a bb,所以只需求出a ,b 即可. 由()⊥+a a b 可得:()20⋅+=+⋅=a a b a a b ,所以9⋅=-a b.进而⋅==a b b ,故选C .2.几何法例2:设a ,b 是两个非零向量,且2==+=a b a b ,则=-a b _______.【答案】【解析】可知a ,b ,+a b 为平行四边形的一组邻边和一条对角线, 由2==+=a b a b 可知满足条件的只能是底角为60o ,边长2a =的菱形,=.3.建立直角坐标系例3:在边长为1的正三角形ABC 中,设2BC BD =uu u v uu u v ,3CA CE =uu v uu u v ,则AD BE ⋅=u u u v u u u v__________.【答案】14AD BE ⋅=-uuu v uu u v【解析】上周是用合适的基底表示所求向量,从而解决问题,本周仍以此题为例,从另一个角度解题,观察到本题图形为等边三角形,所以考虑利用建系解决数量积问题,如图建系:A ⎛ ⎝⎭,1,02B ⎛⎫- ⎪⎝⎭,1,02C ⎛⎫ ⎪⎝⎭,下面求E 坐标:令(),E x y ,∴1,2CE x y ⎛⎫=- ⎪⎝⎭uu u v,12CA ⎛=- ⎝⎭uu v , 由3CA CE =uu v uu u v可得:11132233x x y y ⎧⎛⎫⎧-=-= ⎪⎪⎪⎪⎪⎝⎭⇒⎨⎨⎪⎪==⎪⎪⎩⎩13E ⎛ ⎝⎭,∴0,AD ⎛= ⎝⎭uuu v,56BE ⎛= ⎝⎭uu u v ,∴14AD BE ⋅=-uuu v uu u v .一、单选题1.已知向量a ,b 满足1=a ,2=b ,且向量a ,b 的夹角为4π,若λ-a b 与b 垂直,则实数λ的值为( ) A .12-B .12C. D【答案】D【解析】因为12cos4π⨯⨯=⋅=a b ()40λλλ-⋅=⋅=⇒a b b D . 2.已知向量a ,b 满足1=a ,2=b,+=a b ⋅=a b ( )对点增分集训A .1BCD .2【答案】A【解析】由题意可得:22221427+=++⋅=++⋅=a b a b a b a b ,则1⋅=a b .故选A .3.如图,平行四边形ABCD 中,2AB =,1AD =,60A ∠=o ,点M 在AB 边上,且13AM AB =,则DM DB ⋅=uuu u v uu u v( )A .1-B .1C .D 【答案】B【解析】因为13AM AB =,所以DB AB AD =-uu u v uu u v uuu v ,13DM AM AD AB AD =-=-uuuu v uuu v uuu v uu u v uuu v ,则()22114333DB BM AB AD AB AD AB AB AD AD ⎛⎫⋅=-⋅-=-⋅+ ⎪⎝⎭uu u v uuu v uu u v uuu v uu u v uuu v uu u v uu u v uuu v uuu v14142111332=⨯-⨯⨯⨯+=.故选B . 4.如图,在ABC △中,BE 是边AC 的中线,O 是BE 边的中点,若AB =uu u v a ,AC =u u u v b ,则AO =u u u v( )A .1122+a bB .1124+a bC .1142+a bD .1144+a b【答案】B【解析】由题意,在ABC △中,BE 是边AC 的中线,所以12AE AC =uu u v uuu v,又因为O 是BE 边的中点,所以()12AO AB AE =+uuu v uu u v uu u v,所以()1111122224AO AB AE AB AE =+=+=+u u u v u u u v u u u v u u u v u u u v a b ,故选B .5.在梯形ABCD 中,AB CD ∥,1CD =,2AB BC ==,120BCD ∠=o ,动点P 和Q 分别在线段BC和CD 上,且BP BC λ=uu v uu u v ,18DQ DC λ=uuuv uuu v ,则AP BQ ⋅uu u v uu u v 的最大值为( ) A .2- B .32-C .34 D .98【答案】D【解析】因为AB CD ∥,1CD =,2AB BC ==,120BCD ∠=o , 所以ABCD 是直角梯形,且CM =30BCM ∠=︒,以AB 所在直线为x 轴,以AD 所在直线为y 轴,建立如图所示的平面直角坐标系:因为BP BC λ=uu v uu u v ,18DQ DC λ=uuu v uuu v ,动点P 和Q 分别在线段BC 和CD 上,则(]01λ∈,,()20B ,,()2P λ-,18Q λ⎛ ⎝,所以()1112254848AP BQ λλλλ⎛⋅=-⋅-=+-- ⎝uu u v uu u v , 令()115448f λλλ=+--且(]01λ∈,, 由基本不等式可知,当1λ=时可取得最大值, 则()()max 119154488f f λ==+--=.故选D . 6.已知ABC △中,2AB =,4AC =,60BAC ∠=︒,P 为线段AC 上任意一点,则PB PC ⋅uu v uu u v的范围是( ) A .[]14,B .[]04,C .944⎡⎤-⎢⎥⎣⎦, D .[]24-,【答案】C【解析】根据题意,ABC △中,2AB =,4AC =,60BAC ∠=︒,则根据余弦定理可得2416224cos6012BC =+-⨯⨯⨯︒=,即BC =ABC △为直角三角形以B 为原点,BC 为x 轴,BA 为y 轴建立坐标系,则()02A ,,()C ,则线段AC 12y+=,(0x ≤≤.设(),P x y ,则()()222443PB PC x y x y x y x ⋅=---=+-=+uu v uu u v ,,.∵0x ≤≤944PB PC -≤⋅≤uu v uu uv .故选C . 7.已知非零向量a ,b ,满足a b 且()()320+⋅-=a b a b ,则a 与b 的夹角为( ) A .4π B .2π C .34π D .π【答案】A【解析】非零向量a ,b ,满足=a b 且()()320+⋅-=a b a b ,则()()320+⋅-=a b a b , ∴22320+⋅-=a a b b ,∴223cos 20θ+⨯⨯-=a a b b ,∴2213cos 202θ⨯⨯⨯-=b b b b ,∴cos θ=,4θπ=,∴a 与b 的夹角为4π,故选A .8.在Rt ABC △中斜边BC a =,以A 为中点的线段2PQ a =,则BP CQ ⋅uuv uu u v的最大值为( )A .2-B .0C .2D .【答案】B【解析】∵在Rt ABC △中斜边BC a =,∴BA CA ⊥, ∵A 为线段PQ 中点,且2PQ a =,∴原式()22222cos a BA AQ AQ CA a AQ BA CA a AQ CB a a θ=-+⋅-⋅=-+-=-+⋅=-+u u v u u u v u u u v u u v u u u v u u v u u v u u u v u u v ,当cos 1θ=时,有最大值,0BP CQ ⋅=uu v uu u v.故选B .9.设向量a ,b ,c ,满足1==a b ,12⋅=-a b ,6,0--=oa b c c ,则c 的最大值等于( )A .1BCD .2【答案】D【解析】设OA =uu v a ,OB =uu u v b ,OC =uuu v c ,因为12⋅=-a b ,6,0--=oa b c c ,所以120AOB ∠=︒,60ACB ∠=︒,所以O ,A ,B ,C 四点共圆,因为AB =-uu u v b a ,()222223AB =-=+-⋅=uu u v b a b a a b ,所以AB =由正弦定理知22sin120ABR ==︒,即过O ,A ,B ,C 四点的圆的直径为2,所以c 的最大值等于直径2,故选D .10.已知a 与b 为单位向量,且⊥a b ,向量c 满足2--=c a b ,则c 的取值范围为( )A .1,1⎡⎣B .2⎡+⎣C .D .3⎡-+⎣【答案】B【解析】由a ,b 是单位向量,0⋅=a b ,可设()1,0=a ,()0,1=b ,(),x y =c , 由向量c 满足2--=c a b ,∴()1,12x y --=,2,即()()22141x y +-=-,其圆心()1,1C ,半径2r =,∴OC =22≤≤c B .11.平行四边形ABCD 中,AC uuu v ,BD uu u v 在AB uu u v 上投影的数量分别为3,1-,则BD uu u v 在BC uu uv 上的投影的取值范围是( ) A .()1,-+∞ B .()1,3-C .()0,+∞D .()0,3【答案】A【解析】建立如图所示的直角坐标系:设(),0B a ,则()3,C b ,()1,D a b -,则()31a a --=,解得2a =.所以()1,D b ,()3,C b .BD uu u v 在BC uu u v 上的摄影cos BM BD θθ=uu u v ,当0b →时,cos 1→-,得到:1BM →-,当b →+∞时,0θ→,BM →+∞,故选A .12.如图,在等腰直角三角形ABC 中,AB AC ==D ,E 是线段BC 上的点,且13DE BC =,则AD AE ⋅uuu v uu u v的取值范围是( )A .84,93⎡⎤⎢⎥⎣⎦B .48,33⎡⎤⎢⎥⎣⎦C .88,93⎡⎤⎢⎥⎣⎦D .4,3⎡⎫+∞⎪⎢⎣⎭【答案】A【解析】如图所示,以BC 所在直线为x 轴,以BC 的中垂线为y 轴建立平面直角坐标系,则()0,1A ,()1,0B -,()1,0C ,设(),0D x ,则2,03E x ⎛⎫+ ⎪⎝⎭,113x ⎛⎫-≤≤ ⎪⎝⎭.据此有(),1AD x =-uuu v ,2,13AE x ⎛⎫=+- ⎪⎝⎭uu u v ,则222181339AD AE x x x ⎛⎫⋅=++=++ ⎪⎝⎭uuu v uu u v .据此可知,当13x =-时,AD AE ⋅uuu v uu u v取得最小值89;当1x =-或13x =时,AD AE ⋅uuu v uu u v取得最大值43; AD AE ⋅uuu v uu u v 的取值范围是84,93⎡⎤⎢⎥⎣⎦.故选A .二、填空题13.已知向量()1,2=a ,()2,2=-b ,()1,λ=c ,若()2+∥c a b ,则λ=________. 【答案】12【解析】因为()1,2=a ,()2,2=-b ,所以()24,2+=a b , 又()1,λ=c ,且()2+∥c a b ,则42λ=,即12λ=.14.若向量a ,b 满足1=a ,=b ()⊥+a a b ,则a 与b 的夹角为__________.【答案】34π【解析】由()⊥+a a b 得,()0⋅+=a a b ,即20+⋅=a a b ,据此可得2cos ,⋅=⋅⋅=-a b a b a b a ,∴cos ,2==a b , 又a 与b 的夹角的取值范围为[]0,π,故a 与b 的夹角为34π.15.已知正方形ABCD 的边长为2,E 是CD 上的一个动点,则求AE BD ⋅uu u v uu u v的最大值为________.【答案】4【解析】设DE DC AB λλ==uuu v uuu v uu u v ,则AE AD DE AD AB λ=+=+u u u v u u u v u u u v u u u v u u u v,又BD AD AB =-uu u v uuu v uu u v ,∴()()()22144AE BD AD AB AD AB AD AB AB AD λλλλ⋅=+⋅-=-+-⋅=-uu u v uu u v uuu v uu u v uuu v uu u v uuu v uu u v uu u v uuu v,∵01λ≤<,∴当0λ=时,AE BD ⋅uu u v uu u v取得最大值4,故答案为4.16.在ABC △中,90C ∠=︒,30B ∠=︒,2AC =,P 为线段AB 上一点,则PB PC +uu v uu u v的取值范围为____.【答案】【解析】以C 为坐标原点,CB ,CA 所在直线为x ,y 轴建立直角坐标系,可得()0,0C ,()0,2A ,()B ,则直线AB 12y+=,设(),P x y ,则2y =,0x ≤≤(),PB x y =-uu v ,(),PC x y =--uu u v ,则|()()22222PB PC x y +=+uu v uu u v2222441244212x y x ⎛=+-+=+-+ ⎝22161628333x x ⎛=-+=+ ⎝⎭,由x ⎡=⎣,可得PB PC +uuv uuu v 的最小值为 ,时,则PB PC +uuv uuu v的最大值为即PB PC +uu v uu u v的取值范围为.故答案为.。
