八上平面几何难题集锦
平面几何经典难题与解答
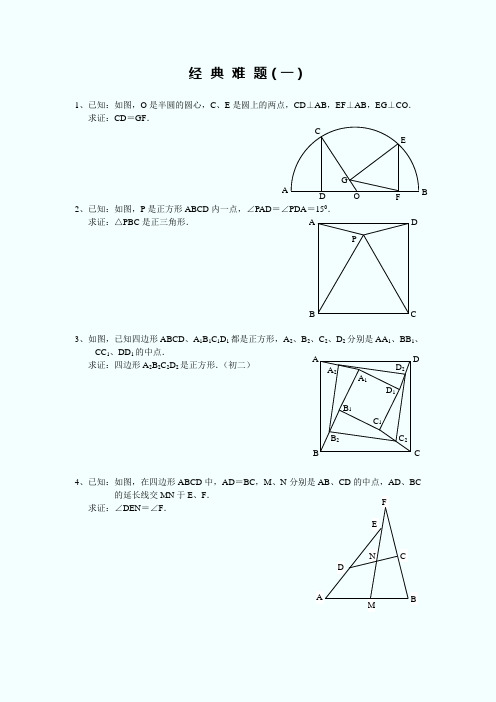
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBP CG FB QA D E1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F F EP C B A O D BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB C B DAF PD E C B A1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB A A CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
八年级上册数学几何难题突破

18.等腰三角形一腰上的高与另一腰的夹角为20°,则该等腰三角形的底角的度为 . 19.如图,已知∠AOB=60°,点P 在边OA 上,OP=12,点M ,N 在边OB 上,PM=PN ,若MN=2,则OM= .%20.如图,在等边△ABC 中,D 为AB 上一点,连接CD ,在CD 上取一点E,∠BEC=120°,连接BE,若CD=314,BE=2,△ACD 的面积为3314, 则△BCE 的面积为 .,24.已知:如图,△ABC 中,AD 平分∠BAC ,BD ⊥AD ,垂足为D , 过D 作DE ∥AC ,交AB 于E , (1) 求证:AE=ED (2) 】(3)若AB=5,求线段DE 的长.·ED CBA (第19题图)(第20题图)P NM O"25.已知:如图, △ABC 中,AB=AC, ∠BAC=90°,AD ⊥BC,AE 平分∠BAD 交BC 于点E, (1) 【(2)求证:AB=CE(3) 点M 在AB 上,BM=2DE ,连接MC 交AD 于点N ,若DN=1,求AB 的长;,27.已知:在平面直角坐标系中,点O 为坐标原点, △ABC 的顶点A(-2,0),点B 、C 分别在 x 轴正半轴上和y 轴正半轴上,∠ACB=90°,∠BAC=60°, (1)求点B 的坐标(2)动点E 从点B 出发以每秒1个单位的速度沿BC 向终点C 运动,设点E 的运动时间为t 秒,△ABE 的面积为S ,求S 与t 的关系式~(3)在(2)的条件下,点E 出发的同时,动点F 从点C 出发以每秒1个单位的速度,沿CO 向终点O 运动,点F 停止时,点E 也随之停止。
连接EF ,以EF 为边在EF 的上方作等边△EFH ,连接CH ,当点C (0,23),CH=3时,求t 的值E DB EDB|~、10. 如图,△ABC ,分别以AB 、AC 为边作等边三角形ABD 与等边三角形ACE ,连接BE 、CD ,BE 的延长线与CD 交于点F , 连接AF ,有以下四个结论:①BE =CD ;②FA 平分∠EFC ; ③FE =FD ;④FE +FC =FA.其中一定正确的结论有( )&17. △ABC 中,DF 是AB 的垂直平分线,交BC 于D ,EG 是AC 的垂直平分线,交BC 于E ,若∠DAE=20°,则∠BAC 等于________°.19. 如图,等边△ABC 中,E 在BA 延长线上,D 在BC 上,F 是DE 与AC 的交点.若AB =4, AE =2,且ED =EC ,则AF =________. —20. 已知Rt △ABC 中,AB =AC ,D 为AB 中点,BE ⊥CD 于E ,BE =2,CD =5 则DE =________.|"19题 20题25.如图,已知△ABC 和△DEF 均为等边三角形,且,AD =2CD ,EF 的延长线交CA 的延长线于点M. 求证:EF =FM.|#。
八年级上册数学几何难题突破

八年级上册数学几何难题突破-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN18.等腰三角形一腰上的高与另一腰的夹角为20°,则该等腰三角形的底角的度为 .19.如图,已知∠AOB=60°,点P 在边OA 上,OP=12,点M ,N 在边OB 上,PM=PN ,若MN=2,则OM= .20.如图,在等边△ABC 中,D 为AB 上一点,连接CD ,在CD 上取一点E,∠BEC=120°,连接BE,若CD=314,BE=2,△ACD 的面积为3314, 则△BCE 的面积为 .24.已知:如图,△ABC 中,AD 平分∠BAC ,BD⊥AD ,垂足为D , 过D 作DE∥AC ,交AB 于E , (1) 求证:AE=ED(2) 若AB=5,求线段DE 的长.ED CBA(第19题(第20题图)PNM O25.已知:如图, △ABC 中,AB=AC, ∠BAC=90°,AD ⊥BC,AE 平分∠BAD 交BC 于点E, (1) 求证:AB=CE(2) 点M 在AB 上,BM=2DE ,连接MC 交AD 于点N ,若DN=1,求AB 的长27.已知:在平面直角坐标系中,点O 为坐标原点, △ABC 的顶点A(-2,0),点B 、C 分别在x 轴正半轴上和y 轴正半轴上,∠ACB=90°,∠BAC=60°, (1)求点B 的坐标(2)动点E 从点B 出发以每秒1个单位的速度沿BC 向终点C 运动,设点E 的运动时间为t 秒,△ABE 的面积为S ,求S 与t 的关系式(3)在(2)的条件下,点E 出发的同时,动点F 从点C 出发以每秒1个单位的速度,沿CO 向终点O 运动,点F 停止时,点E 也随之停止。
连接EF ,EFH 3E DB EDB与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①BE=CD;②FA平分∠EFC;③FE=FD;④FE+FC=FA.其中一定正确的结论有( )A.1B.2C.3D.417. △ABC中,DF是AB的垂直平分线,交BC于D,EG是AC的垂直平分线,交BC于E,若∠DAE=20°,则∠BAC等于________°.19. 如图,等边△ABC中,E在BA延长线上,D在BC上,F是DE与AC的交点.若AB=4,AE=2,且ED=EC,则AF=________.20. 已知Rt△ABC中,AB=AC,D为AB中点,BE⊥CD于E,BE=2,CD=5 则DE=________.19题 20题25.如图,已知△ABC 和△DEF 均为等边三角形,且,AD =2CD ,EF 的延长线交CA 的延长线于点M. 求证:EF =FM.25.已知Rt △ABC 中,∠BAC =90°,∠B =30°,AD ⊥BC , ⑴ 如图1,求证:BC =4CD ;⑵ 如图2,延长CA 至E ,EA =CA ,连接ED ,CM 是△ABC 外角的角平分线,作∠EDF =60°,交CM 于F ,交AC 于H ,若DE =4,求DH 的长.图1 图28.如图,已知∠AOB=60°,点P在边OA上,OP=16,点M,N在边OB上,PM=PN,若MN=4,则OM=()A.3 B.4 C.5 D.69.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是()A.75°B.70°C.65°D.60°10.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有()A.①③④⑤B.①②④⑤C.①②③⑤D.①②③④17.如图,在凸四边形ABCD中,连接BD,已知AB=BC=BD,∠ABC=80°,则∠ADC=18.如图,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DE的度数为19.等腰△ABC被一腰上的中线分成两个三角形周长之差为2,若等腰△ABC 的底边长为6,则等腰△ABC的腰长为20.如图,在直角三角形ABC中∠BAC=90°,AB=3,M为BC上一点,连接AM.如果将三角形ABM沿直线AM翻折后,点B恰好与边AC的中点D重合,那么点M到直线AC的距离为1720 23.(7分)如图,在△ABC中,∠B=60°,延长BC到D,延长BA到E,使AE=BD,连接CE、DE,使EC=DE,求证:△ABC是等边三角形.25. 如图,已知,△ABC和△ADE均为等边三角形,BD、CE交于点F.(1)求证:BD=CE;(2)求锐角∠BFC的度数.27.在平面直角坐标系中,如图所示,△AOB是边长为2的等边三角形,将△AOB绕着点B按顺时针方向旋转得到△DCB,使得点D落在x轴的正半轴上,连接OC,AD.(1)求证:OC=AD;(2)若A到OB的距离为3,求OC的长和C点坐标.28. 如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)何时△PBQ是直角三角形?(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数.。
三等分线八年级较难题

三等分线八年级较难题(最新版)目录1.三等分线的概念2.三等分线的应用3.三等分线的解题技巧正文一、三等分线的概念三等分线,又称为三分线或三等分比例线,是指在平面几何中,将一个线段分割为三等分,使得分割点距离线段两端点的距离相等的线条。
三等分线在许多几何问题中都有广泛的应用,特别是在一些难度较大的题目中,掌握三等分线的解题技巧能够帮助我们快速找到解题思路。
二、三等分线的应用在初中数学中,我们学习了许多与三等分线相关的几何题目。
例如,在解决一些涉及相似三角形、比例线段和面积比的问题时,运用三等分线的概念和性质,可以简化问题,使解题过程更加清晰明了。
此外,在一些复杂的几何图形中,通过作三等分线,我们还可以发现图形之间的内在联系,从而找到解题的突破口。
三、三等分线的解题技巧在解决与三等分线相关的问题时,我们需要掌握一些基本的解题技巧。
以下是一些常用的三等分线解题方法:1.构造三等分线:在解题过程中,我们可以通过作图的方式构造出三等分线。
这需要我们熟练掌握作图技巧,如作平行线、作角平分线、作中线等。
2.利用相似三角形:在解决一些涉及三等分线的相似三角形问题时,我们可以利用相似三角形的性质,如对应角相等、对应边成比例等,来简化问题。
3.利用比例线段:在解决一些涉及三等分线的比例线段问题时,我们可以利用比例线段的性质,如比例线段的乘积相等、比例线段的和差倍分等,来简化问题。
4.利用面积比:在解决一些涉及三等分线的面积比问题时,我们可以利用面积比的性质,如两个三角形的面积比等于它们对应边长的平方比等,来简化问题。
总之,掌握三等分线的概念、应用和解题技巧,对于解决初中数学中的较难题目具有重要意义。
人教八上数学几何习题集含答案

1、如图:在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线,DE⊥AB垂足为E,DF⊥AC,垂足为点F,且BD=CD 求证:BE=CF3、如图,点B和点C分别为∠MAN两边上的点,AB=AC。
(1)按下列语句画出图形:①AD⊥BC,垂足为D;②∠BCN的平分线CE与AD的延长线交于点E;③连结BE;(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD 外的两对全等三角形:____≌____,____≌____;(3)并选择其中的一对全等三角形予以证明。
已知:AB=AC,AD⊥BC,CE平分∠BCN,求证:△ADB≌△ADC;△BDE≌△CDE。
AB D CM NE4、如图,PB、PC分别是△ABC的外角平分线且相交于点P.求证:点P在∠A的平分线上AB CP5、如图,△ABC中,p是角平分线AD,BE的交点. 求证:点p在∠C的平分线上6、下列说法中,错误的是()A.三角形任意两个角的平分线的交点在三角形的内部B.三角形两个角的平分线的交点到三边的距离相等C.三角形两个角的平分线的交点在第三个角的平分线上D.三角形任意两个角的平分线的交点到三个顶点的距离相等7、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC8、如图,AP、CP分别是△ABC外角∠MAC与∠NCA的平分线,它们相交于点P,PD⊥BM于点D,PF⊥BN于点F.求证:BP为∠MBN的平分线。
9、如图,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.10、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;(2)线段DM与AM有怎样的位置关系?请说明理由.11、八(1)班同学上数学活动课,利用角尺平分一个角(如图所示).设计了如下方案:(Ⅰ)∠AOB 是一个任意角,将角尺的直角顶点P 介于射线OA 、OB 之间,移动角尺使角尺两边相同的刻度与M 、N 重合,即PM=PN ,过角尺顶点P 的射线OP 就是∠AOB 的平分线.(Ⅱ)∠AOB 是一个任意角,在边OA 、OB 上分别取OM=ON ,将角尺的直角顶点P 介于射线OA 、OB 之间,移动角尺使角尺两边相同的刻度与M 、N 重合,即PM=PN ,过角尺顶点P 的射线OP 就是∠AOB 的平分线.(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由;(2)在方案(Ⅰ)PM=PN 的情况下,继续移动角尺,同时使PM ⊥OA ,PN ⊥OB .此方案是否可行?请说明理由.12、如图,P 是∠BAC 内的一点,PE ⊥AB ,PF ⊥AC ,垂足分别为点E ,F ,AE=AF 。
八上几何习题集及答案

八上几何习题集1、如图:在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线,DE⊥AB垂足为E,DF⊥AC,垂足为点F,且BD=CD 求证:BE=CF3、如图,点B和点C分别为∠MAN两边上的点,AB=AC。
〔1〕按以下语句画出图形:①AD⊥BC,垂足为D;②∠BCN的平分线CE与AD的延长线交于点E;③连结BE;〔2〕在完成〔1〕后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:____≌____,____≌____;〔3〕并选择其中的一对全等三角形予以证明。
:AB=AC,AD⊥BC,CE平分∠BCN,求证:△ADB≌△ADC;△BDE≌△CDE。
AB D CM NE4、如图,PB、PC分别是△ABC的外角平分线且相交于点P.求证:点P在∠A的平分线上AB C5、如图,△ABC中,p是角平分线AD,BE的交点. 求证:点p在∠C的平分线上6、以下说法中,错误的选项是〔〕A.三角形任意两个角的平分线的交点在三角形的内部B.三角形两个角的平分线的交点到三边的间隔相等C.三角形两个角的平分线的交点在第三个角的平分线上D.三角形任意两个角的平分线的交点到三个顶点的间隔相等7、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC8、如图,AP、CP分别是△ABC外角∠MAC与∠NCA的平分线,它们相交于点P,PD⊥BM于点D,PF⊥BN于点F.求证:BP为∠MBN的平分线。
9、如图,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB 的平分线上.10、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.〔1〕假设连接AM,那么AM是否平分∠BAD?请你证明你的结论;〔2〕线段DM与AM有怎样的位置关系?请说明理由.11、八〔1〕班同学上数学活动课,利用角尺平分一个角〔如下图〕.设计了如下方案:〔Ⅰ〕∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,挪动角尺使角尺两边一样的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.〔Ⅱ〕∠AOB是一个任意角,在边OA、OB上分别取OM=ON,将角尺的直角顶点P介于射线OA、OB之间,挪动角尺使角尺两边一样的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.〔1〕方案〔Ⅰ〕、方案〔Ⅱ〕是否可行?假设可行,请证明;假设不可行,请说明理由;PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.ADEBFC求证:〔1〕PE=PF;〔2〕点P在∠BAC的角平分线上。
平面几何经典难题及解答

1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A PC D B A F G C EBO D D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC=200,求∠BED 的度数.经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答
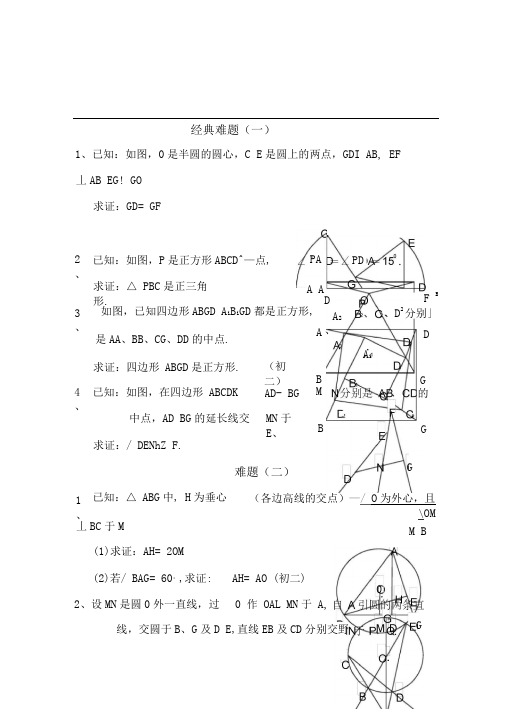
经典难题(一)1、已知:如图,0是半圆的圆心,C E 是圆上的两点,GDI AB, EF丄AB EG! GO 求证:GD= GF2、已知:如图,P 是正方形ABCD^—点, 求证:△ PBC 是正三角形.PA 3、 A A 如图,已知四边形ABGD A i B i GD 都是正方形, 是AA 、BB 、CG 、DD 的中点.求证:四边形 ABGD 是正方形.(初二)4、 已知:如图,在四边形 ABCDK AD- BG 1、中点,AD BG 的延长线交 求证:/ DENhZ F . 已知:△ ABG 中, H 为垂心 丄BC 于M(1)求证:AH= 2OM (2)若/ BAG= 60°,求证:MN 于 E 、难题(二)PD A A iG GB M G 的 D A 2、 B F B、D 2分别」 D (各边高线的交点)—/ O 为外心,且\OMM B0 作 OAL MN 于 A,线,交圆于B 、G 及D E ,直线EB 及CD 分别交野2、设MN 是圆0外一直线,过 AH= AO (初二)G求证:A 吐AQ (初二) 3、如果上题把直线MN 由圆外平移至圆内,贝y 由此可得以下命题: 设MN 是圆0的弦,过MN 的中点A 任作两弦BC DE 设CDEB 分别交MN 于P 、Q求证:AP= AQ (初二)4、如图,分别以^ ABC 的AC 和 BC 为一边,在△ ABC 的NOB1、 F .2、 ACD 审正方形CBFG 点P 是EF 的中点.求证:求证: 点P 到边AB 的距离等于AB 的一半 题(三)经典难四边形ABCD^正方形,CE= CF.(初二)四边形ABC 助正方形,延长线于F . 求证:AE= AF.(初二)-FDE// AC AE = A (A AE 与 CD 相交于(初二)ADE// AC 且 CE= CAK 直线IE3、设P 是正方形ABCD-边BC 上的任CPF 丄求证:PA=PF.(初二)C4、如图,PC 切圆0于C, AC 为圆的直径,PEF 为圆的割线,A E A^F E与直线P0相交于B 、D.求证:AB= DC BC= AD经典难题(四)1、已知:△ ABC 是正三角形,P 是三角形内一点;BC=5.1的正△ ABC 内任一点,L = PA^ PB+PC 求证:< Lv 2.求:/APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且/ PBA=Z PD求证:/ PAB=Z PCB (初二)3、设ABCD 为圆内接凸四边形,求证:AB- CD^ ADi^BC^AB三)4、平行四边形ABC 冲,设E 、F 分别是BC相交于P,且BBCAB 上的一点,AEAE= CF.求证: / DPA=/DPC (初二)经典难题(五)D1、设P 是边长为2、已知:P 是边长为1的正方形 ABCC 内的一点,求 PA ^PB+PC 的最小值.2. 如下图做^ DGC 使与^ ADP 全等,可得△ PDG 为等边△,从而可得△APD^^CGP 得出 PC 二AD 二DC,/ DCG / PCG= 15°所以/ DCP=30,从而得出△ PBC 是正三角形3.如下图连接BC 和AB 分别找其中点F,E.连接QF 与AE 并延长相交于Q 点, 连接EB 并延长交QQ 于H 点,连接FB 并延长交AQ 于G 点,由 A 2E¥AD¥BC I = FB 2 , EB¥AB=2BC二C l,又/ GFQ:+ Q=9(C 和/ GE B 2+Z Q=9(3,所以/ GE52=Z GFC 又/ BFG 二/AEB , 可得△ BFCAEB ,所以 AB 二BG , 又/ GFQ £ H^F=9C 0和/ GFQh EBA , 从而可得/ AB C 2=9C C,同理可得其他边垂直且相等, 从而得出四边形 ABGD 是正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级平面几何难题集锦1.如图,已知等边△ABC ,P 在AC 延长线上一点,以PA 为边作等边△APE,EC 延长线交BP 于M ,连接AM,求证:(1)BP=CE ; (2)试证明:EM-PM=AM.2.点C 为线段AB 上一点,△ACM, △CBN 都是等边三角形,线段AN,MC 交于点E ,BM,CN 交于点F 。
求证:(1)AN=MB.(2)将△ACM 绕点C 按逆时针方向旋转一定角度,如图②所示,其他条件不变,(1)中的结论是否依然成立? (3)AN 与BM 相交所夹锐角是否发生变化。
3.已知,如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AN AM =;(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立.BE A B AB 图①E 图②4.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作正三角形ABC 和正三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下五个结论:① AD=BE ; ② PQ ∥AE ; ③ AP=BQ ;④ DE=DP ; ⑤ ∠AOB=60° ⑥CP=CQ ⑦△CPQ 为等边三角形.⑧共有2对全等三角形 ⑨CO 平分∠AOP ⑩CO 平分∠BCD 恒成立的结论有______________(把你认为正确的序号都填上).5.已知:如图,ABC △是等边三角形,过AB 边上的点D 作DG BC ∥,交AC 于点G ,在GD 的延长线上取点E ,使DE DB =,连接AE CD ,.(1)求证:AGE DAC △≌△;(2)过点E 作EF DC ∥,交BC 于点F ,请你连接AF ,并判断AEF △是怎样的三角形,试证明你的结论.6.如图,以ABC △的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连结EG ,试判断ABC △与AEG △面积之间的关系,并说明理由.7.在ABC △中,2120A B B C A B C ==∠=,°,将ABC △绕点B 顺时针旋转角α(0<°α90)<°得A BC A B 111△,交AC 于点E ,11AC 分别交AC BC 、于D F 、两点.如图1,观察并猜想,在旋转过程中,线段1EA 与FC 有怎样的数量关系?并证明你的结论;ADBECF 1A1CADBECF 1A1CFABC E DO P QCGAE DB F8.如图所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .9.如图1,四边形ABCD 是正方形,M 是AB 延长线上一点。
直角三角尺的一条直角边 经过点D ,且直角顶点E 在AB 边上滑动(点E 不与点A ,B 重合),另一条直角边与∠CBM 的平分线BF 相交于点F.⑴ 如图14―1,当点E 在AB 边的中点位置时:① 通过测量DE ,EF 的长度,猜想DE 与EF 满足的数量关系是 ; ② 连接点E 与AD 边的中点N ,猜想NE 与BF 满足的数量关系是 ; ③ 请证明你的上述两猜想.⑵ 如图14―2,当点E 在AB 边上的任意位置时,请你在AD 边上找到一点N, 使得NE=BF ,进而猜想此时DE 与EF 有怎样的数量关系并证明10.已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F . 当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S +=△△△. 当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABC S △又有怎样的数量关系?请写出你的猜想,不需证明.A BCD E FA E CB DADFCB A DB EDCBA11.已知AC//BD,∠CAB 和∠DBA 的平分线EA 、EB 与CD 相交于点E. 求证:AB=AC+BD.12.等边△ABC ,D 为△ABC 外一点,∠BDC=120°,BD=DC .∠MDN=60°射线DM 与直线AB 相交于点M ,射线DN 与直线AC 相交于点N ,①当点M 、N 在边AB 、AC 上,且DM=DN 时,直接写出BM 、NC 、MN 之间的数量关系.②当点M 、N 在边AB 、AC 上,且DM ≠DN 时,猜想①中的结论还成立吗?若成立,请证明. ③当点M 、N 在边AB 、CA 的延长线上时,请画出图形,并写出BM 、NC 、MN 之间的数量关系.13.如图1,BD 是等腰ABC Rt Δ的角平分线, 90=∠BAC .(1)求证BC =AB +AD ;(2)如图2,BD AF ⊥于F ,BD CE ⊥交延长线于E ,求证:BD =2CE ;AD FE14.已知,如图1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC 。
求证:∠BAD +∠BCD =180°。
15.如图,四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,AD+AB=2AE ,则∠B 与∠ADC 互补.为什么?16.如图4,在△ABC 中,BD=CD ,∠ABD=∠ACD,求证AD 平分∠BAC.17.如图,在△ABC 中∠ABC,∠ACB 的外角平分线交P.求证:AP 是∠BAC 的角平分线 DBEACABCDDCBA18.如图在四边形ABCD 中,AC 平分∠BAD ,∠ADC +∠ABC =180度,CE ⊥AD 于E ,猜想AD 、AE 、AB 之间的数量关系,并证明你的猜想,19.如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD,CE 相交于点O ,求证:OE=OD20.如图所示,已知在△AEC 中,∠E=90°,AD 平分∠EAC ,DF ⊥AC ,垂足为F ,DB=DC ,求证:BE=CF21.如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。
请你参考这个作全等三角形的方法,解答下列问题:(1)如图②,在△ABC 中,∠ACB 是直角,∠B =60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线,AD 、CE 相交于点F 。
请你判断并写出FE 与FD 之间的数量关系;(2)如图③,在△ABC 中,如果∠ACB 不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
O P AM NE B CDF AE F BD图①图②图③EA C图2DBAFDAC B22.已知:如图,BF ⊥AC 于点F ,CE ⊥AB 于点E ,且BD=CD ,求证:(1)△BDE ≌△CDF (2) 点D 在∠A 的平分线上23.如图在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点,求证;AB-AC >PB-PC24.已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
(!)求证:BF =AC ; (2)求证:CE =12BF ; (3)CE 与BC 的大小关系如何?试证明你的结论。
25.如图,在四边形ABCD 中,AB=BC ,BF 是∠ABC 的平分线,AF ∥DC ,连接AC 、CF ,求证:CA 是∠DCF 的平分线。
M N KE DBA M N KDCBA M KN CBA 26.数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平分线CF 于点F ,求证:AE =EF . 经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.27.△ABC 中,∠BAC=60°,∠C=40°,AP 平分∠BAC 交BC 于P ,BQ 平分∠ABC 交AC 于Q ,求证:AB+BP=BQ+AQ 。
28.问题背景,如下命题:① 如图1,在正三角形ABC 中,N 为BC 边上任一点,CM 为正三角形外角∠ACK 的平分线,若∠ANM=60°,则AN=NM② 如图2,在正方形ABCD 中,N 为BC 边上任一点,CM 为正方形外角∠DCK 的平分线,若∠ANM=90°,则AN=NM③ 如图3,在正五边形ABCDE 中,N 为BC 边上任一点,CM 为正五边形外角∠DCK 的平分线,若∠ANM=108°,则AN=NMA D FCGB图1A D F C GB 图2AD FC GB图3任务要求:⑴ 请你证明以上三个命题; ⑵ 请你继续完成下面的探索:① 如图4,在正n (n ≥3)边形ABCDEF …中,N 为BC 边上任一点,CM 为正n 边形外角∠DCK 的平分线,问当∠ANM 等于多少度时,结论AN=NM 成立(不要求证明).② 如图5,在梯形ABCD 中,AD ∥BC,AB=BC=CD,N 为BC 延长线上一点,CM 为∠DCN 的平分线,若∠ANM=∠ABC,请问AN=NM 是否还成立?若成立,请给予证明;若不成立,请说明理由.图5MNDC BA图4N FEDBA29.如图,在△ABC 中,∠A=90°,D 是AC 上的一点,BD=DC ,P 是BC 上的任一点,PE ⊥BD ,PF ⊥AC ,E 、F 为垂足.求证:PE+PF=AB .30.如图,已知△ABC 中,AB=AC=6cm ,∠B=∠C ,BC=4cm ,点D 为AB 的中点.(1)如果点P 在线段BC 上以1cm/s 的速度由点B 向点C 运动,同时,点Q 在线段CA 上由点C 向点A 运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,△BPD 与△CQP 是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点P 与点Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)31.已知:在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的左侧作等腰直角△ADE,解答下列各题:如果AB=AC,∠BAC=90°.(i)当点D在线段BC上时(与点B不重合),如图甲,线段BD,CE之间的位置关系为(ii)当点D在线段BC的延长线上时,如图乙,i)中的结论是否还成立?为什么?32.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.33.在△ABC中,AD⊥BC, BE⊥AC, D、E为垂足,AD与BE交与点H,BD=AD.求证:BH=AC BE⊥ADD CB AE H34.如图14-1,在△ABC 中,BC 边在直线l 上,AC ⊥BC ,且AC = BC .△EFP 的边FP 也在直线l 上,边EF 与边AC 重合,且EF =FP .(1)在图14-1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的数量关系和位置关系;(2)将△EFP 沿直线l 向左平移到图14-2的位置时,EP 交AC 于点Q ,连结AP ,BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;(3)将△EFP 沿直线l 向左平移到图14-3的位置时,EP 的延长线交AC 的延长线于点Q ,连结AP ,BQ .你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.35.如图1,在正方形ABCD 中,点E 、F 分别为边BC 、CD 的中点,AF 、DE 相交于点G ,则可得结论:①AF=DE ;②AF ⊥DE.(不需要证明)(1)如图2,若点E 、F 不是正方形ABCD 的边BC 、CD 的中点,但满足CE=DF.则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)(2)如图3,若点E 、F 分别在正方形ABCD 的边CB 的延长线和DC 的延长线上,且CE=DF ,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.图14-1 (E ) (F )B C P A l l P C F 图14-2l图14-336.如图1,A、E、F、C在同一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试说明BD平分EF;若将△DEC的边EC沿AC方向移动变为图2时,其余条件不变,BD是否还平分EF,请说明理由。
