直线与方程PPT演示文稿
合集下载
高中数学《第三章直线与方程3.3直线的交点坐标与距离公式3.3.4两条平行直线间的距离》310PPT课件

③当P点在直线l上时,有Ax0+By0+C=0, d=|Ax0+A2B+y0B+2 C|=0,适合公式.
两条平行直线间的距离
已知两条平行直线 l1:Ax+By+C1=0,l2:Ax+By
|C1-C2| +C2=0(C1≠C2),则 l1 与 l2 之间的距离为 d A2+B2
=
.
3.l1与l2之间的距离公式是如何推导的? 提示:在直线l1上任取一点P(x0,y0),则Ax0+By0=- C1.点P到直线l2的距离为d=|Ax0+AB2+y0B+2C2|= |CA1-2+CB2|2.
6--3
故所求的直线方程分别为 y-2=-3(x-6)和 y+1=- 3(x+3),即 3x+y-20=0 和 3x+y+10=0.
【解后反思】 通过数形结合思想和函数思想与方法, 根据题中的已知点不动,而两条平行直线可以绕点转动,我 们很容易直观感受到两条平行直线间距离的变化情况,从而 求出两条平行直线间的距离的范围.
4
2 .
1.点到直线的距离的几种特殊情况 (1)点 P(x0,y0)到 x 轴的距离 d=|y0|; (2)点 P(x0,y0)到 y 轴的距离 d=|x0|; (3)点 P(x0,y0)到与 x 轴平行的直线 y=a(a≠0)的距离 d =|y0-a|; (4)点 P(x0,y0)到与 y 轴平行的直线 x=a(a≠0)的距离 d =|x0-a|.
【解】 方法1:设所求直线的方程为5x-12y+C=0. 在直线5x-12y+6=0上取一点P0(0,12), 点P0到直线5x-12y+C=0的距离为 d=|-512+2×-12+12C2|=|C1-3 6|. 由题意,得|C1-3 6|=2. ∴C=32或C=-20. ∴所求直线的方程为5x-12y+32=0或5x-12y-20=0.
两条平行直线间的距离
已知两条平行直线 l1:Ax+By+C1=0,l2:Ax+By
|C1-C2| +C2=0(C1≠C2),则 l1 与 l2 之间的距离为 d A2+B2
=
.
3.l1与l2之间的距离公式是如何推导的? 提示:在直线l1上任取一点P(x0,y0),则Ax0+By0=- C1.点P到直线l2的距离为d=|Ax0+AB2+y0B+2C2|= |CA1-2+CB2|2.
6--3
故所求的直线方程分别为 y-2=-3(x-6)和 y+1=- 3(x+3),即 3x+y-20=0 和 3x+y+10=0.
【解后反思】 通过数形结合思想和函数思想与方法, 根据题中的已知点不动,而两条平行直线可以绕点转动,我 们很容易直观感受到两条平行直线间距离的变化情况,从而 求出两条平行直线间的距离的范围.
4
2 .
1.点到直线的距离的几种特殊情况 (1)点 P(x0,y0)到 x 轴的距离 d=|y0|; (2)点 P(x0,y0)到 y 轴的距离 d=|x0|; (3)点 P(x0,y0)到与 x 轴平行的直线 y=a(a≠0)的距离 d =|y0-a|; (4)点 P(x0,y0)到与 y 轴平行的直线 x=a(a≠0)的距离 d =|x0-a|.
【解】 方法1:设所求直线的方程为5x-12y+C=0. 在直线5x-12y+6=0上取一点P0(0,12), 点P0到直线5x-12y+C=0的距离为 d=|-512+2×-12+12C2|=|C1-3 6|. 由题意,得|C1-3 6|=2. ∴C=32或C=-20. ∴所求直线的方程为5x-12y+32=0或5x-12y-20=0.
《直线的方程》课件

II. 直线的定义
1 直线的特点
直线是由无数个点连成的,没有曲率。
2 直线方程的作用
直线方程可以用来描述和求解直线的性质和 问题。
III. 两点式
1 两点式定义
两点式是通过直线上的两个已知点来表示直线方程。
2 两点式推导过程
我们会学习如何根据两点求解直线方程。
3 两点式的应用场景
两点式可以应用于直线的描绘和求解问题。
《直线的方程》PPT课件
欢迎来到《直线的方程》PPT课件。在本课程中,我们将深入探讨直线方程的 各种推导和应用,从两点式到截距式再到斜截式。让我们一起开始这个精彩 的数学之旅!
ห้องสมุดไป่ตู้
I. 课程介绍
背景知识
学习之前,我们需要掌握坐标系和直线的基本概 念。
本章内容
本章将重点讲解直线的定义以及两点式、截距式、 斜截式等直线方程的推导和应用。
3 斜截式的应用场景
斜截式广泛应用于线性方程和图形的分析。
VI. 综合应用
1
实例解析
我们将基于不同的已知条件,演示如何使用直线方程进行解析和推导。
2
直线方程的综合应用
我们会探讨直线方程在现实生活中的广泛应用,如工程、地理和物理等领域。
VII. 总结
本章内容的回顾
我们将回顾直线方程的不同 形式,强化对各种方程的理 解。
IV. 截距式
1 截距式定义
截距式是通过直线与坐标轴的交点而表示直线方程。
2 截距式推导过程
我们将学习如何从直线的截距求解直线方程。
3 截距式的应用场景
截距式可用于直线的绘图和计算问题。
V. 斜截式
1 斜截式定义
斜截式是通过直线的斜率和截距来表示直线方程。
直线的方程ppt课件
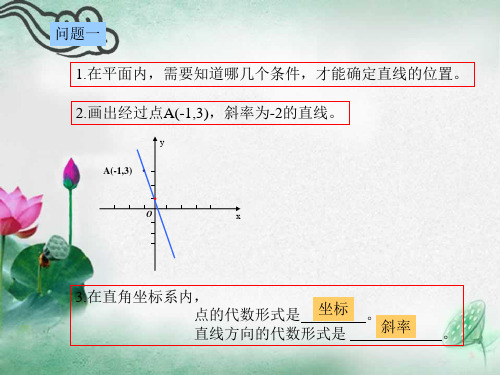
问题一
1.在平面内,需要知道哪几个条件,才能确定直线的位置。
2.画出经过点A(-1,3),斜率为-2的直线。
y
A(-1,3) .
.
O
x
3.在直角坐标系内, 点的代数形式是
坐标
。
直线方向的代数形式是 斜率 。
问题二
若直线l经过点A(-1,3),斜率为-2,点P(x,y)在直线l上运动,那么 点P的坐标x和y之间满足什么关系?
例2: 已知直线l 斜率为k,与y轴的交点是P(0,b),求直线l的方程。
解:由直线的点斜式方程,得 y b k(x 0) 即为 y kx b .
其中,b为直线与y轴交点的纵坐标。 我们称b为直线l 在y轴上的截距。
方程 y kx b 由直线l的斜率和它在y轴上的截距确定 。 所以,这个方程 y kx b 就也叫做直线的斜截式方程。
答 不能。从代数式的表达意义上讲“两点式”
方程使用的前提是x“1 x2 y且1 y2 ”。
它不能表示倾斜角90为 0和 的直线,即
当直线与x轴,y轴不平行时,可以用两点式 表示。
例1:
已知一直线经过两点 A(a, 0), B(0,b). 其中 Байду номын сангаас b 0
求这条直线的方程。
解:由直线的两点式方程,得 y0 xa b0 0a
填空
1.直线y=2x-4的斜率是 2 ,在y轴上的截距是 - 4 。
2.直线2x+y-4=0的斜率是 - 2 ,在y轴上的截距是 4 。
3.直线3x+2y=0的斜率是
3 2
,在y轴上的截距是 0
。
判断
1.直线的点斜式方程 y y1 k(x x1) 可以表示直角坐标系 中的任何一条直线。
1.在平面内,需要知道哪几个条件,才能确定直线的位置。
2.画出经过点A(-1,3),斜率为-2的直线。
y
A(-1,3) .
.
O
x
3.在直角坐标系内, 点的代数形式是
坐标
。
直线方向的代数形式是 斜率 。
问题二
若直线l经过点A(-1,3),斜率为-2,点P(x,y)在直线l上运动,那么 点P的坐标x和y之间满足什么关系?
例2: 已知直线l 斜率为k,与y轴的交点是P(0,b),求直线l的方程。
解:由直线的点斜式方程,得 y b k(x 0) 即为 y kx b .
其中,b为直线与y轴交点的纵坐标。 我们称b为直线l 在y轴上的截距。
方程 y kx b 由直线l的斜率和它在y轴上的截距确定 。 所以,这个方程 y kx b 就也叫做直线的斜截式方程。
答 不能。从代数式的表达意义上讲“两点式”
方程使用的前提是x“1 x2 y且1 y2 ”。
它不能表示倾斜角90为 0和 的直线,即
当直线与x轴,y轴不平行时,可以用两点式 表示。
例1:
已知一直线经过两点 A(a, 0), B(0,b). 其中 Байду номын сангаас b 0
求这条直线的方程。
解:由直线的两点式方程,得 y0 xa b0 0a
填空
1.直线y=2x-4的斜率是 2 ,在y轴上的截距是 - 4 。
2.直线2x+y-4=0的斜率是 - 2 ,在y轴上的截距是 4 。
3.直线3x+2y=0的斜率是
3 2
,在y轴上的截距是 0
。
判断
1.直线的点斜式方程 y y1 k(x x1) 可以表示直角坐标系 中的任何一条直线。
直线与方程ppt(20份) 人教课标版5

灵活运用此公式解决一些简单问题.
4.体会坐标法对于解平面几何问题的重要性.
www.gzjx
www.gzjx
基 础 梳 理
1.求两直线的交点坐标的方法:解方程组,以方程
坐标 的点就是交点. 组的解为______
2.两点间的距离公式:设 A(x1,y1),B(x2,y2)是平 面直角坐标系中的两个点,则|AB|=
www.gzjx
自 测 自 评
5. 以 A(5,5), B(1,4), C(4,1)为顶点的三角形是( A.直角三角形 C.等边三角形 B.等腰三角形 D.等腰直角三角形
)
解析:|AB|=|AC|= 17,|BC|= 18,故△ABC 为 等腰三角形. 答案:B
www.gzjx
www.gzjx
题型一
7
y=3.
由于反射光线为射线,
7 故反射光线的方程为 y=3x≤8.
点评: 光线的入射、 反射的问题以及在某定直线取点,
使它与两定点距离之和最小这类问题均属于点关于直线对 称的问题.
www.gzjx
(1)点 A(x0,y0)关于直线 l:Ax+By+C=0 的对 称点 M(x,y)可由方程组
∵此交点在第四象限,
www.gzjx
∴ m -2 7 <0
2m+3 >0, 7
3 ⇒- <m<2. 2
3 故所求 m 的取值范围是-2,2.
点评:求两条直线的交点坐标就是解联立两直线方程所得方程
组的解.由方程组解的个数可判定两条直线的位置关系:当方程组
仅有一组解时,两直线只有一个交点,故相交;当方程组有无数组
x+x y+y A· 2 +B· 2 +C=0
《直线的点斜式方程》人教版高中数学必修二PPT课件(第3.2.1课时)

∴k=±1
新知探究
(Ⅱ)斜截式方程
y
l
P0(0,b) x
设直线经过点P0( 0,b),其斜率为k,求直线方程. 解:代入点斜式方程,得,
y b k(x 0) y kx b
斜率
截距
说明:(1)当知道斜率和截距时用斜截式. (2)斜率k要存在,纵截距b∈R.
斜截式
新知探究
思考 1.截距b是距离吗? 不是,是数 2.截距与距离有什么区分? 截距为实数,可正,可负,可为零,而距离是大于等于零的实数. 3.b的几何意义是什么? 与y轴交点的纵坐标 4.斜截式方程和点斜式方程的联系: y=kx+b 是 y-y0=k(x-x0)的一种特殊情势
解: =450
k tan = tan 450 1
y 3 1 (x 2)
即:x y 5 0
课堂练习
变式:求经过点D(1,2),且与两坐标轴组成一个等腰直角三角形的直线方程
解:∵直线与坐标轴组成一等腰直角三角形 直线过点(1,2)代入点斜式方程得
y- 2 = x - 1 或y-2=-(x-1) 即x-y+1=0或x+y-3=0
人教版高中数学必修二
第3章 直线与方程
3.2.1直线的点斜式方程
MENTAL HEALTH COUNSELING PPT
讲授人: 时间:20XX.6.1
复习回顾
1.倾斜角 的定义及其取值范围; 0°≤α<1800
2.已知直线上两点 p1(x1, y1), p2 (x2 , y2 )(x1 x2 ) ,则直线的斜率为kk, y2 y1
(1)y 3x 2 (2)y 3x (3)x 3y 2
解:(1)k 3,b 2
(2)k 3,b 0
直线的方程ppt课件

详细描述
斜截式方程的一般形式为y=kx+b,其中k为该直线的斜率,b为截 距。
求解步骤
根据已知的斜率k和截距b,代入斜截式方程中即可求得直线方程 。
两点式方程的求解
总结词
两点式方程是直线方程的一种形式,它表示了直线上任意一点与两 个已知点之间的位置关系。
详细描述
两点式方程的一般形式为(y-y1)/(y2-y1)=(x-x1)/(x2-x1),其中(x1, y1)和(x2, y2)为直线上两个已知点。
求直线的截距
1 2
截距定义
直线的截距是指直线与x轴或y轴的交点坐标,反 映了直线在x轴或y轴上的位置。
截距计算
根据已知直线方程,可以分别计算出直线与x轴 和y轴交点的横坐标和纵坐标。
3
截距与直线斜率
截距为0表示直线与y轴平行,截距不为0表示直 线与x轴垂直。
解决相关问题
01
直线方程的应用范围广泛,包括但不限于解决几何问
05
直线方程的转化
点斜式方程与斜截式方程的转化
01
总结词:点斜式方程是直线方程的一种表示形式,它包含 了直线的斜率和通过的一个点。斜截式方程表示直线与y 轴的交点(截距)和直线的斜率。两者可以通过以下步骤 相互转化
02
给出点斜式方程 y - y1 = k(x - x1)
03
斜截式方程 y = kx + b
向量形式
向量方向
直线的方向向量可以表示为$\overrightarrow{v} = (x_2 - x_1, y_2 - y_1)$,其 中(x1, y1)和(x2, y2)为已知的直线上的两点。
向量法
直线可以表示为$\overrightarrow{P_1P_2} = \lambda\overrightarrow{v}$, 其中$\overrightarrow{P_1P_2}$是从点P1到点P2的向量,$\lambda$为比例系 数。
斜截式方程的一般形式为y=kx+b,其中k为该直线的斜率,b为截 距。
求解步骤
根据已知的斜率k和截距b,代入斜截式方程中即可求得直线方程 。
两点式方程的求解
总结词
两点式方程是直线方程的一种形式,它表示了直线上任意一点与两 个已知点之间的位置关系。
详细描述
两点式方程的一般形式为(y-y1)/(y2-y1)=(x-x1)/(x2-x1),其中(x1, y1)和(x2, y2)为直线上两个已知点。
求直线的截距
1 2
截距定义
直线的截距是指直线与x轴或y轴的交点坐标,反 映了直线在x轴或y轴上的位置。
截距计算
根据已知直线方程,可以分别计算出直线与x轴 和y轴交点的横坐标和纵坐标。
3
截距与直线斜率
截距为0表示直线与y轴平行,截距不为0表示直 线与x轴垂直。
解决相关问题
01
直线方程的应用范围广泛,包括但不限于解决几何问
05
直线方程的转化
点斜式方程与斜截式方程的转化
01
总结词:点斜式方程是直线方程的一种表示形式,它包含 了直线的斜率和通过的一个点。斜截式方程表示直线与y 轴的交点(截距)和直线的斜率。两者可以通过以下步骤 相互转化
02
给出点斜式方程 y - y1 = k(x - x1)
03
斜截式方程 y = kx + b
向量形式
向量方向
直线的方向向量可以表示为$\overrightarrow{v} = (x_2 - x_1, y_2 - y_1)$,其 中(x1, y1)和(x2, y2)为已知的直线上的两点。
向量法
直线可以表示为$\overrightarrow{P_1P_2} = \lambda\overrightarrow{v}$, 其中$\overrightarrow{P_1P_2}$是从点P1到点P2的向量,$\lambda$为比例系 数。
