第五单元 滚动检测试题
《Unit 5 What were you doing when the rainstorm came?》单元检测卷及答案(附听力材料)

《Unit 5 What were you doing when the rainstorm came?》单元检测卷I听小对话,选出与对话内容相符的图片: (5 分)A B C D E1_______ 2._______ 3._______ 4._______ 5._______II. 听下面一段对话,回答6--10题(5分)( )6. What was the weather like yesterday ?A. FineB. CloudyC. Rainy( )7. Why didn’t Tom go to school?A. His father was ill.B. His mother was ill.C. He fell off the bike and the doctor told him to stay in bed..( )8.What was Jack doing when Tom fell off his bike ?A.He was doing his homework.B. He was visiting his parents.C. He was riding around the corner of the park.( )9. What was doing when Tom’s parents got to the hospital ?A.Looking after the patientsB.Beginning patient rounds.C. Looking over Tom( )10. What did the doctor think of Tom ?A. Hurt badlyB. Nothing seriousC. Be in hospitalIII. 听下面一段文章,选择最佳答案(5分)( )11. What was Mr. Bush doing on Sunday morning ?A.Reading a newspaperB. Breaking the windowC. Doing morning exercise ( )12. Where was Mr Bush then ?A.In the kitchen.B. In the bedroomC. In the living room.( )13. Who broke the window of Mr. Bush’s ?A. Mr. Bush himselfB. Two boysC. One of the two children( )14. What was Mrs Bush doing When she heard the noise ?A.Cooking breakfast for the family.B. Talking with her husbandC. Dressing herself in the bedroom( )15. What were her parents doing when Connie went into the living room ?A. Calling up the policeB. Talking beside the windowC. Arguing with each otherIV. 听完下面的短文,完成句子。
第五单元测试卷一答案

第五单元测试卷一答案
一、选择题(每题2分,共20分)
1. A
2. C
3. B
4. D
5. A
6. B
7. D
8. C
9. A
10. B
二、填空题(每空1分,共10分)
1. 请填写正确的术语或概念。
2. 请填写相应的年份或数据。
3. 请填写适当的数学公式或计算结果。
4. 请给出相应的定义或解释。
5. 请填写正确的人名或地点。
三、简答题(每题5分,共20分)
1. 请简述______的概念及其重要性。
2. 描述______的工作原理或过程。
3. 解释______对______的影响。
4. 阐述______的主要特征或特点。
四、计算题(每题10分,共20分)
1. 根据题目所给数据,计算______的值。
2. 解决以下问题:______。
五、论述题(每题15分,共30分)
1. 论述______在______中的作用及其影响。
2. 分析______现象的原因,并提出相应的解决策略。
六、案例分析题(共20分)
1. 阅读以下案例,分析其关键问题,并提出解决方案。
请根据您具体的测试内容,将上述模板中的空白处填写上相应的信息。
如果您需要针对特定学科或主题的详细答案,请提供更多的背景信息
或具体问题。
人教版小学五年级数学下册第五单元测试卷附答案(共8套)

五年级数学下册第五单元测试卷1总分:100 班级:姓名:题号一二三四总分得分一、填空题。
(每空2分,共44分)1、等边三角形有( )条对称轴;正方形有( )条对称轴;圆有( )条对称轴。
2、钟表指针的运动是( )现象,拉抽屉的运动是( )现象。
3、看右图:如果把托盘上的南瓜取下来,指针会( )时针旋转。
如果把托盘上再放一些东西,指针会( )时针旋转。
4、右图中,从2:00到2:25,钟面上的分针( )时针旋转( )O,指向( );从2:00到6:00,钟面上的时针( )时针旋转( )O,指向( )。
5、如右图:(1)指针从“12”绕点O顺时针旋转到“1”时,转了( )O;(2)指针从“1”绕点O顺时针旋转90°到( )。
(3)指针从“1”绕点O逆时针旋转60°到( )。
6、如下图,图①绕中心点O( )时针旋转( )变换成图②;也可以用图③绕中心点O( )时针旋转( )变换成图②;还可以用图④( )时针旋转( )变换成图②。
二、我是小法官。
(10分)1、电风扇的叶片的运动是旋转现象。
( )2、如图,图形A绕点O逆时针旋转90O后,到达图形B的位置。
( )3、图形经过旋转后,位置、大小和形状都发生了变化。
( )4、由平移得到的图形一定不能由旋转得到。
( )5、简单图形经过平移、旋转或轴对称,能形成一个较复杂的图形。
( )三、我会选。
(21分)1、下面的图案( )能通过旋转得到。
A. B. C..2、右图中表示将线段AB( )。
A.以点A为定点顺时针旋转90o.B以点A为定点逆时针旋转90oC.以点B为定点逆时针旋转90o3、把下面的图A绕中心点顺时针旋转90°后再向下平移4个格得到的图形是( )。
A. BB. CC. D4、下列图案,( )不是由该图案的一部分旋转变换得到的。
A. B. C5、把一个图形绕某点逆时针旋转60°,所得的图形与原图形比较( )。
A.变大了B.变小了C.大小不变6、能通过旋转组成长方形的是( );能通过平移组成长方形的是( )。
人教版七年级数学下册第五章相交线与平行线单元检测卷(共6套)
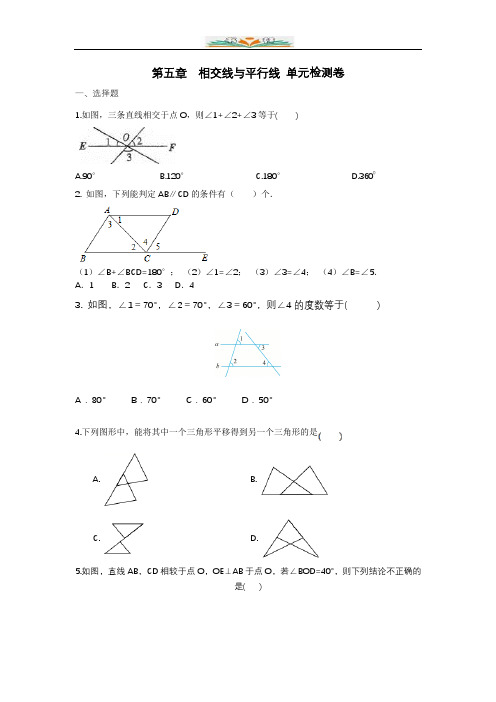
第五章相交线与平行线单元检测卷一、选择题1.如图,三条直线相交于点O,则∠1+∠2+∠3等于( )A.90°B.120°C.180°D.36002. 如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1 B.2 C.3 D.43. 如图,∠1=70°,∠2=70°,∠3=60°,则∠4的度数等于( )A.80°B.70°C.60°D.50°4.下列图形中,能将其中一个三角形平移得到另一个三角形的是A. B.C. D.5.如图,直线AB,CD相较于点O,OE⊥AB于点O,若∠BOD=40°,则下列结论不正确的是( )A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°6.如图,直线a,b被c,d所截,且a∥b,则下列结论中正确的是( )A.∠1=∠2 C.∠3+∠4=180°B.∠3=∠4 D.∠1+∠4=180°7.如图,点A在直线BG上,AD∥BC,AE平分∠GAD,若∠CBA=80°,则( )A.60°B.50°C.40°D.30°8.下列各图中,∠1与∠2互为邻补角的是( )9.对于图中标记的各角,下列条件能推理得到a∥b的是()A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=18010.下列说法正确的是( )A.一个角的补角一定比这个角大B.一个角的余角一定比这个角小C.一对对顶角的两条角平分线必在同一条直线上D.有公共顶点并且相等的两个角是对顶角二、填空题11.如图,直线AB,CD相交于点O, EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为______.12. 如图是由五个形状、大小完全相同的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有_____对平行线.13.如图,,则的度数等于14.如图,点0是直线AB上一点平分,图中与互余的角有______ .图中与互补的角有______ .15. 说明命题“x>-4,则x2>16”是假命题的一个反例可以是x=____________.16.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是三、解答题17.如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.(1)求∠BOD的度数;(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.18.已知:如图,AB∥CD,∠1=∠2,∠3=∠4.(1)求证:AD∥BE;(2)若∠B=∠3=2∠2,求∠D的度数.19.如图,D,E,F是线段AB的四等分点.(1)过点D画DH∥BC交于点H,过点E画EG∥BC交AC于点G,过点F画FM∥BC交AC 于点M;(2)量出线段AH,HG,GM,MC的长度,你有什么发现?(3)量出线段HD,EG,FM,BC的长度,你又有什么发现?20.请写出命题“两直线平行,同位角相等”的题设和结论:题设:,结论:.21.观察下图,寻找对顶角:(1)如图1,图中共有对对顶角(2)如图2,图中共有对对顶角(3)如图3,图中共有对对顶角(4)若有n条直线相交于一点,则可形成多少对对顶角?22.如图,已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC;(2)若∠AMD=75°,求∠AGC的度数.【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
高考英语一轮复习精编单元测试人教版必修五滚动卷测试 Word版含答案

阶段滚动卷(五)(建议用时: 30分钟)Ⅰ. 单项填空1. (2013·成都模拟)It was six hours the French climber Alain Robert reached the top of the world’s tallest building.A. sinceB. thatC. beforeD. when2. (2013·内江模拟)—It’s time to go now. It’s already 5 o’clock.—Dear me! I it at all.A. haven’t realizedB. didn’t realizeC. hadn’t realizedD. don’t realize3. Only you step into society can you learn practical things.A. whileB. thatC. whenD. as4. the doctor’s order that he should take a good rest, he had gone back to work.A. Contrary toB. Similar toC. In terms ofD. In addition to5. More and more high-speed railways have been built in China, it much easier for people to travel.A. to makeB. madeC. havingD. making6. —Thank you so much for changing the flat tire for me.—Don’t mention it. I only did what anyone else in my place.A. must doB. should doC. may have doneD. would have done7. When you go back home, please ring me up to let me know you safely.A. are arrivingB. had arrivedC. have arrivedD. will arrive8. Russia won the host right of the 2018 World Cup England lost it on December 2.A. beforeB. orC. whileD. e ven if9. (2013·西安模拟)More than 100 students have entered for the competition andgains the most points will be the winner.A. whatB. oneC. thatD. whoever10. (2013·青岛模拟)We’ve been looking for a cheap house but haven’t found yet.A. oneB. otherC. itD. thatⅡ. 阅读理解IMAGINE that your parents have bought you the most advancedrobot. He looks like a real person. He talks to you and plays withyou. He can even think for himself and figure out what you need.It may feel as if you have a considerate new brother who keepsyou company all the time. But come to think of it, can you reallytrust him?Ever since the first robot was created decades ago, scientists have obsessed(迷恋)over the task of making robots more like humans. However, as they have gotten closer to that goal, doubts have grown. According to the BBC, Japanese robot designer Masahiro Mori argues that the more lifelike robots become, the more humans feel a connection to them. But once they become too similar to humans, people begin to feel uncomfortable.This theory is what led to the creation of a brand new robot in Switzerland earlier this month. Roboy, as the new machine is called, has various human-like abilities such as hand-shaking and bicycle-riding, but instead of a skin-like covering, Roboy is wrapped in shiny white armor that clearly indicates its robot status.“As long as people can clearly see that the robot is a machine, even if they project their feelings into it, then they feel comfortable, ”Rolf Pfeifer, the creator of Roboy from the University of Zurich, Switzerland, told the BBC.But the problem that people have with robots is not just with the way they look.It also has to do with the roles that they play in our lives.A survey last year of European Union countries showed that 88 percent of those interviewed agreed that robots are“necessary as they can do jobs that are too hard or dangerous for people”, such as space exploration and war fighting. But when it comes to taking care of children, 60 percent of respondents said that robots should not be allowed to participate, because as robots become more sophisticated(先进的), parents may be tempted to hand over too much responsibility to them.No matter what, robots will soon enter our homes, Pfeifer said. What is not yet clear is whether they will act more like servants who work for us or companions who live with us.1. What is the purpose of the text?A. To introduce the newly-invented robot, Roboy.B. To discuss problems related to designing robots.C. To explore the roles robots will play in our future lives.D. To argue what kinds of robots appeal to people more.2. Why did Pfeifer make Roboy look like a robot?A. To better protect it.B. To make it look cool and modern.C. To distinguish it clearly from a human.D. To keep its price down.3. According to the second-to-last paragraph, most of the people interviewed .A. welcome robots into their homesB. believe robots are useful for certain dangerous tasksC. think families with children shouldn’t use robots for houseworkD. are afraid that children will become less responsible if robots take care of them4. Which best describes the author’s tone in the article?A. Objective.B. Critical.C. Admiring.D. Anxious.Ⅲ. 阅读第二节根据对话内容, 从对话后的七个选项中选出能填入空白处的最佳选项。
(高中物理)阶段滚动检测(五)

阶段滚动检测(五) 第十一、十二章 (90分钟100分) 第一卷(选择题共60分) 一、选择题(本大题共12小题,每题5分,共60分,每题只有一个答案正确) 1.(·模拟)在飞机的开展史中有一个阶段,飞机上天后不久,飞机的机翼很快就抖动起来,而且越抖越厉害,后来人们经过了艰苦的探索,利用在飞机机翼前缘处装置一个配重杆的方法解决了这一问题,在飞机机翼前装置配重杆的主要目的是( ) 2.(·怀柔模拟)一列简谐横波以10 m/s的速度沿x轴正方向传播,t=0时刻这列波的波形如下列图,那么a质点的振动图象为( ) 3.(·模拟)图甲为一列横波在t=1.0 s时的波动图象,图乙为该波中x=2 m处质点P的振动图象,以下说法正确的选项是( ) 4 m/s C.再过1.0 s,P点的动能最大 D.再过1.25 s,P点的振动路程为0.5 cm 4.消除噪声污染是当前环境保护的一个重要课题.内燃机、通风机等在排放各种高速气流的过程中都发出噪声,干预型消声器可以用来减弱高速气流产生的噪声.干预型消声器的结构及气流运行如下列图,产生波长为λ的声波沿水平管道自左向右传播.当声波到达a处时,分成两束相干波,它们分别通过r1和r2Δr= r2-r1, 那么Δr等于( ) λ的整数倍λ的奇数倍
2的奇数倍2的偶数倍
5.(·模拟)如图甲为某一波动在t=1.0 s时刻的图象,图乙为参与波动的某一质点的振动图象,那么以下说法正确的选项是( ) 8 m/s C.乙图是甲图x=1 m、2 m、3 m、4 m处四个质点中x=2 m处质点的振动图象 D.假设此波遇到另一列波并发生稳定的干预现象,那么该波所遇到的波的频率一定为1 Hz,振幅一定为0.2 m 6.(·“水面〞时,它也随你靠近而后退.对此现象正确的解释是( ) “海市蜃楼〞,是由于光的折射造成的 B.“水面〞不存在,是由于酷热难耐,人产生的幻觉 C.太阳辐射到地面,使地表温度升高,空气折射率大,发生全反射 D.太阳辐射到地面,使地表温度升高,空气折射率小,发生全反射 7.某玻璃对蓝光的折射率比对红光的折射率大,那么两种光( ) A.在该玻璃中传播时,蓝光的速度较大 B.以相同的入射角从空气斜射入该玻璃中,蓝光折射角较大 C.从该玻璃中射入空气发生全反射时,红光临界角较大 D.用同一装置进行双缝干预实验,蓝光的相邻条纹间距较大 8.(·模拟)在水下同一深度有两个不同颜色的点光源P、Q,P在水面形成的亮斑区域大于Q在水面形成的亮斑区域,以下说法正确的选项是( ) D.同一双缝干预装置,P光条纹间距小于Q光条纹间距 9.(·模拟)如下列图,a、b、c、d四个图是不同的单色光形成的双缝干预或单缝衍射图样.分析各图样的特点可以得出的正确结论是( ) A.a、b是光的干预图样 B.c、d是光的干预图样 10.(·模拟)以下说法中正确的选项是( ) B.太阳能真空玻璃管采用镀膜技术增加透射光,这是利用了光的衍射原理 D.单摆的摆球振动到平衡位置时,所受的合外力为零 11.(滚动交汇考查)如下列图,空间存在一匀强磁场,其方向为垂直于纸面向里,磁场的右边界为MN,在MN右侧有一矩形线圈abcd,ab边与MN重合.线圈在外力作用下以ab边为轴按图示方向匀速转动,规定电流从a→b→c→d→a为正方向,那么以下列图象能正确表示线圈中电流随时间变化规律的是( ) →b→c→d→a的方向为正,那么图中表示线框中感应电流i随bc边位置坐标x变化的图像正确的选项是( ) 第二卷(非选择题共40分) 二、计算题(本大题共4小题,共40分,要有必要的文字说明和解题步骤,有数值计算的要注明单位) 13.(8分)用某一单色光做双缝干预实验时,双缝间距离为0.25 mm,在距离双缝1.2 m处的光屏上,测得5条亮纹间的距离为7.5 mm,试求所用单色光的波长. 14.(10分)一棱镜的截面为直角三角形ABC,∠A=30°,斜边AB=a.棱镜材料的折射率为n=2.在此截面所在的平面内,一条光线以45°的入射角从AC边的中点M射入棱镜,求光线在棱镜上射出的点的位置(不考虑光线沿原路返回的情况). 15.(10分)(滚动交汇考查)如下列图,两根足够长固定平行金属导轨位于倾角θ=30°的斜面上,导轨上、下端各接有阻值R=20 Ω的电阻,导轨电阻忽略不计,导轨宽度L=2 m,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度B=1 T.质量m= 0.1 kg、连入电路的电阻r=10 Ω的金属棒ab在较高处由静止释放,当金属棒ab下滑高度h=3 m时,速度恰好到达最大值v=2 m10 m/s2.求: (1)金属棒ab由静止至下滑高度为3 m的运动过程中机械能的减少量. (2)金属棒ab由静止至下滑高度为3 m的运动过程中导轨上端电阻R中产生的热量. 16.(12分)(滚动交汇考查)自由电子激光器是利用高速电子束射入方向交替变化的磁场,使电子在磁场中摆动着前进,进而产生激光的一种装置.在磁场中建立与磁场方向垂直的平面直角坐标系xOy,如图甲所示.
Unit 5检测卷
Unit 5检测卷(满分:120分时间:100分钟)第I卷听力部分(20分)一、听句子,选出与所听句子内容相符的图片(每小题1分,共5分)A B CD E(1)_________(2)____________(3)____________(4)________ (5)________二、听小对话,选出正确的答语(每小题1分,共5分)6.Where was the pen made?A.Beijing. B.Qinghai. C.Shanghai.7.What is the ruler made of?A.Steel. B.Silver. C.Wood.8.What will they make for the Spring Festival?A.Sky lanterns. B.Clay art. C.Paper cutting. 9.When will the man leave for Weifang?A.Next Sunday. B.This afternoon. C.This evening.10.When was the cup made?A.In 1659. B.Five hundred years ago.C.Thousands of years ago.三、听长对话,选择正确的答案(每小题1分,共5分)听第一段对话,回答第11~12小题。
11.Who does the woman want to buy the skirt for?A.Her daughter. B.Her sister. C.Her cousin. 12.How much is the skirt?A.¥105. B.¥115. C.¥150.听第二段对话,完成13~15题。
13.How long did Jack stay in Shanghai?A.For a month. B.For two months. C.For three months. 14.Where's the tea grown?A.In Hebei. B.In Shandong. C.In Zhejiang. 15.What was made in Japan?A.The TV. B.The radio. C.The orange.四、听短文,判断句子正(T)误(F)(每小题1分,共5分)16.Christmas is one of the most important festivals of the year for the Asian countries.17.Christmas is as important as Chinese New Year to people with English backgrounds.18.December 24 is called Christmas Eve.19.Some children put stockings up for the holding of the presents. They think Santa Claus will come and give them presents.20.Christmas pudding, turkey and dumplings are usually eaten during the Christmas dinner.第II卷:笔试部分(100分)五、单项选择(每小题1分,共15分)21.Books are made ________ paper while paper is mainly made ________ wood.A.of;of B.from;fromC.of;from D.from;of22.—Our chemistry teacher, Mr.Brown, always keeps his lessons ________.—That's why he is so popular among his students.A.lively B.happily C.freely D.heavily23. —Do you know Tai'an?—Yes, it is known ________ Mount Taishan. I have been there three times.A.at B.for C.as D.of24.The novel is read ________ many people today.A.by B.with C.of D.for25. China's hot words, like tuhao, dama and lianghui, ________ in the Western media(媒体).A.use widely B.is widely usedC.uses widely D.are widely used26.How beautiful the world is! It ________ snow and everything is white.A.is covered with B.is put awayC.is turned into D.is picked up27.—Are Sichuan and Yunnan famous for tea?—I think so. ________ I know,maybe onethird of the tea in China is produced in these two provinces.A.As long as B.As far asC.As many as D.As little as28.—Could you please help me to look for my lost dog? ________ name is Gina.—Of course.A.It B.It's C.Its D.Its' 29.It ________ me about two months to learn how to drive a car.A.spent B.paid C.used D.took 30.When you do your homework, you must work carefully to avoid ______ too many mistakes.A.to make B.making C.made D.make 31. Everyone in our class ________ to take part in the English Speech Contest.A.is encouraged B.encouragesC.are encouraging D.are encouraged32.—Are the overseas students all from ________?—No, there are only two ________ in the team.A.Germany; Germany B.Germany; GermansC.German; Germans D.German; Germany33. During the Spring Festival, paper cuttings ________ on windows, doors and walls as symbols of wishes for good luck and a happy new year.A.are put B.were putC.puts D.putting34.Among the four,________ is not metal(金属).A.silver B.glass C.steel D.gold35.—I will take part in an examination tomorrow.—________.A.Good luck B.Quite prettyC.You're welcome D.Have a good time六、完形填空(每小题1分,共10分)(词数:约220;建议用时:6分钟)Have you ever offered a helping hand to those who are in trouble?One day, two ________(36)were walking along the road to school when they saw an old woman carrying a large basket of pears. They thought the woman looked very ________(37). They went up to her and said, “Are you going to the town? If you are, we will help carry your basket.”“T hank you,” ________(38)the woman. “You are very kind. You see I'm weak and ill.” Then she told them that she was going to the market to ________(39) the pears which grew on the only tree in her little garden.“We are all going to the ________(40),” said the boys. “Let us have the basket.” And they took hold of it, one each side. They walked ________(41) with the heavy basket, but happily.The other day, I saw a little girl stop and ________(42) a piece of orange peel (皮), which she threw into the dustbin (垃圾桶). “I wish ________(43)would throw that on the sidewalk,” she said. “Someone may step on it and fall.”Perhaps some may say that these are not ________(44) things. That is right. But such a little thing shows that you have a thoughtful mind and a feeling heart. We must not wait for the ________(45)to do great things. We must begin with little things of love.36.A. boys B.girls C.men D.women37.A. bored B.tired C.pleased D.surprised 38.A. asked B.told C.replied D.spoke39.A. bring B.buy C.take D.sell40.A. town B.market C.garden D.school41.A. weakly B.quickly C.slowly D.quietly42.A. take out B.cut off C.put down D.pick up 43.A. nobody B.everybody C.somebody D.anybody 44.A. little B.good C.great D.bad45.A. pay B.time C.advice D.love七、阅读理解(每小题2分,共30分)A (词数:约160;建议用时:5分钟)Have you heard about paper cutting? Paper cutting is an important art form in China. Papercuts are used for many purposes, and everything can become the theme (主题) of papercuts, from people to the things that can be found in everyday life such as birds, flowers and animals.Each papercut brings out the personal ideas of t he author (作者). People express traditional culture or their own feelings with different styles of papercuts. For example, when someone marries, we put up some red papercuts on the wall, dressing table or other furniture to express our best wishes.It is easy to learn paper cutting but very difficult to make it perfect.We need a longtime practice to learn how to use the scissors and how to paint.Moreover, we need to learn some cutting skills.At present, in many parts of China, papercutting ski ll has become a must for women and a symbol of a clever mind.阅读短文,判断下列句子的正(T)误(F)。
高中数学《第五章 一元函数的导数及其应用》单元检测试卷及答案解析(共四套)
高中数学选择性必修二《第五章 一元函数的导数及其应用》单元检测试卷(一)本试卷分第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若f(x)=sin α-cos x ,则f′(x)等于( )A .sin xB .cos xC .cos α+sin xD .2sin α+cos x 2.以正弦曲线y =sin x 上一点P 为切点的切线为直线l ,则直线l 的倾斜角的范围是( )A.⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎭⎪⎫3π4,π B .[0,π) C.⎣⎢⎡⎦⎥⎤π4,3π4 D.⎣⎢⎡⎦⎥⎤0,π4∪⎝ ⎛⎦⎥⎤π2,3π43.函数f(x)的定义域为开区间(a ,b),导函数f′(x)在(a ,b)内的图象如图所示,则函数f(x)在开区间(a ,b)内有极小值点( )A .1个B .2个C .3个D .4个 4.函数f(x)=x 2-ln x 的单调递减区间是( ) A. ⎝ ⎛⎦⎥⎤0,22 B.⎣⎢⎡⎭⎪⎫22,+∞ C. ⎝⎛⎦⎥⎤-∞,-22,⎝ ⎛⎭⎪⎫0, 22 D.⎣⎢⎡⎭⎪⎫-22, 0,⎝⎛⎦⎥⎤0, 22 5.函数f(x)=3x -4x 3(x ∈[0,1])的最大值是( ) A .1 B.12C .0D .-16.函数f(x)=x 3+ax 2+3x -9,已知f(x)在x =-3处取得极值,则a =( ) A .2 B .3 C .4 D .57.函数f(x)=13ax 3+12ax 2-2ax +1的图象经过四个象限,则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫-310,67B.⎝ ⎛⎭⎪⎫-85,-316C.⎝ ⎛⎭⎪⎫-83,-116D.⎝ ⎛⎭⎪⎫-∞,-310∪⎝ ⎛⎭⎪⎫67,+∞8.已知定义在R 上的函数f(x),f(x)+xf′(x)<0,若a <b ,则一定有( )A .af(a)<bf(b)B .af(b)<bf(a)C .af(a)>bf(b)D .af(b)>bf(a)二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得3分,有选错的得0分)9.下列结论中不正确的是( ) A .若y =cos 1x ,则y′=-1x sin 1xB .若y =sin x 2,则y′=2xcos x 2C .若y =cos 5x ,则y′=-sin 5xD .若y =12xsin 2x ,则y′=xsin 2x10.下列函数中,存在极值点的是( )A .y =x -1xB .y =2|xC .y =-2x 3-x D .y =xln x11.定义在区间⎣⎢⎡⎦⎥⎤-12,4上的函数f(x)的导函数f′(x)图象如图所示,则下列结论正确的是( )A .函数f(x)在区间(0,4)上单调递增B .函数f(x)在区间⎝ ⎛⎭⎪⎫-12,0上单调递减 C .函数f(x)在x =1处取得极大值 D .函数f(x)在x =0处取得极小值12.已知函数f(x)=e x-ax 有两个零点x 1,x 2,且x 1<x 2,则下列说法正确的是( ) A .a >e B .x 1+x 2>2C .x 1x 2>1D .f(x)有极小值点x 0,且x 1+x 2<2x 0第Ⅱ卷(非选择题,共90分)三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.若f(x)=13x 3-f′(1)x 2+x +5,则f′(1)=________.14.已知奇函数 f(x)=⎩⎪⎨⎪⎧e xx-1(x>0),h (x )(x<0),则函数h(x)的最大值为________.15.已知函数f(x)满足f(x)=f(π-x),且当x ∈⎝ ⎛⎭⎪⎫-π2,π2时,f(x)=x +sin x ,设a=f(1),b =f(2),c =f(3),则a ,b ,c 的大小关系是________. 16.若函数f(x)=4xx 2+1在区间(m,2m +1)上单调递增,则实数m 的取值范围是__________.四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知函数f(x)=x 3+ax 2+bx +a 2在x =1处有极值4. (1)求实数a ,b 的值;(2)当a>0时,求曲线y =f(x)在点(-2,f(-2))处的切线方程. 18.(本小题满分12分)已知a ∈R ,函数f(x)=(-x 2+ax)e x. (1)当a =2时,求函数f(x)的单调区间;(2)若函数f(x)在(-1,1)上单调递增,求实数a 的取值范围. 19.(本小题满分12分)已知函数f(x)=ax 3+bx 在x =22处取得极小值- 2. (1)求函数f(x)的解析式;(2)若过点M(1,m)的直线与曲线y =f(x)相切且这样的切线有三条,求实数m 的取值范围.20. (本小题满分12分)设函数f(x)=x22-kln x ,k>0.(1)求f(x)的单调区间和极值;(2)证明:若f(x)存在零点,则f(x)在区间(1, e ]上仅有一个零点. 21.(本小题满分12分)已知函数f(x)=ln x +ax 2+(2a +1)x. (1)讨论f(x)的单调性;(2)当a <0时,证明f(x)≤-34a-2.22.(本小题满分12分)已知函数f(x)=ln x -ax .(1)若f(x)存在最小值且最小值为2,求a 的值;(2)设g(x)=ln x -a ,若g(x)<x 2在(0,e]上恒成立,求a 的取值范围. 答案解析第Ⅰ卷(选择题,共60分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若f(x)=sin α-cos x ,则f′(x)等于( )A .sin xB .cos xC .cos α+sin xD .2sin α+cos x 解析:选A 函数是关于x 的函数,因此sin α是一个常数.2.以正弦曲线y =sin x 上一点P 为切点的切线为直线l ,则直线l 的倾斜角的范围是( )A.⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎭⎪⎫3π4,π B .[0,π) C.⎣⎢⎡⎦⎥⎤π4,3π4 D.⎣⎢⎡⎦⎥⎤0,π4∪⎝ ⎛⎦⎥⎤π2,3π4解析:选A y′=cos x ,∵cos x ∈[-1,1],∴切线的斜率范围是[-1,1],∴倾斜角的范围是⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎭⎪⎫3π4,π.3.函数f(x)的定义域为开区间(a ,b),导函数f′(x)在(a ,b)内的图象如图所示,则函数f(x)在开区间(a ,b)内有极小值点( )A .1个B .2个C .3个D .4个解析:选A 设极值点依次为x 1,x 2,x 3且a <x 1<x 2<x 3<b ,则f(x)在(a ,x 1),(x 2,x 3)上递增,在(x 1,x 2),(x 3,b)上递减,因此,x 1,x 3是极大值点,只有x 2是极小值点. 4.函数f(x)=x 2-ln x 的单调递减区间是( ) A. ⎝ ⎛⎦⎥⎤0,22 B.⎣⎢⎡⎭⎪⎫22,+∞ C. ⎝⎛⎦⎥⎤-∞,-22,⎝ ⎛⎭⎪⎫0, 22 D.⎣⎢⎡⎭⎪⎫-22, 0,⎝⎛⎦⎥⎤0, 22 解析:选A ∵f′(x)=2x -1x =2x 2-1x ,当0<x≤22时,f′(x)≤0,故f(x)的单调递减区间为⎝ ⎛⎦⎥⎤0,22. 5.函数f(x)=3x -4x 3(x ∈[0,1])的最大值是( ) A .1 B.12 C .0 D .-1解析:选A f′(x)=3-12x 2,令f′(x)=0, 则x =-12(舍去)或x =12,f(0)=0,f(1)=-1,f ⎝ ⎛⎭⎪⎫12=32-12=1,∴f(x)在[0,1]上的最大值为1.6.函数f(x)=x 3+ax 2+3x -9,已知f(x)在x =-3处取得极值,则a =( ) A .2 B .3 C .4 D .5 解析:选D f′(x)=3x 2+2ax +3,∵f′(-3)=0. ∴3×(-3)2+2a×(-3)+3=0,∴a =5.7.函数f(x)=13ax 3+12ax 2-2ax +1的图象经过四个象限,则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫-310,67B.⎝ ⎛⎭⎪⎫-85,-316C.⎝ ⎛⎭⎪⎫-83,-116D.⎝ ⎛⎭⎪⎫-∞,-310∪⎝ ⎛⎭⎪⎫67,+∞解析:选D f′(x)=ax 2+ax -2a =a(x +2)(x -1),要使函数f(x)的图象经过四个象限,则f(-2)f(1)<0,即⎝ ⎛⎭⎪⎫103a +1⎝ ⎛⎭⎪⎫-76a +1<0,解得a<-310或a>67. 故选D.8.已知定义在R 上的函数f(x),f(x)+xf′(x)<0,若a <b ,则一定有( ) A .af(a)<bf(b) B .af(b)<bf(a) C .af(a)>bf(b) D .af(b)>bf(a)解析:选C 令y =xf(x),则y′=[xf(x)]′=x′f(x)+xf′(x)=f(x)+xf′(x)<0,∴函数y =xf(x)是R 上的减函数,∵a <b ,∴af(a)>bf(b).二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得3分,有选错的得0分)9.下列结论中不正确的是( ) A .若y =cos 1x ,则y′=-1x sin 1xB .若y =sin x 2,则y′=2xcos x 2C .若y =cos 5x ,则y′=-sin 5xD .若y =12xsin 2x ,则y′=xsin 2x解析:选ACD 对于A ,y =cos 1x ,则y′=1x 2sin 1x ,故错误;对于B ,y =sin x 2,则y′=2xcos x 2,故正确;对于C ,y =cos 5x ,则y′=-5sin 5x ,故错误;对于D ,y =12xsin 2x ,则y′=12sin 2x +xcos 2x ,故错误.10.下列函数中,存在极值点的是( ) A .y =x -1x B .y =2|x|C .y =-2x 3-x D .y =xln x解析:选BD 由题意,函数y =x -1x ,则y′=1+1x 2>0,所以函数y =x -1x在(-∞,0),(0,+∞)内单调递增,没有极值点.函数y =2|x|=⎩⎪⎨⎪⎧2x,x≥0,2-x,x <0根据指数函数的图象与性质可得,当x <0时,函数y =2|x|单调递减,当x≥0时,函数y =2|x|单调递增,所以函数y =2|x|在x =0处取得极小值;函数y =-2x 3-x ,则y′=-6x 2-1<0,所以函数y =-2x 3-x 在R 上单调递减,没有极值点;函数y =xln x ,则y′=ln x +1,x >0,当x ∈⎝ ⎛⎭⎪⎫0,1e 时,y′<0,函数单调递减,当x ∈⎝ ⎛⎭⎪⎫1e ,+∞时,y′>0,函数单调递增,当x=1e时,函数取得极小值,故选B 、D. 11.定义在区间⎣⎢⎡⎦⎥⎤-12,4上的函数f(x)的导函数f′(x)图象如图所示,则下列结论正确的是( )A .函数f(x)在区间(0,4)上单调递增B .函数f(x)在区间⎝ ⎛⎭⎪⎫-12,0上单调递减 C .函数f(x)在x =1处取得极大值 D .函数f(x)在x =0处取得极小值解析:选ABD 根据导函数图象可知,f(x)在区间⎝ ⎛⎭⎪⎫-12,0上,f′(x)<0,f(x)单调递减,在区间(0,4)上,f′(x)>0,f(x)单调递增.所以f(x)在x =0处取得极小值,没有极大值,所以A 、B 、D 选项正确,C 选项错误.故选A 、B 、D.12.已知函数f(x)=e x-ax 有两个零点x 1,x 2,且x 1<x 2,则下列说法正确的是( ) A .a >e B .x 1+x 2>2C .x 1x 2>1D .f(x)有极小值点x 0,且x 1+x 2<2x 0解析:选ABD 由题意,函数f(x)=e x-ax ,则f′(x)=e x-a ,当a≤0时,f′(x)=e x-a >0在R 上恒成立,所以函数f(x)单调递增,不符合题意;当a >0时,令f′(x)=e x-a >0,解得x >ln a ,令f′(x)=e x-a <0,解得x <ln a ,所以函数f(x)在(-∞,ln a)上单调递减,在(ln a ,+∞)上单调递增,因为函数f(x)=e x-ax 有两个零点x 1,x 2且x 1<x 2,则f(ln a)=eln a-aln a =a -aln a =a(1-ln a)<0,且a >0,所以1-ln a <0,解得a >e ,所以A 项正确;又由x 1+x 2=ln(a 2x 1x 2)=2ln a +ln(x 1x 2)>2+ln(x 1x 2),取a =e 22,则f(2)=e 2-2a =0,x 2=2,f(0)=1>0,所以0<x 1<1,所以x 1+x 2>2,所以B 正确;由f(0)=1>0,则0<x 1<1,但x 1x 2>1不能确定,所以C 不正确;由函数f(x)在(-∞,ln a)上单调递减,在(ln a ,+∞)上单调递增,所以函数的极小值点为x 0=ln a ,且x 1+x 2<2x 0=2ln a ,所以D 正确.故选A 、B 、D. 第Ⅱ卷(非选择题,共90分)三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.若f(x)=13x 3-f′(1)x 2+x +5,则f′(1)=________.解析:f′(x)=x 2-2f′(1)x+1,令x =1,得f′(1)=23.答案:2314.已知奇函数 f(x)=⎩⎪⎨⎪⎧e xx-1(x>0),h (x )(x<0),则函数h(x)的最大值为________.解析:先求出x>0时,f(x)=e xx -1的最小值.当x>0时, f′(x)=e x(x -1)x 2,∴x ∈(0,1)时,f′(x)<0,函数单调递减,x ∈(1,+∞)时,f′(x) >0,函数单调递增,∴x =1时,函数取得极小值即最小值,为e -1,∴由已知条件得h(x)的最大值为1-e. 答案:1-e15.已知函数f(x)满足f(x)=f(π-x),且当x ∈⎝ ⎛⎭⎪⎫-π2,π2时,f(x)=x +sin x ,设a=f(1),b =f(2),c =f(3),则a ,b ,c 的大小关系是________. 解析:f(2)=f(π-2),f(3)=f(π-3), 因为f′(x)=1+cos x≥0,故f(x)在⎝ ⎛⎭⎪⎫-π2,π2上是增函数, ∵π2>π-2>1>π-3>0, ∴f(π-2)>f(1)>f(π-3),即c<a<b. 答案:c<a<b 16.若函数f(x)=4xx 2+1在区间(m,2m +1)上单调递增,则实数m 的取值范围是__________.解析:f′(x)=4-4x2(x 2+1)2,令f′(x)>0,得-1<x <1,即函数f(x)的增区间为(-1,1). 又因为f(x)在(m,2m +1)上单调递增, 所以⎩⎪⎨⎪⎧m≥-1,m <2m +1,2m +1≤1.解得-1<m≤0.答案:(-1,0]四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知函数f(x)=x 3+ax 2+bx +a 2在x =1处有极值4. (1)求实数a ,b的值;(2)当a>0时,求曲线y =f(x)在点(-2,f(-2))处的切线方程. 解:(1)∵f(x)=x 3+ax 2+bx +a 2, ∴f′(x)=3x 2+2ax +b.∵f(1)=1+a +b +a 2=4,f′(1)=3+2a +b =0,∴⎩⎪⎨⎪⎧a =3,b =-9或⎩⎪⎨⎪⎧a =-2,b =1.经检验都符合题意.(2)当a>0时,由(1)得f(x)=x 3+3x 2-9x +9, ∴f′(x)=3x 2+6x -9. ∴f(-2)=31,f′(-2)=-9.∴所求的切线方程为y -31=-9(x +2),即9x +y -13=0. 18.(本小题满分12分)已知a ∈R ,函数f(x)=(-x 2+ax)e x. (1)当a =2时,求函数f(x)的单调区间;(2)若函数f(x)在(-1,1)上单调递增,求实数a 的取值范围.解:(1)当a =2时,f(x)=(-x 2+2x)e x,f′(x)=(-x 2+2)e x.令f′(x)>0,即(-x 2+2)e x>0,注意到e x>0,所以-x 2+2>0,解得-2<x< 2.所以,函数f(x)的单调递增区间为(-2,2).同理可得,函数f(x)的单调递减区间为(-∞,-2)和(2,+∞).(2)因为函数f(x)在(-1,1)上单调递增,所以f′(x)≥0在(-1,1)上恒成立. 又因为f′(x)=[-x 2+(a -2)x +a]e x,所以[-x 2+(a -2)x +a]e x≥0,注意到e x>0,因此-x 2+(a -2)x +a≥0在(-1,1)上恒成立,也就是a≥x 2+2x x +1=x +1-1x +1在(-1,1)上恒成立.设y =x +1-1x +1,则y′=1+1(x +1)2>0,即y =x +1-1x +1在(-1,1)上单调递增,则y<1+1-11+1=32,故a≥32.即实数a 的取值范围为⎣⎢⎡⎭⎪⎫32,+∞. 19.(本小题满分12分)已知函数f(x)=ax 3+bx 在x =22处取得极小值- 2. (1)求函数f(x)的解析式;(2)若过点M(1,m)的直线与曲线y =f(x)相切且这样的切线有三条,求实数m 的取值范围.解:(1)由题意得,f′(x)=3ax 2+b.∵函数f(x)=ax 3+bx 在x =22处取得极小值-2, ∴⎩⎪⎨⎪⎧f ⎝ ⎛⎭⎪⎫22=-2,f ′⎝ ⎛⎭⎪⎫22=0,即⎩⎪⎨⎪⎧a +2b =-4,32a +b =0,解得⎩⎪⎨⎪⎧a =2,b =-3,经检验满足条件,则函数f(x)的解析式为f(x)=2x 3-3x.(2)设切点坐标为(x 0,2x 30-3x 0),则曲线y =f(x)的切线的斜率k =f′(x 0)=6x 20-3, 切线方程为y -(2x 30-3x 0)=(6x 20-3)(x -x 0), 代入点M(1,m),得m =-4x 30+6x 20-3,依题意,方程m =-4x 30+6x 20-3有三个不同的实根. 令g(x)=-4x 3+6x 2-3,则g′(x)=-12x 2+12x =-12x(x -1), ∴当x ∈(-∞,0)时,g′(x)<0; 当x ∈(0,1)时,g′(x)>0; 当x ∈(1,+∞)时,g′(x)<0.故g(x)=-4x 3+6x 2-3在(-∞,0)上单调递减,在(0,1)上单调递增,在(1,+∞)上单调递减.∴g(x)极小值=g(0)=-3,g(x)极大值=g(1)=-1.∴当-3<m<-1时,g(x)=-4x 3+6x 2-3的图象与直线y =m 有三个不同的交点, ∴-3<m<-1时,存在这样的三条切线. 故实数m 的取值范围是(-3,-1).20. (本小题满分12分)设函数f(x)=x22-kln x ,k>0.(1)求f(x)的单调区间和极值;(2)证明:若f(x)存在零点,则f(x)在区间(1, e ]上仅有一个零点.解:(1)由f(x)=x22-kln x(k>0),得x>0且f′(x)=x -k x =x 2-kx .由f′(x)=0,解得x =k(负值舍去). f(x)与f′(x)在区间(0,+∞)上的情况如下:所以,f(x)在x =k 处取得极小值f(k)=k (1-ln k )2,无极大值.(2)证明:由(1)知,f(x)在区间(0,+∞)上的最小值为f(k)=k (1-ln k )2.因为f(x)存在零点,所以k (1-ln k )2≤0,从而k≥e.当k =e 时,f(x)在区间(1,e)上单调递减,且f(e)=0, 所以x =e 是f(x)在区间(1, e ]上的唯一零点.当k>e 时,f(x)在区间(1, e ]上单调递减,且f(1)=12>0,f(e)=e -k2<0,所以f(x)在区间(1, e ]上仅有一个零点.综上可知,若f(x)存在零点,则f(x)在区间(1, e ]上仅有一个零点. 21.(本小题满分12分)已知函数f(x)=ln x +ax 2+(2a +1)x. (1)讨论f(x)的单调性;(2)当a <0时,证明f(x)≤-34a -2.解:(1)f(x)的定义域为(0,+∞), f′(x)=1x +2ax +2a +1=(x +1)(2ax +1)x .若a≥0,则当x ∈(0,+∞)时,f′(x)>0, 故f(x)在(0,+∞)上单调递增.若a <0,则当x ∈⎝⎛⎭⎪⎫0,-12a 时,f′(x)>0;当x ∈⎝ ⎛⎭⎪⎫-12a ,+∞时,f′(x)<0.故f(x)在⎝ ⎛⎭⎪⎫0,-12a 上单调递增,在⎝ ⎛⎭⎪⎫-12a ,+∞上单调递减. (2)证明:由(1)知,当a <0时,f(x)在x =-12a 处取得最大值,最大值为f ⎝ ⎛⎭⎪⎫-12a =ln ⎝ ⎛⎭⎪⎫-12a -1-14a .所以f(x)≤-34a -2等价于ln ⎝ ⎛⎭⎪⎫-12a -1-14a ≤-34a -2,即ln ⎝ ⎛⎭⎪⎫-12a +12a +1≤0.设g(x)=ln x -x +1,则g′(x)=1x-1.当x ∈(0,1)时,g′(x)>0;当x ∈(1,+∞)时,g′(x)<0.所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减.故当x =1时,g(x)取得极大值且为最大值,最大值为g(1)=0. 所以当x >0时,g(x)≤0.从而当a <0时,ln ⎝ ⎛⎭⎪⎫-12a +12a+1≤0,即f(x)≤-34a-2.22.(本小题满分12分)已知函数f(x)=ln x -ax .(1)若f(x)存在最小值且最小值为2,求a 的值;(2)设g(x)=ln x -a ,若g(x)<x 2在(0,e]上恒成立,求a 的取值范围. 解:(1)f′(x)=1x +a x 2=x +ax2(x>0),当a≥0时,f′(x)>0,f(x)在(0,+∞)上是增函数, f(x)不存在最小值;当a<0时,由f′(x)=0得x =-a , 且0<x<-a 时,f′(x)<0, x>-a 时,f′(x)>0.∴x =-a 时,f(x)取得最小值, f(-a)=ln(-a)+1=2,解得a =-e. (2)g(x)<x 2即ln x -a<x 2,即a>ln x -x 2,故g(x)<x 2在(0,e]上恒成立,也就是a>ln x -x 2在(0,e]上恒成立. 设h(x)=ln x -x 2,则h′(x)=1x -2x =1-2x2x,由h′(x)=0及0<x≤e 得x =22.当0<x<22时,h′(x)>0,当22<x≤e 时,h′(x)<0,即h(x)在⎝⎛⎭⎪⎫0,22上为增函数,在⎝ ⎛⎦⎥⎤22,e 上为减函数, 所以当x =22时h(x)取得最大值为h ⎝ ⎛⎭⎪⎫22=ln 22-12. 所以g(x)<x 2在(0,e]上恒成立时,a 的取值范围为⎝ ⎛⎭⎪⎫ln 22-12,+∞.高中数学选择性必修二《第五章 一元函数的导数及其应用》单元检测试卷(二)本试卷分第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.等差数列{a n }中,a 3=2,a 5=7,则a 7=( ) A .10 B .20 C .16 D .122.在数列{a n }中,a 1=13,a n =(-1)n·2a n -1(n≥2),则a 5等于( )A .-163 D .163 C .-83 D .833.设等比数列{a n }的前n 项和为S n ,若S 10∶S 5=1∶2,则S 15∶S 5=( ) A .3∶4 B .2∶3 C .1∶2 D .1∶3 4.在等比数列{a n }中,已知前n 项和S n =5n +1+a ,则a 的值为( )A .-1B .1C .5D .-55.已知数列{a n }满足a 1=1,a n +1=⎩⎪⎨⎪⎧2a n ,n 为正奇数,a n +1,n 为正偶数,则254是该数列的( )A .第8项B .第10项C .第12项D .第14项 6.已知数列{a n }是等差数列,其前n 项和为S n ,若a 1a 2a 3=15,且3S 1S 3+15S 3S 5+5S 5S 1=35,则a 2=( )A .2 D .12 C .3 D .137.如果数列a 1,a 2-a 1,a 3-a 2,…,a n -a n -1,…是首项为1,公比为13的等比数列,那么a n =( )A.32⎝ ⎛⎭⎪⎫1-13n D .32⎝ ⎛⎭⎪⎫1-13n -1 C.23⎝ ⎛⎭⎪⎫1-13n D .23⎝ ⎛⎭⎪⎫1-13n -18.若有穷数列a 1,a 2,…,a n (n 是正整数),满足a 1=a n ,a 2=a n -1,…,a n =a 1,即a i =a n-i +1(i 是正整数,且1≤i≤n),就称该数列为“对称数列”.已知数列{b n }是项数不超过2m(m >1,m ∈N *)的对称数列,且1,2,4,…,2m -1是数列{b n }的前m 项,则当m >1 200时,数列{b n }的前2 019项和S 2 019的值不可能为( ) A .2m-2m -2 009B .22 019-1C .2m +1-22m -2 019-1 D .3·2m -1-22m -2 020-1二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得3分,有选错的得0分)9.已知等比数列{a n }的公比q =-23,等差数列{b n }的首项b 1=12,若a 9>b 9且a 10>b 10,则以下结论正确的有( )A .a 9·a 10<0B .a 9>a 10C .b 10>0D .b 9>b 1010.等差数列{a n }的前n 项和为S n ,若a 1>0,公差d≠0,则下列命题正确的是( ) A .若S 5=S 9,则必有S 14=0B .若S 5=S 9,则必有S 7是S n 中最大的项C .若S 6>S 7,则必有S 7>S 8D .若S 6>S 7,则必有S 5>S611.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关”.则下列说法正确的是( ) A .此人第三天走了四十八里路B .此人第一天走的路程比后五天走的路程多六里C .此人第二天走的路程占全程的14D .此人走的前三天路程之和是后三天路程之和的8倍12.若数列{a n }满足:对任意正整数n ,{a n +1-a n }为递减数列,则称数列{a n }为“差递减数列”.给出下列数列{a n }(n ∈N *),其中是“差递减数列”的有( ) A .a n =3n B .a n =n 2+1 C .a n =n D .a n =ln n n +1第Ⅱ卷(非选择题,共90分)三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.已知数列{a n }的通项公式为a n =2 020-3n ,则使a n >0成立的最大正整数n 的值为________.14.已知{a n }是等差数列,S n 为其前n 项和,n ∈N *.若a 3=16,S 20=20,则a n =________,S 10=________.15.已知数列1,a 1,a 2,9是等差数列,数列1,b 1,b 2,b 3,9是等比数列,则b 2a 1+a 2=________.16.设{a n }是由正数组成的等比数列,S n 为其前n 项和,已知a 2a 4=1,S 3=7,则S 5=________.四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知函数f(x)=3xx +3,数列{x n }的通项由x n =f(x n -1)(n≥2且x ∈N *)确定.(1)求证:⎩⎨⎧⎭⎬⎫1x n 是等差数列;(2)当x 1=12时,求x 2 020.18.(本小题满分12分)已知等比数列{a n }的前n 项和为S n ,a 1=-1,S 10S 5=3132.(1)求等比数列{a n }的公比q ; (2)求a 21+a 22+…+a 2n .19.(本小题满分12分)在等差数列{a n }中,S n 为其前n 项和(n ∈N *),且a 2=3,S 4=16. (1)求数列{a n }的通项公式;(2)设b n =1a n a n +1,求数列{b n }的前n 项和T n .20.(本小题满分12分)已知等比数列{a n }的前n 项和为S n ,a 1=1,a n <a n +1,且S 3=2S 2+1.(1)求数列{a n }的通项公式;(2)若数列{b n }满足b n =(2n -1)a n (n ∈N *),求数列{b n }的前n 项和T n . 21.(本小题满分12分)在①a n +1=a n 3a n +1,②⎩⎨⎧⎭⎬⎫1a n 为等差数列,其中1a 2,1a 3+1,1a 6成等比数列,③1a 1+1a 2+1a 3+…+1a n =3n 2-n2这三个条件中任选一个,补充到下面的问题中,然后解答补充完整的题目.已知数列{a n }中,a 1=1,________.(1)求数列{a n }的通项公式;(2)设b n =a n a n +1,T n 为数列{b n }的前n 项和,求证:T n <13.注:如果选择多个条件分别解答,则按第一个解答计分.22.(本小题满分12分)已知等差数列{a n }的前n 项和为S n ,且S 10=55,S 20=210. (1)求数列{a n }的通项公式; (2)设b n =a n a n +1,是否存在m ,k(k>m≥2,m ,k ∈N *)使得b 1,b m ,b k 成等比数列?若存在,请说明理由. 答案解析第Ⅰ卷(选择题,共60分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.等差数列{a n }中,a 3=2,a 5=7,则a 7=( ) A .10 B .20 C .16 D .12 解析:选D ∵{a n }是等差数列, ∴d =a 5-a 35-3=52,∴a 7=2+4×52=12.2.在数列{a n }中,a 1=13,a n =(-1)n·2a n -1(n≥2),则a 5等于( )A .-163 D .163 C .-83 D .83解析:选B ∵a 1=13,a n =(-1)n·2a n -1,∴a 2=(-1)2×2×13=23,a 3=(-1)3×2×23=-43,a 4=(-1)4×2×⎝ ⎛⎭⎪⎫-43=-83,a 5=(-1)5×2×⎝ ⎛⎭⎪⎫-83=163.3.设等比数列{a n }的前n 项和为S n ,若S 10∶S 5=1∶2,则S 15∶S 5=( ) A .3∶4 B .2∶3 C .1∶2 D .1∶3解析:选A 在等比数列{a n }中,S 5,S 10-S 5,S 15-S 10,…成等比数列,因为S 10∶S 5=1∶2,所以S 5=2S 10,S 15=34S 5,得S 15∶S 5=3∶4,故选A.4.在等比数列{a n }中,已知前n 项和S n =5n +1+a ,则a 的值为( )A .-1B .1C .5D .-5 解析:选D 因为S n =5n +1+a =5×5n+a ,由等比数列的前n 项和S n =a 1(1-q n)1-q =a 11-q-a 11-q·q n ,可知其常数项与q n的系数互为相反数,所以a =-5. 5.已知数列{a n }满足a 1=1,a n +1=⎩⎪⎨⎪⎧2a n ,n 为正奇数,a n +1,n 为正偶数,则254是该数列的( )A .第8项B .第10项C .第12项D .第14项 解析:选D 当n 为正奇数时,a n +1=2a n ,则a 2=2a 1=2,当n 为正偶数时,a n +1=a n +1,得a 3=3,依次类推得a 4=6,a 5=7,a 6=14,a 7=15,…,归纳可得数列{a n }的通项公式a n=⎩⎪⎨⎪⎧2n +12-1,n 为正奇数,2n2+1-2,n 为正偶数,则2n2+1-2=254,n =14,故选D.6.已知数列{a n }是等差数列,其前n 项和为S n ,若a 1a 2a 3=15,且3S 1S 3+15S 3S 5+5S 5S 1=35,则a 2=( )A .2 D .12 C .3 D .13解析:选C ∵S 1=a 1,S 3=3a 2,S 5=5a 3,∴1a 1a 2+1a 2a 3+1a 1a 3=35.∵a 1a 2a 3=15,∴35=a 315+a 115+a 215=a 25,∴a 2=3.故选C. 7.如果数列a 1,a 2-a 1,a 3-a 2,…,a n -a n -1,…是首项为1,公比为13的等比数列,那么a n =( )A.32⎝ ⎛⎭⎪⎫1-13n D .32⎝ ⎛⎭⎪⎫1-13n -1 C.23⎝ ⎛⎭⎪⎫1-13n D .23⎝ ⎛⎭⎪⎫1-13n -1解析:选A 由题知a 1=1,q =13,则a n -a n -1=1×⎝ ⎛⎭⎪⎫13n -1.设数列a 1,a 2-a 1,…,a n -a n -1的前n 项和为S n , ∴S n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1)=a n .又∵S n =1×⎝ ⎛⎭⎪⎫1-13n 1-13=32⎝⎛⎭⎪⎫1-13n ,∴a n =32⎝⎛⎭⎪⎫1-13n .8.若有穷数列a 1,a 2,…,a n (n 是正整数),满足a 1=a n ,a 2=a n -1,…,a n =a 1,即a i =a n-i +1(i 是正整数,且1≤i≤n),就称该数列为“对称数列”.已知数列{b n }是项数不超过2m(m >1,m ∈N *)的对称数列,且1,2,4,…,2m -1是数列{b n }的前m 项,则当m >1 200时,数列{b n }的前2 019项和S 2 019的值不可能为( ) A .2m-2m -2 009B .22 019-1C .2m +1-22m -2 019-1 D .3·2m -1-22m -2 020-1解析:选A 若数列{b n }的项数为偶数,则数列可设为1,21,22,…,2m -1,2m -1, (22)2,1,当m≥2 019时, S 2 019=1×(1-22 019)1-2=22 019-1,故B 可能.当1 200<m <2 019时,S 2 019=2×1×(1-2m)1-2-1×(1-22m -2 019)1-2=2m +1-22m -2 019-1,故C 可能.若数列为奇数项,则数列可设为1,21,22,…,2m -2,2m -1,2m -2, (22)2,1,当m≥2 019时,S 2 019=1×(1-22 019)1-2=22 019-1.当1 200<m <2 019时,S 2 019=2×1×(1-2m -1)1-2-1×(1-22m -1-2 019)1-2+2m -1=3·2m -1-22m -2 020-1,故D 可能.故选A.二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得3分,有选错的得0分)9.已知等比数列{a n }的公比q =-23,等差数列{b n }的首项b 1=12,若a 9>b 9且a 10>b 10,则以下结论正确的有( )A .a 9·a 10<0B .a 9>a 10C .b 10>0D .b 9>b 10 解析:选AD ∵等比数列{a n }的公比q =-23,∴a 9和a 10异号,∴a 9a 10=a 29⎝ ⎛⎭⎪⎫-23<0,故A 正确; 但不能确定a 9和a 10的大小关系,故B 不正确; ∵a 9和a 10异号,且a 9>b 9且a 10>b 10,∴b 9和b 10中至少有一个数是负数,又∵b 1=12>0,∴d<0,∴b 9>b 10,故D 正确;∴b 10一定是负数,即b 10<0,故C 不正确.故选A 、D.10.等差数列{a n }的前n 项和为S n ,若a 1>0,公差d≠0,则下列命题正确的是( ) A .若S 5=S 9,则必有S 14=0B .若S 5=S 9,则必有S 7是S n 中最大的项C .若S 6>S 7,则必有S 7>S 8D .若S 6>S 7,则必有S 5>S 6解析:选ABC ∵等差数列{a n }的前n 项和公式S n =na 1+n (n -1)d2,若S 5=S 9,则5a 1+10d =9a 1+36d ,∴2a 1+13d =0, ∴a 1=-13d2,∵a 1>0,∴d <0,∴a 1+a 14=0,∴S 14=7(a 1+a 14)=0,A 对;又∵S n =na 1+n (n -1)d 2=-13nd 2+n (n -1)d 2=d[(n -7)2-49]2,由二次函数的性质知S 7是S n中最大的项,B 对;若S 6>S 7,则a 7=a 1+6d <0,∴a 1<-6d , ∵a 1>0,∴d <0,∴a 6=a 1+5d <-6d +5d =-d ,a 8=a 7+d <a 7<0, S 7>S 8=S 7+a 8,C 对;由a 6<-d 不能确定a 6的符号,所以S 5>S 6不一定成立,D 错.故选A 、B 、C.11.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关”.则下列说法正确的是( ) A .此人第三天走了四十八里路B .此人第一天走的路程比后五天走的路程多六里C .此人第二天走的路程占全程的14D .此人走的前三天路程之和是后三天路程之和的8倍解析:选ABD 设此人第n 天走a n 里路,则{a n }是首项为a 1,公比为q =12的等比数列.所以S 6=a 1(1-q 6)1-q =a 1⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫1261-12=378,解得a 1=192.a 3=a 1q 2=192×14=48,所以A 正确,由a 1=192,则S 6-a 1=378-192=186,又192-186=6,所以B 正确. a 2=a 1q =192×12=96,而14S 6=94.5<96,所以C 不正确.a 1+a 2+a 3=a 1(1+q +q 2)=192×⎝ ⎛⎭⎪⎫1+12+14=336,则后3天走的路程为378-336=42而且42×8=336,所以D 正确. 故选A 、B 、D.12.若数列{a n }满足:对任意正整数n ,{a n +1-a n }为递减数列,则称数列{a n }为“差递减数列”.给出下列数列{a n }(n ∈N *),其中是“差递减数列”的有( ) A .a n =3n B .a n =n 2+1 C .a n =n D .a n =ln nn +1解析:选CD 对A ,若a n =3n ,则a n +1-a n =3(n +1)-3n =3,所以{a n +1-a n }不为递减数列,故A 错误;对B ,若a n =n 2+1,则a n +1-a n =(n +1)2-n 2=2n +1,所以{a n +1-a n }为递增数列,故B 错误;对C ,若a n =n ,则a n +1-a n =n +1-n =1n +1+n,所以{a n +1-a n }为递减数列,故C 正确; 对D ,若a n =lnn n +1,则a n +1-a n =ln n +1n +2-ln n n +1=ln n +1n +2·n +1n =ln ⎝ ⎛⎭⎪⎫1+1n 2+2n ,由函数y =ln ⎝ ⎛⎭⎪⎫1+1x 2+2x 在(0,+∞)递减,所以数列{a n +1-a n }为递减数列,故D 正确. 故选C 、D.第Ⅱ卷(非选择题,共90分)三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.已知数列{a n }的通项公式为a n =2 020-3n ,则使a n >0成立的最大正整数n 的值为________.解析:由a n =2 020-3n>0,得n<2 0203=67313,又∵n ∈N *,∴n 的最大值为673. 答案:67314.已知{a n }是等差数列,S n 为其前n 项和,n ∈N *.若a 3=16,S 20=20,则a n =________,S 10=________.解析:设{a n }的首项,公差分别是a 1,d ,则 ⎩⎪⎨⎪⎧a 1+2d =16,20a 1+20×(20-1)2×d=20,解得a 1=20,d =-2,∴a n =a 1+(n -1)d =20-2(n -1)=22-2n .S 10=10×20+10×92×(-2)=110.答案:22-2n 11015.已知数列1,a 1,a 2,9是等差数列,数列1,b 1,b 2,b 3,9是等比数列,则b 2a 1+a 2=________.解析:因为数列1,a 1,a 2,9是等差数列,所以a 1+a 2=1+9=10.因为数列1,b 1,b 2,b 3,9是等比数列,所以b 22=1×9=9,又b 2=1×q 2>0(q 为等比数列的公比),所以b 2=3,则b 2a 1+a 2=310. 答案:31016.设{a n }是由正数组成的等比数列,S n 为其前n 项和,已知a 2a 4=1,S 3=7,则S 5=________.解析:设{a n }的公比为q ,q>0,且a 23=1, ∴a 3=1.∵S 3=7,∴a 1+a 2+a 3=1q 2+1q +1=7,即6q 2-q -1=0,解得q =12或q =-13(舍去),a 1=1q2=4. ∴S 5=4×⎝ ⎛⎭⎪⎫1-1251-12=8×⎝ ⎛⎭⎪⎫1-125=314.答案:314四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知函数f(x)=3xx +3,数列{x n }的通项由x n =f(x n -1)(n≥2且x ∈N *)确定.(1)求证:⎩⎨⎧⎭⎬⎫1x n 是等差数列;(2)当x 1=12时,求x 2 020.解:(1)证明:∵x n =f(x n -1)=3x n -1x n -1+3(n≥2且n ∈N *),∴1x n =x n -1+33x n -1=13+1x n -1, ∴1x n -1x n -1=13(n≥2且n ∈N *), ∴⎩⎨⎧⎭⎬⎫1x n 是公差为13的等差数列.(2)由(1)知1x n =1x 1+(n -1)×13=2+n -13=n +53.∴1x 2 020=2 020+53=675. ∴x 2 020=1675.18.(本小题满分12分)已知等比数列{a n }的前n 项和为S n ,a 1=-1,S 10S 5=3132.(1)求等比数列{a n }的公比q ; (2)求a 21+a 22+…+a 2n .解:(1)由S 10S 5=3132,a 1=-1,知公比q≠1,S 10-S 5S 5=-132.由等比数列前n 项和的性质知S 5,S 10-S 5,S 15-S 10成等比数列,且公比为q 5,故q 5=-132,q =-12.(2)由(1),得a n =(-1)×⎝ ⎛⎭⎪⎫-12n -1,所以a 2n =⎝ ⎛⎭⎪⎫14n -1,所以数列{a 2n }是首项为1,公比为14的等比数列,故a 21+a 22+…+a 2n =1×⎝ ⎛⎭⎪⎫1-14n 1-14=43⎝ ⎛⎭⎪⎫1-14n .19.(本小题满分12分)在等差数列{a n }中,S n 为其前n 项和(n ∈N *),且a 2=3,S 4=16. (1)求数列{a n }的通项公式;(2)设b n =1a n a n +1,求数列{b n }的前n 项和T n .解:(1)设等差数列{a n }的公差是d ,由已知条件得⎩⎪⎨⎪⎧a 1+d =3,4a 1+6d =16,解得a 1=1,d =2,∴a n =2n -1. (2)由(1)知,a n =2n -1, ∴b n =1a n a n +1=1(2n -1)(2n +1)=12⎝ ⎛⎭⎪⎫12n -1-12n +1,T n =b 1+b 2+…+b n=12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1-13+⎝ ⎛⎭⎪⎫13-15+…+⎝ ⎛⎭⎪⎫12n -1-12n +1 =12⎝⎛⎭⎪⎫1-12n +1=n 2n +1. 20.(本小题满分12分)已知等比数列{a n }的前n 项和为S n ,a 1=1,a n <a n +1,且S 3=2S 2+1.(1)求数列{a n }的通项公式;(2)若数列{b n }满足b n =(2n -1)a n (n ∈N *),求数列{b n }的前n 项和T n .解:(1)设等比数列{a n }的公比为q ,由a n <a n +1,得q>1,又a 1=1,则a 2=q ,a 3=q 2, 因为S 3=2S 2+1,所以a 1+a 2+a 3=2(a 1+a 2)+1,则1+q +q 2=2(1+q)+1,即q 2-q -2=0,解得q =2或q =-1(舍去), 所以数列{a n }的通项公式为a n =2n -1(n ∈N *).(2)由(1)知,b n =(2n -1)·a n =(2n -1)·2n -1(n ∈N *), 则T n =1×20+3×21+5×22+…+(2n -1)×2n -1,2T n =1×21+3×22+5×23+…+(2n -3)×2n -1+(2n -1)×2n,两式相减,得-T n =1+2×21+2×22+…+2×2n -1-(2n -1)×2n,即-T n =1+22+23+24+ (2)-(2n -1)×2n, 化简得T n =(2n -3)×2n+3. 21.(本小题满分12分)在①a n +1=a n 3a n +1,②⎩⎨⎧⎭⎬⎫1a n 为等差数列,其中1a 2,1a 3+1,1a 6成等比数列,③1a 1+1a 2+1a 3+…+1a n =3n 2-n2这三个条件中任选一个,补充到下面的问题中,然后解答补充完整的题目.已知数列{a n }中,a 1=1,________. (1)求数列{a n }的通项公式;(2)设b n =a n a n +1,T n 为数列{b n }的前n 项和,求证:T n <13.注:如果选择多个条件分别解答,则按第一个解答计分. 解:若选条件①:(1)易知a n ≠0,∵a n +1=a n 3a n +1,∴1a n +1-1a n =3.又1a 1=1, ∴数列⎩⎨⎧⎭⎬⎫1a n 是以1为首项,3为公差的等差数列,∴1a n =3n -2,∴a n =13n -2. (2)证明:由(1)可知,b n =1(3n -2)(3n +1)=13⎝ ⎛⎭⎪⎫13n -2-13n +1,∴T n =13⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1-14+⎝ ⎛⎭⎪⎫14-17+…+⎝ ⎛⎭⎪⎫13n -2-13n +1=13⎝ ⎛⎭⎪⎫1-13n +1=13-19n +3<13, 故T n <13.若选条件②:(1)设数列⎩⎨⎧⎭⎬⎫1a n 的公差为d ,则1a 2=1+d ,1a 3+1=2+2d ,1a 6=1+5d ,∵1a 2,1a 3+1,1a 6成等比数列, ∴(2+2d)2=(1+d)(1+5d),解得d =3或d =-1.当d =-1时,1a 2=1+d =0,此时1a 2,1a 3+1,1a 6不能构成等比数列,∴d =3,∴1a n =1+3(n -1)=3n -2, ∴a n =13n -2. (2)由(1)可知,b n =1(3n -2)(3n +1)=13⎝ ⎛⎭⎪⎫13n -2-13n +1,∴T n =13⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1-14+⎝ ⎛⎭⎪⎫14-17+…+⎝ ⎛⎭⎪⎫13n -2-13n +1=13⎝ ⎛⎭⎪⎫1-13n +1=13-19n +3<13, 故T n <13.若选条件③:(1)由1a 1+1a 2+1a 3+…+1a n =3n 2-n 2知,当n≥2时,1a 1+1a 2+1a 3+…+1a n -1=3(n -1)2-(n -1)2,两式相减,得1a n =3n 2-n 2-3(n -1)2-(n -1)2=3n -2,∴a n =13n -2(n≥2),当n =1时,a 1=1也适合上式, ∴a n =13n -2. (2)由(1)可知,b n =1(3n -2)(3n +1)=13⎝ ⎛⎭⎪⎫13n -2-13n +1,∴T n =13⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1-14+⎝ ⎛⎭⎪⎫14-17+…+⎝ ⎛⎭⎪⎫13n -2-13n +1=13⎝ ⎛⎭⎪⎫1-13n +1=13-19n +3<13, 故T n <13.22.(本小题满分12分)已知等差数列{a n }的前n 项和为S n ,且S 10=55,S 20=210. (1)求数列{a n }的通项公式; (2)设b n =a n a n +1,是否存在m ,k(k>m≥2,m ,k ∈N *)使得b 1,b m ,b k 成等比数列?若存在,请说明理由.解:(1)设等差数列{a n }的公差为d ,则S n =na 1+n (n -1)2 d.由已知,得⎩⎪⎨⎪⎧10a 1+10×92d =55,20a 1+20×192d =210,即⎩⎪⎨⎪⎧2a 1+9d =11,2a 1+19d =21,解得⎩⎪⎨⎪⎧a 1=1,d =1.所以a n =a 1+(n -1)d =n(n ∈N *).(2)假设存在m ,k(k>m≥2,m ,k ∈N *)使得b 1,b m ,b k 成等比数列,则b 2m =b 1b k . 因为b n =a n a n +1=nn +1,所以b 1=12,b m =m m +1,b k =kk +1,所以⎝⎛⎭⎪⎫m m +12=12×k k +1.整理,得k =2m2-m 2+2m +1.以下给出求m ,k 的方法: 因为k>0,所以-m 2+2m +1>0, 解得1-2<m<1+ 2. 因为m≥2,m ∈N *, 所以m =2,此时k =8.故存在m =2,k =8使得b 1,b m ,b k 成等高中数学选择性必修二《第五章 一元函数的导数及其应用》单元检测试卷(三)一、单选题1.已知函数()y f x =在0x x =处的导数为1,则()()000lim 2x f x x f x x∆→+∆-=∆( )A .0B .12C .1D .2 2.设函数()f x 在定义域内可导,()y f x =的图象如图所示,则导函数()y f x '=的图象为( )A .B .C .D .3.函数2cos y x x =+在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值是( )A .13π+ B .4π+.6π+.2π4.若函数2()ln 2f x x ax =+-在区间1,22⎛⎫⎪⎝⎭内存在单调递增区间,则实数a 的取值范围是( )A .(,2]-∞-B .1,8⎛⎫-+∞ ⎪⎝⎭C .12,8⎛⎫-- ⎪⎝⎭D .(2,)-+∞ 5.曲线2yx x 在点(1,0)处的切线方程是( )A .210x y --=B .210x y +-=C .10x y --=D .10x y +-=6.已知函数()f x 的导函数()()()1f x a x x a '=+-,若()f x 在x a =处取得极大值,则实数a 的取值范围是( )A .()1,0-B .()2,+∞C .()0,1D .(),3-∞- 7.已知函数()cos xf x e x =+,设()10.3a f -=,()0.32b f -=,()2log0.2c f =,则( )A .c b a <<B .c a b <<C .b a c <<D .b c a << 8.已知偶函数()y f x =对于任意的[0,)2x π∈满足'()cos ()sin 0f x x f x x +>(其中'()f x 是函数()f x 的导函数),则下列不等式中成立的是( )A ()()34f ππ-< B ()()34f ππ-<-C .(0)()4f π>-D .()()63f ππ<二、多选题9.已知定义在R 上的函数()f x 满足()()f x f x '>-,则下列式子成立的是( ) A .()()20192020f ef < B .()()20192020ef f >C .()f x 是R 上的增函数D .若0t >,则有()()tf x e f x t <+10.若直线12y x b =+是函数()f x 图像的一条切线,则函数()f x 可以是( ) A .1()f x x=B .4()f x x =C .()sin f x x =D .()x f x e = 11.已知函数()y f x =的导函数的图象如图所示,下列结论中正确的是( )A .1-是函数()f x 的极小值点B .3-是函数()f x 的极小值点C .函数()f x 在区间()3,1-上单调递增 D .函数()f x 在0x =处切线的斜率小于零 12.已知函数()f x 是定义在R 上的奇函数,当0x >时,()1xx f x e -=.则下列结论正确的是( ).A .当0x <时,()()1xf x e x =-+B .函数()f x 在R 上有且仅有三个零点C .若关于x 的方程()f x m =有解,则实数m 的取值范围是()()22f m f -≤≤D .12,x x ∀∈R ,()()212f x f x -<三、填空题13.已知函数()f x 的导函数为()f x ',且满足关系式()()321xf x x f x e '=-++,则()1f '的值等于__________.14.生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图像,A 对应________;B 对应________;。
高中英语 Unit 5 First aid单元检测5 新人教版必修5
高中英语 Unit 5 First aid单元检测5 新人教版必修5第一卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. How long will the man probably wait in total?A.Two hours.B.Three hours.C.Four hours.2. What can we know about the two speakers?A.They want to have a cup of coffee.B.The woman refused the man’s invitation.C.The woman will write her paper tomorrow.3. What are the two speakers talking about?A.The light.B.Power failure.C.Airconditi oning.4.How much did the man’s sister pay for the coat?A.$172. B.$43. C.$86.5. What do we know about the Grass World?A.It’s a café.B.It’s a supermarket.C.It’s a department store.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
新教材高中英语Unit5单元检测含解析外研版必修第三册
新教材高中英语必修第三册:单元综合检测(五)第一部分阅读(共两节,满分50分)第一节(共15小题;每小题2.5分,满分37.5分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项。
ASince Edmund Hillary and Tenzing Norgay climbed Mount Everest, Mount Qomolangma's peak is no longer a lonely place and is turning into a trash heap.So far,a large number of climbers have successfully reached the peak.And they have complained about waiting for hours in the bottlenecks (狭窄路段) on the way to the peak, a situation that isn't just uncomfortable—it's cold and windy up there —but downright dangerous. If bad weather strikes, climbers can die.As a matter of fact, the dangerous crowds aren't the only problem on Mount Qomolangma. All those climbers need to bring a lot of gear—and much of it ends up being left on the mountain, sometimes even the peak itself. Mount Qomolangma is becoming the world's largest rubbish dump. Here's mountaineer Mark Jenkins' writing in National Geographic about the state of Mount Qomolangma, “The two standard routes, the Northeast Ridge and the Southeast Ridge, are badly polluted with oxygen cans and torn tents everywhere.”But the good news is that some mountaineers are taking on the work to clean up Mount Qomolangma.Mountaineer Paul Thelen and his friend Eberhard Schaaf are part of the annual Eco Everest Expedition,which has been cleaning up rubbish from base camps to the peak since 2008.Some of that rubbish is even being used for a higher purpose. As part of the Mt. Everest 8848 Art Project, a group of 15 artists from Nepal collected 1.5 tons of garbage brought down the mountain by climbers.They've transformed the cans and oxygen tanks—and in one case, part of the remains of a helicopter—into 74 pieces of art that have already gone on exhibition in Nepal's capital. Part of the profit from sales will go to an association, which has helped collect tons of rubbish on the slopes of the mountain.【语篇解读】文章介绍了由于很多人攀登珠穆朗玛峰,现在那里正在变成一个垃圾堆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五单元 滚动检测试题 (时间:60分钟 满分:100分) 编者选题表 考点 题号 第一、二、三、四单元 1、2、3、4、5、6、7 两极格局的形成 8、9、10、11、12、13 世界多极化趋势 14、15、16、17、18、19、20 综合 21、22 一、选择题(本大题共20小题,每小题3分,共60分) 1.(2013湛江一模)东汉政论家仲长统在《昌言》中指出:“汉之初兴,分王子弟,委之以士民之命,假之以杀生之权。”这一记载可以说明西汉初期( ) A.加强了中央集权 B.实现了选贤任能 C.实行了分封制度 D.强化了郡县制度 解析:C 本题关键信息“汉之初兴,分王子弟”,汉初郡国并行制的实行产生了非常严重的消极影响,C项正确。A项与史实相反,B、D两项与材料信息不符。 2.(2013韶关一模)“士的地位介于贵族与平民之间,在社会流动中,成为上下升降的汇聚之所,观念转变也较快”。以下解读正确的是( ) A.察举征辟制导致知识分子最善于接受新思想 B.九品中正制促成士中大部分成为社会的上层 C.科举制为知识分子的上升提供制度性途径 D.农民起义式的社会流动使知识分子地位不能上升 解析:C 首先明确材料中的“士”指社会底层的知识分子,科举制为这些知识分子提供了参政机会,并将其制度化。察举是以“孝廉”为主要选官标准,主要从道德标准评价人才,与知识分子没有必然联系,A项错误。九品中正制选官的标准是门第、出身,而介于贵族与平民之间的士,很难成为社会上层,B项错误。D项说法过于绝对,如汉初明初等很多开国功臣谋士就得益于农民起义运动的成功。 3.(2013年广东文综,18)雅典的陶片放逐法规定,每年召开特别的公民大会,投票决定将那些严重威胁民主政治的人流放海外。据此,下列行为中可能使公民遭到流放的是( ) A.不按时参加公民大会 B.不同意授予外邦人公民权 C.为赢得个人政治声望资助贫穷公民 D.拒绝参加城邦举行的戏剧表演 解析:C 本题考查学生对陶片放逐法的理解。陶片放逐法针对的对象是民主威胁者,分析备选项,C项属于民主威胁者的行为。A、B、D三项均不会对雅典民主政治构成威胁。 4.(2014巢湖模拟)有人说:“美国总统是世界上最令人向往的一个职位。”但即使是伟大的华盛顿,也只连任了两届就引退,其他继任者连任—般也不超过两届。据此分析导致这一现象的原因不包括( ) A.美国受民主思想影响较深 B.美国人民强烈反对再回到封建专制的时代 C.三权分立体制的制约 D.华盛顿等人的榜样作用 解析:B 根据所学知识,A、C、D三项说法正确,是美国民主共和国长期稳定的原因;B项说法错误,美国没有经历封建社会,它是由欧洲移民而形成的国家,并不存在封建专制的时代。 5.(2014清远调研)梁漱溟在报上发表题为《论学生事件》的文章,他说:“纵然曹、章罪大恶极,在罪名未成立时,他仍有他的自由。我们纵然是爱国急公的行为,也不能侵犯他,加暴行于他。”从这段材料中提炼的信息有( ) ①学生有爱国之举 ②学生对传统文化的彻底批判 ③学生爱国且尊重人权、遵守法律 ④学生行为有过激之举 A.①③ B.①④ C.③④ D.②④ 解析:B 本题考查学生对五四运动的认识,主要考查学生获取和解读信息、分析比较以理解问题的能力。通过分析材料的信息“纵然曹、章罪大恶极”可知,这一评论与五四运动要求罢免曹汝霖、陆宗舆、章宗祥的职务有关。由材料“是爱国急公的行为”,说明①正确;材料没有涉及对传统文化的态度,②不正确;由材料“在罪名未成立时,他仍有他的自由”“不能侵犯他,加暴行于他”表明③错误;材料信息说明学生存在过激行为,④正确。综上,选择B项。 6.(2013年福建文综,20)“中国为酷爱和平之民族,过去四年余之神圣抗战,原期侵略者之日本于遭受实际上之惩创后,终能反省„„不料残暴成性之日本,执迷不悟,且更悍然向我英美诸友邦开衅„„兹特正式对日宣战”。这一文告发表的历史背景是( ) A.九一八事变爆发 B.全面抗战开始 C.太平洋战争爆发 D.国共合作宣言公布 解析:C 由“过去四年余之神圣抗战„„向我英美诸友邦开衅„„”可知这一告示发表在全面抗战开始后的第四年,即1941年,这一年爆发了太平洋战争,所以正确答案为C项。A项发生在1931年,B、D两项发生在1937年,所以A、B、D三项在时间上都不符合题干要求。故正确答案为C项。 7.(2013汕头一模)1953年底,美国情报部门一封电报写道:“中国外交政策的目标是在其周边地区(指新兴民族独立国家)促进和建立可以作为缓冲的友好国家。”做出这种判断的依据是( ) A.中国提出“一边倒”外交战略 B.中国提出了和平共处五项原则 C.中国缓和了与美国的外交关系 D.中国和日本建立了外交关系 解析:B 和平共处五项原则是新中国为了发展与周边国家的关系而提出的,因此,B项正确,A、C、D三项与和平共处五项原则没有关系,时间信息也不正确。 8.美国总统杜鲁门说:“我深切地感觉到,如果听任朝鲜沦丧,那么共产党的领袖们就会越发狂妄地向更靠近我们海岸的国家进行侵略。”下列评述正确的是( ) A.为此美国悍然挑起了朝鲜战争 B.这标志着杜鲁门主义的提出 C.美国的随后行动导致了朝鲜的分裂 D.这种思想体现出了典型的冷战思维 解析:D 杜鲁门发表该演说时朝鲜战争已经爆发,并非美国“挑起”,A项错误。杜鲁门主义提出是在1947年,朝鲜战争爆发于1950年,B项错误。朝鲜的分裂是美苏划分势力范围的结果,并非朝鲜战争所致,C项错误。 9.美国在二战后的全球扩张中,高喊着美英有义务和责任“保卫‘自由世界’免受共产主义的影响”;基辛格认为斯大林的“最高原则还是装上共产主义意识形态的苏联国家利益”。上述观点表明( ) ①美苏对抗中意识形态色彩浓厚 ②维护国家利益是美苏的根本目的 ③美苏为其对外扩张寻找合适借口 ④这种行为促进了世界的和平与稳定 A.①②③④ B.①②③ C.①②④ D.③④ 解析:B 此题考查学生对二战后美苏两极格局的理解。根据题干提供的信息和所学史实,二战后美苏由二战中的反法西斯盟友转变为冷战对峙、全面对抗,加剧了世界的紧张。故应该排除④。 10.1948年10月丘吉尔提出“三环外交”:第一环是英联邦,包括英国及其自治领、殖民地;第二环是英语世界,包括英、美、加拿大等讲英语的国家;第三环是联合起来的欧洲。环环相扣,以英国为核心。此项政策的提出主要基于( ) A.美苏为首的两大集团对峙局面的形成 B.遏制共产主义势力在欧洲扩张的需要 C.欧共体的政治联合步伐落后于经济联合 D.二战后英国和欧洲的国际地位被削弱 解析:D 材料反映英国注重发展与本国利益相关的国家的关系,摆脱了工业革命以来的“光荣孤立”政策。“光荣孤立”政策是建立在强大的综合国力基础之上的,“三环外交”是综合国力衰落的选择。 11.(2013泉州一模)“事情的真相是:三四年后,欧洲对外来粮食和其他大部分来自美国主要产品的需要较诸它目前所能偿付的能力要大得多,因而它必须获得实质上的额外援助,否则,便得面对具有非常严重性的经济、社会与政治的危机。”为了避免“危机”,美国( ) A.占领德国 B.建立北约 C.实施马歇尔计划 D.进行核威慑 解析:C 二战后,西欧普遍经济萧条、政局动荡,发生社会主义革命的可能性很高,美国实行马歇尔计划的目的就是稳定西欧的经济秩序,以防止西欧倒向苏联。 12.(2013衢州质检)赫鲁晓夫曾强烈反感甲壳虫乐队,他说“苏联青年不需要这种刺耳的垃圾”,甚至宣称,“从萨克斯管到弹簧刀仅有一步之遥。”对此理解正确的是( ) A.“良知复兴”运动在苏联受挫 B.苏联拒绝无用、堕落的音乐形式 C.经济结构决定苏联的消费水平 D.政治是影响文化传播的重要因素 解析:D 赫鲁晓夫执政时期,处于美苏冷战时期,社会制度和意识形态的对立影响了文化的交流和传播,因此赫鲁晓夫“强烈反感甲壳虫乐队”。 13.“北欧平衡”是指冷战时期的北欧地区以执行武装中立的瑞典为中轴,分别存在受苏联影响和支配的芬兰(保持主权独立且不与西方结盟),及加入北约的挪威、丹麦和冰岛(三国承诺不会对苏联安全构成威胁)。北欧平衡局面一直持续到20世纪80年代后期。对“北欧平衡”理解正确的是( ) A.是美苏冷战政策的恶果 B.有利于维护地区的和平 C.是苏联国力衰弱的表现 D.客观上推动了冷战升级 解析:B 北欧国家的做法本质上是摆脱美苏“冷战”的做法,有利于减少“冷战”对北欧的消极影响,所以,有利于维护地区的和平。 14.(2013宁德质检)美国学者C.W.沃特森认为,任何文明都是历史的产物,有其内在和特定的价值体系,没有一种文明可以宣称比其他更为优越,也没有理由以主流文明自居,并歧视、否定甚至取代其他文明。对此观点理解不准确的是( ) A肯定文明的独特性和价值 B.主张文明之间的平等 C.强调对不同文明的尊重 D.认同西方文明的优越感 解析:D C.W.沃特森认为不同文明之间是平等的,没有主流与非主流之分,故其不可能认同西方文明具有优越感。 15.“世界上有大大小小200多个国家,可是如果没有人管它们,这个世界就是个无政府的世界,肯定会一团糟。所以要有个东西来管,这个东西就是最强大的国家。这个最强大的国家有霸权,但是这个霸权是符合世界稳定的要求的。”该言论属于( ) A.和平共处论 B.独立自主论 C.霸权稳定论 D.联合国安理会表决论 解析:C 材料中的观点认为,霸权有利于世界的稳定,实际是为美国的霸权主义政策辩护,因此,正确的答案为C项。 16.(2013湛江模拟)1968年法国总统戴高乐公开批评越南战争是“一个伟大国家蹂躏一个小国”的“可憎”的战争,能够和这一情景联系起来的是( ) A.美国霸权地位逐渐确立 B.欧洲共同体的实力增强 C.经济全球化的日益加强 D.多极化格局的最终形成 解析:B 题干反映了法国挑战美国的霸主地位,不再对美国惟命是从,其原因在于欧洲共同体的发展,增强了西欧国家的实力。故选B项。 17.(2013潍坊模拟)伊曼纽尔·沃勒斯坦谈到:“苏联解体了。对美国而言,这是个灾!”他提出这一观点的主要依据是( ) A.国际力量失衡引发冲突 B.恐怖主义猖獗
