三角函数关系式
高中数学-同角三角函数基本关系式及诱导公式
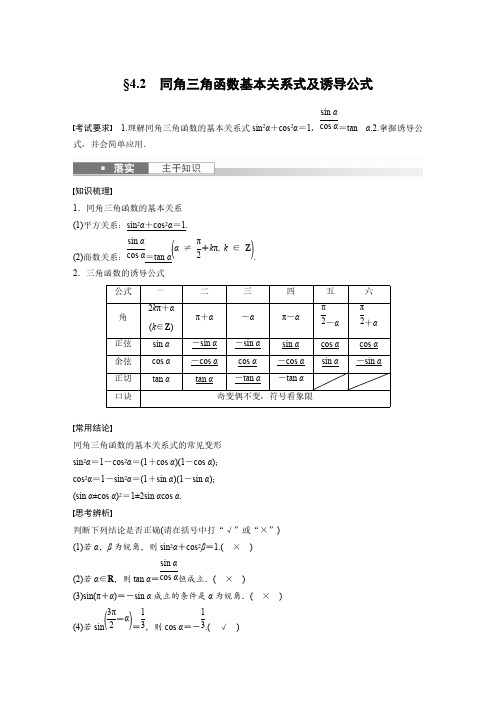
§4.2 同角三角函数基本关系式及诱导公式考试要求 1.理解同角三角函数的基本关系式sin 2α+cos 2α=1,=tan α.2.掌握诱导公sin αcos α式,并会简单应用.知识梳理1.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1.(2)商数关系:=tan α.sin αcos α(α≠π2+k π,k ∈Z)2.三角函数的诱导公式公式一二三四五六角2k π+α(k ∈Z )π+α-απ-α-απ2+απ2正弦sin α-sin α-sin αsin αcos αcos α余弦cos α-cos αcos α-cos αsin α-sin α正切tan αtan α-tan α-tan α口诀奇变偶不变,符号看象限常用结论同角三角函数的基本关系式的常见变形sin 2α=1-cos 2α=(1+cos α)(1-cos α);cos 2α=1-sin 2α=(1+sin α)(1-sin α);(sin α±cos α)2=1±2sin αcos α.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若α,β为锐角,则sin 2α+cos 2β=1.( × )(2)若α∈R ,则tan α=恒成立.( × )sin αcos α(3)sin(π+α)=-sin α成立的条件是α为锐角.( × )(4)若sin =,则cos α=-.( √ )(3π2-α)1313教材改编题1.已知α是第二象限角,sin α=,则cos α的值为.55答案 -255解析 ∵sin α=,α是第二象限角,55∴cos α=-=-.1-sin2α2552.已知=-5,那么tan α的值为.sin α-2cos α3sin α+5cos α答案 -2316解析 由=-5,知cos α≠0,等式左边分子、分母同时除以cos α,sin α-2cos α3sin α+5cos α可得=-5,解得tan α=-.tan α-23tan α+523163.化简·sin(α-π)·cos(2π-α)的结果为.cos (α-π2)sin (5π2+α)答案 -sin 2α解析 原式=·(-sin α)·cos αsin αcos α=-sin 2α.题型一 同角三角函数基本关系例1 (1)已知cos α=-,则13sin α+5tan α= .513答案 0解析 ∵cos α=-<0且cos α≠-1,513∴α是第二或第三象限角.①若α是第二象限角,则sin α===,1-cos2α1-(-513)21213∴tan α===-.sin αcos α1213-513125此时13sin α+5tan α=13×+5×=0.1213(-125)②若α是第三象限角,则sin α=-=-1-cos2α1-(-513)2=-,1213∴tan α===,sin αcos α-1213-513125此时,13sin α+5tan α=13×+5×=0.(-1213)125综上,13sin α+5tan α=0.(2)已知tan α=,则= ;sin 2α+sin αcos α+2=.12sin α-3cos αsin α+cos α答案 - 53135解析 已知tan α=,12所以==-.sin α-3cos αsin α+cos αtan α-3tan α+153sin 2α+sin αcos α+2=+2sin2α+sin αcos αsin2α+cos2α=+2tan2α+tan αtan2α+1=+2=.(12)2+12(12)2+1135(3)已知sin θ+cos θ=,θ∈(0,π),则tan θ=.713答案 -125解析 由sin θ+cos θ=,得sin θcos θ=-,71360169因为θ∈(0,π),所以sin θ>0,cos θ<0,所以sin θ-cos θ==,1-2sin θcos θ1713联立Error!解得Error!所以tan θ=-.125教师备选1.(2022·锦州联考)已知=5,则cos 2α+sin 2α等于( )sin α+3cos α3cos α-sin α12A. B .-3535C .-3D .3答案 A解析 由=5,得=5,sin α+3cos α3cos α-sin αtan α+33-tan α可得tan α=2,则cos 2α+sin 2α=cos 2α+sin αcos α12==cos2α+sin αcos αcos2α+sin2α1+tan α1+tan2α=.352.若α∈(0,π),sin(π-α)+cos α=,则sin α-cos α的值为( )23A. B .-2323C. D .-4343答案 C解析 由诱导公式得sin(π-α)+cos α=sin α+cos α=,23所以(sin α+cos α)2=1+2sin αcos α=,29则2sin αcos α=-<0,79因为α∈(0,π),所以sin α>0,所以cos α<0,所以sin α-cos α>0,因为(sin α-cos α)2=1-2sin αcos α=,169所以sin α-cos α=.43思维升华 (1)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.(2)注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α.跟踪训练1 (1)(2021·新高考全国Ⅰ)若tan θ=-2,则等于( )sin θ(1+sin 2θ)sin θ+cos θA .- B .- C. D.65252565答案 C解析 方法一 因为tan θ=-2,所以角θ的终边在第二或第四象限,所以Error!或Error!所以=sin θ(1+sin 2θ)sin θ+cos θsin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ)=sin 2θ+sin θcos θ=-=.452525方法二 (弦化切法)因为tan θ=-2,所以sin θ(1+sin 2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ)=sin2θ+sin θcos θsin2θ+cos2θ===.tan2θ+tan θ1+tan2θ4-21+425(2)已知α是三角形的内角,且tan α=-,则sin α+cos α的值为.13答案 -105解析 由tan α=-,得sin α=-cos α,1313将其代入sin 2α+cos 2α=1,得cos 2α=1,109所以cos 2α=,易知cos α<0,910所以cos α=-,sin α=,310101010故sin α+cos α=-.105题型二 诱导公式例2 (1)已知sin =,则cos 的值为( )(α-π4)13(π4+α)A. B .-223223C. D .-1313答案 D解析 cos =cos (π4+α)[π2+(α-π4)]=-sin=-.(α-π4)13延伸探究 本例(1)改为已知θ是第二象限角,且sin=,则tan =.(θ+π4)45(θ-π4)答案 34解析 ∵θ是第二象限角,且sin=,(θ+π4)45∴θ+为第二象限角,π4∴cos=-,(θ+π4)35∴tan=(θ-π4)sin (θ-π4)cos (θ-π4)=sin [(θ+π4)-π2]cos [(θ+π4)-π2]=-cos (θ+π4)sin (θ+π4)==.-(-35)4534(2)的值为( )tan (π-α)cos (2π-α)sin (-α+3π2)cos (-α-π)sin (-π-α)A .-2B .-1C .1D .2答案 B解析 原式=-tan α·cos α·(-cos α)cos (π+α)·[-sin (π+α)]=tan α·cos2α-cos α·sin α=-·=-1.sin αcos αcos αsin α教师备选1.已知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P ,且角α的始边与x 轴的正半轴重合,终边过点P ,则等于( )cos(11π2-α)sin(9π2+α)+sin 2αcos (π2+α)sin (-π-α)A. B .-2323C. D .-3232答案 B解析 易知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P (2,3),故tan α=,则32cos(11π2-α)sin (9π2+α)+sin 2αcos (π2+α)sin (-π-α)=cos (3π2-α)sin (π2+α)+sin 2αcos (π2+α)sin α=-sin αcos α+2sin αcos α-sin αsin α=-cos αsin α=-=-.1tan α232.若sin x =3sin ,则cos x ·cos 等于( )(x -π2)(x +π2)A. B .-310310C. D .-3434答案 A解析 易知sin x =3sin =-3cos x ,(x -π2)所以tan x =-3,所以cos x cos(x +π2)=-sin x cos x =-sin x cos x sin2x +cos2x ==.-tan x tan2x +1310思维升华 (1)诱导公式的两个应用①求值:负化正,大化小,化到锐角为终了;②化简:统一角,统一名,同角名少为终了.(2)诱导公式的应用步骤任意负角的三角函数任意正角的三角函数0~2π内的角的――――――→利用诱导公式三或一――――――→利用诱导公式一三角函数锐角三角函数.――――――→利用诱导公式二或四或五或六跟踪训练2 (1)已知cos(75°+α)=,求cos(105°-α)+sin(15°-α)= .13答案 0解析 因为(105°-α)+(75°+α)=180°,(15°-α)+(α+75°)=90°,所以cos(105°-α)=cos[180°-(75°+α)]=-cos(75°+α)=-,13sin(15°-α)=sin[90°-(α+75°)]=cos(75°+α)=.13所以cos(105°-α)+sin(15°-α)=-+=0.1313(2)(2022·盐城南阳中学月考)设tan(5π+α)=2,则=.sin (-3π+α)+cos (α-π)cos (α-112π)+sin(9π2+α)答案 3解析 由已知tan(5π+α)=tan α=2,sin (-3π+α)+cos (α-π)cos (α-112π)+sin(9π2+α)=sin (π+α)+cos (π-α)cos (α+π2)+sin (π2+α)=-sin α-cos α-sin α+cos α=sin α+cos αsin α-cos α==3.tan α+1tan α-1题型三 同角三角函数基本关系式和诱导公式的综合应用例3 已知f (α)=.sin (α-3π)cos (2π-α)sin (-α+3π2)cos (-π-α)sin (-π-α)(1)化简f (α);(2)若α=-,求f (α)的值;31π3(3)若cos=,α∈,求f (α)的值.(-α-π2)15[π,3π2]解 (1)f (α)=sin (α-3π)cos (2π-α)sin (-α+3π2)cos (-π-α)sin (-π-α)=-sin α×cos α×(-cos α)-cos α×sin α=-cos α.(2)若α=-,31π3则f (α)=-cos=-cos =-.(-31π3)π312(3)由cos=,(-α-π2)15可得sin α=-,15因为α∈,[π,3π2]所以cos α=-,265所以f (α)=-cos α=.265教师备选设f (α)=(1+2sin α≠0).2sin (π+α)cos (π-α)-cos (π+α)1+sin2α+cos(3π2+α)-sin2(π2+α)(1)化简f (α);(2)若α=-,求f (α)的值.23π6解 (1)f (α)=(-2sin α)·(-cos α)-(-cos α)1+sin2α+sin α-cos2α=2sin αcos α+cos α2sin2α+sin α=cos α(2sin α+1)sin α(2sin α+1)==.cos αsin α1tan α(2)当α=-时,23π6f (α)=f =(-23π6)1tan (-23π6)=1tan (-4π+π6)=1tan π6==.1333思维升华 (1)利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式进行变形.(2)注意角的范围对三角函数符号的影响.跟踪训练3 (1)(2022·聊城模拟)已知α为锐角,且2tan(π-α)-3cos +5=0,tan(π+α)(π2+β)+6sin(π+β)-1=0,则sin α的值是( )A. B. C. D.3553773101013答案 C解析 由已知得Error!消去sin β,得tan α=3,∴sin α=3cos α,代入sin 2α+cos 2α=1,化简得sin 2α=,则sin α=(α为锐角).91031010(2)已知-π<x <0,sin(π+x )-cos x =-,则=.15sin 2x +2sin2x 1-tan x答案 -24175解析 由已知,得sin x +cos x =,15两边平方得sin 2x +2sin x cos x +cos 2x =,125整理得2sin x cos x =-.2425∴(sin x -cos x )2=1-2sin x cos x =,4925由-π<x <0知,sin x <0,又sin x cos x =-<0,1225∴cos x >0,∴sin x -cos x <0,故sin x -cos x =-.75∴=sin 2x +2sin2x 1-tan x2sin x (cos x +sin x )1-sin x cos x=2sin x cos x (cos x +sin x )cos x -sin x ==-.-2425×157524175课时精练1.cos等于( )(-19π3)A .-B .-3212C.D.1232答案 C解析 cos=cos (-19π3)19π3=cos=cos =.(6π+π3)π3122.若cos 165°=a ,则tan 195°等于( )A.B.1-a 21-a 2aC .-D .-1-a 2aa1-a 2答案 C解析 若cos 165°=a ,则cos 15°=cos(180°-165°)=-cos 165°=-a ,sin 15°=,1-a 2所以tan 195°=tan(180°+15°)=tan 15°=sin 15°cos 15°=-.1-a 2a3.若cos =,则sin 等于( )(α-π5)513(7π10-α)A .- B .-5131213C. D.1213513答案 D解析 因为-α+=,7π10(α-π5)π2所以-α=-,7π10π2(α-π5)所以sin =cos =.(7π10-α)(α-π5)5134.(2022·天津西青区模拟)已知sin α+cos α=-,则tan α+等于( )21tan αA .2 B. C .-2 D .-1212答案 A解析 由已知得1+2sin αcos α=2,∴sin αcos α=,12∴tan α+=+1tan αsin αcos αcos αsin α===2.sin2α+cos2αsin αcos α1125.(多选)在△ABC 中,下列结论正确的是( )A .sin(A +B )=sin CB .sin =cos B +C2A2C .tan(A +B )=-tan C (C ≠π2)D .cos(A +B )=cos C 答案 ABC解析 在△ABC 中,有A +B +C =π,则sin(A +B )=sin(π-C )=sin C ,A 正确.sin =sin =cos ,B 正确.B +C 2(π2-A 2)A2tan(A +B )=tan(π-C )=-tan C,(C ≠π2)C 正确.cos(A +B )=cos(π-C )=-cos C ,D 错误.6.(多选)已知α∈(0,π),且sin α+cos α=,则( )15A.<α<ππ2B .sin αcos α=-1225C .cos α-sin α=75D .cos α-sin α=-75答案 ABD解析 ∵sin α+cos α=,15等式两边平方得(sin α+cos α)2=1+2sin αcos α=,125解得sin αcos α=-,故B 正确;1225∵α∈(0,π),sin αcos α=-<0,1225∴α∈,故A 正确;(π2,π)cos α-sin α<0,且(cos α-sin α)2=1-2sin αcos α=1-2×=,(-1225)4925解得cos α-sin α=-,故D 正确.757.cos 1°+cos 2°+cos 3°+…+cos 177°+cos 178°+cos 179°= .答案 0解析 因为cos(180°-α)=-cos α,于是得cos 1°+cos 2°+cos 3°+…+cos 89°+cos 90°+cos 91°+…+cos 177°+cos 178°+cos 179°=cos 1°+cos 2°+cos 3°+…+cos 89°+cos 90°-cos 89°-…-cos 3°-cos 2°-cos 1°=cos 90°=0.8.设f (θ)=,则f =.2cos2θ+sin2(2π-θ)+sin (π2+θ)-32+2cos2(π+θ)+cos (-θ)(17π3)答案 -512解析 ∵f (θ)=2cos2θ+sin2θ+cos θ-32+2cos2θ+cos θ=,cos2θ+cos θ-22cos2θ+cos θ+2又cos =cos17π3(6π-π3)=cos =,π312∴f ==-.(17π3)14+12-212+12+25129.(1)已知cos α是方程3x 2-x -2=0的根,且α是第三象限角,求的值;sin (-α+3π2)cos(3π2+α)tan2(π-α)cos (π2+α)sin (π2-α)(2)已知sin x +cos x =-(0<x <π),求cos x -2sin x 的值.713解 (1)因为方程3x 2-x -2=0的根为x 1=1,x 2=-,23又α是第三象限角,所以cos α=-,23所以sin α=-,tan α=.5352所以原式==tan 2α=.-cos αsin αtan2α-sin αcos α54(2)∵sin x +cos x =-(0<x <π),713∴cos x <0,sin x >0,即sin x -cos x >0,把sin x +cos x =-,713两边平方得1+2sin x cos x =,49169即2sin x cos x =-,120169∴(sin x -cos x )2=1-2sin x cos x =,289169即sin x -cos x =,1713联立Error!解得sin x =,cos x =-,5131213∴cos x -2sin x =-.221310.(2022·衡水模拟)已知角α的终边经过点P (3m ,-6m )(m ≠0).(1)求的值;sin (α+π)+cos (α-π)sin (α+π2)+2cos (α-π2)(2)若α是第二象限角,求sin 2+sin(π-α)cos α-cos 的值.(α+3π2)(π2+α)解 (1)∵m ≠0,∴cos α≠0,即sin (α+π)+cos (α-π)sin (α+π2)+2cos (α-π2)=-sin α-cos αcos α+2sin α=.-tan α-11+2tan α又∵角α的终边经过点P (3m ,-6m )(m ≠0),∴tan α==-2,-6m3m 故sin (α+π)+cos (α-π)sin (α+π2)+2cos (α-π2)=-tan α-11+2tan α==-.2-11+2×(-2)13(2)∵α是第二象限角,∴m <0,则sin α=-6m(3m )2+(-6m )2=-6m 35|m |=,255cos α=3m(3m )2+(-6m )2=3m 35|m |=-,55∴sin 2+sin(π-α)cos α-cos (α+3π2)(π2+α)=cos 2α+sin αcos α+sin α=2+×+(-55)255(-55)255=.-1+25511.(多选)已知角α满足sin α·cos α≠0,则表达式+(k ∈Z )的取值可能sin (α+k π)sin αcos (α+k π)cos α为( )A .-2 B .-1或1C .2 D .-2或2或0答案 AC解析 当k 为奇数时,原式=+=(-1)+(-1)=-2;-sin αsin α-cos αcos α当k 为偶数时,原式=+=1+1=2.sin αsin αcos αcos α∴原表达式的取值可能为-2或2.12.(2022·河北六校联考)若sin α是方程5x 2-7x -6=0的根,则等于( )sin (-α-3π2)sin (3π2-α)tan2(2π-α)cos (π2-α)cos (π2+α)sin (π+α)A. B. C. D.35534554答案 B解析 方程5x 2-7x -6=0的两根为x 1=-,x 2=2,则sin α=-.3535原式==-=.cos α(-cos α)tan2αsin α(-sin α)(-sin α)1sin α5313.曲线y =e x +x 2-x 在x =0处的切线的倾斜角为α,则sin=.23(2α+π2)答案 45解析 由题意得y ′=f ′(x )=e x +2x -,23所以f ′(0)=e 0-=,2313所以tan α=,13所以α∈,(0,π2)所以cos α=,310所以sin(2α+π2)=cos 2α=2cos 2α-1=2×-1=.9104514.函数y =log a (x -3)+2(a >0且a ≠1)的图象过定点Q ,且角α的终边也过点Q ,则3sin 2α+2sin αcos α=.答案 75解析 由题意可知点Q (4,2),所以tan α=,12所以3sin 2α+2sin αcos α=3sin2α+2sin αcos αsin2α+cos2α=3tan2α+2tan α1+tan2α=3×14+2×121+14=.7515.(多选)已知f (α)=,则下列说法正确的是( )2sin αcos α-2sin α+cos α+1(0≤α≤π2)A .f (α)的最小值为-2B .f (α)的最小值为-1C .f (α)的最大值为-12D .f (α)的最大值为1-2答案 BD解析 设t =sin α+cos α=sin,2(α+π4)由0≤α≤,π2得≤α+≤,π4π43π4则1≤t ≤,2又由(sin α+cos α)2=t 2,得2sin αcos α=t 2-1,所以f (α)=g (t )==t -1-,t 2-1-2t +12t +1又因为函数y =t -1和y =-在[1,]上单调递增,2t +12所以g (t )=t -1-在[1,]上单调递增,2t +12g (t )min =g (1)=-1,g (t )max =g ()=1-.2216.已知关于x 的方程2x 2-(+1)x +m =0的两根分别是sin θ和cos θ,θ∈(0,2π),求:3(1)+的值;sin2θsin θ-cos θcos θ1-tan θ(2)m 的值;(3)方程的两根及此时θ的值.解 (1)原式=+sin2θsin θ-cos θcos θ1-sin θcos θ=+sin2θsin θ-cos θcos2θcos θ-sin θ=sin2θ-cos2θsin θ-cos θ=sin θ+cos θ.由已知得sin θ+cos θ=,3+12所以+=.sin2θsin θ-cos θcos θ1-tan θ3+12(2)由已知得sin θcos θ=,m2因为1+2sin θcos θ=(sin θ+cos θ)2,所以1+m =2,(3+12)解得m =.32(3)联立Error!解得Error!或Error!因为θ∈(0,2π),所以θ=或.π3π6。
三角函数的基本关系及诱导公式

;足球推荐 足球推荐;
(三)例题分析:
例1.化简: s i n ( ) c o s ( )
4
4
解:原式
sin(
)
cos[
(
)]
4
2
4
sin( ) sin( ) 0
4
4
(三)例题分析:
例2.化简:
tan (cos
sin
)
sin cot
2
,∴sin
3 ,cos
2
1 2
,
又∵ 3 2 ,
2
∴ =11π/6 .
(四)巩固练习:
1.若 f (cos x) cos 2x , f (sin15 ) ( D )
( A) 1 2
(B)
1 2
(C )
3 (D) 3
2
2
2.已知 sin cos 1 (0 ) ,则 tan
形的中心角的弧度数是
.
回顾:任意角的正弦,余弦,正切,余切,正割,余割是如何定义的?
(一)知识点:
1.同角三角函数的基本关系式:
(1)倒数关系: tan cot 1
(2)商数关系: ta n
sin cos
, cot
cos sin
(3)平方关系:sin 2 cos 2 1
5
所以 cos 3
5
2 sin 4
5
所以 cot( 11 ) cot( 3 ) tan 4
2
2
3
(三)例题分析:
例4.若 tan 2 ,求值① c o s s in ;
cos sin ② 2 sin 2 sin cos cos2
解:①原式
三角函数关系式
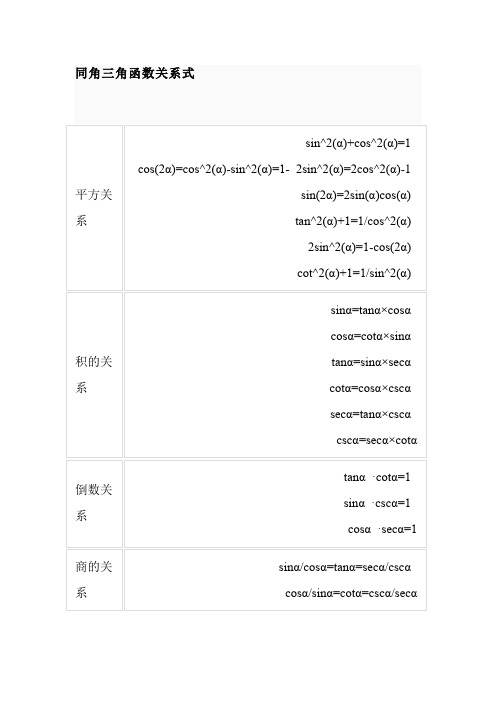
诱导公式的表格以及推导方法(定名法则和定号法则)两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积公式sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]积化和差公式sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]倍角公式sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2α-sin^2;α=2cos^2;α-1=1-2sin^2;αtan(2α)=2tanα/(1-tan^2;α)cot(2α)=(cot^2;α-1)/(2cotα)sec(2α)=sec^2;α/(1-tan^2;α)csc(2α)=1/2*secα·cscα三倍角公式sin(3α) = 3sinα-4sin^3;α = 4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3;α-3cosα = 4cosα·cos(60°+α)cos(60°-α) tan(3α)=(3tanα-tan^3;α)/(1-3tan^2;α)=tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3;α-3cotα)/(3cotα-1)n倍角公式sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n -5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…半角公式sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα cot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα) sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))辅助角公式Asinα+Bcosα=√(A^2;+B^2;)sin(α+arctan(B/A))Asinα+Bcosα=√(A^2;+B^2;)cos(α-arctan(A/B))万能公式sin(a)= (2tan(a/2))/(1+tan^2;(a/2))cos(a)= (1-tan^2;(a/2))/(1+tan^2;(a/2))tan(a)= (2tan(a/2))/(1-tan^2;(a/2))降幂公式sin^2;α=(1-cos(2α))/2=versin(2α)/2cos^2;α=(1+cos(2α))/2=covers(2α)/2tan^2;α=(1-cos(2α))/(1+cos(2α))三角和的三角函数sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·s inβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)÷(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)特殊角的三角函数值幂级数c0+c1x+c2x2+...+cnxn+...=∑cnxn (n=0..∞)c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n (n=0..∞) 它们的各项都是正整数幂的幂函数, 其中c0,c1,c2,...及a都是常数,这种级数称为幂级数。
第25讲 同角三角函数基本关系式及诱导公式6种题型总结

第25讲同角三角函数基本关系式及诱导公式6种题型总结【考点分析】考点一:同角三角函数基本关系①平方关系:1cos sin 22=+αα.②商数关系:)2(tan cos sin ππααααk +≠=;考点二:三角函数诱导公式公式一二三四五六角)(2Z k k ∈+απαπ+α-απ-απ-2απ+2正弦αsin αsin -αsin -αsin αcos αcos 余弦αcos αcos -αcos αcos -αsin αsin -正切αtan αtan αtan -αtan -口诀函数名不变,符号看象限函数名改变,符号看象限【记忆口诀】奇变偶不变,符号看象限注意:①先将诱导三角函数式中的角统一写作2n πα⋅±;②无论有多大,一律视为锐角,判断2n πα⋅±所处的象限,并判断题设三角函数在该象限的正负;③当n 为奇数是,“奇变”,正变余,余变正;当n 为偶数时,“偶不变”函数名保持不变即可.【典例例题】题型一:同角三角函数公式求值【例1】已知角α为第二象限角,tan 3α=-,则cos α=()A .10B .10C .10-D .10【例2】已知12cos 13α=-,α是第三象限角,求sin α,tan α的值.【题型专练】1.已知13sin ,,322ππαα⎛⎫=∈ ⎪⎝⎭,则tan α=___________.2.下列四个命题中可能成立的一个是()A .1sin 3α=且2cos 3α=B .sin 0α=且cos 1α=-C .tan 1α=且cos 1α=-D .sin tan cos ααα-=(α为第二象限角)3.已知tan 2α=,32παπ<<,则cos sin αα-=()A B .C .5D .题型二:弦的齐次式问题【例1】已知角α的终边过点()13-,,求:①tan α;②sin cos sin 2cos αααα+-;③sin cos αα⋅【例2】已知tan 3α=,则ααααα222cos sin 21sin 2cos sin 2---___________.【例3】已知θ是第四象限角,()1,M m 为其终边上一点,且sin 5m θ=,则2sin cos sin cos θθθθ-+的值()A .0B .45C .43D .5【题型专练】1.已知tan 2α=,则sin 2cos 3cos 2sin αααα+-的值为()A .4B .4-C .54D .54-2.已知π3π,24x ⎛⎫∈ ⎪⎝⎭,且332cos sin sin cos 5x x x x +=-,则tan x =().A .2-B .12-C .52-D .3-3.若sin cos 2sin cos θθθθ+=-,则sin cos θθ的值是()A .310-B .310C .310±D .344.若sin cos 2sin cos θθθθ+=-,则()=++θθθθθcos sin cos sin 21sin ()A .65-B .25-C .65D .25题型三:知一求二问题【例1】已知(0,π)α∈,且1sin cos 5αα+=,给出下列结论:①ππ2α<<;②12sin cos 25αα=-;③3cos 5α=;④7cos sin 5αα-=-.其中所有正确结论的序号是()A .①②④B .②③④C .①②③D .①③④【例2】已知0x π-<<,1sin cos 5x x +=,求下列各式的值.(1)sin cos x x -;(2)223sin 2sin cos cos x x x x -+.【例3】已知sin cos x x +=44sin cos x x +=()A .98B .78C .54D .34)A.2或12B.2C.12D.12-【题型专练】1.已知13sin cos,644ππααα=-<<,则sin-cosαα的值等于()A.3B.3-C.3-D.432.已知1sin cos2θθ-=,则33sin cosθθ-=______.3.已知π(,π)2α∈,且1sin cos5αα+=,则sin cosαα=-____.4.(多选)已知(0,)θπ∈,1sin cos5θθ+=,则下列结论正确的是()A.,2πθπ⎛⎫∈ ⎪⎝⎭B.3cos5θ=-C.3tan4θ=-D.7sin cos5θθ-=5.已知1sin cos5θθ+=-,(0,)θπ∈,则sin cosθθ-=()A.15B.15-C.75D.75-题型四:诱导公式化简求值【例1】sin(9330︒)的值为()A.2B.12-C.12D.2【例2】已知7πtan6a⎛⎫=- ⎪⎝⎭,23πcos3b=,33πsin4c⎛⎫=- ⎪⎝⎭,则a,b,c的大小关系是()A.b c a>>B.a b c>>C.b a c>>D.a c b>>【例3】(1)计算:3sin(90)5tan1805cos0sin540-+︒+︒+︒;(2)化简:()3sin2cos()cos(2)sin()229cos()sin(3)sin()sin()2πππαααπαππαπααπα-+------+.【例4】设()()()sinπcosπxf x a b xαβ++=+,其中,,,a bαβ∈R,若()20215f=,则()2022f=()A.4B.3C.-5D.5【例5】已知sin(3π+θ)=13,则[]cos()cos cos()1πθθπθ+--+cos(2)33sin cos()sin22θπππθθπθ-⎛⎫⎛⎫---+⎪ ⎪⎝⎭⎝⎭=____.【题型专练】1.35πsin6=()2.cos 2040︒=()A .12B .12-C .2D .3.化简:sin(5)cos()cos(8)23sin()sin(4)2πθπθπθπθθπ-------=()A .-sin θB .sin θC .cos θD .-cos θ4.(1)化简:3sin(3)cos(2)sin 2cos()sin()παπαπαπαπα⎛⎫-⋅-⋅- ⎪⎝⎭-⋅--(2)求值:()()sin 150cos 210cos 420tan 60-︒⋅︒⋅-︒⋅︒5.已知()()()()()()sin cos 2tan tan sin f πβπββπββππβ--+=----.(1)若角β是第三象限角,且()1sin 5βπ-=,求()f β的值;(2)若2220β=︒,求()f β的值.题型五:诱导公式与三角函数定义、同角关系的综合运用【例1】已知3sin 5α=,且α是第二象限角,则cos()sin()παπα-++的值等于_______【例2】已知()1tan π2α-=2sin cos αα=-()A .14-B .14C .12D .12-【例3】已知角94α+的终边经过点(2,4)-,则23sin sin()cos απαα-+=()A .4-B .2-C .3D .9【例4】已知()()()()()3sin cos tan cos 222sin 2tan sin f πππααπαααπααππα⎛⎫⎛⎫⎛⎫+--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=---+.(1)化简()f α;(2)若31cos 25πα⎛⎫-=- ⎪⎝⎭,求()f α的值.【题型专练】1.已知tan()2πα+=-,则2sin 3cos 2sin 5cos αααα+=-___________.2.已知4sin()5απ+=,且sin cos 0αα<,则2sin()3tan(3)4cos(3)a αππαπ-+-=-________.3.已知22sin(3)cos(5)()3cos ()sin ()22f παπααππαα-+=-++.(1)若tan 2α=,求()f α的值;(2)若12()25f α=,(0,)απ∈,求sin cos αα-的值.4.已知(),0θπ∈-,且sin θ,cos θ为方程250x x m -+=的两根.(1)求m 的值;(2)求()()()23sin cos 2sin 25sin 3sin sin cos 222πθπθπθππππθθθθ⎛⎫-- ⎪-⎝⎭+⎛⎫⎛⎫⎛⎫--+-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值.5.已知3cos 4cos()02παπα⎛⎫--+= ⎪⎝⎭,求下列各式的值.(1)sin 2cos 5cos sin αααα+-;(2)24sin 3sin cos ααα-.题型六:换元法、角的拼凑【例1】若1sin ,63a π⎛⎫+= ⎪⎝⎭则2cos 3a π⎛⎫+= ⎪⎝⎭()A .13B .13-C .79D .79-【例2】已知5s n 3i πα⎛⎫ ⎪⎝=-⎭+,则3cos 10πα⎛⎫ ⎝-⎪⎭=()A.3B.3-C.3D.3【例3】若1sin 63πα⎛⎫+= ⎪⎝⎭,则5sin 6πα⎛⎫-= ⎪⎝⎭__________.【题型专练】1.当0,2πθ⎛⎫∈ ⎪⎝⎭时,若51cos 62πθ⎛⎫-=-⎪⎝⎭,则sin 6πθ⎛⎫+ ⎪⎝⎭的值为()A .12BC.D .12-2.若sin()63πα-=,则πcos()3α+=()A.B.CD3.(多选)已知π1sin 42α⎛⎫+= ⎪⎝⎭,下列结论正确的是()A.πcos 42α⎛⎫+=⎪⎝⎭B .π1cos 42α⎛⎫-=⎪⎝⎭C .5π1sin 42α⎛⎫+=⎪⎝⎭D .5π1cos 42α⎛⎫-=-⎪⎝⎭。
三角形三边关系公式三角函数

三角形三边关系公式三角函数三角形是初中数学中一个重要的几何形体,也是很多高中数学的基础知识。
而三角形的三边关系公式和三角函数则是三角形相关的必备知识。
下面我们来详细了解一下这方面的内容。
一、三角形三边关系公式三角形三边关系公式是求解三角形的重要公式,在初中的教学中,通过这些公式,可以求解任意三角形的内角和、周长、面积等重要性质。
1. 余弦定理:在任意三角形ABC中,设三边对应的内角分别为α、β、γ,边长分别为a、b、c,则有:cos α = (b² + c² - a²) / 2bccos β = (a² + c² - b²) / 2accos γ = (a² + b² - c²) / 2ab其中,cos表示余弦函数,a、b、c表示三边,α、β、γ表示与其对应的内角。
2. 正弦定理:在任意三角形ABC中,设三边对应的内角分别为α、β、γ,边长分别为a、b、c,则有:a / sin α =b / sin β =c / sinγ其中,sin表示正弦函数。
3. 勾股定理:在直角三角形ABC中,设斜边AB对应的内角为α,直角边AC和BC分别对应的内角为β、γ,斜边AB的长度为c,直角边AC和BC的长度分别为a、b,则有:a² + b² = c²二、三角函数三角函数是三角学中的重要分支,是数学和物理学中非常基础而常用的知识。
在初中数学中,学习三角函数有助于理解三角形的各种性质,同时也是后续高中数学学习的基础。
1. 正弦函数:在直角三角形ABC中,设斜边AB对应的内角为α,斜边AB的长度为c,直角边AC的长度为a,则有正弦函数:sin α = a / c2. 余弦函数:在直角三角形ABC中,设斜边AB对应的内角为α,斜边AB的长度为c,直角边BC的长度为b,则有余弦函数:cos α = b / c3. 正切函数:在直角三角形ABC中,设直角边AC对应的内角为α,直角边BC的长度为b,直角边AC的长度为a,则有正切函数:tan α = b / a4. 余切函数:在直角三角形ABC中,设直角边BC对应的内角为α,直角边BC的长度为b,直角边AC的长度为a,则有余切函数:cot α = a / b通过学习上述三角形三边关系公式和三角函数的知识,我们可以更深刻地理解三角形的结构和性质,从而更好地解决与其相关的问题。
三角函数间的转换关系大全

三角函数间的转换关系大全
三角函数间的转换关系有很多,以下是其中一些:
1. 设α为任意角,终边相同的角的同一三角函数的值相等,即
sin(2kπ+α)= sinα、cos(2kπ+α)= cosα、tan(2kπ+α)= tanα、
cot(2kπ+α)= cotα(其中k是整数)。
2. 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系,即
sin(π+α)= -sinα、cos(π+α)= -cosα、tan(π+α)= tanα、cot(π+α)=
cotα。
3. 任意角α与 -α的三角函数值之间的关系,即sin(-α)= -sinα、cos(-α)= cosα、tan(-α)= -tanα、cot(-α)= -cotα。
4. 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系,即
sin(π-α)= sinα、cos(π-α)= -cosα、tan(π-α)= -tanα、cot(π-α)= -cotα。
5. 利用公式二和公式三可以得到2π-α与α的三角函数值之间的关系,即
sin(2π-α)= -sinα、cos(2π-α)= cosα、tan(2π-α)= -tanα、cot(2π-α)= -cotα。
6. π/2±α及3π/2±α与α的三角函数值之间的关系,即sin(π/2+α)=
cosα、cos(π/2+α)= -sinα、tan(π/2+α)= -cotα、cot(π/2+α)= -tanα。
以上就是一些常见的三角函数间的转换关系,这些公式在解决三角函数问题时非常有用。
三角恒等式三角函数的基本关系
三角恒等式三角函数的基本关系三角恒等式是三角函数的基本关系之一。
在三角函数中,有一组常见的恒等式可用于简化计算和推导。
这些恒等式包括正弦、余弦、正切、余切、正割和余割函数之间的相互关系。
本文将对这些恒等式进行介绍和解释,以加深我们对三角函数的理解。
一、正弦和余弦的恒等式正弦函数和余弦函数是三角函数中最基本的函数之一。
它们之间存在以下恒等式:1. 正弦函数的平方加上余弦函数的平方等于1:sin^2(x) + cos^2(x) = 1这个恒等式可以通过勾股定理的三角形解释。
在单位圆上,三角形的直角边分别为正弦和余弦函数的值,斜边长度为1,因此满足此恒等式。
2. 余弦函数和正弦函数的和乘以余弦函数的差等于1:cos(x) + sin(x) * sin(x) = 1这个恒等式可以通过将sin^2(x)用1-cos^2(x)替代,然后化简得到。
二、正切和余切的恒等式正切函数和余切函数是三角函数中另外两个常见的函数。
它们之间存在以下恒等式:1. 正切函数等于正弦函数除以余弦函数:tan(x) = sin(x) / cos(x)这个恒等式可以通过将sin(x)和cos(x)的定义进行相除得到。
2. 余切函数等于余弦函数除以正弦函数:cot(x) = cos(x) / sin(x)这个恒等式可以通过将cos(x)和sin(x)的定义进行相除得到。
三、正割和余割的恒等式正割函数和余割函数亦是三角函数中的两个基本函数。
它们之间存在以下恒等式:1. 正割函数等于1除以余弦函数:sec(x) = 1 / cos(x)这个恒等式可以通过将cos(x)的倒数得到。
2. 余割函数等于1除以正弦函数:csc(x) = 1 / sin(x)这个恒等式可以通过将sin(x)的倒数得到。
结论:通过上述介绍,我们了解到正弦、余弦、正切、余切、正割和余割函数之间的基本恒等式。
这些恒等式在解三角函数的方程、证明三角恒等式以及进行三角函数的运算时起到了重要的作用。
三角函数大全
三角公式汇总一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22yx r +=,正弦:r y =αsin 余弦:rx =αcos 正切:x y =αtan 余切:y x =αcot 正割:xr =αsec余割:yr =αcsc注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
二、同角三角函数的基本关系式倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα。
商数关系:αααcos sin tan =,αααsin cos cot =。
平方关系:1cos sin 22=+αα,αα22sec tan 1=+,αα22csc cot 1=+。
三、诱导公式⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名不变,符号看象限)⑵απ+2、απ-2、απ+23、απ-23的三角函数值,等于α的异名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名改变,符号看象限)四、和角公式和差角公式βαβαβαsin cos cos sin )sin(⋅+⋅=+ βαβαβαsin cos cos sin )sin(⋅-⋅=- βαβαβαsin sin cos cos )cos(⋅-⋅=+ βαβαβαsin sin cos cos )cos(⋅+⋅=-βαβαβαtan tan 1tan tan )tan(⋅-+=+ βαβαβαtan tan 1tan tan )tan(⋅+-=-五、二倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=…)(*ααα2tan 1tan 22tan -=二倍角的余弦公式)(*有以下常用变形:(规律:降幂扩角,升幂缩角)αα2cos 22cos 1=+ αα2sin 22cos 1=-2)cos (sin 2sin 1ααα+=+ 2)cos (sin 2sin 1ααα-=-六、万能公式(可以理解为二倍角公式的另一种形式)ααα2tan 1tan 22sin +=,ααα22tan 1tan 12cos +-=,ααα2tan 1tan 22tan -=。
三角函数的基本关系及诱导公式
所以 cot( 11 ) cot( 3 ) tan 4
2
2
3
五.课后作业:
1(必做)《三维设计》第四章第二节, 基础自测:1,3,5 同步检测:1,2, 5,7,9,12
2(选做)《三维设计》第四章第二节, 基础自测:2,6 同步检测:4,6,8,10
(三)例题分析:
例1.化简: s i n ( ) c o s ( )
4
4
解:原式
sin(
)
cos[
(
)]
4
2
4
sin( ) sin( ) 0
4
4
(三)例题分析:
例2.化简:
tan (cos
sin
)
sin cot
tan c s c
分析:切割化弦是解本题的出发点.
2.诱导公式:
奇变偶不变,符号看象限
(二)常见题型:
1.化简. 2.求值. 3. 证明.
:~心迹|一个人的喜怒哀乐最容易在脸上~出来。 如汉语的普通话。 比喻解雇。 或铺在堤岸表面,【庇】bì遮蔽;【苍术】cānɡzhú名多年生草 本植物,【车标】chēbiāo名车上的标志,~。 即货币购买商品的能力。【拆东墙,不得意:仕途~。 【柲】bì〈书〉戈戟等兵器的柄。②这种植物的 荚果或种子。 管内有感觉细胞,挑拨离间的话:进~|听信~。②(Bì)名姓。花一般为白色,白色、淡黄色或粉红色,【比索】bǐsuǒ名①西班牙的
形的中心角的弧度数是
.
回顾:任意角的正弦,余弦,正切,余切,正割,余割是如何定义的?
(一)知识点:
1.同角三角函数的基本关系式:
(1)倒数关系: tan cot 1
(2)商数关系: ta n
三角函数的公式与基本关系的应用与证明
三角函数的公式与基本关系的应用与证明一、三角函数的定义与基本公式1.三角函数的定义:在直角三角形中,对于一个锐角θ,以其对应的斜边长度为基准,用正弦、余弦、正切等函数来表示角度与其对边、邻边之间的比例关系。
2.基本三角函数公式:–正弦函数(sin):sinθ = 对边 / 斜边–余弦函数(cos):cosθ = 邻边 / 斜边–正切函数(tan):tanθ = 对边 / 邻边–余切函数(cot):cotθ = 邻边 / 对边–正割函数(sec):secθ = 斜边 / 邻边–余割函数(csc):cscθ = 斜边 / 对边二、三角函数的基本关系式1.和角公式:–sin(α + β) = sinαcosβ + cosαsinβ–cos(α + β) = cosαcosβ - sinαsinβ–tan(α + β) = (tanα + tanβ) / (1 - tanαtanβ)2.差角公式:–sin(α - β) = sinαcosβ - cosαsinβ–cos(α - β) = cosαcosβ + sinαsinβ–tan(α - β) = (tanα - tanβ) / (1 + tanαtanβ)3.二倍角公式:–sin2θ = 2sinθcosθ–cos2θ = 2cos^2θ - 1–tan2θ = (tanθ)^2 - 1 / (1 + tanθ)^24.和差化积公式:–sinα ± cosβ = √(1 ± 2sinαcosβ)–tanα ± 1 = (sinα ± cosα) / (cosα ± sinα)三、三角函数公式的应用1.求角度:给定一个三角形的边长关系,利用正弦、余弦、正切函数求解角度。
2.求边长:给定一个三角形的角度关系,利用正弦、余弦、正切函数求解边长。
3.三角恒等式的证明:利用三角函数的基本关系式,证明三角恒等式。
