2018年秋九年级数学上册第1章反比例函数1.3反比例函数的应用课时作业新版湘教版_347
《第六章3反比例函数的应用》作业设计方案-初中数学北师大版12九年级上册

《反比例函数的应用》作业设计方案(第一课时)一、作业目标本作业设计旨在通过反比例函数的应用,加深学生对反比例函数概念的理解,并能够灵活运用反比例函数解决实际问题。
通过作业练习,提高学生的数学思维能力和解题能力。
二、作业内容本课时作业内容主要围绕反比例函数的基本概念、图像特征以及应用展开。
1. 基础知识巩固:要求学生回顾反比例函数的定义、公式及图像特征,并完成相关填空题和选择题。
2. 图像绘制与理解:要求学生根据给定的自变量值,绘制反比例函数的图像,并分析图像的特性和变化规律。
3. 实际问题应用:设计几道与反比例函数相关的实际问题,如路程与时间的关系、费用与数量的关系等,要求学生运用反比例函数的知识进行分析和解答。
4. 拓展延伸:提供一些具有挑战性的题目,如将反比例函数与其他知识点(如一次函数、二次函数)结合的应用问题,培养学生的综合运用能力。
三、作业要求1. 认真审题:学生在完成作业时,要仔细阅读题目,明确题目要求,确保理解题意。
2. 规范答题:要求学生按照数学作业的规范格式进行答题,字迹工整,步骤清晰。
3. 独立思考:鼓励学生独立思考,自主完成作业,不依赖他人答案。
4. 及时订正:学生完成作业后,要及时检查并订正错误,确保答案的准确性。
5. 合理分配时间:学生要合理安排时间,确保在规定时间内完成作业。
四、作业评价1. 评价标准:根据学生完成作业的准确性、规范性、解题思路及解题过程进行评价。
2. 评价方式:教师批改作业时,采用百分制评分,同时给出详细的批语和建议,指出学生的优点和不足。
3. 反馈形式:将学生的作业情况及时反馈给学生,指出错误并要求学生订正。
同时,将共性问题在课堂上进行讲解和讨论。
五、作业反馈1. 个别反馈:针对学生在作业中出现的个别问题,教师进行个别辅导和解答。
2. 集体讲解:将共性问题进行集体讲解和讨论,帮助学生澄清疑惑。
3. 拓展延伸:针对拓展延伸部分的题目,教师可以组织学生进行课堂讨论和交流,分享解题思路和方法。
湘教版九年级上册数学精品教学课件 第1章 反比例函数 反比例函数的应用 (2)

(1) 写出电流 I 与电阻 R 的函数关系式;(2) 如果该电路的
电阻 R 为220Ω,则通过它的电流是多少的值. 解:(1) 因为 U = IR,且 U = 220V ,
所以 IR = 220 ,
即该电路的电流 I 关于电阻 R 的函数表达式为 I 220 .
(2) 因为该电路的电阻 R = 220Ω,
(2) 若到达目的地后,按原路匀速返回,并要求
在 3 小时内回到 A 城,则返回的速度不能低 于__2_4_0_千__米__/_时__.
4. 学校锅炉旁建有一个储煤库,开学时购进一批煤, 现在知道:按每天用煤 0.6 吨计算,一学期 (按 150 天 计算) 刚好用完. 若每天的耗煤量为 x 吨,那么这批煤 能维持 y 天.
解:对当于提F函示=数:40对F0×于 6函120l 0数=,2F0当0时l6>0l,00,由时F2,0随0l =越l 的大60l增0,大F得而越减 小小. .因因此此,,只若要想l求用 出6力00不F=超32,过004N00时N对的应一的半l,的则值, 就动能力确臂定至动少力要臂加l长至201少0.5应m加. 长的量. 3-1.5 = 1.5 (m).
解:由 p= ,得 p= p 是 S 的反比例函数,因为给定一个 S 的值,就有唯一 的一个 p 值和它相对应,这符合反比例函数的定义. (2) 当木板面积为 0.2 m2 时,压强是多少? 解:当 S=0.2 m2 时,p= =3000 (Pa) . 答:当木板面积为 0.2 m2 时,压强是 3000 Pa.
天卸载完,则平均每天至少要卸载 48 吨.
练一练 某乡镇要在生活垃圾存放区建一个老年活动中心,
这样必须把 1200 立方米的生活垃圾运走. (1) 假如每天能运 x 立方米,所需时间为 y 天,写出 y
2022九年级数学上册第1章反比例函数1.3反比例函数的应用习题课件新版湘教版31

(2)当售价为多少元/千克时,水果店销售该种水果的日利润为 200元?
解:依题意得,(x-10)×30x0=200,解得 x=30, 经检验,x=30是原方程的解,并且符合题意. 所以当售价为30元/千克时,水果店销售该种水果的日利 润为200元.
13.心理学家研究发现,一般情况下,一节课40分钟中,学生 的注意力随教师讲课时间的变化而变化.开始上课时,学 生的注意力逐步增强,中间有一段时间学生的注意力保持 较为理想的稳定状态,随后学生的注意力开始分散.经过 实验分析可知,学生的注意力指标数y随时间x(分钟)的变 化规律如图所示(其中AB,BC分别为线段, CD为双曲线的一部分):
A
B
C
D
4.
已知蓄电池的电压为定值,使用蓄电池时,电流
I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的
图象如图所示,如果以此蓄电池为电源的用电器的限制
电流不能超过6 A,那么此用电器的可变电阻R应控制的
范围是( )
A.R>1
B.0<R≤2
C.R≥1 D.0<R≤1
【点拨】设反比例函数的表达式为 I=Rk,把(2,3)代入得 k=2×3 =6,∴反比例函数的表达式为 I=R6, 当 I≤6 时,则R6≤6,∴R≥1.本题易错点:限制电流不能超过 6A 的实质是 I≤6,不能表示为 I<6.
有恒温系统的大棚栽培一种在自然光照且温度为 18 ℃的条
件下生长最快的新品种.如图是某天恒温系统从开启到关闭
及关闭后,大棚内温度 y(℃)随时间 x(小时)变化的函数图象,
其中 BC 段是双曲线 y=kx(k≠0)的一部分,则当 x=16 时,大 棚内的温度为( C )
A.18 ℃
湘教版数学九年级上册1.3《反比例函数的应用》说课稿2

湘教版数学九年级上册1.3《反比例函数的应用》说课稿2一. 教材分析湘教版数学九年级上册1.3《反比例函数的应用》这一节的内容,是在学生已经掌握了反比例函数的定义、性质的基础上进行学习的。
本节课的主要内容是让学生学会如何运用反比例函数解决实际问题,从而提高学生的数学应用能力。
教材中通过实例引入反比例函数的应用,让学生了解反比例函数在实际生活中的应用,接着通过例题和练习题,让学生学会如何运用反比例函数解决实际问题。
教材还设置了“思考题”和“探索题”,激发学生的思考,提高学生的学习兴趣。
二. 学情分析九年级的学生已经掌握了反比例函数的定义和性质,对于如何运用反比例函数解决实际问题,他们可能还存在一定的困难。
因此,在教学过程中,我将会引导学生运用已学的知识解决实际问题,帮助他们克服学习中的困难。
三. 说教学目标1.知识与技能目标:让学生掌握反比例函数的应用,能够运用反比例函数解决实际问题。
2.过程与方法目标:通过实例引入,让学生了解反比例函数在实际生活中的应用,培养学生的数学应用能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的团队合作意识。
四. 说教学重难点1.教学重点:让学生掌握反比例函数的应用。
2.教学难点:如何引导学生运用反比例函数解决实际问题。
五. 说教学方法与手段在教学过程中,我将采用实例引入、小组合作、讨论交流等教学方法,以激发学生的学习兴趣,提高学生的学习积极性。
同时,我还会运用多媒体教学手段,如PPT、网络资源等,以丰富教学内容,提高学生的学习效果。
六. 说教学过程1.导入新课:通过实例引入反比例函数的应用,让学生了解反比例函数在实际生活中的重要性。
2.讲解新课:讲解反比例函数的应用,让学生学会如何运用反比例函数解决实际问题。
3.巩固新课:通过练习题,让学生巩固所学知识。
4.拓展延伸:设置“思考题”和“探索题”,激发学生的思考,提高学生的学习兴趣。
5.课堂小结:对本节课的内容进行总结,让学生掌握反比例函数的应用。
XJ湘教版 初三九年级数学 上册第一学期 同步课堂补习练习题作业 第一章 反比例函数(全章电子作业 分课时)

第一章 反比例函数 1.1 反比例函数(一)1.反比例函数 xm y 1+=的图象经过点(2,1),则m 的值是 . 2.已知反比例函数的图象经过点(m ,2)和(-2,3)则m 的值为 . 3.请你写出一个图象在第一、三象限的反比例函数.答: . 4.已知反比例函数y =xa 2-的图象在第二、四象限,则a 的取值范围是 (二)1.反比例函数xky =)0(<k 的图象与经过原点的直线l 相交于A 、B 两点,已知A 点坐标为)1,2(-,那么B 点的坐标为 .2.P 是反比例函数(0)k y k x=<图象上的一点,由P 分别向x 轴和y 轴引垂线,阴影部分面积为3,则k=3.如图,已知点C 为反比例函数6y x=-上的一点,过点C 向坐标轴引垂线,垂足分别为A 、B ,那么四边形AOBC 的面积为 . (三)1.点A (2,1)在反比例函数y kx=的图像上,当1﹤x ﹤4时,y 的取值范围是2.直线5y x b =-+与双曲线 2y x=- 相交于点P (2,)m -,则 b =3.反比例函数xy 1-=的图象位于( )A .第一、三象限B .第二、四象限C .第一、四象限D .第二、三象限(四)1.下列函数中,图像过点M (-2,1)的反比例函数解析式是( )x y A 2.=2.B y x =- x y C 21.= xy D 21.-=2.如果点(3,-4)在反比例函数ky x =的图象上,那么下列各点中,在此图象上的是( )A .(3,4)B . (-2,-6)C .(-2,6)D .(-3,-4) 3、已知y 是x 的反比例函数,并且当x=3时,y=-8。
(1)写出y 与x 之间的函数关系式。
(2)求y=2时x 的值。
(五)1指出当k>0时,下列图象中哪些可能是y=kx 与y=kx (k ≠0)在同一坐标系中的图象 ( )2.如图13-24,在函数x y 1=的图象上有三点A 、B 、C ,过这三点分别向x 轴、y 轴作垂线,过每一点所作的两条垂线段与x 轴、y 轴围成的矩形的面积分别为1S、2S 、3S ,则( )(A )321S S S >> (B )321S S S <<(C )231S S S << (D )321S S S ==3.函数23)2(m x m y --=是反比例函数,则m=______1.2 反比例函数的图象与性质第1课时 反比例函数xk y =(k >0)的图象与性质1.(对比练习)(1)已知正比例函数3)1(--=m x m y 中,y 随x 的增大而增大,求m 的值;(2)已知反比例函数3)1(--=m x m y 在每一象限内,y 随x 的增大而增大,求m 的值。
湘教版数学九年级上册_课时作业:第3课时_反比例函数y=k÷x(k≠0)的图象与性质
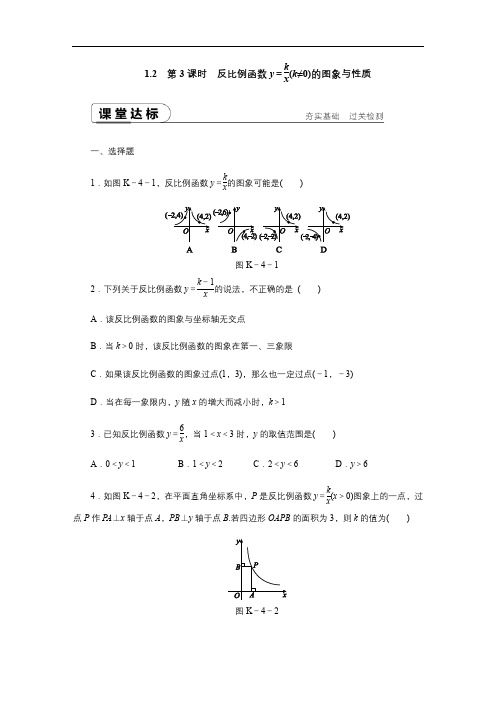
1.2 第3课时 反比例函数y =kx (k ≠0)的图象与性质一、选择题1.如图K -4-1,反比例函数y =kx的图象可能是( )图K -4-12.下列关于反比例函数y =k -1x的说法,不正确的是 ( ) A .该反比例函数的图象与坐标轴无交点B .当k >0时,该反比例函数的图象在第一、三象限C .如果该反比例函数的图象过点(1,3),那么也一定过点(-1,-3)D .当在每一象限内,y 随x 的增大而减小时,k >13.已知反比例函数y =6x ,当1<x <3时,y 的取值范围是( )A .0<y <1B .1<y <2C .2<y <6D .y >64.如图K -4-2,在平面直角坐标系中,P 是反比例函数y =kx (x >0)图象上的一点,过点P 作P A ⊥x 轴于点A ,PB ⊥y 轴于点B .若四边形OAPB 的面积为3,则k 的值为( )图K -4-2A .3B .-3 C.32 D .-325.如果k <0,那么函数y =(1-k )x 与y = kx在同一坐标系中的图象可能是( )图K -4-36.一次函数y =kx +b (k ≠0)的图象经过A (-1,-4),B (2,2)两点,P 为反比例函数y =kbx图象上一动点,O 为坐标原点,过点P 作y 轴的垂线,垂足为C ,则△PCO 的面积为( ) A .2 B .4 C .8 D .不确定二、填空题7.如图K -4-4,反比例函数y =kx 的图象经过点A (2,1).若y ≤1,则x 的取值范围是____________.图K -4-48.已知一次函数y =x +1的图象与反比例函数y =kx 的图象相交,其中有一个交点的横坐标是2,则k 的值为________.9.设函数y =3x 与y =-2x -6的图象的交点坐标为(a ,b ),则1a +2b 的值是________.10.如图K -4-5,在平面直角坐标系中,M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 与反比例函数y =8x (x >0)和y =kx(x >0)的图象分别交于点P ,Q .若S △POQ =14,则k 的值为________.图K -4-5 图K -4-611.函数y 1=x (x ≥0),y 2=4x (x >0)的图象如图K -4-6所示,由有下列结论:①两函数图象的交点A 的坐标为(2,2);②当x >2时,y 2>y 1;③当x =1时,BC =3;④当x 逐渐增大时,y 1随着x 的增大而增大,y 2随着x 的增大而减小.其中正确结论的序号是________.三、解答题12.如图K -4-7,反比例函数y 1=mx (x >0)的图象与一次函数y 2=-x +b (x >0)的图象交于点A ,B ,其中A (1,2).(1)求m ,b 的值;(2)若点B 的坐标为(2,y B ),求y B 的值,并写出y 2>y 1时,x 的取值范围.图K -4-713.如图K -4-8,一次函数y =kx +b (k ≠0)的图象与反比例函数y =ax (a ≠0)的图象在第二象限交于点A (m ,2),与x 轴交于点C (-1,0),过点A 作AB ⊥x 轴于点B ,△ABC 的面积是3.(1)求一次函数和反比例函数的表达式;(2)若直线AC 与y 轴交于点D ,求△ABD 的面积.图K -4-814.反比例函数y =kx (k 为常数,且k ≠0)的图象经过点A (1,3),B (3,m ).(1)求反比例函数的表达式及点B 的坐标;(2)在x 轴上找一点P ,使P A +PB 的值最小,求满足条件的点P 的坐标.图K -4-9新定义问题:在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“倍点”,例如点(-2,-4),(1,2),(3,6)……都是“倍点”,显然这样的“倍点”有无数多个.(1)若点M (2,a )是反比例函数y =kx 的图象上的“倍点”,求这个反比例函数的表达式.(2)对于一次函数y =3mx -1的图象上是否存在“倍点”,嘉琪说:“当m =23时,函数图象上不存在‘倍点’,当m ≠23时,函数图象上存在‘倍点’.”你认为她的说法正确吗?如果正确,请求出存在的“倍点”;如果不正确,请说明理由.详解详析[课堂达标]1.[解析] D A .∵反比例函数的图象在第一、三象限或第二、四象限,∴选项A 不符合题意.B .k =-2×6=-12,k =4×(-2)=-8.∵-12≠-8,∴选项B 不符合题意.C .k =4×2=8,k =-2×(-2)=4.∵8≠4,∴选项C 不符合题意.D .k =4×2=8,k =-2×(-4)=8.∵8=8,∴选项D 符合题意.故选D .2.[解析] B A .反比例函数的图象与坐标轴无交点,正确,不符合题意;B .当k -1>0,即k >1时,该反比例函数的图象在第一、三象限,故错误,符合题意;C .如果该反比例函数的图象过点(1,3),那么也一定过点(-1,-3),正确,不符合题意;D .当在每一象限内,y 随x 的增大而减小时,k -1>0,k >1,正确,不符合题意.故选B .3.[解析] C ∵k =6>0,∴在每个象限内,y 随x 的增大而减小.又∵当x =1时,y =6,当x =3时,y =2,∴当1<x <3时,2<y <6.故选C . 4.[答案] A 5.[答案] C6.[解析] A 将A(-1,-4),B(2,2)代入一次函数表达式,得⎩⎨⎧-k +b =-4,2k +b =2,解得⎩⎨⎧k =2,b =-2,∴反比例函数的表达式为y =-4x .∵P 为反比例函数y =kbx 图象上一动点,O 为坐标原点,过点P 作y 轴的垂线,垂足为C ,∴△PCO 的面积为12|k|=2.故选A .7.[答案] x≥2或x <0 8.[答案] 6[解析] 把x =2代入y =x +1,得y =3,∴这个交点的坐标为(2,3).把(2,3)代入y =kx ,得k =6.9.[答案] -2 10.[答案] -20[解析] ∵S △POQ =S △OMQ +S △OMP ,∴12|k|+12×|8|=14,∴|k|=20.由函数y =kx 的图象可知k<0,∴k =-20.11.[答案] ①③④[解析] ①将y 1=x(x≥0),y 2=4x(x >0)组成方程组,得⎩⎪⎨⎪⎧y =x ,y =4x ,由于x >0,解得x =2,y =2,故点A 的坐标为(2,2).②由图可知,当x >2时,y 1>y 2.③当x =1时,y 1=1,y 2=4,则BC =4-1=3.④当x 逐渐增大时,y 1随着x 的增大而增大,y 2随着x 的增大而减小.综上,正确的结论为①③④.12.解:(1)∵反比例函数y 1=m x (x>0)的图象过点A(1,2),∴2=m1,解得m =2.∵一次函数y 2=-x +b(x>0)的图象过点A(1,2),∴2=-1+b ,解得b =3. (2)将点B 的横坐标2代入y =2x ,得y B =1,∴点B 的坐标为(2,1).根据图象可得,当1<x<2时,y 2>y 1.13.解:(1)∵一次函数y =kx +b(k≠0)的图象与反比例函数y =ax (a≠0)的图象在第二象限交于点A(m ,2),与x 轴交于点C(-1,0),∴点A(a 2,2).∵△ABC 的面积是3,∴3=12·AB·BC.即3=12×2×(-1-a 2),解得a =-8,∴反比例函数的表达式为y =-8x.∴A(-4,2).把A(-4,2),C(-1,0)代入y =kx +b ,得⎩⎨⎧2=-4k +b ,0=-k +b ,解得⎩⎨⎧k =-23,b =-23,∴一次函数的表达式为y =-23x -23.(2)∵直线AC 与y 轴交于点D ,当x =0时,y =-23×0-23=-23,∴D(0,-23),∴OD =23.∴S △ABD =S △BCA +S △BCD =12·BC·(AB +OD)=12×3×(2+23)=4.14.解:(1)因为图象经过点A(1,3),所以3=k1.∴k =3,∴反比例函数的表达式为y =3x .当x =3时,m =33=1,∴点B 的坐标(3,1).(2)如图,作点B 关于x 轴的对称点C ,点C 的坐标为(3,-1).再连接AC 与x 轴交于点P ,此时PA +PB 的值最小. 设直线AC 的函数表达式为y =ax +b(a≠0).因为图象过(1,3)和(3,-1)两点,可得⎩⎨⎧a +b =3,3a +b =-1,解得⎩⎨⎧a =-2,b =5,∴y =-2x +5.当y =0时,x =2.5,∴满足条件的点P 的坐标为(2.5,0).[素养提升]解:(1)∵点M(2,a)是“倍点”, ∴a =2×2=4,∴点M 的坐标为(2,4). ∵点M(2,4)在反比例函数y =kx 的图象上,∴4=k2,解得k =8,∴反比例函数的表达式为y =8x .(2)嘉琪的说法是正确的.设函数y =3mx -1的图象上存在的“倍点”的坐标为(n ,2n), 则有2n =3mn -1.整理,得(3m -2)n =1. ①当3m -2=0时,m =23,此时不存在n 的值,使等式(3m -2)n =1成立,∴函数y =3mx -1的图象上不存在“倍点”; ②当3m -2≠0时,m≠23,由(3m -2)n =1,解得n =13m -2,那么2n =23m -2,∴当m≠23时,函数图象上存在“倍点”为(13m -2,23m -2).。
湘教版数学九年级上册_课时作业:第2课时_反比例函数y=k÷x(k<0)的图象与性质
1.2 第2课时 反比例函数y =kx (k <0)的图象与性质一、选择题1.若点A (-2,3)在反比例函数y =kx 的图象上,则k 的值是( )A .-6B .-2C .2D .62.对于反比例函数y =-2x ,下列说法不正确的是( )A .图象分布在第二、四象限B .当x >0时,y 随x 的增大而增大C .图象经过点(1,-2)D .若点A (x 1,y 1),B (x 2,y 2),都在图象上,且x 1<x 2,则y 1<y 23.已知反比例函数y =kbx (kb ≠0)的图象如图K -3-1所示,则一次函数y =kx +b 的图象可能是( )图K -3-1 图K -3-24.反比例函数y =-2x 的图象上有两点P 1(x 1,y 1),P 2(x 2,y 2).若x 1<0<x 2,则下列结论正确的是( )A .y 1<y 2<0B .y 1<0<y 2C .y 1>y 2>0D .y 1>0>y 25.反比例函数y =-3x(x <0)的图象如图K -3-3所示,则矩形OAPB 的面积是( )图K -3-3A .3B .-3 C.32 D .-326.如图K -3-4,A 为反比例函数y =kx 的图象上的一点,AB ⊥y 轴于点B ,点P 在x 轴上,S △ABP =2,则这个反比例函数的表达式为( )图K -3-4A .y =2xB .y =-2xC .y =4xD .y =-4x二、填空题7.若反比例函数y =2-kx 的图象位于第二、四象限,则k 的取值范围是________.8.如图K -3-5,在平面直角坐标系中,O 为坐标原点,P 是反比例函数y =2x 图象上的一点,P A ⊥x 轴于点A ,则△POA 的面积为________.9.已知反比例函数y =kx 的图象经过点(3,-1),则当1<y <3时,自变量x 的取值范围是________.图K -3-5 图K -3-610.如图K -3-6,D 为矩形OABC 的边AB 的中点,反比例函数y =kx (x >0)的图象经过点D ,交BC 边于点E .若△BDE 的面积为1,则k =________.三、解答题11.已知y 是x 的反比例函数,且当x =2时,y =-3. (1)求反比例函数的表达式;(2)在图K -3-7中画出这个函数的图象; (3)试判断点P (-2,3)是否在这个函数的图象上.图K -3-712.已知函数y =(k -2)xk 2-5为反比例函数. (1)求k 的值;(2)它的图象在第________象限内,在各象限内,y 随x 的增大而________(填变化情况); (3)求出-2≤x ≤-12时,y 的取值范围.13.已知反比例函数y =k -1x(k 为常数,k ≠1).(1)若该反比例函数的图象在每个象限内,y 随x 的增大而增大,求k 的取值范围; (2)若其图象的一支位于第二象限,在这一支上任取两点A (x 1,y 1),B (x 2,y 2),当y 1>y 2时,试比较x 1,x 2的大小.14.如图K -3-8,点A 在反比例函数y =kx 的图象在第二象限内的分支上,AB ⊥x 轴于点B ,O 是原点,且△AOB 的面积为1.试解答下列问题:(1)比例系数k =________;(2)在图K -3-8的平面直角坐标系中,画出这个函数图象的另一个分支; (3)当x >1时,写出y 的取值范围.图K -3-8分类讨论思想如图K -3-9,四边形ABCD 为正方形,点A 的坐标为(0,2),点B 的坐标为(0,-3),反比例函数y =kx(k ≠0)的图象经过点C .(1)求反比例函数的表达式;(2)若P 是反比例函数图象上的一点,△P AD 的面积恰好等于正方形ABCD 的面积,求点P 的坐标.图K -3-9详解详析[课堂达标] 1.[答案] A 2.[答案] D 3.[答案] C4.[解析] D ∵反比例函数y =-2x 中k =-2<0,∴此函数图象在第二、四象限.∵x 1<0<x 2,∴点P 1(x 1,y 1)在第二象限,点P 2(x 2,y 2)在第四象限,∴y 1>0>y 2. 5.[解析] A ∵点P 在反比例函数y =-3x (x <0)的图象上,∴可设P(x ,-3x ),∴OA =-x ,PA =-3x ,∴S 矩形OAPB =OA·PA =-x·(-3x)=3.故选A .6.[解析] D 连接OA.∵△AOB 的面积=△ABP 的面积=2,△AOB 的面积=12|k|,∴12|k|=2,∴k =±4.又∵反比例函数的图象位于第二、四象限,∴k <0,∴k =-4,∴这个反比例函数的表达式为y =-4x.故选D .7.[答案] k >2 8.[答案] 19.[答案] -3<x <-1[解析] ∵反比例函数y =kx 的图象经过点(3,-1),∴k =3×(-1)=-3,∴反比例函数的表达式为y =-3x .∵反比例函数y =-3x 中k =-3<0,∴该反比例函数的图象在第二、四象限,且在每个象限内y 随x 的增大而增大.当y =1时,x =-3;当y =3时,x =-1.∴当1<y <3时,自变量x 的取值范围是-3<x <-1. 10.[答案] 4[解析] 设D(a ,ka).∵D 为矩形OABC 中AB 边的中点, ∴B(2a ,k a ),∴C(2a ,0),∴E(2a ,k2a ).∵△BDE 的面积为1, ∴12·a·(k a -k2a )=1, 解得k =4. 故答案为4.11.解:(1)设反比例函数的表达式为y =kx ,把x =2,y =-3代入,得k =2×(-3)=-6,所以反比例函数的表达式为y =-6x.(2)如图所示:(3)当x =-2时,y =-6x =3,所以点P(-2,3)在这个函数的图象上.12.解:(1)由题意得k 2-5=-1,解得k =±2. ∵k -2≠0,∴k =-2.(2)∵k -2=-4<0,∴反比例函数的图象在第二、四象限,在各象限内,y 随着x 的增大而增大.故答案为二、四 增大.(3)∵反比例函数的表达式为y =-4x ,∴当x =-2时,y =2;当x =-12时,y =8.由(2)得,当-2≤x≤-12时,2≤y≤8.13.解:(1)由题意,得k -1<0,解得k <1.(2)由反比例函数y =k -1x 的图象的一支位于第二象限,得k -1<0,∴在第二象限内,y随x 的增大而增大,∴当y 1>y 2时,x 1>x 2.14.解:(1)-2 (2)如图所示:(3)利用函数图象,可得当x >1时,-2<y <0. [素养提升]解:(1)∵点A 的坐标为(0,2),点B 的坐标为(0,-3),∴AB =5. ∵四边形ABCD 为正方形, ∴点C 的坐标为(5,-3).∵反比例函数y =kx的图象经过点C ,∴-3=k 5,解得k =-15,∴反比例函数的表达式为y =-15x.(2)设点P 到AD 的距离为h.∵△PAD 的面积恰好等于正方形ABCD 的面积, ∴12×5×h =52.解得h =10. ①当点P 在第二象限时,y P =h +2=12.此时,x P =-1512=-54.∴点P 的坐标为⎝⎛⎭⎫-54,12. ②当点P 在第四象限时,y P =-(h -2)=-8.此时,x P =-15-8=158,∴点P 的坐标为⎝⎛⎭⎫158,-8. 综上所述,点P 的坐标为(-54,12) (158,-8).。
九年级数学反比例函数第3课时反比例函数的图象和性质(2)(课堂导练)课件(新版)新人教版
Page 7
,∴6=xy.
分别把点B,C的坐标代入,得
变式练习
3.已知反比例函数的图象经过P(﹣2,3).
(1)求此反比例函数的解析式; 设反比例函数的解析式为y= 把P(﹣2,3)代入y= 所以反比例函数解析式为y=﹣ ,
得k=﹣2×3=﹣6, .
Page 12
巩固提高
8.如图,已知反比例函数y= 的图象经过点A (﹣3,﹣2). (1)求反比例函数的解析式; 因为反比例函数y= 的图象
经过点A(﹣3,﹣2), 把x=﹣3,y=﹣2代入解析式 可得k=6, 所以解析式为y= .
Page 13
巩固提高
(2)若点B(1,m),C(3,n)在该函数的 图象上,试比较m与n的大小.
Page 15
,6), .
中得k=4,则反比例解析式为y=
巩固提高
(2)说出双曲线y= 所在的象限以及在每
个象限内y随x值的增大而变化的情况. ∵y= ,且k=4>0,
∴此函数的图象在第一、三象限,在每 个象限内y随x的增大而减小.
Page
16
巩固提高
10.如图,反比例函数y=
经过点A(1,3).
精典范例
例1.反比例函数y= A.y1<y2 B.y1>y2
C.y1=y2 D.不能确定
的图象经过点(﹣1,y1), A
(2,y2),则下列关系正确的是( )
Page
1
变式练习
1.点(x1,3),(x2,﹣2)在反比例函数
y=﹣ 的图象上,则下列一定正确的是( C ).
A.x1>x2 B.x1≥x2
∵k=6>0, ∴图象在一、三象限,y随x的增大而在第一象限, ∴m>n.
九年级数学作业设计案例(1)北师大版数学九年级第一学期 第六章
初中数学作业设计案例一、单元作业概况二、课时作业设计表以北师大版初中九年级数学上册第六章《反比例函数》为例:三、课时作业、单元测试卷题目属性分析1、课时作业题目属性汇总表2、单元试卷题目属性汇总表s0104Csx09010602选择题中等理解1引用s0104Csx09010603选择题中等理解1引用s0105Csx09010605选择题中等理解2引用s0105Csx09010605选择题较高理解2引用s0106Csx09010603填空题较低知道1引用s0105Csx09010604填空题较低知道1引用s0106Csx09010604填空题中等理解1引用s0107Csx09010606填空题中等理解2引用s0106Csx09010606填空题中等理解3引用s0107Csx09010607解答题中等理解 5 引用s0107Csx09010607解答题较高应用 6 引用s0107Csx09010607 解答题较高应用 6 引用四、课时作业Z0101、设计意图:本题主要考查反比例函数的概念,对反比例函数表达式中0≠k 这一条件的强化.Z0102、设计意图:本题主要考查反比例函数的概念,根据反比例函数概念中x 的次数为-1,且系数不能为0进行作答.Z0103、设计意图:本题主要体现了数学建模素养,借助日常生活中经常遇到的经营问题,通过把售价x 与销量y 之间的变化关系用函数表示出来,建立反比例函数模型,从而达到解决问题的目的.第二节:反比例函数的图象与性质 Z0104、分别画出函数x y 6=和xy 6-=的图象. 设计意图:本题能规范学生画反比例函数图象,使学生进一步体会函数图象与函数表达式之间的关系,感受数形结合的思想.Z0105、设计意图:本题考查了学生对k的几何意义的理解,提高识图能力,进一步体会数形结合的思想.第三节:反比例函数的应用Z0106、设计意图:本题考查学生根据函数图象明确各变量之间的关系,列出函数表达式的能力,并根据实际情况标明自变量的取值范围.体会数学与生活的联系紧密性.Z0107.设计意图:本题考查学生利用待定系数法求函数表达式,利用割补法求图形面积,第(3)考查函数与不等式之间的关系,体会转化思想,数形结合思想.五、单元试卷一、选择题(本大题共10小题,每小题3分,共30分)1.给出下列函数关系式:①12y x =-;②52y x =;③123y x -=;④12y x=+;⑤2xy=1;⑥-xy=2.其中,表示y 是x 的反比例函数的个数为( ) A.3 B.4 C.5 D.62.若反比例函数0k ky x=≠()的图象经过点P (-2,3),则该函数的图象不经过的点是( )A.(3,-2)B.(1,-6)C.(-1,6)D.(-1,-6)3.(2018四川凉山州中考)若ab <0,则正比例函数y =ax 与反比例函数by x=在同一坐标系中的大致图象可能是( )4.(2019甘肃兰州期末)一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v (千米/时)与时间t (小时)的函数关系式为( )A. 480v t =B. =480v t +C. 80v t =D. 6t v t-= 5.(2019湖南娄底中考)将1y x=的图象向右平移1个单位长度,再向上平移1个单位长度所得图象如下图所示,则所得图象的解析式为( )A. 111y x =++ B. 111y x =-+ C. 111y x =+- D. 111y x =-- 6.(2020湖北荆州松滋一模)如下图所示,在平面直角坐标系中,正方形ABCD四个顶点的坐标分别为A (-1,2),B (-1,-1),C (2,-1),D (2,2),当双曲线0k ky x=>()与正方形有四个交点时,k 的取值范围是( )A.0<k <1B.1<k <4C.k >1D.0<k <27.(2020独家原创试题)如下图所示,点A 在反比例函数0ky x x=>()的图象上,过点A 作AB ⊥x 轴,垂足为点B ,点C 在y 轴上,若△ABC 的面积为3,则k 的值为( )A.4B.5C.6D.128.(2017浙江衢州中考)如下图所示,在平面直角坐标系中,点A 在函数04y x x =>()的图象上,AB ⊥x 轴于点B ,AB 的垂直平分线与y 轴交于点C ,与函数04y x x=>()的图象交于点D .连接AC ,CB ,BD ,DA ,则四边形ACBD 的面积等于( )A.2B.C.4D.9.(2020湖南长沙天心期末)如下图所示,平行于x 轴的直线与函数1100,k y k x x =>>(),2200,ky k x x=>>()的图象分别相交于A ,B 两点,点A 在点B 的右侧,C 为x 轴上的一个动点,若△ABC 的面积为6,则12k k -的值为( )A. 12B.-12C.6D.-610.(2015湖北鄂州中考)如下图所示,直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数kyx=的图象在第一象限内交于点A,连接OA,若:1:2AOB BDCS S∆∆=,则k的值为( )A.2B.3C.4D.6二、填空题(本大題共8小题,每小题3分,共24分)11.(2017江苏淮安中考)若反比例函数6yx=-的图象经过点A(m,3),则m的值是_____.12.(2017黑龙江缓化中考)已知反比例函数6yx=,当x>3时,y的取值范围是_____.13.(2018湖南娄底中考)如下图所示,在平面直角坐标系中,O为坐标原点,点P是反比例函数2yx=图象上的点,PA⊥x轴于点A,则△POA的面积为_____.14.(2018湖南张家界中考)如下图所示,矩形ABCD 的边AB 与x 轴平行,顶点A的坐标为(2,1),点B 与点D 都在反比例函数06y x x=>()的图象上,则矩形ABCD的周长为_____.15.(2019贵州毕节中考)如下图所示,在平面直角坐标系中,一次函数y =-4x +4的图象与x 轴、y 轴分别交于A 、B 两点.正方形ABCD 的顶点C 、D 在第一象限,顶点D 在反比例函数0ky k x=≠()的图象上.若正方形ABCD 向左平移n 个单位后,顶点C 恰好落在反比例函数的图象上,则n 的值是_____.三、解答题(共46分)16.(2018湖南常德中考)(8分)如下图所示,已知一次函数111(0)y k x b k =+≠与反比例函数2220k y k x=≠()的图象交于A (4,1),B (n ,-2)两点. (1)求一次函数与反比例函数的解析式;(2)请根据图象直接写出12y y <时x 的取值范围.17.(8分)在压力不变的情况下,某物体承受的压强P (Pa )是它的受力面积S (2m )的反比例函数,其图象如下图所示. (1)求p 与S 之间的函数关系式; (2)求当S =0.5时物体承受的压强p ;(3)若要获得2500Pa 的压强,受力面积应为多少?18.(2019四川雅安中考)(10分)如下图所示,在平面直角坐标系中,一次函数y =-x +m 的图象与反比例函数0ky x x=>()的图象交于A 、B 两点,已知A (2,4).(1)求一次函数和反比例函数的解析式; (2)求B 点的坐标;(3)连接AO 、BO ,求△AOB 的面积.六、答案一、选择题1.答案:B解析:②③⑤⑥均为反比例函数,故选B.2.答案:D解析:由题意得k=-2×3=-6,则6yx=-,因此该函数图象上点的横坐标与纵坐标之积为-6.故选D.3.答案:B解析:因为ab<0,所以正比例函数图象与反比例函数图象不在同一象限内,其中一个在一、三象限时,另一个就在二、四象限.同时,正比例函数的图象是过原点的直线.故选B.4.答案:A解析:由于以80千米/时的平均速度用了6小时到达目的地,因此路程为80×6=480千米,∴汽车的速度v(千米/时)与时间t(小时)的函数关系式为480vt=.故选A.5.答案:C解析:由“左加右减”的原则可知,1yx=的图象向右平移1个单位所得函数图象的关系式是11 yx=-.由“上加下减”的原则可知,函数11yx=-的图象向上平移1个单位长度所得函数图象的关系式是111y x =+-.故选C. 6.答案:A解析: 把点B (-1,-1)代人0ky x x=>(),得k =-1×(-1)=1,由图象可知:当双曲线0ky x x=>()与正方形有四个交点时,k 的取值范围为0<k <1,故选A.7.答案:C解析: 连接OA ,如图∵AB ⊥x 轴,∴OC ∥AB ,∴OAB CAB S S ∆∆=,∴132OAB S k ∆==,∴6k =,∵反比例函数0ky x x=>()的图象在第一象限,∴k >0,∴k =6.故选C.8.答案:C解析:设4,A a a ⎛⎫ ⎪⎝⎭,可求出22,D a a ⎛⎫ ⎪⎝⎭,∵AB ⊥CD ,∴1142422S AB CD a a=⋅=⨯⨯=四边形ACBD .故选C. 9.答案:A解析:设12,,,k k A m B m m m ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,则△ABC 的面积1211622A k k AB y m m m ⎛⎫=⋅⋅=⋅-⋅= ⎪⎝⎭,则1212k k -=.故选A. 10.答案:B解析:易求得点C (0,-2),点B (2,0),所以OC =OB =2,所以2BOC S ∆=.因为:1:2AOB BOC S S ∆∆=,所以1AOB S ∆=.因为OB =2,所以OB 边上的高是1,即点A 的纵坐标是1.把1A y =代入y=x-2中,得3A x =,所以A 点坐标是(3,1).所以k =3.故选B. 二、填空题 11.答案:-2解析:把A (m ,3)代入6y x =-,得63m=-,解得m =-2.12.答案:0<y <2 解析:∵6y x=,6>0, ∴当x >0时,y 随x 的增大而减小,当x =3时,y =2, ∴当x >3时,y 的取值范围是0<y <2. 13.答案:1解析:设点P 的坐标为(x ,y ). ∵P (x ,y )在反比例函数2y x=的图象上,∴xy =2,∴112POA S xy ∆==. 14.答案:12解析:由矩形ABCD 的边AB 与x 轴平行,顶点A 的坐标为(2,1),可知点B 的纵坐标为1,点D 的横坐标为2,因为点B 与点D 都在反比例函数06x y x=>()的图象上,所以点D ,点B 的坐标分别是(2,3),(6,1).所以AB =4,AD =2,所以矩形ABCD 的周长为12. 15.答案:3解析:如图,过点D 作DE ⊥x 轴,过点C 作CF ⊥y 轴,易证△ABO ≌△DAE ,∴AE =BO ,DE =OA ,易求A (1,0),B (0,4),∴D (5,1),∵顶点D 在反比例函数ky x=的图象上,∴k =5,∴5y x=.易证△CBF ≌△BAO ,∴CF =4,BF =1,∴C (4,5),∵点C 向左平移n 个单位后为(4-n ,5),∴5(4-n )=5,∴n =3.三、解答题111(0)y k x b k =+≠与反比例函数2220ky k x=≠()16.解析:(1)将A (4,1)代入2220ky k x=≠(),得24k =,所以反比例函数的解析式为24y x =.将B (n ,-2)代入24y x=,得2n =-,所以点B 的坐标为(-2,-2).将A (4,1),B (-2,-2)代入111(0)y k x b k =+≠,得1141,22,k b k b +=⎧⎨-+=-⎩解得11,21,k b ⎧=⎪⎨⎪=-⎩所以一次函数的解析式为1112y x =-.(2)根据两函数图象可以看出:1y <2y 时,x 的取值范围为2x <-或0<x<4.17.解析:(1)设0kp k S=≠(),∵点(0.25,1000)在这个函数的图象上, ∴10000.25k=,∴k =250, ∴P 与S 之间的函数关系式为0025p S S=>(). (2)当S =0.5时,2505000.5p ==. (3)令P =2500,则2500.12500p ==.故要获得2500Pa 的压强,受力面积应为20.1m .18.解析:(1)将A (2,4)代入y =-x +m 与0k y x x =>()中,得4,22,4km ==-+⎧⎪⎨⎪⎩∴m =6,k =8,∴一次函数的解析式为6y x =-+,反比例函数的解析式为8y x=. (2)解方程组86y x y x ==-+⎧⎪⎨⎪⎩,,得24y x ==⎧⎨⎩,,或42y x ==⎧⎨⎩,, ∴B (4,2).(3)如图,设直线6y x =-+与y 轴交于点D ,易得D (0,6),∴OD =6,∴116462622AOB DOB AOD S S S ∆∆∆=-=⨯⨯-⨯⨯=。
九年级数学上册第1章反比例函数1.3反比例函数的应用课时作业湘教版(2021年整理)
2018年秋九年级数学上册第1章反比例函数1.3 反比例函数的应用课时作业(新版)湘教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年秋九年级数学上册第1章反比例函数1.3 反比例函数的应用课时作业(新版)湘教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年秋九年级数学上册第1章反比例函数1.3 反比例函数的应用课时作业(新版)湘教版的全部内容。
1。
3 反比例函数的应用课时作业(五)一、选择题1.矩形的面积为6,它的长y与宽x之间的函数关系用图象大致可表示为( )图K-5-12.某电子商城推出分期付款购买电脑的活动,一台电脑的售价为1。
2万元,前期付款4000元,后期每个月分期付一定的数额,则每个月的付款额y(元)与付款月数x之间的函数表达式是( )A.y=错误!(x取正整数)B.y=错误!C.y=错误!D.y=8000x3.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图K-5-2所示,则下列说法正确的是( )图K-5-2A.该村人均耕地面积随总人口的增多而增多B.当该村总人口为50人时,人均耕地面积为1公顷C.若该村人均耕地面积为2公顷,则总人口为100人D.该村人均耕地面积y与总人口x成正比例4.某人对地面的压强p与他和地面的接触面积S的函数关系如图K-5-3所示.若某一沼泽地地面能承受的压强不超过300 Pa,则此人必须站立在面积为多大的木板上才不至于下陷(木板的重量忽略不计)( )图K-5-3A.至少2 m2 B.至多2 m2C.大于2 m2 D.小于2 m2二、填空题5.用杠杆撬一块石板,阻力是800 N,阻力臂长为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3 反比例函数的应用
课时作业(五)
一、选择题
1.矩形的面积为6,它的长y 与宽x 之间的函数关系用图象大致可表示为( )
图K -5-1
2.某电子商城推出分期付款购买电脑的活动,一台电脑的售价为1.2万元,前期付款4000元,后期每个月分期付一定的数额,则每个月的付款额y (元)与付款月数x 之间的函数表达式是( )
A .y =8000x
(x 取正整数)
B .y =8x
C .y =8000x
D .y =8000x
3.某村耕地总面积为50公顷,且该村人均耕地面积y (单位:公顷/人)与总人口x (单位:人)的函数图象如图K -5-2所示,则下列说法正确的是( )
图K -5-2
A .该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口为100人
D.该村人均耕地面积y与总人口x成正比例
4.某人对地面的压强p与他和地面的接触面积S的函数关系如图K-5-3所示.若某一沼泽地地面能承受的压强不超过300 Pa,则此人必须站立在面积为多大的木板上才不至于下陷(木板的重量忽略不计)( )
图K-5-3
A.至少2 m2 B.至多2 m2
C.大于2 m2 D.小于2 m2
二、填空题
5.用杠杆撬一块石板,阻力是800 N,阻力臂长为0.5 m,则杠杆平衡时,动力F与动力臂长L之间的函数表达式是________;若动力臂长为2 m,则需要________N的动力才能撬动石板.
6.一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变.已知密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图K-5-4所示.当V=2 m3时,气体的密度是________kg/m3.
图K-5-4
7.某气球内充满了一定质量的气体,当温度不变时,气球内气体的压强p(kPa)是气体体积V(m3)的反比例函数,其图象如图K-5-5所示,则当气球内气体体积V(m3)的范围是0.8<V<2时,气体的压强p(kPa)的范围是________.
图K -5-5
三、解答题
8.2017·丽水丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时间为t 小时,平均速度为v 千米/时(汽车行驶速度不超过100千米/时).根据经验,
v ,t 的一组对应值如下表:链接听课例1归纳总结
(1)根据表中的数据,求出平均速度v (千米/时)关于行驶时间t (时)的函数表达式; (2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由; (3)若汽车到达杭州市场的行驶时间t 满足3.5≤t ≤4,求平均速度v 的取值范围.
9.某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15~20 ℃的新品种.如图K -5-6是某天恒温系统从开启到关闭及关闭后,大棚里温度y (℃)随时间x (h)变化的函数图象,其中AB 段是恒温阶段,BC 段是双曲线y =k x
的一部分,请根据图中信息解答下列问题:
(1)求k 的值;
(2)恒温系统在一天内保持大棚里温度在15 ℃及15 ℃以上的时间有多少小时?链接听课例2归纳总结
图K-5-6
10.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到800 ℃,然后停止煅烧进行锻造操作.第8 min时,材料温度降为600 ℃.煅烧时,温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图K-5-7).已知该材料的初始温度是32 ℃.
(1)分别求出材料煅烧和锻造时y与x之间的函数表达式,并写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480 ℃时,必须停止操作,那么锻造的操作时间有多长?
图K-5-7
分类讨论与方程思想一辆客车从甲地出发前往乙地,平均速度v(千米/时)与所用时间t(时)之间的函数关系如图K-5-8所示,其中60≤v≤120.
(1)直接写出v与t之间的函数表达式.
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A,B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
图K-5-8
详解详析
【作业高效训练】 [课堂达标]
1.[解析] D 由题意,得y =6
x (x >0),所以y 是x 的反比例函数,图象在第一象限,
故选D .
2.[解析] A ∵购买的电脑价格为1.2万元,交了首付4000元之后每期付款y 元,x 个月结清余款,∴xy +4000=12000,∴y =8000
x
(x 取正整数),故选A .
3.[解析] B 由题图知人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,∴y 随x 的增大而减小,∴A ,D 错误.设y =
k
x (k >0,x >0),把x =50,y =1代入得k =50,∴y =50
x
.把y =2代入上式得x =25,∴C 错误.由图象知B 正确.故答案为B .
4.解析] A 设函数的表达式为p =F
S .∵函数图象经过点(10,60),
∴F =pS =10×60=600,
∴p =600
S ,当p≤300时,S ≥2,故选A .
5.[答案] F =400
L
200
[解析] 阻力×阻力臂=动力×动力臂. 6.[答案] 4
7.[答案] 48<p <120
[解析] 设函数表达式为p =k
V ,∵点A(0.8,120)在函数图象上,将点A 的坐标代入可
得120=k 0.8,∴k =0.8×120=96,∴函数表达式为p =96V .∵当V =0.8时,p =96
0.8=120,
当V =2时,p =96
2
=48.又p 随V 的增大而减小,所以48<p <120.故答案为:48<p <120.
8.解:(1)根据表中的数据,可画出v 关于t 的函数图象(如图所示),根据图象形状,选择反比例函数模型进行尝试.设v 与t 的函数表达式为v =k
t ,∵当v =75时,t =4,∴k
=4×75=300,∴v =300
t .将点(3.75,80),(3.53,85),(3.33,90),(3.16,95)的坐标
代入v =300t 验证:30080=3.75,30085≈3.53,30090≈3.33,300
95≈3.16,∴v 与t 的函数表达式
是v =300
t
(t≥3).
(2)∵10-7.5=2.5,∴t =2.5时,v =300
2.5=120>100,∴汽车上午7:30从丽水出
发,不能在上午10:00之前到达杭州市场.
(3)由图象或反比例函数的性质,得当3.5≤t≤4时,75≤v ≤600
7.
答:平均速度v 的取值范围是75≤v≤600
7.
9.解:(1)把B(12,20)代入y =k
x 中,得
k =12×20=240.
(2)设线段AD 所在直线的函数表达式为y =mx +n. 把(0,10),(2,20)代入y =mx +n 中,得
⎩⎪⎨⎪⎧n =10,2m +n =20,解得⎩
⎪⎨⎪⎧m =5,n =10, ∴线段AD 所在直线的函数表达式为y =5x +10. 当y =15时,15=5x +10,解得x =1; 15=240x ,解得x =240
15
=16,
∴16-1=15(h ).
答:恒温系统在一天内保持大棚里温度在15 ℃及15 ℃以上的时间有15 h . 10.解:(1)设锻造时y 与x 之间的函数表达式为y =k 1x ,则600=k 1
8,∴k 1=4800,
∴y =4800
x
.
当y =800时,800=4800
x ,x =6,
∴点B 的坐标为(6,800).
∴锻造时的函数表达式为y =4800
x
(x≥6).
设煅烧时的函数表达式为y =k 2x +b ,则⎩⎪⎨⎪⎧b =32,6k 2+b =800,解得⎩
⎪⎨⎪⎧k 2=128,
b =32,
∴煅烧时y 与x 之间的函数表达式为y =128x +32(0≤x<6). (2)当y =480时,x =4800
480=10,
10-6=4(min ),
∴锻造的操作时间有4 min . [素养提升]
解:(1)设v 与t 之间的函数表达式为v =s
t .
∵当t =5时,v =120, ∴s =120×5=600, ∴当v =60时,t =600
60
=10,
∴v 与t 之间的函数表达式为v =600
t (5≤t≤10).
(2)①依题意,得3(v +v -20)=600, 解得v =110,
经检验,v=110符合题意.
当v=110时,v-20=90.
答:客车和货车的平均速度分别为110千米/时和90千米/时.②当A加油站在甲地和B加油站之间时,
110t-(600-90t)=200,
解得t=4,此时110t=110×4=440;
当B加油站在甲地和A加油站之间时,
110t+200+90t=600,
解得t=2,此时110t=110×2=220.
答:甲地与B加油站的距离为220千米或440千米.。
