线性代数综合测试题
西安工业大学线性代数第二学期试题(B卷)--11月4日

22
212
1213352626x x x x x x x ,则此二次型的秩为命题教师:1.出题用小四号、宋体输入打印, 纸张大小为8K.
考 生:1.不得用红色笔,铅笔答题,不得在试题纸外的其他纸张上答题,否则试卷无效。
2.参加同卷考试的学生必须在“备注”栏中填写“同卷”字样。
3.考试作弊者,给予留校察看处分;叫他人代考或代他人考试者,双方均给予开除学籍处理。
并取消授予学士学位资
命题教师:1.出题用小四号、宋体输入打印, 纸张大小为8K.
考 生:1.不得用红色笔,铅笔答题,不得在试题纸外的其他纸张上答题,否则试卷无效。
2.参加同卷考试的学生必须在“备注”栏中填写“同卷”字样。
3.考试作弊者,给予留校察看处分;叫他人代考或代他人考试者,双方均给予开除学籍处理。
并取消授予学士学位资
命题教师:1.出题用小四号、宋体输入打印, 纸张大小为8K.
考 生:1.不得用红色笔,铅笔答题,不得在试题纸外的其他纸张上答题,否则试卷无效。
2.参加同卷考试的学生必须在“备注”栏中填写“同卷”字样。
3.考试作弊者,给予留校察看处分;叫他人代考或代他人考试者,双方均给予开除学籍处理。
并取消授予学士学位资。
线性代数考试题及答案3
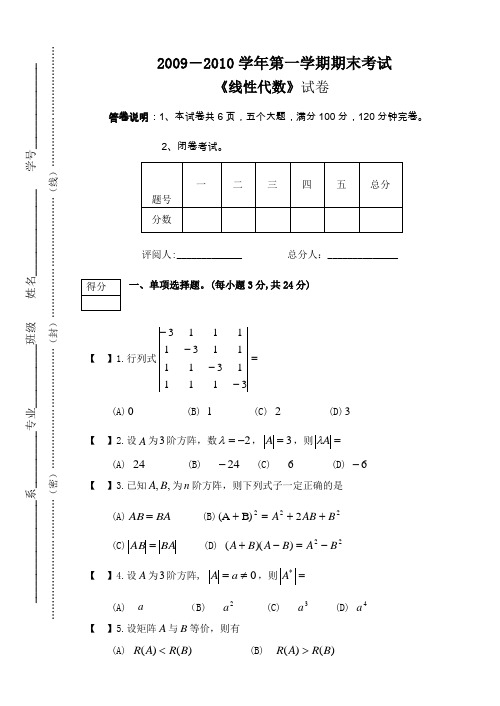
2009-2010学年第一学期期末考试 《线性代数》试卷 答卷说明:1、本试卷共6页,五个大题,满分100分,120分钟完卷。
2、闭卷考试。
评阅人:_____________ 总分人:______________ 一、单项选择题。
(每小题3分,共24分) 【 】1.行列式=----3111131111311113 (A)0 (B) 1 (C) 2 (D)3 【 】2.设A 为3阶方阵,数2-=λ,3=A ,则=A λ (A) 24 (B) 24- (C) 6 (D) 6- 【 】3.已知,,B A 为n 阶方阵,则下列式子一定正确的是 (A)BA AB = (B)2222B)(A B AB A ++=+ (C)BA AB = (D) 22))((B A B A B A-=-+ 【 】4.设A 为3阶方阵, 0≠=a A ,则=*A (A) a (B) 2a (C) 3a (D) 4a【 】5.设矩阵A 与B 等价,则有__________________系__________专业___________班级姓名_______________学号_______________………………………………(密)………………………………(封)………………………………(线)………………………………(C) )()(B R A R = (D) 不能确定)(A R 和)(B R 的大小【 】6.设n 元齐次线性方程组0=Ax 的系数矩阵A 的秩为r ,则0=Ax 有非零解的充分必要条件是(A) n r = (B) n r ≥ (C) n r < (D) n r >【 】7. 向量组)2(,,,21≥m a a a m 线性相关的充分必要条件是(A) m a a a ,,,21 中至少有一个零向量(B) m a a a ,,,21 中至少有两个向量成比例(C) m a a a ,,,21 中每个向量都能由其余1-m 个向量线性表示(D) m a a a ,,,21 中至少有一个向量可由其余1-m 个向量线性表示【 】8. n 阶方阵A 与对角阵相似的充分必要条件是(A)n A R =)( (B)A 有n 个互不相同的特征值(C)A 有n 个线性无关的特征向量 (D)A 一定是对称阵二、填空题。
《经济数学基础》综合练习(线性代数)

《经济数学基础》综合练习(线性代数)一、单项选择题1.设A 为23⨯矩阵,B 为32⨯矩阵,则下列运算中( )可以进行. A .AB B .AB T C .A +B D .BA T 2.设B A ,为同阶可逆矩阵,则下列等式成立的是( ) A . T T T )(B A AB = B . TT T )(A B AB = C . 1T 11T)()(---=B A AB D . T 111T )()(---=B A AB3.设B A ,为同阶可逆方阵,则下列说法正确的是( ). A . 若AB = I ,则必有A = I 或B = I B .TTT)(B A AB = C . 秩=+)(B A 秩+)(A 秩)(B D .111)(---=A B AB4.设B A ,均为n 阶方阵,在下列情况下能推出A 是单位矩阵的是( ). A .B AB = B .BA AB = C .I AA = D .I A=-15.设A 是可逆矩阵,且A AB I +=,则A -=1( ). A . B B . 1+B C . I B + D . ()I AB --16.设)21(=A ,)31(-=B ,I 是单位矩阵,则I B A -T=( ).A .⎥⎦⎤⎢⎣⎡--6231 B .⎥⎦⎤⎢⎣⎡--6321 C .⎥⎦⎤⎢⎣⎡--5322 D .⎥⎦⎤⎢⎣⎡--5232 7.设下面矩阵A , B , C 能进行乘法运算,那么( )成立.A .AB = AC ,A ≠ 0,则B = C B .AB = AC ,A 可逆,则B = C C .A 可逆,则AB = BAD .AB = 0,则有A = 0,或B = 08.设A 是n 阶可逆矩阵,k 是不为0的常数,则()kA -=1( ).A .kA -1B .11kA n- C . --kA 1D . 11k A - 9.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=314231003021A ,则r (A ) =( ). A .4 B .3 C .2 D .110.设线性方程组b AX =的增广矩阵通过初等行变换化为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--00000120004131062131,则此线性方程组的一般解中自由未知量的个数为( ).A .1B .2C .3D .4 11.线性方程组⎩⎨⎧=+=+012121x x x x 解的情况是( ).A . 无解B . 只有0解C . 有唯一解D . 有无穷多解 12.若线性方程组的增广矩阵为⎥⎦⎤⎢⎣⎡=01221λA ,则当λ=()时线性方程组无解.A .12B .0C .1D .2 13. 线性方程组AX =0只有零解,则AX b b =≠()0( ).A . 有唯一解B . 可能无解C . 有无穷多解D . 无解14.设线性方程组AX=b 中,若r (A , b ) = 4,r (A ) = 3,则该线性方程组( ). A .有唯一解 B .无解 C .有非零解 D .有无穷多解15.设线性方程组b AX =有唯一解,则相应的齐次方程组O AX =( ). A .无解 B .有非零解 C .只有零解 D .解不能确定二、填空题1.两个矩阵B A ,既可相加又可相乘的充分必要条件是 .2.计算矩阵乘积[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡10211000321= .3.若矩阵A = []21-,B = []132-,则A T B=.4.设A 为m n ⨯矩阵,B 为s t ⨯矩阵,若AB 与BA 都可进行运算,则m n s t ,,,有关系式 .5.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=13230201a A ,当a = 时,A 是对称矩阵. 6.当a 时,矩阵⎥⎦⎤⎢⎣⎡-=a A 131可逆. 7.设B A ,为两个已知矩阵,且B I -可逆,则方程X BX A =+的解=X.8.设A 为n 阶可逆矩阵,则r (A )= .9.若矩阵A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--330204212,则r (A ) = .10.若r (A , b ) = 4,r (A ) = 3,则线性方程组AX = b.11.若线性方程组⎩⎨⎧=+=-002121x x x x λ有非零解,则=λ.12.设齐次线性方程组01=⨯⨯n n m X A ,且秩(A ) = r < n ,则其一般解中的自由未知量的个数等于 .13.齐次线性方程组0=AX 的系数矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=000020103211A 则此方程组的一般解为 .14.线性方程组AX b =的增广矩阵A 化成阶梯形矩阵后为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-→110000012401021d A则当d 时,方程组AX b =有无穷多解.15.若线性方程组AX b b =≠()0有唯一解,则AX =0 .三、计算题1.设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=113421201A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=303112B ,求B A I )2(T -.2.设矩阵 ⎥⎦⎤⎢⎣⎡-=021201A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=200010212B ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=242216C ,计算C BA +T .3.设矩阵A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------1121243613,求1-A .4.设矩阵A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-012411210,求逆矩阵1-A . 5.设矩阵 A =⎥⎦⎤⎢⎣⎡--021201,B =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡142136,计算(AB )-1. 6.设矩阵 A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-022011,B =⎥⎦⎤⎢⎣⎡--210321,计算(BA )-1. 7.解矩阵方程⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--214332X .8.解矩阵方程⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡02115321X . 9.设线性方程组⎪⎩⎪⎨⎧=-+=-+=+bax x x x x x x x 321321312022讨论当a ,b 为何值时,方程组无解,有唯一解,有无穷多解.10.设线性方程组 ⎪⎩⎪⎨⎧=+-=-+--=+052231232132131x x x x x x x x ,求其系数矩阵和增广矩阵的秩,并判断其解的情况.11.求下列线性方程组的一般解:⎪⎩⎪⎨⎧=-+-=+-+-=-+03520230243214321431x x x x x x x x x x x 12.求下列线性方程组的一般解:⎪⎩⎪⎨⎧=-+-=-+-=+-126142323252321321321x x x x x x x x x 13.设齐次线性方程组⎪⎩⎪⎨⎧=+-=+-=+-0830352023321321321x x x x x x x x x λ问λ取何值时方程组有非零解,并求一般解.14.当λ取何值时,线性方程组⎪⎩⎪⎨⎧=+-=-+=++1542131321321x x x x x x x x λ 有解?并求一般解.15.已知线性方程组b AX =的增广矩阵经初等行变换化为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----→→300000331013611λ A问λ取何值时,方程组b AX =有解?当方程组有解时,求方程组b AX =的一般解.四、证明题1.试证:设A ,B ,AB 均为n 阶对称矩阵,则AB =BA .2.试证:设A 是n 阶矩阵,若3A = 0,则21)(A A I A I ++=--. 3.已知矩阵 )(21I B A +=,且A A =2,试证B 是可逆矩阵,并求1-B . 4. 设n 阶矩阵A 满足A I 2=,T AA I =,证明A 是对称矩阵.5.设A ,B 均为n 阶对称矩阵,则AB +BA 也是对称矩阵.。
线性代数模拟考试题(4套)

线性代数模拟考试题(4套)模拟试题⼀⼀、判断题:(正确:√,错误:×)(每⼩题2分,共10分)1、若B A ,为n 阶⽅阵,则 B A B A +=+. ……………………( )2、可逆⽅阵A 的转置矩阵T A 必可逆. ……………………………( )3、n 元⾮齐次线性⽅程组b Ax =有解的充分必要条件n A R =)(.…( )4、A 为正交矩阵的充分必要条件1-=A A T .…………………………( )5、设A 是n 阶⽅阵,且0=A ,则矩阵A 中必有⼀列向量是其余列向量的线性组合.…………………………………………………………( ) ⼆、填空题:(每空2分,共20分)1、,A B 为 3 阶⽅阵,如果 ||3,||2A B ==,那么 1|2|AB -= .2、⾏列式中元素ij a 的余⼦式和代数余⼦式,ij ij M A 的关系是 .3、在5阶⾏列式中,项5541243213a a a a a 所带的正负号是 .4、已知()??-==256,102B A 则=AB .5、若?--=1225A ,则=-1A . 6、设矩阵--2100013011080101是4元⾮齐次线性⽅程组b Ax =的增⼴矩阵,则b Ax =的通解为 .7、()B A R + ()()B R A R +.8、若*A 是A 的伴随矩阵,则=*AA .9、设=A-500210111t ,则当t 时,A 的⾏向量组线性⽆关.10、⽅阵A 的特征值为λ,⽅阵E A A B 342+-=,则B 的特征值为 . 三、计算:(每⼩题8分,共16分) 1、已知4阶⾏列式1611221212112401---=D ,求4131211132A A A A +-+.2、设矩阵A 和B 满⾜B A E AB +=+2,其中=101020101A ,求矩阵B .四、(10分) 求齐次线性⽅程组=++-=-++=--+-=++-0242205230204321432143214321x x x x x x x x x x x x x x x x 的基础解系和它的通解.五、(10分) 设三元⾮齐次线性⽅程组b Ax =的增⼴矩阵为+-+----22)1)(1()2)(1(00)1(11011λλλλλλλλλλ,讨论当λ取何值时,b Ax =⽆解,有唯⼀解和有⽆穷多解,并在⽆穷多解时求出通解.六、(10分) 判断向量组---=? --=? =? -=1622,4647,3221,1123:4321a a a a A 的线性相关性,如果线性相关,求⼀个最⼤⽆关组,并⽤它表⽰其余向量. 七、综合计算:(本题14分)已知⼆次型31232221321422),,(x x x x x x x x f --+= (1)求⼆次型所对应的矩阵A ,并写出⼆次型的矩阵表⽰;(2)求A 的特征值与全部特征向量;(3)求正交变换PY X =化⼆次型为标准形, 并写出标准形;(4)判断该⼆次型的正定性。
考研线性代数综合竞赛试题

考研线性代数综合竞赛试题 时间:150分 满分:150分一、 选择题(每题1分,共20分)1、 记行列式212322212223333245354435743x x x x x x x x x x x x xx x x ---------------为()f x ,则方程()0f x =的根的个数为()A 1 ()B 2 ()C 3 ()D 42、 设n 维行向量11,0,,0,22α⎛⎫=⎪⎝⎭ ,矩阵,2T T A E B E αααα=-=+,其中E 为n 阶单位矩阵,则AB =()A 0 ()B E - ()C E ()D T E αα+3、设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为 ( )(A )**32O B AO ⎛⎫ ⎪⎝⎭ (B )**23O B AO ⎛⎫⎪⎝⎭ (C )**32O A BO ⎛⎫⎪⎝⎭ (D )**23O A BO ⎛⎫⎪⎝⎭4、设1112131414131211212223242423222131323334343332314142434444434241,a a a a a a a a a a a a a a a a A B a a a a a a a a a a a a a a a a ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,10001010000101000P ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦, 21000001001000001P ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,其中A 可逆,则1B -= ()A 112A PP - ()B 112P A P - ()C 112PP A - ()D 121P A P -5、设A 为m n ⨯矩阵,C 是n 阶可逆矩阵,矩阵A 的秩为r ,矩阵B AC =的秩为1r ,则()A 1r r > ()B 1r r < ()C 1r r = ()D r 与1r 的关系依C 而定6、设矩阵m n A ⨯的秩()r A m n =<,m E 为m 阶单位矩阵,下述结论中正确的是()A A 的任意m 个列向量必线性无关 ()B A 的任意一个m 阶子式不等于零()C A 通过初等行变换,必可以化为(),0m E 形式()D 非齐次方程Ax b =一定有无穷多组解7、设3阶矩阵a b b A b a b b b a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,若A 的伴随矩阵的秩为1,则必有 ()A a b =或20a b += ()B a b =或20a b +≠ ()C a b ≠或20a b += ()D a b ≠或20a b +≠8、设矩阵001010100B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,已知矩阵A 相似于B ,则秩()2A E -与秩()A E -之和等于 ()A 2 ()B 3 ()C 4 ()D 59、设向量组123,,ααα线性无关,向量1β可由123,,ααα线性表示,而向量2β不能由123,,ααα线性表示,则对于任何常数k ,必有()A 123,,ααα,12k ββ+线性无关 ()B 123,,ααα,12k ββ+线性相关()C 123,,ααα,12k ββ+线性无关 ()D 123,,ααα,12k ββ+线性相关10、设向量组()()()()12341,1,2,4,0,3,1,2,3,0,7,14,1,2,2,0,αααα=-===-()52,1,5,10α=,则该向量组的极大线性无关组是()A 123,,ααα ()B 124,,ααα()C 125,,ααα ()D 1245,,,αααα11、设A 是m n ⨯矩阵,B 是n m ⨯矩阵,则线性方程组()0AB x =()A 当n m >时仅有零解 ()B 当n m >时必有非零解 ()C 当m n >时仅有零解 ()D 当m n >时必有非零解12、设n 阶矩阵A 的伴随矩阵*0A ≠,若1234,,,ξξξξ是非齐次线性方程组Ax b =的互不相等的解,则对应的齐次线性方程组0Ax =的基础解系()A 不存在 ()B 仅含一个非零解向量 ()C 含有两个线性无关的解向量 ()D 含有三个线性无关的解向量13、设),,,(4321αααα=A 是4阶矩阵,*A 是A 的伴随矩阵,若T)0,1,0,1(是方程组0=Ax 的一个基础解系,则0*=x A 的基础解系可为 ( )()A 31,αα ()B 21,αα ()C 321,,ααα ()D 432,,ααα14、设123,,ααα是四元非齐次线性方程组Ax b =的三个解向量,且()3r A =,()()1231,2,3,4,0,1,2,3,T TC ααα=+=表示任意常数,则线性方程组Ax b =的通解x 等于()A 11213141C ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ ()B 10213243C ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ ()C 12233445C ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦()D 13243546C ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦15、设2λ=是非奇异矩阵A 的一个特征值,则矩阵1213A -⎛⎫⎪⎝⎭有一个特征值等于()A43 ()B 34 ()C 12 ()D 14 16、设A 是n 阶实对称矩阵,P 是n 阶可逆矩阵。
线代期末综合考试及答案

线性代数期末综合练习(二)班级 姓名 学号一、 填空题 1、设1234555533325422221146523A =,则3132333435()()A A A A A ++-+= . 2、设1212,,,,ααββγ都是3维行向量,且行列式 112212122ααααββββγγγγ====,则12122ααββγ++= . 3、设A 是4阶矩阵,12,ξξ是齐次线性方程组0Ax =的两个线性无关的解,则A 的伴随矩阵A *= .4、方阵A 可表示成一个对称矩阵与一个反对称矩阵之和,其为 .5、设A 是n 阶可逆矩阵,若行列式1A n=-,则1A -= . 6、设矩阵0,0C A D ⎡⎤=⎢⎥⎣⎦若C 、D 可逆,则A 也可逆,且1A -= . 7、设α与β是4阶正交矩阵A 的前两列,则内积(,)αβ= . 8、设3阶矩阵A 的3个特征值为2,3,4,则行列式2A = .9、三阶矩阵122121330A ⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦有一个2重特征值,其值为3, 则它的另一个特征值为 . 二、设A 是n 阶方阵,2A I =,证明矩阵的秩的关系式:()()r A I r A I n ++-=三、 计算n 阶行列式:111111111111n n n n----四、 设矩阵A 、B 满足:AB A B =+,求A B +,其中211264213A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦五、设三维向量123(1,1,1),(,1,1),(1,2,),(2,3,4)a b αααβ====,问当a 、b取何值时,(1)β可由123,,ααα线性表示,且表法不唯一. (2)β不能由123,,ααα线性表示.六、设线性方程组123123123(2)2212(5)4224(5)1x x x x x x x x x λλλλ-+-=⎧⎪+--=⎨⎪--+-=--⎩a) 问λ为何值时,方程组有唯一解,无解,有无穷多解? b) 当有无穷多解时求出其解.七、设12,αα是矩阵A 的分别属于不同特征值12λλ≠的 特征向量,证明12αα+不是A 的特征向量.八、对实对称矩阵A ,求一个正交矩阵P ,使1P AP -为一个对角矩阵.212151212A -⎛⎫⎪=-- ⎪⎪-⎝⎭线性代数期末综合练习(二)班级 姓名 学号 一、填空题1、设1234555533325422221146523A =,则3132333435()()A A A A A ++-+= 0 . 解析: 将3132333435()()A A A A A ++-+还原成行列式 即31323334351234555533()()1111102221146523A A A A A ++-+=--= 2、设1212,,,,ααββγ都是3维行向量,且行列式 112212122ααααββββγγγγ====,则12122ααββγ++= 16 . 解析:12122ααββγ++=1122αββγ++2112212121222222αααααββββββγγγγγ+=+++112212122222ααααββββγγγγ=+++ 3、设A 是4阶矩阵,12,ξξ是齐次线性方程组0Ax =的两个线性无关的解,则A 的伴随矩阵A *= 0 .解析:12,ξξ是齐次线性方程组0Ax =的两个线性无关的解,则0Ax =的基 础解系中至少含有两个解向量,则()22r A n ≤-=,所以A 中所有3阶子 式都为0。
线性代数练习卷1-340
一、选择题(每题2分,共20分)1. 若齐次线性方程组⎪⎩⎪⎨⎧=λ++=+λ+=++λ000321321321x x x x x x x x x 有非零解,则=λ( ).A . 1或2B . -1或-2C . 1或-2D . -1或22. 已知4阶矩阵A 的第三列元素依次为1,3,2,2-,它们的余子式的值分别为3,2,1,1-,则=A (). A .5 B .-5 C .-3 D .33. 设A 、B 均为n 阶矩阵,满足O AB =,则必有( ).A .0=+B A B .))B r A r ((=C .O A =或O B =D .0=A 或0=B4. 设21β,β是非齐次线性方程组b X A =的两个解向量,则下列向量中仍为该方程组解的是( ).A .21+ββB .()212351ββ+ C .()21221ββ+ D .21ββ-5. 以下乘积中( )是4阶行列式ij D a =中取负号的项.A .11233344a a a aB .14233142a a a aC .12233144a a a aD .23413211a a a a6.下列行列式的值不一定为零的是( ).A .行列式中每行元素之和为aB .n 阶行列式中,零的个数多于2n n -个C .行列式中两行元素完全相同D .行列式中两行元素成比例7.设,,A B C 为n 阶方阵,则下列方阵中为对称矩阵的是( ).A .T A A - B. T AA C .T CAC D .()T AA B8.下列矩阵中,不为初等矩阵的是( ).A .001010100⎛⎫ ⎪⎪ ⎪⎝⎭ B .100010301⎛⎫⎪ ⎪ ⎪-⎝⎭ C .100010001-⎛⎫ ⎪- ⎪ ⎪⎝⎭ D .100020001⎛⎫ ⎪⎪ ⎪⎝⎭9. n 元齐次线性方程组0Ax =的系数矩阵A 的秩为r ,则它有非零解的充要条件是( ).A. r n =B. r n <C. r n ≥D. r n >10. 下列论述错误的是( ).A. 含有零向量的向量组必线性相关B. n+1个n 维向量构成的向量组必线性相关C. 向量组12,,,m ααα中的每一个向量i α都可以由该向量组线性表示D. 向量组A :1α、2α、… 、m α(2)m ≥线性相关的充要条件是向量组中每一个向量可由其余m-1个向量线性表示二、填空题(每题3分,共24分)1. 排列953876421的逆序数为 .2.设11223524A t ⎛⎫ ⎪= ⎪ ⎪⎝⎭的秩为2,则t = . 3.已知111213212223313233a a a a a a m a a a =,则111112132121222331313233453453453a a a a a a a a a a a a -+-+=-+ . 4.设12,ηη为三元非齐次线性方程组AX b =的两个不同解,且()2r A =,则AX b =的通解为 .5.设102113A -⎛⎫= ⎪⎝⎭,112013B ⎛⎫= ⎪⎝⎭,则T AB = . 6. 设矩阵1200230000320022A ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,则10||A = . 7. 设方阵A 满足20A A E ++=,则1()A E -+= .8. 设A 为5阶方阵,且3A =,则1*T A A A A -= .三、计算题(每小题8分,共40分)1.计算行列式1123010130231211D --=--. 2. 计算n 阶行列式121121121121n n n n n n n ax x x x ax x D x x a x x x x a ------=.(对角线元素都为a ,每行其余元素为1x 至1n x -) 3. 设矩阵1410,1102P D ---⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭,矩阵A 满足关系式D AP P =-1,试求5A .4.求向量组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=0221,8451,6352,2130,421154321ααααα的秩与它的一个最大无关组,并把其余向量用该最大无关组线性表示.5.已知线性方程组⎪⎩⎪⎨⎧=+--=+++=+++a x x x x x x x x x x x x 4321432143219105363132,(1)问a 为何值时方程组有解?(2)当方程组有解时求出它的通解(用解的结构表示).四、综合题(每小题8分,共16分)1.设,A B 均为n 阶方阵. 证明:AB 可逆当且仅当,A B 均可逆,并求1()AB -.2.一个投资者想把1万元钱投入给3个企业1A 2A 3A ,所得利润率分别为12%,15%,22%,他想得到2000元的利润.(1) 如果投入给2A 的钱是投入给1A 的2倍,那么应当分别给1A 2A 3A 投资多少?(2) 可不可以投给3A 的钱等于投给1A 2A 的钱的和?。
郑州工业应用技术学院 线性代数(高起专) 综合作业
1. (单选题) 设A为3阶矩阵,|A|=1,则|-2A T|=( )(本题1.0分)A. -8B. -2C. 2D. 8答案: A解析: 无2. (单选题) 下列矩阵中不是初等矩阵的是( )(本题1.0分)A.B.C.D.答案: A解析: 无3. (单选题) 设行列式,则()(本题1.0分)A. -6B. -3C. 3D. 6答案: D解析: 无4. (单选题) 设齐次线性方程组有非零解,则为( )(本题1.0分)A. 1B. 0C. -1D. 2答案: C解析: 无5. (单选题) 若向量α=(1,-2,1)与β=(2,3,t)正交,则t=( )(本题1.0分)A. -2B. 0C. 2D. 4答案: D解析: 无6. (单选题) 设三阶方阵A的特征值分别为,则的特征值为( )(本题1.0分)A. 2,4,B.C.D. 2,4,3-答案: A解析: 无7. (单选题) 对于任意两个事件A与B,若A B,则P(A-B)= ( )。
(本题1.0分)A. P(A) -P(B)B. 1C. 0D. P(A)答案: C解析: 无8. (单选题) 设为某连续型随机变量的概率密度函数, 则必有( )。
(本题1.0分)A.B.C. 在定义域内单调不减D.答案: B解析: 无9. (单选题) 若P( )=0.1,P( )=0.6,独立,则=( )(本题1.0分)A. 0.9B. 0.4C. 1.3D. 0.94答案: D解析: 无10. (单选题) 已知随机变量X服从参数为2的指数分布,则随机变量X的期望为( )(本题1.0分)A. -B. 0C.D. 2答案: C解析: 无11. (单选题) 设行列式,,则行列式等于( )(本题1.0分)A. m+nB. -(m+n)C. n-mD. m-n答案: D解析: 无12. (单选题) 已知4阶矩阵A的第三列的元素依次为1,3,-2,2,它们的余子式的值分别为3,-2,1,1,则( )(本题1.0分)A. 5B. -5C. -3D. 3答案: A解析: 无13. (单选题) 设A是方阵,如有矩阵关系式AB=AC,则必有( )(本题1.0分)A. A =0B. B C时A=0C. A0时B=D. |A|0时B=C答案: D解析: 无14. (单选题) .设矩阵A的秩为r,则A中( )(本题1.0分)A. 所有r-1阶子式都不为0B. 所有r-1阶子式全为0C. 至少有一个r阶子式不等于0D. 所有r阶子式都不为0答案: C解析: 无15. (单选题) 设n阶方阵A不可逆,则必有( )(本题1.0分)A. 秩(A)<nB. 秩(A)=n-1C. A=0D. 方程组Ax=0只有零解答案: A解析: 无16. (单选题) 设是非齐次线性方程组的两个解向量,则下列向量中仍为该方程组解的是( )(本题1.0分)A.B.C.D.答案: B解析: 无17. (单选题) 设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,则必有( )(本题1.0分)A. k≤3B. k<3C. k=3D. k>3答案: A解析: 无18. (单选题) .设A是正交矩阵,则下列结论错误的是( )(本题1.0分)A. |A|2必为1B. |A|必为1C. A-1=A TD. A的行(列)向量组是正交单位向量组答案: B解析: 无19. (单选题) 设A=,则下列矩阵中与A相似的是( )(本题1.0分)A.B.C.D.答案: A解析: 无20. (单选题) 设矩阵A=有特征值1、2、-4,则=( ) (本题1.0分)A. 3B. -3C. 2D. -4答案: B解析: 无21. (单选题) 设行列式,则( )(本题1.0分)A. -6B. -3C. 3D. 6答案: D解析: 无22. (单选题) 设矩阵,为同阶方阵,且可逆,若则矩阵=( )(本题1.0分)A.B.C.D.答案: A解析: 无23. (单选题) 已知向量,,则=( )(本题1.0分)A.B.C.D.答案: A解析: 无24. (单选题) 已知A为3阶方阵,且∣A∣=3,则∣-2A∣=( )(本题1.0分)A. -6B. 6C. -24D. 24答案: C解析: 无25. (单选题) 设三阶方阵A的特征值分别为,则的特征值为( )(本题1.0分)A. 2,4,B.C.D. 2,4,3答案: A解析: 无26. (单选题) 设A是正交矩阵,则下列结论错误的是( )(本题1.0分)A. |A|2必为1B. |A|必为1C.D. A的行(列)向量组是正交单位向量组答案: B解析: 无27. (单选题) 对于任意两个事件A与B,若A B,则P(A-B)= ( )。
线性代数 综合复习资料
《线性代数(经)》综合复习资料第一章 n 阶行列式一、判断题 1.1122121233443434a b a b a a b b a b a b a a b b ++=+++ ). ( ) 3、如果行列式0=D ,则D 中必有一行为零。
4. 设A 为n 级方阵:|A|=2 ,则|-3A|= -6 ( ) 5.ij ijA a D ,33⨯=为ij a 的代数余子式,则0231322122111=++A a A a A a . ( )二.填空题:2、设行列式1112132122233132333a a a a a a a a a =,则313233213122322333111213222222222222a a a a a a a a a a a a +++= 。
3、n 个方程、n 个未知量的齐次线性方程组0Ax =有非零解的充要条件是 。
4、设,A B 均为3阶方阵,且2,3A B ==-,则13A B *-= 。
5.设行列式30402222075322D =--,则41424344A A A A +++=____________.三.选择题1、设A 为3阶矩阵且行列式0A =,则下列说法正确的是( ) (A )矩阵A 中元素都等于0;(B )矩阵A 中必有两列元素对应成比例;(C )矩阵A 中必有一列向量是其余列向量的线性组合; (D )矩阵A 中任一列向量是其余列向量的线性组合。
2、一个n 级方阵的行列式的值不为零,经若干次初等变换后,其行列式的值( )(A) 保持不变; (B ) 保持不为零; (C) 可变成任何值; ( D)保持相同的符号。
4. 已知4阶行列式D 的第三行元素分别是1,0,2,-3;第四行元素对应的代数余子式依次是5,10,t ,5,则t=( )(A) 3 (B) 4 (C)5 (D) 65.下列说法错误的是( )(A )若n 阶线性方程组Ax b =的系数矩阵行列式0A ≠,则该方程组存在唯一解; (B )若n 阶线性方程组0Ax =的系数矩阵行列式0A ≠,则该方程组只有零解; (C )一个行列式交换两列,行列式值不变;(D )若一个行列式的一列全为零,则该行列式的值为零。
线性代数考试题及答案解析
WORD 格式整理 2009-2010学年第一学期期末考试 《线性代数》试卷 答卷说明:1、本试卷共6页,五个大题,满分100分,120分钟完卷。
2、闭卷考试。
评阅人:_____________ 总分人:______________ 一、单项选择题。
(每小题3分,共24分) 【 】1.行列式=----3111131111311113 (A)0 (B) 1 (C) 2 (D)3 【 】2.设A 为3阶方阵,数2-=λ,3=A ,则=A λ (A) 24 (B) 24- (C) 6 (D) 6- 【 】3.已知,,B A 为n 阶方阵,则下列式子一定正确的是 (A)BA AB = (B)2222B)(A B AB A ++=+ (C)BA AB = (D) 22))((B A B A B A -=-+【 】4.设A 为3阶方阵, 0≠=a A ,则=*A (A) a (B) 2a (C) 3a (D) 4a 【 】5.设矩阵A 与B 等价,则有(A) )()(B R A R < (B) )()(B R A R >__________________系__________专业___________班级姓名_______________学号_______________………………………………(密)………………………………(封)………………………………(线)………………………………(C) )()(B R A R = (D) 不能确定)(A R 和)(B R 的大小【 】6.设n 元齐次线性方程组0=Ax 的系数矩阵A 的秩为r ,则0=Ax 有非零解的充分必要条件是(A) n r = (B) n r ≥ (C) n r < (D) n r >【 】7. 向量组)2(,,,21≥m a a a m 线性相关的充分必要条件是(A) m a a a ,,,21 中至少有一个零向量(B) m a a a ,,,21 中至少有两个向量成比例(C) m a a a ,,,21 中每个向量都能由其余1-m 个向量线性表示(D) m a a a ,,,21 中至少有一个向量可由其余1-m 个向量线性表示【 】8. n 阶方阵A 与对角阵相似的充分必要条件是(A)n A R =)( (B)A 有n 个互不相同的特征值(C)A 有n 个线性无关的特征向量 (D)A 一定是对称阵二、填空题。
