1-机构的动态静力分析
案例1机构的动态静力分析

4 M 4 p4 x FR4 y p4 y FR4 x q4 x FR3 y q4 y FR3x J 4
三个构件,得到9方程,组成一个线性方程组,可 表示为:
AR B
1 0 q2 y 0 A 0 0 0 0 0
A
2 l2
C
φ2
l3 3
φ1
4 l4
D
φ3
x
x:
y:
l1 cos 1 l 2 cos 2 l 4 l3 cos 3 l1 sin 1 l 2 sin 2 l3 sin 3
位移方程式
以上方程组可求解φ2、φ3。
2、速度分析 y l1 cos 1 l 2 cos 2 l 4 l3 cos 3 l1 sin 1 l 2 sin 2 l3 sin 3 上式对t求导,得: l l11 sin 1 l 2 2 sin 2 l3 3 sin 3 1 1 l11 cos 1 l 2 2 cos 2 l3 3 cos 3
G ( FP0 ks) fFR 2 x ms FR cos 0
FR 2 x FR sin 0
FR (r0 s) sin FR 2 x H M 2 0
对凸轮1: FR1y FR cos 0 FR1x FR sin 0
M d FR (r0 s) sin 0
按照上述表示方法可将三个构件的平衡方程展开为: 构件2:
s2 F2 x FR2 x FR1x m2 x
s2 F2 y FR2 y FR1y m2 y
机械分析应用基础03第三章 机构静力分析基础

根据合力投影定理,有:
FRx= ΣFx=F1x+ F2x + F3x + F4x =F1cosα1+F2cosα2+F3 cosα3+F4 cosα4 =0.2 cos30°+0.3cos45°+0.5 cos0+0.4cos60° = 1.085kN
FRy = ΣFy=F1y+ F2y + F3y + F4y = - F1sinα1+F2sinα2+F3sinα3-F4sinα4 = - 0.2sin30°+0.3sin45°+0.5sin0-0.4 sin60° = -0.234kN
刚体和变形体 刚体——忽略受力后微小变形的力学模型。
F
F´
F
F´
例如:研究塔吊不致倾倒,确定所需配重时,视其为刚体。
刚体和变形体 变形体——不能忽略受力后微小变形的力学模型。
F
F´
例如:研究组成塔吊的每一根杆件时,视其为变形体。
2.力的性质 性质1 二力平衡公理 不计自重的构件在二力作用下平衡 的必要和充分条件: 二力等值、反向、共线。
矢量表达式为: F1= -F2
二力构件(二力杆)——作用有二力而处于平衡的构件 。
二力杆上的两个力必沿两力作用点的连线(与构件形状无 关),且等值、反向。
2.力的性质 性质1 二力平衡公理 例如:
性质2 加减平衡力系公理 在作用于构件的力系中,加上或减去任意个平衡力系,不改 变原力系对构件的作用效应。
第三章 机构静力分析基础
第一节 静力分析的基本概念 第二节 平面机构中约束类型及约束反力 第三节 平面机构中约束反力的求解 第四节 运动副的摩擦与自锁 第五节 回转件平衡的动态静力分析
第三章 机构静力分析基础
第7章机械动力学
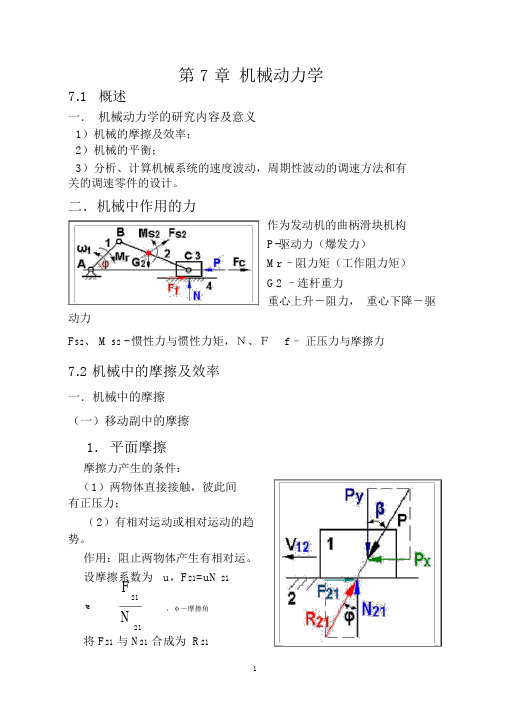
第 7 章机械动力学7.1概述一.机械动力学的研究内容及意义1)机械的摩擦及效率;2)机械的平衡;3)分析、计算机械系统的速度波动,周期性波动的调速方法和有关的调速零件的设计。
二.机械中作用的力作为发动机的曲柄滑块机构P-驱动力(爆发力)Mr –阻力矩(工作阻力矩)G2 –连杆重力重心上升-阻力,重心下降-驱动力F S2、 M S2 - 惯性力与惯性力矩,N、F f –正压力与摩擦力7.2 机械中的摩擦及效率一.机械中的摩擦(一)移动副中的摩擦1.平面摩擦摩擦力产生的条件:(1)两物体直接接触,彼此间有正压力;(2)有相对运动或相对运动的趋势。
作用:阻止两物体产生有相对运。
设摩擦系数为u,F21=uN 21F21tg,φ-摩擦角N21将 F21与 N21合成为 R21R21-总反力(全反力)P X P分解为 P和 P ,tgX Y P Y( P X P sin、 P Y P cos )F21P X,有F21tgY 方向平衡: Py=N 21,即:tg tg P Xtg讨论:①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ, P X > F21,滑块作加速运动;当β =φ, P X = F21,动则恒动,静则恒静;当β <φ, P X < F21,原来运动,作减速运动,原来静止,永远静止,称自锁。
③ 自锁条件:β≤φβ=φ,条件自锁(静止);β<φ,无条件自锁。
2.斜面摩擦斜面机构如图,滑块置于升角α的斜面上,摩擦角为φ,作用于滑块上的铅垂力为Q,求滑块等速上升和下降时所需水平平衡力P 和 P’。
(1)求等速上升水平平衡力 PP-驱动力, Q-阻力PQ R 21 0 ,tg ()P,P Qtg () (1)Q( 2)求等速下降水平平衡力 P ’Q -驱动力, P ’-阻力P'Q R 21 0 ,tg () P ',P 'Qtg () (2)Q讨论:① 欲求下滑 (反行程) P ’,只需将式 ( 1)中 P →P ’,φ→ (-φ )② 下滑时,当α >φ, P ’为平衡力α <φ, P ’为负,成为驱动力的一部分,该条件下,若无 P ’,则无论 Q 多大,滑块不下滑,称自锁,自锁条件:α≤φ。
6.1平面机构的动态静力分析
M3 C32 M32 ~rDCC32 R32 0
第六章 机构的动态静力分析
M3 C32 M32 ~rDCC32 R32 0
u03 c3
v03
s3c
23
M 3 s3s23
s3 c 3c 23 c3s23
0 u32
[C12
]s32
s21
0
0 0
c2 s2c12 s2s12 r32 r21
s2
c2c12
c
2s12
s32
s21
0
0
s12
c12 0 0
r32c2 s32s2c12 r21 0 r32s2 s32c2c12 s21 0 s32s12 0
r32c2 r21 0 r32s2 s21 0
第六章 机构的动态静力分析
6.1 平面机构的动态静力分析
6.1.1 构件的受力分析
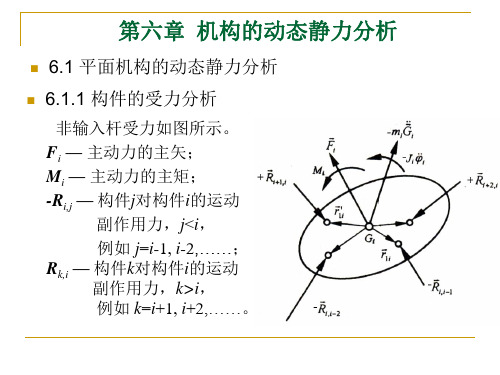
非输入杆受力如图所示。 Fi — 主动力的主矢; Mi — 主动力的主矩; -Ri,j — 构件j对构件i的运动
副作用力,j<i, 例如 j=i-1, i-2,……; Rk,i — 构件k对构件i的运动 副作用力,k>i, 例如 k=i+1, i+2,……。
共有9个方程:
R10x R21x
F1x
m1G1x
R10 y R21y F1y m1G1y
r1y R10x r1x R10 y r1y R21x r1x R21y M1N M1 J11
R21x R32x F2x m2G2x R21y R32 y F2 y m2G2 y
构件2的力和力矩平衡方程为
R32 R21 m2G2
(d e3 ) R32 r2 R21 J22
第一章机构的动态静力分析

其中A为系数矩阵
0 0 0 1 0 p3 y 1 0 q4 y 0 0 0 0 1 p3 x 0 1 q4 x 0 0 0 0 0 0 1 0 p4 y 0 0 0 0 0 0 0 1 p4 x 0 0 1 0 0 0 0 0 0
系数矩阵中的元素与各构件的质心位置有关。
Md为平衡力矩:
驱动力矩。
构件4:
4 F4 FR 4 FR3 m4 s 4 M 4 p4FR 4 q4FR3 J 4
构件2:
2 F2 FR 2 FR1m2 s 2 M 2 p2FR 2 q2FR1 Md J 2
凸轮作用于从动件的力:FR
FR cos 0 (a) G( FP 0 ks)fFR 2 x m s 从动件的平衡方程:FR 2 x FR sin 0 (b) FR (r0 s)sin FR 2 x H M 2 0 (c )
凸轮的平衡方程:
FR1 y FR cos 0 (d ) FR1x FR sin 0 (e) M d FR (r0 s)sin 0 ( f )
对质心的矩式平衡方程 pI FRi qI FRi1 M I J II 0
方程可改写为
I FRi FRi1FI mI s I pI FRi qI FRi1 M I J I
其中:pI , qI 为从质心至铰链 的矢径
二、平面连杆机构的动态静力分析
第i个构件的力平衡方程 FRi为第(i+1)个构件作用在第i个构件上 的约束反力。
二、平面梁杆机构的动态静力分析
第I个构件在约束反力、主动力主矢、主矩、惯 性力、惯性力偶矩的共同作用下处于平衡状态。
列出矢量形式的平衡方程
二、平面连杆机构的动态静力分析
机械原理课程设计压床机构

机械原理课程设计说明书设计题目:学院:班级:设计者:学号:指导老师:目录目录....................................................................................一、机构简介与设计数据.......................................................................1.1.机构简介.............................................................................1.2机构的动态静力分析....................................................................1.3凸轮机构构设计........................................................................1.4.设计数据.............................................................................二、压床机构的设计...........................................................................2.1.传动方案设计.........................................................................基于摆杆的传动方案...................................................................六杆机构A ............................................................................六杆机构B ............................................................................2.2.确定传动机构各杆的长度...............................................................三.传动机构运动分析..........................................................................3.1.速度分析.............................................................................3.2.加速度分析...........................................................................3.3. 机构动态静力分析....................................................................3.4.基于soildworks环境下受力模拟分析: ..................................................四、凸轮机构设计.............................................................................五、齿轮设计.................................................................................5.1.全部原始数据.........................................................................5.2.设计方法及原理.......................................................................5.3.设计及计算过程....................................................................... 参考文献.....................................................................................一、机构简介与设计数据1.1.机构简介图示为压床机构简图,其中六杆机构为主体机构。
1-机构的动态静力分析

Machinery Dynamics
静力分析是基础
加入惯性力,成为动态静力分析
力平衡是根本 矢量形式和标量形式是统一的; 力平衡和力矩平衡是独立的。 重视对机架的附加反动 摆动力和摆动力矩对机器的影响 研究平衡力矩的特性 在动态设计中的指导意义
Machinery Dynamics
机械动力学
Raymond Ding ©
Question 1
pi FRi qi FRi1 Mi Jii
vector equation & scalar equation
Machinery Dynamics
机械动力学
Raymond Ding ©
1 0 0 1 q2 y q2 x 0 0 0 A 0 0 0 0 0 0 0 0 0 1 0 p2 y 1 0 q3 y 0 0 0 0 1 p2 x 0 1 q3 x 0 0 0 0 0 0 1 0 p3 y 1 0 q4 y 0 0 0 0 1 p3 x 0 1 q4 x 0 0 0 0 0 0 1 0 p4 y 0 0 0 0 0 0 0 1 p4 x 0 0 1 0 0 0 0 0 0
FR1x FR1 y FR 2 x FR 2 y R FR 3 x FR 3 y FR 4 x FR 4 y Md
m2 s 2 F2 x x m2 s 2 F2 y y J 22 M 2 m3 s 3 F3 x x B m3 s 3 F3 y y J 33 M 3 m4 s 4 F4 x x m4 s 4 F4 y y J 44 M 4
Raymond Ding ©
平面连杆机构的动态静力分析
导杆机构
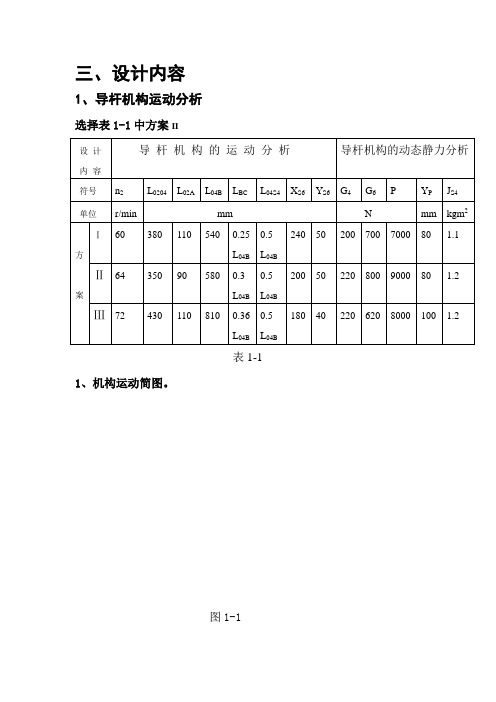
三、设计内容1、导杆机构运动分析选择表1-1中方案II设计内容导杆机构的运动分析导杆机构的动态静力分析符号n2 L0204 L02A L04B L BC L04S4 X S6 Y S6 G4 G6 P Y P J S4 单位r/min mm N mm kgm2方案Ⅰ60 380 110 540 0.25L04B0.5L04B240 50 200 700 7000 80 1.1 Ⅱ64 350 90 580 0.3L04B0.5L04B200 50 220 800 9000 80 1.2 Ⅲ72 430 110 810 0.36L04B0.5L04B180 40 220 620 8000 100 1.2表1-11、机构运动简图。
图1-12、曲柄位置“7”速度分析,加速度分析(列矢量方程,画速度图,加速度图)取曲柄位置“7”进行速度分析,其分析过程同曲柄位置“1”。
取构件3和4的重合点A进行速度分析。
列速度矢量方程,得υA4=υA3+υA4A3大小? √?方向⊥O4A⊥O2A∥O4B代表pa4 pa3 a3a4V A3=ω2l o2A=64/60×6.28×0.09=0.603m/s取速度极点P,速度比例尺µv=0.01(m/s)/mm,作速度多边形如图1-2则由图1-2知,υA4=pa4·μv=29×0.01=0.29m/sυA4A3=a3a4·μv=52×0.01m/s=0.52m/s图1-2υB5=υB4=υA4·O4B/ O4A=0.44m/s取5构件为研究对象,列速度矢量方程,得υC5=υB5+υC5B5大小? √?方向∥XX⊥O4B⊥BC代表pc5 pb4 b4b5其速度多边形如图1-2所示,有υC5=5Pc·μv=42×0.01=0.42m/s取曲柄位置“7”进行加速度分析,取曲柄构件3和4的重合点A进行加速度分析.列加速度矢量方程,得:a A4 =a A4n +a A4t= a A3n +a A4A3k+a A4A3r 大小? ω42l O4A ?√2ω4υA4A3 ? 方向? A→O4⊥O4B A→O2⊥O4B(向右)∥O4B代表pA4’pn4’n4’A4’p’A3’A3’k’k’A4’取加速度极点为P',加速度比例尺μa=0.02(m/s2)/mm作加速度多边形图1-3图1-3则由图1─3知:a A4t= n4’A4’·μa =137×0.02m/s2=2.74m/s2α4= a A4t/l O4A = 7.17 m/s2a A4 = pA4’·μa = 138×0.01m/s2 =2.76 m/s2用加速度影象法求得a B5 = a B4 = a A4 ×l O4B/l O4A=4.19m/s2取5构件的研究对象,列加速度矢量方程,得a C5=a B5+ a C5B5n+ a C5B5t大小?√√?方向∥xx √ C→B ⊥BC代表 P’c5’ P’B5’ n5’B5’ C5’n5’加速度比例尺μa=0.02(m/s2)/mm其加速度多边形如图1─4所示,有图1-4a C5B5t= n5’c5’·μa =31×0.02m/s2 =0.62m/s2a C5 = P’c5’·μa =179×0.02m/s2 =3.58m/s23、曲柄位置“10”速度分析,加速度分析(列矢量方程,画速度图,加速度图)取曲柄位置“10”进行速度分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M d FR (r0 s) sin 0
G FP 0 ks m s M d (r0 s) tan 1 f tan
Machinery Dynamics
机械动力学
Raymond Ding ©
平面凸轮机构的动态静力分析
AR B
Machinery Dynamics
机械动力学
Raymond Ding ©
摆动力和摆动力矩 shaking of the base
惯性载荷引起的附加动反力
周期性波动 惯性载荷 贡献度
激励→振动
Machinery Dynamics
机械动力学
Raymond Ding ©
平面凸轮机构的动态静力分析
机械动力学
Raymond Ding ©
平面机构的动态静力分析
Kinetostatic Analysis of Planar Mechanism
Machinery Dynamics
机械动力学
Raymond Ding ©
1. 几个相关的概念 2. 平面连杆机构的动态静力分析 3. 平面凸轮机构的动态静力分析 4. 小结
pi FRi qi FRi1 Mi Jii
vector equation & scalar equation
Machinery Dynamics
机械动力学
Raymond Ding ©
1 0 0 1 q2 y q2 x 0 0 0 A 0 0 0 0 0 0 0 0 0 1 0 p2 y 1 0 q3 y 0 0 0 0 1 p2 x 0 1 q3 x 0 0 0 0 0 0 1 0 p3 y 1 0 q4 y 0 0 0 0 1 p3 x 0 1 q4 x 0 0 0 0 0 0 1 0 p4 y 0 0 0 0 0 0 0 1 p4 x 0 0 1 0 0 0 0 0 0
Prob. 图为一对心直动从动件圆 盘凸轮机构,假定凸轮作等速回转 运动,忽略凸轮轴可能存在的速度 波动。求作用于凸轮上维持其等速 回转的平衡力矩。
看成上述分析方法的 一个应用例子
Md ?
Machinery Dynamics
机械动力学
Raymond Ding ©
Equation s
Machinery Dynamics
静力分析是基础
加入惯性力,成为动态静力分析
力平衡是根本 矢量形式和标量形式是统一的; 力平衡和力矩平衡是独立的。 重视对机架的附加反动 摆动力和摆动力矩对机器的影响 研究平衡力矩的特性 在动态设计中的指导意义
Machinery Dynamics
机械动力学
Raymond Ding ©
Question 1
大小:固有性质+运动状态 方向:反动 广义力:效果形式 两个特例:平动;绕质心转动
Fi mi i s
M i J ii
Machinery Dynamics
机械动力学
Raymond Ding ©
平面连杆机构的动态静力分析
Machinery Dynamics
机械动力学
Machinery Dynamics
机械动力学
Raymond Ding ©
机器在运转过程中,受到其各部件本身所具有的 质量和转动惯量在运动状态下产生的惯性作用。 周期性变化的惯性作用是产生机器振动、噪音和 疲劳等现象的主要原因→机构的运动和动力性能。
动力平衡就是为解决这一问题所进行的研究,
它是机构学领域,特别是机构动力学重要的前沿课 题之一。
G FP 0 ks m s M d (r0 s) tan 1 f tan
Machinery Dynamics
机械动力学
Raymond Ding ©
Any questions?
Machinery Dynamics
机械动力学
Raymond Ding ©
Summary
“二力杆”的受力,与运动构件的受力分析为什么不同?
Machinery Dynamics
Machinery Dynamics
机械动力学
Raymond Ding ©
Several Basic Definitions
机构 mechanism 结构 structure 构件 part;element;components 运动副 kinematic pair 自由度 DOF
Machinery Dynamics
机械动力学
Raymond Ding ©
作用在机械上的力
动力 输入功 抗力 阻抗功
⊙生产阻力
F=F(x), F=F(t), F=F(v), F=C
⊙重力 ⊙摩擦力 ⊙其它介质阻力
Machinery Dynamics
机械动力学
Raymond Ding ©
Inertia Force & Inertia Moment 惯性力和惯性矩
Raymond Ding ©
平面连杆机构的动态静力分析
equations of equilibrium
原动构件→平衡力矩 Md
FRi FRi 1 Fi mi i s
pi FRi qi FRi1 Mi Jii
Machinery Dynamics
机械动力学
机械动力学
Raymond Ding ©
G ( FP0 ks) fFR 2 x ms FR cos 0
FR 2 x FR sin 0
FR (r0 s) sin FR 2 x H M 2 0
FR1y FR cos 0
G FP 0 ks m s FR cos f sin
FR1x FR1 y FR 2 x FR 2 y R FR 3 x FR 3 y FR 4 x FR 4 y Md
m2 s 2 F2 x x m2 s 2 F2 y y J 22 M 2 m3 s 3 F3 x x B m3 s 3 F3 y y J 33 M 3 m4 s 4 F4 x x m4 s 4 F4 y y J 44 M 4
Raymond Ding ©
平面连杆机构的动态静力分析
平衡力矩 为维持原动构 件按假定的理想运动规律 运动,所需施加于原动构 件上的驱动力矩。
Md
Machinery Dynamics
机械动力学
Raymond Ding ©
平面连杆机构的动态静力分析
FRi FRi 1 Fi mi i s
