第一章 机构的动态静力分析
案例1机构的动态静力分析

4 M 4 p4 x FR4 y p4 y FR4 x q4 x FR3 y q4 y FR3x J 4
三个构件,得到9方程,组成一个线性方程组,可 表示为:
AR B
1 0 q2 y 0 A 0 0 0 0 0
A
2 l2
C
φ2
l3 3
φ1
4 l4
D
φ3
x
x:
y:
l1 cos 1 l 2 cos 2 l 4 l3 cos 3 l1 sin 1 l 2 sin 2 l3 sin 3
位移方程式
以上方程组可求解φ2、φ3。
2、速度分析 y l1 cos 1 l 2 cos 2 l 4 l3 cos 3 l1 sin 1 l 2 sin 2 l3 sin 3 上式对t求导,得: l l11 sin 1 l 2 2 sin 2 l3 3 sin 3 1 1 l11 cos 1 l 2 2 cos 2 l3 3 cos 3
G ( FP0 ks) fFR 2 x ms FR cos 0
FR 2 x FR sin 0
FR (r0 s) sin FR 2 x H M 2 0
对凸轮1: FR1y FR cos 0 FR1x FR sin 0
M d FR (r0 s) sin 0
按照上述表示方法可将三个构件的平衡方程展开为: 构件2:
s2 F2 x FR2 x FR1x m2 x
s2 F2 y FR2 y FR1y m2 y
《构件的静力分析》PPT课件

(一)柔性约束
由线绳、链条或胶带等非刚性体所形成的约束。它们 只能受拉不能受压,约束反力的方向沿着中心线而背离被 约束物体。约束反力通常用符号FT来表示。图中线绳上的 约束反力FT1 和FT2 。
(二)光滑面约束 物体与光滑面成点、线、面刚性接触(摩擦力很小,
固定端约束的构件可以用一端插入刚体内的 悬臂梁来表示(图a),这种约束限制物体沿任 何方向的移动和转动,其约束作用包括限制移动 的两个正交约束反力FAx、FAy和限制转动的约束 反力偶MA(图c)。
四、受力图 在对物体进行受力分析时,为了清楚地表示物体的
受力情况,需将研究对象从周围的物体中分离出来,即 解除全部约束,成为分离体。为了使分离体的受力情况 与原来的受力情况一致,必须在分离体上画出所有主动 力,在解除约束的地方画出相应的约束反力。这样所得 到的画有分离体及其全部主动力和约束反力的简图称为 受力图。
二、静力学公理 1.二力平衡公理
刚体仅受两力作用而保持平衡的充分必要条件是: 两力大小相等、方向相反,且作用在同一直线上。如图 所示,即F1=F2
在两个力作用下处于平衡 的刚体,称为二力构件,又称 为二力杆。二力构件受力的特 点是两个力的作用线必沿其作 用点的连线,且等值、反向。
2.加减平衡力系公理 在任意一个已知力系上加上或减去任意的平衡力系, 并不会改变原力系对刚体的作用效应。 力的可传性推理:作用在刚体上的力,沿其作用线移 到刚体上任意一点,不会改变它对刚体的作用效应。
一、平面汇交力系合成的几何法 (一)力的三角形法则
第一章 构件的静力分析
机器的运行是由于力的作用引起的,构件的受力情 况直接影响机器的工作能力。
力是物体间相互的机械作用。力的作用有两种效应: 使物体的机械运动状态发生变化和使物体的形状发生 改变,前者称为运动效应,后者称为变形效应。
机械原理课程设计六杆机构运动与动力分析

机械原理课程设计六杆机构运动与动⼒分析⽬录第⼀部分:六杆机构运动与动⼒分析⼀.机构分析分析类题⽬ 3 1分析题⽬ 32.分析内容 3 ⼆.分析过程 4 1机构的结构分析 42.平⾯连杆机构运动分析和动态静⼒分析 53机构的运动分析8 4机构的动态静⼒分析18 三.参考⽂献21第⼆部分:齿轮传动设计⼀、设计题⽬22⼆、全部原始数据22三、设计⽅法及原理221传动的类型及选择22 2变位因数的选择22四、设计及计算过程241.选取两轮齿数242传动⽐要求24 3变位因数选择244.计算⼏何尺⼨25 五.齿轮参数列表26 六.计算结果分析说明28 七.参考⽂献28第三部分:体会⼼得29⼀.机构分析类题⽬3(⽅案三)1.分析题⽬对如图1所⽰六杆机构进⾏运动与动⼒分析。
各构件长度、构件3、4绕质⼼的转动惯量如表1所⽰,构件1的转动惯量忽略不计。
构件1、3、4、5的质量G1、G3、G4、G5,作⽤在构件5上的阻⼒P⼯作、P空程,不均匀系数δ的已知数值如表2所⽰。
构件3、4的质⼼位置在杆长中点处。
2.分析内容(1)对机构进⾏结构分析;(2)绘制滑块F的运动线图(即位移、速度和加速度线图);(3)绘制构件3⾓速度和⾓加速度线图(即⾓位移、⾓速度和⾓加速度线图);(4)各运动副中的反⼒;(5)加在原动件1上的平衡⼒矩;(6)确定安装在轴A上的飞轮转动惯量。
图1 六杆机构⼆.分析过程:通过CAD制图软件制作的六杆机构运动简图:图2 六杆机构CAD所做的图是严格按照题所给数据进⾏绘制的。
并机构运动简图中活动构件的序号从1开始标注,机架的构件序号为0。
每个运动副处标注⼀个字母,该字母既表⽰运动副,也表⽰运动副所在位置的点,在同⼀点处有多个运动副,如复合铰链处或某点处既有转动副⼜有移动副时,仍只⽤⼀个字母标注。
见附图2所⽰。
1.机构的结构分析如附图1所⽰,建⽴直⾓坐标系。
机构中活动构件为1、2、3、4、5,即活动构件数n=5。
第一章机构的动态静力分析

其中A为系数矩阵
0 0 0 1 0 p3 y 1 0 q4 y 0 0 0 0 1 p3 x 0 1 q4 x 0 0 0 0 0 0 1 0 p4 y 0 0 0 0 0 0 0 1 p4 x 0 0 1 0 0 0 0 0 0
系数矩阵中的元素与各构件的质心位置有关。
Md为平衡力矩:
驱动力矩。
构件4:
4 F4 FR 4 FR3 m4 s 4 M 4 p4FR 4 q4FR3 J 4
构件2:
2 F2 FR 2 FR1m2 s 2 M 2 p2FR 2 q2FR1 Md J 2
凸轮作用于从动件的力:FR
FR cos 0 (a) G( FP 0 ks)fFR 2 x m s 从动件的平衡方程:FR 2 x FR sin 0 (b) FR (r0 s)sin FR 2 x H M 2 0 (c )
凸轮的平衡方程:
FR1 y FR cos 0 (d ) FR1x FR sin 0 (e) M d FR (r0 s)sin 0 ( f )
对质心的矩式平衡方程 pI FRi qI FRi1 M I J II 0
方程可改写为
I FRi FRi1FI mI s I pI FRi qI FRi1 M I J I
其中:pI , qI 为从质心至铰链 的矢径
二、平面连杆机构的动态静力分析
第i个构件的力平衡方程 FRi为第(i+1)个构件作用在第i个构件上 的约束反力。
二、平面梁杆机构的动态静力分析
第I个构件在约束反力、主动力主矢、主矩、惯 性力、惯性力偶矩的共同作用下处于平衡状态。
列出矢量形式的平衡方程
二、平面连杆机构的动态静力分析
机械原理课程设计压床机构

机械原理课程设计说明书设计题目:学院:班级:设计者:学号:指导老师:目录目录....................................................................................一、机构简介与设计数据.......................................................................1.1.机构简介.............................................................................1.2机构的动态静力分析....................................................................1.3凸轮机构构设计........................................................................1.4.设计数据.............................................................................二、压床机构的设计...........................................................................2.1.传动方案设计.........................................................................基于摆杆的传动方案...................................................................六杆机构A ............................................................................六杆机构B ............................................................................2.2.确定传动机构各杆的长度...............................................................三.传动机构运动分析..........................................................................3.1.速度分析.............................................................................3.2.加速度分析...........................................................................3.3. 机构动态静力分析....................................................................3.4.基于soildworks环境下受力模拟分析: ..................................................四、凸轮机构设计.............................................................................五、齿轮设计.................................................................................5.1.全部原始数据.........................................................................5.2.设计方法及原理.......................................................................5.3.设计及计算过程....................................................................... 参考文献.....................................................................................一、机构简介与设计数据1.1.机构简介图示为压床机构简图,其中六杆机构为主体机构。
导杆机构
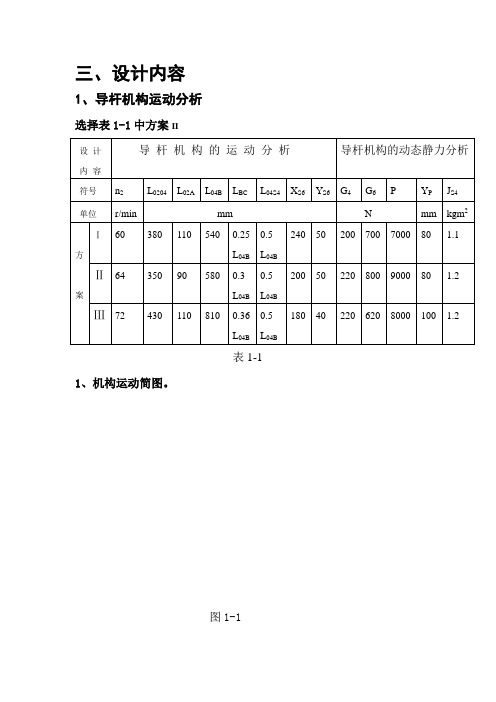
三、设计内容1、导杆机构运动分析选择表1-1中方案II设计内容导杆机构的运动分析导杆机构的动态静力分析符号n2 L0204 L02A L04B L BC L04S4 X S6 Y S6 G4 G6 P Y P J S4 单位r/min mm N mm kgm2方案Ⅰ60 380 110 540 0.25L04B0.5L04B240 50 200 700 7000 80 1.1 Ⅱ64 350 90 580 0.3L04B0.5L04B200 50 220 800 9000 80 1.2 Ⅲ72 430 110 810 0.36L04B0.5L04B180 40 220 620 8000 100 1.2表1-11、机构运动简图。
图1-12、曲柄位置“7”速度分析,加速度分析(列矢量方程,画速度图,加速度图)取曲柄位置“7”进行速度分析,其分析过程同曲柄位置“1”。
取构件3和4的重合点A进行速度分析。
列速度矢量方程,得υA4=υA3+υA4A3大小? √?方向⊥O4A⊥O2A∥O4B代表pa4 pa3 a3a4V A3=ω2l o2A=64/60×6.28×0.09=0.603m/s取速度极点P,速度比例尺µv=0.01(m/s)/mm,作速度多边形如图1-2则由图1-2知,υA4=pa4·μv=29×0.01=0.29m/sυA4A3=a3a4·μv=52×0.01m/s=0.52m/s图1-2υB5=υB4=υA4·O4B/ O4A=0.44m/s取5构件为研究对象,列速度矢量方程,得υC5=υB5+υC5B5大小? √?方向∥XX⊥O4B⊥BC代表pc5 pb4 b4b5其速度多边形如图1-2所示,有υC5=5Pc·μv=42×0.01=0.42m/s取曲柄位置“7”进行加速度分析,取曲柄构件3和4的重合点A进行加速度分析.列加速度矢量方程,得:a A4 =a A4n +a A4t= a A3n +a A4A3k+a A4A3r 大小? ω42l O4A ?√2ω4υA4A3 ? 方向? A→O4⊥O4B A→O2⊥O4B(向右)∥O4B代表pA4’pn4’n4’A4’p’A3’A3’k’k’A4’取加速度极点为P',加速度比例尺μa=0.02(m/s2)/mm作加速度多边形图1-3图1-3则由图1─3知:a A4t= n4’A4’·μa =137×0.02m/s2=2.74m/s2α4= a A4t/l O4A = 7.17 m/s2a A4 = pA4’·μa = 138×0.01m/s2 =2.76 m/s2用加速度影象法求得a B5 = a B4 = a A4 ×l O4B/l O4A=4.19m/s2取5构件的研究对象,列加速度矢量方程,得a C5=a B5+ a C5B5n+ a C5B5t大小?√√?方向∥xx √ C→B ⊥BC代表 P’c5’ P’B5’ n5’B5’ C5’n5’加速度比例尺μa=0.02(m/s2)/mm其加速度多边形如图1─4所示,有图1-4a C5B5t= n5’c5’·μa =31×0.02m/s2 =0.62m/s2a C5 = P’c5’·μa =179×0.02m/s2 =3.58m/s23、曲柄位置“10”速度分析,加速度分析(列矢量方程,画速度图,加速度图)取曲柄位置“10”进行速度分析。
第1章 机构静力分析基础
第1章机构静力分析基础学习目标正确理解力的概念及静力学基本定理;理解常见的约束及约束力的特点;掌握物体受力分析的方法,能画出研究对象的受力图;掌握力投影的概念及求法、合力投影定理;会求解平面汇交力系合成的解析法;熟悉力对点之矩的概念,合力矩定理,力对点之矩的求法,力偶及力偶矩的概念,力偶的性质;掌握力的平移定理,平面任意力系的简化,固定端约束,不考虑摩擦的平面力系的平衡方程及应用。
1.1力的基本概念及其性质1.1.1 力的概念人们在长期的生产实践活动中,经过不断地观察和总结,建立了力的概念。
1.定义力是物体问相互的机械作用。
这种作用使物体的运动状态、形状或尺寸发生改变。
力使物体的运动状态发生改变称为力的外效应;力使物体的形状或尺寸发生改变称为力的内效应。
例如:用手推门时,手指与门之间有了相互作用,这种作用使门产生了运动;用空气锤锻打工件,空气锤和工件问有了相互作用,工件的形状和尺寸发生了改变。
2.刚体在外力作用下不发生变形的物体称为刚体。
例如,用脚踢皮球,脚和球体之间产生了相互作用,球体的运动状态和形状尺寸同时发生了改变,力对球体的这两种效应并不是单独发生的,而是同时发生的。
当研究物体的运动规律(包括平衡)时,可以忽略不计形状尺寸改变对运动状态改变的影响,把物体抽象为不变形的理想化模型——刚体,这是将物体抽象化的一个最基本的力学模型。
3.力的三要素力对物体的效应取决于力的三要素,即力的大小、方向和作用点。
力是一个既有大小又有方向的量,称为力矢量,用一个有向线段表示。
线段的长度按一定的比例尺表示力的大小;线段箭头的指向表示力的方向;线段的始端A(图1—1)或末端B表示力的作用点。
力的单位为牛顿(N)。
4.力系与等效力系若干个力组成的系统称为力系。
若一个力系与另一个力系对物体的作用效果相同,那么这两个力系互为等效力系。
若一个力与一个力系等效,则称这个力为该力系的合力,图1—1力矢量而该力系中的各力称为这个力的分力。
1-机构的动态静力分析
静力分析是基础
加入惯性力,成为动态静力分析
力平衡是根本 矢量形式和标量形式是统一的; 力平衡和力矩平衡是独立的。 重视对机架的附加反动 摆动力和摆动力矩对机器的影响 研究平衡力矩的特性 在动态设计中的指导意义
Machinery Dynamics
机械动力学
Raymond Ding ©
Question 1
Prob. 图为一对心直动从动件圆 盘凸轮机构,假定凸轮作等速回转 运动,忽略凸轮轴可能存在的速度 波动。求作用于凸轮上维持其等速 回转的平衡力矩。
看成上述分析方法的 一个应用例子
Md ?
Machinery Dynamics
机械动力学
Raymond Ding ©
Equation s
Machinery Dynamics
机械动力学
Raymond Ding ©
G ( FP0 ks) fFR 2 x ms FR cos 0
FR 2 x FR sin 0
FR (r0 s) sin FR 2 x H M 2 0
FR1y FR cos 0
G FP 0 ks m s FR cos f sin
Raymond Ding ©
平面连杆机构的动态静力分析
equations of equilibrium
原动构件→平衡力矩 Md
FRi FRi 1 Fi mi i s
pi FRi qi FRi1 Mi Jii
Machinery Dynamics
机械动力学
G FP 0 ks m s M d (r0 s) tan 1 f tan
Machinery Dynamics
牛头刨床导杆机构的运动分析、动态静力分析
摘要——牛头刨床运动和动力分析一、机构简介与设计数据1、机构简介牛头刨床是一种用于平面切削加工的机床,如图1-1a。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。
刨床工作时,由导杆机构2 –3 –4 –5 –6 带动刨头6和刨刀7作往复运动。
刨头右行时,刨刀进行切削,称工作行程,此时要求速度较低并且均匀,以减少电动机容量和提高切削质量;刨头左行时,刨刀不切削,称空回行程,此时要求速度较高,以提高生常率。
为此刨床采用有急回作用的导杆机构。
刨刀每切削完一次,利用空回行程的时间,凸轮8通过四杆机构1 – 9 – 10 – 11 与棘轮带动螺旋机构(图中未画),使工作台连同工件做一次进给运动,以便刨刀继续切削。
刨头在工作行程中,受到很大的切削阻力(在切削的前后各有一段约0.05H的空刀距离,图1-1b),而空回行程中则没有切削阻力。
因此刨头在整个运动循环中,受力变化是很大的,这就影响了主轴的匀速运转,故需安装飞轮来减小主轴的速度波动,以提高切削质量和减少电动机容量a b图目录摘要 (III)1设计任务 (1)2 导杆机构的运动分析 (2)导杆机构的动态静力分析 (4)3.1运动副反作用力分析 (4)3.2力矩分析 (6)4方案比较 (7)5总结 (10)6参考文献 (10)《机械原理课程设计》说明书1设计任务机械原理课程设计的任务是对机器的主题机构进行运动分析。
动态静力分析,确定曲柄平衡力矩,并对不同法案进行比较,以确定最优方案。
要求根据设计任务,绘制必要的图纸和编写说明书等。
2 导杆机构的运动分析2.1 速度分析取曲柄位置1’对其进行速度分析,因为2和3在以转动副相连,所以V A2=V A3,其大小等于ω2l02A,指向于ω2相同。
取构件3和4的重合点A进行速度分析。
列速度矢量方程,得υA4 = υA3 + υA4A3大小 ? √ ?方向⊥O4A ⊥O2A ∥O4B选比例尺μv=0.004(m/s)/mm,做出速度矢量图(见图a)νA4=0.088m/sνA3=0.816m/s取5构件作为研究对象,列速度矢量方程,得υC5 = υB5 + υC5B5大小 ? √ ?方向∥XX ⊥O4B ⊥BC取速度极点p,选比例尺μv=0.004(m/s)/mm,做出速度矢量图(见图a)νC5=0.16m/sνC5B5=0.044m/s2.2 加速度分析取曲柄位置“1”进行加速度分析。
平面机构的动态静力分析
▼对相应构件加上惯性力;
▼动力学反问题求解。已知运动状态和工作阻力,求平衡力
矩,运动副反力及变化规律。在此基础上求机座的摆动力和
摆动力矩。
主要内容
§1-1刚体运动惯性力的简化 §1-2平面连杆机构的动态静力分析 §1-3平面凸轮机构的动态静力分析
机械动力学
§1-1刚体运动惯性力的简化
机械系统是由各种构件组成,每一个构件是一个刚体,刚体的
yc3
xc3
2
3 xd
(2)取整体为对象:受力如图。
F3 yI
其中:
Md
F3 xI
F4 xI
FRAy
M 3Ic
FRDy
机械动力学
(3)列方程求解
取AB为对象:
F3 yIMd来自F4 xIFRAx FRAy
M 3Ic
F3 xI
FRDy
机械动力学
§1-2平面连杆机构的动态静力分析 方法2:达朗贝尔原理求解
机械动力学
§1-1刚体运动惯性力的简化
一、刚体作平移 向质心C简化:
刚体平移时惯性力系合成为一过质心的合力。
FI1
FI
FI2
FIn
机械动力学
§1-1刚体运动惯性力的简化
二、定轴转动刚体
条件: 具有质量对称平面,质量对称 平面垂直于转轴,质心在质量对称平面内 的简单情况。
直线 i :平移,过Mi点,
作用线过C点
机械动力学
§1-2平面连杆机构的动态静力分析
一、构件的惯性力简化
当构件作一般的平面运动时, 某瞬时的角速度和角加速度及 质心加速度分别为
构件的质量及对质心的转动惯 量为
mi riC
J iCi
将虚加在构件上的惯性力向质心简化
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运动学方程(三种方法) 运动学方程(三种方法)
r1 + l 2 + l 3 + l 4 + l1 + ( − r1 ) = 0 r1 + l 2 + l 3 + l 4 + l1 = r1
r1 + l 2 + l 3 + l 4 = r4
运动学方程窍门: 运动学方程窍门:找所有运动学 闭环通路,只要有运动部件处, 闭环通路, 只要有运动部件处, 闭环就要经过
将三组方程相加得
− FR1 + FR4 + ( F2 + F3 + F4 ) − ∑ mi ɺɺi = 0 s
i=2
4
ɺɺ r4 × FR4 + ∑ ( si × Fi ) + M d − ∑ M i − ∑ ( si × mi ɺɺi ) − ∑ J iϕ i = 0 s
i=2 i=2 i=2 i=2
牛顿—欧拉方程
牛顿方程 s − FRi −1 + FRi + FI = mi ɺɺi ɺɺ 欧拉方程(力矩方程, qi × (− FRi −1 ) + pi × FRi + M I = J iϕ i 向构件质心简化。
建立所有构件动力方程 1、先建立坐标系(放在特殊点处); 、先建立坐标系(放在特殊点处) 2、给构件、铰链编号; 、给构件、铰链编号; 3、画出构件质心、铰点矢径。 、画出构件质心、铰点矢径。 4、确定构件受力。 、确定构件受力。 5、运用牛欧方程建立所有构件动力方程。 、运用牛欧方程建立所有构件动力方程。 6、根据运动学方程和动力方程求解平衡 、 所需驱动力和各运动副约束反力。 所需驱动力和各运动副约束反力。
摆动力和摆动力矩当然可通过前面得到的运动副约 束反力而直接获得。 但为了明确其物理意义, 束反力而直接获得 。 但为了明确其物理意义 , 下面 通过达朗贝尔方程进行推导,得到其数学表达式: 通过达朗贝尔方程进行推导,得到其数学表达式:
平面四连杆机构 运动构件对机座 的反作用力和反 作用力矩
F0 = FR1 − FR4
M 0 = r4 × (− FR4 )
s − FR1 + FR2 + F2 − m2 ɺɺ2 = 0 ɺɺ ɺɺ r1 × (− FR1 ) + r2 × FR2 + s2 × F2 + s2 × (−m2 s2 ) + M 2 + M d − J 2ϕ 2 = 0 s − FR2 + FR3 + F3 − m3ɺɺ3 = 0 ɺɺ ɺɺ r2 × (− FR2 ) + r3 × FR3 + s3 × F3 + s3 × (−m3 s3 ) + M 3 − J 3ϕ 3 = 0 s − FR3 + FR4 + F4 − m4 ɺɺ4 = 0 ɺɺ ɺɺ r3 × (− FR3 ) + r4 × FR4 + s4 × F4 + s4 × (−m4 s4 ) + M 4 − J 4ϕ 4 = 0
分析构件I的受力和运动状态 分析构件 的受力和运动状态 1、先建立坐标系 、 2、分析受力 、 3、运动分析 , 画出关键点的 、 运动分析, 矢径。 矢径。 运用达朗贝尔原理( 运用达朗贝尔原理 ( 最简单 的力学理论)建立构个I的动 的力学理论 ) 建立构个 的动 力方程: 力方程:
力平衡方程 s − FRi −1 + FRi + FI − mi ɺɺi = 0 ɺɺ ɺɺ ri −1 × (− FRi −1 ) + ri × FRi + s I × FI + s I × (−mi si ) + M I − J iϕ i = 0 力矩平衡方程,可向任意位置简化。
动力学方程
三、 机构的摆动力和摆动力矩
动态静力分析的任务除了求得驱动力和运动副反力 以外, 以外 , 还要关注和求解运动构件与机座相连的运动 副约束反力中的动载荷( 摆动力和摆动力矩) 副约束反力中的动载荷 ( 摆动力和摆动力矩 ) 。 因 为在高速下惯性载荷占主要成份, 为在高速下惯性载荷占主要成份 , 而且惯性载荷是 周期性波动的,是引起振动的主要激励。 周期性波动的,是引起振动的主要激励。
1.1 平面连杆机构的动态静力分析 一、 构件的惯性力和惯性力矩
平面机构中作一般平面运动的构件会产生一个惯性力
ɺɺ − mi ɺɺi 和一个惯性力矩 − J iϕ i s
。
二、 平面连杆机构的动态静力分析
关键:根据达朗贝尔原理建 立动力学模型。 建立每个构件的力和力矩平 衡方程。 衡方程 。 所以要分析每个构 件的受力和运动状态。 件的受力和运动状态。
4
4
4
4
最终得到摆动力和摆动力矩(平面连杆机构)的表达式
Fs = − ∑ mi ɺɺi s
i=2
4
ɺɺ M s = − ∑ ( si × mi ɺɺi + J i静力分析
在动态静力分析中要计入惯性力, 在动态静力分析中要计入惯性力,而为求出惯性力又需知 道构件的加速度, 道构件的加速度,所以在动态静力分析中首先要进行运动分 析。在进行运动分析时是假定运动构件按某种理想的运动规 律运动的(多数机构的驱动构件均假定为作等速回转运动) 律运动的(多数机构的驱动构件均假定为作等速回转运动), 由于采用了这样一种假定, 由于采用了这样一种假定,在动态静力分析中便不涉及到原 动机的特性。因而, 动机的特性。因而,这在本质上是一种理想化运动状态下的 力分析。它应用于动力学反问题中: 力分析。它应用于动力学反问题中:已知机构的运动状态和 工作阻力,求解平衡力矩、各运动副反力及其变化规律, 工作阻力,求解平衡力矩、各运动副反力及其变化规律,并 在此基础上求出对机座的摆动力和摆动力矩。 在此基础上求出对机座的摆动力和摆动力矩。
