安徽省对口高考数学模拟试题(一).pdf

合集下载

安徽“小高考”2024届模拟考试数学试题

一、单选题二、多选题1.复数的虚部是（）A ．5B．C．D．2. 已知角终边上点坐标为，则（）A．B．C．D．3. 设集合，，，则（）A．B．C．D．4.（）A．B ．C．D ．5.已知函数（a ，b 为常数，且，）的图象经过点，，下列四个结论：①；②；③函数仅有一个零点；④若不等式在时恒成立，则实数m 的取值范围为．其中所有正确结论的序号是（）A ．①②③B ．①②④C ．①③④D ．②③④6. 若函数在区间内恒有，则的单调递增区间是A．B．C．D．7. 已知函数，，则大致图象如图的函数可能是（）A．B．C．D．8. 如表所示的数阵称为“森德拉姆素数筛”，表中每行每列的数都成等差数列，设表示该数阵中第m 行、第n 列的数，则下列说法正确的是（）234567…35791112…4710131619…5913172125…6111212631…71319253137……………………A．B．C．D．安徽“小高考”2024届模拟考试数学试题安徽“小高考”2024届模拟考试数学试题三、填空题四、解答题9. 下列命题中正确的是（）A ．已知一组数据6，6，7，8，10，12，则这组数据的分位数是7.5B ．样本相关系数的绝对值越接近1时，成对样本数据的线性相关程度越强C．已知随机变量，则D ．已知经验回归方程，则y 与x 具有负线性相关关系10. 某统计机构对1000名拥有汽车的人进行了调查，对得到的数据进行整理并制作了如图所示的统计图表，下列关于样本的说法错误的是（）A ．30岁以上人群拥有汽车的人数为720B ．40～45岁之间的人群拥有汽车的人数最多C ．55岁以上人群每年购买车险的总费用最少D ．40～55岁之间的人群每年购买车险的总费用，比18～30岁和55岁以上人群购买车险的总费用之和还要多11. 已知a ，b 为空间中两条不同直线，，为空间中两个不同的平面，则下列命题一定成立的是（）A ．，，B．，，C ．，，D ．，，12. 下列计算正确的是（）A．B．C．D．13. 已知，则______.14.若实数满足，则称为函数与的“关联数”.若与在实数集上有且只有3个“关联数”，则实数的取值范围为__________.15. 将3封不同的信随机放入2个不同的信箱中，共有种不同的放法，则在的展开式中，含项的系数为______．16. 在平面直角坐标系中，已知椭圆：的离心率为，右焦点为，上顶点为，点到直线的距离等于1．（1）求椭圆的标准方程；（2）若直线：与椭圆相交于，两点，为中点，直线，分别与圆：相切于点，，求的最小值．17. 如图，在三棱柱中，，，，.（1）证明：平面平面.（2）若，求二面角的余弦值.18. 如图，正方形与梯形所在的平面互相垂直，，，，，为的中点.(1)求证：平面平面；(2)求二面角的正弦值.19. 已知椭圆：经过点，离心率为.(1)求椭圆的标准方程；(2)若直线：与椭圆C有两个不同的交点A，B，原点到直线的距离为2，求的面积的最大值.20. 如图，已知椭圆的离心率为，直线与圆交于M，N两点，．(1)求椭圆E的方程；(2)A，B为椭圆E的上、下顶点，过点A作直线交圆O于点P，交椭圆E于点Q（P，Q位于y轴的右侧），直线BP，BQ的斜率分别记为，，试用k表示，并求当时，△面积的取值范围．21. 已知函数是大于0的常数，记曲线在点处的切线为在轴上的截距为.(1)若函数，求的单调区间；(2)当时，求的取值范围.。

高考数学模拟试题（一）

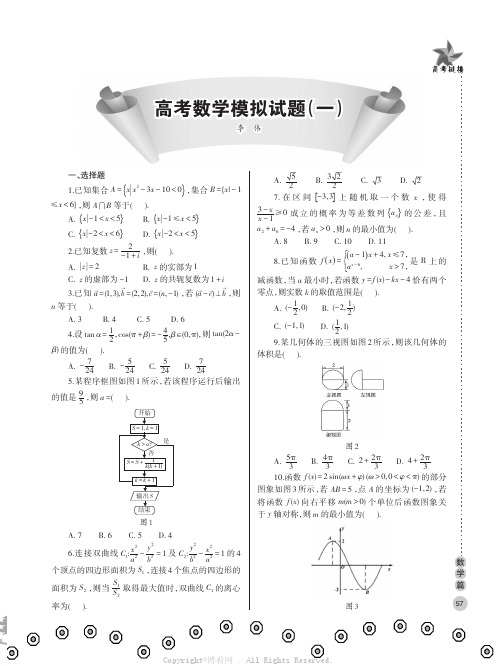
一、选择题1.已知集合A ={}x |x 2-3x -10<0，集合B ={x |-1≤x <6}，则A ⋂B 等于().A.{}x |-1<x <5B.{}x |-1≤x <5C.{}x |-2<x <6 D.{}x |-2<x <52.已知复数z =2-1+i，则().A.||z =2B.z 的实部为1C.z 的虚部为-1D.z 的共轭复数为1+i3.已知a =(1,3),b =(2,2),c =(n ,-1)，若(a -c )⊥b ，则n 等于().A.3B.4C.5D.64.设tan α=12，cos(π+β)=-45,β∈(0,π)，则tan(2α-β)的值为().A.-724B.-524C.524D.7245.某程序框图如图1所示，若该程序运行后输出的值是95，则a =().图1A.7B.6C.5D.46.连接双曲线C 1:x 2a2-y 2b 2=1及C 2:y 2b 2-x 2a2=1的4个顶点的四边形面积为S 1，连接4个焦点的四边形的面积为S 2，则当S 1S 2取得最大值时，双曲线C 1的离心率为().A.B. C.3 D.27.在区间[]-3,3上随机取一个数x ，使得3-x x -1≥0成立的概率为等差数列{}a n 的公差，且a 2+a 6=-4，若a n >0，则n 的最小值为().A.8B.9C.10D.118.已知函数f ()x =ìíî()a -1x +4,x ≤7，a x -6,x >7，是R 上的减函数，当a 最小时，若函数y =f (x )-kx -4恰有两个零点，则实数k 的取值范围是().A.(-12,0)B.(-2,12)C.(-1,1)D.(12,1)9.某几何体的三视图如图2所示，则该几何体的体积是().图2A.5π3B.4π3C.2+2π3D.4+2π310.函数f (x )=2sin(ωx +φ)(ω>0,0<φ<π)的部分图象如图3所示，若AB =5，点A 的坐标为(-1,2)，若将函数f (x )向右平移m (m >0)个单位后函数图象关于y 轴对称，则m 的最小值为().图357高考链接A.12 B.1 C.π3 D.π211.在等腰直角三角形BCD 与等边三角形ABD中，∠C =90°，BD =6，现将△ABD 沿BD 折起，则当直线AD 与平面BCD 所成角为45°时，直线AC 与平面ABD().A.B.C.D.12.已知函数f (x )=13ax 3+x 2(a >0).若存在实数x 0∈(-1,0)，且x 0≠-12，使得f (x 0)=f (-12)，则实数a 的取值范围为().A.(23,5)B.(23,3)⋃(3,5)C.(187,6)D.(187,4)⋃(4,6)二、填空题13.已知C 4n =C 6n ，设(3x -4)n =a 0+a 1(x -1)+a 2(x -1)2+⋯+a n ()x -1n，则a 1+a 2+⋯+a n =_____．14.已知数列{a n }的各项均为正数，满足a 1=1，a k +1-a k =a i .(i ≤k ,k =1,2,3,⋯,n -1)，若{a n }是等比数列，数列{a n }的通项公式a n =_______．15.实数x ，y 满足ìíîïïy ≥1，y ≤2x -1，x +y ≤m ，如果目标函数z =x -y 的最小值为-2，则yx的最小值为_______．16.已知M 是抛物线y 2=2x 上一点，N 是圆x 2+(y -2)2=1关于直线x -y =0对称的曲线C 上任意一点，则||MN 的最小值为_______．三、解答题17.已知在△ABC 中，a 、b 、c 分别为角A ，B ，C 的对边，且b =a sin A -c sin Csin B -sin C.(1)求角A 的值；(2)若a =3，设角B =θ，△ABC 周长为y ，求y =f (θ)的最大值．18.如图4，已知三棱柱ABC -A 1B 1C 1中，△ABC 与△B 1BC 是全等的等边三角形.(1)求证：BC ⊥AB 1；(2)若cos ∠BB 1A =14，求二面角B -B 1C -A 的余弦值.图419.移动支付(支付宝及微信支付)已经渐渐成为人们购物消费的一种支付方式，为调查市民使用移动支付的年龄结构，随机对100位市民做问卷调查得到2×2列联表如下：使用移动支付不使用移动支付合计35岁以下（含35岁）4035岁以上40合计50100（1）将上2×2列联表补充完整，并请说明在犯错误的概率不超过0.10的前提下，认为支付方式与年龄是否有关？（2）在使用移动支付的人群中采用分层抽样的方式抽取10人做进一步的问卷调查，从这10人随机中选出3人颁发参与奖励，设年龄都低于35岁(含35岁)的人数为X ，求X 的分布列及期望．(参考公式：K 2=n ()ad -bc 2()a +b ()c +d ()a +c ()b +d (其中n =a +b +c +d )20.已知椭圆x2a 2+y 2b2=1()a >b >0右焦点F ()1,0，离心率为，过F 作两条互相垂直的弦AB ,CD ，设AB ,CD 中点分别为M ,N ．（1）求椭圆的标准方程；（2）求以A ,B ,C ,D 为顶点的四边形的面积的取值范围.21.已知函数f (x )=bx 2-2ax +2ln x ．(1)若曲线y =f (x )在(1,f (1))处的切线为y =2x +4，试求实数a ，b 的值；(2)当b =1时，若y =f (x )有两个极值点x 1，x 2，且x 1<x 2，a ≥52，若不等式f (x 1)≥mx 2恒成立，试求实数m 的取值范围．四、选做题22.过点P ()-1,0作倾斜角为α的直线与曲线C :ìíîx =3cos θ，y =2sin θ，(θ为参数)相交于M 、N 两点．(1)写出曲线C 的一般方程；(2)求||PM ∙||PN 的最小值．23.已知函数f (x )=16-||2x -1．(1)解不等式f (x )≤||x +2；(2)若函数y =f (x )-a 存在零点，求a 的求值范围．58参考答案以及解析一、选择题1-12BCCDD DDAAB AD二、填空题13.1023；14.2n-1；15.17；16.3-1.三、解答题17.解：（1）由已知b=a sin A-c sin Csin B-sin C可得b sin B-b sin c=a sin A-c sin C，由正弦定理可得b2+c2=a2+bc，∴cos A=b2+c2-a22bc=12，又A∈()0,π，∴A=π3．(2)由a=3，A=π3及正弦定理得bsin B=c sin C=a sin A=2，∴b=2sin B=2sinθ，c=2sin C=2sinæèöø2π3-B=2sinæèöø2π3-θ，∴y=a+b+c=3+2sinθ+2sinæèöø2π3-θ，即y=23sinæèöøθ+π6+3，由0<θ<2π3得π6<θ+π6<5π6，∴当θ+π6=π2，即θ=π3时，y max=33．18.解：（1）取BC的中点O，连接AO，B1O，由于△ABC与△B1BC是等边三角形，所以有AO⊥BC，B1O⊥BC，且AO⋂B1O=O，所以BC⊥平面B1AO，AB1⊂平面B1AO，所以BC⊥AB1．（2）设AB=a，△ABC与△B1BC是全等的等边三角形，所以BB1=AB=BC=AC=B1C=a，又cos∠BB1A=14，由余弦定理可得AB21=a2+a2-2a∙a×14=32a2，在△AB1C中，有AB21=AO2+B1O2，所以以OA，OB，OB1分别为x，y，z轴建立空间直角坐标系，如图5所示，则Aèöø÷,0,0，Bæèöø0,a2,0，B1æèçø，设平面ABB1的一个法向量为n =()x,y,z，则ìíîn ∙ AB=0，n ∙ AB1=0，即ìíîïïïï+12ay=0，2+=0，令x=1，则n =()1,3,1，又平面BCB1的一个法向量为m =()1,0,0，所以二面角B-B1C-A的余弦值为cosθ=n ∙m ||n ∙||m=．图519.解：（1）根据题意及2×2列联表可得完整的2×2列联表如下：使用移动支付不使用移动支付合计35岁以下(含35岁)40105035岁以上104050合计5050100根据公式可得K2=100()40×40-10×10250×50×50×50=36>6.635，所以在犯错误的概率不超过0.10的前提下，认为支付方式与年龄有关．（2）根据分层抽样，可知35岁以下(含35岁)的人数为8人，35岁以上的有2人，所以获得奖励的35岁以下(含35岁)的人数为X，则X的可能为1，2，3，P()X=1=C18C22C310=8120，P()X=2=C28C12C310=5610，P()X=3=C38C310=56120，其分布列为XP1812025612035612059高考链接EX =1×8120+2×56120+3×56120=125．20.解：（1）由题意得c =1,c a 则a =2,b =c =1，所以椭圆的方程为x 22+y 2=1.（2）①当两直线一条斜率不存在一条斜率为0时，S =12||AB ·||CD =12×22×2=2,②当两直线斜率存在且都不为0时，设直线AB 方程为y =k ()x -1,A ()x 1,y 1,B ()x 2,y 2,将其代入椭圆方程整理得：()1+2k 2x2-4k 2x +2k 2-2=0,x 1+x 2=4k 21+2k 2,x 1x 2=2k 2-21+2k 2,||AB =1+k 2||x 1-x 2=22()k 2+11+2k 2,同理可得||CD =22()k 2+1k 2+2,S =12||AB ·||CD =2-22æèöøk +1k 2+1∈éëöø169,2，当k =±1时，S =169，综上所述四边形面积范围是éëùû169,2.21.解：(1)由题可知f ()1=2×1+4=6=b -2a ，f ′()x =2bx -2a +2x，∴f ′()1=2b -2a +2=2，联立可得a =b =-6．(2)当b =1时，f ()x =x 2-2ax +2ln x ，∴f ′()x =2x -2a +2x =2()x 2-ax +1x，∵f ()x 有两个极值点x 1，x 2，且x 1<x 2，∴x 1，x 2是方程x 2-ax +1=0的两个正根，∴x 1+x 2=a ≥52，x 1∙x 2=1，不等式f ()x 1≥mx 2恒成立，即m ≤f ()x 1x 2恒成立，∴f (x 1)x 2=x 21-2ax 1+2ln x 1x 2=-x 31-2x 1+2x 1ln x 1，由∴x 1+x 2=a ≥52，x 1∙x 2=1，得x 1+1x 1≥52，∴0<x 1≤12，令h ()x =-x 312，h ′()x =-3x 2+2ln x <0，∴h ()x 在æèùû0,12上是减函数，∴h ()x ≥h æèöø12=-98-ln 2，故m ≤-98-ln 2．四、选做题22.解：（1）由曲线C 的参数方程ìíîx =3cos θ，y =2sin θ，(θ是参数)，可得x 23+y 22=cos 2θ+sin 2θ=1，即曲线C 的一般方程为x 23+y 22=1．(2)直线MN 的参数方程为{x =-1+t cos α，y =t sin α，(t 为参数)，将直线MN 的参数方程代入曲线x 23+y 22=1，得()3-cos 2α∙t 2-4cos α∙t -4=0，设M ，N 对应的对数分别为t 1，t 2，则||PM ∙||PN =||t 1∙t 2=43-cos 2α，当cos α=0时，||PM ∙||PN 取得最小值为43．23.解：（1）不等式可化为||x +2+||2x -1≥16，当x ≤-2时，原不等式可化为-x -2-2x +1≥16，解得x ≤-173；当-2<x ≤12时，原不等式可化为x +2-2x +1≥16，解得x ≤-13，不满足，舍去；当x >12时，原不等式可化为x +2+2x -1≥16，解得x ≥5，所以不等式的解集为{}x |x ≤-173或x ≥5．（2）因为f ()x =ìíîïï17-2x ,x ≥12，15+2x ,x <12，所以若函数y =f ()x -a 存在零点则可转化为函数y =f ()x 与y =a 的图象存在交点，函数f (x )在(-∞,12]上单调增，在[12,+∞)上单调递减，且f (12)=16.数形结合可知a ≤16．60。

2023高考数学模拟卷(一)(含答案解析)

A.1B.2C.3D.4
9.已知抛物线的焦点为，准线为，是上一点，直线与抛物线交于两点，若，则
A B.8C.16D.
10.已知函数的图象过点，且在上单调，同时的图象向左平移个单位之后与原来的图象重合，当，且时，，则
A. B.-1C.1D.
11.下图是某四棱锥的三视图，网格纸上小正方形的边长为1，则该四棱锥的外接球的表面积为
20.已知椭圆的一个焦点为，离心率为 .不过原点的直线与椭圆相交于两点，设直线，直线，直线的斜率分别为，且成等比数列.
（1）求的值；
（2）若点在椭圆上，满足直线是否存在？若存在，求出直线的方程；若不存在，请说明理由.
21.已程的两个实数根为，求证：；
设M（x1，y1），N（x2，y2），M，N到准线的距离分别为dM，dN，
由抛物线的定义可知|MF|=dM=x1+1，|NF|=dN=x2+1，于是|MN|=|MF|+|NF|=x1+x2+2．
∵ ，
∴ ，即，∴ .
∴ ,∴直线AB的斜率为，
∵F（1，0），∴直线PF的方程为y= （x﹣1），
将y= （x﹣1），代入方程y2=4x，得3（x﹣1）2=4x，化简得3x2﹣10x+3=0，
A. B. C. D.
6.已知展开式中的系数为0，则正实数
A.1B. C. D.2
7.已知数列的前项和，若，则
A. B.
C. D.
8.如图是正四面体的平面展开图，分别是的中点，在这个正四面体中：① 与平行；② 与为异面直线；③ 与成60°角；④ 与垂直.以上四个命题中，正确命题的个数是（）

2021年安徽省马鞍山市普通高校对口单招数学摸底卷(含答案)

2021年安徽省马鞍山市普通高校对口单招数学摸底卷(含答案)一、单选题(20题)1.函数y=f（x）存在反函数，若f（2）=-3，则函数y=f-1（x）的图像经过点（）A.（-3，2）B.（1，3）C.（-2，2）D.（-3，3）2.将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是（）A.4πB.3πC.2πD.π3.设a，b为实数，则a2=b2的充要条件是（）A.a=bB.a=-bC.a2=b2D.|a|=|b|4.执行如图的程序框图，那么输出S的值是( )A.-1B.1/2C.2D.15.设为双曲线的两个焦点，点P在双曲线上，且满足，则的面积是（）A.1B.C.2D.6.一元二次不等式x2＋x- 6<0的解集为A.(-3,2)B.(2,3）C.(-∞,-3)∪(2,＋∞)D.(-∞,2)∪(3,＋∞)7.在等差数列{a n}中，a5=9,则S9等于( )A.95B.81C.64D.458.袋中装有4个大小形状相同的球，其中黑球2个，白球2个，从袋中随机抽取2个球，至少有一个白球的概率为（）A.B.C.D.9.设集合A={x|x≤2或x≥6}，B={x||x-1|≤3}，则为A∩B( )A.[-2,2]B.[-2,4]C.[-4,4]D.[2,4]10.A.(-2.3)B.(2,3]C.[2,3）D.[-2,3]11.若不等式|ax+2|＜6的解集是{x|-1＜x＜2}，则实数a等于（）A.8B.2C.-4D.-812.tan960°的值是（）A.B.C.D.13.下列各组数中成等比数列的是（)A.B.C.4，8，12D.14.已知i是虚数单位，则1+2i/1+i=()A.3-i/2B.3+i/2C.3-iD.3+i15.已知a=(1，-1)，b=(-1，2)，则(2a+b)×a=( )A.1B.-1C.0D.216.17.若f(x)=4log2x+2,则f⑵+f⑷+f(8)=()A.12B.24C.30D.4818.下列函数中，是增函数，又是奇函数的是（〕A.y=B.y=1/xC.y=x2D.y=x1/319.已知拋物线方程为y2=8x，则它的焦点到准线的距离是（）A.8B.4C.2D.620.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异，拟从这三个年级中按人数比例抽取部分学生进行调查，则最合理的抽样方法是（）A.抽签法B.系统抽样法C.分层抽样法D.随机数法二、填空题(20题)21.22.某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为2:3:4,现用分层抽样方法抽出一个容量为n的样本，样本中A种型号产品有6件，那么n= 。

(2021年整理)2018安徽对口高考数学真题

(完整版)2018安徽对口高考数学真题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)2018安徽对口高考数学真题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)2018安徽对口高考数学真题的全部内容。

(完整版)2018安徽对口高考数学真题编辑整理：张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是我们任然希望 (完整版）2018安徽对口高考数学真题这篇文档能够给您的工作和学习带来便利.同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉,前进的动力。

本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为 <（完整版）2018安徽对口高考数学真题〉这篇文档的全部内容。

2018年安徽省对口高考数学试卷31. 已知集合}2,1,0,2{},3,0{-==B A ，则=B A(A)∅ (B ）}0{ （C ）}3,0{ （D ）}3,2,1,0,2{- 32.函数3-=x y 的定义域是（A ）}3{≥x x （B ）}3{>x x （C ）}3{≤x x （D ）}3{<x x33.过B(2,3)A(-1,2),两点的直线的斜率为（A ）3- （B ）3 （C ）31-（D ）31 34。

已知向量b a ,的夹角060，且4,2==b a ，则=⋅b a（A ）8 （B ）34 （C)24 （D ）435。

=0390sin（A ）21- (B ）23- （C ）21（D ）2336.椭圆1422=+y x 的离心率是（A ）23 （B ）21 （C ）43 （D ）43 37。

安徽对口高考数学真卷

2012年安徽省普通高校对口招收中等职业学校毕业考试数学试题姓名：__________得分：_________(本卷满分150分,时间120分钟)一. 选择题(每小题5分,共60分。

每小题的4个选项中，只有一个选项是符合题目要求的) 1.已知集合A ＝{1，2，4}，B ＝{1，2，3，4}，则A ∩B ＝（） A. {1，2，3，4} B. {1，2，4} C.{3} D. 2.下列函数是奇函数的是（）A.y = x 3－xB. y = lg xC. y = 2x + 1D. y = cos x 3.函数y =x⎪⎪⎫⎛1的图像大致是（）4.下列选项正确的是（）A. +⎪⎪⎭⎫ ⎝⎛41 <+⎪⎪⎭⎫ ⎝⎛61 B. 0.46 > 0.45C. 70.6 > 70.5D. log 4+<log 4+5.设sin a > 0且tin a < 0，则角a 是（） A.第一象限的角 B. 第二象限的角 C. 第三象限的角 D. 第四象限的角 6. sin15°×cos15°值为（） A.43B.23 C.41D.21 7.不等式| x + 2 | > 3的解集是（）A. { x | x <－5}B. { x | x > 1}C. { x | －5 < x < 1}D. { x | x <－5或x > 1} 8.已知向量a = (1,4), b = (x ,2),要使a ⊥b ,则x 的值为（）A.21B. －21C. 8D. －8 9.双曲线92x ―y 2＝1的焦点坐标为（）A. (±10,0)B.( 0,±10)C. (±210,0)D. (0,±210) 10.下列说法正确的是（）A. 经过空间的任意三个点,只能确定一个平面B. 三条直线相交,最多可确定两个平面C. 一条直线和这条直线外的一点,可以确定一个平面D. 四条线段首尾相接,所得图形一定是平面图形O / A CD11. (2x + 1)6的展开式中含x 3的项的系数为（）A. 20B. 120C. 160D. 960 12. 函数y =⎪⎪⎭⎫⎝⎛-42sin πx 的最小正周期为（）A. 2πB. πC. 2πD. 4π二．填空题（每小题4分，共16分） 13.计算2 lg 2 + lg 25_____________.14. 电视台在球赛休息时连续播放4个广告,则这4个广告的编排顺序共____种(用数字作答．．．．．).15. 如果点A (2, ―8),B (―1,4),的坐标为_________. 16. 圆x 2 + y 2―2x +4y ―4 = 0的圆心坐标为_________.三.解答题（共74分，解答时应写出简要的文字说明、证明过程及演算步骤.）17.（本小题满分12分）已知函数y = ax 2 + 2x + c 的图像经过(0,1)和(1,2)两点. ⑴求a 、c 的值； ⑵求当y >―2时, x 的取值范围.18. （本小题满分12分）已知sin α=53, cos β=22,且为钝角.求cos(α―β)的值.19. （本小题满分12分）甲、乙二人独立地解答一道数学题,他们会做的概率分别为0.4和0.3,求 ⑴两人都会做该题的概率； ⑵该题能被解出的概率.20. （本小题满分12分）已知抛物线y 2 = 2px (p > 0)的准线方程为x =23 .⑴求抛物线方程；⑵过焦点F 作垂直于x 轴的直线交抛物线于A 、B 两点,求△OAB 的面积.21. （本小题满分12分）如图所示,在四面体S －ABC 中, AB = AC , SB = SC , E 、F 分别为AC , BC 的中点. 求证:⑴EF ∥面SAB ； ⑵BC ⊥SA.22. （本小题满分14分） ⑴写出寻找满足条件S=1 + 3+ 32 +…+3n -1 > 2012的最小正整数n 的算法；⑵画出相应的算法程序框图.A BS EFC。

2019年安徽省普通高校分类考试招生和对口招生文化素质测试数学试题及参考答案

2019 年安徽省普通高校分类考试招生和对口招生文化素质测试数学试题及参考答案数学试题( 120 分)选择题(共 30 小题;每小题 4 分,满分 120 分)在每小题给出的四个选项中 ,选出一个符合题目要求的选项 ,并在答题卡上将该项涂黑31. 设集合 A={1,2m+1},B={3,1}, 若 A=B.则 m= (A)0 (B)1 (C)2 (D)3 32. 函数 f (x) =的定义域为(A) ( - 1,+w) (B)(1,+w) (C) (- w,-1)同 (- 1,+w ) (D) (w ,-1)同 (1,+w ) 33.若向量 a=(2,-4) ,b=(2,1),则 a+2b=(A)(4,-3) (B)(4.0) (C)(6.-3) (D)(6,-2) 34.不等式 x 2 - 4x +3 < 0 的解集为(A) {xx > 3} (B) {x x <1} (C) {x 1< x < 3} (D) {x x <1或x > }3 35.过点(0.1)且与直线 x-y+2=0 平行的直线方程为(A)x - y +1 = 0 (B)x - y - 1 = 0 (C) x + y +1 = 0 (D)x + y - 1 = 0 36.在数列{a n } 中, a 1 = 4, a n+1 - a n = 2(n = N * ) ,则 a 6 =(A)12 (B)14 (C)16 (D)1837.双曲线x 24- y 2 = 1 的渐近线方程 (A) y = 士 1 x (B) y = 士2x (C) y = 士 1 x (D) y = 士4x2 437. 某校共有学生 1200 名,其中男生 700 名,女生 500 名.为了解该校学生的安全意识情况 ,采、用分层抽样方法 ,从全校学生中抽取 60 名进行调查,则应抽取的女生人数为(A)15 (B)20 (C)25 (D)3038. 下列函数中,最小正周期为二的是(A)(B) y = sin (|2x + " )|( 6 ) ( 6 )(C) y = sin (|3x + " )| (D) y = sin (|4x + " )|( 6 ) ( 6 )39. 在等比数列 {a n } 中, a 2 = 4, a 2 = 2 ,则该数列的前 4 项和S 4 = (A)7 (B)12 (C)13 (D)1540. 若一个球的表面积为 12" ,则该球的半径为 (A) 7 (B) 3 (C) 2 3 (D)3 42. 已知函数 f (x) =〈,若 f (a) = 21,则 a = (A) 1 (B) 3 (C) - 1 (D) - 14 4 243. cos 5" 的值是3(A) - 3244.某闭支部 30 名团员在某月内阅读中国古典名著的时间 ( (单位:小时)统计如下 :现从这 30 名团员中随机抽取 1 名,则抽到的团员是在该月内阅读时间不少于 25 小时的概率为阅读时间人数[20,25)8 [25,30)9 [35,40)3[30,35)8 [15,20)2 (B) - 12(D) 32(C) 12(D) 141545.设函数 y = f (x) 在 R 上是增函数,实数值范围是(A) ( 一 w,3) (B)( 一 w,5) (C) (3,+w )46.若 cosa > 0 .则asin a(A)第一或第三象限 (B)第一或第四象限角(C)第二或第三象限角 (D)第二或第四象限角 47." a 一 b = 0"是" a 2 一 b 2 = 0 "的 (A)充分条件 (B)必要条件(C)充要条件 (D)既不充分也不必要条件48.下列式子中正确的是(A) 1.90.3 > 1.90.4 (B) log 1.9 0.3 > log 1.9 0.4 (C) 0.90.3 > 0.90.4 (D) log 0.9 0.3 < log 0.9 0.4 49.下列函数中为奇函数的是(A) y = x 3 +1 (B) y = x 3 + x (C) y = x 2 +1 (D) y = x 2 + x 50.两数 f (x) = 2sin x cosx +1的最大值为(A)0 (B)1 (C)2 (D)351. 如图 ,在四棱锥 P-ABCD 中 , PA 」平面 ABCD. 四边形 ABCD 是正方形 ,PA = 2AB .则直线 PC 与平面 ABCD 所成角的大小为(D )90°(C )60° (B)45° (A )30° (A) (B) a 满足 f(2a-1)>f(a+4), 则 a 的取(D) (5,+w )1323310(C)52. 在△ABC 中,角 A,B,C 所对的边分别为 a ，b,c,且 b=12,c=13、cosA = 12 ,13则 a= (A)13 (B)12 (C)10 (D)553. 若椭圆 x 2+ y 2 = 1的一个焦点坐标为(2.0),则此椭圆的方程为a 2(A) x2+ y 2 = 1 (B) x 2+ y 2 = 1 (C) x2+ y 2 = 1 2 3 4(D) x 2 + y 2= 1554. sin(a +β)cos B-cos(a+B)sin β=(A)sin a (B)cosa (C)sin(a +2 β) (D)cos(a +2 β) 55. 已知两个非零向量 a 和b 满足 a ·b=0.则 a 与b 的夹角为 (A )180° (B )90° (C )45° (D)056. 已知 A(-1,2),B(3,0), 则以线段 AB 的中点为圆心， 1 为半径的圆的方程是(A) (x 1)2 +(y 1)2 = 1 (B) (x 2)2 +(y 2)2 = 1 (C) (x +1)2 +(y +1)2 = 1 (D) (x + 2)2 +(y + 2)2 = 1 57.设 a > 0，则 a a =1(A) a 41(B) a 23(C) a 4(D)a58.若直线 x+y-3=0 过抛物线 y=2px 的焦点,则 p= (A) 3 (B)3 (C)6 (D)12259.如阁、在正方体 ABCD A 1B 1 C 1D 1 中.点 E,F 分别是接 BB 1 ,DC 的中点,则下列结论错误的是(A) AE 」D 1F (B) DE 」D 1F (C) AE 」BC (D) DE 」BC60. 函数y = logx + b ( a > 0且a 1)的图象如图所示,则函数y = (1 a)x2 + b 的图a象可能是(A) (B) (C) (D)数字试题参考答案31. B 32. C 33.D 34.C 35. A36.B 37. A 38.C 39.D 40.D41.B 42.B 43.C 44.B 45.D 46.A 47.A 48.C 49.B 50.C 51.B 52.D 53.D 54.A 55.B 56.A57.C58.C59.D50.A。

2024年新高考数学模拟卷A卷(解析版)

2024年新高考数学模拟卷A 卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的.1．集合{}2468M =，，，，{}2|280N x x x =--≤，则M N ⋂=（）A ．{}2,4B ．{}2,4,6C ．{}2,4,6,8D ．[]24，【答案】A【详解】由题意{}2|280{|24}N x x x x x =--≤=-≤≤，∴{2,4}M N ⋂=．故选：A ．2．复数2(2)i z i-=i 为虚数单位，则A ．25B ．C ．5D ．【答案】C【详解】()()()223443,1i i i z i i--⨯-===--()()2243 5.z -+-=3．已知()1,3a =-，()2,1b =- ，且()()2//a b ka b +-，则实数k =（）A ．2-B ．2C ．12D ．12-【答案】D【详解】 (1,3)=- a ，()2,1b =- ，(1ka b k ∴-= ，3)(2---，1)(2k =+，13)k --，2(3,1)a b +=--，()//(2)ka b a b +-，(2)3(13)k k ∴-+=---，∴解得：12k =-．故选：D ．4．已知函数2,(1)()4,(1)x a x ax x f x a x ⎧-++<⎪=⎨⎪≥⎩，若()y f x =在(),-∞+∞上单调递增，则实数a 的取值范围是（）A ．[]2,4B ．()2,4C ．()2,+∞D ．[)2,+∞【答案】A【详解】()f x 在(),-∞+∞上单调递增；∴2112211414aa a a a a a a⎧≥⎪≥⎧⎪⎪>⇒>⎨⎨⎪⎪≤⎩⎪-++≤⎩，解得24a ≤≤；所以实数a 的取值范围为[]2,4．故选：A ．5．若椭圆X ：()22211x y a a +=>与双曲线H ：2213x y -=的离心率之和为736，则=a （）A ．2B 3C 2D ．1【答案】A【详解】椭圆X ：()22210x y aa +=>H ：2213x y -==，=2a=.故选：A.6．设过点(0,P 与圆22:410C x y x +--=相切的两条直线的夹角为α，则cos α=（）A ．19BC ．19-D ．【答案】A【详解】解法1：如图，圆22410x yx +--=，即22(2)5x y -+=，则圆心(2,0)C ，半径r ，过点(0,P 作圆C 的切线，切点为,A B ，连接AB .因为3PC =，则2PA PB ==，得2sin 3APC APC ∠∠=，则221cos cos sin 09APB APC APC∠=∠-∠=-<，即APB ∠为钝角，且α为锐角，所以1cos cos(π)9APB α=-∠=.故选A.解法2：如图，圆22410x y x +--=，即22(2)5x y -+=，则圆心(2,0)C ，半径r =，过点(0,P 作圆C 的切线，切点为,A B ，连接AB .因为3PC =，则2PA PB ==，因为22222cos 2cos PA PB PA PB APB CA CB CA CB ACB+-⋅∠=+-⋅∠，且πACB APB ∠=-∠，则448cos 5510cos APB ACB +-∠=+-∠，即44cos 55cos APB ACB -∠=-∠，解得1cos 09APB ∠=-<，即APB ∠为钝角，且α为锐角，则1cos cos(π)9APB α=-∠=.故选：A.解法3：圆22410x y x +--=，即22(2)5x y -+=，则圆心(2,0)C ，半径r =线方程为0x=，则圆心到切点的距离2d r =<，不合题意；若切线斜率存在，则设切线方程为y kx =，即0kx y -=，则圆心到切线的距离d =120,k k ==-1212sin tan 1cos k k k k ααα-==+，又α为锐角，由22sin cos 1αα+=解得1cos 9α=.故选：A.7．若数列{}n a 满足212n na p a +=（p 为常数，n ∈N ，1n ≥），则称{}n a 为“等方比数列”．甲：数列{}n a 是等方比数列；乙：数列{}n a 是等比数列，则（）．A ．甲是乙的充分非必要条件B ．甲是乙的必要非充分条件C ．甲是乙的充要条件D ．甲是乙的既非充分也非必要条件【答案】B【详解】若{}n a 为等比数列，设其公比为q ，则()222112n n n n a a q p a a ++⎛⎫=== ⎪⎝⎭，p 为常数，所以{}2n a 成等比数列，即{}n a 是等方比数列，故必要性满足.若{}n a 是等方比数列，即{}2n a 成等比数列，则{}n a 不一定为等比数列，例如23452,2,2,2,2,...--，有()221224n na a +=±=，满足{}n a 是等方比数列，但{}n a 不是等比数列，充分性不满足.故选：B8．若ππ2sin sin sin 44βααβ⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭，则()tan αβ+=（）A ．－1B ．1C ．－2D ．2【答案】A【详解】解法一：由题得()()2sin sin cos 2222βαααβαβ⎫-=-+-⎪⎪⎝⎭，所以2sin sin 2cos sin sin cos cos sin cos cos sin sin αβαβαβαβαβαβ-=-++，即sin cos cos sin cos cos sin sin 0αβαβαβαβ++-=，即()()sin cos 0αβαβ+++=，显然()cos 0αβ+≠，故()tan 1αβ+=-.解法二：令π4αθ-=，则π4αθ=+，所以ππ2sin sin sin 44βααβ⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭可化为π2sin sin sin 2βθθβ⎛⎫=-+ ⎪⎝⎭，即()2sin sin cos βθθβ=-，所以2sin sin cos cos sin sin βθθβθβ=+，即cos cos sin sin 0θβθβ-=，所以()cos 0θβ+=，则ππ2k θβ+=+，k ∈Z ，所以()πππ3πtan tan tan πtan 14424k αβθβ⎛⎫⎛⎫+=++=++==- ⎪ ⎪⎝⎭⎝⎭，k ∈Z .故选：A.二、多选题：本题共3小题，每小题6分，共18分。

2021年安徽省淮北市普通高校对口单招数学摸底卷(含答案)

2021年安徽省淮北市普通高校对口单招数学摸底卷(含答案)一、单选题(20题)1.{已知集合A={-1，0，1}，B={x|-1≤x＜1}则A∩B=()A.{0}B.{-1,0}C.{0，1}D.{-1，0，1}2.A.3B.8C.3.4.下列句子不是命题的是A.B.C.D.5.A.(6,7)B.(2,-1)C.(-2,1)D.(7,6)6.5人排成一排，甲必须在乙之后的排法是（）A.120B.60C.24D.127.函数f（x）=x2+2x-5，则f（x-1）等于（）A.x2-2x-6B.x2-2x-5C.x2-6D.x2-58.下列四组函数中表示同一函数的是( )A.y=x与y=B.y=2lnx与y=lnx2C.y=sinx与y=cos()D.y=cos(2π - x)与y=sin(π - x)9.若输入-5,按图中所示程序框图运行后，输出的结果是（）A.-5B.0C.-1D.110.从1，2，3，4，5这5个数中，任取四个上数组成没有重复数字的四个数，其中5的倍数的概率是（）A.B.C.D.11.等差数列{a n}中，若a2+a4+a9+a11=32，则a6+a7=()A.9B.12C.15D.1612.拋物线y2-4x+17=0的准线方程是（）A.x=2B.x=-2C.x=1D.x=-113.设A-B={x|x∈A且x B}，若M={4，5，6，7，8}，N={7，8，9，10}则M-N等于（）A.{4，5，6，7，8，9，10}B.{7，8}C.{4，5，6，9，10}D.{4，5，6}14.函数的定义域是()A.(-1，1)B.[0,1]C.[-1，1)D.(-1，1]15.直线：y+4=0与圆(x-2)2+(y+l)2=9的位置关系是（）A.相切B.相交且直线不经过圆心C.相离D.相交且直线经过圆心16.下列立体几何中关于线面的四个命题正确的有（）（1）垂直与同一平面的两个平面平行（2）若异面直线a，b不垂直，则过a的任何一个平面与b都不垂直（3）垂直与同一平面的两条直线一定平行（4）垂直于同一直线两个平面一定平行A.1个B.2个C.3个D.4个17.若不等式x2+x+c＜0的解集是{x|-4＜x＜3}，则c的值等于（）A.12B.-12C.11D.-1118.下列函数为偶函数的是A.B.y=7xC.y=2x+119.函数y=f（x）存在反函数，若f（2）=-3，则函数y=f-1（x）的图像经过点（）A.（-3，2）B.（1，3）C.（-2，2）D.（-3，3）20.设一直线过点（2，3）且它在坐标轴上的截距和为10，则直线方程为（）A.B.C.D.二、填空题(20题)21.22.数列{a n}满足a n+1=1/1-a n，a2=2，则a1=_____.23.24.25.己知0<a<b<1，则0.2a 0.2b。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学海无涯
2018年安徽省对口高考数学模拟试题（一）
题型：选择题共30小题，每小题4分，满分120分。在每小题给出的四个选项中只有
一项是符合题目要求，把正确选项写在表格中。

1.I =｛0,1,2,3,4｝,M=｛0,1,2,3｝ ,N=｛0,3,4｝,
)(NCM
I

=( )

A.｛2,4｝ B.｛1,2｝ C.｛0,1｝ D.｛0,1,2,3｝
2.下列命题中的真命题共有( );
① x=2是022=−−xx的充分条件 ② x≠2是022−−xx的必要条件
③yx=是x=y的必要条件 ④ x=1且y=2是0)2(12=−+−yx的充要条件
A.1个 B.2个 C.3个 D.4个

3.设、、均为实数，且＜，下列结论正确的是( )。
(A)＜ (B)＜ (C)－＜－ (D)＜
4.三个数30.7、3log0.7、0.73的大小关系是（）
A. 30.730.73log0.7 B. 30.730.7log0.73
C. 30.73log0.70.73 D. 0.733log0.730.7
5. yxa=−与logayx=在同一坐标系下的图象可能是（）

6．不等式0|)|1)(1(−+xx的解集是
( )
1 yxO1 -1 A 1 yxO1 -1 B 1 yxO1 -1 C 1 D -1 1
y

x
O
学海无涯
A．}10|{xx B．0|{xx且}1−x
C．}11|{−xx D．1|{xx且}1−x
7．函数xay=在]1,0[上的最大值与最小值这和为3，则a＝ ( )
A．21 B．2 C．4 D．41
8．在)2,0(内，使xxcossin成立的x的取值范围是 ( )
A．)45,()2,4( B．),4(
C．)45,4( D．
)23,45(),4(



9．椭圆5522=+kyx的一个焦点是)2,0(，那么=k
( )
A．1− B．1 C．5 D．5−
10．一个圆锥和一个半球有公共底面，如果圆锥的体积恰好与半球的体积相等，那么这个圆
锥轴截面顶角的余弦值是 ( )
A．43 B．54 C．53 D．53−
11．直线01)1(=+++yxa与圆0222=−+xyx相切，则a的值为( )
A．1,1− B．2.2− C．1 D．1−
12．抛物线2yax=的准线方程是2,ya=则的值为（）

（A）18 （B）18− （C）8 （D）8−

13．等差数列na中，已知1251,4,33,3naaaan=+==则为（）
（A）48 （B）49 （C）50 （D）51

14．设函数−=−2112)(xxfx 00xx，若1)(0xf，则0x的取值范围是（）
（A）（1−，1）（B）（1−，+）
（C）（−，2−）（0，+）（D）（−，1−）（1，+）

15．已知5()lg,(2)fxxf==则（）
学海无涯
（A）lg2 （B）lg32 （C）1lg32 （D）1lg25
16．已知集合M＝{x|x2＜4}，N＝{x|x2－2x－3＜0}，则集合M∩N＝( )
（A）{x|x＜－2} （B）{x|x＞3}
（C）{x|－1＜x＜2} （D）{x|2＜x＜3}
17．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为 ( )
（A）75° （B）60° （C）45° （D）30°

18．已知向量a、b满足：|a|＝1，|b|＝2，|a－b|＝2，则|a＋b|＝( )

（A）1 （B）2 （C）5 （D）6

19．
双曲线19422=−yx的渐近线方程是（）

A. xy32= B. xy94= C. xy23= D. xy49=
20．已知向量a=（4，2），向量b=（x，3），且a∥b，则x= ( )
（A）9 （B）6 （C）5 （D）3
21．函数sin2cos2yxx=的最小正周期是( )

（A）2 （B）4 （C）4 （D）2
22．如图，平面⊥平面，,,ABAB与两平面、所成的角分别为4和6。
过A、B分别作两平面交线的垂线，垂足为'A、',B若AB=12，则'A'B=( )
（A）4
（B）6
（C）8
（D）9

23．已知数列﹛na﹜为等差数列，且17134aaa++=，则212tan()aa+的值为( )
A．3 B．3− C．3 D．33−

A'
B'
A
B



学海无涯
24．直线l过点(1,2)−且与直线垂直，则l的方程是( )
A．3210xy+−= B. 3270xy++=
C. 2350xy−+= D. 2380xy−+=
25．有三个命题：①垂直于同一个平面的两条直线平行；②过平面α的一条斜线l有且仅有
一个平面与α垂直；③异面直线a、b不垂直，那么过a的任一个平面与b都不垂直。其中
正确命题的个数为（）
A．0 B．1 C．2 D．3

26．函数)42sin(−=xy的递增区间是( )

A.−8,8 B.)(8,8Zkkk+−
C. 87,83 D. )(83,8Zkkk+−
27．已知等比数列的公比为21，且则,6099531=++++aaaa
100321
aaaa++++
等于( )

A.30 B.90 C.100 D.120
28．设点P(3，-6)、Q(-5，2)，R(x,-9)，且P、Q、R三点共线，则x等于( )
A.-9 B.-6 C.9 D.6
29．10名工人某天生产同一零件，生产的件数是15，17，14，10，15，17，17、16，14，
14．设其平均数为a，中位数为b，众数为c，则有( )．
A．a>b>c B．b>c>a C．c>a>b D．c>b>a
29．从1、2、3、4、5、6、7、8、9、10这十个数中随机取出一个数，取出的数是3的倍
数的概率是（）

A 51 B 103 C 31 D 21
答题卡：
题号
1 2 3 4 5 6 7 8 9 10

答案
题号
11 12 13 14 15 16 17 18 19 20
学海无涯
答案
题号
21 22 23 24 25 26 27 28 29 30
答案