基于商空间粒度理论的三维网格分割方法
原创_abaqus三维筒体过渡网格划分
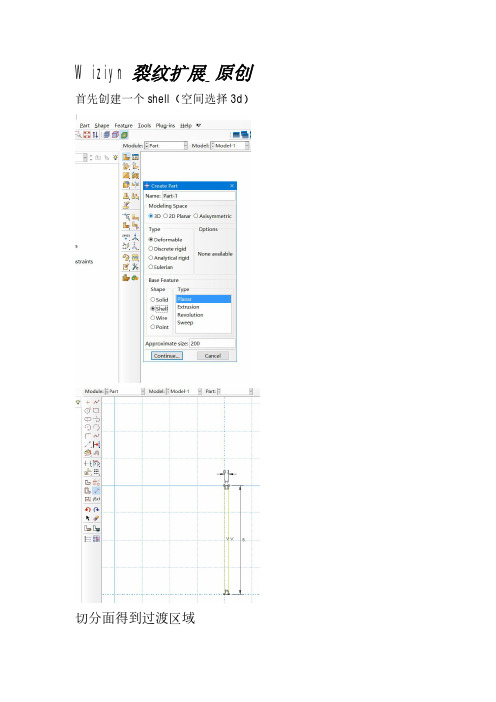
Wiziyn裂纹扩展_原创首先创建一个shell(空间选择3d)
切分面得到过渡区域
布置种子划分网格
熟悉的都知道如何布置的),过渡区域要约束种子不能增加或者减少
点击mesh ,创建网格部件
编辑网格获得三维实体网格,可以设置单元类型c3d8R等(厚度方向上设置自己需要的厚度及单元层
数)
创建instance
使用这两个点创建基准线作为旋转轴
进行周向阵列(旋转轴选择上方定义的基准线)
最终效果如下图:局部和整体图
欢迎大家加入abaqus断裂分析群交流:327237913(群内各种大手)
主攻断裂失效(裂纹扩展):
collapse element
Cohesive element
cohesive surface
debond VCCT
XFEM
cohesive单元的二次开发xfem单元的二次开发
批量嵌入cohesive单元France2d/3d
zencrack
abaqus的二次开发等等。
基于谱聚类的三维网格分割算法(SpectralClustering)

基于谱聚类的三维⽹格分割算法(SpectralClustering) 谱聚类(Spectral Clustering)是⼀种⼴泛使⽤的数据聚类算法,[Liu et al. 2004]基于谱聚类算法⾸次提出了⼀种三维⽹格分割⽅法。
该⽅法⾸先构建⼀个相似矩阵⽤于记录⽹格上相邻⾯⽚之间的差异性,然后计算相似矩阵的前k个特征向量,这些特征向量将⽹格⾯⽚映射到k维谱空间的单位球上,最后使⽤K-means⽅法对谱空间中的数据点进⾏聚类。
具体算法过程如下:⼀.相似矩阵 ⽹格分割以⾯⽚为基本单元,为了能使算法沿着⼏何模型的凹形区域进⾏分割,⽹格相邻⾯⽚之间的距离采⽤[Katz et al. 2003]中提到的⽅法,具体形式在“”中有所解释,距离由测地距离Geod_Dist和⾓度距离Ang_Dist两部分组成,如下所⽰: 上式中有两个重要的参数δ和η,参数δ通常取值范围为[0.01, 0.05],其⽤于控制测地距离和⾓度距离之间的权重⽐例,参数η通常取值范围为[0.1, 0.2],其使得分割边界更倾向于凹形区域。
计算完相邻⾯⽚之间的距离后,相似矩阵中对应位置的值由距离的⾼斯函数得到:其中:⼆.⽹格谱聚类 谱聚类⽅法在本质上都是类似的,都是利⽤相似矩阵的特征向量将原始空间中的数据映射到谱空间,并在谱空间中进⾏聚类。
⽹格上的谱聚类⽅法如下: 1 由上述定义计算相似矩阵W; 2 计算归⼀化矩阵N:N = D-1/2WD-1/2; 3 计算矩阵N的前k个最⼤特征向量e1, e2, … , e k,以这k个特征向量为列组成矩阵U = [e1, e2, … , e k]; 4 将矩阵U的每⼀⾏单位化后得到矩阵Ȗ; 5 提取出k个初始聚类中⼼⽤于K-means聚类,该过程先计算矩阵Q = ȖȖT,然后查找矩阵Q中的最⼩元素Q rs,那么r和s点就是两个距离最远的点,然后继续查找后续点; 6 以Ȗ的⾏向量为数据样本进⾏K-means聚类。
平面分割算法

平面分割算法
平面分割算法是计算机图形学中常用的算法,用于将三维空间中的物
体分割成多个平面进行处理。
以下是一些常见的平面分割算法:
1.基于网格的平面分割算法:将三维物体通过三角面片等网格结构进
行表示,然后对网格进行切割,生成多个平面。
2.基于距离场的平面分割算法:通过计算三维物体中每个点到最近平
面的距离,获得距离场,然后以距离场中的局部最小值作为平面的分割线。
3.基于约束优化的平面分割算法:将三维物体分割为多个部分,并对
不同的部分设置不同的约束条件,然后通过优化算法获得最优的平面分割
方案。
4.基于图论的平面分割算法:将三维物体转化为无向图,对图进行遍历,找到合适的平面分割方案。
5.基于点云的平面分割算法:通过激光扫描或者摄像头得到三维物体
的点云数据,并对点云进行聚类,找到平面点的集合,然后使用RANSAC
算法求解平面参数,从而实现平面分割。
基于投影法三维模型全六面体网格的划分方法

基于投影法三维模型全六面体网格的划分方法
任辉龙;巩生龙;蔡永昌
【期刊名称】《计算机辅助工程》
【年(卷),期】2013(22)5
【摘要】针对六面体网格自动划分的难度远高于四面体网格的问题,用投影法对简单形状的初始网格进行投影变换得到每个块体的实际网格,用节点合并算法和再分割技术实现不同块体之间的不同密度网格的过渡,从而生成复杂三维几何形体的全六面体网格.算例表明:该方法生成的网格质量很好,易于实施,适用性广.
【总页数】7页(P122-128)
【作者】任辉龙;巩生龙;蔡永昌
【作者单位】同济大学土木工程地下建筑与工程系,上海200092;同济大学土木工程地下建筑与工程系,上海200092;同济大学土木工程地下建筑与工程系,上海200092
【正文语种】中文
【中图分类】O241.82
【相关文献】
1.基于子域重构的扫掠体六面体网格划分方法 [J], 代星;崔汉国;李正民;张立平
2.基于子域分解的全六面体网格生成方法 [J], 汪攀;张见明;韩磊;鞠传明;池宝涛
3.基于有限元弹性变形运算的全六面体网格生成方法研究 [J], 邹静;纪洪广
4.基于拓扑的再制造叶轮全六面体网格生成方法 [J], 许磊;曹华军;舒林森;李浩
5.基于拓扑分割的泵叶轮六面体网格划分方法 [J], 许磊;杜彦斌;张磊
因版权原因,仅展示原文概要,查看原文内容请购买。
基于网格分割的三维模型轻量化算法及构建

( 同济 大学 软件 学院 ,上海
摘
2 0 1 8 0 4 )
要:三维建模指通过三维制作软件构建 出具有三维 数据的模 型。三 维建模技 术可 以大 大
增加物体 的真实感 。传统的三维建模技术 首先对 真实物 体进行抽象 ,用 多边形构 造物体 的三
维模型 ,往往伴随着缓慢的生成 速度 。为保证 三维建模 以及模型展 现的效率 ,三 维模型 的轻 量化技术必不可少。基 于重 复的网格 分割算法 通过发现重 复单元来 提高模 型展现效率 ,但 是 该算法对于单连通模型的效 果不佳 , 因此在 引入几何描述符的基础上 , 提出一种基于网格分 割
c o n s t uc r t t h r e e - d i me n s i o n a l mo d e l b y p o l y g o n s . T h i s k i n d o f t e c h n i q u e s i s a l wa y s w i t h s l o w l y g e n e r a —
Ab s t r a c t :T h r e e —d i me n s i o n a l mo d e l i n g i s t h e p r o c e s s o f c o n s t r u c t i n g t h r e e—d i me n s i o n a l mo d e l b y
i r n g s pe e d .L i g h t we i g h t t e c h n o l o g y i s t h e k e y t o i mp r o v e t h e e ic f i e n c y a n d p e r f o r ma n c e o f t h r e e—d i - me n s i o n a l mo d e l i n g.S e g me n t a t i o n a l g o it r h m b a s e d o n r e p e a t e d g r i d c a n a c hi e v e a h i g h c o mp r e s s i o n r a — t i o b y in f d i n g r e p e a t e l e me n t s.b u t t h i s a l g o r i t h m h a s n o t g o o d e f f e c t i n t h e s i t u a t i o n o f s i n g l e c o n n e c — t i v i t y mo d e 1 .Th i s pa p e r p r e s e nt s a me s h s e g me n t a t i o n a l g o it r hm f o r r e p e a t e d u n i t ba s e d o n i mp o r t i n g
三维几何模型分割和对齐算法

三维几何模型分割和对齐算法三维几何模型分割和对齐算法是在三维计算机视觉领域中的一种重要技术,主要用于处理三维模型的分割和对齐任务。
三维模型分割是将一个三维模型划分成多个部分或物体的过程,而三维模型对齐是将多个三维模型以一定的准则对齐到同一个坐标系中的过程。
本文将详细介绍三维几何模型分割和对齐算法的原理、方法以及在实际应用中的一些应用案例。
一、三维几何模型分割算法1.数据预处理:对三维模型进行预处理,包括去噪、平滑等操作,以减少后续算法的误差和噪声。
2.特征提取:从三维模型中提取出特征信息,如曲率、法向量等。
这些特征信息对于分割算法非常关键,可以用来判断分割边界和区域。
3.区域生长:根据预定义的条件和阈值,从特征点开始,逐步生长出一个个区域。
区域的生长过程可以基于邻域信息,也可以基于一定的几何约束。
4.分割验证:对生长出的区域进行验证,剔除不符合条件的区域。
这一步骤通常需要根据应用场景和模型特点进行适当的调整。
5.后处理:对分割结果进行平滑处理,修复边界,减少噪声。
这一步骤可以使用一些图像处理或曲面重建的技术。
二、三维几何模型对齐算法1.数据预处理:对多个三维模型进行预处理,包括去噪、平滑等操作,以减少后续算法的误差和噪声。
2.特征提取:从每个三维模型中提取出特征信息,如特征点、特征曲线等。
这些特征信息对于对齐算法非常关键,可以用来匹配和对齐不同模型之间的相同部分。
3.特征匹配:将特征信息进行匹配,找到多个模型之间的对应关系。
匹配可以基于特征点、特征曲线等信息进行。
4.刚体变换:根据特征匹配的结果,计算出刚体变换矩阵,将不同模型对齐到同一个坐标系中。
5.优化调整:对刚体变换进行优化调整,以进一步提高对齐的准确性。
这一步可以使用一些优化算法,如最小二乘法等。
三维几何模型对齐算法在许多领域都有广泛应用,如三维建模、医学图像处理、机器人导航等。
例如,在机器人导航中,对齐算法可以将多个传感器采集到的三维地图对齐到同一个坐标系中,以提供一致的地图信息,便于机器人进行导航和路径规划。
基于投影法三维模型全六面体网格的划分方法
基于投影法三维模型全六面体网格的划分方法作者:任辉龙巩生龙蔡永昌来源:《计算机辅助工程》2013年第06期摘要:针对六面体网格自动划分的难度远高于四面体网格的问题,用投影法对简单形状的初始网格进行投影变换得到每个块体的实际网格,用节点合并算法和再分割技术实现不同块体之间的不同密度网格的过渡,从而生成复杂三维几何形体的全六面体网格.算例表明:该方法生成的网格质量很好,易于实施,适用性广.关键词:全六面体网格;投影法;超限插值;再分割技术;网格过渡;爆炸模拟中图分类号: O241.82 文献标志码: AFull hexahedral meshing method for 3D model based onprojection methodREN Huilong, GONG Shenglong, CAI Yongchang(Department of Geotechnical Engineering, Tongji University, Shanghai 200092,China)Abstract: As to the issue that the automatic hexahedral meshing is far more difficult than the automatic tetrahedral meshing, the projection method is used to transform the initial mesh of simple shapes into the actual mesh of each block, the mesh transition among blocks with different mesh density is implemented by node merging algorithm and resegmentation technique. The numerical examples show that the mesh quality generated by the method is good and the method is easy to bring into effect with wide applicability.Key words: full hexahedral mesh; projection method; transfinite interpolation;resegmentation technique; mesh transition; explosion simulation收稿日期: 2013-03-29 修回日期: 2013-05-24基金项目:西部交通建设科技项目(2011ZB04)作者简介:任辉龙(1989—),男,江西宜春人,硕士研究生,研究方向为岩土工程稳定性分析,(E-mail)hl.ren@0 引言目前,在三维有限元模型网格生成中普遍采用四面体单元或六面体单元.与四面体单元相比,六面体单元具有更好的力学性能,达到同样精度所需的六面体单元和节点数远少于四面体单元,故六面体单元在有限元分析领域有较高的价值,是一种十分重要的单元.[1]很多专家认为,在诸如锻压成形和爆炸冲击等三维有限元仿真领域中,六面体应该是首选单元.在某些情况下,如当用有限体积法和边界适应坐标系统求解复杂形体的控制守恒方程时,只能采用六面体单元进行有限元分析.[2-3]从技术角度讲,六面体网格自动划分的难度远远高于四面体网格.目前,有代表性的全六面体网格生成方法有映射法、扫描法、基于栅格法、扩展的AFT方法、多子区域法和投影法等.映射法的优点是速度快、网格质量高、密度可控制,但同时也有2个严重的问题:复杂三维域自动分解问题和网格密度过渡问题.近年来,一些研究者采用中面法[4]进行子域自动分解,但对于复杂的几何形体难以实现全自动分区.扫描法是通过对离散化的基本单元形体进行旋转、扫描和拉伸等操作获得高维网格的一种方法.该方法难度较低,容易实现,但只适合于形状简单的三维物体.单元转换法将其他单元转化为六面体单元,可以实现全自动化[5-7],但这种方法的边界拟合能力弱,生成的网格质量较差.左旭等[8] 改进单元转换法,将十节点曲边四面体转换为六面体,并采用非线性约束优化算法大幅提高六面体网格的单元质量.基于栅格法能实现网格生成的自动化,生成速度也非常快,但其最大弱点是边界单元的质量较差,网格密度很难控制.AFT方法的扩展主要有编须算法[9]和粘贴算法[10].编须算法基于空间缠绕连续集[11]概念,将AFT方法扩展到三维空间,生成的六面体网格质量是所有算法中最好的,但程序实现非常困难;粘贴算法可能会留下一些孔洞,这些未被划分的区域只能用四面体填充.LI等[12]提出一种带梯度的全六面体网格划分方法,利用单元分割模板得到不同块体之间节点的约束关系,建立整数规划数学模型,解得不同块体之间的单元划分数量关系.该方法可以实现不同网格密度的合理过渡,但求取约束关系过于复杂.SU等[13]利用单元分割模板提出一种基于复合投影法建立多块体的全六面体网格划分方法,但该方法涉及到三棱柱单元的再划分.本文基于投影法,利用单元分割技术实现不同块体的单元节点协调过渡,建立疏密有致的全六面体网格模型.1 投影法投影法的理论基础是射影几何,通过投影法将点投影到曲面上,将普通形状变换成具有相同拓扑性质的曲面形状.[14-15]复杂的三维模型都能分解为简单块体,而简单块体又可以通过简单形状经过布尔运算和投影得到.投影法生成六面体网格正是基于这样一种思想,将复杂几何模型分解为简单块体,提取所有简单块体的边界几何信息;生成具有初始六面体网格的简单实体,删除某些区域,使其与简单块体具有相同的拓扑结构,将具有初始网格的简单实体表面节点投影到简单块体的边界表面,内部网格节点通过超限插值分布在简单块体的内部,形成具有六面体网格的简单块体,最后将简单块体组装起来形成全六面体的复杂几何模型.基于投影法划分网格是一种自顶向下的建模方法,与普通商业软件先建立实体模型再进行网格划分的流程相反,而正是这种自顶向下的建模方法可以建立任意复杂几何形状的全六面体网格模型.基于投影法的六面体网格生成算法可以分解成以下步骤:(1)形成具有初始网格的初始结构;(2)将初始网格的自由节点投影到模型表面;(3)用最小变形角法匹配网格边界;(4)用最小扭转角法匹配模型顶点;(5)用超限插值技术获得网格内部节点坐标;(6)用再分割技术和节点合并算法形成整体网格模型.1.1 超限插值法超限插值法是最重要的映射方法,它将一个单位立方体映射到任意曲棱线的六面体区域,见图1.图 1 基于曲棱线的六面体超限插值Fig.1 Hexahedral transfinite interpolation based on ridge由文献[16]有P(ξ,η,γ)=(1-η)(1-γ)f1(ξ)+(1-η)γf2(ξ)+ηγf3(ξ)+η(1-γ)f4(ξ)+(1-ξ)(1-γ)f5(η)+(1-ξ)γf6(η)+ξγf7(η)+ξ(1-γ)f8(η)+(1-ξ)(1-η)f9(γ)+(1-ξ)ηf10(γ)+ξηf11(γ)+ξ(1-η)f12(γ)+C(ξ,η,γ)(1)C(ξ,η,γ)=-2((1-ξ)(1-η)(1-γ)v(0,0,0)+(1-ξ)(1-η)γv(0,0,1)+(1-ξ)η(1-γ)v(0,1,0)+(1-ξ)ηγv(0,1,1)+ξ(1-η)(1-γ)v(1,0,0)+ξ(1-η)γv(1,0,1)+ξη(1-γ)v(1,1,0)+ξηγv(1,1,1))(2)式中:P(ξ,η,γ)={x(ξ,η,γ),y(ξ,η,γ),z(ξ,η,γ)}为六面体区域中任意一插值点;fi(s)(i=1,2,…,12,s=ξ,η,γ)为边界曲线函数; v(i,j,k)={x(i,j,k),y(i,j,k),z(i,j,k)},(i,j,k=0,1)为8个顶点;ξ∈[0,1];η∈[0,1];γ∈[0,1].六面体区域内插值点的坐标(x,y,z)与12条边界曲线、8个顶点及在立方体中相应坐标(ξ,η,γ)有关,而在生成六面体网格时只需要区域内有限的插值点,因此,对于边界曲线只需要有限节点的坐标值.设线1,5和9上节点分别为m+1,n+1和p+1,取ξ=(i-1)/m,i=1,2,…,m+1η=(j-1)/n, j=1,2,…,n+1γ=(k-1)/p, k=1,2,…,p+1(3)则可求得曲棱线六面体内任意节点的插值坐标.1.2 形成整体协调模型在简单块体的组装过程中,会面临不同块体对应面上节点的协调性问题.当单元节点不协调时,可以通过添加节点耦合方程获得整体网格模型.本文通过共用节点法形成全六面体网格模型.在组装简单块体时,建立交界面的局部坐标,见图2,ζ和η方向的单元个数分别为n和m.需要合并节点的2个交界面分别称为主面和从面,不妨称网格数目较多的交界面为主面,单元数目为nm×mm;网格数目较少的交界面为从面,单元数目为ns×ms.如果块体交界面上节点满足一定的关系,就可通过节点合并算法和再分割模板形成整体模型.图 2 交界面上节点局部坐标Fig.2 Local coordinates of interface node1.2.1 节点合并算法节点合并算法指若主面和从面在ζ和η方向的单元数目对应相等,则可以建立主面和从面上节点的一一对应,实现对应节点的合并.1.2.2 再分割技术再分割技术 [14]指通过按一定的规则再分割已有的六面体单元,在适当位置添加相应节点,再经过适当组合,形成多个六面体单元的方法.通过再分割技术,可以使主面和从面上ζ和η方向单元节点数目相等,再利用节点合并算法就可实现简单块体的组装,形成协调的全六面体网格有限元模型.本文采用几种较简单、方便实施的再分割模板,单元再分割模板见图3.图 3 单元再分割模板Fig.3 Element resegmentation templates1.2.3 不同网格密度过渡交界面上ζ和η方向的节点数目相同是实现网格协调的充要条件,然而当交界面上主面与从面之间的网格数量满足一定的比例条件时,利用如图3所示的再分割模板,使得交界面上主、从面的节点数量相等.这些比例条件有:(1)当nm∶ns=1∶1,mm∶ms=1∶1时,通过节点合并技术就可以实现单元协调过渡.(2)当nm∶ns=4∶2,mm∶ms=1∶1或nm∶ns=1∶1,mm∶ms=4∶2时,用节点合并和再分割法过渡,见图4(a).(3)当nm∶ns=4∶2,mm∶ms=4∶2时,用图4(b)方法过渡.(4)当nm∶ns=3∶1,mm∶ms=1∶1或nm∶ns=1∶1,mm∶ms=3∶1时,用图4(c)方法过渡.(5)当nm∶ns=3∶1,mm∶ms=3∶1时,用图4(d)方法过渡.(6)当nm∶ns=3∶1,mm∶ms=4∶2时,用图4(e)方法过渡.因此,对于复杂三维模型,首先将三维模型分解为简单块体,简单块体的实质就是拓扑形状较简单,简单块体通过之间的共用面形成整体三维模型,利用共用面就可以快速匹配交界面.确定初始网格的数目,使得交界面上的网格数目满足比例条件(1)~(6)中的一条,就可以实现块体之间不同网格密度的过渡,满足节点协调性要求.已有的有限元软件主要通过逐步扩大过渡实现节点协调性,但这只是比例条件(1)的特殊情况.当简单块体之间有2个或多个相邻的交界面,或从面有其他单元时,则采用图4中5种过渡方法之一,就会在过渡面块体之外产生节点不协调的单元,见图5.(a)过渡方法1(b)过渡方法2(c)过渡方法3(d)过渡方法4(e)过渡方法5图 4 交界面上不同密度网格过渡Fig.4 Transition of mesh with different density at interface图 5 单元节点不协调网格Fig.5 Unconformable mesh of element nodes不协调单元产生的原因是从面内的单元进行再分割,而从面周围的单元没有进行分割,产生一层节点不协调的单元.分析图4中5种过渡方法,从面周围若有其他单元,再分割的单元与周围的单元是不协调的.因此,对于节点不协调的单元需进行再分割.对于图5中节点不协调的单元,可采用图3(f)和3(g)模板进行再分割,实现单元节点的协调.1.2.4 六面体模型修复假设简单块体已通过投影法和过渡方式1~5组合生成八节点六面体复杂模型,模型由n 个节点和m个单元组成.节点为(Ni,xi,yi,zi),i=1,2,…n.单元为(Eid,Aj,Bj,Cj,Dj,Ej,Fj,Gj,Hj),j=1,2,…,m;Aj,Bj,…,Hj为节点编号,顺序见图6.图 6 八节点实体单元Fig.6 8-node solid elements单元的8个节点组成6个面,依次为(A,D,C,B),(A,E,H,D),(A,B,F,E),(B,C,G,F),(C,D,H,G)和(E,F,G,H),右手手指沿面上节点顺序,大拇指方向为面的法向方向,如图6中面EFGH的法向方向为n,n=(EF×EH)/|EF×EH|(4)式中:EF=(xF-xE,yF-yE,zF-zE);EH=(xH-xE,yH-yE,zH-zE).提取所有六面体单元的6个面,总共有6m个面,Si=(Ni1,Ni2,Ni3,Ni4),i=1,2,…,6m.单元之间的交界面上节点不协调,则该界面不协调,见图7,设交界面S1=(1,4,3,2),S2=(1,2,6,5):(1)具有公共节点(1,2);(2)面法向量n1与n2反向;(3)面积|S1|图 7 不协调交界面Fig.7 Unconformable interface图 8 节点不协调单元交界面Fig.8 Unconformable element interface of nodes图8中,情况1和2是以2∶4为过渡方式的节点不协调单元的交界面,情况3和4是以1∶3为过渡方式的节点不协调单元的交界面.基于对不协调交界面的分析,提出消除上述节点不协调的算法.步骤1 读入全六面体网格模型的节点数据和单元数据.每个节点包括有节点号和x,y,z 方向的坐标;每个单元由8个节点、6个面组成,其中每个面由4个节点构成,形成每个节点的面数据.步骤2 找出需要分割的六面体单元:比较所有单元的面,找出属于图8(a)~8(d)的不协调面,找出需要分割的六面体单元.步骤3 对步骤2中找出的六面体单元,按模板6或7的方式进行再分割,形成新的六面体单元,并删除原单元.步骤4 通过节点合并算法,合并图8(a)~8(d)中交界面上的节点,更新节点数据和单元数据.步骤5 按一定格式输出全六面体网格模型.按该步骤编制MATLAB程序,对存在部分节点不协调的六面体网格模型进行修复,形成协调的全六面体网格复杂模型.2 全六面体网格建模实例若几何模型较规则,按照该方法能确保单元质量;若几何模型过于复杂,按照该方法就不可避免地会产生少量畸变单元.虽然这些不良单元数量不多,占总单元数比例也不是很大,但会影响计算精度,甚至无法进行计算.因此,检测网格单元是否已经畸变必不可少,可依次检查最大和最小顶角以及纵横比确定.(1)最大顶角,即单元表面相邻两边夹角的最大值,其警戒值为155°.(2)最小顶角,即单元表面相邻两边夹角的最小值,其警戒值为18°.(3)纵横比.过单元表面投影图形的四边中点做一个矩形,其长边与短边的比值就是纵横比.该比值的警戒值为5.实例1 具有初始网格的简单实体向边界曲面投影,得到简单块体的六面体网格,利用单元的再分割和简单块体的组装形成整体六面体网格模型,实例1的六面体网格见图9.通过单元质量检查,最大顶角为151°,最小顶角为26°,纵横比为1~2.3,均小于警戒值.图 9 实例1的六面体网格Fig.9 Hexahedral mesh of example 1实例2 浅埋连拱隧道爆破数值模型的建模.爆破模拟可以利用高性能炸药单元或等效炮轰载荷的方法.第一种方法的理论更可靠,该方法能很好地模拟爆源近区的冲击响应问题,也可以研究中远区的爆破震动传播问题;但第一种方法存在数值模型建立困难的问题.这是因为该方法要求炸药材料单元和炮孔周围网格划分得十分细小,而地下工程爆破震动数值模拟的计算模型又很大,如果没有合理的网格过渡,就会使模型单元数量太多,超过普通计算机的处理能力.合理的数值建模是爆破模拟中的一个难题.由于精细模型建立的复杂性,数值模型只能降低单元质量,即采用过于刚硬的四面体单元或采用扫掠拉伸方法建立的六面体单元,但采用扫掠拉伸方法建立的部分六面体单元过于细长,纵横比超过20;或者只能缩小模型规模,简化为平面应变模型,无法真正建立疏密有致、又很好控制单元质量和单元总数的模型.利用本文提出的方法,选取计算区域:140 m(x方向)×80 m(z方向)×72 m(y方向),隧道掌子面爆破施工,前、后洞掌子面部分区域采用边长为20 cm的六面体网格,经过多面过渡,依次过渡边长为60, 100, 200和400 cm的单元.该隧道爆破数值模型见图10,所有六面体单元的长宽比均不超过4,严格控制单元质量,模型单元总数193 256个,节点总数202 817个.通过单元质量检查,模型的最小顶角为16°,低于18°的单元少于总数0.5%,最大顶角为154°,纵横比为1.0~6.3,超过警戒值5的单元总数少于0.3%,单元质量总体合格.如果按20 cm边长的六面体网格进行精细划分,网格数量会超过1 000万个,而通过本文的方法将单元数量控制在20万个以内,普通的计算机也能计算.在文献[17]中,利用该模型模拟分析浅埋连拱隧道爆破过程,见图11~12,监测结果与模拟结果一致,振速合矢量波形很接近,特征节点最大振速为15.951 cm/s,实测为15.726 cm/s,说明六面体网格模型有效,网格质量很好.(a)开挖区网格划分(b)隧道整体网格模型图 10 浅埋连拱隧道爆破数值模型Fig.10 Numerical explosive model of shallow buried multi-arch tunnel图 11 测点处振速合矢量Fig.11 Resultant vibration velocity at measurement point图 12 特征节点合速度Fig.12 Resultant velocity of feature node3 结束语将复杂三维几何模型分为简单块体,基于投影法,对简单形状初始网格进行投影变换,得到每个块体的实际网格,利用节点合并算法和再分割技术,实现不同块体之间的不同网格密度过渡,生成整体全六面体单元模型.算例表明,本文所提出的方法简单易行,生成的网格质量很好,可以有效解决爆炸与冲击数值模拟中模型建立问题,适合于各种要求六面体单元数值计算.在以后的工作中,将考虑如何使用更多形式分割模板及其组合形式实现不同密度网格过渡,以及寻找三维几何模型简单块体的自动划分方法.参考文献:[1] 金晶,吴新跃. 有限元网格划分相关问题分析研究[J]. 计算机辅助工程, 2005, 14(2): 75-78.JIN Jing, WU Xinyue. Analysis of finite element mesh problems[J]. Comput Aided Eng,2005, 14(2): 75-78.[2] 关振群,宋超,顾元宪,等. 有限元网格生成方法研究的新进展[J]. 计算机辅助设计与图形学学报, 2003, 15(1): 1-14.GUAN Zhenqun, SONG Chao, GU Yuanxian, et al. Recent advances of research on finite element mesh generation methods[J]. J Computer-aided Des & Compu Graphics, 2003, 15(1): 1-14.[3] LANDER S F, STEFFAN H. Method to generate complex computational meshes efficiently[J]. Int J Commun Numer Methods Eng, 1994, 10(5): 373-384.[4] PRICE M, ARMSTRONG C. Hexahedral mesh generation by medial surface subdivision:Part II: solids with flat and concave edges[J]. Int J Numer Methods Eng, 1997, 40(1): 111-136.[5] 关振群,单菊林,顾元宪. 基于转换模板的三维实体全六面体网格生成方法[J]. 计算力学学报, 2005, 22(1): 32-37.GUAN Zhenqun, SHAN Julin, GU Yuanxian. All hexahedral mesh generation method for 3D solid model based on extended transform templates[J]. Chin J Comput Mech, 2005, 22(1):32-37.[6] 陈沸镔,谢步瀛. 建筑结构模型的四边形网格生成算法[J]. 计算机辅助工程, 2010,19(1): 17-21.CHEN Feibin, XIE Buying. Quadrilateral mesh generation algorithm of building structure model[J]. Comput Aided Eng, 2010, 19(1): 17-21.[7] 徐敏艳,陈华书,范秦寅,等. 多块网格划分技术在CFD仿真中的应用[J]. 计算机辅助工程, 2012, 21(4): 65-68.XU Minyan, CHEN Huashu, FAN Qinyin, et al. Application of multi-block meshing technology in CFD simulation[J]. Comput Aided Eng, 2012, 21(4): 65-68.[8] 左旭,卫原平,陈军,等. 三维六面体有限元网格自动划分中的一种单元转换优化算法[J]. 计算力学学报, 1999, 16(3): 343-348.ZUO Xu, WEI Yuanping, CHEN Jun, et al. An element transformation and optimization method in 3D automatic hexahedral meshes generation[J]. Chin J Comput Mech, 1999, 16(3):343-348.[9] TAUTGES T J, BLACKER T, MITCHELL S. The whisker-weaving algorithm: a connectivity based method for constructing all hexahedral finite element meshes[J]. Int J Numer Methods Eng, 1996, 39(19): 3327-3349.[10] BLACKER T D, MEYERS R J. Seams and wedges in plastering: a 3D hexahedral mesh generation algorithm[J]. Eng Computers, 1993, 9(2): 83-93.[11] MURDOCH P, BENZLEY S E. The spatial twist continuum[C]//Proc 4th Int Meshing Roundtable, Albuquerque, 1995: 243-251.[12] LI H, CHENG G. New method for graded mesh generation of all hexahedral finite elements[J]. Computers & Structures, 2000, 76(6): 729-740.[13] SU Y, LEE H K, KUMAR A S. Automatic hexahedral mesh generation for multi-domain composite models using a hybrid projective mesh-based method[J]. Computer-Aided Des,2004, 36(3): 203-215.[14] GORDON W J, THIEL L C. Transfinite mappings and their application to mesh generation[J]. Appl Math & Comput, 1982(10): 171-233.[15] MIDDLECOFF J F, THOMAS P D. Direct control of the mesh point distribution in meshes generated by elliptic equations[J]. AIAA J, 1980, 18(6): 652-656.[16] COOK W A. Body oriented (natural) co-ordinates for generating three-dimensional meshes[J]. Int J Numer Methods Eng, 1974, 8(1): 27-43.[17] 任辉龙,段群苗,蔡永昌. 浅埋连拱隧道爆破的数值模拟[J]. 爆破, 2012, 29(4): 70-75.REN Huilong,DUAN Qunmiao,CAI Yongchang. Numerical simulation on explosion of shallow buried multi-arch tunnel[J]. Blasting, 2012, 29(4): 70-75.(编辑于杰)。
三维网格模型的局部三角剖分算法
三维网格模型的局部三角剖分算法
李岩席;贺可太;朱冬梅
【期刊名称】《机电产品开发与创新》
【年(卷),期】2024(37)1
【摘要】为了提高三维网格模型的渲染显示效率和提高网格质量以满足有限元分析,提出了一种新的三维网格模型的局部三角剖分方法。
本方法的三角剖分基于Bowyer-Watson插点算法实现。
通过在新插入点的邻域内搜索三角形来提高三角剖分的效率,通过对网格的几何形状和连通性进行局部修改来提高网格质量。
通过尺寸场来约束控制三角剖分区域,使得生成的网格质量和算法性能有较好的综合表现。
【总页数】5页(P6-10)
【作者】李岩席;贺可太;朱冬梅
【作者单位】北京科技大学机械工程学院
【正文语种】中文
【中图分类】TP39
【相关文献】
1.用随机增量局部转换算法实现三维点集的Delaunay三角剖分
2.地质模型网格剖分中Delaunay三角剖分算法的实现及优化
3.面向局部突起的三维网格分割算法研究
4.基于改进三角剖分算法与微惯导技术的三维模型构建方法
5.基于三角剖分局部搜索的三维滑移面算法
因版权原因,仅展示原文概要,查看原文内容请购买。
多维分割论之二—平面分割空间的全套理论和方法
多维分割论之二—平面分割空间的全套理论和方法平面分割空间理论和方法是多维分割论的重要组成部分,它是一种将多维数据集划分为不同的区域或簇的方法,以便对数据进行分析和处理。
在这篇文章中,我们将介绍平面分割空间的基本理论和全套方法。
1.空间划分空间划分是平面分割空间的核心概念,它将多维数据集划分为多个不相交的区域或簇。
常用的空间划分方法包括K-means聚类、DBSCAN和层次聚类等。
K-means聚类是一种基于距离度量的划分方法,它将数据集划分为K个不同簇,每个簇包含与该簇中心最近的数据点。
DBSCAN是一种基于密度的划分方法,它将数据点分为核心对象、边界对象和噪声对象等不同的类型,并根据数据点之间的密度关系将它们划分为不同的簇。
层次聚类是一种自底向上的划分方法,它通过计算数据点之间的相似度或距离来决定数据点的聚类关系,从而形成层次化的簇结构。
2.空间分割方法空间分割方法是指将空间划分应用到实际数据集中的具体方法,常用的空间分割方法包括Voronoi图、R树和网格划分等。
Voronoi图是一种基于距离的空间分割方法,它将空间划分为多个区域,每个区域包含与该区域中心点最近的数据点。
R树是一种哈希树结构,它将数据点划分为不同的层次结构,以便高效地进行空间查询。
网格划分是将空间划分为规则网格的方法,它可以快速地进行空间查询操作。
3.空间索引空间索引是平面分割空间中的关键技术之一,它用于提高空间查询的效率。
常见的空间索引方法包括R树、kd树和Quadtree等。
R树是一种基于矩形包围框的空间索引方法,它将数据点分为不同的层次结构,并按照矩形包围框的大小关系进行索引。
kd树是一种二叉树结构,它将数据点递归地划分为不同的子空间,并将每个节点对应的子空间划分为两个相等大小的子空间。
Quadtree是一种四叉树结构,它将二维空间划分为四个相等大小的子空间,并递归地划分每个子空间。
4.空间查询空间查询是在划分空间后对数据进行查询操作的过程,常见的空间查询包括范围查询、最近邻查询和k近邻查询等。
测绘技术中的三维网格模型构建与拓扑关系处理方法
测绘技术中的三维网格模型构建与拓扑关系处理方法测绘技术在现代社会发展中发挥着重要作用,其中三维网格模型的构建与拓扑关系处理是其中的重要环节。
三维网格模型是一种用于表示三维物体表面的数学模型,广泛应用于虚拟现实、计算机图形学、仿真等领域。
在这篇文章中,我们将探讨三维网格模型构建的方法以及处理其拓扑关系的技术。
首先,我们来讨论三维网格模型构建的方法。
三维网格模型的构建可以通过多种途径实现,其中最常见的方法是从三维扫描仪获取物体的点云数据,并利用网格重构算法将其转换为三维网格模型。
点云数据是由一系列离散的点组成的,在构建三维网格模型之前,需要对点云数据进行预处理,例如去噪、滤波等操作,以提高模型的质量和精度。
接下来,可以利用曲面重建算法或三角化算法将点云数据转化为三维网格模型。
曲面重建算法通过拟合曲面来填补点云数据之间的空白,常用的方法有最小二乘拟合和高斯过程拟合。
而三角化算法则根据点云数据之间的距离关系,将其连接为三角面片,常用的算法有Delaunay三角剖分和Alpha形状三角剖分。
通过这些方法,可以得到具有一定拓扑结构的三维网格模型。
其次,我们谈论三维网格模型的拓扑关系处理方法。
在三维网格模型中,拓扑关系是指模型中各个面片之间相邻、连通或分离的关系。
处理三维网格模型的拓扑关系是为了实现模型的精确表示和高效计算。
常见的拓扑关系处理方法包括边界提取、正则化和拓扑修复等。
边界提取是为了提取网格模型的边界或边缘,可以通过算法判断网格模型中哪些面片是边界面片,从而进行边界提取。
正则化是指对三维网格模型进行优化,使其满足一定的规则或约束条件,例如将面片的法向量进行统一化,去除模型中的重复面片等。
拓扑修复是在三维网格模型中修复非法或错误的拓扑关系,例如合并相邻面片、修复缺失面片等。
这些处理方法可以有效地改善三维网格模型的质量和准确度。
综上所述,三维网格模型的构建与拓扑关系处理是测绘技术中的重要环节。
通过三维网格模型的构建,可以将实际物体转化为具有一定拓扑结构的数学模型,为后续的分析和应用提供了基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
me tt n b s d o h r n l r y c mp t go u t n p c e r na i a e n t eg a u a t o u i f oi t a e t oy,a d t e rp u d d me h s g n ain b s d O ir o i n q e s h n n p o o n e s e me tt a e n he - h o ac ia a d s n h sstc n q e F r d t e df r n a u ai r a y e t ci g r s e t ey te g o t c lc a a tr - rh c l n y t e i h i u . o me h i e e t n l r y a e sb xr t e p ci l h e mer a h rc ei e f r g t a n v i s
第2 7卷 第 4期
21 0 0年 4月
计 算 机 应 用 研 究
Ap l a in Re e r h o o u e s p i t s a c fC mp tr c o
Vo J 7 No 4 l2 .
A r 2 1 p. 0 0
基 于 商 空 间粒 度 理 论 的 三 维 网格 分 割 方 法
关键词 :网格 分割 ;商空间 ;粒度 ;粗分割 ;合 成
中图分类号 :T 1 P8 文 献标 志码 :A 文章编 号 :10 —6 5 2 L )4 19 —3 0 13 9 ( O O O — 5 80
d i1 .9 9 ji n 10 -6 52 1 . . l3 o:0 3 6 /.s . 0 13 9 .0 0 0 0 1 s 4
算 法通过 成不 同的粒度 区域 , 再根据 粒度合 成理论 。将这 些所
形成 的粒度组 织起 来 , 而 实现对 三维 网格 的最终分割 , 从 为三 角网格模 型的 简化提 供 了快速 有 效的 方法 。实验 表 明了该算法对 于网格 分割 的有效性和 正确性。
( colfEet n s& C m ue Si c Tcn l y o hU i rt o hn ,Tiun0 0 5 , hn ) Sho l r i o coc o pt c ne& eho g ,N a nv syf C ia aya 3 0 1 C i r e o e i a
Absr c : T r u h te su y o xsi s e me ain a d lsrIlfc to t ds hi p ra a y e h rnu ta t h o g h td fe it me h sg ntt nd mo e i p i a in meho ,t spa e n l zd te g a — ng o e i
ss 8 st e ie t na e m e tto ft e — i n ina s e wh c r vd d f s n fe tv t o o h d l i 0a o ra z hef l s g nai n o hre d me so lme h s, i h p o ie a ta d efci e meh d fr te mo e l i smp i c t n. er s l h w h tt rpo e lo i i lf ai T e ut s o t a he p o s d ag rt i o h s hm sef cie a d v ld frt e me h s g n ain. i fe tv n a i o h s e me t t o
石 晓敬 ,韩 燮
( 中北 大学 电子与计 算机科 学技 术 学院,太原 0 0 5 ) 30 1 摘 要 :通过研 究 已有 的网格分割 和模型 简化 方法 , 分析三 维模 型的 网格 分割 中的商 空 间粒 度 思想 , 并将 商 空
间粒度 计算 引入到 网格分割 中, 网格分割过 程进行描 述 , 出了基 于 粒度 分层合 成技 术 的 网格 分 割方 法。该 对 提
lrt o ui g o u t n p c h oy i h D me h s g n ain a d i t d c d te g a u a i o u ig o u t n ai c mp t fq oi ts a e te r n t e 3 s e me tt n n r u e h rn lr y c mp t fq oi t y n e o o t n e s a e t e r h s e me tt n a d d s r e h rc s f s e me tt n u r a d te p i cp eo s e — p c h oy t t e me h s g na i n e c b d t ep o e s h s g n ai .P t o w r r il f o o i o me o f h n me h s g
3 me h s g n a i n b s d o r n l rt fq oi n p c h o y D s e me t to a e n g a u a i o u te ts a e t e r y
S I i -n , A i H a j g H NX e X oi
