垂直关系1:线面垂直的判定
2.3.1直线与平面垂直的判定(经典)

如图,点Q是_点_P_在_平_面_内_的_射_影_ _线_段_PQ_是点P到平面 的垂线段
(2)斜线
一条直线和一个平面相交,但不和
这个平面垂直,这条直线叫做这个平面
的斜线.
P
斜线和平面的交点
叫做斜足。
从平面外一点向平 面引斜线,这点与斜
R
足间的线段叫做这点
到这个平面的斜线段
思考:平面外一点到一个平面的垂线段有 几条?斜线段有几条?
A
B
O
D
α
C
这条直线垂直于梯形所在的平面。(√ )
(4)若一条直线与一个平面不垂直,则这个平面内
没有与这条直线垂直的直线。(× )
定理应用
四:典型例题
例1 如图,已知 a//b,a,求证 b.
证明:在平面 内作两条相交
直线m,n.
a
b
m n
巩固练习
例2 如图,在三棱锥V—ABC中,VA=VC, AB=BC,求证:VB⊥AC。
如图,长方体ABCD—A1B1C1D1中,棱
AA1,BB1,CC1,DD1 所在直线与底面ABCD的 位置关系如何?它们彼此之间具有什么
位置关系? C1
D1
B1
A1
C
D
B
A
一、线面垂直的性质定理
垂直于同一个平面的两条直线平行
已知:a⊥α, b⊥α, 求证:a // b
证明:
假设 a与b不平行.
记直线b和α的交点为o,
A
A
B
D
CB
C D
过 ABC 的顶点A翻折纸片,得到折痕AD,将翻
折后的纸片竖起放置在桌面上(BD,DC于桌面接
触).
(1)折痕AD与桌面垂直吗?
5 第5讲 直线、平面垂直的判定及其性质

GH∥平面ABC.
证明 (1)因为EF∥DB,所以EF与DB确定平面BDEF,
图① 如图①,连接DE.因为AE=EC,D为AC的中点, 所以DE⊥AC.同理可得BD⊥AC.又BD∩DE=D, 所以AC⊥平面BDEF. 因为FB⊂平面BDEF,所以AC⊥FB.
-AB-C的正切值.
S
解:过C作CH⊥AB于点H,连结SH
∵SC⊥平面ABC, AB⊂平面ABC A
∴ AB ⊥ SC
又∵SC∩CH=H
∴ AB ⊥平面 SCH
H
又∵SH⊂平面SCH ∴ AB ⊥ SH
∴ ∠SHC是二面角S-AB-C的平面角
…………
棱的垂面法
C B
4.PB 平面 ABC, PB BC CA 4, 且 BCA 90, 求二面角 B PA C 的大小
2.(2014·浙江高考)设 m,n 是两条不同的直线,α,β是两个不同的
平面( C )
A.若 m⊥n,n∥α,则 m⊥α B.若 m∥β,β⊥α,则 m⊥α C.若 m⊥β,n⊥β,n⊥α,则 m⊥α D.若 m⊥n,n⊥β,β⊥α,则 m⊥α
(山东卷) 在如图所示的几何体中,D是AC的 中点,EF∥DB.
(2)因为平面 ABD⊥平面 BCD, 平面 ABD∩平面 BCD=BD, BC⊂平面 BCD,BC⊥BD, 所以 BC⊥平面 ABD. 因为 AD⊂平面 ABD, 所以 BC⊥AD. 又 AB⊥AD,BC∩AB=B,AB⊂平面 ABC,BC⊂平面 ABC, 所以 AD⊥平面 ABC. 又因为 AC⊂平面 ABC, 所以 AD⊥AC.
第11讲 空间中垂直关系的判定与性质
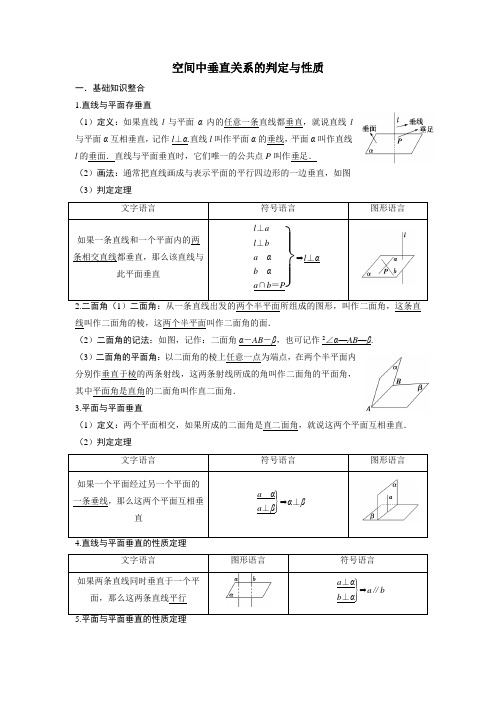
空间中垂直关系的判定与性质一.基础知识整合1.直线与平面存垂直(1)定义:如果直线l 与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直,记作l ⊥α.直线l 叫作平面α的垂线,平面α叫作直线l 的垂面.直线与平面垂直时,它们唯一的公共点P 叫作垂足.(2)画法:通常把直线画成与表示平面的平行四边形的一边垂直,如图(3)判定定理 ⎭⎪⎬⎪⎫l ⊥a l ⊥b a αb αa ∩b =P ⇒l ⊥α从一条直线出发的两个半平面所组成的图形,叫作二面角,这条直线叫作二面角的棱,这两个半平面叫作二面角的面.(2)二面角的记法:如图,记作:二面角α-AB -β,也可记作2∠α—AB —β.(3)二面角的平面角:以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角,其中平面角是直角的二面角叫作直二面角.3.平面与平面垂直(1)定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.(2)判定定理⎭⎪⎬⎪⎫a αa ⊥β⇒α⊥β符号语言⎭⎪⎬⎪⎫α⊥βα∩β=l a αa ⊥l ⇒a ⊥β 题型一:线面垂直的判定 例1:如图所示,在Rt △ABC 中,∠B =90°,且S 为所在平面外一点,满足SA =SB =SC .D为AC 的中点.求证:SD ⊥平面ABC .证明:∵在Rt △ABC 中,∠B =90°,且D 为AC 的中点,∴BD =AD =DC .又∵SA =SB =SC ,SD为公共边,∴△SBD ≌△SAD ≌△SCD , ∴∠SDB =∠SDA =∠SCD =90°,∴SD ⊥AD ,SD ⊥BD ,∵AD ∩BD =D ,∴SD ⊥平面ABC .变式训练1:如图,已知AB 是⊙O 的直径,C 是圆周上不同于A ,B 的点,P A ⊥⊙O 所在的平面,AF ⊥PC 于F ,求证:BC ⊥平面PAC .证明:因为AB 为⊙O 的直径,所以BC ⊥AC .因为P A ⊥平面ABC ,BC平面ABC ,所以P A ⊥BC .因为P A ∩AC =A ,所以BC ⊥平面P AC .题型二:面面垂直的判定例2:已知四面体ABCD 的棱长都相等,E ,F ,G ,H 分别为AB ,AC ,AD ,BC 的中点.求证:平面EHG ⊥平面FHG .证明:如图,取CD 的中点M ,连接HM ,MG ,FM ,则四边形MHEG为平行四边形.连接EM 交HG 于O ,连接FO .在△FHG 中,O 为HG的中点,且FH =FG ,所以 FO ⊥HG .同理可证FO ⊥EM .又HG ∩EM =O ,所以FO ⊥平面EHMG .又FO 平面FHG ,所以平面EHG ⊥平面FHG .变式训练2:如图,在空间四边形ABDC中,AB =BC ,CD =DA ,E 、F 、G 分别为CD 、DA 和对角线AC 的中点.:求证:平面BEF ⊥平面BDG .证明:∵AB =BC ,CD =AD ,G 是AC 的中点,∴BG ⊥AC ,DG ⊥AC ,又EF ∥AC ,∴EF ⊥BG ,EF ⊥DG .∴EF ⊥平面BGD .∵EF 平面BEF ,∴平面BDG ⊥平面BEF .题型三:垂直关系的综合应用例3:如图,在三棱锥P —ABC 中,P A ⊥底面ABC ,P A =AB ,∠BCA=90°.点D ,E 分别在棱PB ,PC 上,且DE ∥BC .(1)求证:BC ⊥平面P AC ;(2)是否存在点E 使得二面角A —DE —P 为直二面角?并说明理由.证明:(1)∵P A ⊥底面ABC ,∴P A ⊥BC .又∠BCA =90°,∴AC ⊥BC .又P A ∩AC =A ,∴BC ⊥平面P AC .(2)存在点E 使得二面角A —DE —P 为直二面角.由(1)知BC ⊥平面P AC ,又∵DE ∥BC ,∴DE ⊥平面P AC .又∵AE 平面P AC ,PE 平面P AC ,∴DE ⊥AE ,DE ⊥PE .∴∠AEP 为二面角A —DE —P 的平面角.又∵P A ⊥底面ABC ,∴P A ⊥AC .∴∠P AC =90°.∴在棱PC 上存在一点E ,使得AE ⊥PC .这时,∠AEP =90°.故存在点E 使得二面角A —DE —P 是直二面角.变式训练3:如图所示,P A ⊥平面ABC ,AC ⊥BC ,AB =2,BC =2,PB =6,求二面角P —BC —A 的大小.解:∵P A ⊥平面ABC ,BC 平面ABC ,∴P A ⊥BC .又AC ⊥BC ,P A ∩AC =A ,∴BC ⊥平面P AC .又PC 平面P AC ,∴BC ⊥PC .又BC ⊥AC ,∴∠PCA 为二面角P —BC —A 的平面角.在Rt △PBC 中,∵PB =6,BC =2,∴PC =2.在Rt △ABC 中,∵AB =2,BC =2,∴AC = 2.∴在Rt △P AC 中,cos ∠PCA =22,∴∠PCA=45°,即二面角P —BC —A 的大小为45°.题型四:线面垂直性质定理的应用例4:如图,在正方体ABCD -A 1B 1C 1D 1中,点E 、F 分别在A 1D 、AC 上,且EF ⊥A 1D ,EF ⊥AC .求证:EF ∥BD 1.证明:如图所示,连接AB 1、B 1C 、BD .∵DD 1⊥平面ABCD ,AC 平面ABCD .∴DD 1⊥AC .又∵AC ⊥BD ,且BD ∩DD 1=D ,∴AC ⊥平面BDD 1. ∵BD 1平面BDD 1,∴BD 1⊥AC .同理可证BD 1⊥B 1C .∴BD 1⊥平面AB 1C .∵EF ⊥A 1D ,A 1D ∥B 1C ,∴EF ⊥B 1C .又EF ⊥AC ,且AC ∩B 1C =C ,∴EF ⊥平面AB 1C ,∴EF ∥BD 1.变式训练3:如图,在正方体ABCD -A 1B 1C 1D 1中,点E 、F 分别在A 1D 、AC上,且EF ⊥A 1D ,EF ⊥AC .若G 是AB 的中点,则E 在A 1D 上什么位置时,能使EG ⊥平面AB1C?解:若EG⊥平面AB1C,因为BD1⊥平面AB1C,所以EG∥BD1.因为G为AB的中点,所以E为AD1的中点,即E为A1D的中点时,EG⊥平面AB1C.题型五:面面垂直性质定理的应用例5:已知平面P AB⊥平面ABC,平面P AC⊥平面ABC,求证:P A⊥平面ABC.证明:如图所示,在BC上任取一点D,作DF⊥AC于F,DG⊥AB于G,∵平面P AC⊥平面ABC,且平面P AC∩平面ABC=AC,∴DF⊥平面P AC,又∵P A平面P AC,∴DF⊥P A,同理DG⊥P A,又∵DF∩DG=D且DF平面ABC,DG平面ABC,∴P A⊥平面ABC.变式训练5:如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=22,M为BC的中点.求证:AM⊥PM.证明:如图连接AP.矩形ABCD中,AD⊥DC,BC⊥DC,又∵平面PDC⊥平面ABCD,平面PDC∩平面ABCD=DC,∴AD⊥平面PDC,BC⊥平面PDC,又∵PD平面PDC,PC平面PDC,∴AD⊥PD,BC⊥PC,在Rt△P AD和Rt△PMC中,易知AP2=AD2+PD2=(22)2+22=12,PM2=PC2+MC2=22+(2)2=6,又∵Rt△ABM中,AM2=AB2+BM2=22+(22)2=6,∴AP2=PM2+AM2,∴AM⊥PM.题型六:垂直关系的综合应用例6:如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,F A=FE,∠AEF=45°.(1)求证:EF⊥平面BCE;(2)设线段CD、AE的中点分别为P,M,求证:PM∥平面BCE.证明:(1)因为平面ABEF⊥平面ABCD,BC平面ABCD,BC⊥AB,平面ABEF∩平面ABCD =AB,所以BC⊥平面ABEF.所以BC⊥EF.因为△ABE为等腰直角三角形,AB=AE,所以∠AEB=45°.又因为∠AEF =45°,所以∠FEB =90°,即EF ⊥BE .因为BC 平面BCE ,BE 平面BCE ,BC ∩BE =B ,所以EF ⊥平面BCE .(2)取BE 的中点N ,连接CN ,MN ,则MN 綊12AB 綊PC ,所以PMNC 为平行四边形.所以PM ∥CN . 因为CN 在平面BCE 内,PM 不在平面BCE 内,所以PM ∥平面BCE .变式训练6:如图,四棱锥S -ABCD 中,SD ⊥平面ABCD ,AB ∥DC ,AD ⊥DC ,AB =AD=1,SD =2,BC ⊥BD ,E 为棱SB 上的一点,平面EDC ⊥平面SBC .(1)证明:DE ⊥平面SBC ;(2)证明:SE =2EB .证明:(1)连接BD ,∵SD ⊥平面ABCD ,故BC ⊥SD ,又∵BC ⊥BD ,BD ∩SD =D ,∴BC ⊥平面BDS ,∴BC ⊥DE . 作BK ⊥EC ,K 为垂足,因平面EDC⊥平面SBC ,故BK ⊥平面EDC ,BK ⊥DE . 又∵BK 平面SBC ,BC 平面SBC ,BK ∩BC =B ,∴DE ⊥平面SBC .(2)由(1)知DE ⊥SB ,DB =2AD = 2.∴SB =SD 2+DB 2=6,DE =SD ·DB SB =233,EB =DB 2-DE 2=63,SE =SB -EB =263,∴SE =2EB . 三.方法规律总结1.线面垂直的判定定理是证明线面垂直的主要方法,证明的关键是在平面内找到两条相交直线与已知直线垂直.2.在证明面面垂直时,一般方法是从一个平面内寻找另一个平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决(所作辅助线要有利于题目的证明),即由线面垂直证面面垂直.3.空间中线线、线面、面面之间的垂直关系可以相互转化,其转化关系如下:4.会用线面垂直的性质定理证明平行问题,用面面垂直的性质定理证明垂直问题.四:课后练习作业一、选择题1.设l、m为不同的直线,α为平面,且l⊥α,下列为假命题的是(B) A.若m⊥α,则m∥l B.若m⊥l,则m∥αC.若m∥α,则m⊥l D.若m∥l,则m⊥α【解析】A中,若l⊥α,m⊥α,则m∥l,所以A正确;B中,若l⊥α,m⊥l,则m∥α或mα,所以B错误;C中,若l⊥α,m∥α,则m⊥l,所以C正确;若l⊥α,m∥l,则m⊥α,所以D正确.2.在正方体ABCD—A1B1C1D1中,与AD1垂直的平面是(A)A.平面A1DCB1 B.平面DD1C1C C.平面A1B1C1D1D.平面A1DB【解析】连接A1D、B1C,由ABCD—A1B1C1D1为正方体可知,AD1⊥A1B1,AD1⊥A1D.故AD1⊥平面A1DCB1.3.如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是(C)A.BC∥平面PDF B.DF⊥平面P AEC.平面PDF⊥平面ABC D.平面P AE⊥平面ABC【解析】由题意知BC∥DF,且BC⊥PE,BC⊥AE.∵PE∩AE=E,∴BC⊥平面P AE,∴BC∥平面PDF成立,DF⊥平面P AE成立,平面P AE⊥平面ABC也成立.4.设α、β是两个不同的平面,l是一条直线,以下命题正确的是(C) A.若l⊥α,α⊥β,则lβB.若l∥α,α∥β,则lβC.若l⊥α,α∥β,则l⊥βD.若l∥α,α⊥β,则l⊥β【解析】A错,可能l∥β;B错,可能l∥β;C正确;D错,不一定l⊥β.5.设平面α⊥平面β,且α∩β=l,直线aα,直线bβ,且a不与l垂直,b不与l垂直,那么a与b (B)A.可能垂直,不可能平行B.可能平行,不可能垂直C.可能垂直,也可能平行D.不可能垂直,也不可能平行【解析】当a,b都平行于l时,a与b平行,假设a与b垂直,如图所示,由于b与l不垂直,在b上任取一点A,过点A作b′⊥l,∵平面α⊥平面β,∴b′⊥平面α,从而b′⊥a,又由假设a⊥b易知a⊥平面β,从而a⊥l,这与已知a不与l垂直矛盾,∴假设不正确,a与b不可能垂直.6.空间四边形ABCD,若AB、AC、AD与平面BCD所成角相等,则A点在平面BCD的射影是△BCD的(A)A.外心B.内心C.重心D.垂心【解析】设A点在平面BCD内的射影为O.可知,△OAB≌△OAC≌△OAD.∴OB=OC=OD,∴点O为外心.7.下列说法中正确命题的个数为(B)①如果直线l与平面α内的无数条直线垂直,则l⊥α;②如果直线l不垂直于α,则α内没有与l垂直的直线;③如果一条直线与平面内的一条直线垂直,则该直线与此平面必相交;④如果一条直线和平面的一条垂线垂直,该直线必在这个平面内;⑤如果一条直线和一个平面垂直,该直线垂直于平面内的任一直线.A.0B.1C.2D.3【解析】如图(1)所示,l与α相交(不垂直),此时也有无数条直线与l垂直.故①②错误;如图(2)所示,l与α平行,此时平面内也存在无数条直线与l垂直,故③④错误;如图(3)所示,直线l与平面α的垂线m垂直,但l不在平面α内;由线面垂直的定义可知,⑤正确.8.如图,在正方形ABCD中,E、F分别为边BC,CD的中点,H是EF的中点,现沿AE、AF,EF把这个正方形折成一个几何体,使B、C、D三点重合于点G,则下列结论中成立的是(A)A.AG⊥平面EFG B.AH⊥平面EFGC.GF⊥平面AEF D.GH⊥平面AEF【解析】∵AG⊥GF,AG⊥GE,GF∩GE=G,∴AG⊥平面EFG.9.如图,在四边形ABCD中,AD∥BC,AB=AD,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列命题正确的是(B)A.平面ADC⊥平面BDCB.平面ABD⊥平面ABCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC【解析】在图①中,∵∠BAD=90°,AD=AB,∴∠ADB=∠ABD=45°.∵AD∥BC,∴∠DBC=45°.又∵∠BCD=45°.∴∠BDC=90°,即BD⊥CD.在图②中,此关系仍成立.∵平面ABD⊥平面BCD,∴CD⊥平面ABD.∵BA平面ADB,∴CD⊥AB.∵BA⊥AD,∴BA⊥平面ACD.∵BA平面ABC,∴平面ABC⊥平面ACD.10.如图,在正方体ABCD—A1B1C1D1中,点P在侧面BCC1B1上运动,并且总保持AP⊥BD1,则动点P在(A)A.线段B1C上B.线段BC1上C.BB1中点与CC1中点的连线上D.B1C1中点与BC中点的连线上【解析】连接AC,B1C,AB1,由线面垂直的判定可知BD1⊥平面AB1C.若AP平面AB1C,则AP⊥BD1.这样只要P在B1C上移动即可.二、填空题11.如图,在正方体ABCD—A1B1C1D1中,平面ACD1与平面BB1D1D的位置关系是________.垂直D⊥平面ABCD,AC平面【解析】∵ABCD是正方形,∴AC⊥BD.又∵DABCD,∴D1D⊥AC.∵D1D∩DB=D,∴AC⊥平面BB1D1D.∵AC平面ACD1,∴平面ACD1⊥平面BB1D1D.12.如图所示,已知P A⊥平面α,PB⊥平面β,垂足分别为A、B,α∩β=l,∠APB=50°,则二面角α-l-β的大小为________.130°【解析】如图,设平面P AB∩l=O,连接AO,BO,AB,∵P A⊥α,lα,∴P A⊥l.同理PB⊥l,而PB∩P A=P,∴l⊥平面P AB,∴l⊥AO,l⊥BO,∴∠AOB即为二面角α-l-β的平面角.结合图形知∠AOB+∠APB=180°,∴∠AOB=130°.13.如图,已知平面α⊥平面β,在α与β的交线l上,取线段AB=4,AC、BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=3 cm,BD=12 cm,则CD=______.13 cm【解析】连接BC.因为平面α⊥平面β,且α∩β=l,又因为BD平面β,且BD⊥l,所以BD⊥平面α.又∵BC平面α,∴BC⊥BD.所以△CBD也是直角三角形.在Rt △BAC 中,BC =32+42=5.在Rt △CBD 中,CD =52+122=13.所以CD 长为13 cm.14.α,β是两个不同的平面,m ,n 是平面α与β之外的两条不同直线,给出四个论断:①m ⊥n ;②α⊥β;③n ⊥β;④m ⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________.若①③④,则②(或若②③④,则①)【解析】利用面面垂直的判定,可知①③④⇒②为真;利用面面垂直的性质,可知②③④⇒①为真.15.如图平面ABC ⊥平面BDC ,∠BAC =∠BDC =90°,且AB =AC =a ,则AD =_______a【解析】如图所示,取BC 的中点E ,连接ED ,AE ,∵AB =AC ,∴AE ⊥BC ,∵平面ABC ⊥平面BDC .∴AE ⊥平面BDC ,∴AE ⊥ED .在Rt △ABC 和Rt △BCD 中,AE =ED =12BC =22a ,∴在Rt △AED 中,AD =AE 2+ED 2=a .三、解答题16.如图所示,AB 是圆O 的直径,P A 垂直于圆O 所在的平面,M 是圆周上任意一点,AN ⊥PM ,垂足为N .求证:AN ⊥平面PBM .证明:设圆O 所在的平面为α,∵P A ⊥α,且BM α,∴P A ⊥BM .又∵AB 为⊙O 的直径,点M 为圆周上一点,∴AM ⊥BM ,∵直线P A ∩AM =A ,∴BM ⊥平面P AM .又AN 平面P AM ,∴BM ⊥AN .这样,AN 与PM ,BM 两条相交直线垂直.故AN ⊥平面PBM .17.如图所示,过S 引三条长度相等但不共面的线段SA ,SB ,SC 且∠ASB =∠ASC =60°,∠BSC =90°.求证:平面ABC ⊥平面BSC .【证明】(法一)取BC 的中点D ,连接AD ,SD .∵∠ASB =∠ASC ,且SA =SB=AC ,∴AS =AB =AC .∴AD ⊥BC .又△ABS 是正三角形,△BSC 为等腰直角三角形,∴BD =SD .∴AD 2+SD 2=AD 2+BD 2=AB 2=AS 2.由勾股定理的逆定理,知AD ⊥SD .又∵SD ∩BC =D ,∴AD⊥平面BSC .又AD 平面ABC ,∴平面ABC ⊥平面BSC .(法二)同法一证得AD ⊥BC ,SD ⊥BC ,则∠ADS 即为二面角A —BC —S 的平面角.∵∠BSC =90°,令SA =1,则SD =22,AD =22,∴SD 2+AD 2=SA 2.∴∠ADS =90°.∴平面ABC ⊥平面BSC .18.如图,在三棱锥S -ABC 中,SA ⊥平面ABC ,AB ⊥BC ,DE 垂直平分SC ,分别交AC 、SC 于D 、E ,且SA =AB =a ,BC =2a .(1)求证:SC ⊥平面BDE ;(2)求平面BDE 与平面BDC 所成二面角的大小.(1)证明:∵SA ⊥平面ABC ,又AB 、AC 、BD 平面ABC ,∴SA ⊥AB ,SA ⊥AC ,SA ⊥BD ,∴SB =SA 2+AB 2=2a .∵BC =2a ,∴SB =BC .∵E 为SC 的中点,∴BE ⊥SC .又DE ⊥SC ,BE ∩DE =E ,∴SC ⊥平面BDE .(2)由(1)及BD 平面BDE ,得BD ⊥SC .又知BD ⊥SA ,∴BD ⊥平面SAC .∴BD ⊥AC 且BD ⊥DE .∴∠CDE 为平面BDE 与平面BDC 所成二面角的平面角.∵AB ⊥BC ,AC =AB 2+BC 2=3a .∴Rt △SAC中,tan ∠SCA =SA AC =33,∴∠SCA =30°.∴∠CDE =60°,即平面BDE 与平面BDC 所成二面角为60°.19.如图,已知三棱锥A BPC -中,AP PC ⊥,AC BC ⊥,M为AB 中点,D 为PB 中点,且PMB ∆为正三角形.(1)求证:DM APC ∥平面;(2)求证:ABC APC ⊥平面平面.证明:(1)∵M 为AB 中点,D 为PB 中点,∴MD //AP ,又MD不在平面APC 上,∴MD //平面APC.(2)∵△PMB 为正三角形,又D 为PB 中点. ∴MD ⊥PB .又由(1)知MD //A P , ∴AP ⊥PB . 又AP ⊥PC , 且PB ∩PC =P ,∴AP ⊥平面PBC , ∴AP ⊥BC , 又∵AC ⊥BC , 且AP ∩AC =A ∴BC ⊥平面APC , 又BC 在平面ABC 内,∴平面ABC ⊥平面APC .20.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M 是AB 上一点,N 是A 1C 的中 点,MN ⊥平面A 1DC .求证:(1)MN ∥AD 1;(2)M 是AB 的中点.证明:(1)∵ADD 1A 1为正方形,∴AD 1⊥A 1D .又∵CD ⊥平面ADD 1A 1,AD 1平面ADD 1A 1,∴CD ⊥AD 1.∵A 1D ∩CD =D ,∴AD 1⊥平面A 1DC .又∵MN ⊥平面A 1DC ,∴MN ∥AD 1. MD B P C A(2)连接ON ,在△A 1DC 中,A 1O =OD ,A 1N =NC .∴ON 綊12CD 綊12AB ,∴ON ∥AM .又∵MN ∥OA ,∴四边形AMNO 为平行四边形,∴ON =AM .∵ON =12AB ,∴AM =12AB ,∴M 是AB 的中点. 21.如图所示,P 是四边形ABCD 所在平面外一点,ABCD 是∠DAB =60°且边长为a 的菱形,侧面P AD 为正三角形,其所在平面垂直于底面ABCD .(1)若G 为AD 边的中点,求证:BG ⊥平面P AD ;(2)求证:AD ⊥PB .证明:(1)连接PG ,BD .由题知△P AD 为正三角形,G 是AD 的中点,∴PG ⊥AD .又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,PG 平面P AD ,∴PG ⊥平面ABCD ,∴PG ⊥BG .又∵四边形ABCD 是菱形且∠DAB =60°,∴△ABD 是正三角形,∴BG ⊥AD .又AD 平面P AD ,PG 平面P AD ,且AD ∩PG =G ,∴BG ⊥平面P AD .(2)由(1)可知BG ⊥AD ,PG ⊥AD .又BG 平面PBG ,PG 平面PBG ,且BG ∩PG =G ,AD ⊥平面PBG ,∴AD ⊥PB .。
平面垂直的判定及其性质

立体几何综合复习一、直线与平面垂直1.定义如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直.记作:l⊥α.2.直线与平面垂直的判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.简记为:线线垂直⇒线面垂直数学描述:l⊥a,l⊥b,a⊂α,b⊂α,a b P=⇒l⊥α3.直线与平面垂直的性质定理垂直于同一个平面的两条直线平行.简记为:线面垂直⇒线线平行数学描述:abαα⊥⎫⎬⊥⎭⇒a b∥4.直线与平面所成的角(1)定义:一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点叫做斜足.过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的锐角..,叫做这条直线和这个平面所成的角.(2)规定:一条直线垂直于平面,我们说它们所成的角等于90;一条直线和平面平行,或在平面内,我们说它们所成的角等于0.因此,直线与平面所成的角.........α.的范围是....π[0,]2.5.常用结论(熟记)(1)若两条平行线中一条垂直于一个平面,则另一条也垂直于这个平面.(2)若一条直线垂直于一个平面,则这条直线垂直于这个平面内任何一条直线.(3)过空间任一点有且只有一条直线与已知平面垂直.(4)过空间任一点有且只有一个平面与已知直线垂直.二、平面与平面垂直1.定义两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.平面α与平面β垂直,记作αβ⊥.2.平面与平面垂直的判定定理文字语言一个平面过另一个平面的垂线,则这两个平面垂直.简记为:线面垂直⇒面面垂直图形语言符号语言l⊥α,lβ⊂⇒α⊥β作用判断两平面垂直3.平面与平面垂直的性质定理文字语言两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.简记为:面面垂直⇒线线平行图形语言=laaa lαβαββα⎫⎪⎪⇒⎬⊂⎪⎪⊥⎭⊥⊥4.二面角(1)二面角的定义:平面内的一条直线把平面分成两部分,这两部分通常称为半平面.从一条直线出发的两个半平面所组成的图形叫做二面角....这条直线叫做二面角的棱,这两个半平面叫做二面角的面.(2)二面角的平面角的定义:在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的射线,则这两条射线构成的角叫做这个二面角的平面角.(3)二面角的范围:[0,π].三、垂直问题的转化关系考向一线面垂直的判定与性质典例1如图所示,和都是以为直角顶点的等腰直角三角形,且,下列说法中错误的是A.平面B.平面C.平面D.平面1.如图,在棱长为1的正方体1111ABCD A B C D -中,点E 、F 分别是棱BC 、1CC 的中点,P 是底面ABCD 上(含边界)一动点,且满足1A P EF ⊥,则线段1A P 长度的取值范围是A .51,⎡⎤⎢⎥⎣⎦B .53,2⎡⎤⎢⎥⎣⎦C .1,3⎡⎤⎣⎦D .2,3⎡⎤⎣⎦典例2 如图,在三棱柱中,各个侧面均是边长为的正方形,为线段的中点.()求证:平面; ()求证:直线平面;2.如图1所示,在Rt ABC △中,∠C =90°,D ,E 分别为AC ,AB 的中点,点F 为线段CD 上的一点,将ADE △沿DE 折起到1A DE △的位置,使A 1F ⊥CD ,如图2所示.(1)求证:1A F BE ⊥;(2)线段1A B 上是否存在点Q ,使1A C ⊥平面DEQ ?说明理由.考向二面面垂直的判定与性质判定面面垂直的常见策略:(1)利用定义(直二面角).(2)判定定理:可以通过直线与平面垂直来证明平面与平面垂直.(3)在运用面面垂直的性质定理时,若没有与交线垂直的直线,则一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线,这样就把面面垂直转化为线面垂直,进而转化为线线垂直.典例4 如图,直三棱柱中,分别是的中点,.(1)证明:平面;(2)证明:平面平面.考向三 线面角与二面角求直线与平面所成的角的方法: (1)求直线和平面所成角的步骤: ①寻找过斜线上一点与平面垂直的直线;②连接垂足和斜足得到斜线在平面上的射影,斜线与其射影所成的锐角或直角即为所求的角; ③把该角归结在某个三角形中,通过解三角形,求出该角. (2)求线面角的技巧:在上述步骤中,其中作角是关键,而确定斜线在平面内的射影是作角的关键,几何图形的特征是找射影的依据,射影一般都是一些特殊的点,比如中心、垂心、重心等. 求二面角大小的步骤:简称为“一作二证三求”.作平面角时,一定要注意顶点的选择.典例5 正三棱柱111ABC A B C 的所有棱长都相等,D 是11A C 的中点,则直线AD 与平面1B DC 所成角的正弦值为 A .35 B .45 C .34D .55典例6 如图,直三棱柱111ABC A B C -的底面是边长为2的正三角形,,E F 分别是1,BC CC 的中点. (1)证明:平面AEF ⊥平面11B BCC ;(2)若直线1A C 与平面11A ABB 所成的角为45°,求三棱锥F AEC -的体积.4.如图,四边形为矩形,四边形为直角梯形,.(1)求证:; (2)求证:平面; (3)若二面角的大小为,求直线与平面所成的角.1.下列命题中不正确的是A.如果平面α⊥平面β,且直线l∥平面α,则直线l⊥平面βB.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βC.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βD.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ2.设a,b,c表示三条直线,α,β表示两个平面,则下列命题中不正确的是A.ccαβαβ⊥⎫⇒⊥⎬⎭∥B.a bb b cc aββ⊥⎫⎪⊂⇒⊥⎬⎪⎭是在内的射影C.b cb ccααα⎫⎪⊂⇒⎬⎪⊄⎭∥∥D.abb aαα⎫⇒⊥⎬⊥⎭∥3.如图,在三棱锥中,⊥底面,,则直线与平面所成角的大小为A .B .C .D .4.如图,三条相交于点P的线段P A,PB,PC两两垂直,P在平面ABC外,PH⊥平面ABC于H,则垂足H是△ABC的A.外心B.内心C.垂心D.重心5.如图,A,B,C,D为空间四点,在△ABC中,AB=2,AC=BC=,等边三角形ADB以AB为轴旋转,当平面ADB⊥平面ABC时,CD=A.B.2C.D.16.如图,已知六棱锥P-ABCDEF的底面是正六边形,P A⊥平面ABC,P A=2AB,则下列结论正确的是A.PB⊥AD B.平面PAB⊥平面PBCC.直线BC∥平面PAE D.直线PD与平面ABC所成的角为45°7.《九章算术》卷五《商功》中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何?问题中“刍甍”指的是底面为矩形的屋脊状的几何体,如图1,该几何体可由图2中的八边形沿,向上折起,使得与重合而成,设网格纸上每个小正方形的边长为1,则此“刍甍”中与平面所成角的正弦值为A.B.C.D.8.如图,在矩形ABCD中,AB=2,AD=3,点E为AD的中点,现分别沿BE,CE将△ABE,△DCE翻折,使得点A,D 重合于点F,此时二面角E-BC-F的余弦值为(1)(2)A.34B.7C.23D.59.已知α,β是平面,m、n是直线,给出下列命题:①若m⊥α,m⊂β,则α⊥β;②若m⊂α,n⊂α,m∥β,n∥β,则α∥β;③如果m⊂α,n⊄α,m,n是异面直线,那么n与α相交;④若α∩β=m,n∥m,且n⊄α,n⊄β,则n∥α且n∥β.其中命题正确的是__________.10.如图,三棱锥,平面平面,若,则△的形状为__________.11.在四面体中,平面,,,,,为棱上一点,且平面平面,则__________.12.如图,在三棱锥P-ABC中,P A⊥底面ABC,∠BAC=90°,F是AC的中点,E是PC上的点,且EF⊥BC,则PEEC________.中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当13.如图所示,在四棱锥P ABCDDM⊥________时,平面MBD⊥平面PCD.14.四棱锥中,,且平面是棱的中点.(1)证明:平面;(2)求三棱锥的体积.。
2.3.1.1线面垂直的判定定理

C线线垂直Fra bibliotek线面垂直的定义 线面垂直的判定定理
线面垂直
例2:已知PA 平面ABC,AB是圆O的直径,C是圆周上的一点 求证:BC 平面PAC
证明: PA 平面ABC, BC 平面ABC PA BC AB是圆O的直径,
BC AC
又 PA AC A, PA 平面PAC, AC 平面PAC
线线垂直
线面垂直
3.数学思想方法:转化的思想 空间问题
平面问题
今日作业
课本P67练习1,
zxxk
课本P74 B组 第2题.
C1 C
CC1
A
D
检查自学效果:
3.直线与平面垂直的判定定理:
文字语言
一条直线和一个平面内的两条相交直线 都垂直,则这条直线垂直于这个平面.
“线线垂直,则线面垂直”
符号语言
m n mn P l l m l n
图形语言
l
m O
α
n
例题示范,巩固新知
的问题
自学导引:
自学课本64—65 页 思考: (时间5分钟)
1. 直线与平面垂直的定义是什么?如何表示? 2. 若直线与平面垂直,则该直线与平面内的直线 有何位置关系? 3. 线面垂直的判定定理.
检查自学效果:
1.直线与平面垂直的定义: 如果直线 l 与平面 内的任意一条直线都 垂直,则称 直线 l 和平面 互相垂直. 记作: l⊥ 平面α
探究活动:请同学们拿出一块
zxxk
A A1
A1
三角形的纸片,做如图所示的 试验: D B 过△ABC的顶点A翻折纸片, B D1 B1 D 1 B 1 D C 得到折痕AD,将翻折后的纸片 A1 竖起放置在桌面上(BD、DC与 C1 桌面接触). (1)折痕AD与桌面垂直吗? D1 (2)如何翻折才能保证折痕AD B1 B 与桌面所在平面肯定垂直?
直线、平面垂直的判定及其性质

2.3 直线、平面垂直的判定及其性质线面垂直→线线垂直:如果一条直线a与一个平面α内的任意一条直线都垂直,我们就说直线a垂直于平面α。
【线面垂直定义】线线垂直→线面垂直:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面。
【判定】线面垂直→线线平行:如果两条直线同时垂直于一个平面,那么这两条直线平行。
【性质】线面垂直→面面垂直:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
【判定】面面垂直→线面垂直:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
【性质】三垂线定理:在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
一、选择题1.给定空间中的直线l及平面α,条件“直线l与平面α内两条相交直线都垂直”是“直线l与平面α垂直”的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分又不必要条件【解析】直线l与平面α内两条相交直线都垂直,是线面垂直判定定理的条件,故为充要条件.【答案】 C2.空间四边形ABCD中,若AB=BC,AD=CD,E为对角线AC的中点,下列判断正确的是( ) A.面ABD⊥面BDC B.面ABC⊥面ABDC.面ABC⊥面ADC D.面ABC⊥面BED【解析】在等腰三角形ABC、ADC中,E为底边AC的中点,则BE⊥AC,DE⊥AC.又∵BE∩DE=E,∴AC⊥面BDE,故面ABC⊥面BDE,面ADC⊥面BDE.【答案】 D3.对两条不相交的空间直线a和b,必定存在平面α,使得 ( )A.a⊂α,b⊂α B.a⊂α,b∥αC.a⊥α,b⊥α D.a⊂α,b⊥α【解析】当a,b异面时,A不成立;当a,b不平行时,C不成立;当a,b不垂直时,D不成立.故选B.【答案】 B4.设直线m与平面α相交但不垂直,则下列说法中正确的是( )A.在平面α内有且只有一条直线与直线m垂直B.过直线m有且只有一个平面与平面α垂直C.与直线m垂直的直线不可能与平面α平行D.与直线m平行的平面不可能与平面α垂直【解析】在平面α内有无数条彼此平行的直线与直线m垂直,与直线m垂直的直线可能与平面α平行,与直线m平行的平面可能与平面α垂直.故A,C,D错误.【答案】 B5.设a,b,c是空间三条直线,α,β是空间两个平面,则下列命题中,逆命题不成立...的是( )A.当c⊥α时,若c⊥β,则α∥βB.当b⊂α,且c是a在α内的射影时,若b⊥c,则a⊥bC.当b⊂α时,若b⊥β,则α⊥βD.当b⊂α,且c⊄α时,若c∥α,则b∥c【解析】α⊥β,b⊂α,b不一定垂直于β.故C错误.【答案】 C6.命题p:若平面α⊥β,平面β⊥γ,则必有α∥γ;命题q:若平面α上不共线的三点到平面β的距离相等,则必有α∥β.对以上两个命题,下列结论中正确的是( ) A.命题“p且q”为真 B.命题“p或綈q”为假C.命题“p或q”为假 D.命题“綈p且綈q”为假【解析】命题p,命题q皆为假,所以命题C正确.【答案】 C7.如图,已知△ABC 为直角三角形,其中∠ACB =90°,M 为AB 的中点,PM 垂直于△ABC 所在的平面,那么( )A .PA =PB >PCB .PA =PB <PCC .PA =PB =PCD .PA ≠PB ≠PC【解析】 ∵M 为AB 的中点,△ACB 为直角三角形,∴BM =AM =CM ,又PM ⊥平面ABC ,∴Rt △PMB ≌Rt △PMA ≌Rt △PMC ,故PA =PB =PC .【答案】 C二、填空题8.m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:①若α∥β,α∥γ,则β∥γ;②若α⊥β,m ∥α,则m ⊥β;③若m ⊥α,m ∥β,则α⊥β;④若m ∥n ,n ⊂α,则m ∥α.其中真命题的序号是________.【解析】 由平面平行的传递性知①正确,由面面垂直的判定定理知③正确.【答案】 ①③9.P 为△ABC 所在平面外一点,AC =2a ,连接PA 、PB 、PC ,得△PAB 和△PBC 都是边长为a 的等边三角形,则平面ABC 和平面PAC 的位置关系为________.【解析】如图所示,由题意知PA =PB =PC =AB =BC =a ,取AC 中点D ,连接PD 、BD ,则PD ⊥AC ,BD ⊥AC ,则∠BDP 为二面角P -AC -B 的平面角,又∵AC =2a ,∴PD =BD =22a , 在△PBD 中,PB 2=BD 2+PD 2,∴∠PDB =90°.【答案】 垂直10.(精选考题·四川高考)如图所示,二面角α-l -β的大小是60°,线段AB ⊂α,B ∈l ,AB 与l 所成的角为30°,则AB 与平面β所成的角的正弦值是________________________________________________________________________.【解析】 如图,过点A 作平面β的垂线,垂足为C ,在β内过C 作l 的垂线,垂足为D ,连接AD ,由线面垂直关系可知AD ⊥l ,故∠ADC 为二面角α-l -β的平面角,∴∠ADC =60°.连接CB ,则∠ABC 为AB 与平面β所成的角.设AD =2,则AC =3,CD =1,AB =AD sin30°=4,∴sin ∠ABC =AC AB =34. 【答案】34 三、解答题11.如图所示,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60°,PA =AB =BC ,E 是PC 的中点.求证:(1)CD ⊥AE ;(2)PD ⊥平面ABE .【证明】 (1)在四棱锥P -ABCD 中,∵PA ⊥底面ABCD ,CD ⊂平面ABCD ,∴PA ⊥CD .∵AC ⊥CD ,PA ∩AC =A ,∴CD ⊥平面PAC .而AE ⊂平面PAC ,∴CD ⊥AE .(2)由PA =AB =BC, ∠ABC =60°,可得AC =PA .∵E 是PC 的中点,∴AE ⊥PC .由(1)知,AE ⊥CD ,且PC ∩CD =C ,∴AE ⊥平面PCD ,而PD ⊂平面PCD ,∴AE ⊥PD .∵PA ⊥底面ABCD ,∴PA ⊥AB .又∵AB ⊥AD 且PA ∩AD =A ,∴AB ⊥平面PAD ,而PD ⊂平面PAD ,∴AB ⊥PD .又∵AB ∩AE =A ,∴PD ⊥平面ABE .12.如图,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,PD =DC =BC =1,AB =2,AB ∥DC ,∠BCD =90°.(1)求证:PC ⊥BC ;(2)求点A 到平面PBC 的距离.【解析】 (1)证明:∵PD ⊥平面ABCD ,BC ⊂平面ABCD ,∴PD ⊥BC .由∠BCD =90°,得BC ⊥DC .又PD ∩DC =D ,∴BC ⊥平面PCD .∵PC ⊂平面PCD ,∴PC ⊥BC .(2)如图,连接AC .设点A 到平面PBC 的距离为h .∵AB ∥DC ,∠BCD =90°,∴∠ABC =90°.从而由AB =2,BC =1,得△ABC 的面积S △ABC =1.由PD ⊥平面ABCD 及PD =1,得三棱锥P -ABC 的体积V =13S △ABC ·PD =13.∵PD ⊥平面ABCD ,DC ⊂平面ABCD ,∴PD ⊥DC .又PD =DC =1,∴PC =PD 2+DC 2= 2.由PC ⊥BC ,BC =1,得△PBC 的面积S △PBC =22.由V =13S △PBC h =13×22h =13,得h = 2.因此点A 到平面PBC 的距离为 2.。
231线面垂直的判定定理
在正方体ABCD-A1B1C1D1中, (1)与平面CD1垂直的直线 (2)与直线AA1垂直的平面 (3)与直线AC垂直的平面
A A1
D1 B1
C1
D C B
3、已知:a∥b,a⊥α求证:b⊥α
a
P
b
a m
b
α
m
n
α
两条平行线中一条直线与一个平面垂直,则 另一条直线也与此平面垂直
例1
有一根旗杆AB高8m如图,它的顶端A挂有一条 10m的绳子,拉紧绳子并把它的下端放在地面上 的两点(和旗杆脚不在同一条直线上)C、D。 如果这两点都和旗杆脚B的距离是6m, 那么旗杆就和地面垂直,为什么? 在⊿ABC和⊿ABD中, ∵AB=8m,BC=BD=6m,AC=AD=10m, ∴AB2+BC2=62+82=102=AC2, AB2+BD2=62+82=102=AD2, ∴ ∠ABC= ∠ABD=90o 即AB⊥BC,AB⊥BD 又知B、C、D三点不共线 ∴AB⊥平面BCD
动画演示
二(一)直线和平面垂直的判定定理(1)
如果一条直线和一个平面 内的两条相交直线都垂直,那 猜想: 么这条直线垂直于这个平面。
符号表示?
lm ln m l n m n B
l
m
n
练习、
1、判断正误 (1)若一条直线垂直于平面内的两条直线,则这条直线垂直于这个平面 ( ) (2)若一条直线垂直于平面内的无数条直线,则这条直线垂直于这个平面( )
2.3.1直线与平面垂直的判定
引入
显然它们都是垂直的.AB和桌面 的 位置关系,给我们一种直线和平面垂 直的形象
将书打开放在桌面 上,观察书脊 AB和各页面与桌面 的交线的位置 关系,
2.3.1线面垂直的判定(三课时)
A
C
B
真题演练
4.在正方体ABCD—A1B1C1D1 中,求直线A1B与平 面A1B1CD所成的角 C1 D1 D1 C
A1
Q
1
B1
P
A1 C D
B1 F
C
O
D
1
A
B
A
B
E
1
变式:(1)求直线AC与平面A1B1CD所成的角 (2)E,F分别是BC,CC1的中点,求EF与面ACC1A1所成的角
真题演练
线不在多 相交则行
m
m 符号语言: n m I n=O l m l n
线线垂直 线面垂直
α
O
n
l
长方体中,直线AD与AB、AA1、A1 B1 、 EB、GH分别是什么位置关系?
D1 A1
E G
C1 B1
H
D A B
C
理论依据: 若a , b , 则a b
例题分析
三垂线定理 : 在平面内的一条直线,如果和这个平面的一条斜线在这个平面内 的射影垂直,那么它也和这条斜线垂直;反之,如果和这个平面 的一条斜线垂直,那么它也和这条斜线的射影垂直。
P
斜线 垂线 A
O
斜线在平面上的射影
第2个 空间角 平面的一条斜线和它在平 面内的射影所成的锐角,叫做 这条直线和这个平面所成的角
例1.如图,AB是圆O的直径,PA垂直于圆O所在 的平面α,C是圆周上不同于A,B的任意一点,
求证: BC⊥PC P
C A
O
B
真题演练
练习1.如图,在三棱锥V-ABC中,VA=VC,BA=BC, 求证: VB⊥AC.
V
直线与平面垂直的判定定理
四 中 南 校 杨 英
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
在阳光下直立于地面的 旗杆及它在地面的影子
A
可以观察到,随着时间的变化, 尽管影子BC的位置在移动, 但是旗杆AB所在直线始终与 BC所在直线垂直。也就是说, 旗杆AB所在直线与地面内任 意一条过点B的直线垂直。 B
.
C1
C
事实上,旗杆AB所在直线与地面内任意一条直线垂直
1.线面垂直定义
直线与平面垂直的定义 如果直线a与平面α内的任意一条直线都 垂直,我们就说直线a与平面α互相垂直, 记作:a⊥α.直线a 叫做平面α的垂线,平 面α叫做直线a的垂面.直线与平面垂直时, 它们惟一的公共点P 叫做垂足.
a
m是平面内任一条直线 a α am
如果两条平行 直线中的一条 垂直于一个平 面,那么另一 条也垂直于同 一个平面。
“平面化”是解决立体几何问题的一般思路。
线面垂直的定义 线面垂直的判定理 线线垂直 线面垂直
线面垂直的定义 关键:线不在多 相交则行
五、课时作业:完成课时作业(九)
谢谢合作!
下课了!
2:已知△ABC 在平面α内,直线a与平 面α相交,且 a⊥AC,a⊥BC. 求证:a⊥AB
四:课堂小结:
直线与平面垂直的判定方法
定义:如果一 条直线垂于一 个平面内的任 何一条直线, 则此直线垂直 于这个平面.
判定定理:如果 一条直线垂直于 一个平面内的两 条相交直线,那 么此直线垂直于 这个平面。
线面垂直关系的判定
研一研·问题探究、课堂更高效
6.1
如图,已知 a∥b,a⊥α.求证: b⊥α.
本 课 时 栏 目 开 关
证明 在平面 α 内作两条相交直线 m,n.
因为直线 a⊥α,根据直线与平面垂直的定义知 a⊥m, a⊥n.
又因为 b∥a,所以 b⊥m,b⊥n.
6.1
三角板绕 AC 转动,在转动过程中,直角边 CB 与地面紧贴, 这表明了什么?
答 表明了 AC 与地面垂直.
研一研·问题探究、课堂更高效
问题 3 (1)阳光下直立于地面的旗杆 AB 与它在地面上
6.1
的影子 BC 的位置关系是什么?随着太阳的移 动,旗杆 AB 与影子 BC 所成的角度会发生改 变吗? (2)旗杆 AB 与地面上任意一条不过旗杆底部 B 的直线 B′C′的位置关系又是什么?依据是 什么?由此得到什么结论?
又因为 m α,n
所以 b⊥α.
α,m, n 是两条相交直线,
6.1
小结 (1)如果两条平行直线有一条垂直于平面,那么
另一条直线也垂直于这个平面.
(2)证明线面垂直的一般思路是依据线面垂直的判定定理,寻
找满足定理的条件,当条件满足了,也就证明了线面垂直; 线面垂直的定义说明了直线垂直平面,则直线垂直这个 平面内的任意直线,常用此性质证线线垂直.
竖起放置在桌面上折痕 AD 与桌面不垂直;当 AD 与 BC 垂直时, 翻折后的纸片竖起放置在桌面上折痕 AD 与桌面 垂直.
研一研·问题探究、课堂更高效
问题 3
答
6.1
由 折 痕 AD⊥BC , 翻折 之后 垂直关 系 不变 ,即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线与平面垂直的判定一个人走在灯火通明的大街上,会在地面上形成影子,随着人不停走动,这个影子忽前忽后、忽左忽右,但无论怎样,人始终与影子相交于一点,并始终保持垂直.你承认这个事实吗?为什么?1.直线与平面垂直定义如果直线l与平面α内的__任意一条__直线都垂直,我们就说直线l与平面α互相垂直记法l⊥α有关概念直线l叫做平面α的__垂线__,平面α叫做直线l的___垂面__.它们唯一的公共点P叫做__垂足__.图示画法画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直[归纳总结](1)定义中的“任意一条直线”这一词语与“所有直线”是同义语,与“无数条直线”不是同义语.(2)直线与平面垂直是直线与平面相交的一种特殊形式.(3)由直线与平面垂直的定义,得如果一条直线垂直于一个平面,那么这条直线垂直于该平面内的任意一条直线.2.判定定理文字语言一条直线与一个平面内的两条__相交__直线都垂直,则该直线与此平面垂直图形语言符号语言l⊥a,l⊥b,a⊂α,b⊂α,__a∩b=P__⇒l⊥α作用判断直线与平面垂直[归纳总结]直线与平面垂直的判定定理告诉我们:可以通过直线间的垂直来证明直线与平面垂直.通常我们将其记为“线线垂直,则线面垂直”.因此,处理线面垂直转化为处理线线垂直来解决.也就是说,以后证明一条直线和一个平面垂直,只要在这个平面内找到两条相交直线和已知直线垂直即可.3.直线和平面所成的角(1)定义:一条直线和一个平面相交,但不和这个平面__垂直__,这条直线叫做这个平面的斜线,斜线和平面的__交点__叫做斜足.过斜线上斜足以外的一点向平面引垂线,过__垂足__和__斜足__的直线叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的__锐角__,叫做这条直线和这个平面所成的角.(2)规定:一条直线垂直于平面,我们说它们所成的角等于__90°__;一条直线和平面平行,或在平面内,我们说它们所成的角等于__0°__.因此,直线与平面所成的角的范围是__[0°,90°]__.预习自测1.直线l⊥平面α,直线m⊂α,则l与m不可能(A)A.平行B.相交C.异面D.垂直[解析]∵直线l⊥平面α,∴l与α相交又∵m⊂α,∴l与m相交或异面,由直线与平面垂直的定义,可知l⊥m.故l与m不可能平行.2.直线l与平面α内的无数条直线垂直,则直线l与平面α的关系是(D)A.l和平面α相互平行B.l和平面α相互垂直C.l在平面α内D.不能确定[解析]如下图所示,直线l和平面α相互平行,或直线l和平面α相互垂直或直线l 在平面α内都有可能.故选D.3.(2016~2017·福州高二检测)在△ABC中,AB=AC=5,BC=6,P A⊥平面ABC,P A =8,则P到BC的距离是(D)A. 5 B.2 5C.3 5 D.4 5[解析]取BC的中点D∵AB=AC∴AD⊥BC.又∵P A⊥平面ABC,∴P A⊥BC.又P A∩AD=D∴BC⊥平面P AD,∴BC⊥PD.∵在△ABC中,AB=AC=5,BC=6∴AD=4∴PD=P A2+AD2=45.故选D.命题方向1⇨线面垂直的判定典例1 如图,P为△ABC所在平面外一点,P A⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F.求证:(1)BC⊥平面P AB;(2)AE⊥平面PBC;(3)PC⊥平面AEF.[思路分析]本题是证线面垂直问题,要多观察题目中的一些“垂直”关系,看是否可利用.如看到P A⊥平面ABC,可想到P A⊥AB、P A⊥BC、P A⊥AC,这些垂直关系我们需要哪个呢?我们需要的是P A⊥BC,联系已知,问题得证.[解析](1)∵P A⊥平面ABC,BC⊂平面ABC∴P A⊥BC.∵∠ABC=90°,∴AB⊥BC.又AB∩P A=A,∴BC⊥平面P AB.(2)∵BC⊥平面P AB,AE⊂平面P AB,∴BC⊥AE.∵PB⊥AE,BC∩PB=B∴AE⊥平面PBC.(3)∵AE⊥平面PBC,PC⊂平面PBC∴AE⊥PC.∵AF⊥PC,AE∩AF=A∴PC⊥平面AEF.『规律方法』线面垂直的判定方法:(1)证明线面垂直的方法①线面垂直的定义.②线面垂直的判定定理.③如果两条平行直线的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.④如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.(2)利用直线与平面垂直的判定定理判定直线与平面垂直的步骤:①在这个平面内找两条直线,使它和这条直线垂直;②确定这个平面内的两条直线是相交的直线;③根据判定定理得出结论.(3)利用直线与平面垂直的判定定理判定直线与平面垂直的技巧:证明线面垂直时要注意分析几何图形,寻找隐含的和题目中推导出的线线垂直关系,进而证明线面垂直.三角形全等、等腰三角形底边的中线、高;菱形、正方形的对角线、三角形中的勾股定理的逆定理等都是找线线垂直的方法.〔跟踪练习1〕如图,在△ABC中,∠ABC=90°,D是AC的中点,S是△ABC所在平面外一点,且SA=SB=SC.(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC.[解析](1)因为SA=SC,D是AC的中点所以SD⊥AC.在Rt△ABC中,AD=BD由已知SA=SB,所以△ADS≌△BDS所以SD⊥BD,又AC∩BD=D所以SD⊥平面ABC.(2)因为AB=BC,D为AC的中点所以BD⊥AC,由(1)知SD⊥BD又因为SD ∩AC =D ,所以BD ⊥平面SAC . 命题方向2 ⇨直线与平面所成的角 典例2 在正方体ABCD -A 1B 1C 1D 1中,(1)求直线A 1C 与平面ABCD 所成的角的正切值; (2)求直线A 1B 与平面BDD 1B 1所成的角.[思路分析] (1)求线面角的关键是找出直线在平面内的射影,为此须找出过直线上一点的平面的垂线.(2)中过A 1作平面BDD 1B 1的垂线,该垂线必与B 1D 1、BB 1垂直,由正方体的特性知,直线A 1C 1满足要求.[解析] (1)∵直线A 1A ⊥平面ABCD ,∴∠A 1CA 为直线A 1C 与平面ABCD 所成的角,设A 1A =1,则AC = 2∴tan ∠A 1CA =22. (2)连接A 1C 1交B 1D 1于O ,在正方形A 1B 1C 1D 1中,A 1C 1⊥B 1D 1,∵BB 1⊥平面A 1B 1C 1D 1,A 1C 1⊂平面A 1B 1C 1D 1,∴BB 1⊥A 1C 1又BB 1∩B 1D 1=B 1,∴A 1C 1⊥平面BDD 1B 1,垂足为O . ∴∠A 1BO 为直线A 1B 与平面BDD 1B 1所成的角在Rt △A 1BO 中,A 1O =12A 1C 1=12A 1B ,∴∠A 1BO =30°.即A 1B 与平面BDD 1B 1所成的角为30°.『规律方法』 求线面角的方法:(1)求直线和平面所成角的步骤:①寻找过斜线上一点与平面垂直的直线;②连接垂足和斜足得到斜线在平面上的射影,斜线与其射影所成的锐角或直角即为所求的角;③把该角归结在某个三角形中,通过解三角形,求出该角.(2)求线面角的技巧:在上述步骤中,其中作角是关键,而确定斜线在平面内的射影是作角的关键,几何图形的特征是找射影的依据,射影一般都是一些特殊的点,比如中心、垂心、重心等.〔跟踪练习2〕如图,在三棱柱ΑΒC -A 1B 1C 1中,∠BAC =90°,AB =AC =2,A 1A =4,A 1在底面ABC的射影为BC的中点,D是B1C1的中点.(1)证明:A1D⊥平面A1BC;(2)求直线A1B和平面BB1C1C所成的角的正弦值.[解析](1)取BC的中点E,连接A1E、DE、AE,由题意得A1E⊥平面ABC,所以A1E ⊥AE因为AB=AC,所以AE⊥BC,故AE⊥平面A1BC由D、E分别是B1C1、BC的中点,得DE∥B1B且DE=B1B,所以DE∥A1A所以四边形A1AED是平行四边形,故A1D∥AE又因为AE⊥平面A1BC,所以A1D⊥平面A1BC.(2)作A1F⊥DE,垂足为F,连接BF.因为A1E⊥平面ABC,所以BC⊥A1E.因为BC⊥AE,所以BC⊥平面AA1DE.所以BC⊥A1F,A1F⊥平面BB1C1C.所以∠A1BF为直线A1B与平面BB1C1C所成的角.由AB=AC=2,∠CAB=90°,得EA=EB=2.由∠A1EA=∠A1EB=90°,得A1A=A1B=4,A1E=14.由DE=BB1=4,DA1=EA= 2∠DA1E=90°,得A1F=7 2.所以sin∠A1BF=7 8.易错系列逻辑推理不严密致误典例3 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,D是AB的中点,连接CD.求证:CD⊥平面ABB1A1.[错解]∵AA1⊥平面ABC,CD⊂平面ABC,∴CD⊥AA1.又BB1∥AA1,∴CD⊥BB1又AA1⊂平面ABB1A1,BB1⊂平面ABB1A1∴CD⊥平面ABB1A1.[错因分析]错解中AA1和BB1是平面ABB1A1内的两条平行直线,不是相交直线,故不满足直线与平面垂直的判定定理的条件.[正解]∵AA1⊥平面ABC,CD⊂平面ABC∴CD⊥AA1.又AC=BC,D是AB的中点∴CD⊥AB.∵AB⊂平面ABB1A1,AA1⊂平面ABB1A1AB∩AA1=A∴CD⊥平面ABB1A1.[警示]用判定定理证明线面垂直时,必须要找全条件,这些条件必须是已知的、或明显成立的、或已经证明的.〔跟踪练习3〕如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A2C1=90°,D为BB1的中点.求证:AD⊥平面A1DC1.[错解]在三棱柱中,∵AA1⊥平面ABC,∠B1A1C1=90°∴AD⊥A1C1;又从图可知AD⊥平面BCC1B1∴AD⊥C1D∴AD⊥平面A1DC1.[辨析]前半部分,虽然由罗列条件能够推证出AD⊥A1C1,但推理过程不严密;后半部分AD⊥平面BCC1B1纯属臆想,无任何推理依据.[分析]先推证C1A1⊥平面ABB1A1得出AD⊥C1A1;再在矩形ABB1A1中,通过计算证明AD⊥A1D.[证明]∵AA1⊥底面ABC,平面A1B1C1∥平面ABC∴AA1⊥平面A1B1C1.∴A1C1⊥AA1.又∠B1A1C1=90°,∴A1C1⊥A1B1.而A1B1∩AA1=A∴A1C1⊥平面AA1B1B,AD⊂平面AA1B1B∴A1C1⊥AD.由已知计算得AD=2,A1D=2,AA1=2.∴AD2+A1D2=AA21∴A1D⊥AD.∵A1C1∩A1D=A1∴AD⊥平面A1DC1.1.线线垂直和线面垂直的相互转化典例4 一期末)如图,在棱长均为1的直三棱柱ABC-A1B1C1中,D是BC的中点.(1)求证:AD⊥平面BCC1B1;(2)求直线AC1与平面BCC1B1所成角的正弦值.[解析](1)证明:直三棱柱ABC-A1B1C1中,BB1⊥平面ABC∴BB1⊥AD∵AB=AC,D是BC的中点∴AD⊥BC.又BC∩BB1=B∴AD⊥平面BCC1B1.(2)解:连接C1D.由(1)AD⊥平面BCC1B1则∠AC1D即为直线AC1与平面BCC1B1所成角.在Rt△AC1D中,AD=32,AC1=2,sin∠AC1D=ADAC1=64即直线AC1与平面BCC1B1所成角的正弦值为6 4.〔跟踪练习4〕如图,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE.求证:AE⊥BE.[证明]∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE.又AE⊂平面ABE,∴AE⊥BC.∵BF⊥平面ACE,AE⊂平面ACE,∴AE⊥BF.∵BF⊂平面BCE,BC⊂平面BCE,BF∩BC=B∴AE⊥平面BCE.又BE⊂平面BCE,∴AE⊥BE.2.关于垂直的存在型探索性问题典例5 在矩形ABCD中,AB=1,BC=a,P A⊥平面ABCD,且P A=1,边BC上是否存在点Q,使得PQ⊥QD?为什么?[思路分析]关键是将PQ⊥QD转化为DQ⊥AQ,再使DQ⊥AP即可,但AD=BC=a 是变化的,故需对a进行讨论.[解析]∵P A⊥平面ABCD,∴P A⊥QD.若边BC上存在一点Q,使得QD⊥AQ则有QD ⊥平面P AQ ,从而QD ⊥PQ .在矩形ABCD 中,当AD =a <2时,直线BC 与以AD 为直径的圆相离,故不存在点Q ,使AQ ⊥DQ .∴当a ≥2时,才存在点Q ,使得PQ ⊥QD .[点评] 本题运用平面几何知识,借助以AD 为直径的圆与BC 交点的个数推断点Q 是否存在.课堂检测1.如果一条直线垂直于一个平面内的:①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边. 则能保证该直线与平面垂直( A ) A .①③ B .①② C .②④D .①④[解析] 三角形的两边,圆的两条直径一定是相交直线,而梯形的两边,正六边形的两条边不一定相交,所以保证直线与平面垂直的是①③.2.如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为( D )A .223B .23C .24D .13[解析] ∵AA 1⊥平面A 1B 1C 1D 1∴∠AC 1A 1为直线AC 1与平面A 1B 1C 1D 1所成角 ∵AA 1=1,AB =BC =2,∴AC 1=3 ∴sin ∠AC 1A 1=AA 1AC 1=13.3.如图所示,P A ⊥平面ABC ,△ABC 中BC ⊥AC ,则图中直角三角形的个数有__4__.[解析] ∵P A ⊥平面ABC∴P A ⊥AB ,P A ⊥AC ,P A ⊥BC . ∴△P AB 、△P AC 为直角三角形. ∵BC ⊥AC ,P A ∩AC =A∴BC ⊥平面P AC .∴BC ⊥AC ,BC ⊥PC . ∴△ABC 、△PBC 为直角三角形.4.如图所示,在四棱锥P -ABCD 中,底面ABCD 是矩形,侧棱P A ⊥平面ABCD ,E 、F 分别是AB 、PC 的中点,P A =AD .求证:EF ⊥平面PCD .[解析] 如图,取PD 的中点H ,连接AH 、HF .∴FH 綊12CD∴FH 綊AE ,∴四边形AEFH 是平行四边形,∴AH ∥EF . ∵底面ABCD 是矩形,∴CD ⊥AD .又∵P A ⊥底面ABCD ,∴P A ⊥CD ,P A ∩AD =A ∴CD ⊥平面P AD .又∵AH ⊂平面P AD ,∴CD ⊥AH . 又∵P A =AD ,∴AH ⊥PD ,PD ∩CD =D ∴AH ⊥平面PCD又∵AH ∥EF ,∴EF ⊥平面PCD .A 级 基础巩固一、选择题1.一条直线和平面所成角为θ,那么θ的取值范围是( B ) A .(0°,90°)B .[0°,90°]C .(0°,90°]D .[0°,180°][解析] 由线面角的定义知B 正确.2.在正方体ABCD -A 1B 1C 1D 1的六个面中,与AA 1垂直的平面的个数是( B ) A .1 B .2 C .3D .6[解析] 仅有平面AC 和平面A 1C 1与直线AA 1垂直.3.如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,则图中共有直角三角形的个数为( D )A .1B .2C .3D .4[解析] ∵P A ⊥平面ABCD∴P A ⊥AB ,P A ⊥AD ,P A ⊥BC ,P A ⊥CD .⎭⎪⎬⎪⎫AB ⊥BCP A ⊥BC P A ∩AB =A ⇒BC ⊥平面P AB ⇒BC ⊥PB 由⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫CD ⊥AD CD ⊥P A P A ∩AD =A ⇒CD ⊥平面P AD ⇒CD ⊥PD . ∴△P AB ,△P AD ,△PBC ,△PCD 都是直角三角形.4.直线a 与平面α所成的角为50°,直线b ∥a ,则直线b 与平面α所成的角等于( B ) A .40° B .50° C .90°D .150°[解析] 根据两条平行直线和同一平面所成的角相等,知b 与α所成的角也是50°. 5.下列说法中,正确的是( B ) A .垂直于同一直线的两条直线互相平行 B .垂直于同一平面的两条直线互相平行 C .垂直于同一平面的两个平面互相平行 D .平行于同一平面的两条直线互相平行[解析] A 中两直线可相交、异面、平行,故A 错;B 中l ⊥α,m ⊥α则l ∥m ,正确;C 中两平面可平行、相交,故C 错;D 中两直线可平行、相交、异面,故D 错.6.如图,已知六棱锥P-ABCDEF的底面是正六边形,P A⊥平面ABC,P A=2AB,则下列结论正确的是(D)A.PB⊥ADB.平面P AB⊥平面PBCC.直线BC∥平面P AED.直线PD与平面ABC所成的角为45°[解析]设AB长为1,由P A=2AB得P A=2又ABCDEF是正六边形,所以AD长也为2又P A⊥平面ABC,所以P A⊥AD所以△P AD为直角三角形.∵P A=AD,∴∠PDA=45°∴PD与平面ABC所成的角为45°,故选D.二、填空题7.已知△ABC所在平面外一点P到△ABC三顶点的距离都相等,则点P在平面ABC 内的射影是△ABC的__外心__.(填“重心”、“外心”、“内心”、“垂心”) [解析]P到△ABC三顶点的距离都相等,则点P在平面ABC内的射影到△ABC三顶点的距离都相等,所以是外心.8.等腰直角三角形ABC的斜边AB在平面α内,若AC与α所成的角为30°,则斜边上的中线CM与α所成的角为__45°__.[解析]如图,设C在平面α内的射影为O点连结AO,MO则∠CAO=30°,∠CMO就是CM与α所成的角.设AC=BC=1,则AB= 2∴CM=22,CO=12.∴sin CMO=COCM=22,∴∠CMO=45°.三、解答题9.如图,在三棱锥A-BCD中,CA=CB,DA=DB.作BE⊥CD,E为垂足,作AH⊥BE 于H .求证:AH ⊥平面BCD .[解析] 取AB 的中点F ,连接CF 、DF . ∵CA =CB ,DA =DB ,∴CF ⊥AB ,DF ⊥AB .∵CF ∩DF =F ,∴AB ⊥平面CDF . ∵CD ⊂平面CDF ,∴AB ⊥CD .又CD ⊥BE ,AB ∩BE =B ,∴CD ⊥平面ABE . ∵AH ⊂平面ABE ,∴CD ⊥AH .∵AH ⊥BE ,BE ∩CD =E ,∴AH ⊥平面BCD .10.如图在三棱锥P -ABC 中,P A =PB =PC =13,∠ABC =90°,AB =8,BC =6,M 为AC 的中点.(1)求证:PM ⊥平面ABC ;(2)求直线BP 与平面ABC 所成的角的正切值.[解析] (1)∵P A =PC ,M 为AC 的中点,∴PM ⊥AC .① 又∠ABC =90°,AB =8,BC =6 ∴AM =MC =MB =12AC =5.在△PMB 中,PB =13,MB =5. PM =PC 2-MC 2=132-52=12. ∴PB 2=MB 2+PM 2,∴PM ⊥MB .② 由①②可知PM ⊥平面ABC . (2)解:∵PM ⊥平面ABC∴MB 为BP 在平面ABC 内的射影∴∠PBM 为BP 与底面ABC 所成的角. 在Rt △PMB 中tan ∠PBM =PM MB =125.B 级 素养提升一、选择题1.如图,在正方体ABCD -A 1B 1C 1D 1中,E 为A 1C 1上的点,则下列直线中一定与CE 垂直的是( B )A .ACB .BDC .A 1D 1D .A 1A[解析] ∵BD ⊥AC ,BD ⊥A 1A ,AC ∩A 1A =A ,∴BD ⊥平面ACC 1A 1. 又∵CE ⊂平面ACC 1A 1,∴BD ⊥CE .2.空间四边形ABCD 的四边相等,则它的两对角线AC 、BD 的关系是( C ) A .垂直且相交 B .相交但不一定垂直 C .垂直但不相交D .不垂直也不相交[解析] 取BD 中点O ,连接AO 、CO则BD ⊥AO ,BD ⊥CO ∴BD ⊥面AOC ,BD ⊥AC 又BD 、AC 异面,∴选C .3.如图,三条相交于点P 的线段P A ,PB ,PC 两两垂直,P 在平面ABC 外,PH ⊥平面ABC 于H ,则垂足H 是△ABC 的( C )A .外心B .内心C .垂心D .重心[解析]∵PC⊥P A,PC⊥PBP A∩PB=P,∴PC⊥平面P AB.又∵AB⊂平面P AB,∴AB⊥PC.又∵AB⊥PH,PH∩PC=P,∴AB⊥平面PCH.又∵CH⊂平面PCH,∴AB⊥CH.同理BC⊥AH,AC⊥BH.∴H为△ABC的垂心.4.(2018·全国卷Ⅰ文,10)在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C 所成的角为30°,则该长方体的体积为(C)A.8 B.6 2C.8 2 D.8 3[解析]在长方体ABCD-A1B1C1D1中,连接BC1根据线面角的定义可知∠AC1B=30°因为AB=2,所以BC1=23,从而求得CC1=2 2所以该长方体的体积为V=2×2×22=82,故选C.二、填空题5.已知P A垂直于平行四边形ABCD所在的平面,若PC⊥BD,则平行四边形ABCD 一定是__菱形__.[解析]由于P A⊥平面ABCD,BD⊂平面ABCD所以P A⊥BD.又PC⊥BD,且PC⊂平面P AC,P A⊂平面P AC,PC∩P A=P,所以BD⊥平面P AC.又AC⊂平面P AC,所以BD⊥AC.又四边形ABCD是平行四边形,所以四边形ABCD是菱形.6.如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),P A⊥平面AC,且P A=1,若BC边上存在点Q,使得PQ⊥QD,则a的取值范围是__[2,+∞)__.[解析]因为P A⊥平面AC,QD⊂平面AC,∴P A⊥QD.又∵PQ⊥QD,P A∩PQ=P∴QD⊥平面P AQ,所以AQ⊥QD.①当0<a<2时,由四边形ABCD是矩形且AB=1知,以AD为直径的圆与BC无交点,即对BC上任一点Q,都有∠AQD<90°,此时BC边上不存在点Q,使PQ⊥QD;②当a=2时,以AD为直径的圆与BC相切于BC的中点Q,此时∠AQD=90°,所以BC边上存在一点Q,使PQ⊥QD;③当a>2时,以AD为直径的圆与BC相交于点Q1、Q2,此时∠AQ1D=∠AQ2D=90°,故BC边上存在两点Q(即Q1与Q2),使PQ⊥QD.C级能力拔高1.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F 是棱CD上的动点.试确定点F的位置,使得D1E⊥平面AB1F.[解析]当F为CD的中点时,D1E⊥平面AB1F.连接A1B、CD1,则A1B⊥AB1,A1D1⊥AB1,又A1D1∩A1B=A1,∴AB1⊥面A1BCD1又D1E⊂面A1BCD1,∴AB1⊥D1E.又DD1⊥平面BD∴AF⊥DD1.又AF⊥DE,∴AF⊥平面D1DE∴AF⊥D1E.∴D1E⊥平面AB1E.即当点F是CD的中点时,D1E⊥平面AB1F.2.如图,在锥体P-ABCD中,底面ABCD是菱形,且∠DAB=60°,P A=PD,E,F 分别是BC,PC的中点.求证:AD⊥平面DEF.[证明] 取AD 的中点G ,连接PG ,BG .因为P A =PD所以AD ⊥PG . 设菱形ABCD 边长为1.在△ABG 中,因为∠GAB =60°,AG =12,AB =1所以∠AGB =90° 即AD ⊥GB . 又PG ∩GB =G 所以AD ⊥平面PGB 从而AD ⊥PB .因为E ,F 分别是BC ,PC 的中点,所以EF ∥PB ,从而AD ⊥EF . 易证DE ∥GB ,且AD ⊥GB 所以AD ⊥DE ,因为DE ∩EF =E 所以AD ⊥平面DEF .。
