2018年高考数学考试大纲解读专题03函数的概念与基本初等函数I理 Word版含答案

合集下载

2018年高考数学考纲与考试说明解读.docx

2018年高考数学考纲与考试说明解读2018年高考数学考纲与考试说明解读专题一：函数、极限与导数的综合问题（一）不等式、函数与导数部分考查特点分析与建议类年份全国Ⅰ全国Ⅱ全国Ⅲ别2 / 883 / 88全国课标卷考查内容分析（考什么）（一）结论：考查的核心知识为:函数的概念、函数的性质、函数的图象、导数的应用函数的概念：函数的定义域、值域、解析式（分段函数）;函数的性质：函数的奇偶性、单调性、对称性、周期性;函数的图象：包含显性与隐性；导数的应用：导数的概念及其几何意义;利用导数求单调区间、极值、最值与零点；结合函数的单调性解不等式或证明不等式、求参数范围．4 / 88（二）试题题型结构：全国卷基本上是2道选择题或填空题、1道解答题，共3道题.分值为22分．（三）试题难度定位：全国卷对函数与导数的考查难度相对稳定，选择、填空题中，有一道为中等难度，另一道作为选择、填空的“压轴题”进行考查；解答题均放置于“压轴”位置．小题考点可总结为八类：（1）分段函数；（2）函数的性质；（3）基本函数；（4）函数图像；（5）方程的根（函数的零点）；（6）函数的最值；（7）导数及其应用；（8）定积分。

解答题主要是利用导数处理函数、方程和5 / 88不等式等问题，有一定的难度，往往放在解答题的后面两道题中的一个．纵观近几年全国新课标高考题，常见的考点可分为六个方面：（1）变量的取值范围问题；（2）证明不等式的问题；（3）方程的根（函数的零点）问题；（4）函数的最值与极值问题；（5）导数的几何意义问题；（6）存在性问题。

考点：题型1 函数的概念例1 有以下判断：①f(x)＝|x |x与g(x)＝⎩⎨⎧1 x≥0－1 x<0表示6 / 887 / 88同一函数；②函数y ＝f (x )的图象与直线x ＝1的交点最多有1个；③f (x )＝x 2－2x ＋1与g (t )＝t 2－2t ＋1是同一函数；④若f (x )＝|x －1|－|x |，则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫12＝0.其中正确判断的序号是________.题型2 函数的概念、性质、图象和零点（2017年全国新课标Ⅰ卷理科第8题）例 2、已知函数()()2112x x f x x x a e e --+=-++有唯一零点，则a = A. 12-B.13C.12D. 1C【解析】函数()f x 的零点满足()2112e e x x x x a --+-=-+，设()11eex x g x --+=+，则()()21111111e 1eeee e x x x x x x g x ---+----=-=-='，当()0g x '=时， 1x =；当1x <时， ()0g x '<，函数()g x 单8 / 88调递减；当1x >时， ()0g x '>，函数()g x 单调递增，当1x =时，函数()g x 取得最小值，为()12g =.设()22h x xx=-，当1x =时，函数()h x 取得最小值，为1-，若0a ->，函数()h x 与函数()ag x -没有交点；若0a -<，当()()11ag h -=时，函数()h x 和()ag x -有一个交点，即21a -⨯=-，解得12a =.故选C.例3、（2012理科）（10）已知函数1()ln(1)f x x x=+-；则()y f x =的图像大致为（）B9 / 88（1）定义域（2）奇偶性（3）对称性（4）单调性（求导）（5）周期性（6）特征点（7）变化趋势1.考查角度(1)以指、对、幂函数为载体考查函数的单调性、奇偶性等性质;(2)考查分段函数的求值以及指数、对数的运算;(3)函数图象的考查主要是函数图象的识别及应用;(4)高考一般不单独考查函数零点的个数以及函数零点所在区间,有时在导数中考查函数的零点问题;(5)函数与方程的考查既可以是结合函数零点存在性定理或函数图象判断零点的存在性,也1,ln(1)y t x x t==+-1'111x t x x -=-=++(1)0,31()034ln 44f f <-=<-10 / 88可以是利用函数零点的存在性求参数的值、范围或判断零点所在区间. 2.题型及难易度选择题或填空题.难度:中等或偏上.2求函数定义域常见结论：(1)分式的分母不为零；(2)偶次根式的被开方数不小于零；(3)对数函数的真数必须大于零；(4)指数函数和对数函数的底数大于零且不等于1；(5)正切函数y ＝tan x ，x ≠k π＋ (k ∈Z)； (6)零次幂的底数不能为零；(7)实际问题中除要考虑函数解析式有意义外，还应考虑实际问题本身的要求.题型3、函数、方程、不等式及导数的综合应用例3（2013理科）若函数=的图像关于直线2x =-对称，则的最(1)(3)8(1)(5)15f f a f f b -=-=⎧⎧⇒⇒⎨⎨=-=⎩⎩法一：导数求最值问题大值是______. 1616)5()(,910)3(16)()3(16)34)(34()2(max 2222222==⇒-+-=+-=⇒+-=++-+-=-g t g t t t t t g x x x x x x x f 法二：知识点：函数的奇偶性、对称性和导数的应用数学思想：考查转化、数形结合体现了多角度、多维度、多层次题型4 函数、方程、不等式及导数的综合应用例4、已知函数()f x =x ﹣1﹣alnx ．（1）若()0f x ≥ ，求a 的值；（2）设m 为整数，且对于任意正整数n ，21111++1+)222n ()(1)(﹤m ，求m 的最小值．解：（1）()f x 的定义域为()0，+∞.①若0a ≤，因为11=-+2＜022f a ln ⎛⎫ ⎪⎝⎭，所以不满足题意；②若＞0a ，由()1a x a f 'x x x-=-=知，当()0x ,a ∈时，()＜0f 'x ；当()，+x a ∈∞时，()＞0f 'x ，所以()f x 在()0,a 单调递减，在()，+a ∞单调递增，故x=a 是()f x 在()0，+x ∈∞的唯一最小值点. 由于()10f =，所以当且仅当a=1时，()0f x ≥. 故a=1（2）由（1）知当()1，+x ∈∞时，1＞0x ln x --令1=1+2nx 得111+＜22nnln ⎛⎫ ⎪⎝⎭，从而 2211111111++1+++1+＜+++=1-＜12222222nn nln ln ln ⎛⎫⎛⎫⎛⎫⋅⋅⋅⋅⋅⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故21111+1+1+＜222ne⎛⎫⎛⎫⎛⎫⋅⋅⋅ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭而231111+1+1+＞2222⎛⎫⎛⎫⎛⎫⎪⎪⎪⎝⎭⎝⎭⎝⎭，所以m 的最小值为3.（6）复习重点函数作为几大主干知识之一，其主体知识包括 1个工具：导数研究函数的单调性、极值、最值和证明不等式；1个定理：零点存在性定理； 1个关系：函数的零点是方程的根；2个变换：图象的平移变换和伸缩变换；2大种类：基本初等代数函数(正比例函数、反比例函数、一次函数、二次函数、三次函数、指数函数、对数函数、幂函数)和基本初等函数的复合函数(对勾函数、双曲函数、分段函数和其它函数)；2个最值：可行域背景下的二元函数最值和均值不等式背景下的一元函数最值;2个意义：导数的几何意义和定积分的几何意义；3个要素：定义域、值域、解析式；3个二次：二次函数、二次方程、二次不等式；5个性质：单调性、奇偶性、周期性、凸凹性、对称性.关注二阶导数在研究函数中的拓展应用虽然高中数学没有涉及二阶导数的提法和应用，但将函数的导数表示为新的函数，并继续研究函数的性质的试题比比皆是．因此有必要关注二阶导数在研究函数中的拓展应用，但要注意过程性的学习，而不是定理的记忆．① 当a 1≥时，恒有()'≥h x ()00'≥h ，从而()h x 是增函数，()00h =，()0h x ≥在[)0,+∞恒成立② 当a 1时，()h x '在[)0,+∞是增函数，()00=a 10,0,使'-∃h x ()0x 0'=h ，所用当()()0x 0,0时'∈x h x ，从而()h x 是减函数，()00h =，()0≤h x ，所以()0h x ≥在[)0,+∞不恒成立故1a ≥即为所求.全国（2）卷文设函数f(x)=(1-x 2)e x . （1）讨论f(x)的单调性；（2）当x ≥0时，f(x)≤ax +1，求a 的取值范围. （2）∵0x ≥时，()1f x ax ≤+，∴()211x x e ax -≤+ ∴210x x x e e ax -++≥，令()21x x h x x e e ax =-++，即[)0,x ∈+∞时，()0h x ≥，而()00h =再令()()22x x x x h x x e xe e a ϕ'==+-+，()()241x x x x e ϕ'=++ 0x ≥时，()0x ϕ'>恒成立. ∴()h x '在[)0,+∞是增函数（理21）已知函数()2ln f x ax ax x x =--，且()0f x ≥。

2018年高考新课标数学理一轮考点突破课件：第二章函

方程 lnx＝8－2x 的实数根 x∈(k，k＋1)，k∈Z，则 k＝ ________.
1 解：构造函数 f(x)＝lnx＋2x－8，所以 f′(x)＝＋2＞0(x＞ x 0)，则 f(x)在(0，＋∞)上单调递增，又 f(1)＝－6＜0，f(2)＝ln2 －4＜0，f(3)＝ln3－2＜0，f(4)＝ln4＞0，所以 f(x)的唯一零点在(3，4)内，因此 k＝3.故填 3.
2
பைடு நூலகம்
2
类型一
判断函数零点所在的区间
6 (2014·北京)已知函数 f(x)＝－log2x.在下列区间 x 中，包含 f(x)零点的区间是( ) A．(0，1) B．(1，2) C．(2，4) D．(4，＋∞)
解：f(x)在(0，＋∞)为减函数，又 f(1)＝6＞0，f(2) 3 1 ＝2＞0，f(4)＝－2＝－＜0.故选 C. 2 2
(2014·苏锡模拟)已知奇函数 f(x)是 R 上的 2 单调函数，若函数 y＝f(x )＋f(k－x)只有一个零点，则实数 k 的值是________．
解：由 f(x )＋f(k－x)＝0 得 f(x )＝－f(k－x)，因为 f(x)是 2 奇函数，有－f(k－x)＝f(x－k)，故有 f(x )＝f(x－k)，又 f(x) 2 2 是 R 上的单调函数，所以方程 x ＝x－k 即 x －x＋k＝0 有唯一解， 1 1 由 Δ＝0 解得 k＝ .故填 . 4 4
2 － g(x)＝7－x ，x≥2，作图易知函数 y＝f(x)与 y＝1－g(x)有两个交 x2－1，1＜x＜2，－1，0＜x＜1， 2 点，又 y＝－1－g(x)＝5－x ，x≥2，作图易知函数 y＝f(x)与 y＝－1 x2－3，1＜x＜2，

专题03 基本初等函数(解析版)

专题03 基本初等函数命题规律内容典型１指数式与对数式的化简与求值2018年高考全国Ⅲ卷理数２同一坐标系中含参数的两个基本初等函数图象识别2019年高考浙江３比较对数式的大小 2018年高考天津理数４比较指数式、对数式的大小2020年高考全国Ⅲ卷理数12５给定参数满足的条件判定含参数的对数式、指数式的范围2019年高考全国Ⅱ卷理数命题规律一指数式与对数式的化简与求值【解决之道】解决此类问题的关键在于掌握指数运算、对数运算法则、对数换底公式、对数常用恒等式，常用解法：首先利用幂的运算把底数或真数进行变形，化成分数指数幂的形式，使幂的底数最简，然后正用对数运算性质化简合并；其次将对数式化为同底数对数的和、差、倍数运算，然后逆用对数的运算性质，转化为同底对数真数的积、商、幂的运算．【三年高考】1.【2018年高考全国Ⅲ卷理数】设0.2log 0.3a =，2log 0.3b =，则 A ．0a b ab +<<，0ab ∴<， ∴0ab a b <+<，故选B ．命题规律二同一坐标系中含参数的两个基本初等函数图象识别【解决之道】根据其中一个函数的图象确定参数的范围，再根据参数范围确定另一个函数图象是不是正确. 【三年高考】1.【2019年高考浙江】在同一直角坐标系中，函数1xy a =，1(2log )a y x =+(a >0，且a ≠1)的图象可能是【答案】D【解析】当01a <<时，函数xy a =的图象过定点(0,1)且单调递减，则函数1x y a=的图象过定点(0,1)且单调递增，函数1log 2a y x ⎛⎫=+⎪⎝⎭的图象过定点1(,0)2且单调递减，D 选项符合；当1a >时，函数xy a =的图象过定点(0,1)且单调递增，则函数1xy a =的图象过定点(0,1)且单调递减，函数1log 2a y x ⎛⎫=+ ⎪⎝⎭的图象过定点1(,02）且单调递增，各选项均不符合，综上，选D.命题规律三比较对数式的大小【解决之道】利用对数的运算法则、换底公式、对数恒等式将不同底的对数式化为同底的对数，再利用对数函数的单调性比较大小，较复杂的可以用作差比较法（或作商比较法）判定大小. 【三年高考】1.【2018年高考天津理数】已知2log e a =，ln2b =，121log 3c =，则a ，b ，c 的大小关系为 A ．a b c >> B ．b a c >> C ．c b a >> D ．c a b >>【答案】D【解析】由题意结合对数函数的性质可知：2log e 1a =>，()21ln20,1log eb ==∈，12221log log 3log e 3c ==>，据此可得：c a b >>，故选D. 命题规律四比较指数式、对数式的大小【解决之道】首项利用指数的运算法则将不同底化为同底数或同指数的指数式，利用指数函数或幂函数的图象与性质比较大小并估算出范围，然后利用对数的运算法则、对数恒等式、对数换底公式将对数式化为同底数或同真数的对数式，利用对数函数的图象与性质比较大小并估算出范围，再根据其各自的范围即可比较出大小. 【三年高考】1.【2020年高考全国Ⅲ卷理数12】已知544558,138<<．设5813log 3,log 5,log 8a b c ===，则（）A ．a b c <<B ．b a c <<C ．b c a <<D ．c a b << 【答案】A【解析】解法一：由题意可知a 、b 、()0,1c ∈，()222528log 3lg 3lg81lg 3lg8lg 3lg8lg 241log 5lg 5lg 522lg 5lg 25lg 5a b ⎛⎫⎛⎫++⎛⎫==⋅<⋅==< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，a b ∴<；由8log 5b =，得85b =，由5458<，得5488b <，54b ∴<，可得45b <；由13log 8c =，得138c =，由45138<，得451313c <，54c ∴>，可得45c >．综上所述，a b c <<．故选A ．解法二：易知(01)a,b,c ,∈，由()()2225555558log 3log 8log 24log 32log 3log 81log 5444a b +==⋅<=<=，知a b <．∵8log 5b =，13log 8c =，∴85b =，138c =，即5585b =，44138c =又∵5458<，45138<，∴445541385813c b b =>=>，即b c <．综上所述：a b c <<，故选A ．2.【2020年高考天津卷6】设0.80.70.713,,log 0.83a b c -⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系为（）A ．a b c <，0.80.80.71333b a -⎛⎫==>= ⎪⎝⎭，0.70.7log 0.8log 0.71c =<=，所以1c a b <<<，故选D ．3.【2019年高考全国Ⅰ卷理数】已知0.20.32log 0.220.2a b c ===，，，则 A ．a b c <=0.3000.20.21,c <=<=即01,c <<则a c b <<，故选B ．4.【2019年高考天津理数】已知5log 2a =，0.5og 2.l 0b =，0.20.5c =，则,,a b c 的大小关系为 A ．a c b <=，10.200.50.50.5c <=<，即112c <<，所以a c b <<，故选A. 5.【2019年高考天津文数】已知0.223log 7,log 8,0.3a b c ===，则a ，b ，c 的大小关系为 A ．c b a <=，331log 8log 92b <=<=， ∴c b a <<.故选A.命题规律五给定参数满足的条件判定含参数的对数式、指数式的范围【解决之道】①若根据给定的条件是等式，利用条件将二元式子化为一元函数，利用相应函数的图象与性质作出判定；②若给出的条件是不等式，利用相应的函数的图象与性质，判定式子的范围. 【三年高考】1.【2020年高考山东卷11】已知0a >，0b >，且1a b +=，则（）A ．2212a b +≥B ．122a b -> C ．22log log 2a b +≥- D 2 【答案】ABD【解析】对于A ，()222221221a b a a a a +=+-=-+21211222a ⎛⎫⎪⎭+ ⎝≥-=，当且仅当12a b ==时，等号成立，故A 正确；对于B ，211a b a -=->-，所以11222a b-->=，故B 正确；对于C ，2222221log log log log log 224a b a b ab +⎛⎫+=≤==- ⎪⎝⎭，当且仅当12a b ==时，等号成立，故C 不正确；对于D ，因为2112a b =+≤++=≤，当且仅当12a b ==时，等号成立，故D 正确，故选：ABD ．2.【2019年高考全国Ⅱ卷理数】若a >b ，则 A ．ln(a −b )>0 B ．3a <3b C ．a 3−b 3>0 D ．│a │>│b │【答案】C【解析】取2,1a b ==，满足a b >，但ln()0a b -=，则A 错，排除A ；由219333=>=，知B 错，排除B ；取1,2a b ==-，满足a b >，但|1||2|<-，则D 错，排除D ；因为幂函数3y x =是增函数，a b >，所以33a b >，即a 3−b 3>0，C 正确. 故选C ．。

【理科专题二】函数概念与基本初等函数(带答案)

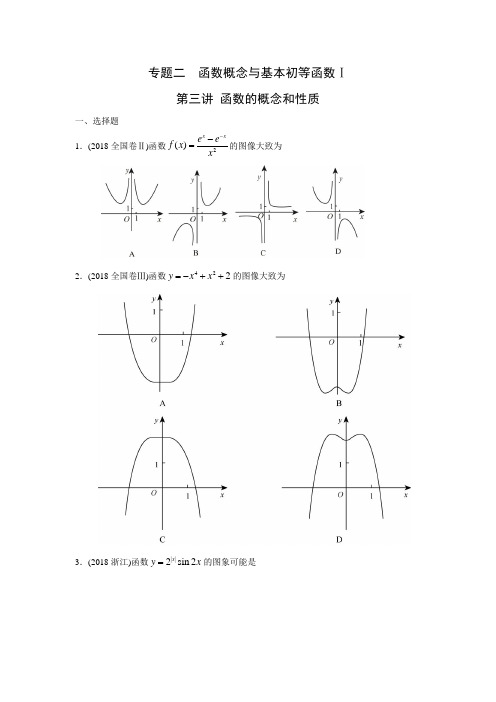
专题二函数概念与基本初等函数Ⅰ第三讲函数的概念和性质一、选择题1．(2018全国卷Ⅱ)函数2()--=x xe ef x x 的图像大致为2．(2018全国卷Ⅲ)函数422y x x =-++的图像大致为3．(2018浙江)函数||2sin 2x y x =的图象可能是A ．B ．C ．D ．4．(2018全国卷Ⅱ)已知()f x 是定义域为(,)-∞+∞的奇函数，满足(1)(1)-=+f x f x ．若(1)2=f ，则(1)(2)(3)(50)++++=…f f f fA ．50-B ．0C ．2D ．505．（2017新课标Ⅰ）函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(1)1f =-，则满足1(2)1f x --≤≤ 的x 的取值范围是A ．B ．C ．D ． 6．（2017浙江）若函数2()f x x ax b =++在区间[0，1]上的最大值是M ，最小值是m ，则M m -A ．与a 有关，且与b 有关B ．与a 有关，但与b 无关C ．与a 无关，且与b 无关D ．与a 无关，但与b 有关7．（2017天津）已知奇函数()f x 在R 上是增函数，()()g x xf x =．若2(log 5.1)a g =-，0.8(2)b g =，(3)c g =，则a ，b ，c 的大小关系为A ．a b c <<B ．c b a <<C ．b a c <<D ．b c a <<8．（2017北京）已知函数1()3()3x x f x =-，则()f x A ．是奇函数，且在R 上是增函数 B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数9．(2016山东)已知函数f (x )的定义域为R ．当x <0时，3()1f x x =- ；当11x -≤≤ 时，()()f x f x -=-；当12x >时，11()()22f x f x +=-，则f (6)= A ．−2 B ．−1C ．0D ．2 10．(2016全国I) 函数2||2x y x e =-在[–2,2]的图像大致为A ．B ．C ．D ．11．(2016全国II) 已知函数()()f x x ∈R 满足()()2f x f x -=-，若函数1x y x +=与()y f x =图像的交点为()11x y ，，()22x y ，，…，()m m x y ，，则()1m i i i x y =+=∑ A ．0 B ．m C ．2m D ．4m12．(2015福建)下列函数为奇函数的是A．y B ．sin y x = C ．cos y x = D ．x x y e e -=-13．(2015广东)下列函数中，既不是奇函数，也不是偶函数的是A．y = B ．1y x x =+ C ．122x x y =+ D ．x y x e =+ 14．(2015湖南)设函数()ln(1)ln(1)f x x x =+--，则()f x 是A ．奇函数，且在(0,1)上是增函数B ．奇函数，且在(0,1)上是减函数C ．偶函数，且在(0,1)上是增函数D ．偶函数，且在(0,1)上是减函数15．(2015湖北)已知符号函数1,0,sgn 0,0,1,0.x x x x >⎧⎪==⎨⎪-<⎩()f x 是R 上的增函数，()()g x f x =-()f ax (1)a >，则A ．sgn[()]sgn g x x =B ．sgn[()]sgn g x x =-C ．sgn[()]sgn[()]g x f x =D ．sgn[()]sgn[()]g x f x =-16．(2015安徽)函数()()2ax bf x x c +=+的图象如图所示，则下列结论成立的是A ．0a >，0b >，0c ，0c >C ．0a <，0b >，0c <D ．0a <，0b <，0c <17．(2014新课标1)设函数()f x ，()g x 的定义域都为R ，且()f x 是奇函数，()g x 是偶函数，则下列结论正确的是A ．()f x ()g x 是偶函数B ．()f x |()g x |是奇函数C ．|()f x |()g x 是奇函数D ．|()f x ()g x |是奇函数18．(2014山东)函数1)(log 1)(22-=x x f 的定义域为A ．)210(，B ．)2(∞+，C ．),2()210(+∞ ，D ．)2[]210(∞+，， 19．(2014山东)对于函数()f x ，若存在常数0a ≠，使得x 取定义域内的每一个值，都有 ()(2)f x f a x =-，则称()f x 为准偶函数，下列函数中是准偶函数的是A．()f x = B ．2()f x x = C ．()tan f x x = D ．()cos(1)f x x =+20．(2014浙江)已知函数32()f x x ax bx c =+++，且0(1)(2)(3)3f f f -=-=-≤≤，则A ．3≤cB ．63≤<cC ．96≤<cD ．9>c21．(2015北京)下列函数中，定义域是R 且为增函数的是A ．x y e -=B ．3y x =C ．ln y x =D ．y x =22．(2014湖南)已知(),()f x g x 分别是定义在R 上的偶函数和奇函数，且()()f x f x -=321x x ++，(1)(1)f g +则＝A ．－3B ．－1C ．1D ．323．(2014江西)已知函数||5)(x x f =，)()(2R a x ax x g ∈-=，若1)]1([=g f ，则=aA ．1B ．2C ．3D ．-124．(2014重庆)下列函数为偶函数的是A ．()1f x x =-B ．3()f x x x =+C ．()22x x f x -=-D ．()22x x f x -=+ 25．(2014福建)已知函数()⎩⎨⎧≤>+=0,cos 0,12x x x x x f 则下列结论正确的是A ．()x f 是偶函数B ．()x f 是增函数C ．()x f 是周期函数D ．()x f 的值域为[)+∞-,126．(2014辽宁)已知()f x 为偶函数，当0x ≥时，1cos ,[0,]2()121,(,)2x x f x x x π⎧∈⎪⎪=⎨⎪-∈+∞⎪⎩，则不等式1(1)2f x -≤的解集为 A ．1247[,][,]4334 B ．3112[,][,]4343-- C ．1347[,][,]3434 D ．3113[,][,]4334-- 27．(2013辽宁)已知函数()3)1f x x =+，则1(lg 2)(lg )2f f +=A ．1-B ．0C ．1D ．2 28．(2013新课标Ⅰ)已知函数()f x =22,0ln(1),0x x x x x ⎧-+≤⎨+>⎩，若|()f x |≥ax ，则a 的取值范围是A ．(,0]-∞B ．(,1]-∞C ．[－2,1]D ．[－2,0]29．(2013广东)定义域为R 的四个函数3y x =,2x y =,21y x =+,2sin y x =中，奇函数的个数是A ．4B ．3C ．2D ．130．(2013广东)函数lg(1)()1x f x x +=-的定义域是 A ．(1,)-+∞ B ．[1,)-+∞ C ．(1,1)(1,)-+∞ D ．[1,1)(1,)-+∞31．(2013山东)已知函数()f x 为奇函数，且当0x >时，()21f x x x=+ ，则()1f -= A ．－2 B ．0 C ．1 D ．232．(2013福建)函数)1ln()(2+=x x f 的图象大致是A ．B ．C ．D ．33．(2013北京)下列函数中，既是偶函数又在区间(0,)+∞上单调递减的是A ．1y x= B ．x y e -= C ．21y x =-+ D ．lg y x = 34．(2013湖南)已知()f x 是奇函数，()g x 是偶函数，且()()112f g -+=，()()114f g +-=，则()1g 等于A ．4B ．3C ．2D ．1 35．(2013重庆)已知函数3()sin 4(,)f x ax b x a b R =++∈，2(lg(log 10))5f =，则(lg(lg 2))f =A ．5-B ．1-C ．3D ．436．(2013湖北)x 为实数，[]x 表示不超过x 的最大整数，则函数()[]f x x x =-在R 上为A ．奇函数B ．偶函数C ．增函数D ．周期函数37．(2013四川)函数133-=x x y 的图像大致是A B C D38．(2012天津)下列函数中，既是偶函数，又在区间(1,2)内是增函数的为A ．cos 2,y x x R =∈B ．2log ||,0y x x R x =∈≠且C ．,2x xe e y x R --=∈ D ．31y x =+ 39．(2012福建)设1,0,()0,0,1,0,xf x x x >⎧⎪= =⎨⎪- <⎩⎩⎨⎧=为无理数为有理数x x x g ,0,1)(，则(())f g π的值为A ．1B ．0C ．1-D ．π40．(2012山东)函数1()ln(1)f x x =++ A ．[2,0)(0,2]- B ．(1,0)(0,2]- C ．[2,2]- D ．(1,2]-41．(2012陕西)下列函数中，既是奇函数又是增函数的为A 1y x =+B 3y x =-C 1y x =D ||y x x = 42．(2011江西)若()f x =，则)(x f 的定义域为 A ．(21-,0) B ．(21-,0] C ．(21-,∞+) D ．(0,∞+) 43．(2011新课标)下列函数中，既是偶函数又在+∞（0，）单调递增的函数是A ．3y x =B ．1y x =+C ．21y x =-+D ．2x y -=44．(2011辽宁)函数)(x f 的定义域为R ，2)1(=-f ，对任意R ∈x ，2)(>'x f ，则42)(+>x x f 的解集为A ．(1-，1)B ．(1-，+∞)C ．(∞-，1-)D ．(∞-，+∞)45．(2011福建)已知函数2,0()1,0x x f x x x >⎧=⎨+≤⎩．若()(1)0f a f +=，则实数a 的值等于 A ．－3 B ．－1C ．1D ．346．(2011辽宁)若函数))(12()(a x x x x f -+=为奇函数，则a = (A)21 (B)32 (C)43 (D)1 47．(2011安徽)设)(x f 是定义在R 上的奇函数，当0x ≤时，2()2f x x x =-，则(1)f =A ．－3B ．－1C ．1D ．348．(2011陕西)设函数()()f x x R ∈满足()(),(2)(),f x f x f x f x -=+=,则()y f x =的图像可能是49．(2010山东)函数()()2log 31x f x =+的值域为 A ．()0,+∞ B ．)0,+∞⎡⎣ C ．()1,+∞ D ．)1,+∞⎡⎣ 50．(2010年陕西)已知函数()f x =221,1,1x x x ax x ⎧+<⎨+≥⎩，若((0))f f =4a ，则实数a = A ．12 B ．45C ．2D ．9 51．(2010广东)若函数()33x x f x -=+与()33x x g x -=-的定义域均为R ，则A ．()f x 与()g x 均为偶函数B ．()f x 为偶函数，()g x 为奇函数C ．()f x 与()g x 均为奇函数D ．()f x 为奇函数，()g x 为偶函数52．(2010安徽)若()f x 是R 上周期为5的奇函数，且满足()()11,22f f ==，则()()34f f -=A ．－1B ．1C ．－2D ．2二、填空题53．(2018江苏)函数()f x =的定义域为．54．(2018江苏)函数()f x 满足(4)()()f x f x x +=∈R ，且在区间(2,2]-上，cos ,02,2()1||,20,2x x f x x x π⎧<⎪⎪=⎨⎪+<⎪⎩≤-≤则((15))f f 的值为． 55．(2018上海)已知11{2,1,,,1,2,3}22α∈---，若幂函数()α=f x x 为奇函数，且在0+∞（，）上递减，则α=_____56．(2018北京)能说明“若()(0)f x f >对任意的(0,2]x ∈都成立，则()f x 在[0,2]上是增函数”为假命题的一个函数是__________．57．（2017新课标Ⅲ）设函数1,0()2,0x x x f x x +⎧=⎨>⎩≤，则满足1()()12f x f x +->的x 的取值范围是___．58．（2017江苏）已知函数31()2x xf x x x e e =-+-，其中e 是自然数对数的底数，若2(1)(2)0f a f a -+≤，则实数a 的取值范围是．59．（2017山东）若函数e ()xf x (e=2．71828 ，是自然对数的底数)在()f x 的定义域上单调递增，则称函数()f x 具有M 性质，下列函数中具有M 性质的是①()2x f x -= ②()3xf x -= ③3()=f x x ④2()2=+f x x 60．（2017浙江）已知a ∈R ，函数4()||f x x a a x=+-+在区间[1，4]上的最大值是5，则a 的取值范围是．61．(2016天津)已知f (x )是定义在R 上的偶函数，且在区间(,0)-∞上单调递增.若实数a 满足1(2)(a f f ->，则a 的取值范围是______.62．(2016江苏)设()f x 是定义在R 上且周期为2的函数，在区间[)1,1-上，(),10,2,01,5x a x f x x x +-<⎧⎪=⎨-<⎪⎩≤≤其中a ∈R ，若59()()22f f -=，则()5f a 的值是． 63．(2015新课标Ⅰ)若函数()ln(f x x x =+为偶函数，则a =64．(2015浙江)已知函数223,1()lg(1),1x x f x xx x ⎧+-⎪=⎨⎪+<⎩≥，则((3))f f -=_______，()f x 的最小值是______．65．(2015山东)已知函数()(0,1)x f x a b a a =+>≠ 的定义域和值域都是[1,0]-，则a b += ．66．(2015福建)若函数()6,2,3log ,2,a x x f x x x -+⎧=⎨+>⎩≤(0a > 且1a ≠ )的值域是[)4,+∞，则实数a 的取值范围是．67．(2014新课标Ⅱ)偶函数()f x 的图像关于直线2x =对称，(3)3f =，则(1)f -=___．67．(2014湖南)若()()ax e x f x ++=1ln 3是偶函数，则=a ____________．68．(2014四川)设()f x 是定义在R 上的周期为2的函数，当[1,1)x ∈-时，242,10,(),01,x x f x x x ⎧-+-≤<=⎨≤<⎩，则3()2f = ． 70．(2014浙江)设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ，则实数a 的取值范围是___. 71．(2014湖北)设()x f 是定义在()+∞,0上的函数，且()0>x f ，对任意0,0>>b a ，若经过点(,())a f a ，(,())b f b -的直线与x 轴的交点为()0,c ，则称c 为b a ,关于函数()x f 的平均数，记为),(b a M f ，例如，当())0(1>=x x f 时，可得2),(b a c b a M f +==，即),(b a M f 为b a ,的算术平均数． (Ⅰ)当())0_____(>=x x f 时，),(b a M f 为b a ,的几何平均数；(Ⅱ)当())0_____(>=x x f 时，),(b a M f 为b a ,的调和平均数ba ab +2； (以上两空各只需写出一个符合要求的函数即可) 72．(2013安徽)函数1ln(1)y x =++的定义域为_____________． 73．(2013北京)函数12log ,1()2,1x x x f x x ≥⎧⎪=⎨⎪ <⎩的值域为．74．(2012安徽)若函数()|2|f x x a =+的单调递增区间是),3[+∞，则a =________． 75．(2012浙江)设函数()f x 是定义在R 上的周期为2的偶函数，当[0,1]x ∈时，()1f x x =+，则3()2f =_______________．76．(2011陕西)设2lg 0()30ax x f x x t dt x >⎧⎪=⎨+⎪⎩⎰…，若((1))1f f =，则a = ． 77．(2011江苏)已知实数0≠a ，函数⎩⎨⎧≥--<+=1,21,2)(x a x x a x x f ，若)1()1(a f a f +=-，则a 的值为________78．(2011福建)设V 是全体平面向量构成的集合，若映射:f V R →满足：对任意向量11(,)x y a =∈V ，22(,)x y b =∈V ，以及任意λ∈R ，均有((1))()(1)(),f f f λλλλ+-=+-a b a b则称映射f 具有性质P ．现给出如下映射：①12:,(),,(,);f V R f m x y m x y V →=-=∈ ②222:,(),(,);f V R f m x y m x y V →=+=∈ ③33:,()1,(,).f V R f m x y m x y V →=++=∈其中，具有性质P 的映射的序号为________．(写出所有具有性质P 的映射的序号)79．(2010福建)已知定义域为0+∞（，）的函数()f x 满足：①对任意0x ∈+∞（，），恒有(2)=2()f x f x 成立；当(1,2]x ∈时，()=2f x x -．给出如下结论：①对任意Z m ∈，有(2)=0mf ；②函数()f x 的值域为[0+∞，）；③存在Z n ∈，使得(2+1)=9n f ；④“函数()f x 在区间(,)a b 上单调递减”的充要条件是 “存在Z k ∈，使得1(,)(2,2)kk a b +⊆”．其中所有正确结论的序号是．80．(2010江苏)设函数()()xxf x x e ae -=+(x ∈R)是偶函数，则实数a =______．专题二函数概念与基本初等函数Ⅰ第三讲函数的概念和性质答案部分1．B 【解析】当0<x 时，因为0--<xxe e ，所以此时2()0--=<x xe ef x x，故排除A ．D ；又1(1)2=->f e e，故排除C ，选B ． 2．D 【解析】当0x =时，2y =，排除A ，B ．由3420y x x '=-+=，得0x =或2x =±，结合三次函数的图象特征，知原函数在(1,1)-上有三个极值点，所以排除C ，故选D ．3．D 【解析】设||()2sin 2x f x x =，其定义域关于坐标原点对称，又||()2sin(2)()x f x x f x --=⋅-=-，所以()y f x =是奇函数，故排除选项A ，B ；令()0f x =，所以sin 20x =，所以2x k π=(k ∈Z )，所以2k x π=(k ∈Z )，故排除选项C ．故选D ．4．C 【解析】解法一 ∵()f x 是定义域为(,)-∞+∞的奇函数，()()-=-f x f x ．且(0)0=f ．∵(1)(1)-=+f x f x ，∴()(2)=-f x f x ，()(2)-=+f x f x ∴(2)()+=-f x f x ，∴(4)(2)()+=-+=f x f x f x ，∴()f x 是周期函数，且一个周期为4，∴(4)(0)0==f f ，(2)(11)(11)(0)0=+=-==f f f f ，(3)(12)(12)(1)2=+=-=-=-f f f f ，∴(1)(2)(3)(50)120(49)(50)(1)(2)2+++⋅⋅⋅+=⨯++=+=f f f f f f f f ，故选C ．解法二由题意可设()2sin()2f x x π=，作出()f x 的部分图象如图所示．由图可知，()f x 的一个周期为4，所以(1)(2)(3)(50)+++⋅⋅⋅+f f f f ，所以(1)(2)(3)(50)120(1)(2)2+++⋅⋅⋅+=⨯++=f f f f f f ，故选C ． 5．D 【解析】由函数()f x 为奇函数，得(1)(1)1f f -=-=，不等式1(2)1f x --≤≤即为(1)(2)(1)f f x f --≤≤，又()f x 在(,)-∞+∞单调递减，所以得121x --≥≥，即13x ≤≤，选D ． 6．B 【解析】函数()f x 的对称轴为2a x =-， ①当02a-≤，此时(1)1M f a b ==++，(0)m f b ==，1M m a -=+； ②当12a-≥，此时(0)M f b ==，(1)1m f a b ==++，1M m a -=--；③当012a <-<，此时2()24a a m fb =-=-，(0)M f b ==或(1)1M f a b ==++，24a M m -=或214a M m a -=++．综上，M m -的值与a 有关，与b 无关．选B ．7．C 【解析】由题意()g x 为偶函数，且在(0,)+∞上单调递增，所以22(log 5.1)(log 5.1)a g g =-= 又2222log 4log 5.1log 83=<<=，0.8122<<，所以0.822log 5.13<<，故b a c <<，选C ．8．A 【解析】11()3()(3())()33xx x x f x f x ---=-=--=-，得()f x 为奇函数， ()(33)3ln33ln30x x x x f x --''=-=+>，所以()f x 在R 上是增函数．选A ．9．D 【解析】当11x-剟时，()f x 为奇函数，且当12x >时，(1)()f x f x +=，所以(6)(511)(1)f f f =⨯+=．而3(1)(1)[(1)1]2f f =--=---=，所以(6)2f =，故选D ．10．D 【解析】当0x ?时，令函数2()2x f x x e =-，则()4x f x x e '=-，易知()f x '在[0，ln 4）上单调递增，在[ln 4，2]上单调递减，又(0)10f '=-<，1()202f '=->，(1)40f e '=->，2(2)80f e '=->，所以存在01(0,)2x ∈是函数()f x 的极小值点，即函数()f x 在0(0,)x 上单调递减，在0(,2)x 上单调递增，且该函数为偶函数，符合条件的图像为D ．11．B 【解析】由()()2f x f x -=-得()()2f x f x -+=，可知()f x 关于()01，对称，而111x y x x+==+也关于()01，对称， ∴对于每一组对称点0i i x x '+= =2i i y y '+， ∴()111022m m miiiii i i mx y x ym ===+=+=+⋅=∑∑∑，故选B ． 12．D【解析】∵函数y 的定义域为[0,)+∞，不关于原点对称，所以函数y =为非奇非偶函数，排除A ；因为|sin |y x =为偶函数，所以排除B ；因为cos y x =为偶函数，所以排除C ；因为()xxy f x e e -==-，()()()x x x x f x e e e e f x ---=-=--=-，所以()x x y f x e e -==-为奇函数．13．D 【解析】选项A 、C 为偶函数，选项B 中的函数是奇函数；选项D 中的函数为非奇非偶函数．14．A 【解析】由题意可知，函数()f x 的定义域为(1,1)-，且12()lnln(1)11x f x x x+==---，易知211y x=--在(0,1)上为增函数，故()f x 在(0,1)上为增函数，又()ln(1)ln(1)()f x x x f x -=--+=-，故()f x 为奇函数．15．B 【解析】因为()f x 是R 上的增函数，令x x f =)(，所以x a x g )1()(-=，因为1>a ，所以)(x g 是R 上的减函数，由符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩知，1,0sgn[()]0,0sgn 1,0x g x x x x ->⎧⎪===-⎨⎪<⎩.16．C 【解析】∵2()()ax bf x x c +=+的图象与,x y 轴分别交于,N M ，且点M 的纵坐标与点N的横坐标均为正，∴0b x a =->，20by c=>，故0,0a b <>，又函数图象间断的横坐标为正，∴0c ->，故0c <．17．B 【解析】()f x 为奇函数，()g x 为偶函数，故()f x ()g x 为奇函数，()f x |()g x |为奇函数，|()f x |()g x 为偶函数，|()f x ()g x |为偶函数，故选B ．18．C 【解析】2222(log )10log 1log 1x x x ->⇒><-或，解得1202x x ><<或． 19．D 【解析】由()(2)f x f a x =-可知，准偶函数的图象关于y 轴对称，排除A ，C ，而B 的对称轴为y 轴，所以不符合题意；故选D ． 20．C 【解析】由已知得184212793a b c a b c a b c a b c -+-+=-+-+⎧⎨-+-+=-+-+⎩，解得611a b =⎧⎨=⎩，又0(1)63f c <-=-≤，所以69c <≤． 21．B 【解析】四个函数的图象如下显然B 成立．22．C 【解析】用x -换x ，得32()()()()1f x g x x x ---=-+-+，化简得32()()1f x g x x x +=-++，令1x =，得(1)(1)1f g +=，故选C ．23．A 【解析】因为[(1)]1f g =，且||()5x f x =，所以(1)0g =，即2110a ⋅-=，解得1a =．24．D 【解析】函数()1f x x =-和2()f x x x =+既不是偶函数也不是奇函数，排除选项A和选项B ；选项C 中()22x x f x -=-，则()22(22)()x x x x f x f x ---=-=--=-，所以()f x =22xx--为奇函数，排除选项C ；选项D 中()22x x f x -=+，则()22()x x f x f x --=+=，所以()22x x f x -=+为偶函数，选D ．25．D 【解析】2()1,()1f f πππ=+-=-，所以函数()x f 不是偶函数，排除A ；因为函数()x f 在(2,)ππ--上单调递减，排除B ；函数()x f 在(0,)+∞上单调递增，所以函数()f x 不是周期函数，选D ．26．A 【解析】当102x ≤≤时，令1()cos 2f x x π=≤，解得1132x ≤≤，当12x >时，令1()212f x x =-≤，解得1324x <≤，故1334x ≤≤．∵()f x 为偶函数，∴1()2f x ≤的解集为3113[,][,]4334--⋃，故1(1)2f x -≤的解集为1247[,][,]4334⋃．27．D 【解析】11lg 2lg lg(2)lg1022+=⨯==，()()3)13()]1f x f x x x +-=-++--+3)3)2x x =++ln 33)2x x ⎡⎤=+⎣⎦2ln (3)2x ⎡⎤=-+⎣⎦ln122=+=．28．D 【解析】∵|()f x |=22,0ln(1),0x x x x x ⎧-≤⎨+>⎩，∴由|()f x |≥ax 得，202x x x ax ≤⎧⎨-≥⎩ 且0ln(1)x x ax>⎧⎨+≥⎩，由202x x x ax ≤⎧⎨-≥⎩可得2a x ≥-，则a ≥-2，排除A ，B ，当a =1时，易证ln(1)x x +<对0x >恒成立，故a =1不适合，排除C ，故选D ． 29．C 【解析】是奇函数的为3y x =与2sin y x =，故选C ．30．C 【解析】1010x x +>⎧⎨-≠⎩，∴11x x >-⎧⎨≠⎩．31．A 【解析】()()112f f ---=-．32．A 【解析】本题考查的是对数函数的图象．由函数解析式可知)()(x f x f -=，即函数为偶函数，排除C ；由函数过)0,0(点，排除B ，D ． 33．C 【解析】1y x=是奇函数，x y e -=是非奇非偶函数，而D 在(0,)+∞单调递增．选C ． 34．B 【解析】由已知两式相加得，()13g =． 35．C 【解析】因为21(lg(log 10))(lg())(lg(lg 2))5lg 2f f f ==-=，又因为 ()()8f x f x +-=，所以(lg(lg 2))(lg(lg 2))5(lg(lg 2))8f f f -+=+=，所以(lg(lg 2))f =3，故选C ．36．D 【解析】由题意f (1.1)＝1.1－[1.1]＝0.1，f (－1.1)＝－1.－[－1.1]＝－1.1－(－2)＝0.9，故该函数不是奇函数，也不是偶函数，更不是增函数．又对任意整数a ，有f (a ＋x )＝a ＋x －[a ＋x ]＝x －[x ]＝f (x )，故f (x )在R 上为周期函数．故选D ．37．C 【解析】由函数解析式可得，该函数定义域为(－∞，0)∪(0，＋∞)，故排除A ；取x ＝－1，y ＝1113--＝32＞0，故再排除B ；当x →＋∞时，3x －1远远大于x 3的值且都为正，故331x x -→0且大于0，故排除D ，选C ．38．B 【解析】函数x y 2log =为偶函数，且当0>x 时，函数x x y 22log log ==为增函数，所以在)2,1(上也为增函数，选B ．39．B 【解析】∵π是无理数 ∴g （π）=0 则(())f g π=f （0）=0 ，故选B ．40．B 【解析】210,11,100 2.40,x x x x x +>⎧⎪+≠∴-<<<≤⎨⎪-≥⎩或故选B ．41．D 【解析】A 是增函数，不是奇函数；B 和C 都不是定义域内的增函数，排除，只有D正确，因此选D ．42．A 【解析】12log (21)0x +>，所以0211x <+<，故102x -<<． 43．B 【解析】3y x =为奇函数，21y x =-+在(0,)+∞上为减函数，2xy -=在(0,)+∞上为减函数．44．B 【解析】令函数()()24g x f x x =--，则()()20g x f x ''=->，所以()g x 在R 上为增函数，又(1)(1)240g f -=-+-=，所以不等式可转化为()(1)g x g >-，由()g x 的单调性可得1x >-．45．A 【解析】当0a >时，由()(1)0f a f +=得220a+=，无解；当0a <时，由()(1)0f a f +=得120a ++=，解得3a =-，故选A ．46．A 【解析】∵))(12()(a x x xx f -+=为奇函数，∴(1)(1)0f f -+=，得12a =．47．A 【解析】因为)(x f 是定义在R 上的奇函数，且当0x …时，2()2f x x x =-，∴2(1)(1)2(1)(1)3f f =--=-⨯-+-=-，选A ．48．B 【解】由()()f x f x -=得()y f x =是偶函数，所以函数()y f x =的图象关于y 轴对称，可知B ，D 符合；由(2)()f x f x +=得()y f x =是周期为2的周期函数，选项D 的图像的最小正周期是4，不符合，选项B 的图像的最小正周期是2，符合，故选B ．49．A 【解析】因为311x+>，所以()()22log 31log 10x f x =+>=，故选A ．50．C 【解析】∵()21200=+=f ，∴()()()a a f f f 2422202+=+==．于是，由()()a f f 40=得2424=⇒=+a a a ．故选C ． 51．B 【解析】()33(),()33()xx x x f x f x g x g x ---=+=-=-=-．52．A 【解析】∵()f x 是R 上周期为5的奇函数，∴(3)(4)(2)(1)(2)(1)211f f f f f f -=---=-+=-+=-．53．[2,)+∞【解析】要使函数()f x 有意义，则2log 10x -≥，即2x ≥，则函数()f x 的定义域是[2,)+∞．54．【解析】因为函数()f x 满足(4)()f x f x +=(x ∈R )，所以函数()f x 的最小正周期是4．因为在区间(2,2]- 上，cos ,02,2()1||,20,2x x f x x x π⎧<⎪⎪=⎨⎪+<⎪⎩≤-≤，所以1((15))((1))()cos24f f f f f π=-===． 55．1-【解析】由题意()f x 为奇函数，所以α只能取1,1,3-，又()f x 在(0,)+∞上递减，所以1α=-．56．sin y x =（不答案不唯一）【解析】这是一道开放性试题，答案不唯一，只要满足()(0)f x f >对任意的(0,2]x ∈都成立，且函数()f x 在[0,2]上不是增函数即可，如，()sin f x x =，答案不唯一．57．1(,)4-+∞【解析】当12x >时，不等式为12221x x-+>恒成立；当102x <≤，不等式12112xx +-+>恒成立；当0x ≤时，不等式为11112x x ++-+>，解得14x >-，即104x -<≤；综上，x 的取值范围为1(,)4-+∞．58．1[1,]2-【解析】因为31()2e ()e xx f x x f x x -=-++-=-，所以函数()f x 是奇函数，因为22()32e e 320x x f 'x x x -=-++≥-+≥，所以数()f x 在R 上单调递增，又21)02()(f f a a +-≤，即2())2(1a a f f ≤-，所以221a a ≤-，即2120a a +-≤，解得112a -≤≤，故实数a 的取值范围为1[1,]2-． 59．①④【解析】①()2()2xxxx ee f x e -=⋅=在R 上单调递增，故()2x f x -=具有M 性质； ②()3()3xxx x ee f x e -=⋅=在R 上单调递减，故()3x f x -=不具有M 性质； ③3()xxe f x e x =⋅，令3()xg x e x =⋅，则322()3(2)xxxg x e x e x x e x '=⋅+⋅=+，∴当2x >-时，()0g x '>，当2x <-时，()0g x '<，∴3()x x e f x e x =⋅在(),2-∞-上单调递减，在()2,-+∞上单调递增，故()3f x x =不具有M 性质；④2()(2)x x e f x e x =+，令()()22xg x ex=+，则22()(2)2[(1)1]0xxxg x e x e x e x '=++⋅=++>，∴2()(2)x x e f x e x =+在R 上单调递增，故2()2f x x =+具有M 性质．60．9(,]2-∞【解析】∵[1,4]x ∈，∴4[4,5]x x+∈ ①当5a ≥时，44()2224f x a x a a x a a x x =--+=---=-≤，所以()f x 的最大值245a -=，即92a =（舍去） ②当4a ≤时，44()5f x x a a x x x=+-+=+≤，此时命题成立．③当45a <<时，max ()max{|4|,|5|}f x a a a a =-+-+，则|4||5||4|5a a a a a a -+-+⎧⎨-+=⎩≥或|4||5||5|5a a a a a a -+<-+-+=，解得92a =或92a <，综上可得，实数a 的取值范围是9(,]2-∞．61．13(,)22【解析】由()f x 是偶函数可知，()0-∞，单调递增；()0+∞，单调递减又()(12a f f ->，(f f =可得，12a -112a -<∴1322a <<． 62．25-【解析】由题意得511()()222f f a -=-=-+，91211()()225210f f ==-=，由59()()22f f -=可得11210a -+=，则35a =，则()()()325311155f a f f a ==-=-+=-+=-． 63．1【解析】由题意()ln(())==-=-f x x x f x x x ，=x ，解得1a =．64．0、3【解析】∵(3)1f -=，(1)0f =，即((3))0f f -=．又()f x 在(,0)-∞上单调递减，在(0,1)上单调递增，在上单调递减，在)+∞上单调递增，所以min ()min{(0),3f x f f ==．65．32-【解析】当1a >时1010a b a b -⎧+=-⎨+=⎩，无解；当01a <<时1001a b a b -⎧+=⎨+=-⎩，解得2b =-，12a =，则13222a b +=-=-．66．(1,2]【解析】因为6,2()3log ,2a x x f x x x -+⎧=⎨+>⎩≤，所以当2x ≤时，()4f x ≥；又函数()f x 的值域为[4,)+∞，所以13log 24a a >⎧⎨+⎩≥，解得12a <≤，所以实数a 的取值范围为(1,2]．67．3【解析】∵函数()f x 的图像关于直线2x =对称，所以()(4)f x f x =-，()(4)f x f x -=+，又()()f x f x -=，所以()(4)f x f x =+，则(1)(41)(3)3f f f -=-==． 68．32-【解析】函数3()ln(1)xf x e ax =++为偶函数，故()()f x f x -=，即33ln(1)ln(1)xxeax e ax -+-=++，化简得32361ln 2ln xax x x e ax e e e+==+，即32361x ax x xe e e e+=+，整理得32331(1)x ax x xe e e ++=+，所以230ax x +=，即32a =-． 69．1【解析】2311()()4()21222f f =-=-⨯-+=．70．(-∞结合图形（图略），由()()2f f a ≤，可得()2f a -≥，可得a ． 71．【答案】（Ⅱ）x（或填（Ⅰ）k （Ⅱ）2k x ，其中12,k k 为正常数均可）【解析】过点(,())a f a ，(,())b f b -的直线的方程为()()()()f a f b y f a x a a b+-=--，令0y =得()()()()af b bf a c f a f b +=+．()()()()af b bf a f a f b +=+()()()()a b bf a af b =+，可取()0)f x x =>．（Ⅱ）令调和平均数2()()()()ab af b bf a a b f a f b +=++，得()()()()ab ba af b bf a a b f a f b ++=++，可取()(0)f x x x =>．72．(]0,1【解析】2110011011x x xx x ⎧+>⇒><-⎪⎨⎪-≥⇒-≤≤⎩或，求交集之后得x 的取值范围(]0,1. 73．(),2-∞【解析】由分段函数1x ≥，1122log log 10x ≤=；1x <，10222x<<=．74．6-【解析】由22()22a x a x f x ax a x ⎧--<-⎪⎪=⎨⎪+-⎪⎩…可知()f x 的单调递增区间为[,)2a -+∞，故362aa -=⇔=-． 75．32【解析】331113()(2)()()1222222f f f f =-=-==+=．76．1【解析】因为10x =>，所以(1)lg10f ==，又因为230()3af x x t dt x a =+=+⎰，所以3(0)f a =，所以31a =，1a =．77．34-【解析】30,2212,2a a a a a a >-+=---=-， 30,1222,4a a a a a a <-+-=++=- ．78．①③【解析】∵11(,)x y a =，22(,)x y b =，R λ∈，所以1212(1)((1),(1))x x y y λλλλλλ+-=+-+-a b对于①1111212(),((1))((1),(1))f m x y f a b f x x y y λλλλλλ=-+-=+-+-12121122(1)(1)()(1)()x x y y x y x y λλλλλλ=+----=-+--()(1)()f a f b λλ=+-,具有性质P 的映射,同理可验证③符合,②不符合,答案应填．79．①②④【解析】①0)2(2)2(2)22()2(111====⋅=---f f f f m m m m ，正确； ②取]2,2(1+∈m m x ，则]2,1(2∈m x ；mm x x f 22)2(-=，从而 x xf x f x f m m m -====+12)2(2)2(2)( ，其中， ,2,1,0=m ，从而),0[)(+∞∈x f ，正确；③122)12(1--=++n m n f ，假设存在n 使9)12(=+n f ，∵121[2,2)n n n ++∈，∴1(21)22121n n n n f ++=--=-，∴219,210n n +==，这与n Z ∈矛盾，所以该命题错误；④根据前面的分析容易知道该选项正确；综合有正确的序号是①②④.80．－1【解析】设(),()x x g x x h x e ae -==+，∵()g x 为奇函数，由题意()h x 也为奇函数．所以(0)0h =，解得1a =-．专题二函数概念与基本初等函数Ⅰ 第四讲指数函数、对数函数、幂函数一、选择题1．(2018全国卷Ⅰ)已知函数0()ln 0⎧=⎨>⎩，≤，，，x e x f x x x ()()=++g x f x x a ．若()g x 存在2个零点，则a 的取值范围是 A ．[1,0)-B ．[0,)+∞C ．[1,)-+∞D ．[1,)+∞2．(2018全国卷Ⅲ)设0.2log 0.3a =，2log 0.3b =，则A ．0a b ab +<> B ．b a c >>C ．c b a >>D ．c a b >>4．（2017新课标Ⅰ）设,,x y z 为正数，且235xyz==，则A ．235x y z <<B ．523z x y <<C ．352y z x <<D ．325y x z << 5．（2017天津）已知奇函数()f x 在R 上是增函数，()()g x xf x =．若2(log 5.1)a g =-，0.8(2)b g =，(3)c g =，则a ，b ，c 的大小关系为A ．a b c <<B ．c b a <<C ．b a c <<D ．b c a <<6．（2017北京）已知函数1()3()3x xf x =-，则()f xA ．是奇函数，且在R 上是增函数B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数 7．（2017北京）根据有关资料，围棋状态空间复杂度的上限M 约为3613，而可观测宇宙中普通物质的原子总数N 约为8010．则下列各数中与M N最接近的是（参考数据：lg 3≈0．48）A ．3310B ．5310C ．7310D ．9310 8．(2016全国I) 若1a b >>，01c <<，则A ．c c a b <B ．c c ab ba <C ．log log b a a c b c <D ．log log a b c c < 9．(2016全国III) 已知432a =，254b =，1325c =，则A ．b a c <<B ．a b c <<C ．b c a <<D ．c a b << 10．（2015新课标Ⅱ）设函数211log (2),1()2,1x x x f x x -+-<⎧=⎨⎩≥，则2(2)(log 12)f f -+=A ．3B ．6C ．9D ．1211．（2015北京）如图，函数()f x 的图像为折线ACB ，则不等式()()2log 1f x x +≥的解集是A ．{}|10x x -<≤B ．{}|11x x -≤≤C ．{}|11x x -<≤D ．{}|12x x -<≤12．（2015天津）已知定义在R 上的函数()21x mf x -=- （m 为实数）为偶函数，记0.5log 3a =，()2log 5b f =，()2c f m =则,,a b c 的大小关系为A ．a b c <>”是“log 3log 3a b <”的A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件 14．（2015山东）设函数31,1()2,1xx x f x x -<⎧=⎨⎩≥，则满足()(())2f a f f a =的a 的取值范围是 A ．2[,1]3B ．[0,1]C ．2[,)3+∞ D ．[1,)+∞15．（2014山东）已知函数log ()a y x c =+（,a c 为常数，其中0,1a a >≠）的图象如图，则下列结论成立的是A ．0,1a c >>B ．1,01a c ><<C ．01,1a c <<>D ．01,01a c <<<<16．（2014安徽）设3log 7a =， 1.12b =， 3.10.8c =，则A ．c a b <<B ．b a c <<C ．a b c <<D ．b c a <<17．（2014浙江）在同意直角坐标系中，函数x x g x x x f a a log )(),0()(=≥=的图像可能是18．（2014天津）函数212()log (4)f x x =-的单调递增区间是A ．(0,)+¥B ．(,0)-?C ．(2,)+¥D ．(),2-? 19．（2013新课标）设357log 6,log 10,log 14a b c ===，则A ．c b a >>B ．b c a >>C ．a c b >>D ．a b c >> 20．（2013陕西）设a , b , c 均为不等于1的正实数, 则下列等式中恒成立的是A ．·log log log a c c b a b = B ．·log lo log g a a a b a b = C ．()log og g l lo a a a b c bc =D ．()log g og o l l a a a b b c c +=+ 21．（2013浙江）已知y x ,为正实数，则A ．y x yx lg lg lg lg 222+=+ B ．lg()lg lg 222x y x y += C ．y x yx lg lg lg lg 222+=∙ D ．lg()lg lg 222xy x y =22．（2013天津）已知函数()f x 是定义在R 上的偶函数，且在区间[0,)+∞单调递增．若实数a 满足212(log )(log )2(1)f a f f a ≤+，则a 的取值范围是A ．[1,2]B ．10,2⎛⎤ ⎥⎝⎦C ．1,22⎡⎤⎢⎥⎣⎦D ．(0,2]23．（2012安徽）23(log 9)(log 4)⋅=A ．14 B ．12C ． 2D ． 4 24．（2012新课标）当102x <≤时，4log xa x <，则a 的取值范围是A．(0,2 B．(2C． D． 25．（2012天津）已知122a =，0.212b -⎛⎫= ⎪⎝⎭，52log 2c =，则,,a b c 的大小关系为A ．c b a <<B ．c a b <<C ．b a c <<D ．b c a << 26．（2011北京）如果,0log log 2121<<y x 那么A ．1y x <⎩≤，则满足()2f x ≤的x 的取值范围是A ．1[-，2]B ．[0，2]C ．[1，+∞）D ．[0，+∞） 29．（2010山东）函数22x y x =-的图像大致是30．（2010天津）设5log 4a =，5(log 3)b =2，4log 5c =，则A ．a <c <bB ．b <c <aC ．a 0，y >0，函数f (x )满足f （x ＋y ）＝f （x ）f （y ）”的是A ．幂函数B ．对数函数C ．指数函数D ．余弦函数34．（2010新课标）已知函数212log ,0()log (),0x x f x x x >⎧⎪=⎨-<⎪⎩，若a ，b ，c 均不相等，且()f a =()f b =()f c ，则abc 的取值范围是A ．（1，10）B ．(5，6)C ．(10，12)D ．(20，24)35．（2010天津）若函数212log ,0()log (),0x x f x x x >⎧⎪=⎨-<⎪⎩,若()()f a f a >-,则实数a 的取值范围是A ．(1,0)(0,1)-B ．(,1)(1,)-∞-+∞C ．(1,0)(1,)-+∞D ．(,1)(0,1)-∞- 二、填空题36．(2018江苏)函数()f x =的定义域为． 37．(2018上海)已知11{2,1,,,1,2,3}22α∈---，若幂函数()α=f x x 为奇函数，且在(0,)+∞上递减，则α=_____．38．(2018上海)已知常数0a >，函数2()(2)xx f x ax =+的图像经过点6()5P p ，、1()5Q q -，，若236p qpq +=，则a =__________．39．(2016年浙江) 已知1a b >>，若5log log 2a b b a +=，b aa b =，则a = ，b = ． 40．（2015江苏）不等式224x x-<的解集为_______．41．（2015浙江）若4log 3a =，则22aa-+=_______．42．(2014新课标)设函数()113,1,,1,x e x f x x x -⎧<⎪=⎨⎪≥⎩则使得()2f x ≤成立的x 的取值范围是__．43．（2014天津）函数2()lg f x x =的单调递减区间是________． 44．（2014重庆）函数2()log )f x x =的最小值为_________．45．（2013四川）____________．46．（2012北京）已知函数()lg f x x =，若()1f ab =，则22()()f a f b += ．47．（2012山东）若函数()(0,1)x f x a a a =>≠在[1,2]-上的最大值为4，最小值为m ，且函数()(14g x m =-[0,)+∞上是增函数，则a ＝＿＿＿＿．48．（2011天津）已知22log log 1a b +≥，则39ab+的最小值为__________． 49．（2011江苏）函数)12(log )(5+=x x f 的单调增区间是__________．专题二函数概念与基本初等函数Ⅰ 第四讲指数函数、对数函数、幂函数答案部分1．C 【解析】函数()()=++g x f x x a 存在 2个零点，即关于x 的方程()=--f x x a 有2个不同的实根，即函数()f x 的图象与直线=--y x a 有2个交点，作出直线=--y x a 与函数()f x 的图象，如图所示，由图可知，1-≤a ，解得1≥a ，故选C ． 2．B 【解析】由0.2log 0.3a =得0.31log 0.2a =，由2log 0.3b =得0.31log 2b=，所以0.30.30.311log 0.2log 2log 0.4a b +=+=，所以1101a b <+<，得01a bab+<<．又0a >，0b <，所以0ab <，所以0ab a b <+<．故选B ．3．D 【解析】因为2log e >1a =，ln 2(0,1)b =∈，12221log log 3log 13c e ==>>．所以c a b >>，故选D ．4．D 【解析】设235x y zk ===，因为,,x y z 为正数，所以1k >，则2log x k =，3log y k =，5log z k =，所以22lg lg3lg913lg 23lg lg8x k y k =⨯=>，则23x y >，排除A 、B ；只需比较2x 与5z ， 22lg lg5lg 2515lg 25lg lg32x k z k =⨯=<，则25x z <，选D ． 5．C 【解析】由题意()g x 为偶函数，且在(0,)+∞上单调递增，所以22(log 5.1)(log 5.1)a g g =-= 又2222log 4log 5.1log 83=<<=，0.8122<<，所以0.822log 5.13<<，故b a c <<，选C ． 6．A 【解析】11()3()(3())()33xx x x f x f x ---=-=--=-，得()f x 为奇函数， ()(33)3ln33ln30x x x x f x --''=-=+>，所以()f x 在R 上是增函数．选A ．7．D 【解析】设36180310M x N ==，两边取对数得，36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-≈，所以93.2810x =，即M N最接近9310，选D ．8．C 【解析】选项A ，考虑幂函数c y x =，因为0c >，所以cy x =为增函数，又1a b >>，所以c c a b >，A 错．对于选项B ，c cab ba <()cb b aa ⇔<，又()xb y a=是减函数，所以B 错．对于选项D ，由对数函数的性质可知D 错，故选C ．9．A 【解析】因为4133216a ==，2155416b ==，1325c =，且幂函数13y x =在R 上单调递增，指数函数16x y =在R 上单调递增，所以b a c <<，故选A ． 10．C 【解析】由于2(2)1log 43f -=+=，22log 121log 62(log 12)226f -===，所以2(2)(log 12)f f -+=9．11．C 【解析】如图，函数2log (1)y x =+的图象可知，2()log (1)f x x +≥的解集是{|11}x x -<≤．。

2018版高考数学大一轮温习第二章节函数概念与基本初等函数I 第3讲函数的奇偶性与周期性讲义理北师大版

B.y＝ex
C.y＝cos x
D.y＝ex－e－x
解析 A，B中显然为非奇非偶函数；C中y＝cos x为偶函数. D中函数定义域为R，又f(－x)＝e－x－ex＝－(ex－e－x)＝－f(x)，∴y＝ex－e－x为奇函数.
答案 D
3.已知 f(x)＝ax2＋bx 是定义在[a－1，2a]上的偶函数，那么
2
∴f(log2a)＋f(－log2a)≤2f(1)⇒f(log2a)≤f(1)，又 f(log2a)＝f(|log2a|)且 f(x)在[0，＋∞)上递增， ∴|log2a|≤1⇔－1≤log2a≤1.解得12≤a≤2. 答案 (1)D (2)C
规律方法 (1)函数单调性与奇偶性的综合.注意函数单调性及奇偶性的定义以及奇、偶函数图像的对称性. (2)周期性与奇偶性的综合.此类问题多考查求值问题，常利用奇偶性及周期性进行变换，将所求函数值的自变量转化到已知解析式的函数定义域内求解. (3)单调性、奇偶性与周期性的综合.解决此类问题通常先利用周期性转化自变量所在的区间，然后利用奇偶性和单调性求解.
答案 (1)C (2)1
规律方法 (1)已知函数的奇偶性求参数，一般采用待定系数法求解，根据f(x)±f(x)＝0得到关于待求参数的恒等式，由系数的对等性得参数的值或方程(组)，进而得出参数的值. (2)已知函数的奇偶性求函数值或解析式，首先抓住在已知区间上的解析式，将待求区间上的自变量转化到已知区间上，再利用奇偶性求出，或充分利用奇偶性构造关于f(x)的方程(组)，从而得到f(x)的解析式或函数值.
解析 (1)易知 f(－x)＝22－－xx＋－1a＝12－x＋a21x，由 f(－x)＝－f(x)，得12－x＋a21x＝－22xx＋－1a，即 1－a2x＝－2x＋a，化简得 a(1＋2x)＝1＋2x，所以 a＝1， f(x)＝22xx＋－11，由 f(x)>3，得 0<x<1.

专题03函数的概念与基本初等函数(含答案解析)

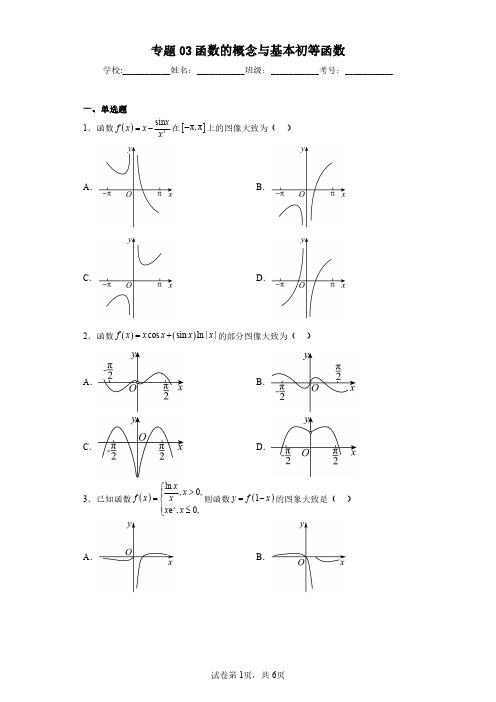
专题03函数的概念与基本初等函数学校:___________姓名：___________班级：___________考号：___________．．．．．函数()cos f x x x =+的部分图像大致为（）．．．．．已知函数()ln ,e ,x xx f x x x x ⎧⎪=⎨⎪⎩)的图象大致是（）．．．．．函数2cos ()xf x x x =+的大致图象为（．．．．．已知函数()2,x f x ⎧⎪=⎨⎛-⎪ ⎝⎩)a -，则实数a 的取值范围是（．()3,-+∞B ()3,+∞D ．已知函数5()2f x ⎧⎛⎫⎪ ⎪=⎨⎝⎭⎪⎩()f x x =-的零点个数为（．13二、多选题．已知函数()f x ⎧=⎨⎩则下列结论正确的是（）．()f x 是偶函数312f f π⎛⎫⎛⎫-= ⎪⎪⎝⎭⎝⎭()f x 是增函数()f x 的值域为[-三、填空题8．已知函数()()211log 2,12,1x x x f x x -⎧+-<=⎨≥⎩，则()()2f f -=__________.四、单选题五、多选题13．已知定义在R 上的函数()f x ，对于给定集合A ，若12,R x x ∀∈，当12x x A -∈时都有()()12f x f x A -∈，则称()f x 是“A 封闭”函数.则下列命题正确的是（）A ．()2f x x =是“[]1,1-封闭”函数B ．定义在R 上的函数()f x 都是“{}0封闭”函数C ．若()f x 是“{}1封闭”函数，则()f x 一定是“{}k 封闭”函数()*N k ∈D ．若()f x 是“[],a b 封闭”函数()*,N a b ∈，则()f x 不一定是“{}ab 封闭”函数14．对于定义在区间D 上的函数()f x ，若满足：1x ∀，2x D ∈且12x x <，都有()()12f x f x ≤，六、单选题15．已知函数()f x 的定义域为R ，且()21f x +为偶函数，()()()12f x f x f x =+-+，若()12f =，则()18f =（）A ．1B ．2C ．1-D ．2-八、单选题18．已知函数()f x 的定义域为R ，若函数()21f x +为奇函数，且()()4f x f x -=，2023 1()1kf k ==∑，则()0f=（）A．1-B．0C．1D．2九、多选题十、单选题十一、多选题十二、单选题十三、多选题27．已知2336x y ==，则下列说法正确的是（）A ．()2xy x y =+B ．16xy >C ．9x y +<D ．2232x y +<参考答案：由图象可知，函数()y f x =与即函数()g x 有3个零点，故选：C.7．BD【分析】利用反例可判断AC 选项.【详解】()12f =，而()1f -因为77cos 33f ππ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭()3012f f f π⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭，故当0x <时，()[]1,1f x ∈-，当故()f x 的值域为[1,)-+∞，故故选：BD.8．4【分析】根据分段函数的定义求解即可【详解】由()(211log 22,1x f x x -⎧+=⎨≥⎩所以()()(221log 22f -=+--所以()()()31232f f f --===【点睛】本题考查分段函数的单调性，小是关键，属于中档题．10．C【分析】根据已知可得{min sin 的单调性，可得()()12g g >>而得到实数m 的取值范围，即可得出答案【详解】当sin cos x x ≥时，原不等式可化为cos x mx >；所以，()333sin cos sin x x x =>，即()33sin cos sin 0x x ->.令()()sin cos sin F x x x =-，()0,1x ∈，因为函数sin y x =在()0,1上单调递增，cos y x =在()0,1上单调递减，且0cos 1x <<，根据复合函数的单调性可知，函数()sin cos y x =在()0,1上单调递减，所以()F x 在()0,1上单调递减.又()10F x =，()()310F x F x >=，所以31x x <.因为cos y x =在()0,1上单调递减，22sin x x <，所以()22cos sin cos x x >.又()22cos sin x x =，所以22cos x x >，即22cos 0x x -<.令()cos G x x x =-，()0,1x ∈，则()sin 10G x x '=--<恒成立，所以，()G x 在()0,1上单调递减.又()111cos 0G x x x =-=，()()2221cos 0G x x x G x =-<=，所以21x x >.综上可得，213x x x >>.故选：C.【点睛】关键点点睛：证明sin x x >在()0,1上恒成立.然后即可采用放缩法构造函数，进而根据函数的单调性得出大小关系.13．BC【分析】A 特殊值124,3x x ==判断即可；B 根据定义及函数的性质即可判断；C 根据定义得到R x ∀∈都有(1)()1f x f x +=+，再判断所给定区间里是否有22()()f x k f x k +-=成立即可判断，D 选项可判断出其逆否命题的正误，得到D 选项的正误.【详解】A ：当124,3x x ==时，121[1,1]x x -=∈-，而12()()1697[1,1]f x f x -=-=∉-，A 错误；B ：对于区间{}0，12,R x x ∀∈使120x x -=，即12x x =，必有12()()0f x f x -=，所以定义在R 上的函数()f x 都是“{}0封闭”函数，B 正确；C ：对于区间{}1，12,R x x ∀∈使{}121x x -∈，则121x x =+，而()f x 是“{}1封闭”函数，则22(1)()1f x f x +-=，即R x ∀∈都有(1)()1f x f x +=+，对于区间{}k ，12,R x x ∀∈使{}12x x k -∈，则12x x k =+，*N k ∈，而22()(1)1f x k f x k +=+-+，22(1)(2)1f x k f x k +-=+-+，...，22(1)()1f x f x +=+，所以222222()(1)...(1)(1)(2)...()1f x k f x k f x f x k f x k f x k +++-+++=+-++-+++-，即22()()f x k f x k +=+，故22()()f x k f x k +-=，()f x 一定是“{}k 封闭”函数()*N k ∈，C正确；D 选项，其逆否命题为，若()f x 是“{}ab 封闭”函数，则()f x 不是“[],a b 封闭”函数()*,N a b ∈，只需判断出其逆否命题的正误即可，12,R x x ∀∈使12x x ab -=，则12()()f x f x ab -=，若[],ab a b ∈，则ab a ab b a b ≥⎧⎪≤⎨⎪<⎩，由ab b ≤解得1a ≤，因为*N a ∈，所以1a =，即12,R x x ∀∈使[]12,x x ab b a b -==∈，则[]12()(),f x f x ab b a b -==∈，满足()f x 是“[],a b 封闭”函数()*,N a b ∈，故逆否命题为假命题，故原命题也时假命题，D 错误.故选：BC【点睛】关键点点睛：对于C ，根据给定的条件得到R x ∀∈都有(1)()1f x f x +=+，R x ∀∈有()()f x a f x b +=+恒成立，利用递推关系及新定义判断正误.14．ACD【分析】利用已知条件和函数的性质对选项逐一判断即可得正确答案.【详解】A.因为()()22f x f x +-=，所以令1x =得()()1212f f +-=，所以()11f =，故A 正确；()1y f x =+为()y f x =向左平移1个单位得到，是偶函数，故()3y f x =+为()y f x =向左平移3个单位得到，是奇函数，故由lg y x =在(,0)-∞上递减，且lg 101-=，lg 10-=；在(0,结合图象：看出()y f x =和lg y x =的图象有10个交点，即故C 错误：由()10f =，()21f =，()30f =，()41f =-，()50f =，则()()()1280f f f ++⋅⋅⋅+=，所以()()()()2023125201271k f k f f f ==⨯+++⋅⋅⋅+=-⎡⎤⎣⎦∑，故故选：AB17．ABD。

2018年高考数学大纲

咼考数学018年的高考中，核心考点仍然是函数与导数、三角函数、解三角形、数列、立体几何、解析几何、概率与统计、选考内容等•在选择题或填空题中，集合、复数、程序框图、三视图、三角函数的图象和性质、线性规划、平面向量、数列的概念与性质、圆锥曲线的简单几何性质、解三角形、导数与不等式的结合、函数的性质仍然是高频考点.在解答题中，除数列和三角函数轮流命题外，立体几何、概率与统计、解析几何、函数导数与不等式、选考内容仍然是必考内容数学考点（一）函数和导数函数是高中数学内容的主干知识，是高考考查的重点•高考中主要考查函数的概念与表示、函数的奇偶性、单调性、极大（小）值、最大（小）值和周期性；考查幕函数、指数函数、对数函数的图像和性质以及函数的应用；考查导数的概念、导数的几何意义、导数的运算以及导数的应用；重点考查利用导数的方法研究函数的单调性、极大（小）值、最大（小）值，研究方程和不等式.对函数和导数的考查侧重于理解和应用，试题有一定的综合性，并与数学思想方法紧密结合，对函数与方程思想、数形结合思想、分类讨论思想等都进行深入的考查，体现能力立意的命题原则. （二）数列数列是高中数学的重要内容，高考主要考查数列的概念以及等差数列、等比数列的概念、性质、通项公式与前n项和公式.其中，等差数列、等比数列的通项公式与求和公式是考查的重点. 数列试题的考查突出基础性，重点考查考生对数列通性通法的理解与应用；数列试题也具有一定的综合性，将对基础知识的考查和对能力的考查有机结合.（三）不等式不等式是高中数学的基本内容，高考主要考查不等式的性质、简单不等式的解法、基本不等式的应用以及二元一次不等式组与简单线性规划问题•对不等式的考查体现综合性和应用性，与其他知识综合，与数学思想方法紧密结合.（四）三角函数三角函数是高中数学的重要内容.高考主要考查任意角三角函数的概念和正弦函数、余弦函数、正切函数的图像和性质，突出考查形如的函数的图像与性质，考查两角和与差的三角函数公式及简单的三角恒等变换，重点考查正弦定理和余弦定理及其应用.对三角函数的考查重点是基本概念、基本公式的理解和应用以及运算求解能力.（五）平面向量平面向量具有几何形式和代数形式，是中学数学知识的一个交汇点.高考主要考查平面向量的概念、线性运算、平面向量基本定理、坐标表示、数量积及其应用.平面向量的考查重点是基础知识、基本技能和数形结合的思想方法，考查中将几何知识和代数知识有机结合，体现思维的灵活性. （六）立体几何立体几何是高中数学的重点内容，是考查空间想象能力的重要载体.高考主要考查三视图，柱、锥、球的表面积和体积，直线与直线、直线与平面、平面与平面的位置关系，其中，几何元素间的位置关系和度量关系是考查重点.立体几何试题突出综合性，综合考查考生的空间想象能力、推理论证能力和运算求解能力.（七）解析几何解析几何是高中数学的重要内容.高考主要考查直线与圆、椭圆、抛物线、双曲线的定义、标准方程和简单的几何性质.其中，直线与圆、直线与圆锥曲线的位置关系是考查重点.运动与变化是研究几何问题的基本观点，利用代数方法研究几何问题是基本方法.试题强调综合性，综合考查数形结合的思想、函数与方程的思想、特殊与一般的思想等思想方法，突出考查考生的推理论证能力和运算求解能力.（八）统计与概率统计与概率是高中数学的重要内容.高考主要考查随机抽样、用样本估计总体、变量的相关性、随机事件的概率、古典概型、几何概型、回归分析、独立性检验.其中，用样本估计总体、古典概率的计算、应用回归分析与独立性检验思想方法解决简单实际问题的能力是考查的重点.试题强调应用性，以实际问题为背景，构建数学模型，突出考查统计与概率的思想及考生的数据处理能力和应用意识.（九）算法算法是高中数学的基本内容，高考主要考查算法的含义、程序框图、基本算法语句.理科数学1・考核目标与要求根据音通吝寻学校对新主文化亲质的要求，依据中华人民共和国救育部2003年预布的《普通高中课程方案〔实验D和《普通高中数学课程标准（实验）》的必修漂程、:i三逞巨壬列2和系列4的内容，确定理工类高考数学科考试内容.一、知识要求知识是指《習通吝中数学谍谨标崔（实验”（以下简称：课豆标准O=P所刼定的必修澡程、选修课移妄列2和系列4中的数学槪念、性更、法则、公弍、公理、定理以及由其内容反咬的数学思想方法，还包括按照一定隹序与步骤进行运算、处理数据、绘削图表寻基本技能・各部分知识的整体要求及其定位参照《课移标准》柜应填块的有关说明.对知识的要求依次是了解.理解.拿夷三个层次・1.了禅：要求对所列気识的含文有初步的.感性的认识，知道这一丹识内容是尸么，按黑一定的穫序和步骥照样模仿，并能（或会）在有关的问题中识别和认识它.这一层次所涉及的主要行为动词有：了解，丸道、识别，模仿，会求.会解等・2.亘蒔:要求对所列知识内容有絞深刻的理性认识，知道知识闾的逻辑关系，能够对所列知识做正魂的玮述说明并用数学语言表达,能務利用所学的知识内容对有关问题进行比较. 判别、讨论,具备利用所学知识解决简单问題的能力.这一昙次所涉及的主要行为动诃有：描述，说退表达，推孤想象•比较、判别,初步应用等.3.拿捏:要求能够对所列的知识内容进行推导证明，能够利用所学知识对问題进行分析. 研究.讨论，并且加以解决.这一层次所涉及的主要行为动词有：事握.昌出■分析,推导、证明，研究.讨论、运用、解决问題等.二.能力要求能力是指空间想鉄能力、抬象槻括能力.推進论证能力、运算求解能力、数捋处理能力以及应用意识和创靳意识.1.空间炬象能力：能很捋条件作出正确的图形，很据茎形想象出宜观形象：能正确地分析出图形中的基去元袁及其相互关丢：能对茎形进行分解、组台：会运乏图形与匿表等手段形象地掲示问題的本质.空伺姬象能力是对空间形式的观察.分析、主象的能力，主要表现为识荃、亘图和对图形的想象能力.识匡杲指观察餅究所给图形中几何元素之伺的相互关丢：画丕是指将文字语言和符号语言转化为国形语言以及对因形添加辅助国形或对国形进行各种变按;对图形的想象主要色括有国想图和无图想图两种，是空伺想象能力高层次的标志.2•希象槻括能力：抽象是指舍弃事物非本质的属性，捲示其本质的属性：奄括是指狂仅仅爱于某一类对象的共同壤性区分出来的思维过程.生皺和概括是鹉互联系的，没有社欽零不可能有概括，而概括必须在把象的基础上得出某种观点或某个结论.抽彖概括能力是对具体的•生动的实例，经过分析提炼-•发现窃究对象的本眞：从给是的犬量信息材料中概括出一些结论，并能埒其应用亍解决问題或傲出新的判鲂.3•生理论证能力：推理是思维的基本形式之一，它主前提和结论两歆分组成；论证是由己有的正确的前提到祓论证的结论的一连串的推理过程.推理啜色括演绎推理，也包括舍情圣理：论证方法既色話按形式划分的演经法和归纳法,徑色括按患考方法划分的宜接迁法和面接证法一般运用合倩推理迸行猜鶴再运用演绎推理进行证明.中学数学的推逢论还能力是根捋己知的事实和己获得的正縫数学命題,论证某一数学命题真实性的初步的推理能力.4.运算求解能力：会視捋法则、公式进行丘确运算、变形和数据处理，能根寿问题的条•牛寻接与设计合理、简捷的运算途径,能根据要求对数据进行估计和近似计算.运算求解能力是思维能力和运算技能的结合•运算包括对数字的计算、估值和近似计算，对弍子的坦合变形与分解变形,对几何国形各几何量的计算求解等.运算能力包矣分析运算条件、税究运算方向.选择运算公式、确定运算程序尊一系列过程中1的恿维能力，也包括在实施运算过程中遇到隨碍而调整运算的能力.5•魅捋处蚕能力：会收集、至理.分析麹氐能从大量数据中抽取对研兖叵题有审的信息，并做出判断・数务处妾能力主要是指针对研究对欽的特殊性，选择合蚕的牧集数空的方法，根空问题的具体情况，选择合适的统计方法整蚕数推，并构建模型对雄进行分析、推断，获得结论.6•应用怠识：能综合应用所学数学知识.思想和方法解决何题■包括解决相关学科、生产、生活中简单的数学问题：能理解对问題陈述的材料,并对所提供的信息资料进行归纳、整理和分类，将实际问題招彖为数学问題：能应巨相关的数学方法解决问题进而加以验证，并能用数学淆言正确地表达和说明.应臣的主要过程長依摊现实的兰活背長，実炼相关的数量关系，将现实问題扶化为数学问題，构造数学模型,并加以解决.7•创新意识：能发现问题、提出问题，综合与灵活地应用所学的数学知识、思坦方法，选择有效的方法和手段分析信息,进行独立的思考、探素和研究，畫出解决问题的思躡创造性地解决问题.创蔚意识是理性思维的高层次表观.对数学问题的“观聚、猜测、毛象、槪君、证明”，杲发现问题和解决问題的重要送径，对数学知识的迁移、组台、融会的程更越哥，显示出的创新意识也就越程.三、个性品质要求个性品质是指考生个体的情超、态度和价值观•要求冬生具有一定的数学规野，认识数学的科学价值和人文价值,崇尚数学的理性緒格形成审慎的思维习惯，体会数学的美学意义.要求考生克服緊张情绻，以平和的心态参加考试,合理支配考试时闾，以实事求是的科学态度解答试题,钙立战往困难的信心，体现螟而不舍的靖禅.四、考査要求数学学科的系统性和严密性决定了数学気识之阖深刻的内在联系，包括各部分知识的纵向联系和模向联系••要善于从本质上抓住这些联系，进而通过分类、梳理.综合，构建数学试卷的框架结构.1.对数学荃碇知识的考奁，匪要全面文要突出垂点•对于支撞学科知识体来的垂点内容, 要占有较大的比例，构或数学试巻的主体.注更学科的内在醱系和辺识的综合性，不刻意追求知识的茨苣面•从学科的整体高度和思维价值的高度考虑问题，在知识网络的交汇点处设计试题，使对数学基础知识的考査达到必要的深度.2.对数学•更想方法的考查是对数学知识在更咅层次上的抽象和概括的考査，考査时必须要与数学矩识梅结台，通过对数学丸识的考查•反映考生对数学思炬方法的拿灸程度・23・对数学能力射考査•謝虎“以能力立意J就是以数学気识为载亦从问题入手••把徨学科的整体怠义，用统一的数学观•点组织材料，侧更体现对知识的亘蒔和应巨••尤其是淙合和灵活的应甩•以此来检滾考生将知识迁移到不同情境中去的能力,从而检测出考主个体理性思维的广度和深度以及进一步学习的潜能・对能力的考査要全面再茧谓综台性、应用性，并要切合考生实际•对推灸论证能力和拒叙覆括能力的考查英穿于全卷•，是考査的篡.钛再调其科学性、严谨性、抽象性：对空阿想象能力的考查主要竹现在对文字语言、符号语言及图形语言的互絹转化上：对运算求解能力的考査主要是对算法和走理的考査••考査以代数运算为主：对数据处理能力的考查主要是考查运用概率统计的基本方:去和思想解决实际问題的能力.4.对应用意识的考査主要采用解决应用问题的形式•金题时要坚持“贴近主活,背養公平，控创难度”的原则，试题设计要切合中学数学教学的实际和考生的年龄特点，并结合实践经验,便数学应用问题的难燮為合考生的水平.5.对创新言识的考査是对高层次理性思维的考奁•在考试中创设餉紙的问趣倩境,构這有一定浜度和广度的数学问题时,要注重问题的多样化，体现思维的发散性:猜心设计考查数学主体内容.体现数学袁质的试题：徑要有反咲数、形运动变化的试题以及硏究型、探素型、开放型等类型的试题.数学科的锂题佐考查基砒知识的基咄上注重对数学恿想方法的考查••注重对数学能力的考査婆现数学的科学价直和人文价值••同时兼颈试題的基咄性、综合性和应用性,亘观试題间的层次性，台理调M综合程度.坚持多角雯、多层次的冬查••努力实现全面考査综台数学素养的要求.DL考试范围与要求本部分包括必考内容和选考内容两部分•必考内容为《课程标進$的必修内容和选修系列2的内容：选考内容为：课隹标進》的选修系列4的“坐标系与参数方程”、“不等式选讲”等2个专题・必考内客(―)集合1.集合的含义与表示(D 了號集台的含义.元素与集合的履于关杀.(2)饋用自然语言、图形语言.裳合语言(列举法或描述法)描述不同的具体问题.2.集合间的基本关系(1)理解集合之何包含与相等的含义，能识别给定集合的子笑.⑵在具体情境中，了解全集与空集的含义.3.集合的基本运算(D婕解两个集合的并集与交集的含义,会求两个简至集合的并集与交冥.⑵屋解在给定集合中一个子集的补笑的含义，会求给定子冥的补集.(3)能论用韦恩(Venn)冕表达集合的关系及运算.(二)函数概念与基本初等函数I (指数函数.对数函数.專函数)1 •函数(D了解构成函数的要素，会求一些简单函数的定文域和值域；了解鉄射的概念.⑵在实际倩境中,会根捋不同的需要选择恰当的方法(如图像法、列表法、解析法)表示函数.(3)了解简单的分段函数，井能倚单应用.(4)理解函数的車谩性、最大值、冬小值及其几何意文：结合具体函数，了解函数奇偶性的含义(5)会运用函数图線理解和硏究函数的性氐2.指数函数(1)了解指数函数模型的实际背最.(2)理解肓亘务数驀的含义，了解实数指数幕的意义，掌握幕的运算.(3)瘻解指数函数的概念，雀解指数函数的单谓性，事再务数函数运像適过的特殊点.(4)知道指数函数是一类重要的函数模型.3.对数劇数(1)W 对数的概念及其运算性质，知道用換克公式能将一般对数銭化成自然对数或常用对数：了解对数在简化运算中的作用.⑵理解对数函数的概念，蚕幕对啟函数的单谓性,事捏对数函数匡像通过的粹殊点.(3)知道对数函数是一类里要的函数模翌.(4)7解指数函数J = a'与对数函数y = kg X互为反函数(a >0,且“ I)・4.慕函数(1)7解禧函数的概念.⑵结台函数尸小v = x2, y = x\ y = l,尸，的图缴，了籬它们的变化情込x5.函数与方程(1)结台二次函数的图爼了解函数的零点与方程根的联系，判新一元二次方移根的存在性及根的个数.(2)根毎具体函数的图嫁•，能够用二分法求相应方程的近似解.6.函数模型及其应用(1)了解指数函数、对数函数以及慕函数的增长特征，知道亘线上升、指数増冬、对数増长等不同函数类型增长的含义.(2)了解函数模型如指数逅数、对数西数、基函数、分段函数尊在社会生活中普這便乏的函数模型)的广泛应月.(三)立体几何初步1.空间几何体⑴认识柱、铿、台、球及其简单组合体的结构特征,并能运巨这些特征描述现实生活中简单物传的结构.⑵能画出简单空间图形(长方体、球、楚柱、圆链、棱柱等的简易组合)的三视国，能识别上述三视图所表示的立体模型，会用斜二画法画出它们的直观适.⑶会用平行投影与中心投影两种方法画出简单空间图形的三视图与亶观图，了解空间图形的不同表示形式.(4)会逼茶些建氏初的视国与宜观图(在不影旄图形特征的基础上,尺寸、钱冬寻不作严络要求).(5)7解球、棱性、棱链、台的表面积和体积的计算公式.2•点、直线、平面之间的位置关慕(D理輕空叵亘线、平面住宣关系的是文,并了解如下可以作为挂亘※掲的公理和定蚕.•公理1：妁果一条亘践上的两.点在一个平面内，那么这条豊线上所有的点都在此平面内.•公長2：过不在同一条言线上的三点，有且只有一个平面••公理3：妇果两个不重合的平面有一个公关，点，那么它们有且只有一条过该点的公共直线.・公理4：平行于同一条宜线的两条直线互相平行.•走理^空囱中如果一个角的两边与另一个角的两边分别宁行，那么这两个角相等或互补.(2)以立体几何的上述走义、公理和走理为出发点，认识和理解空伺中线面平行、垂宣的有关性质与判定走理.理解以下判定走理.4•妇果平肓外一条直线与此平面内的一条直线平行，那么该直找与此平页平行.•如果一个平面内的两*柜交直线与另一个平面茹平行，那么这两个平肓平行.•妁果一条苣践与一个平面内的两条相交直践至垂宣••茹么该直裟与此平面垂豊.•如果一个平面经过另一个平面的垂线，那么这两个平面互柜垂宜.理解以下性质定理,并能够证明.•如果一条宣践与一个平面平行，那么经过该直线的任一个平面与此平豆的交线和该直线平行.•如果两个平行平面同时和第三个平面柜交,那么它们的交线相互平行.•垂直于同一个平面的两条直线平行.•如果两个平面垂1L•那么一个平面内垂宜亍它们交线的直线与另一个平面垂建.3・能运甬公理.定理和己获得的结论证明一些空伺芟形的位宣关系的简单创题.(四)平面解析几何初步1.直线与方程(1)左平面直角坐标系中，结合具体图形,确是宜线位置的几何要素.(2)爰解直线的倾斜角和斜率的概念，拿握过:两•点的直线斜率的计算公式.(3)能根捋两条直线的斜率判走这两条直线孚行或垂直.(4)拿翼魂走直线泣置的几何姜素,拿握直线方程的几种形式(点斜式.两点式及一般弍), 了翘斜截式与一次函数的关系.(5)能用解方程组的方法求两冬相交直线的交点坐标.(6)事霆两点间的距离公式、点到直钱的距离公式，会求两*平行直践间的距複.2.圆与方程(D事霆魂定圆的几何要素，拿提圆的标准方程与一般方程.(2)能很捋给定直缴更的方程判断宜线与圆的位置关系；能抿盘给走两个艾的方程判断两圆的位置关系(3)能用直践和圆的方隹解决一些简单的问题.(4)初步了解用代数方法处理几何问題的患想.3.空闾直角坐标系(D 了解空直宜角坐标来，会用空底亘角坐标表示点的住宣.⑵会生导空间两点阿的距离公式(五)算法初步1.算法的含义、程序框国(1)7解算法的含义，了解算法的恿想.(2)W程宇框国的三种基本逻辑结构：顺序、条件分支「繪环.2.基本算法语句56理解几种基本算法语句一复入语句、输出语句、赋直语句、黃件语句、循环语句的含义.(六) 统计1. 随机抽样(D 理解随机抽样的必要性和重要性.(2) 会用简单随机抽样方法从总体中抽取样本：了解分层抽样和来统抽样方法.2. 用样本估计总体(D 了解分布的意义和作用，会列频坚分布表，会画频率分布直方罢、频率折线图、茎廿图，笔解它们各自的特点.(2) 理解样本数据标進差的意JC 和作用，会计算数圣标進差.(3) 能从样本数据中提取基本的数孚特征(妁平均瓠标准差)，并给出台瘵的解轻.⑷会用样本的频率分布估计总体分杞会用样本的基本数字特征估计总体的基本数孚特征，理鲜用样本估计总体的思花.(5) 会用随机推样的基本方法和样本估计总体的思想解决一些置单的实际问题.3. 变量的相关性⑴会作两个有关駐变量的数据的敢点園会利巨敢点国认识变量⑧的昭关关系.(2) 了解最小二乘法的恿想••能根捋给出的线性回归方隹系数公式建立线性回归方程.(七) 概率1. 事件与概率(1) 了解随机爭件发生的不确定性和頻率的稳定性，了解概率的意义，了解频率与概率的区别.(2) 7解两个互丘事件的概率加法公式.2. 古典概型(D 理解古英概型及其概率计算公式.(2)会计算一些随机事件所含的基本爭件数及爭件发生的概率.3. 随机数与几何概型(1) 了解随机数的意义,能运用模拟方法估计概率.(2) 了解几何概型的意义.(八) 基本初等函数U(三角函数)1•任意角的概念.拆度測(1) 了解任意角的概念•(2) 7解弧受刨的概念,能进行弧燮与角度的互化•2. 三角函数(D 理解任意角三角函数(正弦、余弦、正切)的定文.(2)能利用单位圆中的三角更数线推导出彳士a, 的正弦、余弦、正切的诱导公式,能画出y-srnx, j = cosx, y = tanx 的国象了解三角更数的周期性・⑶理解正弦函数、余弦函数在区间［0.2K ］上的性质(妇单调性.最大值和最小疽以及⑷理解同角三角逐数的基本关系式:与：r 袖的交点尊),理解正切函数在区间内的至谓性.sin 2x + cos 2x-L — tanx.COST 7⑸了解函数y = /15in(g・ + e)的物理意义：能画出,v = Jsin(^.v + ^)的匿爼了解参数・4, 孙卩对函数图像变化的影戦(6)了解三角函数是描述周期变化现象的重要函数模型,会乏三角函数解决一些筍单实际问题・(九)平面向量1.平面向量的实际背景及基本概念(1)7解向量的实际背最.(2)理解平面向量的概念,理解两个向量柜等的含义.(3)理解向量的几何表示.2.向量的线性运算⑴事湼向量加法、减法的运算,并理解其几何意文.(2)事涅向量软乘的运算及其几何意义，理解两个向量共线的含文.(3)了解向量线性运算的性质及其几何意义.3.平面向虽的基本定理及坐标表示(1)7解平面向量的基本定理及其意义.(2)事徨平面向量的正交分解及其坐标表示.(3)会用坐标表示平面向董的加法、减法与数乘运算.(4)長解用坐标表示的平面向量共线的条件.4・平面向童的数量积(1)長解平面向量敦量秩的含义及其初理意义.(2)了解平面向量的数量积与向量授影的关系.(3)拿霆数量积的坐标表达式，会送行平面向量数量积的运算.⑷能运足数量秩表示两个向量的夹角，会用数量秩裁断两个平面向莹的垂直关系.5.向量的应用(1)会用向量方法解决某些匱单的平页几何问題.(2)会用向量方法筋决简单的力学问题与其他一些实际何题.(十)三角恒铮变换1.和与誉的三角函数公式(1)会用向量的数量积推导出两角巻的余弦公式.(2)能利用两角蚤的余弦公式导出两角差的正弦、正切公式.(3)能利冃两角差的余弦公式导出两角和的正弦、余弦、正切公弍，导出二铠龟的正弦、余弦.正切公式，了解它们的内在联系.2.简单的三角這尊变涣髭运扁上述公式送行筍单的恒尊变换(包括导出积化和垒、和雀化积、半角公式,但对这三组公弍不要求记忆).(十一)解三角形1.正弦定理和余弦定理拿睜正弦定理、余弦是理，并能解决一些简单的三角形度重问题.2•应用能哆运用正弦是理.余弦定爰尊远识和方法解决一些与瀝量和几何计算有关的实际问题.(十二)数列1 •敢列的概念和简单表示法。

新高考数学总复习专题三函数及其性质课件

考点五函数的周期性对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有f(x+T)=f(x),那么就称函数y=f(x)为周期函数,称T为这个函数的周期.如果在周期函数f(x)的所有周期中存在最小的正数,那么这个最小正数就叫做f(x)的最小正周期. 【注意】并不是所有的周期函数都有最小正周期,如f(x)=5.
偶函数
考点四函数的奇偶性
满足的充要条件
图象特征
对定义域中任意的x,都关于原
有f(-x)=-f(x)
点对称
对定义域中任意的x,都关于y轴
有f(-x)=f(x)
对称
【注意】既是奇函数又是偶函数的函数只有一个,即f(x)=0,x∈D.其中定义域D是关于原点对称的非空数集. 【知识拓展】 1)对于奇函数: ①如果定义域中包含0,那么f(0)=0; ②若函数在关于原点对称的区间上有最值,则f(x)max+f(x)min=0; ③在关于原点对称的区间上单调性相同. 2)对于偶函数: ①f(x)=f(|x|); ②在关于原点对称的区间上单调性相反.
减函数,又因为f(-4)=0,所以f(4)=0,作出函数f(x)的大致图象如图所示.
由 f (x 4) f (x 4) >0,得 f (x 4) f [(x 4)] >0,即 2 f (x 4) >0,
x
x
x
则有
f x
(x 0
4)
0,
或
f x
(x 0,
4)
0,
则 x 40,x
C. f(x)=ln 2 x
2 x
D. f(x)=e-x-ex
(2)(202X河北张家口一模,8)设f(x)是R上的奇函数,且f(x)在(-∞,0)上是减

2018年高考数学一轮复习第二章函数概念与基本初等函数Ⅰ2.1函数及其表示课件文新人教A版

§2.1 函数及其表示
考纲展示► 1.了解构成函数的要素，会求一些简单函数的定义域和值域，了解映射的概念． 2．在实际情境中，会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数． 3．了解简单的分段函数，并能简单地应用(函数分段不超过三段)．考点1函数的概念
1.函数与映射的概念
解析：①②中，对于定义域内任意一个数 x，可能有两个不同的 y 值，不满足对应的唯一性，所以①②错误；③中，定义域是空集，而函数的定义域是非空的数集，所以③错误．
函数与映射理解的误区：唯一性；非空数集．
①②④ 是映如图表示的是从集合A到集合B的对应，其中________ ①② 是函数．射，________
解析：函数与映射都要求对于集合A中的任一元素在集合B 中都有唯一确定的元素与之对应，所以③不是映射也不是函数；①②④表示的对应是映射；①②是函数，由于④中集合A， B不是数集，所以不是函数．
[典题1]
(1)下列四个图象中，是函数图象是( B )
A．① C．①②③
B．①③④ D．③④
[解析]
①中每一个 x 的值对应唯一的 y 值，因此是函数图
象，②中当 x>0 时，每一个 x 的值对应两个不同的 y 值，因此不是函数图象，③④中每一个 x 的值对应唯一的 y 值，因此是函数图象．故选 B.
(2)已知函数 f(x)和 g(x)的定义域和值域都是集合{1,2,3}，对应法则如下表. x f(x) g(x) 1 2 1 2 3 3 3 1 2
考点2 函数的定义域
对函数 y＝f(x)，x∈A，其中 x 叫做自变量，x 的取值范围 A 叫做定义域，与 x 的值对应的 y 值叫做函数值，函数值的集合 {f(x)|x∈A}叫做值域．求函数定义域的常见结论： (1)分式的分母不为零； (2)偶次根式的被开方数不小于零； (3)对数函数的真数必须大于零；

全国通用2018版高考数学一轮复习第二章函数概念与基本初等函数I第1讲函数及其表示课件理北师大版

解析 (1)要使函数 f(x)有意义，应满足x－x 1>0，解得 x>1，故 x≥0，
函数 f(x)＝lnx－x 1＋x12的定义域为(1，＋∞).
(2)∵y＝f(x)的定义域为[1，2 017]，
∴g(x)有意义，应满足1x－≤1x＋ ≠10≤ . 2
017， ∴0≤x≤2
016，且
x≠1.因此 g(x)的定义域为{x|0≤x≤2 016，且 x≠1}.
答案 (1)C (2)[－1，0]
考点二求函数的解析式【例 2】 (1)已知 f2x＋1＝lg x，则 f(x)＝________.
(2)已知 f(x)是二次函数且 f(0)＝2，f(x＋1)－f(x)＝x－1，则 f(x)＝________. (3)已知函数 f(x)的定义域为(0，＋∞)，且 f(x)＝2f1x· x－ 1，则 f(x)＝________.
第1讲函数及其表示
最新考纲 1.了解构成函数的要素，会求一些简单函数的定义域和值域，了解映射的概念；2.在实际情境中，会根据不同的需要选择恰当的方法(如图像法、列表法、解析法)表示函数；3.了解简单的分段函数，并能简单地应用(函数分段不超过三段).
知识梳理
1.函数的基本概念 (1)函数的定义给定两个非空_数__集_A和B，如果按照某个对应关系f，对于集合A中_任__何__的一个数x，在集合B中都存在唯一的数f(x)与之对应，那么就把对应关系f叫作定义在集合A上的函数，记作 f：A→B或_y_=_f_(_x_),_x_∈__A_，此时x叫作自变量，集合A叫作函数的定义域，集合{f(x)|x∈A}叫作函数的值域.
【训练 1】 (1)(2015·湖北卷)函数 f(x)＝ 4－|x|＋lgx2－x－5x3＋6的

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题03 函数的概念与基本初等函数I
（二）函数概念与基本初等函数Ⅰ（指数函数、对数函数、幂函数）
1．函数
（1）了解构成函数的要素，会求一些简单函数的定义域和值域；了解映射的概念.
（2）在实际情境中，会根据不同的需要选择恰当的方法（如图象法、列表法、解析法）表示函数.
（3）了解简单的分段函数，并能简单应用.
（4）理解函数的单调性、最大值、最小值及其几何意义；结合具体函数，了解函数奇偶性的含义.
（5）会运用函数图象理解和研究函数的性质.
2．指数函数
（1）了解指数函数模型的实际背景.
（2）理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算.
（3）理解指数函数的概念，理解指数函数的单调性，掌握指数函数图象通过的特殊点.
（4）知道指数函数是一类重要的函数模型.
3．对数函数
（1）理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用.
（2）理解对数函数的概念，理解对数函数的单调性，掌握对数函数图像通过的特殊点.
（3）知道对数函数是一类重要的函数模型.
（4）了解指数函数与对数函数互为反函数（a>0，且a≠1 ).
4．幂函数
（1）了解幂函数的概念.
（2）结合函数
1
232
1
,,,,
y x y x y x y y x
x
=====的图象，了解它们的变化情况.
5．函数与方程
（1）结合二次函数的图象，了解函数的零点与方程根的联系，判一元二次方程根的存在性及根
的个数.
（2）根据具体函数的图象，能够用二分法求相应方程的近似解. 6．函数模型及其应用
（1）了解指数函数、对数函数以及幂函数的增长特征，知道直线上升、指数增长、对数增长等不同函数类型增长的含义.
（2）了解函数模型（如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型）的广泛应用.
1．涉及本专题知识的考题，大多以选择题、填空题的形式出现，可易可难，预测2018年高考仍然会出小题.
2．函数的概念及其表示：考查函数的概念、定义域和值域，函数的解析表示法，其中常以分段函数为载体考查函数、方程、不等式等知识的综合.
3．函数的性质：考查单调性，可以从函数图象、单调性定义、导数来理解；考查奇偶性，可以从图象和定义入手，尤其要注意抽象函数奇偶性的判断；对称性和周期性结合，用以考查函数值重复出现的特征以及求解析式.
4．基本初等函数：比较大小，基本初等函数的图象和性质，基本初等函数的综合应用，其中常以分段函数为载体考查函数、方程、不等式等知识的综合.
考向一函数的单调性、奇偶性的应用
样题1 （2017北京理科）已知函数1()3()3
x x
f x =-，则()f x
A ．是奇函数，且在R 上是增函数
B ．是偶函数，且在R 上是增函数
C ．是奇函数，且在R 上是减函数
D ．是偶函数，且在R 上是减函数
【答案】A
样题2 （2017天津理科）已知奇函数()f x 在R 上是增函数，()()g x xf x =．若2(log 5.1)a g =-，
0.8(2)b g =，(3)c g =，则a ，b ，c 的大小关系为
A ．a b c <时，()0f x >，从而()()g x xf x =是R 上的偶函数，且在[0,)+∞上是增函数，22(log 5.1)(log 5.1)a g g =-=，0.822<，又
4 5.18<<，则2
2l o g 5.13<<，所以0.8202log 5.13<<<，0.82(2)(log 5.1)(3)g g g <<，所以b a c <<，故选C ．
【名师点睛】比较大小是高考的常见题型，指数式、对数式的大小比较要结合指数函数、对数函数，借助指数函数和对数函数的图象，利用函数的单调性、奇偶性等进行大小比较，要特别关注灵活利用函数的奇偶性和单调性，数形结合进行大小比较或解不等式．
考向二函数图象的判断
样题3 (2016高考新课标Ⅰ) 函数y =2x 2
–e |x |
在[–2,2]的图象大致为
A ．
B ．
C ．
D ．
【答案】D
样题4 函数()x
f x x x
=+的图象是
A
B C D
【答案】C
【解析】对x 进行讨论，将函数()x
f x x x
=+
转化为所熟知的基本初等函数即可作图．当x ＞0时，()1f x x =+，故图象为直线1y x =+上0x >的部分；当x ＜0时，()1f x x =-，故图象为直线1y x =-上0x <的部分；当x =0时，()f x 无意义.
综上，1,0
()1,0
x x f x x x +>⎧=⎨-<⎩的图象为直线1y x =+上0x >的部分，1y x =-上0x <的部分，
即两条射线.故选C.
【名师点睛】作分段函数图象的关键是根据定义域的不同部分，分别由解析式作出对应的图象.作图时一定要注意每段自变量的取值范围，且要标出关键点的横、纵坐标.
考向三函数的最值问题
样题5 （2017浙江）若函数f (x )=x 2
+ ax +b 在区间[0，1]上的最大值是M ，最小值是m ，则M –
m
A ．与a 有关，且与b 有关
B ．与a 有关，但与b 无关
C ．与a 无关，且与b 无关
D ．与a 无关，但与b 有关
【答案】B
样题6 （2017浙江）已知a ∈R ，函数4
()||f x x a a x
=+
-+在区间[1，4]上的最大值是5，则a 的取值范围是___________．【答案】9(,]2
-∞
【解析】[][]4
1,4,4,5x x x
∈+∈，分类讨论：
①当5a ≥时，()442f x a x a a x x x
=--
+=--，函数的最大值为9
245,2
a a -=∴=，舍去；
②当4a ≤时，()44
5f x x a a x x x
=+
-+=+≤，此时命题成立； ③当45a <<时，(){}max max 4,5f x a a a a =-+-+，则：
4545a a a a a a ⎧-+≥-+⎪⎨-+=⎪⎩或4555
a a a a a a ⎧-+<-+⎪⎨
-+=⎪⎩，解得92a =或92a <．综上可得，实数a 的取值范围是9,2⎛
⎤-∞ ⎥⎝
⎦．
【名师点睛】本题利用基本不等式，由[]1,4x ∈，得[]4
4,5x x
+∈，通过对解析式中绝对值符
号的处理，进行有效的分类讨论：①5a ≥；②4a ≤；③45a <<，问题的难点在于对分界点的确认及讨论上，属于难题．解题时，应仔细对各种情况逐一进行讨论．
样题7 (2016北京理科)设函数33,()2,⎧-≤=⎨->⎩x x x a
f x x x a
.
①若0a =，则()f x 的最大值为____________________； ②若()f x 无最大值，则实数a 的取值范围是_________________. 【答案】2 (,1)-∞-
【名师点睛】1.求分段函数的函数值时，应首先确定所给自变量的取值属于哪一个范围，然后选取相应的对应关系．若自变量的值为较大的正整数，一般可考虑先求函数的周期．若给出函数值求自变量的值，应根据每一段函数的解析式分别求解，但要注意检验所求自变量的值是否属于相应段自变量的范围；2.在研究函数的单调性时，需要先将函数化简，转化为讨论一些熟知的函数的单调性，因此掌握一次函数、二次函数、幂函数、对数函数等的单调性，将大大缩短我们的判断过程．。