北京航空航天大学材料力学2004年真题
第十三章北航 材料力学 全部课件 习题答案
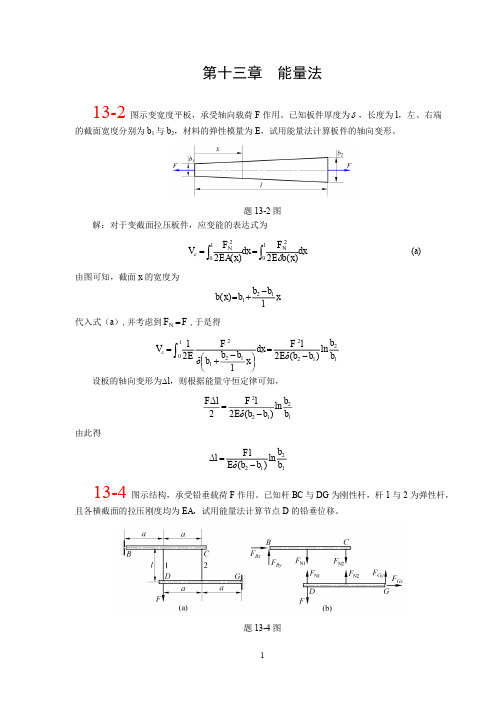
M ( x2 ) Fx2 M C ,
图 13-9 根据卡氏定理,得
C
1 [ EI
a 0
( Fx1 )(
x1 )dx1 a
a 0
( Fx2 )(1)dx2 ]
5Fa 2 () 6EI
A A
13-10 图示各梁,弯曲刚度 EI 均为常数,试用卡氏定理计算横截面 A 的挠度 与转角 。
3 3
3 3
–F
F 2
3 Fa 3 3 Fa 12
3 Fa 12
3
a
3 6
9
故有
ΔB
求 AB 的运算过程列表如下: i 1 2 3
i 1
3
F Ni FNi li 3Fa (←) EA 12EA
li
a a a
F Ni
2 3a 1
FNi
F
F Ni FNi l i
2 3 F 3
3a 1
–F
3 F 3
3 F 6
3a
F 2
故有
5 3 F 6
AB
F Ni FNi li 5 3F () EA 6 EA i1
3
(b) 解:求Δ B 和 AB 的单位状态分别示如图 13-17b(1)和 b(2) 。
图 13-17b 求 Δ B 的运算过程列表如下:
i 1 2 3 4
转角。
图示刚架,承受载荷 F 作用。设弯曲刚度 EI 为常数,试用卡氏定理计算截面 C 的
题 13-9 图 解:在截面 C 处假想附加一矩为 M C 的力偶(见图 13-9) ,由图可得
M x1 ( F
孙训方《材料力学》考研配套材料力学考研真题库

孙训方《材料力学》考研配套材料力学考研真题库第一部分考研真题精选一、选择题1卡氏定理可用于求()的相应位移。
[北京航空航天大学2013研]A.任意结构B.非弹性结构C.非线性弹性结构D.线弹性结构【答案】D查看答案【解析】在13章能量法里,讨论的应变能表达式都是基于小变形和线弹性材料建立的,所以由应变能得到的克拉贝依隆原理、互等定理和卡氏定理都只适用于线弹性结构;单位载荷法是基于虚功原理建立起来的,适用范围更广,但是常用到的莫尔积分方法也只是适用于线弹性结构。
2压杆的下端固定,上端通过水平弹簧与固定面连接,则其长度系数μ的取值范围为______。
[中国科学技术大学2016研]A.μ<0.5B.0.5<μ<0.7C.0.7<μ<2D.μ>2【答案】C查看答案【解析】压杆端面的约束是介于自由端和铰支座约束。
一段固定,另一端为自由端的长度系数为2,另一端为铰支座约束的长度系数为0.7,所以本题的长度系数介于0.7和2之间。
3如图1-1-1所示,在σa-σm坐标系中(σa为交变应力的幅度,σm为平均应力),C1、C2两点均位于一条过原点O的直线上,设C1、C2两点对应的两个应力循环特征为r1、r2,最大应力分别为σmax1、σmax2,则()。
[哈尔滨工业大学2009年研]图1-1-1A.r1=r2,σmax1>σmax2B.r1=r2,σmax1<σmax2C.r1≠r2,σmax1>σmax2D.r1≠r2,σmax1<σmax2【答案】B查看答案【解析】在射线OC2上,σa+σm=σmax,且tanα=σa/σm=(1-r)/(1+r),因此,C1、C2的循环特征相同,且C2的最大应力比C1的大。
1根据均匀、连续性假设,可以认为()。
[北京科技大学2012研]A.构件内的变形处处相同B.构件内的位移处处相同C.构件内的应力处处相同D.构件内的弹性模量处处相同【答案】D查看答案【解析】连续性假设认为组成固体的物质不留空隙地充满固体的体积,均匀性假设认为在固体内到处有相同的力学性能。
09-10年度北航材料力学试题第一学期期末试卷

09-10第一学期期末试卷一、选择题 (单选,共15分,每小题3分) 1、下列说法正确的是: __ 。
A 、切应力互等定理是指微体的两个截面上,垂直于这两个截面交线的切应力数值相等;B 、材料能经受较大塑性变形而不破坏的能力,称为材料的塑性;C 、在工程中,延伸率较大的材料称为脆性材料,延伸率较小的材料称为塑性材料;D 、所有塑性材料拉伸时的应力-应变图都会存在明显的屈服阶段。
2、下列说法正确的是: _ 。
A 、应力集中是指载荷集中作用在构件的某个部位;B 、圆轴扭转切应力公式适用于矩形和椭圆形截面轴的扭转切应力计算;C 、梁或梁段各横截面的剪力为零而弯矩为常数的受力状态,称为纯弯曲;D 、当梁的长度远大于其截面高度时,梁的最大弯曲切应力远大于最大弯曲正应力。
3、在下列杆件中,图 _ 所示杆是轴向拉伸杆。
A 、B 、C 、D 、4、下图所示组合梁,采用积分法确定梁的挠曲轴方程时,需要根据边界条件和连续条件确定方程中的积分常数,下列条件中正确的是: _ 。
FFFFF /2A、w A=0,w B=0,θB=0;B、w A=0,θA(左)=θA(右),w B=0,θB=0,w C(左)= w C(右),θC(左)=θC(右);C、w A=0,θA=0,w B=0,θB=0,w C=0,θC=0;D、w A=0,θA(左)=θA(右),w B=0,w C(左)= w C(右),θC(左)=θC(右)=0。
5、某等截面轴的扭矩图面积的代数和等于零,则其两端面的相对转角__ 。
A、大于零;B、小于零;C、等于零;D、不能确定。
二、填空题(10分,每空1分)1、材料力学的基本假设为________ 、_______ 和_______ 。
2、几个载荷同时作用产生的效果,等于各载荷单独作用产生的效果总和,此原理称为_______ 。
3、静不定问题未知力的数目多于有效平衡方程的数目,二者之差称为______ 。
北京航空航天大学经济学2004年考研真题参考答案

北京航空航天大学2004年硕士试题经济学482一、解释下列概念(本题共20分,每小题2分)1.边际效用2.经济成本3.Ceteris paribus4.逆向选择5.自然垄断6.外部性7.潜在产出8.实际利率9.公开市场操作(业务)10.购买力平价二、选择题(ABCD四个备选答案中,只有一个是最合适的,将其选出。
本题共40分,每小题2分)1.在无差异曲线上的任何一点,商品X和Y的边际替代率等于它们的()A.价格之比B.数量之比C.边际效用之比D.边际成本之比2.如果两种商品的需求的交叉弹性小于零,这两种商品的关系是()A.替代品B.互补品C.无关商品D.可能是替代品也可能是互补品3.过原点的线性供给各点的弹性为()A.大于1B.小于1C.等于1D.不确定4.下面关于平均成本与边际成本关系的说法,哪一个是正确的()A.平均成本上升,边际成本可能上升也可能下降B.在边际成本曲线的最低点,边际成本等于平均成本C.如果边际成本上升,平均成本一定上升D.在平均成本曲线的最低点,边际成本等于平均成本5.等成本线的斜率表示的是()A.横轴要素价格对纵轴要素价格的比率B.纵轴要素价格对横轴要素价格的比率C.既定成本下的各种可能的产量D.既定产量下的总成本6.完全竞争厂商的主要策略手段是()A.广告B.涨价C.降价D.降低成本7.垄断厂商达到均衡时,下列公式成立的是()A.P=MC=MRB.P>MC=MRC.P>MC=ARD.ABC都对8.垄断竞争厂商短期达到均衡时候,它()A.一定能够获得超额利润B.一定不能获得超额利润C.只能得正常利润D.获得超额利润、获得正常利润和亏损都有可能9.哪一年,苏格兰人亚当·斯密出版了《国民财富的性质和原因的研究》一书,从而创立了近代经济学体系。
()A.1759年B.1776年C.1817年D.1794年10.一个厂商,有3个不同的项目可以生产,那么,从经济学家的角度,它阳多可以在几个项目中获利。
第十一章北航 材料力学 全部课件 习题答案

弹簧支持。试证明压杆的临界载荷满足下述方程:
sin
kl 2
sin
kl 2
kl 2
1
4k 2EI cl
cos
kl 2
0
式中, k F /(EI) 。
8
题 11-10 图 解:该细长压杆的微弯状态如图 11-10 所示。
图 11-10 按图中所取坐标,左、右段压杆得弯矩方程分别为
N/mm 时,截面 B 的挠度分别为何值。横梁与立柱均用低碳钢制成,弹性模量 E = 200 GPa,
比例极限 p =200 MPa。
11
题 11-13 图 解:1.求立柱的临界载荷
给立柱和梁编号分别为 1 和 2,我们有
λp π
E π σp
200109 200106
99.3
i I1 d 10mm0.010m A1 4
6
由此得
FN1 FN2 FN3 FN4
F 2
Fcr
2
(
π
2
l
EI
2
)
2π 2 EI l2
11-9 图 a 所示细长压杆,弯曲刚度 EI 为常数,试证明压杆的临界载荷满足下述方程:
式中,k2=F/(EI)。
sinkl(sinkl2klcoskl)0
题 11-9 图
解:在临界载荷作用下,压杆可在图 b 所示微弯状态保持平衡。
w2
A2sinkx2
B2coskx2
Fc 2F
x2
由此得
当x1 0,w1 0; 当x2 0,w2 0
位移连续条件为 代入通解后,得
重排后,得
07-08年度北航材料力学试题第一学期期末试卷

2007~2008第1学期期末考试A 卷一、选择题(每小题4分,共20分)1. 为计算图示拉压杆m-m 截面的内力, 建立平衡方程。
A 只能对m-m 截面左段;B 只能对m-m 截面右段;C 既能对m-m 截面左段也能对m-m 截面右段;D 需取整体为研究对象。
2.低碳钢拉伸、压缩屈服极限分别为+s σ,-s σ,灰口铸铁拉伸、压缩强度极限分别为+b σ,-b σ,则有 。
A -+-+==b b s s σσσσ,;B -+-+=<b b s s σσσσ,;C -+-+<=b b s s σσσσ,;D -+-+<<b b s s σσσσ,。
3.图示等腰三角形O 为形心,y 为对称轴,设y I 、z I 分别为整个图形对y 、z 轴的惯性矩,'y I 、'z I 分别为图形阴影部分对y 、z 轴的惯性矩,则A ''2,2z z y y I I I I ==; B ''2,2z z y y I I I I ≠=;C ''2,2z z y y I I I I =≠;D ''2,2z z y y I I I I ≠≠。
m4.设图示简支梁的弯矩为M (x ),则挠曲轴方程可以写为⎰⎰++=D Cx dxdx x M EIw )(,其中EI 为弯曲刚度,w 为挠度,对于积分常数有 。
A 0,0==D C ;B 0,0≠=DC ; C 0,0=≠D C ; D 0,0≠≠D C 。
5.中性轴是梁的 的交线。
A 纵向对称面与横截面;B 横截面与中性层;C 纵向对称面与中性层;D 横截面与顶面。
二、作图题(5分)试绘制图示梁的挠曲轴的大致形状,并标明凹凸性和拐点。
q29qa M 图三、计算题(五道小题,共70分)1. 画图示外伸梁的剪力和弯矩图(15分)2. 图示结构中,杆1与杆2刚度均为EA ,梁BD 为刚体,载荷kN F 50=,许用拉应力为MPa t 160][=σ,许用压应力为MPa c 120][=σ,试确定各杆的横截面面积。
第四章北航的材料力学全部课件习题答案
第四章 扭 转4-5 一受扭薄壁圆管,外径D = 42mm ,内径d = 40mm ,扭力偶矩M = 500N •m ,切变模量G =75GPa 。
试计算圆管横截面与纵截面上的扭转切应力,并计算管表面纵线的倾斜角。
解:该薄壁圆管的平均半径和壁厚依次为mm 122 mm 5.20)22(210=-==+=d D d D R δ,于是,该圆管横截面上的扭转切应力为189.4MPa Pa 10894.1m001.00.02052πN 500π282220=⨯=⨯⨯==δτR T 依据切应力互等定理,纵截面上的扭转切应力为 MPa 4.189=='ττ 该圆管表面纵线的倾斜角为rad 102.53rad 1075104.189396-⨯=⨯⨯==G τγ 4-7 试证明,在线弹性范围内,且当R 0/δ≥10时,薄壁圆管的扭转切应力公式的最大误差不超过4.53%。
解:薄壁圆管的扭转切应力公式为δR Tτ20π2=设βδR =/0,按上述公式计算的扭转切应力为3220π2π2δβTδR T τ== (a)按照一般空心圆轴考虑,轴的内、外直径分别为 δR D δR d +=-=002 2,极惯性矩为 )4(2π])2()2[(32π)(32π2200404044p δR δR δR δR d D I +=--+=-=由此得)14(π)12()2()4(π)2(23022000p max ++=++=+=ββδβδδδT R R R TδR I T τ (b)比较式(a)与式(b),得)12(214)12()14(ππ222332max++=++⋅=ββββββδδβT Tττ 当100==δβR 时,9548.0)1102(10211042max=+⨯⨯⨯+⨯=ττ可见,当10/0≥δR 时,按薄壁圆管的扭转切应力公式计算τ的最大误差不超过4.53%。
4-8 图a 所示受扭圆截面轴,材料的γτ-曲线如图b 所示,并可用mC /1γτ=表示,式中的C 与m 为由试验测定的已知常数。
2004年材力期中试题
哈工大2004年春季学期期中材料力学试题25分)一、(4分)、已知,试作梁的剪力、弯矩图。
q a y S F zM 二、(4分)矩形截面细长悬臂梁如图所示。
试求A 、B 、C 三点的应力,并用单元体分别表示这三点的应力状态。
三、(4分)外径,内径,长的空心圆轴,承受分布集度为的均D d l q m 匀分布外力偶作用。
若材料的切变模量为,试求:G 1)圆轴的最大切应力;2)整个圆轴的扭转角;3)整个圆轴的变形能。
题号一二三四五六七八九十总分分数四、(4分)已知构件内某点处的应力状态为两种应力状态的叠加结果,试求叠加后该点该平面内的(1)主应力与主应变;(2)主切应力;(3)该点的形变应变能密度。
f e (已知材料的弹性模量,横向变形系数)GPa 200=E 3.0=ν五、(5分)图示静不定结构。
各杆的横截面面积、长度、弹性模量均相同,分别为A 、l 、E ,在节点A 处受铅垂方向载荷F 作用。
试求节点A 的铅垂位移。
六、选择题以下4题为选择题(每题1分,合计4分),各题中均备有4个答案,但均只有1个正确。
请将正确答案的标号写在每题的“__________”处。
1、轴向拉伸细长杆件如图所示,__________A.1-1、2-2面上应力皆均匀分布;B.1-1面上应力非均匀分布,2-2面上应力均匀分布;C.1-1面上应力均匀分布,2-2面上应力非均匀分布;D.1-1、2-2面上应力皆非均匀分布。
2、塑性材料试件拉伸试验时,在强化阶段__________A.只发生弹性变形;B.只发生塑性变形;C.只发生线弹性变形;D.弹性变形与塑性变形同时发生。
3、比较脆性材料的抗拉、抗剪、抗压性能,__________><A.抗拉性能抗剪性能抗压性能;<<B.抗拉性能抗剪性能抗压性能;>>C.抗拉性能抗剪性能抗压性能;D.没有可比性。
4、水平面内放置的薄壁圆环平均直径为d,横截面面积为A。
北京航空航天大学 材料力学课件 Chapt7-2004
a
x
2
y
x
2
y
cos2a
xsin2a
a
x
2
y
sin2a
xcos2a
上述关系式是建立在静力学基础上,故所得结论既适用于各向同性 与线弹性情况,也适用于各向异性、非线弹性与非弹性问题
a
x
2
y
x
2
y
cos2a
xsin2a
a
x
2
y
sin2a
Constructing Mohr's Circle 绘制应力圆
C
x y
2
- 圆心横坐标
图解法求斜截面应力
a Hx 2OyCCxD2cosy(2coas02a 2a)xsin2a
H OC CD cos2a0cos2a CD sin2a0sin2a
a
x
2
y
sin2a
xcos2a
解: x 100 MPa x 60 MPa y 50 MPa a 30
m
(-100
50) 2
MPa
(-100
50) 2
MPa cos(-60)
(-60 MPa)sin(-60) -114.5 MPa
m
σ occur (no shear stresses in existence) 切应力为零的截面 Principal Stresses主应力 - the normal stresses acting on principal planes主平面上的正应力
北航材料力学试题库
λ=
400 = 320 >100 5 4
AC 杆的柔度大于临界柔度, 采用 Euler 公式
Fcr =
π 2 EI = l2
π 2 × 200000 ×
400 2
π × 54 64 = 378.5 N
当 F=350N 时,AC 杆不会失稳,则前面的分析是正确的
FN = 0.9885F
( F − FN )l 3 FN l ' 0.992 × 350 × 400 δ= = = = 0.035mm π 3EI EA' 2 200000 × × 5 4
出 ε x = 230 × 10
−6
, ε y = 100 × 10 与 ε 45o = −40 × 10
−6
−6
, [σ]=70MPa 。(1) 求沿 x,y 方向的
正应力;(2)试求气体压强p;(3)用第三强度理论校核筒壁强度。
M p
εy
ε 45o εx
l
F
知识点:广义胡克定律,任意方向的应变分析,主应力分析,薄壁圆筒的强度计算; 难度:B,综合性较强。 解: (1)首先,根据广义胡克定律计算正应力
σ max σ x + σ y ⎛σ x −σ y = ± ⎜ ⎜ σ min 2 2 ⎝ τ max =
79.45 − 0 = 39.725 2
79.45 ⎞ 2 ⎟ + τ = 45 . 85 ± 33 . 60 = x ⎟ 12.25 ⎠
2
得到主应力及三向应力状态下的最大切应力
由第三强度理论
τ max = 39.725 >
北航材料力学试题库&习题集
为了建立材料力学试题库及编写辅导书,根据上次开会讨论所提意见,将原定开学每人交 50 题改为 6 月下旬完成,可以包含以前提到的 30 题。请大家首先列出自己编写部分的相关知识点, 根据主要问题类型及分析方法进行编写(含题、解答、及难度分析) 。
