综合练习8。30
人教版七年级数学下册8.3实际问题与二元一次方程组同步测试及答案

人教版七年级下学期8.3实际问题与二元一次方程组同步测试一、选择题1.既是方程23x y-=的解,又是方程3410x y+=的解是()A.12xy=⎧⎨=⎩B.21xy=⎧⎨=⎩C.43xy=⎧⎨=⎩D.45xy=-⎧⎨=-⎩2.甲、乙两数这和为16,甲数的3倍等于乙数的5倍,若设甲数为x,乙数为y,则方程组(1)1635x yx y+=⎧⎨=⎩,;(2)1653x yx y+=⎧⎨=⎩,;(3)16530x yy x-=⎧⎨-=⎩,;(4)1653y xx y-=⎧⎪⎨=⎪⎩,中,正确的有()A.1组B.2组C.3组D.4组3.某校150名学生参加竞赛,平均分为55分,其中及格学生平均分为77分,不及格学生平均分为47分,则不及格学生的人数为()A.49B.101C.40D.1104.某个体商店在一次买卖中同时卖出两件上衣,每件都是以135元卖出,若按成本计算,其中一件赢利25%,另一件亏损25%,则这家商店在这次买卖中() A.不赔不赚 B.赚9元 C.赔8元 D.赔18元5.甲、乙两地相距100千米,一艘轮船往返两地,顺流用4小时,逆流用5小时,•那么这艘轮船在静水中的航速与水速分别是()A.24千米/时,8千米/时 B.22.5千米/时,2.5千米/时C.18千米/时,24千米/时 D.12.5千米/时,1.5千米/时6.今年哥哥的年龄是妹妹的2倍,2年前哥哥的年龄是妹妹的3倍,求2年前哥哥和妹妹的年龄,设2年前哥哥x岁,妹妹y岁,依题意,得到的方程组是()A.23(2),2x yx y+=+⎧⎨=⎩B.23(2),2x yx y-=-⎧⎨=⎩C.22(2),3x yx y+=+⎧⎨=⎩D.23(2),3x yx y-=-⎧⎨=⎩7.某文具店出售单价分别为120元和80•元的两种纪念册,•两种纪念册每册都有30%的利润.某人共有1080元钱,欲买一定数量的某一种纪念册,若买单价为120•元的纪念册则钱不够,但经理知情后如数付给了他这种纪念册,结果文具店获利和卖出同数量的单价为80元的纪念册获利一样多,那么这个人共买纪念册()A.8册 B.9册 C.10册 D.11册8.某校初三(2)班40名同学为“希望工程”捐款,•共捐款100元.捐款情况如下表:表格中捐款2若设捐款2元的有x 名同学,捐款3元的有y 名同学,根据题意,可得方程组( )A .27,2366x y x y +=⎧⎨+=⎩B .27,23100x y x y +=⎧⎨+=⎩C .27,3266x y x y +=⎧⎨+=⎩D .27,32100x y x y +=⎧⎨+=⎩9.足球比赛的记分规则是:胜一场得3分,平一场得1分,负一场得0分.•一支青年足球队参加15场比赛,负4场,共得29分,则这支球队胜了( )A .2场B .5场C .7场 C .9场10.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3:2,•求两种球各有多少个?若设篮球有x 个,排球有y 个,依题意,得到的方程组是( )A .23,32x y x y =-⎧⎨=⎩B .23,32x y x y =+⎧⎨=⎩C .23,23x y x y =-⎧⎨=⎩D .23,23x y x y =+⎧⎨=⎩二、填空题11.某人买了60分的邮票和80分的邮票共20张,用去了13元2角,则60分的邮票买了 枚,80分的邮票买了 枚。
《综合练习》学习与巩固-完整PPT课件

90000÷30÷40=75〔块〕 答:第二种方案要用75块地砖。
〔 米〕。
m²
3有两个长24厘米、宽12厘米的长方形。 〔1〕把它们拼成一个长方形,这个长方形的周长是多少?
〔24+24+12〕×2=120〔厘米〕 答:这个长方形的周长120厘米。 〔2〕把它们拼成一个正方形,这个正方形的周长是多少?
24×4=96〔厘米〕 答:这个正方形的周长是96厘米。
4小明家的厨房改造后要铺地砖,现有两种方案可供选择〔如以下图〕。 〔1〕第一种方案正好用了100块地砖,请你计算厨房的面积。
综合练习
1下面图形的面积各是多少?〔每个小方格代表1平方厘米。 2〕5平方厘米
2在括号里填上适宜的单位。
我家住的房子约有3〔 米〕高,实用面积约是138〔 〕。m门²前的那棵
树高达25〔 〕,每米到夏天能提供18〔 〕的树荫,m人²们在下面可以
乘凉。树前的那块绿地长约40〔 〕,宽约16〔米〕,面积大约是600
小学三年级下册数学题混合运算和应用题练习

以下是为⼤家整理的关于⼩学三年级下册数学题混合运算和应⽤题练习的⽂章,供⼤家学习参考!(⼀)混合运算1.三步式题【知识要点精讲】三步式题的混合运算与两步式题的混合运算⼀样,都要先算乘、除法,后算加、减法。
如果有⼩括号就要先算上括号⾥⾯的;如果⼩括号中⼜有乘、除法,⼜有加、减法时,也要先算乘、除法,后算加、减法。
这⾥要注意:不要认为“先算乘、除法”,就是不管乘、除法谁在前,总是先算乘。
要看谁在前,就要先算谁。
即有乘、除混运算时,要从左往右依次计算。
在⼀个没有括号的算式⾥。
如果式题中有两步计算是乘、除法,但这两步运算被加、减法运算隔开,在计算时可以同时计算乘、除法。
在同⼀个算式⾥,如果有两个⼩括号,在计算时,也可以同时计算。
【重点难点点拨】本节知识的重点是三步式题的运算顺序。
本节知识主要学习的是带有乘、除混合的三步式题与带有⼩括号的三步式题。
本节知识的难点是带有⼩括号的三步式题及三步式题计算的书写格式。
【典型例题⽰解】例1 160+300÷25×8分析:这道题中,有加法、乘法和除法,按照运算顺序,先算除法(因为除法在前),再算乘法,最后算加法。
即:160+300÷25×8②160+300÷25×8=160+12×8=160+96=256例2 7050÷5-51×8分析:这道题中含有⼆级运算乘除法,⼜含有⼀级运算减法,但这题中的乘除法运算中间被减法隔开了,那么,乘除法两步计算可以同⼀次脱式计算,也就是同时计算7050÷5和51×8,最后算减法。
即:7050÷5-51×8①7050÷5-51×8=1410-408=1002例3 在算式420-180÷5×12中,怎样才能改变运算顺序,使得最后⼀步运算是除法,并将结果计算出来。
分析:要最后⼀步算除法,也就是要先算减法和乘法。
八大时态综合练习

1 八大时态综合练习 一、选择最佳答案填空(动词及搭配): 1. A policeman saw two thieves ______a girl’s mobile phone on the bus and hecaught them at once. A. to steal B. stealing C. stole D. stolen 2. The Chinese pingpong players will join in the match.Let’s ______them success. A.wish B.to wish C.hope D.to hope 3. He is so careless that he always ______his school things at home. A.forgets B.forgot C.leaves D.left 4. ----Who ______the computer? I want to use it. ----Timmy. He ______ it for a week. A.borrowed, has borrowed B.has borrowed, bought C.has borrowed, has kept D.bought, has borrowed 5. Look! One of the girls ______the door. A.cleans B.is cleaning C.clean D.are cleaning 6. If you don’t feel well, you may just ______. A.stopped reading B.stop reading C.stopped to read D.stop to read 7. ----Where can we get a baseball? ----Let’s ______. A. lend Jim one B.lend one to Jim C.borrow one from Jim D.borrow one of Jim 8. ----My model ship doesn’t work. ----Don’t worry. I’ll have it ______this afternoon. A. repairing B.made C.repaired D.mend 9. You ______wash your hands before meals. A. need B.must C.can D.may 10. Will you ______the light? It’s dark in the room. A.get on B.get off C.trun on D.turn off 11. My name is Zhang Mingjian. You may ______me Zhang Mingjian or Mr Zhang. A. ask B.say C.tell D.call 12. There is going to ______a game in our school this afternoon. A.has B.have C.be D.are 13. You’d better______smoking. It’s bad for your health. A.eat up B.give up C.come up D.get up 2
人教版五年级数学上册期末综合复习练习题(含答案)

人教版五年级数学上册期末综合复习练习题(含答案) 一、填空题 1.根据
18641152,可知1.80.64( ),11526.4( )。
2.2.45×16可以转化成245×16,计算后把所得的积缩小到它的( ). 3.小红骑自行车每分钟行a米,她10分钟可以骑行( )米;她骑行b米,
需要( )分钟。 4.为庆祝“元旦”,学校准备在65米宽的教学楼前挂一排灯笼,每隔5米挂一个
(一端挂,一端不挂),一共要挂( )个。 5.在括号里填上“>”“<”或“=”。 7.3×0.99( )7.3×1.1 0.059( )0.059 1.6×0.13( )0.13
2.07÷3.1( )1 0.55÷0.89( )0.99×0.55 6.小强两天看一本书,第一天看了m页,第二天比第一天多看8页,这本书共 页. 7.丹丹在计算一个数除以2.6时,把除号误看成乘号,得到的结果是3.38,正确
的结果应该是( )。 8.某小区内有一个人工湖,周长为150米,要在湖岸边每隔5米植一棵树,每
两棵树之间放一个石凳。这个人工湖周围一共要植( )棵树,放( )个石凳。 9.5(2)班的座位设了6列,每列座位一样多,第6列最后一个同学的位置是
(6,7)。5(2)班一共有( )人。 10.实验小学组织师生共120人参观三线建设博物馆,如果每辆车限乘客35人,
至少需要这样的车( )辆。 二、选择题 11.下列各式中,积比两个因数都小的是( )。 A.2.35×3.2 B.0.88×0.64 C.0.38×1.02 D.1.35×1 12.下面哪个图形不能密铺( ) A.正五边形 B.长方形 C.正方形 D.正三角形 13.在计算0.89×101时,运用( )能使计算简便。 A.乘法交换律 B.乘法结合律 C.乘法分配律 D.加法交
换律 14.因为65×39=2535,所以下列各式错误的是( )。 A.6.5×39=253.5 B.0.65×3.9=0.2535 C.65×0.39=25.35 D.25.35÷0.039=650 15.简算1.25×2.5×4时,要用到的运算定律是( )。 A.乘法交换律B.加法结合律C.乘法分配律 D.乘法结合律 三、判断题 16.在同一间教室里,乐乐的位置用数对表示是(5,2),明明的位置用数对表
综合练习课
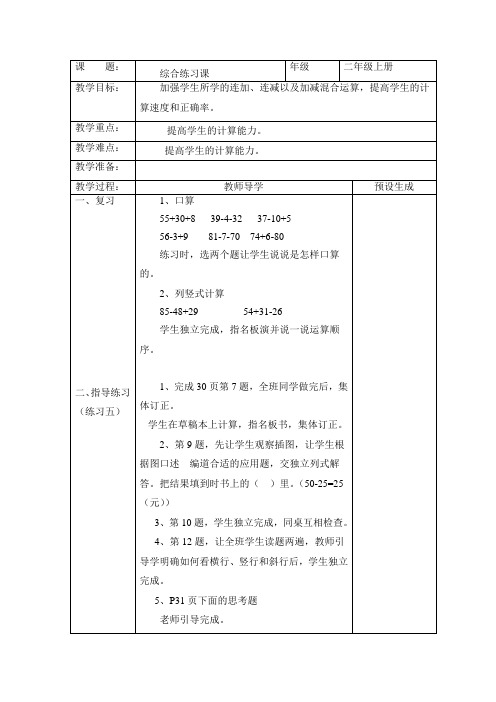
2、列竖式计算
85-48+29 54+31-26
学生独立完成,指名板演并说一说运算顺序。
1、完成30页第7题,全班同学做完后,集体订正。
学生在草稿本上计算,指名板书,集体订正。
2、第9题,先让学生观察插图,让学生根据图口述编道合适的应用题,交独立列式解答。把结果填到时书上的()里。(50-25=25(元))
课题:
综合练习课
年级
二年级上册
教学目标:
加强学生所学的连加、连减以及加减混合运算,提高学生的计算速度和正确率。
教学重点:
提高学生的计算能力。
教学难点:
提高学生的计算能力。
复习
二、指导练习(练习五)
三、小结
1、口算
55+30+8 39-4-32 37-10+5
56-3+9 81-7-70 74+6-80
3、第10题,学生独立完成,同桌互相检查。
4、第12题,让全班学生读题两遍,教师引导学明确如何看横行、竖行和斜行后,学生独立完成。
5、P31页下面的思考题
老师引导完成。
6、笔算下面各题
69+30-45 65+18-39
26+40-8 71-65+45
板书设计:
教学后记:
《24时计时法》综合习题 - 2 (1)
《24时计时法》综合习题
1、填空题。
1时=()分 1分=()秒 1周=()天
1天=()时 120秒=()分 1时30分=()分
2、愉快的一天。
3、用普通计时法表示。
7时() 12时30分() 14时()
24时() 17时45分() 20时15分()
4、下面是小华的妈妈上、下班的时间。
小华的妈妈一天要工作多少小时?
5、小丽晚上9时睡觉,第二天早上6时起床,她一共睡了几个小时?
6、小军的爸爸在银行工作,早上8:30上班,中午休息2小时,一共要工作8小时,那么小军的爸爸几点下班?
7、从北京南站到上海的动车,7:40从北京南站开出,行驶了10小时3分到达上海,到上海的时间是几时几分?
1、小亮家附近超市的营业时间是早上8:30到晚上10:30,请你用24时计时法表示门前挂的营业时间牌。
小亮从家到超市只需15分钟,早晨小亮什么时刻从家走,到超市刚好开始营业?
2、小红的爸爸早上7:00开始劳动,下午5:00收工。
八上数学目标答案
数学八年级(上)目标参考答案2010.8第十一章 全等三角形11.11.D2.A3.D4.B C ;∠D ;∠DBA5. 50°,66.DC ,∠BFC7.∠ABC =70°8.周长为12,面积为69.相等且垂直 10.∠F ,FC 11.80°12.(1)对应边:AB 和AD , BC 和DE ,AC 和AE ; 对应角:∠B 和∠D ,∠BAC 和∠DAE .(2)∵△ABC ≌△ADE ∴DE =BC =5cm .13.∠OAD =95°.14.BE =DC 且BE ⊥DC . 证明:如图,∵△ACD ≌△AEB ∴BE =DC .∠ADC =∠ABE.又∵∠AOD =∠BOC ∴∠BPO =∠DAO =90°∴BE ⊥DC .11.2(1)1. C2. A3. 20°4. SSS 公理5. 证明:∵AE =DB (已知)∴AE+ BE =DB+ BE 即 AB = DE .在△ABC 与△DEF 中,BC = EF (已知) ∴△ABC ≌△DEF ( SSS ) 6. 用SSS 公理直接证明.7. 先用SSS 公理证△ABC ≌△DCB ,再得∠ACB =∠DBC ;(2)由△ABC ≌△DCB ,可得∠ABC =∠DCB ,再用∠ABC -∠ACB =∠DCB -∠DBC ,就得到∠1=∠2.8. (1)∵D 是BC 中点,∴BD =CD ,再用SSS 证△ABD ≌△ACD. (2)由△ABD ≌△ACD ,可得∠ADB =∠ADC ,∵∠ADB+∠ADC =180°,∴∠ADB =90°,∴AD ⊥BC. (3) 由△ABD ≌△ACD ,可得∠BAD =∠CAD ,∵∠BAD =25°,∴∠BAC =2∠BAD =50°. 9. 连接AC ,用SSS 证△ABC ≌△ADC ,可得∠B =∠D11.2 (2)DO EDC B AP1. D2. B3. C4. △AEC,SAS5. AB=DE6. ∵∠1=∠2(已知),∴∠1﹢∠_DAE_=∠2﹢∠_DAE__即∠_BAE__=∠__CAD__.在△__ABE___和△_ACD___中,__AB__=_AC_(已知),∠_BAE__=∠__CAD__(已证). 图11 -26_AE__=_AD__(已知)∴△_BAE_≌△_CAD_(SAS ).7. ∵DC⊥CA,EA⊥CA,∴∠C=∠A=90°,用SAS证△DCB≌△BAE.8. ∵AD=AE,BD=CE,∴AD+BD=AE+CE,∴AB=AC 再用SAS证△ADC≌△AEB.9. (1)∵AB∥ED,∴∠A=∠D,∵AF=DC,∴AF+FC=DC+FC,即AC=DF 再用SAS 证△ABC≌△DEF,得到BC=EF (2)由△ABC≌△DEF,得到∠BCA=∠EFD,∴BC∥EF.10. 连接AC.AD,先用SAS证△ABC≌△AED,得到AC=AD,又∵F是CD中点,∴CF=DF,再用SSS证△ACF≌△ADF,得到∠AFC=∠AFD,∵∠AFC+∠AFD=180°,∴∠AFC=90°,∴AF⊥CD.11.2 (3)1. C2. B3. 54.AC=AB或BD=CE5.AC∥DF或∠A=∠D6. ∠D=∠E或∠DAC=EAB或∠DAB=∠EAC.7. ∵AD∥BC,DF∥BE ∴∠A=∠C,∠AFD=∠CEB,再用AAS证△ADF≌△CBE.8. ∵∠1=∠2,∠CAD=∠DBC,∴∠1+∠CAD=∠2+∠DBC,即∠CAB=∠DBA,再用AAS 证△CAB≌△DBA,得到AC=BD.9. ∵BM∥CN,∴∠ABM=∠D,∵AC=BD,∴AC+CB=BD+CB,即AB=CD 再用AAS证△ABM≌△CDN,得到∠A=∠DCN,∴MN∥CN.10. 可补充的条件有:∠B=∠D(用AAS证明);∠E=∠C(可用ASA证明);AD=AB (可用SAS证明)等.11. 先证∠EAC=∠ABD(同角的余角相等),再用AAS证△ABD≌△CAE,得到AD=CE,BD=AE,∴BD=AE=AD+DE=CE+ED ∴BD=EC+ED.11.2 (4)1. C2. C3. D4. AB =AC ,AAS5. 3对儿6. ∵AD ⊥BD ,AE ⊥EC ∴∠ADB =∠AEC =90°然后用HL 证△ABD ≌△ACE7. ∵AE =BF ,∴AE+EF =BF+EF ,即AF =BE 再用HL 证△ACF ≌△DBE8. ∵DE =CF ∴DE -EF =CF -EF 即DF =CE 再用HL 证△ADF ≌△BCE ,得到∠D =∠C. 9. 因为AC ⊥CE ,BD ⊥DF 所以∠ACE =∠BDF =90° 在Rt △ACE 和Rt △BDF 中 AE =BF (已知) AC =BD (已知) ∴Rt △ACE ≌Rt △BDF (HL ) ∴∠A =∠B ∵AE =BF ∴AE+EF =BF+EF 即AF =BE 在△ACF 和△BDE 中∴△ACF ≌△BDE (SAS ) ∴CF =DE10.可选择:△AA′E ≌△C′CF ,△A′DF ≌△CBE (证明略.)11.2 (5)1. B2. B3. D4. HL5. 120°6. ∵AB ∥CD ,∴∠B =∠D 再用ASA 证△ABE ≌△CDF 得到AE =CF7. 先用HL 证△ABF ≌△ACG ,得到∠BAF =∠CAG ,∴∠BAF -∠BAC =∠CAG -∠BAC 即∠DAF =∠EAG 再用AAS 证△GAE ≌△DAF ,得到AD =AE.8. 先用SSS 证△AED ≌△ABE ,得到∠DAE =∠BAE ,再用SAS 证△DAC ≌△BAC ,得到CB =CD.9. 先用等角的余角相等证明∠C =∠F ,再用AAS 证△ABC ≌△DFE ,得到AC =EF 10. (1)已知:OA =OC ,OB =OD ,求证:AB ∥DC.证明:可证△OAB ≌△OCD (SAS )∴∠OAB =∠OCD ∴AB ∥CD (2)已知:OA =OC ,AB ∥DC ,求证:OB =OD.证明:可证△OAB ≌△OCD (AAS )∴OB =OD (3)已知:AB ∥DC ,OB =OD ,求证:OA =OC.证明:可证△OAB ≌△OCD (AAS )∴OA =OC.11. (1)①与∠A 相等的角是∠BOD (或∠COE );②证明:如图,作CG ⊥BE 于G 点,作BF ⊥CD 交CD 延长线于F 点.因为∠DCB=∠EBC=12∠A ,BC 为公共边, 所以△BCF ≌△CBG . 所以BF=CG .因为∠BDF=∠ABE+∠EBC+∠DCB ,∠BEC=∠ABE+∠A , 所以∠BDF=∠BEC . 可证△BDF ≌△CEG . 所以BD=CE . (2)成立 11.3 (1)1.A2.到角两边距离相等的所有3.3,角平分线上的点到角两边的距离相等4.BD =75.128cm 26.证明:由已知可得OD =OF.可证△ODG ≌△OFE (ASA )∴OE =OG .7.(1)△ABP 与△PCD 不全等.理由:不具备全等的条件. (2)△ABP 与△PCD 的面积相等.理由:等底等高. 8.证明:连接BE 、CE ,可证△BED ≌△CED (SAS )从而可证Rt △EBF ≌Rt △ECG (HL )∴BF =CG .9.可证DE =DA ,∠BED =∠BAD =90°,CE+DE+CD =CE+AD+CD =CE+AC =CE+AB ∵BD 是角平分线∴∠EBD =∠ABD ,可证△BED ≌△BAD (AAS )∴EB =AB ∴CE+DE+CD =CE+AD+CD =CE+AB =CE+EB =12cm 10.作EN ⊥CA ,EM ⊥BD ,EP ⊥CB ,垂足分别是N 、M 、P . ∵∠ABD =∠ABC -∠CBD =105°-30°=75°,∠AFB =180°-105°=75°,∴∠AFB =∠ABD ,∵EM ⊥BD 于M ,EP ⊥CB 于P ,∴EP =EM ,又CE 平分∠ACB ,EN ⊥CA ,EP ⊥CB ,∴EN =EP ,∴EN =EM , ∴ED 平分∠ADB , ∴∠ADE =21∠ADB =21×70°=35°.11.3 (2) 1.A 2.∠A 3.∠DAP =18° 4.∵BD ⊥AM ,CE ⊥AN ,∴∠FDC =∠FEB =90° 又∵∠DFC =∠EFB ,BF =CF ∴△DFM ≌△EFB(AAS) ∴FD =FE ∵BD ⊥AM ,CE ⊥AN ,∴点F 在∠A 的平分线上. 5.过P 作PE ⊥AC 于E . ∵P A ,PC 分别为∠MAC 与∠NCA 的平分线.且PD ⊥BM ,PF ⊥BN ∴PD =PE ,PF =PE ,∴PD =PF又∵PD ⊥BM ,PF ⊥BN ,∴点P 在∠MBN 的平分线上, 即BP 是∠MBN 的平分线.6.作CE ⊥AB 于E ,CF ⊥AD 交AD 的延长线于F .∵AC 平分∠BAD ,∴CE =CF . 在△CBE 和Rt △CDF 中,∵CE =CF ,CB =CD , ∴Rt △CBE ≌Rt △CDF ,∴∠B =∠1,∵∠1+∠ADC =180°, ∴∠B +∠ADC =180°, 即∠B +∠D =180°.NMP F E D CB A 17.证明:过点P 作PE ⊥DC ,垂足是E ,∴3490A ===︒∠∠∠,∵DP 平分∠ADC ,∴12=∠∠, ∴PA PE =,∵P 为AB 的中点,∴PA PB PE PB ==,, ∵90AD BC A =︒,∥∠,∴∠B =90°. ∴AB ⊥BC. ∴P 点在∠DCB 的平分线上. ∴CP 平分∠DCB .8.(1)FE =FD ; (2)成立.证明:过F 作FM ⊥AB 于M ,过F 作FN ⊥BC 于N ∴FM =FN ,∠EMF =∠DNF =90°∵∠ABC =60°∴∠MEF =∠BAC+∠ACE =12 ∠BAC+12 (∠BAC+∠ACB )=12 ∠BAC+60°,∠NDF =∠ABC+∠BAD =60°+12∠BAC ∴∠MEF =∠NDF.∴△EMF ≌△DNF (AAS )∴FE =FN.第十一章综合练习题1.C2.B3.C4.B5.B6.D7.D8.60°9.BC =EF(答案不惟一) 10.7,2,20 11.110° 12.1<AD <3 13.可证△ADE ≌△BFE (AAS )∴AE = BE 14.先证△AOC ≌△BOD ,再证 △ACE ≌△BDF ,或△COE ≌△DOF ∴CE =DF 15.AD 是△ABC 的中线 证明:由△BDE ≌△CDF (AAS ) ∴BD =CD ∴AD 是△ABC 的中线. 16.Rt △DEC ≌Rt △BFA(HL) ∴AF CE = ∠C =∠A ,∴AB CD ∥ 17.AD 平分∠BAC DE ⊥AB 于E ,DF ⊥AC 于F ,∴DE =DF 又∵DB =DC ∴Rt △DBE ≌Rt △DCF(HL) ∴EB =FC 18.过D 作DE ⊥AB ,交AB 于E 点,则E 点即可满足要求. ∵AD 平分∠CAB 且CD ⊥AC .ED ⊥AB , ∴CD =DE .由“H L”可证Rt △ACD ≌Rt △AED . ∴AC =AE .∵AC =BC ∴AE =CB ∴L △BDE =BD +DE +EB =BD +DC +EB =BC +EB =AC +EB =AE +EB =AB .4321BACFED19.证明:在AB 上截取AF ,使AF =AD ,连接EF.BCAD AB BC BF ECB EFB BE BE 43C BFE ECB EFB C,BFE 180AFE BFE 180C D BC //AD AFE ADE AFE ADE AE AE 21AF AD AFE ADE +=,=,=,=,中,和在,又=+,,=,=,=,=中,和在∴∴∆≅∆∴∠∠∠=∠∆∆∠=∠∴︒=∠+∠︒∠∠∴∠∠∴∆≅∆∴∠∠∆∆20.(1) ① ∵∠ADC =∠ACB =90° ∴∠CAD+∠ACD =90° ∴∠BCE+∠ACD =90° ∴∠CAD =∠BCE ∵AC =BC ∴△ADC ≌△CEB ② ∵△ADC ≌△CEB ∴CE =AD ,CD =BE ∴DE =CE+CD =AD+BE (2) ∵∠ADC =∠CEB =∠ACB =90° ∴∠ACD =∠CBE 又∵AC =BC ∴△ACD ≌△CBE ∴CE =AD ,CD =BE ∴DE =CE -CD =AD -BE(3) 当MN 旋转到图3的位置时,AD.DE.BE 所满足的等量关系是DE =BE -AD(或AD =BE -DE ,BE =AD+DE 等) ∵∠ADC =∠CEB =∠ACB =90° ∴∠ACD =∠CBE , 又∵AC =BC , ∴△ACD ≌△CBE , ∴AD =CE ,CD =BE , ∴DE =CD -CE =BE -AD.第十二章 轴对称12.1(1)1.B2.D3.略4.H ,A ,B5. 2条6.(3)n 条12.1(2)1.B2.B3.C4.直线CD 垂直平分线段AB5.一点,相等6.157.先证ACB ∆≌ABD ∆,再证ACO ∆≌DOB ∆8.连结AO9.(1)BGD ∆≌CFD ∆(2)利用两边之和大于第三边:EF CF BE >+12.1(3) 1.略 2 .3.N M4.(答案不惟一)12.2.1(1)1.C2. B3.25度4.略5. (1)(2)12.2.1(2)1.B2.D3. A4.115度 5. 80度6. QM与PM 的和最小,作Q关于BC的对称点Q’,连结PM’与BC的交点就是M点7. 作点A关于直线l的对称点A’,连结BA’并延长交直线l与点P 8. 连结AE交BD于点P 9.作B点关于y轴B’,点A关于x轴对称点A’,连结A’ B’交x轴与点C,交y轴于D点12.2.21.B2.D3.(2,3)4.m=0.5,n=-3.55.(3,3),(0,1)或(0,5)6.略7.略8.(1)略(2)(8,-3)(3)(6-a,0)12.3.1(1)1.D2.C3.D4.55°5.22.5°6.25°7. 45°8.略9.连结AD,证ΔADE≌ΔBDF 10.如图.12.3.1(2)1.D2.B3.44.55.略6.略7.略12.3.2(1)1.D2.B3.120°4.轴5.略6.略7.略8.30°12.3.2(2)1.C2.C3.A4.B5.86.17.10cm8.连结AD9.连结OE.OF 10.(1)BE=AD;(2)等边三角形;(3)MN∥BD.第十二章综合练习题1.C2.B3.A4.A5.D6. −2,−57. 82.5°8.59.40°10.(答案不惟一)C311.(1)①和②;②和③;(2)图略. 12.90° 13.略 14.略 15.略 16过点D 作DM ∥AC ,交BC 于M 17.(1)略 (2)等腰直角三角形;(3)(如图)点D 是AB 的中点,AD =1.18.略 19.60°第十三章 实数13.1(1)1.C2.C3.D4.(1)16 (2)35.36.(1)算术平方根 (2)4和5 (3)767.11;47;0.5;6 8.34;10;2;3 9.0.1;-53;7;3110.(略) 11.<;< 12.(略) 13.1(2)1.C2.C3.D4.D5.D6.07.169;±138. ±5,±4; 10.3和4 11.±12,512.±6;± 153;±0.4;±11 3.20;-35;±0.9;6 14.±7;±16;±23; 15.y =—57,y 1011-=5 16.x =±3,y =±21,|x+2y|=4或2 16.0.313.21.B2.C3.D4.C5.D6.07.1,-18.>9.4 10.31- 11.27,3 12.80;-34;5;-7 13.10;-0.6;-2514.-3;4;-1 15.<;< 1 16.8000 17.128π 18. 边长是10米的正方形比较适合13.31..C2.A3.D4.C5.C6.C7.3-3,8.22,14.3-π;3-59.π(答案不惟一) 10.-1 11.152 12.(1) 64,42,20,3.14,1+π (2) 75- ,39- (3)64,42,75- 3.14 , 0 (4) 39-,20,1+π13.(1)322- (2)55103- (3)172- (4)23+ 14. 略15.(1)2(2)—400(3)23±16. P >Q.第十三章综合练习题1. B2.A3.D4.B5.C6.D7.A8.D9.7,—13 10.-2,1.4,—7 11.8± 12.49413. -28 14. <,>,> 15.(1)±20;(2)-0.7;(3)7;(4)-2;(5)略;(6)略;16. .略 17. 20 18. 0.125;0.5 19. A(-22,-22),B(22,-22),C(22,22) ,D(-22,22) 20 . >,< 21. 9cm第十四章 一次函数14.1.11. C 2.C 3. 34,π;v ,r 4. m =3n+1;3,1;m ,n 5.x30y =;30,x ,y 6.0.4,0.8,1.2,1.6,y =0.4x 7. ①S =x (10-x ),S 和x 是变量,10是常量; ②α=90°-β,α和β是变量, 90°是常量; ③y =30-0.5t ,y 和t 是变量,30和-0.5是常量;8. (1)V =100h ,变量:v ,h ;常量:100;(2) 3700cm ;(3) 3100cm ,35000cm . 14.1.2(1)1. D2.C3.D4.315y x =- 5.y =2x 6.y =90+2x 7. y =π2r + 30πr 8. Q =30—0.5t ,60t 0≤≤,40 9. y =24-6x (0≤x≤11) 自变量:x 自变量的函数:y ;14.1. 2(2) 1.C 2. A 3. 32-4.-14;585.S =4(n —1)7.(1)x 为任意实数 ; (2)x≠21(3)x≤5; (4)x >-3 (5) x≤1且x≠0;(6) x≤1 ;8. (1) v = 331+0.6 t ;(2) 332.5米/秒 ;(3)115℃9. (1) S =x(24-2x) ; (2) 7≤x <12; (3) 当x =10时, s =402m ; (4)x =8,s 最大64; 10. 2110050200s m =⨯= ∵60>50 ∴此时刹车不会有危险. 14.1.3(1)1. B2.B3.B4.(1)100千米;6小时,2小时;(2)摩托车先到达乙地,早到了1小时;(3)骑自行车的先匀速行驶了2小时,行驶40千米后休息了1小时,然后用3小时到达乙地.骑摩托车的在自行车出发3小时后出发,行驶2小时后到达乙地.(4)摩托车行驶的平均速度是50千米/时. 14.1.3(2)1.B2.C3.B4.A5. 图象略;6. (1) (-3.0) (-1,0) (4,0); (0,2.5) (2)(1.5,4);1. 5;大,大,4; (3)上升,增大 (4)-3<x <-114.1.3(3)1.A2.B3.B4.100,甲,325米/秒,8米/秒 5.20 6.y =12+1.8(x -10)=1.8x —6 7. (1)y =12+0.5x ;(2) 17cm 8.(1)y =⎩⎨⎧〉-+≤的整数)3)(3(1.02.0)3(2.0t t t (2) 图象略; 9. (1) y =17x+2 ;(2)图象略;(3) 118个; 14.2.1 (1)1. D ;2.C ;3.B ;4.D ;5.C;6.S =80t ;49小时 7. C =2πr ;正比例 ; 8.m≠-2 9.1 ; 10.-3 ; 11.(1)y =4x ,是正比例函数;(2)s =h 25,是正比例函数.(3)y =0.1x ,正比例函数(4)x =28-5y ,不是正比例函数(5)t 2.3y =;是正比例函数 14.2.1 (2)1.B2.A3. y =-2x4.k =45. m >326.y =-3x ;7.0,1,减小8.b a -=(a b -=,0=+b a ,相反数)9.二、四,减小 10.答案不惟一 11.6 12.314.2.2(1)1.C 2 .C 3. B 4. y =-x+90 5 .k≠1;k =-1 6.y =75x+100 7. (1)y =-16x+1920;(2) x ≤721, 13人. 8.(1)甲:y =0.7x+3;乙:y =0.85x; (2)一样都是17(3)在甲买30本 14.2.2(2)1.A2.B3.D4.D5.A6.C7.y =-x+38. (3,0) , (0,3) ,299 .一、二、四 ,减小 10. >,> 11. 上 ,3 12.○1○2○4,○1○3,○2○3 13.32- 14. (1) m >-41;(2) m >-1;(3) - 1<m < -4115. y =4x 先到达16. ①y =75x+145(x≥3);②7元;③21元;④20千米 17.(1)y =x+1;(2)m =1或-314.2.2(3)1.D2.C3.B4.y =21x -3 5. 答案不惟一 6.y =x+2 ;x =1 7. ±6 8.31432+-=x y 9. y =2x+2 10. 1 11. 221+-=x y 12. y =-x+313. ①y =x+5;图象略;②12.5 14. y =4x -3 15. y =2x -916. (1) k 1=-2,k 2=-3;(2) (1,0) 17. l 1 : y =-2x ; l 2 : y =3x+5或y = -43x +4518. (1)y =32535+x (2) y =3254.4235+⨯=79,配套 19.54y x =;1525+-=x y 20.(1)y = 39200 -30x (0≤x≤70);(2)x =70时,y 最小=37100元21. (1)⎩⎨⎧>-=≤≤=)100(25.0)1000(48.0x x y x x y (2)63(元)(3)144度14.3.11. B2. D3. B4. A5. -5,0252=--x ,-2 6. (-4,0)、(0,8),16 7. (-7,0) 8. 2,2 9. 4 10. 图略,3=x 11. 图略,(1)当x =-2时,y =1 (2)当y =3时,x =2 (3)(-4,0)、(0,2) (4)x =4 12. 41714.3.21. A2.. D3. C4. D5. 2>x6. 34-< 7. 2>x 8. (3,0) 9. ①2->x②2-=x ③2-<x 10. (-1,0),1-<x 11. (1)12-≤x (2)2-<x12.(1)1l :1211+=x y ,2l :x y =2 (2)盈利 (3)121-=x y13.(1)x <1500(2)x =1500(3)个体;14. (1)甲树苗400株,乙树苗100株 (2)甲种树苗应不小于200株(3)选购甲树苗300株,乙树苗200株14.3.31.C2. B3.B4.D5.B6.11,17. 114x y =⎧⎨=⎩,(11,4) 8. 21 9. 1,1 10. 72-11. x>5,x<5 12.(1)⎩⎨⎧==12y x (2)⎩⎨⎧-==5.15.1y x 13.24514. (1)30,25;2小时,2.5小时 (2) y = -15x+30 ;y = -10x+25(3) 燃烧1小时,高度相等; 0≤x <1,甲高;1<x <2.5,乙高; 15.(1)(0,1),(0,—2);(2)(1,—1);(3)2 第十四章综合练习题1. D2. C3. B4.A5.A6.C7.D8.D9.A 10. B 11. 2 12. -3 13. x >-2 14. y = 2x+1 15.-1 ,-25 16. y =-43x+27 17. y =1000+1.5x 18.6 19.33-=x y 20.(—6,2)或(—2,6)21.(1)a =1.5,c =6 (2) 1.5y x =(x≤6),627y x =-(x>6) (3)21元 22. x y 34=,153y x =-+或35y x =-,图略 23.图略,(1)x<-3 (2) ⎩⎨⎧-==13y x 24.(1)620.02y x =- (2)180个 25. (1)(—1,1)或(—7,—5) (2)(1,3)第十五章 整式的乘除15.1.11.D2.C3.4,4-,8-4.(1)810 (2)3a (3)5a 5. 6 6.0 7.nm a a ,8.(1)7m (2)5m - (3)43+m y (4)5)b a -( (5)10102⨯(6)72x (7)0 (8)0 9. (1)18105⨯ (2)1510248.1⨯ 10.b c a 2=+15.1.21.C2.D 3.①65②63-③63④-6a ⑤6x - 4.3 5.96.(1)64 (2)64729(3)6y - (4)10x (5)62x (6)10x (7)12a - (8)24x (9)13-n a 7.32x = 8. 263913324<< 9. 10815.1.31.B2.C3.D4.38m ;42y x 5.3;2x ;x 6.4 ;37.(1)36271y x (2)864b a (3)12a (4)924-a (5)0 8. 52- 9. 8 15.1.4(1)1.A2.D3.D4.(1)357a (2)3361y x - 5.52.510-⨯ 6.(1)366a b (2)23310c b a - (3)99x (4)44371z y x (5)443a b c (6)538x y(7)1121++-n n b a 7.(1)2)1(3-+=x y (2)1215.1.4(2)1.C2.D3. (1)12x x 62+ (2)2293xy y x +- 4.-12 5.(1)3222242a b a b a b +-(2)233242x y x y -+ (3)34512106-x x x ++ (4)545384y x y x +-6.(1) x 11;311- (2)xy x 3032--;87 15.1.4(3)1.D2.C3.232++x x 4. 3,-28 5.(1)652++x x (2)652-+-x x(3)2249b a - (4)2215196y xy x +- (5)x x x 67223+- (6)2222a ac c b ++-(7)33y x + (8)2212314y xy x -+ 6. 0 7.224y x x =-+ 15.2.11.B2.D3.(1)12-x (2)94-x 4.(1))y x -( (2))(x y - 5.(1)+3y ,x (2)53,a 6.241a - 7.①2499;②40084009 8. =-+))((b a b a 22b a - 9. 减少9 10.(1)492-x (2)21x - (3)249m n - (4)164124-y x (5)22425y a -(6)814-x 11.-2 12.1+n x-1 13. 115.2.21.D2.C3.A4.412+-y y ;mn 4 5.10x ;5 6.6± 7.(1)91242+-x x ;(2)224b a -4ab+1;(3)1442++m m (4)2244b ab a -- (5)a b ab a 6222-++96+-b (6)42816x x -+ 8.xy x 252- 9.ab a -2;5 10. 59-x ;-8 11. 2 12.225-; 13.27 15.3.11. C2. A3.(1)5a (2)3x 4.(1)-27 (2)-3x 5. (1)1 (2)21xy6.(1)6x (2)2a - (3)x (4)13a (5)1 (6) 51032b a - 7.解:根据题意,得.1,01032-=∴⎩⎨⎧=+≠-x x a8. 解:64943)()(32323232=÷=÷=÷=-n m n m nm a a a a a9. 周长=4018)]5(5)3()5([222++=+++++a a a a a a 15.3.2(1)1. B2.D3.(1)4a (2)a (3)24a 4.5104⨯ 5.(1)316x (2)524a b c -;(3)2259x -(4)7289x y - (5)c b a 3716- (6)656432-a a + 6.29.610⨯小时 15.3.2(2)1. C2.(1)1242+-a a (2)m n 23- 3.2m 4.122+-b a 5.(1)224743a b ab -++;(2)544010y xy +- 6.(1)y x 2141-;3017(2)y x 21-,515.4.11.B2.B3.D.4.(1))2(-a a ;(2))13(5--a a5.156-6.(1)- (2)+ (3)-7.(1))1(b ab + (2))431(52a a a +- (3)()239ab a - (4)()22342xyz x y y z xz -+(5)))((b a y x -+ (6))3(-x x (7))1)(1)((-++x x b a (8)()()272---y x y x8. 171.15.4.2(1)1.A2.D3.(1))1)(1(-+x x (2))51)(51b b -+( (3))1)(1(3-+a a (4))3)(3(b a b a ab -+. 4.-+=-a b a b a )((22)b5.(1)()()2525a a +- (2))1)(1(-+xy xy (3)()()22ab a b a b +-(4)()()()22422x yx y x y ++- (5))3)(3(8-+x x (6))32)(32)((n m n m n m -++ 6. 0 7. 10215.4.2(2)1.C2.B3.C4.2)(2y x +5.2)(b a a -6.(1)1 (2)x 217.±20 8. (1)()223b a -; (2)()231y -; (3)2)21(m +; (4)2)12(-a a (5))1)(1(y x y x -+++;(6)()()c b a c b a --++22 9.b a 25+10.(1)49 (2)))((22b a b a b a -+=-(答案不惟一) 第十五章综合练习题1.C2. B3.D4.C5.三;三6.xy -7. 128x -;5a 8. 1 9.1-b 10.(1)2)3(-x (2))2)(2(-+x x x11.(1)y 5 (2)132+-ab (3)2413x y (4)5445364042a b a b a b -+- (5)4312ab c - (6)223103b ab a -+- 12.322+-a a ,13 13.(1))2(2-x x (2))2)((x y y x -- (3)()2ab a b - (4)()()224x b x b a -+- 14.(1)6 (2)515. ()222222342224a b a b a ab cm πππππ++⎛⎫⎛⎫⎛⎫--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭16.(1)425-=x (2)21>x 17. 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
综合练习
1、对于任意的两个数a和b,规定a*b=3×a-b÷3。求8*9的值。
2、已知ab表示(a-b)÷(a+b),试计算:53
3 、定义新的运算a⊖babab.求(1⊖2)⊖3.
4、 有一个数学运算符号“○”,使下列算式成立:21○6332,54○
451197,65○42671.求113○5
4
=( )
5、甲每小时行9千米,乙每小时行11千米,两人同时同地相背而行。
问:6小时后两人相距多少千米?
6、甲、乙两只轮船同时从一个港口向相反方向的两地开出。甲船每
小时行25千米,乙船每小时行18千米。经过几小时,两船相距645
千米?
7、一列长300米的列车,完全通过一座长450米的桥梁,一共用了
2分钟。这列火车过桥时每分钟行多少米?
8、长100米的列车,以每秒20米的速度通过一座长500米的大桥。
列车通过这座桥要用多少秒?
9、一列火车通过一座长500米的桥梁用了40秒,用同样的速度通过
另一座600米的桥梁用了45秒。这列火车过桥时每秒钟行多少米?
10、一列火车通过一座400米的桥梁用了20秒,通过一座700米的
桥梁用了30秒。这列火车过桥时每秒钟行多少米?这列火车有多
长?
11、两个码头相距192千米,一艘汽艇顺水行完全程需要8小时,已
知这条河的水流速度为4千米/小时,求逆水行完全程需几小时?
12、一艘每小时行25千米的客轮,在大运河中顺水航行140千米,
水速是每小时3千米,需要行几个小时?
13、一只小船静水中速度为每小时30千米。在176千米长河中逆水
而行用了11个小时.求返回原处需用几个小时。
14、向阳小学有730个学生,问:至少有几个学生的生日是同一天?
15、有一个布袋中有5种不同颜色的球,每种都有20个,问:一次
至少要取出多少个小球,才能保证其中至少有3个小球的颜色相同?
16、一个口袋里分别有4个红球,7个黄球,8个黑球,为保证取出
的球中有6个球颜色相同,则至少要取多少个小球?
