2018_2019学年八年级数学下册专题2勾股定理课件新人教版
八年级数学人教版下勾股定理的常见题型课件优秀课件

D、7
∴BE=AB-AE=10-6=4,y 在Rt△BDE中,由勾股5 定理得,
DE2+BE2=BD2 4
P( 3,4 )
即CD2+42=(8-CD)2,3
解得:CD=3cm4. 2
平面直角坐标系内有两点A(
5
),B(
4 ) ,则这两点之间的距离为AB=
如图,长方体的高为4,长1为5,宽为3,一只蚂蚁从顶点
)A、48 B、60 C、76 D、80 )A、48 B、60 C、76 D、80
1、如图,在RtΔABC中,∠A=90°,BD平分∠ABC,交AC于点D, 且AB=4,BD=5,求点D到BC的距离。
A出发沿长方体的表面爬到顶点B,求蚂蚁经过的最短
完成导学提纲 解:设AE=x,EB=ED=10-x
),B(
) ,则这两点之间的距离为AB=
1、矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=_______cm.
A.、 4 │P1P2│=10
解:由折叠的性质知CD=DE,AC=AE. 在Rt△BDE中,由勾股定理得,AB=10.
B、 3
C、 5 由折叠的性质知,AE=AC=6,DE=CD, ∠AED=∠C=90°.
)2
12
12
2、立体图形中的最短距离
B
B
如图,长方体的高为4,长为5,宽为3,一只蚂蚁从顶点
A出发沿长方体的表面爬到顶点B,求蚂蚁经过的最短
路程。
4
B
3ห้องสมุดไป่ตู้
B
AA
5
4 3
B
A
5
3
4
A
5
数学人教版八年级下册勾股定理的应用(2)——作图

学习目标:1.能用勾股定理直角三角形全等的“斜边、直角边”判定定理。
2.能应用勾股定理在数轴上画出表示无理数的点。
3.体会勾股定理在数学中的地位和作用。
学习重点:用勾股定理作出长度为无理数的线段。
教学活动流程活动1:复习孕新,引入课题1.回顾勾股定理,并以针对性练习为画作铺垫;(2)用“数学海螺”图创设情境并导入新课,明确学习目标。
活动2:运用勾股定理证明(HL)用三角板作辅助演示活动3:课件动画演示作图演示的两种作法以及“数学海螺”的作法.活动4:动手实践,会“数形互变”以前面的练习题为作图思路导向,以课件演示类比模仿,教师演示规范作图,学生会作图也会求点.活动5:当堂检测教材第27页习题活动6:拓展应用,服务生活1.用无刻度的直尺在网格上按要求画含无理数线段的三角形;(2)求蚂蚁沿圆柱表面爬行的最短路径。
活动7:小结梳理数轴图——网格图——展开图;实际问题——数学问题——建模活动8:布置作业教学过程活动1:复习孕新,引入课题1.问题(1)勾股定理的内容是什么?怎样求斜边长c或直角边长a、b?(2)求以线段a、b为直角边的直角三角形的斜边长。
a=1 b=1 (c=)a=1 b= (c=)a=2 b=3 (c=)设计意图:在复习的基础上为新课画无理数线段作铺垫,实现知识正迁移。
(3)如果直角三角形ABC的两边长分别为3和4,求第三边长。
设计意图:第三边应考虑为直角边或斜边,渗透分类讨论思想。
2.课件展示“数学海螺”图片并明确学习目标设计意图:创设情境并明确本节课学习任务。
活动2:运用勾股定理证明(HL)用三角板作演示,并要求画图并写出已知、求证并证明,利用勾股定理求得第三边长,再利用(SSS)或(SAS)可证得。
活动3:课件动画演示作图1.对比的两种作法,明确当直角边为正整数时作图方便,并引导学生如何规范作图。
2.“数学海螺”的作法活动4:动手实践,会“数形互变”1.在数轴上画出表示的点,的点呢?2.求点A在数轴上表示的点(1-)设计意图:以练习为画的思路导向,以活动3为类比模仿会作图也会求点,实现数形互变,以“数”化“形”,以“形”变“数”,渗透数形结合思想。
(第9套)人教版八年级数学下册 17.1 勾股定理精品教学课件

中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
勾股定理
看
发们映友 现,直家
一
什我角作相 么们三客传
2500
看
?也角, 来形发
观三现年
察边朋前
下的友,
面某家一
的种用次
图数砖毕
案量铺达
,关成哥
看系的拉
看,地斯
你同面去
能学反朋
A
图乙
C
A
B
C B
图甲
SA+SB=SC
A的面积 B的面积 C的面积
图甲 图乙 49 4 16 8 25
填表:若小方格的边长 为1.
思考:正方形A、B、C 的面积有什么关系?
C Aa c
b B 图甲
A
图乙
a
Bb c C
猜想:a、b、c 之间的关系? SA+SB=SC
问题:边长为任意长度的直 角三角形还成立吗?
2、等腰△ABC中 ,AB=Aห้องสมุดไป่ตู้,AD是底边上的高,若 AB=5cm,BC=6cm 求 ①AD的长;
②ΔABC的面积
小结: ①本节课学到了什么数学知
识? ②你了解了勾股定理的发现
方法了吗? ③你还有什么困惑?
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
a2 +b2 =c2
SA+SB=S C
C
图乙 a
Aa c b
bc C
图甲 B
SA+SB=S
C
3.猜想:a、b、c 之间的关系? a2 +b2
新人教版2019八年级数学下册第十七章勾股定理小专题二利用勾股定理解决最短路径问题练习新版
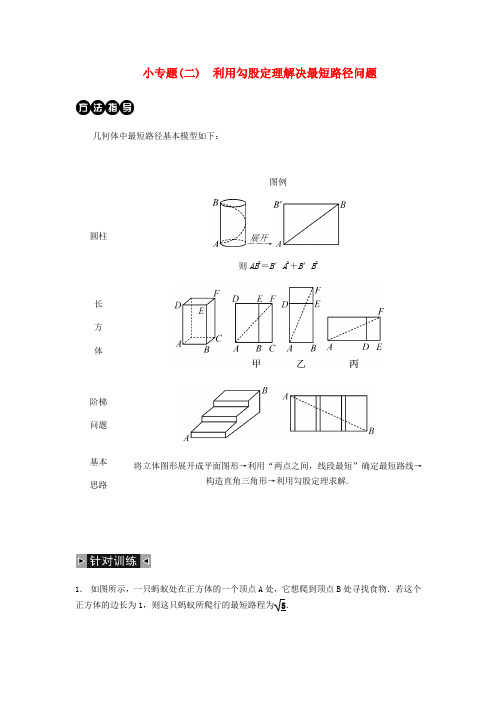
小专题(二) 利用勾股定理解决最短路径问题几何体中最短路径基本模型如下:
图例
圆柱
――→
展开
则AB2=B′A2+B′B2
长
方
体
阶梯
问题
基本思路将立体图形展开成平面图形→利用“两点之间,线段最短”确定最短路线→构造直角三角形→利用勾股定理求解.
1.如图所示,一只蚂蚁处在正方体的一个顶点A处,它想爬到顶点B处寻找食物.若这个
正方体的边长为1
第1题图第2题图
2.(2018·黄冈)如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm 的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为20cm.(杯壁厚度不计)
3.如图,在一个长为2 m,宽为1 m的长方形草地上,放着一根长方体的木块,它的棱和草地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达点C处需要走的最短路程是2.60m(精确到0.01 m).。
2019八年级数学下册第十七章勾股定理小专题(二)利用勾股定理解决最短路径问题练习新人教版
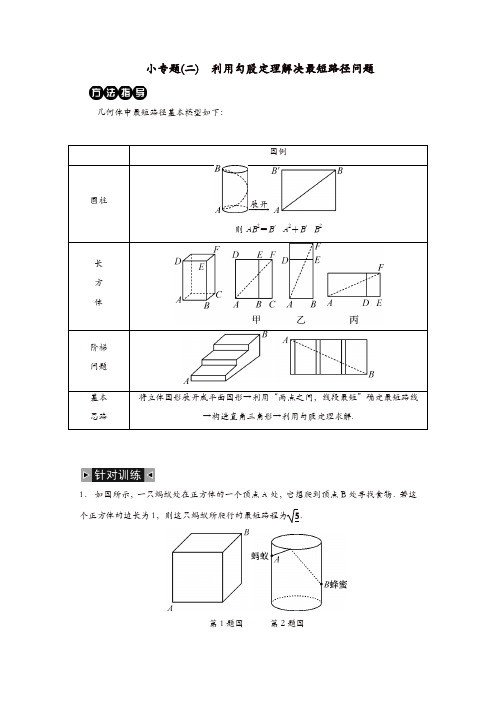
小专题(二) 利用勾股定理解决最短路径问题
几何体中最短路径基本模型如下:
――→展开
则
AB
2=
B ′A 2+B ′B 2
将立体图形展开成平面图形→利用“两点之间,线段最短”确定最短路线
1. 如图所示,一只蚂蚁处在正方体的一个顶点A 处,它想爬到顶点B 处寻找食物.若这个正方体的边长为1
第1题图 第2题图
2.(2018·黄冈)如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm 的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为20cm.(杯壁厚度不计)
3.如图,在一个长为2 m,宽为1 m的长方形草地上,放着一根长方体的木块,它的棱和草地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达点C处需要走的最短路程是2.60m(精确到0.01 m).。
17-1第1课时 勾股定理(共42张ppt)2022-2023学年八年级下学期数学人教版

5.求斜边长17 cm、一条直角边长15 cm的直角三 角形的面积.
解:设另一条直角边长是x cm. 由勾股定理得152+ x2 =172, 即x2=172-152=289–225=64, ∴ x=±8(负值舍去), ∴另一直角边长为8 cm,
直角三角形的面积是
(cm2).
a
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”. 如图,图中的三个三角形都是直角三角形,求证: a2 + b2 = c2.
a
b
c
证明:
S梯形
1 (a 2
b)(a
b),
S梯形
1 2
ab
1 2
ab
1 2
c2,
c a
∴a2 + b2 = c2.
AC2+ 1
4
BC2.
∴阴影部分的面积为
1 2
AB2= 9 .
2
8.(创新题)如图17-10-12,在△ABD中,∠D=90°,C是BD上一点,已知BC=9,AB=17,AC=10,求 AD的长.
解:∵∠D=90°,
∴AD2=AB2-BD2=AC2-CD2.
∴172-(9+CD)2=102-CD2.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图,BC 42 32 7;
当BC为斜边时,如图,BC 42 32 5.
B B
4
3
C 图 A
4
A
3
图
C
归纳 当直角三角形中所给的两条边没有指明是斜边或 直角边时,其中一较长边可能是直角边,也可能是斜
精品课件:人教版八年级下册数学第十七章17.1.3利用勾股定理作图和计算
6、 如图,四边形ABCD中∠A=60°,∠B=∠D=90°, AB=2,CD=1,求四边形ABCD的面积.
解:如图,延长AD、BC交于E. A ∵∠B=90°,∠A=60°, D ∴∠E=90°-60°=30°, 在Rt△ABE和Rt△CDE中, E B ∵AB=2,CD=1, C ∴AE=2AB=2×2=4,CE=2CD=2×1=2, 由勾股定理得 BE 42 22 2 3,DE 22 12 3,
D
∵ AB 12 22 5
3 3 5 CD 5 5
此类网格中求格点三角形的高的题,常用的 归纳 方法是利用网格求面积,再用面积法求高.
课堂练习
1、已知:如图,等边△ABC的高AD是 3 .
(1)求边长;
(2)求S△ABC .
A
2x
3
B
x D
C
2、如图为4×4的正方形网格,以格点与点A为 端点,你能画出几条边长为 10 的线段?
3.如图,网格中的小正方形边长均为1,△ABC的 8 13 三个顶点均在格点上,则AB边上的高为_______. 13
4、如图,折叠长方形ABCD的一边AD,使点D落在BC边 的F点处,若AB=8cm,BC=10cm,求EC的长.
解:在Rt△ABF中,由勾股定理得 A
BF2=AF2-AB2=102-82=36,
典例精析
例1、已知:如图,等边△ABC的边长是 6 . (1)求高AD的长; 解: ( 1) ∵AD⊥BC (2)求S△ABC .
∴∠BAD=30° 1 BD AB 3
AD AB2 BD2 3 3
1 (2)SΔABC= 2 BC AD 1 63 3 2
A
6 ?
【最新】人教版八年级数学下册第17章《勾股定理的逆定理》优质公开课课件.ppt
解:∵ AB=3,BC=4,∠B=90°,
D
∴ AC=5.又∵ CD=12,AD=13,
∴ AC2+CD2=52+122=169.
又∵ AD2=132=169,
A
即 AC2+CD2=AD2,
∴ △ACD是直角三角形. B
C
∴
四边形ABCD的面积为
134+1512=36.
2
2
巩固练习
如图,在四边形ABCD中,AB=BC=CD=DA,
追问1 类似这样的关系6,8,10;9,12,15是否 也是勾股数?如何验证?
追问2 通过对以上勾股数的研究,你有什么样的 猜想?
拓展练习
问题2 通过例1及例2的学习,我们进一步学习了 像18,24,30;3,4,5;5,12,13这样的勾股数,大 家有没有发现18,24,30;3,4,5 这两组勾股数有什 么关系?
小时航行12 n mile.它们离开港口一个半小时后分别位
于点Q,R处,且相距
N
30 n mile .如果知道 “远航”号沿东北方
S
Q
向航行,能知道“海
R
天”号沿哪个方向航
行吗?
P
E
巩固练习
A、B、C三地的两两距离如图所示,A地在B 地的正东方向,C地在B地的什么方向?
正北方向
例题讲解
例2 如图,在四边形ABCD中,AB=3,BC=4, CD=12,AD=13,∠B=90°,求四边形ABCD的面积.
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
勾股定理(第2课时)(课件)-2022-2023学年八年级数学下册同步精品课堂(人教版)
勾股定理应用的常见类型
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路径问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、
生活中的实际问题.
课堂练习
1.一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯
三角形的面积公式可求BD,再利用
勾股定理便可求CD.
北东
A
C
D
Q
课堂练习
P
解:∵AC10,BC8,AB6,
B
∴AC2AB2BC2
北东
A
即△ABC是直角三角形,
C
D
Q
1
1
而S△ABC BC AB AC BD
2
2
24
解得:BD .
5
2
24
在Rt△BCD中,CD = BC 2 BD 2 82 6.4
路线最短?
B
A
B
A
方案①
B
A
方案②
方案③
针对练习
(2)如图,将圆柱侧面剪开展成一个长方形,点A到点B的最短路线是什么?
你画对了吗?
B
A
B
A
B
∵两点之间线段最短,
∴方案③的路线最短.
A
针对练习
(3)蚂蚁从点A出发,想吃到点B上的食物,它沿圆柱侧面爬行的最短路程是
多少?
解:在Rt△ABC中,
C
B
AC=12 cm,BC=18÷2=9(cm).
在Rt△A′DB中,由勾股定理得
