大学物理简明教程第三版课后习题答案
大学物理简明教程滕道祥课后答案

大学物理简明教程滕道祥课后答案1、37.用同种金属制成的体积相等的甲、乙两种金属球,其中有一种是实心的,有一种是空心的。
在调节好的天平左盘放3个甲球,在天平的右盘放5个乙球,天平恰好平衡,则下列说法不正确的是()[单选题] *A.乙金属球是空心的B.甲、乙两种金属球的质量之比为5:3C.空心的金属球中空心部分体积与整个球的体积之比为2:3(正确答案)D.空心的金属球中空心部分体积与整个球的体积之比为2:52、其原因错误的是()*A.使用的用电器总功率过大B.电路中有断路(正确答案)C.开关接触不良(正确答案)D.电路的总电阻过大(正确答案)3、2022年北京-张家口将举办第24届冬季奥林匹克运动会,我国提出“三亿人参与冰雪运动”的目标。
右图是滑雪运动员从山上滑下的情景,下列有关说法中正确的是()[单选题]A.运动员加速下滑是因为运动员具有惯性B.运动员穿上滑雪板,是为了减小对地面的压力C.运动员加速下滑过程中重力势能减小、动能增加(正确答案)D.若运动员下滑过程中一切外力都消失,他将立即停止运动4、空中运动的足球,若所受力都消失,它将静止在空中[判断题] *对错(正确答案)答案解析:空中运动的足球所受合力为零时将做匀速直线运动5、重锤线可以检测墙上的画是否挂正,这利用重力的方向垂直于支持面[判断题] *对错(正确答案)答案解析:重力的方向是竖直向下6、4.如图所示,打开水龙头,放出细细的水流。
小红用塑料梳子在干燥的头发上梳过后,将梳子靠近水流。
下列说法正确的是()[单选题] *A.梳过的头发不带电荷,梳子带负电荷B.水流靠近梳子,因为摩擦后的梳子带上电荷,吸引水流(正确答案)C.水流靠近梳子,因为摩擦后的梳子带有磁性,吸引水流D.水流方向不变,因为梳子离开头发后失去电子7、将钢棒一端靠近验电器,若验电器金属箔没有张开,则钢棒没有磁性[判断题] *对错(正确答案)答案解析:验电器是检测物体是否带电的8、21.用托盘天平测量物体的质量时,将被测物体和砝码放反了,若天平平衡时,左盘放着100g和20g的砝码各一个,游码所在位置读数为6g。
大学物理简明教程(吕金钟)第四章习题答案
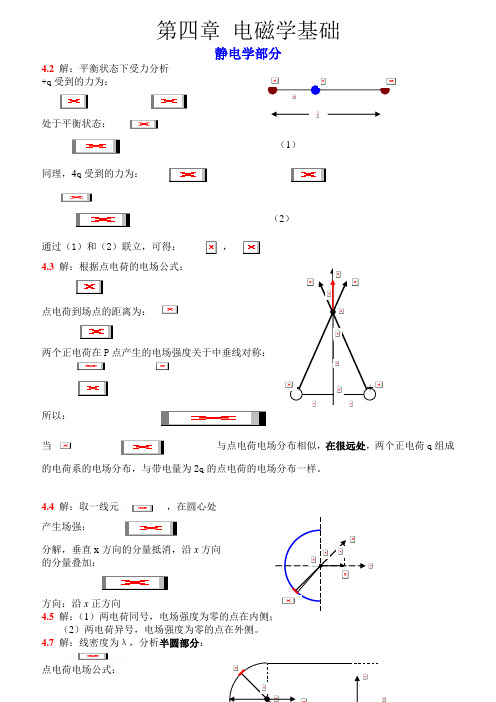
第四章电磁学基础静电学部分4.2解:平衡状态下受力分析+q受到的力为:处于平衡状态:(1)同理,4q 受到的力为:(2)通过(1)和(2)联立,可得:,4.3解:根据点电荷的电场公式:点电荷到场点的距离为:两个正电荷在P点产生的电场强度关于中垂线对称:所以:当与点电荷电场分布相似,在很远处,两个正电荷q组成的电荷系的电场分布,与带电量为2q的点电荷的电场分布一样。
4.4解:取一线元,在圆心处产生场强:分解,垂直x方向的分量抵消,沿x方向的分量叠加:方向:沿x正方向4.5解:(1(2)两电荷异号,电场强度为零的点在外侧。
4.7解:线密度为λ,分析半圆部分:点电荷电场公式:++在本题中:电场分布关于x 轴对称:,进行积分处理,上限为,下限为:方向沿x轴向右,正方向分析两个半无限长:,,,两个半无限长,关于x轴对称,在y方向的分量为0,在x方向的分量:在本题中,r为场点O到半无限长线的垂直距离。
电场强度的方向沿x轴负方向,向左。
那么大O点的电场强度为:4.8解:E的方向与半球面的轴平行,那么通过以R为半径圆周边线的任意曲面的电通量相等。
所以通过S1和S2的电通量等效于通过以R为半径圆面的电通量,即:4.9解:均匀带电球面的场强分布:球面R 1、R2的场强分布为:根据叠加原理,整个空间分为三部分:根据高斯定理,取高斯面求场强:图4-94 习题4.8用图S1S2RO场强分布:方向:沿径向向外4.10解:(1)、这是个球对称的问题当时,高斯面对包围电荷为Q当,高斯面内包围电荷为q方向沿径向(2)、证明:设电荷体密度为这是一个电荷非足够对称分布的带电体,不能直接用高斯定理求解。
但可以把这一带电体看成半径为R、电荷体密度为ρ的均匀带电球体和半径为R`、电荷体密度为-ρ的均匀带电体球相叠加,相当于在原空腔同时补上电荷体密度为ρ和-ρ的球体。
由电场叠加原理,空腔内任一点P的电场强度为:在电荷体密度为ρ球体内部某点电场为:在电荷体密度为-ρ球体内部某点电场为:所以4.11解:利用高斯定理,把空间分成三部分场强分布:方向:沿径向向外4.12 解:取闭合圆柱面为高斯面,高斯定理场强分布:方向沿径矢方向4.14 解:无限大带电平面的电场分布为:,场强叠加(1)电荷面密度均为σ在一区:在二区:在三区:(2)电荷面密度分别为σ和-σ在一区:在二区:在三区:方向为垂直于平面方向4.16解:把总的电场力做功看做是正电荷+q电场力做功和负电荷-q电场力做功的叠加,得用公式(4—14):(1)把单位正电荷从O点沿OCD移到D点,电场力做功。
大学物理简明教程课后习题参考答案-陈执平

∵
∴
由图中比例关系可知
矢量图
2-1质量为0.5kg的物体沿x轴作直线运动,在沿x方向的力 的作用下,t = 0时其位置与速度分别为x0 =5,v0 =2,求t = 1时该物体的位置和速度.(其中F以N为单位,t以s为单位,x0以m为单位,v0以m/s为单位)
分析当作用于物体的力是时间的函数时,由建立的运动方程积分可以求得速度.所求出的速度必定也是时间的函数,当还需要计算t时刻该物体的位置时,就应该利用速度的定义式 ,再积分求出位置的表示式.
(1)
如图所示,在距A为x远处取厚度为 的薄圆盘,半径为r,面积为 ,体积为 ,因 为一无穷小量,薄圆盘上电荷面密度 ,代入(1)式,得薄圆盘在A点产生的电场强度为
利用几何关系 ,对上式积分得圆锥体在A点的电场强度为
方向为沿对称轴向
5-4求真空中电荷面密度为 的无限大均匀带电平面的场强。
解:选取垂直于平面的圆柱面为高斯面。圆柱侧面上场强 与轴线平行,通过侧面电通量为零,而在两底面 上,场强方向与平面法线方向都一致。
分析由于木块与水平面间存在摩擦,子弹嵌入木块后与弹簧并不构成一个通常意义的弹簧振子,机械能不守恒,但是可以应用功能原理分析摩擦力作功与机械能的变化的关系.
解在子弹 和木块 碰撞的瞬间,因时间很短,木块的位置还未发生改变,因而还不受弹簧的作用,子弹和木块组成的系统水平方向无外力作用,水平方向动量守恒,设子弹质量为m1,速度为v10,木块质量为m2,子弹击中木块后,共同的速度为v2,得
1-1一质点在xy平面内运动,在 时它的位置矢量 ,经 后,其位移 m,求:(1) 时的位矢;(2)在Δt时间内质点的平均速度.
解(1)据题意,在 时刻,该质点的位矢为
大学物理简明教程陈执平参考解答(完整版)7.恒定磁场习题.

7-1 如图AB 、CD 为长直导线,BC 是一段圆心为O 、半径为R 的圆弧形导线,若导线通有电流I ,求O 点的磁感应强度。
解: AB 段产生:0B 1= BC 段产生:R12IB 02μ=,方向垂直向里CD 段产生:)231(R 2I )60sin 90(sin 2R 4IB 00003-=-=πμπμ方向垂直向里 )6231(R 2I B B B B 03210ππμ+-=++=,垂直纸面向内7-2 两条无限长直载流导线垂直且不相交,它们相距最近处为cm 0.2d =,电流分别为A 0.4I 1=和A 0.6I 2=, P 点到两导线距离都是d ,求P 处的磁感应强度大小。
解: 电流I 1在P 点产生 T 100.4d2I B 5101-⨯==πμ 方向垂直向里 电流I 2在P 点产生 T 100.6d2I B 5202-⨯==πμ 方向在纸面里垂直指向电流I 1P 点 T 102.7B B B 52221-⨯=+=5.1B B tg 12==θ,91560'=θ7-3 一宽度为b 的半无限长金属板置于真空中,均匀通有电流0I 。
P 点为薄板边线延长线上的一点,与薄板边缘的距离为d 。
如图所示。
试求P 点的磁感应强度B 。
解 建立坐标轴OX ,如图所示,P 点为X 轴上的一点。
整个金属板可视为由无限多条无限长的载流导线所组成,其中取任意一条载流线,其宽度为dx ,其上载有电流dx b I dl 0=,它在P 点产生的场强为()x d b b dx I r dIdB P -+==πμπμ44000的方向垂直纸面向里。
由于每一条无限长直载流线在P 点激发的磁感强度dB 具有相同的方向,所以整个载流金属板在P 点产生的磁感应强度为各载流线在该点产生dB 的代数和,即⎰⎰-+==bP P x d b dx bI dB B 004πμbx d b b I 0001ln 4-+=πμb d d b I πμ4ln 00+=P B 方向垂直于纸面向里。
大学物理简明教程答案

v船
v船
再对 t 求导,即得船的加速度
dl ds l dv v0 s lv 船 a 船 dt 2 dt v0 v0 dt s s2 l2 2 ( s )v 0 2 h 2 v0 s 3 s2 s 2 2 1-5 质点沿 x 轴运动,其加速度和位置的关系为 a =2+6 x , a 的单位为 m s , x 的单 1 位为 m. 质点在 x =0 处,速度为 10 m s ,试求质点在任何坐标处的速度值. s
dr v 3i (t 3) j m s 1 dt (4) v 3 i 7 j m s 1 4 则 v 3 i 3 j , v 3 i 7 j 0 4 (5)∵ v v4 v0 4 a 1j m s 2 t 4 4 dv a 1 j m s 2 dt (6) y 这说明该点只有 方向的加速度,且为恒量。
v2 v0 20 m s 1 ,
而
an2 g cos 60 o
2 v2 (20) 2 2 80 m a n2 10 cos 60
2
∴
1-10 飞轮半径为 0.4 m,自静止启动,其角加速度为 β=0.2 rad· s ,求 t =2s 时边缘 上各点的速度、法向加速度、切向加速度和合加速度. 解:当
b.
v
解: (1 )
ds v0 bt dt
dv b dt v 2 (v0 bt ) 2 an R R a
2 a a2 a n b2
则 加速度与半径的夹角为
(v0 bt ) 4 R2
arctan
(2)由题意应有
a Rb a n (v0 bt ) 2
大学物理简明教程课后习题参考答案-陈执平

1-1 一质点在xy 平面内运动,在 s 0t =时 它的位置矢量m )j 5i 4(r+-=,经s 5t Δ=后,其位移)j 8i 6(r Δ-=m ,求:(1) s 5t =时的位矢;(2)在Δt 时间内质点的平均速度.解 (1)据题意,在t t ∆+时刻,该质点的位矢为m32m )8-(6m )54(1)(j i j i j i r r r -=++-=∆+=(2)在Δt 时间内质点的平均速度为m/s )1.6-(1.2m/s 586j i j i r v =-=∆∆=t1-3 已知质点运动方程为k t 2j t sin R i t cos R r ++=,R 为常量。
求,t=0及2t π=时质点的速度和加速度。
解:(1)jˆt sin R i ˆt cos R dtv d a ,kˆ2j ˆt cos R i ˆt sin R dt r d v ,kˆt 2j ˆt sin R i ˆt cos R r --==++-==++= 当t=0时,a a ,R a ,2v ,R v ,0v,i ˆR a ,k ˆ2j ˆR v z y x z y x ==-====-=+= 当t=π/2时,z a ,R y a ,0x a ,2z v ,0y v ,R x v,j ˆR a ,k ˆ2i ˆR v =-====-=-=+-=1-6 在铅直平面内运动的质点,其运动方程为j t t i t r )515(52-+=,求t=1秒时的法向加速度、切向加速度。
解:j)t 1015(i 5v-+=,22)t 1015(5v -+=j 10a -= ,10a =, 25dtdva t ==而2t 2n 2a a a += ,故25a n =因此j5i 5v 1+=,j 22i 22v v 111+==τ j 5i 5)a (a 11t --=⋅=ττ ,j 5i 5a a a t n-=-=1-7 当一轮船在雨中航行时,它的雨篷遮着篷的垂直投影后2 m 的甲板上,篷高4 m 但当轮船停航时,甲板上干湿两部分的分界线却在篷前3 m ,如雨滴的速度大小为8 m ·s -1,求轮船的速率. 解: 依题意作出矢量图∵ 船雨雨船v v v-= ∴ 船雨船雨v v v+=由图中比例关系可知1s m 8-⋅==雨船v v 矢量图2-1 质量为0.5kg 的物体沿x 轴作直线运动,在沿x 方向的力t F 610-=的作用下,t = 0时其位置与速度分别为x0 =5,v0 =2,求t = 1时该物体的位置和速度.(其中F 以N 为单位,t 以s 为单位,x0以m 为单位,v0以m/s 为单位)分析 当作用于物体的力是时间的函数时,由建立的运动方程积分可以求得速度.所求出的速度必定也是时间的函数,当还需要计算t 时刻该物体的位置时,就应该利用速度的定义式txd d =v ,再积分求出位置的表示式. 解 由加速度的定义ta d d v=,应用牛顿第二定律,可得 t t m F t 122050610d d -=-==.v 分离变量:t t d 1220d )(-=v两边积分得C t t +-=2620v由初始条件:t = 0时v=v0 =2,得20==v C ,即26202+-=t t v (1)因txd d =v ,上式可写为 2620d d 2+-=t t tx分离变量:t t t x d 2620d 2)(+-=两边积分得1322210C t t t x ++-=由初始条件:t = 0时x=x0 =5,得501==x C ,即5221032++-=t t t x (2)当t = 1s 时,由(1)和(2)式得m/s 16=v ,m 15=x .2-3 光滑水平面上有一固定的圆环,半径为R 。
物理学简明教程(马文蔚等著)第三章课后练习题答案详解

物理学简明教程(马文蔚等著)第三章课后练习题答案详解物理学简明教程(马文蔚等著)第三章课后练习题答案详解3 -1有两个力作用在一个有固定转轴的刚体上:(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零;(4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零.对上述说法下述判断正确的是( )(A) 只有(1)是正确的(B)(1)、(2)正确,(3)、(4)错误(C) (1)、(2)、(3)都正确,(4)错误 (D)(1)、(2)、(3)、(4)都正确分析与解力对轴之力矩通常有三种情况:其中两种情况下力矩为零:一是力的作用线通过转轴,二是力平行于转轴(例如门的重力并不能使门转).不满足上述情况下的作用力(含题述作用力垂直于转轴的情况)对轴之矩不为零,但同时有两个力作用时,只要满足两力矩大小相等,方向相反,两力矩对同一轴的合外力矩也可以为零,由以上规则可知(1)(2)说法是正确.对于(3)(4)两种说法,如作用于刚体上的两个力为共点力,当合力为零时,它们对同一轴的合外力矩也一定为零,反之亦然.但如这两个力为非共点力,则以上结论不成立,故(3)(4)说法不完全正确.综上所述,应选(B).3-2关于力矩有以下几种说法:(1) 对某个定轴转动刚体而言,内力矩不会改变刚体的角加速度;(2) 一对作用力和反作用力对同一轴的力矩之和必为零;(3) 质量相等,形状和大小不同的两个刚体,在相同力矩的作用下,它们的运动状态一定相同.对上述说法下述判断正确的是( )(A) 只有(2)是正确的 (B) (1)、(2)是正确的(C)(2)、(3)是正确的 (D) (1)、(2)、(3)都是正确的分析与解刚体中相邻质元之间的一对内力属于作用力与反作用力,且作用点相同,故对同一轴的力矩之和必为零,因此可推知刚体中所有内力矩之和为零,因而不会影响刚体的角加速度或角动量等,故(1)(2)说法正确.对说法(3)来说,题述情况中两个刚体对同一轴的转动惯量因形状、大小不同有可能不同,因而在相同力矩作用下,产生的角加速度不一定相同,因而运动状态未必相同,由此可见应选(B).3-3均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动,如图所示,今使棒从水平位置由静止开始自由下落,在棒摆到竖直位置的过程中,下述说法正确的是( )(A) 角速度从小到大,角加速度不变(B) 角速度从小到大,角加速度从小到大(C) 角速度从小到大,角加速度从大到小(D) 角速度不变,角加速度为零分析与解如图所示,在棒下落过程中,重力对轴之矩是变化的,其大小与棒和水平面的夹角有关.当棒处于水平位置,重力矩最大,当棒处于竖直位置时,重力矩为零.因此在棒在下落过程中重力矩由大到小,由转动定律知,棒的角加速亦由大到小,而棒的角速度却由小到大(由机械能守恒亦可判断角速度变化情况),应选(C).3 -4 一汽车发动机曲轴的转速在12 s 内由1.2×103 r·min-1均匀的增加到2.7×103 r·min-1.(1) 求曲轴转动的角加速度;(2) 在此时间内,曲轴转了多少转?分析这是刚体的运动学问题.刚体定轴转动的运动学规律与质点的运动学规律有类似的关系,本题为匀变速转动.解 (1) 由于角速度ω=2π n (n 为单位时间内的转数),根据角加速度的定义tωαd d =,在匀变速转动中角加速度为()200s rad 1.13π2-?=-=-=tn n t ωωα (2) 发动机曲轴转过的角度为()0020π221n n t ωωt αt ωθ-=-=+= 在12 s 内曲轴转过的圈数为3902π20=+==t n n θN 圈3 -5 一飞轮由一直径为30㎝,厚度为2.0㎝的圆盘和两个直径为10㎝,长为8.0㎝的共轴圆柱体组成,设飞轮的密度为7.8×103 kg·m -3,求飞轮对轴的转动惯量.分析根据转动惯量的可叠加性,飞轮对轴的转动惯量可视为圆盘与两圆柱体对同轴的转动惯量之和;而匀质圆盘、圆柱体对轴的转动惯量的计算可查书中公式,或根据转动惯量的定义,用简单的积分计算得到.解根据转动惯量的叠加性,由匀质圆盘、圆柱体对轴的转动惯量公式可得2424122221121m kg 136.021π161 2212212?=??? ??+=??+??? ???=+=ad ld ρd m d m J J J3 -6 一燃气轮机在试车时,燃气作用在涡轮上的力矩为2.03×03N·m ,涡轮的转动惯量为25.0kg·m 2 .当轮的转速由2.80×103 r·min -1 增大到1.12×104 r·min -1时,所经历的时间t 为多少?分析由于作用在飞轮上的力矩是恒力矩,因此,根据转动定律可知,飞轮的角加速度是一恒量;又由匀变速转动中角加速度与时间的关系,可解出飞轮所经历的时间.该题还可应用角动量定理直接求解.解1 在匀变速转动中,角加速度t ωωα0-=,由转动定律αJ M =,可得飞轮所经历的时间()s 8.10200=-=-=n n M J πJ M ωωt 解2 飞轮在恒外力矩作用下,根据角动量定理,有()00d ωωJ t M t-=? 则()s 8.10π200=-=-=n n MJ J M ωωt3-7 电风扇接通电源后一般经5s 后到达额定转速10min r 300-?=n ,而关闭电源后经16 s 后风扇停止转动,已知电风扇的转动惯量为2m kg 5.0?,设启动时电磁力矩M 和转动时的阻力矩f M 均为常数,求启动时的电磁力矩M .分析由题意知M 和f M 均为常数,故启动时电风扇在M 和f M 共同作用下,作匀加速转动,直至到达额定转速,关闭电源后,电风扇仅在f M 的作用下作匀减速转动.运用匀变速转动的运动学规律和转动定律既可求解.解设启动时和关闭电源后,电风扇转动时的角加速度分别为1α和2α,则启动过程αJ M M =-f110t αω=关闭电源后2f αJ M =-0220=+t αω 联解以上各式并将60200n πω=以及0n 、1t 、2t 、J 值代入,得 m N 12.4?=M3 -8 一质量为m′、半径为R 的均匀圆盘,通过其中心且与盘面垂直的水平轴以角速度ω转动,若在某时刻,一质量为m 的小碎块从盘边缘裂开,且恰好沿垂直方向上抛,问它可能达到的高度是多少?破裂后圆盘的角动量为多大?分析盘边缘裂开时,小碎块以原有的切向速度作上抛运动,由质点运动学规律可求得上抛的最大高度.此外,在碎块与盘分离的过程中,满足角动量守恒条件,由角动量守恒定律可计算破裂后盘的角动量.解 (1) 碎块抛出时的初速度为R ω=0v由于碎块竖直上抛运动,它所能到达的高度为g R ωg h 222220==v(2) 圆盘在裂开的过程中,其角动量守恒,故有L L L '-=0 式中ωR m L 221'=为圆盘未碎时的角动量;ωmR L 2='为碎块被视为质点时,碎块对轴的角动量;L 为破裂后盘的角动量.则ωR m m L 221??-'=3-9 一位溜冰者伸开双臂来以1.01s r -?绕身体中心轴转动,此时的转动惯量为1.33 2m kg ?,她收起双臂来增加转速,如收起双臂后的转动惯量变为0.48 2m kg ?.求(1)她收起双臂后的转速;(2)她收起双臂前后绕身体中心轴的转动动能各为多少?分析各种物体(含刚体和变形体)在运动过程中,只要对空间某定点或定轴的外力矩之和为零,则物体对同一点或轴的角动量就守恒,在本题中当溜冰者绕身体中心轴转动时,人体重力和地面支持力均与该轴重合,故无外力矩作用,满足角动量守恒.此时改变身体形状(即改变对轴的转动惯量)就可改变转速,这是在体育运动中经常要利用的物理规律.解(1)由分析知,有ωωJ J =00则 1-00s r 77.2?==ωωJJ (2)收起双臂前 J 26.2212001k ==ωJ E收起双臂后 J 72.6212k2==ωJ E此时由于人体内力做功,有 1k 2k E E >的上端点,开始时棒自由悬挂.以100 N 的力打击它的下端点,打击时间为0.02 s .(1) 若打击前棒是静止的,求打击时其角动量的变化;(2) 棒的最大偏转角.分析该题属于常见的刚体转动问题,可分为两个过程来讨论:(1) 瞬间的打击过程.在瞬间外力的打击下,棒受到外力矩的角冲量,根据角动量定理,棒的角动量将发生变化,则获得一定的角速度.(2) 棒的转动过程.由于棒和地球所组成的系统,除重力(保守内力)外无其他外力做功,因此系统的机械能守恒,根据机械能守恒定律,可求得棒的偏转角度.解 (1) 由刚体的角动量定理得120s m kg 0.2d -??====?t ΔFl t M ωJ L Δ(2) 取棒和地球为一系统,并选O 处为重力势能零点.在转动过程中,系统的机械能守恒,即()θmgl ωJ cos 1212120-= 由式(1)、(2)可得棒的偏转角度为8388Δ31arccos o 222'=-=gl m t F θ棒的一端的水平轴转动.如将此棒放在水平位置,然后任其落下,求:(1) 当棒转过60°时的角加速度和角速度;(2) 下落到竖直位置时的动能;(3) 下落到竖直位置时的角速度.分析转动定律M =Jα是一瞬时关系式,为求棒在不同位置的角加速度,只需确定棒所在位置的力矩就可求得.由于重力矩()θl mg θM cos 2=是变力矩,角加速度也是变化的,因此,在求角速度时,就必须根据角加速度用积分的方法来计算(也可根据转动中的动能定理,通过计算变力矩的功来求).至于棒下落到竖直位置时的动能和角速度,可采用系统的机械能守恒定律来解,这是因为棒与地球所组成的系统中,只有重力作功(转轴处的支持力不作功),因此,系统的机械能守恒.解 (1) 棒绕端点的转动惯量231ml J=由转动定律M =Jα可得棒在θ 位置时的角加速度为()l θg J θM α2cos 3==当θ =60°时,棒转动的角加速度2s 418-=.α 由于θωωt ωαd d d d ==,根据初始条件对式(1)积分,有=o 6000d d θαωωω 则角速度为1600s 98.7sin 3o-==l θg ω(2) 根据机械能守恒,棒下落至竖直位置时的动能为J 98.021==mgl E K (3) 由于该动能也就是转动动能,即221ωJ E K =,所以,棒落至竖直位置时的角速度为1s 57.832-==='lg J E ωK。
大学物理简明教程习题解答第8章 2010.9(1)

第8章 变化的电场和磁场8-1 变化的磁场中有一电阻R =1.9Ω的闭合回路,通过回路的磁通量与时间的关系为 Wb 10)(32-⨯++=c bt at Φ,式中t 以秒计,a =5.0 1/s 2,b =8.0 1/s ,c =2,求:(1)t =2s时回路中的感应电动势;(2)t 从2s 到3s时通过回路截面的电量。
解 (1)根据法拉第电磁感应定律tΦd d i -=εV 10)810()d(32-⨯+-=++-=t dtc bt at当t =2s 时V 108.22i -⨯-=ε,负号表示方向为顺时针。
(2)2s 到3s 间通过回路截面的电量 ⎰⎰⎰-⨯+===323d 9.110)810(d d t t t R t I Q εC 107.12-⨯=8-2 通过一导线回路的磁通量为t k t Φωsin )(=,式中常量 Wb 105.93-⨯=k ,rad/s 377=ω。
求:在s 100.33-⨯=t 时刻回路中感应电动势的大小。
解 根据法拉第电磁感应定律,感应电动势 tΦd d i -=ε在s 100.33-⨯=t 时刻回路中感应电动势的大小V52.1cos )sin d(d d i ===-=t k dttk tΦωωωε8-3 一段导线长20.0cm ,在b 处弯折成30︒角,且ab 与bc 长度相同。
若使导线置于页面内。
在均匀磁场中以匀速度v =1.50m/s 运动,方向如图。
磁场方向垂直页面向内,磁感应强度B =2.50⨯10-2T 。
问ac 间的电势差是多少?哪一点电势高?解 弯折导线切割磁感应线的有效长度m 187.030cos =︒+=bc ab ac l l l 导线ac 的动生电动势的大小 V 1000.73i -⨯==ac Bl v εac 间电势差的绝对值与动生电动势大小相等,即V 1000.73-⨯=-c a U U 。
a 点电势高于c 点。
8-4 如图所示,在磁感应强度为B 的匀强磁场中,有一根金属棒在顶角为θ 的导线架上滑动,它们组成的回路平面与磁场方向垂直。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物理简明教程第三版课后习题及答案习题一1-1 |r ∆|与r ∆有无不同?t d d r 和t d d r 有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r ϖϖ-=∆; (2)t d d r 是速度的模,即t d d r ==v tsd d .t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆr ˆtr t d d d d d d r rr += 式中t rd d 就是速度径向上的分量,∴t r t d d d d 与r 不同如题图所示.(3)t d d v 表示加速度的模,即t v a d d ϖϖ=,t v d d 是加速度a 在切向上的分量. ∵有ττϖϖ(v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττϖϖϖ+=式中dt dv就是加速度的切向分量.1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r ϖϖϖ+=,jt y i t x t r a jt y i t x t r v ϖϖϖϖϖϖϖϖ222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x y x而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作。
22d d d d t r a trv ==其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
在1-1题中已说明t r d d 不是速度的模,而只是速度在径向上的分量,同样,22d d t r 也不是加速度的模,它只是加速度在径向分量中的一部分⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=222d d d d t r t r a θ径。
或者概括性地说,前一种方法只考虑了位矢r ϖ在径向(即量值)方面随时间的变化率,而没有考虑位矢r ϖ及速度v ϖ的方向随间的变化率对速度、加速度的贡献。
1-3 一质点在xOy 平面上运动,运动方程为x =3t +5, y =21t 2+3t -4.式中t 以 s 计,x ,y 以m 计.(1)以时间t 为变量,写出质点位置矢量的表示式;(2)求出t =1 s 时刻和t =2s 时刻的位置矢量,计算这1秒内质点的位移;(3)计算t =0 s 时刻到t =4s 时刻内的平均速度;(4)求出质点速度矢量表示式,计算t =4 s 时质点的速度;(5)计算t =0s 到t =4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算t =4s 时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).解:(1)jt t i t r ϖϖϖ)4321()53(2-+++=m (2)将1=t ,2=t 代入上式即有j i r ϖϖϖ5.081-= mj j r ϖϖϖ4112+=mj j r r r ϖϖϖϖϖ5.4312+=-=∆m(3)∵ j i r j j r ϖϖϖϖϖϖ1617,4540+=-= ∴ 104s m 534201204-⋅+=+=--=∆∆=j i j i r r t r v ϖϖϖϖϖϖϖϖ(4) 1s m )3(3d d -⋅++==j t i t rv ϖϖϖϖ则 j i v ϖϖϖ734+= 1s m -⋅ (5)∵ j i v j i v ϖϖϖϖϖϖ73,3340+=+=204s m 1444-⋅==-=∆∆=jv v t v a ϖϖϖϖϖ(6) 2s m 1d d -⋅==j t v a ϖϖϖ这说明该点只有y 方向的加速度,且为恒量。
1-4 在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.图1-4解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知222s h l +=将上式对时间t 求导,得ts s t l ld d 2d d 2=根据速度的定义,并注意到l ,s 是随t 减少的,∴t s v v t l v d d ,d d 0-==-=船绳即θcos d d d d 00v v s lt l s l t s v ==-=-=船或 s v s h s lv v 02/1220)(+==船将船v 再对t 求导,即得船的加速度3202220202002)(d d d d d d s v h s v s l s v slv s v v s t s l t l st v a =+-=+-=-==船船1-5 质点沿x 轴运动,其加速度和位置的关系为 a =2+62x ,a 的单位为2s m -⋅,x 的单位为 m. 质点在x =0处,速度为101s m -⋅,试求质点在任何坐标处的速度值.解: ∵x v v t x x v t v a d d d d d d d d ===分离变量: x x adx d )62(d 2+==υυ两边积分得 cx x v ++=322221由题知,0=x 时,100=v ,∴50=c∴ 13s m 252-⋅++=x x v1-6 已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x=5 m ,v =0,求该质点在t =10s 时的速度和位置.解:∵t t va 34d d +==分离变量,得 t t v d )34(d +=积分,得 12234c t t v ++=由题知,0=t ,00=v ,∴01=c故2234t t v += 又因为2234d d t t t x v +==分离变量, tt t x d )234(d 2+= 积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c故 521232++=t t x所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-7 一质点沿半径为1 m 的圆周运动,运动方程为 θ=2+33t ,θ式中以弧度计,t 以秒计,求:(1) t =2 s时,质点的切向和法向加速度;(2)当加速度的方向和半径成45°角时,其角位移是多少?解:t t t t 18d d ,9d d 2====ωβθω(1)s 2=t 时, 2s m 362181-⋅=⨯⨯==βτR a2222s m 1296)29(1-⋅=⨯⨯==ωR a n(2)当加速度方向与半径成ο45角时,有145tan ==︒na a τ即 βωR R =2 亦即 t t 18)9(22=则解得923=t 于是角位移为rad67.29232323=⨯+=+=t θ1-8 质点沿半径为R 的圆周按s =2021bt t v -的规律运动,式中s 为质点离圆周上某点的弧长,0v ,b 都是常量,求:(1)t 时刻质点的加速度;(2) t 为何值时,加速度在数值上等于b .解:(1)bt v t sv -==0d dR bt v R v a b tva n 202)(d d -==-==τ则 240222)(R bt v b a a a n-+=+=τ加速度与半径的夹角为20)(arctanbt v Rb a a n --==τϕ(2)由题意应有2402)(R bt v b b a -+==即 0)(,)(4024022=-⇒-+=bt v R bt v b b∴当b v t 0=时,b a =1-9 以初速度0v =201s m -⋅抛出一小球,抛出方向与水平面成幔60°的夹角, 求:(1)球轨道最高点的曲率半径1R ;(2)落地处的曲率半径2R . (提示:利用曲率半径与法向加速度之间的关系) 解:设小球所作抛物线轨道如题1-10图所示.题1-9图 (1)在最高点,o0160cos v v v x == 21s m 10-⋅==g a n又∵1211ρv a n =∴m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点,2002==vv 1s m -⋅,而o60cos 2⨯=g a n∴m8060cos 10)20(22222=︒⨯==n a v ρ1-10飞轮半径为0.4 m ,自静止启动,其角加速度为β=0.2 rad ·2s -,求t =2s 时边缘上各点的速度、法向加速度、切向加速度和合加速度.解:当s 2=t 时,4.022.0=⨯==t βω1s rad -⋅ 则16.04.04.0=⨯==ωR v 1s m -⋅064.0)4.0(4.022=⨯==ωR a n 2s m -⋅08.02.04.0=⨯==βτR a 2s m -⋅22222s m 102.0)08.0()064.0(-⋅=+=+=τa a a n习题二2-1 一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB 平行,如图所示,求这质点的运动轨道.解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v ϖ方向为X轴,平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-1图X 方向: 0=x F t v x 0= ① Y方向:yy ma mg F ==αsin ②0=t 时 0=y 0=y v2sin 21t g y α=由①、②式消去t ,得220sin 21x g v y ⋅=α2-2 质量为16 kg 的质点在xOy 平面内运动,受一恒力作用,力的分量为x f =6 N ,y f =-7 N ,当t =0时,==y x 0,x v =-2 m ·s-1,y v =0.求当t =2 s时质点的 (1)位矢;(2)速度.解:2s m 83166-⋅===m f a x x2s m 167-⋅-==m f a y y(1)⎰⎰--⋅-=⨯-=+=⋅-=⨯+-=+=20101200s m 872167s m 452832dt a v v dt a v v y y y x x x于是质点在s 2时的速度1s m 8745-⋅--=ji v ϖϖϖ(2)m874134)167(21)4832122(21)21(220j i ji jt a i t a t v r y x ϖϖϖϖϖϖϖ--=⨯-+⨯⨯+⨯-=++=2-3 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mkev )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m ke )(-];(3)停止运动前经过的距离为)(0k m v ;(4)证明当k m t =时速度减至0v 的e 1,式中m 为质点的质量.答: (1)∵t vm kv a d d =-=分离变量,得m tk v v d d -=即 ⎰⎰-=vv t m t k vv00d dmkt e v v -=ln ln 0∴tm k ev v -=0(2)⎰⎰---===tttm k m ke k mv t ev t v x 000)1(d d(3)质点停止运动时速度为零,即t →∞,故有⎰∞-=='00d kmv t ev x tm k(4)当t=k m时,其速度为ev ev e v v km m k 0100===-⋅-即速度减至0v 的e 1.2-4一质量为m 的质点以与地的仰角θ=30°的初速0v ϖ从地面抛出,若忽略空气阻力,求质点落地时相对抛射时的动量的增量.解: 依题意作出示意图如题2-6图题2-4图在忽略空气阻力情况下,抛体落地瞬时的末速度大小与初速度大小相同,与轨道相切斜向下,而抛物线具有对y 轴对称性,故末速度与x 轴夹角亦为o30,则动量的增量为v m v m p ϖϖϖ-=∆由矢量图知,动量增量大小为v m ϖ,方向竖直向下.2-5 作用在质量为10 kg 的物体上的力为i t F ϖ)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化,以及力给予物体的冲量.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j ϖ6-m ·s-1的物体,回答这两个问题. 解: (1)若物体原来静止,则it i t t F p t ϖϖϖϖ10401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向, ip I im p v ϖϖϖϖϖϖ111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t t tF v m t m F v m p v m p 000000d )d (,ϖϖϖϖϖϖϖ于是⎰∆==-=∆t p t F p p p 0102d ϖϖϖϖϖ,同理, 12v v ϖϖ∆=∆,12I I ϖϖ=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理.(2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t解得s 10=t ,(s 20='t 舍去) 2-6 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量.解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得b a t =(2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将b at =代入,得b a I 22=(3)由动量定理可求得子弹的质量0202bv a v I m ==2-7设N67j i F ϖϖϖ-=合.(1) 当一质点从原点运动到m 1643k j i r ϖϖϖϖ++-=时,求F ϖ所作的功.(2)如果质点到r 处时需0.6s ,试求平均功率.(3)如果质点的质量为1kg ,试求动能的变化.解: (1)由题知,合F ϖ为恒力,∴ )1643()67(k j i j i r F A ϖϖϖϖϖϖϖ++-⋅-=⋅=合J 452421-=--= (2)w 756.045==∆=t A P(3)由动能定理,J 45-==∆A E k2-8 如题2-18图所示,一物体质量为2kg ,以初速度0v =3m ·s-1从斜面A 点处下滑,它与斜面的摩擦力为8N ,到达B 点后压缩弹簧20cm 后停止,然后又被弹回,求弹簧的劲度系数和物体最后能回到的高度.解: 取木块压缩弹簧至最短处的位置为重力势能零点,弹簧原 长处为弹性势能零点。
