非经典数理逻辑与近似推理(王国俊著)思维导图
王道数据结构 第七章 查找思维导图-高清脑图模板
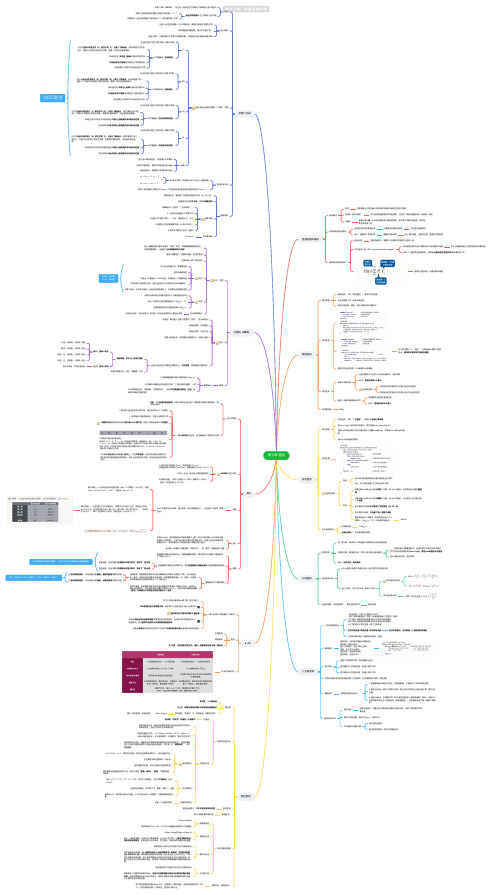
每次调整的对象都是“最小不平衡子树”
插入操作
在插入操作,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡
在A的左孩子的左子树中插入导致不平衡
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增
至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。
LL
将A的左孩子B向右上旋转代替A成为根节点 将A结点向右下旋转成为B的右子树的根结点
RR平衡旋转(左单旋转)
而B的原左子树则作为A结点的右子树
在A的左孩子的右子树中插入导致不平衡
由于在结点A的左孩子(L)的右子树(R)上插入了新结点,A的平衡因子由1增
LR
至2,导致以A为根的子树失去平衡,需要两次旋转操作,先左旋转再右旋转。
将A的左孩子B的右子树的根结点C向左上旋转提升至B结点的位置
本质:永远保证 子树0<关键字1<子树1<关键字2<子树2<...
当左兄弟很宽裕时,用当前结点的前驱、前驱的前驱来填补空缺 当右兄弟很宽裕时,用当前结点的后继、后继的后继来填补空缺
兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限,且与此结点 右(或左)兄弟结点的关键字还很宽裕,则需要调整该结点、右(或左)兄弟结 点及其双亲结点及其双亲结点(父子换位法)
LL平衡旋转(右单旋转)
而B的原右子树则作为A结点的左子树
在A的右孩子的右子树中插入导致不平衡
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1
减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。
RR
将A的右孩子B向左上旋转代替A成为根节点 将A结点向左下旋转成为B的左子树的根结点
推理闭包子空间的基本性质及其交并运算

推理闭包子空间的基本性质及其交并运算高超;赵彬【摘要】文中在推理闭包空间基础上结合拓扑学的思想和方法,引入推理闭包子空间的概念,研究推理闭包空间之间连续映射的基本性质,并讨论原有推理闭包子空间与推理闭包空间中两个子空间的交(并)集形成的子空间的关系,明确了交(并)集上的结论闭域.【期刊名称】《西北大学学报(自然科学版)》【年(卷),期】2014(044)003【总页数】4页(P351-354)【关键词】模糊逻辑;推理闭包空间;推理闭包算子;推理闭包子空间;连续映射【作者】高超;赵彬【作者单位】陕西师范大学数学与信息科学学院,陕西西安710062;陕西师范大学数学与信息科学学院,陕西西安710062【正文语种】中文【中图分类】O189.1;O141.1模糊命题演算系统是模糊逻辑学中一个重要研究方面。
典型的模糊命题演算系统有Lukasiewicz模糊命题演算系统[1],模糊命题演算的形式演绎系统[2],基础模糊命题演算系统BL*[3]等。
吴洪博教授通过对命题演算系统L*共同特征的研究[4-5]提出了基于命题演算系统的一种推理闭包算子,并且建立了一般非空集合上的推理闭包空间[6],并在推理闭包空间之间引入了连续映射[7]。
本文结合拓扑学的思想和方法[8-12],研究了推理闭包子空间的基本性质及它们之间连续映射的性质。
进一步通过推理闭包空间中的两个子空间的交集和并集运算,探索了推理闭包空间中两个子空间与它们的交集(并集)形成的推理闭包子空间的关系,给出了交集(并集)上的结论闭域形式,这有助于更深入地理解全体推理闭包子空间的结构,为范畴论中研究万有空间做了必要的准备。
1 预备知识定义1[6]设X是一个非空集合。
若c:2X→2X,满足条件:1)c(∅)≠∅;2)∀A∈2X,A⊆c(A);3)∀~D⊆2X,如果~D是2X的定向子集,c(∪~D)=∪D∈~D c(D);4)∀A ∈2X,c(c(A))=c(A),则称c为X上的一个推理闭包算子,这里2X为X的幂集,称c(A)为A的推理闭包。
厦门大学_应用所研究生培养方案

附件3厦门大学硕士研究生培养方案(报表)一级学科名称计算机科学与技术专业名称计算机应用技术专业代码081203厦门大学研究生院制表填表日期:2006年6月25日一、主要研究方向序号研究方向名称主要研究内容、特色与意义研究生导师(博导注明)1人工智能集人工智能理论、应用技术和实际项目开发为一体,在人工智能的逻辑基础、自然语言处理和信息检索、神经网络及其应用、进化计算和智能控制等方面开展了较为深入的研究。
周昌乐(博导)史晓东李绍滋(博导)冯寅邹丰美2计算机检测与控制主要开展新一代城市交通实时控制系统的研究与开发,承担了厦门、深圳、昆明、福州、威海等城市交通实时监控系统的软件研制和部分硬件开发、多项网络信息系统的软件开发、”厦门大典”多媒体信息光盘(福建省出版总社正式出版)软件设计等。
陆达郑建德李名世黎忠文3计算机在医学工程中的应用技术主要研究生物医学信息的获取、处理、显示、传输的新理论、新技术;研究设计人体生理信息,医学图像的监测诊断仪器;综合应用计算机、电子、信息等工程技术与方法,解决生物医学的问题。
还在脑神经核团三维重建、眼科成像与图像处理方面取得了一定的研究成果。
王博亮(博导)陆达达力4计算机视觉与图象处理主要开展计算机视觉、图象处理与分析、小波变换理论及其应用、人工神经网络、非线性动力系统与智能信息处理、数字水印处理技术、软件雷达技术等应用研究。
李翠华(博导)雷蕴奇杨晨晖邹丰美5计算模型与程序设计方法学主要开展各种新型分布式计算模型、分布式基础算法以、分布式软件技术理论和容错计算技术应用于未来网络与分布式计算的研究。
赵致琢黎忠文6LUNIX开发及应用嵌入式系统及LUNIX开发应用陈辉煌(博导)陈启安洪景新7数据库技术数据库理论及其应用、分布式数据库、知识挖掘郑建德倪子伟冯少荣注:本表不够可加页。
二、培养目标、学习年限及学分要求培养目标:(本表可不填政治标准)培养德智体全面发展,能够独立承担计算机学科的教学、理论研究、计算机系统设计与开发的高层次科技工作者。
《学好数学并不难:代数+几何(套装共2册)》读书笔记思维导图PPT模板

让数据告诉 我们宇宙的 过去和未来
数学是这个 世界的普遍 真理吗
当然,我们老师也该反思自己,教学的方式,有真正在调动学生的好奇心吗?我们的起点,究竟是生硬的 拔成绩,还是让孩子从小通过数学培养对世界的那份好奇心? 答案是肯定的,也是必然的,因为这个世界,是因 为好奇心去做那些“无意义”的事,才变得越来越有意思。 当然,我们老师也该反思自己,教学的方式,有真正 在调动学生的好奇心吗?我们的起点,究竟是生硬的拔成绩,还是让孩子从小通过数学培养对世界的那份好奇心? 答案是肯定的,也是必然的,因为这个世界,是因为好奇心去做那些“无意义”的事,才变得越来越有意思。你 是想教数学?不,你是想割韭菜! 还好奇心,还抽象?说得谁好像不知道一样。 数学是百分百确定的?你怕是 不知道哥德尔不完备定理。你是想教数学?不,你是想割韭菜! 还好奇心,还抽象?说得谁好像不知道一样。我 个人数学极差,属于看见数字犯晕的人,觉得数学在生活中的作用不大,读完《学好数学并不难》才明白,数学 与生活关系密切,数学不好的人,逻辑思维不会好,对生活的关注也有限。一眼看出答案,如果不尝试写出思考 过程,找不到最优解,也不行。 书里说,这是思考过程:1、发现问题、2、分析问题、3、解决问题。其实一般 情况下我是静不下心来在手机上看书或听书的,总想着去追追剧看看小视频,但这本书我是真的挺喜欢,我的数 学成绩还算可以,对数学也有一定的兴趣,我也很喜欢听小故事,而这本书里,作者就举了好多名人的故事,顺 变讲着学习态度方法等,甚至出现了一些公式,这些呢也就又让我有了更多的兴趣。
乘方开方混合运 算:规律和禁忌
改变世界的二次 方程:算出最优
解
多项式乘法:一 个公式的多种变
形
完全平方公式: 代数、图形和类 比
平方差公式:平 方差和差的平方
