18学年高中数学立体几何初步1.2.2第2课时平面与平面平行学案新人教B版21802262163
高中数学 第一章 立体几何初步 1.2.2 第2课时 平面与平面平行学业分层测评 新人教B版必修2

1.2.2 第2课时平面与平面平行学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.若直线l不平行于平面α,且l⊄α,则( )A.α内的所有直线与l异面B.α内不存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交【解析】直线l不平行于平面α,且l⊄α,所以l与α相交,故选B.【答案】 B2.已知m,n是两条直线,α,β是两个平面.有以下说法:①m,n相交且都在平面α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;②若m∥α,m∥β,则α∥β;③若m∥α,n∥β,m∥n,则α∥β.其中正确的个数是( )A.0B.1C.2D.3【解析】把符号语言转换为文字语言或图形语言.可知①是面面平行的判定定理;②③中平面α、β还有可能相交,所以选B.【答案】 B3.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为( )A.平行B.相交C.平行或相交D.可能重合【解析】若三点分布于平面β的同侧,则α与β平行,若三点分布于平面β的两侧,则α与β相交.【答案】 C4.如果AB、BC、CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC 的位置关系是( )A.平行B.相交C.AC在此平面内D.平行或相交【解析】把这三条线段放在正方体内如图,显然AC∥EF,AC⊄平面EFG.EF⊂平面EFG,故AC∥平面EFG.故选A.【答案】 A5.以下四个命题:①三个平面最多可以把空间分成八部分;②若直线a⊂平面α,直线b⊂平面β,则“a与b相交”与“α与β相交”等价;③若α∩β=l,直线a⊂平面α,直线b⊂平面β,且a∩b=P,则P∈l;④若n条直线中任意两条共面,则它们共面.其中正确的是( )A.①②B.②③C.③④D.①③【解析】对于①,正确;对于②,逆推“α与β相交”推不出“a与b相交”,也可能a∥b;对于③,正确;对于④,反例:正方体的共顶点的侧棱任意两条都共面,但这4条侧棱却不共面,故④错.所以正确的是①③.【答案】 D二、填空题6.若夹在两个平面间的三条平行线段相等,那么这两个平面的位置关系为________.【解析】三条平行线段共面时,两平面可能平行也可能相交,当三条平行线段不共面时,两平面一定平行.【答案】平行或相交7.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是________(写出所有符合要求的图形序号).图1234【解析】①设MP中点为O,连接NO.易得AB∥NO,又AB⊄平面MNP,所以AB∥平面MNP.②若下底面中心为O,易知NO∥AB,NO⊄平面MNP,所以AB与平面MNP不平行.③易知AB∥MP,所以AB∥平面MNP.④易知存在一直线MC∥AB,且MC⊄平面MNP,所以AB与平面MNP不平行.【答案】①③8.在如图1235所示的几何体中,三个侧面AA1B1B,BB1C1C,CC1A1A都是平行四边形,则平面ABC与平面A1B1C1平行吗?图1235______(填“是”或“否”).【解析】因为侧面AA1B1B是平行四边形,所以AB∥A1B1,因为AB⊄平面A1B1C1,A1B1⊂平面A1B1C1,所以AB∥平面A1B1C1,同理可证:BC∥平面A1B1C1.又因为AB∩BC=B,AB⊂平面ABC,BC⊂平面ABC,所以平面ABC∥平面A1B1C1.【答案】是三、解答题9.如图1236所示,在三棱柱ABCA1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.图1236【证明】由棱柱性质知,B1C1∥BC,B1C1=BC,又D,E分别为BC,B1C1的中点,所以C1E═∥DB,则四边形C1DBE为平行四边形,因此EB∥C1D,又C1D⊂平面ADC1,EB⊄平面ADC1,所以EB∥平面ADC1.连接DE,同理,EB1═∥BD,所以四边形EDBB1为平行四边形,则ED═∥B1B.因为B1B═∥A1A(棱柱的性质),所以ED═∥A1A,则四边形EDAA1为平行四边形,所以A1E∥AD,又A1E⊄平面ADC1,AD⊂平面ADC1,所以A1E∥平面ADC1.由A1E∥平面ADC1,EB∥平面ADC1.A1E⊂平面A1EB,EB⊂平面A1EB,且A1E∩EB=E,所以平面A1EB∥平面ADC1.10.如图1237所示,在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E,F分别是A1C1,BC的中点.图1237(1)证明:C1F∥平面ABE;(2)设P是BE的中点,求三棱锥P-B1C1F的体积.【解析】(1)证明:如图,取AC的中点M,连接C1M,FM.又F是BC的中点,∴FM∥AB,而FM⊄平面ABE,∴FM∥平面ABE.在矩形ACC1A1中,∵E,M分别是A1C1,AC的中点,∴C1M∥AE.而C1M⊄平面ABE,∴C1M∥平面ABE.又C1M∩FM=M,∴平面ABE∥平面FMC1,∵C 1F ⊂平面FMC 1,∴C 1F ∥平面ABE .(2)由AC =4,CB =2,∠ACB =60°知AB =23,AB ⊥BC .取B 1C 1的中点H ,连接EH ,如图,则EH ∥AB 且EH =12AB = 3. 易知AB ⊥平面BB 1C 1C ,∴EH ⊥平面BB 1C 1C ,∵P 是BE 的中点,∴VP -B 1C 1F =12VE -B 1C 1F =12×13S △B 1C 1F ·EH =12×13×2×3=33. [能力提升]1.设平面α∥平面β,A ∈α,B ∈β,C 是AB 的中点,当点A 、B 分别在平面α,β内运动时,动点C ( )A.不共面B.当且仅当点A 、B 分别在两条直线上移动时才共面C.当且仅当点A 、B 分别在两条给定的异面直线上移动时才共面D.无论点A ,B 如何移动都共面【解析】 无论点A 、B 如何移动,其中点C 到α、β的距离始终相等,故点C 在到α、β距离相等且与两平面都平行的平面上.【答案】 D2.在正方体EFGH -E 1F 1G 1H 1中,下列四对截面彼此平行的一对是( )A.平面E 1FG 1与平面EGH 1B.平面FHG 1与平面F 1H 1GC.平面F 1H 1H 与平面FHE 1D.平面E 1HG 1与平面EH 1G【解析】 如图,∵EG ∥E 1G 1,EG ⊄平面E 1FG 1,E 1G 1⊂平面E 1FG 1,∴EG ∥平面E 1FG 1,又G 1F ∥H 1E ,同理可证H 1E ∥平面E 1FG 1,又H 1E ∩EG =E ,∴平面E 1FG 1∥平面EGH 1.【答案】 A3.如图1238,在正四棱柱ABCDA1B1C1D1中,E,F,G,H分别是棱C1C,C1D1,D1D,DC 的中点,点M在四边形EFGH及其内部运动,则M只需满足条件________时,就有MN∥平面B1BDD1,其中N是BC的中点.(填上一个正确的条件即可,不必考虑全部可能的情况)图1238【解析】连接FH(图略),因为N∉FH,所以平面FHN∥平面B1BDD1,若M∈FH,则MN ⊂平面FHN,所以MN∩平面B1BDD1=∅,所以MN∥平面B1BDD1.【答案】M∈FH4.如图1239,三棱柱ABCA1B1C1中,底面是边长为2的正三角形,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2,当点M在何位置时,BM∥平面AEF.图1239【解】如图,取EC的中点P,AC的中点Q,连接PQ,PB,BQ,则PQ∥AE.因为EC=2FB=2,所以PE=BF.所以四边形BFEP为平行四边形,所以PB∥EF.又AE,EF⊂平面AEF,PQ,PB⊄平面AEF,所以PQ∥平面AEF,PB∥平面AEF.又PQ∩PB=P,所以平面PBQ∥平面AEF.又BQ⊂平面PBQ,所以BQ∥平面AEF.故点Q 即为所求的点M,即点M为AC的中点时,BM∥平面AEF.。
高中数学第一章立体几何初步1.2.2第3课时平面与平面平行学案新人教B版必修2(2021年整理)

(鲁京辽)2018-2019学年高中数学第一章立体几何初步1.2.2 第3课时平面与平面平行学案新人教B版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((鲁京辽)2018-2019学年高中数学第一章立体几何初步1.2.2 第3课时平面与平面平行学案新人教B版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(鲁京辽)2018-2019学年高中数学第一章立体几何初步1.2.2 第3课时平面与平面平行学案新人教B版必修2的全部内容。
第3课时平面与平面平行学习目标 1.掌握平面与平面的位置关系,会判断平面与平面的位置关系。
2.学会用图形语言、符号语言表示平面间的位置关系。
3。
掌握空间中面面平行的判定定理及性质定理,并能应用这两个定理解决问题.知识点一平面与平面平行的判定思考三角板的两条边所在直线分别与平面α平行,这个三角板所在平面与平面α平行吗?答案平行.梳理平面平行的判定定理及推论判定定理推论文字语言如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行符号语言l⊂α,m⊂α,l∥β,m∥β,l∩m=A⇒α∥βa∥c,b∥d,a∩b=A,a⊂α,b⊂α,c⊂β,d⊂β⇒α∥β图形语言知识点二平面与平面平行的性质观察长方体ABCD-A1B1C1D1的两个面:平面ABCD及平面A1B1C1D1。
思考1 平面A1B1C1D1中的所有直线都平行于平面ABCD吗?答案是的.思考2 过BC的平面交平面A1B1C1D1于B1C1,B1C1与BC是什么关系?答案平行.梳理平面平行的性质定理及推论性质定理推论文字语言如果两个平行平面同时与第三个平面相交,那么它们的交线平行两条直线被三个平行平面所截,截得的对应线段成比例符号语言α∥β,α∩γ=a,β∩γ=b⇒a∥bα∥β∥γ,m∩α=A,m∩β=B,m∩γ=C,n∩α=E,n∩β=F,n∩γ=G⇒错误!=错误!图形语言1.若一个平面内的两条直线都与另一个平面平行,则这两个平面平行.(×)2.若一个平面内的两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行.( √) 3.如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.(√)类型一平面与平面平行的判定例1 如图所示,在正方体AC1中,M,N,P分别是棱C1C,B1C1,C1D1的中点,求证:平面MNP∥平面A1BD。
2019_2020学年高中数学第一章立体几何初步1.2.2空间中的平行关系第2课时平面与平面平行学案新人教B版必修2
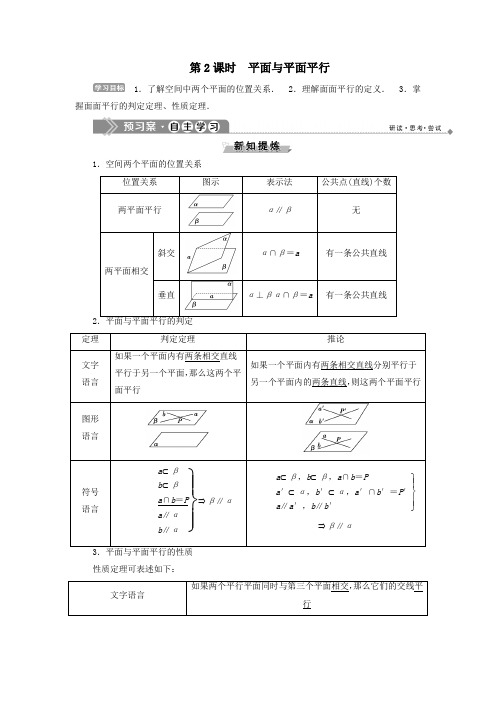
第2课时 平面与平面平行1.了解空间中两个平面的位置关系. 2.理解面面平行的定义. 3.掌握面面平行的判定定理、性质定理.1.空间两个平面的位置关系位置关系 图示表示法公共点(直线)个数两平面平行α∥β无两平面相交斜交α∩β=a 有一条公共直线垂直α⊥βα∩β=a 有一条公共直线2定理 判定定理推论文字 语言如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行 图形 语言符号 语言⎭⎪⎬⎪⎫a ⊂βb ⊂βa ∩b =P a ∥αb ∥α⇒β∥α⎭⎪⎬⎪⎫a ⊂β,b ⊂β,a ∩b =Pa ′⊂α,b ′⊂α,a ′∩b ′=P ′a ∥a ′,b ∥b ′⇒β∥α性质定理可表述如下:文字语言如果两个平行平面同时与第三个平面相交,那么它们的交线平行符号语言⎭⎬⎫α∥βα∩γ=aβ∩γ=b⇒a∥b图形语言1.若α∥β,a⊂α,b⊂β,下列几种说法中正确的是( )①a∥b;②a与β内无数条直线平行;③a与β内的任何一条直线都不垂直;④a∥β.A.①②B.②④C.②③D.①③④答案:B2.已知三棱锥PABC中,D,E,F分别是棱PA,PB,PC的中点.求证:平面DEF∥平面ABC.证明:如图所示,在△PAB 中,因为D,E 分别是PA,PB的中点,所以DE∥AB.又知AB⊂平面ABC,因此DE∥平面ABC.同理,EF∥平面ABC.又因为DE∩EF=E,所以平面DEF∥平面ABC.3.平行于同一个平面的两条直线是否也一定平行?解:不一定.平行、相交、异面都有可能.平面与平面平行的判定正方体ABCDA1B1C1D1中,E、F分别是CC1、AA1的中点,求证:平面BDE∥平面B1D1F.【证明】 设G 是BB 1的中点,连接CG 、DF 、FG . 因为FG ═∥AB ,AB ═∥DC , 所以FG ═∥DC .所以四边形FGCD 是平行四边形, 则DF ═∥CG . 由题设可得EB 1═∥CG ,则DF ═∥EB 1. 所以四边形DFB 1E 是平行四边形.所以B 1F ∥ED ,因为B 1F ⊄平面BDE ,ED ⊂平面BDE , 所以B 1F ∥平面BDE . 又因为B 1D 1∥BD ,B 1D 1⊄平面BDE ,BD ⊂平面BDE ,所以B 1D 1∥平面BDE .因为B 1D 1∩B 1F =B 1,所以平面BDE ∥平面B 1D 1F .证明面面平行的方法(1)要证明两平面平行,只需在其中一个平面内找到两条相交直线平行于另一个平面. (2)判定两个平面平行与判定线面平行一样,应遵循先找后作的原则,即先在一个面内找到两条与另一个平面平行的相交直线,若找不到再作辅助线.在正三棱柱ABC A 1B 1C 1中,E 、F 、G 是侧面对角线上的点,且BE =CF =AG .求证:平面EFG ∥平面ABC .证明:作EP ⊥BB 1于P ,连接PF . 在正三棱柱ABC A 1B 1C 1的侧面ABB 1A 1中, 易知A 1B 1⊥BB 1.又EP ⊥BB 1,所以EP ∥A 1B 1∥AB .所以BE BA 1=BPBB 1,EP ∥平面ABC . 又因为BE =CF ,BA 1=CB 1, 所以CF CB 1=BP BB 1, 所以PF ∥BC ,则PF ∥平面ABC .因为EP ∩PF =P ,所以平面PEF ∥平面ABC . 因为EF ⊂平面PEF ,所以EF ∥平面ABC . 同理,GF ∥平面ABC .因为EF ∩GF =F ,所以平面EFG ∥平面ABC .面面平行的性质已知点S 是正三角形ABC 所在平面外的一点,且SA =SB =SC ,SG 为△SAB 上的高,D 、E 、F 分别是AC 、BC 、SC 的中点,试判断SG 与平面DEF 的位置关系,并给予证明.【解】SG ∥平面DEF ,证明方法如下:法一:连接CG 交DE 于点H ,连接FH , 因为DE 是△ABC 的中位线, 所以DE∥AB.在△ACG 中,D 是AC 的中点,且DH ∥AG , 所以H 为CG 的中点.所以FH 是△SCG 的中位线,所以FH ∥SG . 又SG ⊄平面DEF ,FH ⊂平面DEF , 所以SG ∥平面DEF .法二:因为EF 为△SBC 的中位线,所以EF ∥SB . 因为EF ⊄平面SAB ,SB ⊂平面SAB ,所以EF ∥平面SAB . 同理DF ∥平面SAB ,EF ∩DF =F , 所以平面SAB ∥平面DEF .又因为SG ⊂平面SAB ,所以SG ∥平面DEF .两平面平行问题常常转化为线面平行,而线面平行又可转化为线线平行,所以要注意转化思想的应用.两平面平行的性质定理是证明空间两直线平行的重要依据,故应切实掌握好.如图所示,在底面是平行四边形的四棱锥P ABCD 中,点E 在PD 上,且PE ∶ED =2∶1,在棱PC 上是否存在一点F ,使BF ∥平面AEC ?并证明你的结论.解:当F 是棱PC 的中点时,BF ∥平面AEC ,证明如下: 取PE 的中点M ,连接FM ,则FM ∥CE ,①由EM =12PE =ED ,知E 是MD 的中点,连接BM ,BD ,设BD ∩AC =O ,则O 为BD 的中点,连接OE , 则BM ∥OE ,②由①②可知,平面BFM ∥平面AEC ,又BF ⊂平面BFM ,所以BF ∥平面AEC .面面平行的判定与性质的综合问题如图,在正方体ABCD -A 1B 1C 1D 1中,点N 在BD 上,点M 在B 1C 上,且CM =DN .求证:MN ∥平面AA 1B 1B .【证明】 如图,作MP ∥BB 1交BC 于点P ,连接NP , 因为MP ∥BB 1, 所以CM MB 1=CP PB. 因为BD =B 1C ,DN =CM ,所以B 1M =BN , 所以CM MB 1=DN NB, 所以CP PB =DN NB, 所以NP ∥CD ∥AB . 因为NP ⊄平面AA 1B 1B ,AB ⊂平面AA 1B 1B ,所以NP ∥平面AA 1B 1B . 因为MP ∥BB 1,MP ⊄平面AA 1B 1B ,BB 1⊂平面AA 1B 1B .所以MP ∥平面AA 1B 1B .又因为MP ⊂平面MNP ,NP ⊂平面MNP ,MP ∩NP =P ,所以平面MNP ∥平面AA 1B 1B . 因为MN ⊂平面MNP , 所以MN ∥平面AA 1B 1B .要证面面平行需先在一个平面内找出两条相交直线,证这两条直线分别与另一平面平行,再根据面面平行的判定定理得出结论.如图,平面α∥平面β,△ABC 与△A ′B ′C ′分别在α、β内,线段AA ′、BB ′、CC ′相交于点O ,点O 在α、β之间,若AB =2,AC =1,∠BAC =60°,OA ∶OA ′=3∶2,求△A ′B ′C ′的面积.解:根据题意有S △ABC =32. 因为AA ′、BB ′相交.所以直线AA ′、BB ′确定一个平面ABA ′B ′, 因为平面α∥平面β,所以AB ∥A ′B ′, 易得△ABO ∽△A ′B ′O , ① △ABC ∽△A ′B ′C ′, ②由①得AB A ′B ′=OA OA ′=32, 由②得S △ABCS △A ′B ′C ′=⎝ ⎛⎭⎪⎫AB A ′B ′2=(32)2,所以S △A ′B ′C ′=239.1.平面与平面平行的判定方法 (1)定义法:两个平面没有公共点;(2)判定定理:一个平面内的两条相交直线分别平行于另一个平面;(3)转化为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则α∥β;(4)利用平行平面的传递性:若α∥β,β∥γ,则α∥γ. 2.利用面面平行的性质定理证明线线平行的基本步骤(1)先找两个平面,使这两个平面分别经过这两条直线中的一条; (2)判定这两个平面平行;(3)再找一个平面,使这两条直线都在这个平面上; (4)由定理得出结论.3.对“线线平行”“线面平行”“面面平行”之间的关系认识. 三者之间的转化关系如图所示从线线平行、线面平行、面面平行之间的关系可以看出证明立体几何问题所用的核心思想是转化思想.面面平行的判定定理中有五个条件,也是缺一不可.若没有两“相交”直线这个条件,不一定有面面平行,也可能相交.1.设直线l⊄平面α,则过l作平面β,使β∥α,这样的β( )A.只能作一个B.至多可作一个C.不存在D.至少可作一个解析:选B.当l与平面α相交时,平面β不存在,当l∥α时,可作一个平面.2.下列说法中,错误的是( )A.平行于同一直线的两个平面平行B.平行于同一平面的两个平面平行C.一个平面与两个平行平面相交,交线平行D.一条直线与两个平行平面中的一个相交,则必与另一个相交解析:选A.平行于同一直线的两个平面有可能相交,如正方体ABCDA1B1C1D1中,平面ABCD与A1ABB1都与C1D1平行,但平面ABCD与A1ABB1相交.3.平面α∥平面β,直线a⊂α,则直线a和平面β的位置关系是.答案:a∥β4.过正方体ABCDA1B1C1D1的三顶点A1、C1、B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是.解析:因为平面ABCD∥平面A1B1C1D1,平面ABCD∩平面A1C1B=l,平面A1B1C1D1∩平面A1C1B=A1C1,所以l∥A1C1(面面平行的性质定理).答案:平行[学生用书P95(单独成册)])[A 基础达标]1.若三条直线,a,b,c满足a∥b∥c,且a⊂α,b⊂β,c⊂β,则两个平面α、β的位置关系是( )A.平行B.相交C.平行或相交D.不能确定答案:C2.若平面α∥平面β,直线a∥平面α,点B∈β,则在平面β内过B的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一与a平行的直线答案:A3.已知m、n是不重合的直线,α,β是不重合的平面,有下列命题,其中正确的命题的个数是( )①若m⊂α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α,m∥β.A.0 B.1C.2 D.3解析:选A.①不正确,n∥α,过n作平面β与α相交,n与其交线平行,m⊂α,m 不一定与其交线平行;②不正确,设α∩β=l,m∥l,也可有m∥α,且m∥β;③不正确,有m⊂α或m⊂β的可能.4.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为( )A.平行B.相交C.平行或相交D.可能重合解析:选C.若三点分布于平面β的同侧,则α与β平行,若三点分布于平面β的两侧,则α与β相交.5.在正方体EFGHE1F1G1H1中,下列四对截面彼此平行的一对是( )A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G解析:选A.如图,因为EG ∥E 1G 1,EG ⊄平面E 1FG 1, E 1G 1⊂平面E 1FG 1,所以EG ∥平面E 1FG 1, 又G 1F ∥H 1E ,同理可证H 1E ∥平面E 1FG 1, 又H 1E ∩EG =E ,所以平面E 1FG 1∥平面EGH 1.6.已知平面α∥β∥γ,两条直线l ,m 分别与平面α,β,γ相交于点A ,B ,C 和D ,E ,F ,已知AB =6,DE DF =25,则AC = .解析:因为α∥β∥γ,所以AB BC =DEEF.由DE DF =25,得DE EF =23,所以AB BC =23. 而AB =6,所以BC =9, 所以AC =AB +BC =15. 答案:157.已知a ,b 表示两条不同直线,α,β,γ表示三个不重合的平面,给出下列命题: ①若α⊥β,β⊥γ,则α∥γ;②若a ,b 相交,且都在α,β外,a ∥α,b ∥α,a ∥β,b ∥β,则α∥β; ③若a ⊂α,a ∥β,α∩β=b ,则a ∥b . 其中,正确命题的序号是 .解析:①错误,α与γ也可能相交;②正确,依题意,由a ,b 确定的平面γ,满足γ∥α,γ∥β,故α∥β;③正确,由线面平行的基本性质可知.答案:②③8.如图是正方体的平面展开图,在这个正方体中,①BM ∥平面DE ; ②CN ∥平面AF ; ③平面BDM ∥平面AFN ; ④平面BDE ∥平面NCF .以上四个命题中,正确命题的序号是.解析:以ABCD为下底面还原正方体,如图,则易判定四个命题都是正确的.答案:①②③④9.如图,在几何体ABCA′B′C′中,∠1+∠2=180°,∠3+∠4=180°,求证:平面ABC∥平面A′B′C′.证明:在四边形ABB′A′中,因为∠1+∠2=180°,所以A′B′∥AB.又因为A′B′⊄平面ABC,AB⊂平面ABC,所以A′B′∥平面ABC.同理可证B′C′∥平面ABC.又因为A′B′∩B′C′=B′,所以平面ABC∥平面A′B′C′.10.如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.(1)求证:PQ∥平面DCC1D1;(2)求PQ的长;(3)求证:EF∥平面BB1D1D.解:(1)证明:法一:如图,连接AC,CD1.因为P ,Q 分别是AD 1,AC 的中点, 所以PQ ∥CD 1. 又PQ ⊄平面DCC 1D 1,CD 1⊂平面DCC 1D 1,所以PQ ∥平面DCC 1D 1.法二:取AD 的中点G ,连接PG ,GQ , 则有PG ∥DD 1,GQ ∥DC ,且PG ∩GQ =G , 所以平面PGQ ∥平面DCC 1D 1. 又PQ ⊂平面PGQ , 所以PQ ∥平面DCC 1D 1.(2)由第一问易知PQ =12D 1C =22a .(3)证明:法一:取B 1D 1的中点O 1, 连接FO 1,BO 1, 则有FO 1═∥12B 1C 1. 又BE ═∥12B 1C 1, 所以BE ═∥FO 1. 所以四边形BEFO 1为平行四边形, 所以EF ∥BO 1,又EF ⊄平面BB 1D 1D ,BO 1⊂平面BB 1D 1D , 所以EF ∥平面BB 1D 1D .法二:取B 1C 1的中点E 1,连接EE 1,FE 1, 则有FE 1∥B 1D 1,EE 1∥BB 1,且FE 1∩EE 1=E 1, 所以平面EE 1F ∥平面BB 1D 1D . 又EF ⊂平面EE 1F , 所以EF ∥平面BB 1D 1D .[B 能力提升]11.已知m 、n 表示两条直线,α、β、γ表示三个平面,则下列命题中正确的个数是( )①若α∩γ=m ,β∩γ=n ,m ∥n ,则α∥β;②若存在a 、b ⊂α,c 、d ⊂β使a ∥c ,b ∥d ,则α∥β; ③若m ∥α,n ∥β,m ∥n ,则α∥β. A .0 B .1 C .2D .3解析:选A .①错,可考虑三棱柱模型,三棱柱的三个侧面中任意两个与第三个侧面相交,两条交线即侧棱相互平行,但这两个侧面不平行;②错;③错.故选A .12.几何体ABCD A 1B 1C 1D 1是棱长为a 的正方体,M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点,P 是上底面的棱AD 上的一点,AP =a3,过P 、M 、N 三点的平面交上底面于PQ ,Q 在CD上,则PQ 等于 .解析:取CD 上一点Q ,使CQ =a 3,又由AP =a3,所以PQ ∥AC .而由正方体的性质知:AC ∥A 1C 1,M 、N 分别为A 1B 1、B 1C 1的中点,所以MN ∥A 1C 1,所以MN ∥AC ,所以MN ∥PQ ,所以面MNQP 为过点P 、M 、N 的平面,在△DAC 中,AP =CQ =a 3,所以PQ =2DQ =223a .答案:223a13.如图所示,四边形EFGH 为三棱锥A BCD 的一个截面,若截面为平行四边形, (1)求证:AB ∥平面EFGH ,CD ∥平面EFGH ;(2)若AB =4,CD =6,求四边形EFGH 周长的取值范围. 解:(1)证明:因为四边形EFGH 为平行四边形, 所以EF ∥HG .因为HG ⊂平面ABD ,所以EF ∥平面ABD . 因为EF ⊂平面ABC ,平面ABD ∩平面ABC =AB , 所以EF ∥AB ,所以AB ∥平面EFGH .同理可证CD ∥平面EFGH . (2)设EF =x (0<x <4),则CF CB =x4,FG 6=BF BC =BC -CF BC =1-x 4,从而FG =6-32x . 于是四边形EFGH 的周长为l =2⎝ ⎛⎭⎪⎫x +6-32x =12-x ,又0<x <4,所以8<l <12.14.(选做题)如图所示,在三棱柱ABC -A 1B 1C 1中,D 是棱CC 1的中点,问在棱AB 上是否存在一点E ,使DE ∥平面AB 1C 1?若存在,请确定点E 的位置;若不存在,请说明理由.解:法一:存在点E ,且E 为AB 的中点时,DE ∥平面AB 1C 1. 下面给出证明:如图,取BB 1的中点F ,连接DF ,则DF ∥B 1C 1,因为AB 的中点为E ,连接EF ,则EF ∥AB 1,B 1C 1∩AB 1=B 1,EF ∩DF =F ,所以平面DEF ∥平面AB 1C 1.而DE ⊂平面DEF ,所以DE ∥平面AB 1C 1.法二:假设在棱AB 上存在点E ,使得DE ∥平面AB 1C 1.如图,取BB 1的中点F ,连接DF ,EF ,则DF ∥B 1C 1, 又DF ⊄平面AB 1C 1, 所以DF ∥平面AB 1C 1,又DE ∥平面AB 1C 1,DE ∩DF =D , 所以平面DEF ∥平面AB 1C 1,因为EF⊂平面DEF,所以EF∥平面AB1C1.又因为EF⊂平面ABB1,平面ABB1∩平面AB1C1=AB1,所以EF∥AB1,因为点F是BB1的中点,所以点E是AB的中点.即当点E是AB的中点时,DE∥平面AB1C1.。
高中数学第一章立体几何初步1.2.3第2课时平面与平面垂直课件新人教B版必修2

知识点二 平面与平面垂直的判定定理
思考 建筑工人常在一根细线上拴一个重物,做成“铅锤”,用这种 方法来检查墙与地面是否垂直.当挂铅锤的线从上面某一点垂下时,如 果墙壁贴近铅锤线,则说明墙和地面什么关系?此时铅锤线与地面什 么关系?
解析 ∵AF⊥平面ABCD,DE⊥平面ABCD, ∴AF∥DE. 又AF=DE,∴四边形AFED为平行四边形, 故EF=AD=6.
1 2 34 5
解析 答案
5.如图所示,在四棱锥S-ABCD中,底面四边形ABCD是平行四边形,
SC⊥平面ABCD,E为SA的中点.
求证:平面EBD⊥平面ABCD.
证明 连接AC与BD交于O点,连接OE.梳理文字语言图形语言符号语言
如果两个平面互相 垂直,那么在垂直一于个它们 平交线面的内直_线_________
垂直于 另一个平面
α⊥β,α∩β=CD, BA⊂α,BA⊥CD, B为垂足⇒BA⊥β
[思考辨析 判断正误] 1.若l⊥α,则过l有无数个平面与α垂直.( √ ) 2.若平面α⊥平面β,任取直线l⊂α,则必有l⊥β.( × ) 3.已知两个平面垂直,过一个平面内任意一点作交线的垂线,则此 垂线必垂直于另一个平面.×( )
谢谢
√A.平面PAB与平面PBC、平面PAD都垂直
B.它们两两垂直 C.平面PAB与平面PBC垂直,与平面PAD不垂直 D.平面PAB与平面PBC、平面PAD都不垂直
1 2 34 5
解析 答案
3.如图,在四面体ABCD中,已知AB⊥AC,BD⊥AC,那么D在面ABC内
18版高中数学第一章立体几何初步1.2.1平面的基本性质与推论学案(含解析)新人教B版必修2

1.2.1 平面的基本性质与推论1.了解平面的概念,掌握平面的画法及表示方法.(难点)2.掌握平面的基本性质及推论,能用符号语言描述空间点、直线、平面之间的位置关系.(重点)3.能用图形、文字、符号三种语言描述三个公理,并能解决空间线面的位置关系问题.(难点)[基础·初探]教材整理1 平面阅读教材P35的内容,完成下列问题.1.平面的概念几何里所说的“平面”,是从课桌面、黑板面、海面这样的一些物体中抽象出来的.几何里的平面是无限延展的.2.平面的画法(1)水平放置的平面通常画成一个平行四边形,它的锐角通常画成45°,且横边长等于其邻边长的2倍.如图121①.(2)如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用虚线画出来.如图121②.①②图1213.平面的表示法上图中图①的平面可表示为平面α、平面ABCD、平面AC或平面BD.下列说法正确的是( )A.生活中的几何体都是由平面组成的B.平面无厚薄,但有边界线C.任何一个平面图形都是一个平面D.平面多边形和圆都可以表示平面【解析】 由平面的特性是无限延展性知,选项A 、B 错误;平面图形和平面是两个完全不同的概念,平面图形是有大小的,不能无限延展,选项C 错误;选项D 正确.【答案】 D教材整理2 平面的基本性质及推论阅读教材P 35~P 37“思考”以上的内容,完成下列问题.图122推论1 经过一条直线和直线外的一点,有且只有一个平面(图122①). 推论2 经过两条相交直线,有且只有一个平面(图122②). 推论3 经过两条平行直线,有且只有一个平面(图122③).判断(正确的打“√”,错误的打“×”) (1)三点可以确定一个平面.( )(2)一条直线和一个点可以确定一个平面.( ) (3)四边形是平面图形.( )(4)两条相交直线可以确定一个平面.( )【解析】 (1)错误.不共线的三点可以确定一个平面. (2)错误.一条直线和直线外一个点可以确定一个平面. (3)错误.四边形不一定是平面图形. (4)正确.两条相交直线可以确定一个平面.【答案】 (1)× (2)× (3)× (4)√ 教材整理3 共面与异面直线阅读教材P 37~P 38“练习”以上内容,完成下列问题. 1.异面直线(1)定义:把不同在任何一个平面内的两条直线叫做异面直线. (2)画法:(通常用平面衬托)图1232.空间两条直线的位置关系⎩⎨⎧共面直线⎩⎪⎨⎪⎧相交直线:同一平面内,有且只有一个公共点.平行直线:同一平面内,没有公共点.异面直线:不同在任何一个平面内,没有公共点.判断(正确的打“√”,错误的打“×”) (1)两条直线无公共点,则这两条直线平行.( ) (2)两直线若不是异面直线,则必相交或平行.( )(3)过平面外一点与平面内一点的连线,与平面内的任意一条直线均构成异面直线.( )(4)和两条异面直线都相交的两直线必是异面直线.( )【解析】 (1)错误.空间两直线无公共点,则可能平行,也可能异面. (2)正确.因空间两条不重合的直线的位置关系只有三种:平行、相交或异面. (3)错误.过平面外一点与平面内一点的连线,和平面内过该点的直线是相交直线. (4)错误.和两条异面直线都相交的两直线也可能是相交直线. 【答案】 (1)× (2)√ (3)× (4)×[小组合作型]形:(1)A∈α,B∉α;(2)l⊂α,m⊄α,m∩α=A,A∉l;(3)P∈l,P∉α,Q∈l,Q∈α.【精彩点拨】解答本题要正确理解立体几何中表示点、线、面之间位置关系的符号“∈”,“∉”,“⊂”,“⊄”,“∩”的意义,在此基础上,由已知给出的符号表示语句,写出相应的点、线、面的位置关系,画出图形.【自主解答】(1)点A在平面α内,点B不在平面α内;(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上;(3)直线l经过平面α外一点P和平面α内一点Q.图形分别如图(1),(2),(3)所示.图(1) 图(2) 图(3)1.用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.2.要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“∉”表示,直线与平面的位置关系只能用“⊂”或“⊄”表示.3.由符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.[再练一题]1.根据图形用符号表示下列点、直线、平面之间的关系.图124(1)点P与直线AB;(2)点C与直线AB;(3)点M与平面AC;(4)点A1与平面AC;(5)直线AB与直线BC;(6)直线AB与平面AC;(7)平面A1B与平面AC.【解】(1)点P∈直线AB;(2)点C∉直线AB;(3)点M∈平面AC;(4)点A1∉平面AC;(5)直线AB∩直线BC=点B;(6)直线AB⊂平面AC;(7)平面A1B∩平面AC=直线AB..【导学号:45722037】【精彩点拨】四条直线两两相交且不共点,可能有两种情况:一是有三条直线共点;二是任意三条直线都不共点,故要分两种情况.【自主解答】已知:a,b,c,d四条直线两两相交,且不共点,求证:a,b,c,d 四线共面.证明:(1)若a,b,c三线共点于O,如图所示,∵O∉d,∴经过d与点O有且只有一个平面α.∵A、B、C分别是d与a、b、c的交点,∴A、B、C三点在平面α内.由公理1知a、b、c都在平面α内,故a、b、c、d共面.(2)若a、b、c、d无三线共点,如图所示,∵a∩b=A,∴经过a、b有且仅有一个平面α,∴B、C∈α.由公理1知c⊂α.同理,d⊂α,从而有a、b、c、d共面.综上所述,四条直线两两相交,且不共点,这四条直线在同一平面内.证明点线共面常用的方法1.纳入法:先由部分直线确定一个平面,再证明其他直线也在这个平面内.2.重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.[再练一题]2.一条直线与三条平行直线都相交,求证:这四条直线共面.【解】已知:a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:直线a,b,c,l共面.证明:法一∵a∥b,∴a,b确定一个平面α,∵l∩a=A,l∩b=B,∴A∈α,B∈α,故l⊂α.又∵a∥c,∴a,c确定一个平面β.同理可证l⊂β,∴α∩β=a且α∩β=l.∵过两条相交直线a、l有且只有一个平面,故α与β重合,即直线a,b,c,l共面.法二由法一得a、b、l共面α,也就是说b在a、l确定的平面α内.同理可证c在a、l确定的平面α内.∵过a和l只能确定一个平面,∴a,b,c,l共面.如图125,正方体ABCDA1B1C1D1中,判断下列直线的位置关系:图125①直线A1B与直线D1C的位置关系是________;②直线A1B与直线B1C的位置关系是________;③直线D1D与直线D1C的位置关系是________;④直线AB与直线B1C的位置关系是________.【精彩点拨】判断两直线的位置关系,主要依据定义判断.【自主解答】根据题目条件知直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线“平行”,所以①应该填“平行”;点A1、B、B1在一个平面A1BB1内,而C不在平面A1BB1内,则直线A1B与直线B1C“异面”.同理,直线AB与直线B1C“异面”.所以②④都应该填“异面”;直线D1D与直线D1C相交于D1点,所以③应该填“相交”.【答案】①平行②异面③相交④异面1.判定两条直线平行与相交可用平面几何的方法去判断.2.判定两条直线是异面直线有定义法和排除法,由于使用定义判断不方便,故常用排除法,即说明这两条直线不平行、不相交,则它们异面.[再练一题]3.若a、b是异面直线,b、c是异面直线,则( )A.a∥cB.a、c是异面直线C.a、c相交D.a、c平行或相交或异面【解析】若a、b是异面直线,b、c是异面直线,那么a、c可以平行,可以相交,可以异面.【答案】 D[探究共研型]探究1 如图126,在正方体ABCDA1B1C1D1中,设A1C∩平面ABC1D1=E.能否判断点E在平面A1BCD1内?图126【提示】如图,连接BD1,∵A1C∩平面ABC1D1=E,∴E∈A1C,E∈平面ABC1D1.∵A1C⊂平面A1BCD1,∴E∈平面A1BCD1.探究2 上述问题中,你能证明B,E,D1三点共线吗?【提示】由于平面A1BCD1与平面ABC1D1交于直线BD1,又E∈BD1,根据公理3可知B,E,D1三点共线.如图127,在正方体ABCDA1B1C1D1中,点M,N,E,F分别是棱CD,AB,DD1,AA1上的点,若MN与EF交于点Q,求证:D,A,Q三点共线.图127【精彩点拨】欲证D、A、Q三点共线,只需说明三点均在平面AD1和平面AC的交线DA上即可.【自主解答】∵MN∩EF=Q,∴Q∈直线MN,Q∈直线EF,又∵M∈直线CD,N∈直线AB,CD⊂平面ABCD,AB⊂平面ABCD.∴M、N∈平面ABCD,∴MN⊂平面ABCD.∴Q∈平面ABCD.同理,可得EF⊂平面ADD1A1.∴Q∈平面ADD1A1,又∵平面ABCD∩平面ADD1A1=AD,∴Q∈直线AD,即D,A,Q三点共线.点共线与线共点的证明思路1.点共线的思路:证明这些点都分别在两个相交的平面内,因此也在两个平面的交线上.2.线共点的思路:先由两条直线交于一点,再证明该点在第三条直线上.[再练一题]4.如图128,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.图128求证:E,F,G,H四点必定共线.【证明】∵AB∥CD,∴AB,CD确定一个平面β,又∵AB∩α=E,AB⊂β,∴E∈α,E∈β,即E为平面α与β的一个公共点.同理可证F,G,H均为平面α与β的公共点,∵两个平面有公共点,它们有且只有一条通过公共点的公共直线,∴E,F,G,H四点必定共线.1.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )A.平行或异面B.相交或异面C.异面D.相交【解析】如图,在正方体ABCDA1B1C1D1中,AA1与BC是异面直线,又AA1∥BB1,AA1∥DD1,显然BB1∩BC=B,DD1与BC是异面直线,故选B.【答案】 B2.下列说法中正确的个数为( )①三角形一定是平面图形;②若四边形的两对角线相交于一点,则该四边形是平面图形;③圆心和圆上两点可确定一个平面;④三条平行线最多可确定三个平面.A.1B.2C.3D.4【解析】圆上两点为直径端点时,它们与圆心共线,此时这三个点不能确定平面,故③不正确,①②④正确,故选C.【答案】 C3.设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β=________.【导学号:45722038】【解析】∵α∩β=l,AB∩l=C,∴C∈β,C∈AB,∴AB∩β=C.【答案】 C4.有以下三个说法:①平面外的一条直线与这个平面最多有一个公共点;②直线l在平面α内,可以用符号“l∈α”表示;③已知平面α与β不重合,若平面α内的一条直线a与平面β内的一条直线b相交,则α与β相交.其中正确的序号是________.【解析】若直线与平面有两个公共点,则这条直线一定在这个平面内,故①正确;直线l在平面α内用符号“⊂”表示,即l⊂α,②错误;由a与b相交,说明两个平面有公共点,因此一定相交,故③正确.【答案】①③5.如图129,三个平面α,β,γ两两相交于三条直线,即α∩β=c,β∩γ=a,γ∩α=b,若直线a和b不平行.图129求证:a,b,c三条直线必过同一点.【证明】∵α∩γ=b,β∩γ=a,∴a⊂γ,b⊂γ.由于直线a和b不平行,∴a、b必相交.设a∩b=P,如图,则P∈a,P∈b.∵a⊂β,b⊂α,∴P∈β,P∈α.又α∩β=c,∴P∈c,即交线c经过点P.∴a、b、c三条直线相交于同一点.。
2018版高中数学第一章立体几何初步1.2.2平行直线直线与平面平行学业分层测评新人教B版

1.2.2 第1课时平行直线、直线与平面平行学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.如图1219所示,长方体ABCD A1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG与AB的位置关系是( )图1219A.平行B.相交C.异面D.平行和异面【解析】由题意可知EF∥AB,∴EF∥平面ABCD.又平面EFGH∩平面ABCD=GH,∴EF∥GH,∴GH∥AB,故选A.【答案】 A2.已知下列叙述:①一条直线和另一条直线平行,那么它就和经过另一条直线的任何平面平行;②一条直线平行于一个平面,则这条直线与这个平面内所有直线都没有公共点,因此这条直线与这个平面内的所有直线都平行;③若直线l与平面α不平行,则l与α内任一直线都不平行;④与一平面内无数条直线都平行的直线必与此平面平行.其中正确的个数是( )A.0B.1C.2D.3【解析】两直线可能共面,①错;一条直线平行于一个平面,这个平面内的直线可能与它异面,②错;对于③④,直线有可能在平面内.【答案】 A3.l1,l2,l3是空间三条不同的直线,则下列命题正确的是( )A.l1⊥l2,l2⊥l3⇒l1∥l3B.l1⊥l2,l2∥l3⇒l1⊥l3C.l1∥l2∥l3⇒l1,l2,l3共面D.l1,l2,l3共点⇒l1,l2,l3共面【解析】当l1⊥l2,l2⊥l3时,l1也可能与l3相交或异面,故A不正确;l1⊥l2,l2∥l3⇒l1⊥l3,故B正确;当l1∥l2∥l3时,l1,l2,l3未必共面,如三棱柱的三条侧棱,故C不正确;l1,l2,l3共点时,l1,l2,l3未必共面,如正方体中从同一顶点出发的三条棱,故D 不正确.【答案】 B4.在长方体ABCD-A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D1、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有( )A.2个B.3个C.4个D.5个【解析】如图所示,结合图形可知AA1∥平面BC1,AA1∥平面DC1,AA1∥平面BB1D1D.【答案】 B5.如图1220,在正方体ABCD-A1B1C1D1中,E、F、G、H、M、N分别是棱AB、BC、A1B1、BB1、C1D1、CC1的中点,则下列结论正确的是( )图1220A.直线GH和MN平行,GH和EF相交B.直线GH和MN平行,MN和EF相交C.直线GH和MN相交,MN和EF异面D.直线GH和EF异面,MN和EF异面【解析】易知GH∥MN,又∵E、F、M、N分别为所在棱的中点,由平面基本性质3可知EF、DC、MN交于一点,故选B.【答案】 B二、填空题6.平行四边形的一组对边平行于一个平面,则另一组对边与这个平面的位置关系是________.【答案】平行或相交7.如图1221,ABCD-A1B1C1D1是正方体,若过A、C、B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的关系是________.图1221【解析】 连接A 1C 1,∵AC ∥A 1C 1,∴AC ∥面A 1B 1C 1D 1, 又∵AC ⊂面AB 1C ,面AB 1C ∩面A 1B 1C 1D 1=l , ∴AC ∥l . 【答案】 平行8.如图1222,P 为▱ABCD 所在平面外一点,E 为AD 的中点,F 为PC 上一点,当PA ∥平面EBF 时,PF FC=__________.图1222【解析】 连接AC 交BE 于G ,连接FG ,因为PA ∥平面EBF ,PA ⊂平面PAC ,平面PAC ∩平面BEF =FG ,所以PA ∥FG , 所以PF FC =AGGC.又因为AD ∥BC ,E 为AD 的中点, 所以AG GC =AE BC =12,所以PF FC =12.【答案】 12三、解答题9.如图1223所示,三棱锥A -BCD 被一平面所截,截面为平行四边形EFGH . 求证:CD ∥EF .图1223【证明】∵四边形EFGH为平行四边形,∴EF∥GH,又GH⊂平面BCD,EF⊄平面BCD,∴EF∥平面BCD.而EF所在的平面ACD∩平面BCD=CD,∴EF∥CD.10.一块长方体木块如图1224所示,要经过平面A1C1内一点P和棱BC将木块锯开,应该怎样画线?图1224【解】在平面A1B1C1D1内,经过点P作EF∥B1C1,且交A1B1于E,交D1C1于F;连接BE、CF,则BE、CF即为平面与长方体侧面的交线,可知,要满足题意,只要沿BE、EF、FC画线即可.如图所示.[能力提升]1.对于直线m、n和平面α,下面命题中的真命题是( )A.如果m⊂α,n⊄α,m、n是异面直线,那么n∥αB.如果m⊂α,n与α相交,那么m、n是异面直线C.如果m⊂α,n∥α,m、n共面,那么m∥nD.如果m∥α,n∥α,m、n共面,那么m∥n【解析】对于A,如果m⊂α,n⊄α,m、n是异面直线,则n∥α或n与α相交,故A错;对于B,如果m⊂α,n与α相交,则m、n相交或是异面直线,故B错;对于C,如果m⊂α,n∥α,m、n共面,由线面平行的性质定理,可得m∥n,故C对;对于D,如果m∥α,n∥α,m、n共面,则m∥n或m、n相交,故D错.【答案】 C2.若∠AOB=∠A1O1B1且OA∥O1A1,OA与O1A1的方向相同,则下列结论中正确的是( )A.OB∥O1B1且方向相同B.OB∥O1B1C.OB与O1B1不平行D.OB与O1B1不一定平行【解析】如图①②所示,OB,O1B1不一定平行.图①图②【答案】 D3.已知直线l∥平面α,P∈α,那么过点P且平行于l的直线有________条.【解析】如图所示,∵l∥平面α,P∈α,∴直线l与点P确定一个平面β,α∩β=m,∴P∈m,∴l∥m且m是唯一的.【答案】 14.如图1225所示,已知P是▱ABCD所在平面外一点,M、N分别是AB、PC的中点,平面PAD∩平面PBC=l.图1225(1)求证:l∥BC;(2)MN与平面APD是否平行?试证明你的结论.【解】(1)因为BC∥AD,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD.又因为平面PBC∩平面PAD=l,所以BC∥l.(2)平行.取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.可知四边形AMNE为平行四边形.所以MN∥AE,又因为MN⊄平面APD,AE⊂平面APD,所以MN∥平面APD.。
18版高中数学第一章立体几何初步1.2.2第1课时平行直线
[基础· 初探] 教材整理 1 公理 4 及等角定理
阅读教材 P39~P39“例题”以上内容,完成下列问题. 1.公理 4 文字表述:平行于同一条直线的两条直线互相平行 .这一性质叫做空间平行 线的 传递性 . a∥b ⇒ a∥c . 符号表述: b∥c
2.等角定理 空间中如果两个角的两边分别对应平行 , 并且方向 相同, 那么这两个角相等 .
【精彩点拨】
解答本题要牢牢地抓住直线和平面三种位置关系的特征,
【答案】 (1)× (2)× (3)× (4)×
教材整理 3
直线与平面平行的判定及性质
阅读教材 P42~P43 的内容,完成下列问题. 定理 条件 结论 图形语言 符号语言
不在一个平面内 的一 这条直线
判定 条直线和 平面内的一 和 这 个 平 条直线平行 面 平行
l⊄α, m⊂ ,⇒ l ∥m
【解析】 行.
(1)错误.若直线与平面不相交,则直线在平面内或直线与平面平
(2)错误.当点在已知直线上时,不存在过该点的直线与已知直线平行,故(2) 错. (3)错误.直线 l 也可能与平面 α 相交. (4)错误.在棱柱的上底面内, 过一点任意作一条直线都与棱柱的下底面平行, 所以过平面外一点与已知平面平行的直线有无数条,故(4)错.
l∥
一条直线和一个平 这 条 直 线 性质 面 平行 ,经过这条直 和 这 两 个 线的平面和这个平面 平面的 交线
l∥α, l⊂β ,
相交
平行
⇒l∥m
下列条件中能确定直线 a 与平面 α 平行的是( A.a⊄α,b⊂α,a∥b B.b⊂α,a∥b C.b⊂α,c⊂α,a∥b,a∥c
图 1215
【精彩点拨】 (1)欲证四边形 BB1M1M 是平行四边形,可证其一组对边平 行且相等;(2)可结合(1)利用等角定理证明或利用三角形全等证明.
2018版高中数学第一章立体几何初步1.2.1平面的基本性质与推论学案新人教B版必修2
1.2.1 平面的基本性质与推论学习目标 1.理解平面的基本性质与推论,能运用平面的基本性质及推论去解决有关问题.2.会用集合语言来描述点、直线和平面之间的关系以及图形的性质.3.理解异面直线的概念.知识点一平面的基本性质与推论思考1 直线l与平面α有且仅有一个公共点P.直线l是否在平面α内?有两个公共点呢?思考2 观察图中的三脚架,你能得出什么结论?思考3 观察正方体ABCD—A1B1C1D1(如图所示),平面ABCD与平面BCC1B1有且只有两个公共点B、C吗?梳理(1)平面的基本性质平面内容作用图形基本性质1如果一条直线上的________在一个平面内,那么这条直线上的所有点判断直线是否在平面内的依据都在这个平面内(即直线在________或______经过直线)基本性质2经过不在同一条直线上的________,有且只有一个平面(即________确定一个平面)确定平面及两个平面重合的依据基本性质3如果不重合的两个平面有________公共点,那么它们有且只有一条过这个点的公共直线判断两平面相交,线共点,点共线的依据(2)平面基本性质的推论推论1:经过一条直线和直线外的一点,________平面.推论2:经过两条________直线,有且只有一个平面.推论3:经过两条________直线,有且只有一个平面.知识点二点、直线、平面之间的关系及表示思考直线和平面都是由点组成的,联系集合的观点,点和直线、平面的位置关系,如何用符号来表示?直线和平面呢?梳理点、直线、平面之间的基本位置关系及表示文字语言符号语言图形语言A在l上A∈lA在l外A∉lA在α内A∈αA在α外A∉αl在α内l⊂αl在α外l⊄αl,m相交于A l∩m=Al,α相交于A l∩α=Aα,β相交于l α∩β=l知识点三共面与异面直线思考如图,直线AB与平面α相交于点B,点A在α外,那么直线l与直线AB能不能在同一个平面内?为什么?直线l与直线AB的位置关系是怎样的?梳理共面与异面直线(1)共面①概念:空间中的几个点或几条直线,都在________________内.②特征:共面的直线________或者________.(2)异面直线①概念:既不________又不________的直线.②判断方法:与一平面相交于一点的直线与这个平面内________________的直线是异面直线.类型一点、直线、平面之间的位置关系的符号表示例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.反思与感悟(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.(2)根据符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.跟踪训练1 根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:(1)A∈α,B∉α;(2)l⊂α,m∩α=A,A∉l;(3)平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC.类型二平面的基本性质的应用命题角度1 点、线共面问题例2 如图,已知:a⊂α,b⊂α,a∩b=A,P∈b,PQ∥a,求证:PQ⊂α.引申探究将本例中的两条平行线改为三条,即求证:和同一条直线相交的三条平行直线一定在同一平面内.反思与感悟证明多线共面的两种方法(1)纳入法:先由部分直线确定一个平面,再证明其他直线在这个平面内.(2)重合法:先说明一些直线在一个平面内,另一些直线也在另一个平面内,再证明两个平面重合.跟踪训练2 已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1,l2,l3在同一平面内.命题角度2 点共线与线共点问题例3 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE、D1F,DA三线交于一点.反思与感悟(1)点共线:证明多点共线通常利用基本性质3,即两相交平面交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,然后证明其他点也在其上.(2)三线共点:证明三线共点问题可把其中一条作为分别过其余两条直线的两个平面的交线,然后再证两条直线的交点在此直线上,此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得三线共点.跟踪训练3 已知△ABC在平面α外,其三边所在的直线满足AB∩α=P,BC∩α=Q,AC∩α=R,如图所示.求证:P,Q,R三点共线.类型三异面直线的判定例4 如图是一个正方体的展开图,如果将它还原为正方体,那么NC,DE,AF,BM这四条线段所在的直线是异面直线的有多少对?试以其中一对为例进行证明.反思与感悟判定两条直线是异面直线的方法(1)证明两条直线既不平行又不相交.(2)重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A∉α,B∈α,l⊂α,B∉l⇒AB与l是异面直线(如图).跟踪训练4 分别在两个相交平面内的两条直线间的位置关系是( )A.异面B.平行C.相交D.以上都有可能1.若A∈平面α,B∈平面α,C∈直线AB,则( )A.C∈αB.C∉αC.AB⊄αD.AB∩α=C2.平行六面体ABCD—A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )A.3 B.4C.5 D.63.如图所示,在长方体ABCD-A1B1C1D1中,与AA1异面的是( )A.AB B.BB1C.DD1D.B1C14.线段AB在平面α内,则直线AB与平面α的位置关系是________.5.如图,已知D,E分别是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB 与平面α的交点是P,则点P与直线DE的位置关系是________.1.解决立体几何问题首先应过好三大语言关,即实现这三种语言的相互转换,正确理解集合符号所表示的几何图形的实际意义,恰当地用符号语言描述图形语言,将图形语言用文字语言描述出来,再转换为符号语言.文字语言和符号语言在转换的时候,要注意符号语言所代表的含义,作直观图时,要注意线的实虚.2.在处理点线共面、三点共线及三线共点问题时初步体会三个公理的作用,突出先部分再整体的思想.3.异面直线是既不平行也不相交的直线.答案精析问题导学知识点一思考1 前者不在,后者在.思考2 不共线的三点可以确定一个平面.思考3 不是,平面ABCD与平面BCC1B1相交于直线BC.梳理(1)两点平面内平面三点不共线的三点一个(2)有且只有一个相交平行知识点二思考点和直线、平面的位置关系可用数字符号“∈”或“∉”表示,直线和平面的位置关系,可用数学符号“⊂”或“⊄”表示.知识点三思考不可能在同一个平面内,因为如果在同一个平面内,点A就在α内,这与点A在α外矛盾.由图知,直线l与直线AB没有公共点,所以它们不相交,直线l与直线AB不可能平行,否则它们就会同在平面α内,所以直线l与直线AB既不相交也不平行.梳理(1)①同一平面②相交平行(2)①平行相交②不经过交点题型探究例1 解在(1)中,α∩β=l,a∩α=A,a∩β=B.在(2)中,α∩β=l,a⊂α,b⊂β,a∩l=P,b∩l=P.跟踪训练1 解(1)点A在平面α内,点B不在平面α内,如图①.(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上,如图②.(3)平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC,如图③.例2 解因为PQ∥a,所以PQ与a确定一个平面β.所以直线a⊂β,点P∈β.因为P∈b,b⊂α,所以P∈α.又因为a⊂α,所以α与β重合,所以PQ⊂α.引申探究解已知:a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:a,b,c和l共面.证明:如图,∵a ∥b ,∴a 与b 确定一个平面α.∵l ∩a =A ,l ∩b =B ,∴A ∈α,B ∈α. 又∵A ∈l ,B ∈l ,∴l ⊂α. ∵b ∥c ,∴b 与c 确定一个平面β, 同理l ⊂β.∵平面α与β都包含l 和b ,且b ∩l =B , 由推论2知:经过两条相交直线有且只有一个平面, ∴平面α与平面β重合,∴a ,b ,c 和l 共面. 跟踪训练2 证明 方法一 (纳入平面法) ∵l 1∩l 2=A ,∴l 1和l 2确定一个平面α. ∵l 2∩l 3=B ,∴B ∈l 2.又∵l 2⊂α,∴B ∈α.同理可证C ∈α. ∵B ∈l 3,C ∈l 3,∴l 3⊂α. ∴直线l 1,l 2,l 3在同一平面内. 方法二 (辅助平面法)∵l 1∩l 2=A ,∴l 1和l 2确定一个平面α. ∵l 2∩l 3=B ,∴l 2,l 3确定一个平面β. ∵A ∈l 2,l 2⊂α,∴A ∈α. ∵A ∈l 2,l 2⊂β,∴A ∈β.同理可证B ∈α,B ∈β,C ∈α,C ∈β.∴不共线的三个点A ,B ,C 既在平面α内,又在平面β内. ∴平面α和β重合,即直线l 1,l 2,l 3在同一平面内. 例3 证明 如图,连接EF ,D 1C ,A 1B .∵E 为AB 的中点,F 为AA 1的中点, ∴EF 綊12A 1B .又∵A 1B 綊D 1C , ∴EF 綊12D 1C ,∴E ,F ,D 1,C 四点共面, ∴D 1F 与CE 相交,设交点为P . 又D 1F ⊂平面A 1D 1DA ,CE ⊂平面ABCD ,∴P 为平面A 1D 1DA 与平面ABCD 的公共点. 又平面A 1D 1DA ∩平面ABCD =DA , 根据基本性质3,可得P ∈DA , 即CE 、D 1F 、DA 相交于一点.跟踪训练3 证明 方法一 ∵AB ∩α=P , ∴P ∈AB ,P ∈平面α.又AB ⊂平面ABC ,∴P ∈平面ABC .∴由基本性质3可知:点P 在平面ABC 与平面α的交线上, 同理可证Q 、R 也在平面ABC 与平面α的交线上. ∴P 、Q 、R 三点共线. 方法二 ∵AP ∩AR =A ,∴直线AP 与直线AR 确定平面APR .又∵AB ∩α=P ,AC ∩α=R ,∴平面APR ∩平面α=PR .∵B ∈平面APR ,C ∈平面APR ,∴BC ⊂平面APR .∵Q ∈BC ,∴Q ∈平面APR ,又Q ∈α, ∴Q ∈PR ,∴P 、Q 、R 三点共线.例4 解 将展开图还原为正方体(如图).NC 与DE ,NC 与AF ,NC 与BM ,DE 与AF ,DE 与BM ,AF 与BM ,都是异面直线,共有6对.以NC 与AF 是异面直线为例证明如下: 方法一 连接BE ,若NC ∥AF , 则由NC ∥BE ,可知AF ∥BE , 这与AF 与BE 相交矛盾. 故NC 与AF 不平行.若NC与AF相交,则平面ABFE与平面CDNM有公共点,这与正方体的性质矛盾.故NC与AF 不相交.所以NC与AF异面.方法二连接BE,如图,因为直线NC⊂平面BCNE,直线AF∩平面BCNE=O.O∉直线NC,所以NC与AF异面.跟踪训练4 D [如图(1)所示,直线a与b互相平行;如图(2)所示,直线a与b相交;如图(3)所示,直线a与b异面.]当堂训练1.A 2.C 3.D4.直线AB⊂α解析由基本性质1知直线AB在平面α内.5.P∈直线DE解析因为P∈AB,AB⊂平面ABC,所以P∈平面ABC.又P∈α,平面ABC∩平面α=DE,所以P∈直线DE.。
2018版高中数学第一章立体几何初步1.2.2第1课时平行直线学案新人教B版
1.2.2 第1课时 平行直线学习目标 1.掌握空间中两条直线的位置关系,理解空间平行性的传递性.2.理解并掌握基本性质4及等角公理.知识点一 基本性质4思考 在平面内,直线a ,b ,c ,若a ∥b ,b ∥c 则a ∥c .该结论在空间中是否成立?梳理 基本性质4(1)文字表述:平行于同一条直线的两条直线互相________.这一性质叫做________________________. (2)符号表达:⎭⎪⎬⎪⎫a ∥b b ∥c ⇒________.知识点二 等角定理思考 观察图,在长方体ABCD —A ′B ′C ′D ′中,∠ADC 与∠A ′D ′C ′,∠ADC 与∠D ′A ′B ′的两边分别对应平行,这两组角的大小关系如何?梳理 等角定理如果一个角的两边与另一个角的两边分别________________,并且________________,那么这两个角相等. 知识点三 空间四边形顺次连接________的四点A ,B ,C ,D 所构成的图形,叫做空间四边形.这四个点中的各个点叫做空间四边形的________;所连接的相邻顶点间的线段叫做空间四边形的________;连接不相邻的顶点的线段叫做空间四边形的________.空间四边形用表示顶点的四个字母表示.类型一基本性质4的应用例1 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,E,F,G,H分别为PA,PB,PC,PD的中点,求证:四边形EFGH是平行四边形.反思与感悟证明两条直线平行的两种方法(1)利用平行线的定义:证明两条直线在同一平面内且无公共点.(2)利用基本性质4:寻找第三条直线,然后证明这两条直线都与所找的第三条直线平行,根据基本性质4,显然这两条直线平行.若题设条件中含有中点,则常利用三角形的中位线性质证明直线平行.跟踪训练1 如图所示,E,F分别是长方体A1B1C1D1-ABCD的棱A1A,C1C的中点.求证:四边形B1EDF是平行四边形.类型二等角定理的应用例2 如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.求证:(1)四边形BB1M1M为平行四边形;(2)∠BMC=∠B1M1C1.反思与感悟有关证明角相等问题,一般采用下面三种途径(1)利用等角定理及其推论. (2)利用三角形相似.(3)利用三角形全等.本例是通过第一种途径来实现的.跟踪训练2 已知棱长为a 的正方体ABCD -A 1B 1C 1D 1中,M 、N 分别是棱CD 、AD 的中点.求证: (1)四边形MNA 1C 1是梯形; (2)∠DNM =∠D 1A 1C 1.类型三 空间四边形的认识例3 如图,设E ,F ,G ,H 分别是四面体A -BCD 的棱AB ,BC ,CD ,DA 上的点,且AE AB =AHAD=λ,CF CB =CGCD=μ,求证:(1)当λ=μ时,四边形EFGH 是平行四边形; (2)当λ≠μ时,四边形EFGH 是梯形.反思与感悟 因空间图形往往包含平面图形,在解题时容易混淆,所以把相似的概念辨析一下,区分异同,有利于解题时不出错,如本例中明确给出了“空间四边形ABCD ”,不包含平面四边形,说明“A ,B ,C ,D 四点必不共面”,不能因直观图中AD 与BC 看似平行的关系认为它们是平行的.跟踪训练3 已知空间四边形ABCD 中,AB ≠AC ,BD =BC ,AE 是△ABC 的边BC 上的高,DF 是△BCD 的边BC 上的中线,判定AE 与DF 的位置关系.1.直线a∥b,直线b与c相交,则直线a,c一定不存在的位置关系是( )A.相交B.平行C.异面D.无法判断2.下列四个结论中假命题的个数是( )①垂直于同一直线的两条直线互相平行;②平行于同一直线的两直线平行;③若直线a,b,c满足a∥b,b⊥c,则a⊥c;④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线.A.1 B.2 C.3 D.43.下列结论正确的是( )A.若两个角相等,则这两个角的两边分别平行B.空间四边形的四个顶点可以在一个平面内C.空间四边形的两条对角线可以相交D.空间四边形的两条对角线不相交4.下面三个命题,其中正确的个数是( )①三条相互平行的直线必共面;②两组对边分别相等的四边形是平行四边形;③若四边形有一组对角都是直角,则这个四边形是圆的内接四边形.A.1个B.2个C.3个D.0个5.两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )A.全等B.不相似C.仅有一个角相等D.相似1.判定两直线的位置关系的依据就在于两直线平行、相交、异面的定义.很多情况下,定义就是一种常用的判定方法.另外,我们解决空间有关线线问题时,不要忘了我们生活中的模型,比如说教室就是一个长方体模型,里面的线线关系非常丰富,我们要好好地利用它,它是我们培养空间想象能力的好工具.2.3.注意:等角定理的逆命题不成立.答案精析问题导学 知识点一 思考 成立.梳理 (1)平行 空间平行线的传递性 (2)a ∥c 知识点二思考 从图中可以看出,∠ADC =∠A ′D ′C ′,∠ADC +∠D ′A ′B ′=180°. 梳理 对应平行 方向相同 知识点三不共面 顶点 边 对角线 题型探究例1 解 在△PAB 中,因为E ,F 分别是PA ,PB 的中点, 所以EF ∥AB ,EF =12AB ,同理GH ∥DC ,GH =12DC .因为四边形ABCD 是平行四边形, 所以AB ∥CD ,AB =CD . 所以EF ∥GH ,EF =GH .所以四边形EFGH 是平行四边形. 跟踪训练1 证明设Q 是DD 1的中点, 连接EQ ,QC 1.∵E 是AA 1的中点, ∴EQ 綊A 1D 1. 又在矩形A 1B 1C 1D 1中,A 1D 1綊B 1C 1,∴EQ 綊B 1C 1(基本性质4). ∴四边形EQC 1B 1为平行四边形, ∴B 1E 綊C 1Q .又∵Q ,F 是DD 1,C 1C 的中点, ∴QD 綊C 1F .∴四边形QDFC 1为平行四边形. ∴C 1Q 綊DF ,∴B 1E 綊DF . ∴四边形B 1EDF 为平行四边形.例2 证明 (1)在正方形ADD 1A 1中,M ,M 1分别为AD ,A 1D 1的中点, ∴A 1M 1綊AM ,∴四边形AMM 1A 1是平行四边形, ∴A 1A 綊M 1M .又∵A 1A 綊B 1B ,∴M 1M 綊B 1B , ∴四边形BB 1M 1M 为平行四边形. (2)由(1)知四边形BB 1M 1M 为平行四边形, ∴B 1M 1∥BM .同理可得四边形CC 1M 1M 为平行四边形, ∴C 1M 1∥CM .由平面几何知识可知, ∠BMC 和∠B 1M 1C 1都是锐角. ∴∠BMC =∠B 1M 1C 1.跟踪训练2 证明 (1)如图,连接AC ,在△ACD 中,∵M 、N 分别是CD 、AD 的中点, ∴MN 是△ACD 的中位线, ∴MN ∥AC ,MN =12AC .由正方体的性质得:AC ∥A 1C 1,AC =A 1C 1.∴MN ∥A 1C 1,且MN =12A 1C 1,即MN ≠A 1C 1,∴四边形MNA 1C 1是梯形. (2)由(1)可知MN ∥A 1C 1,又∵ND ∥A 1D 1,∴∠DNM 与∠D 1A 1C 1相等或互补.而∠DNM 与∠D 1A 1C 1均是直角三角形的一个锐角, ∴∠DNM =∠D 1A 1C 1.例3 证明 (1)∵AE AB =AH AD=λ, ∴EH ∥BD ,∴EH BD=λ. 同理,GF ∥BD ,GF BD=μ. 又∵λ=μ,∴EH =GF , ∴EH 綊GF .∴四边形EFGH 是平行四边形. (2)由(1)知EH ∥GF , 又∵λ≠μ,∴EH ≠GF . ∴四边形EFGH 是梯形.跟踪训练3 解 由已知,得E ,F 不重合. 设△BCD 所在平面为α, 则DF ⊂α,A ∉α,E ∈α,E ∉DF , 所以AE 与DF 异面. 当堂训练1.B 2.B 3.D 4.D 5.D。
18版高中数学第一章立体几何初步1.2.3第2课时平面与平面垂直学业分层测评新人教B版必修2
1.2.3 第2课时平面与平面垂直学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.△ABC所在的平面为α,直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则直线l,m的位置关系是( )A.相交B.异面C.平行D.不确定【解析】因为l⊥AB,l⊥AC且AB∩AC=A,所以l⊥平面ABC.同理可证m⊥平面ABC,所以l∥m,故选C.【答案】 C2.设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( )A.若α⊥β,m⊂α,n⊂β,则m⊥nB.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β【解析】A中,m,n可能为平行、垂直、异面直线;B中,m,n可能为异面直线;C 中,m应与β中两条相交直线垂直时结论才成立.【答案】 D3.已知平面α、β和直线m、l,则下列命题中正确的是( )【导学号:45722059】A.若α⊥β,α∩β=m,l⊥m,则l⊥βB.若α∩β=m,l⊂α,l⊥m,则l⊥βC.若α⊥β,l⊂α,则l⊥βD.若α⊥β,α∩β=m,l⊂α,l⊥m,则l⊥β【解析】选项A缺少了条件l⊂α;选项B缺少了条件α⊥β;选项C缺少了条件α∩β=m,l⊥m;选项D具备了面面垂直的性质定理的全部条件.故选D.【答案】 D4.如图1265所示,PA⊥矩形ABCD,下列结论中不正确的是( )图1265A.PD⊥BDB.PD⊥CDC.PB⊥BCD.PA⊥BD【解析】若PD⊥BD,则BD⊥平面PAD,又BA⊥平面PAD,则过平面外一点有两条直线与平面垂直,不成立,故A不正确;因为PA⊥矩形ABCD,所以PA⊥CD,AD⊥CD,所以CD⊥平面PAD,所以PD⊥CD,同理可证PB⊥BC.因为PA⊥矩形ABCD,所以由直线与平面垂直的性质得PA⊥BD.故选A.【答案】 A5.如图1266所示,三棱锥PABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )图1266A.一条线段B.一条直线C.一个圆D.一个圆,但要去掉两个点【解析】∵平面PAC⊥平面PBC,AC⊥PC,平面PAC∩平面PBC=PC,AC⊂平面PAC,∴AC⊥平面PBC.又∵BC⊂平面PBC,∴AC⊥BC.∴∠ACB=90°.∴动点C的轨迹是以AB为直径的圆,除去A和B两点.【答案】 D二、填空题6.如图1267所示,在三棱锥P ABC 中,PA ⊥底面ABC ,∠BAC =90°,F 是AC 的中点,E 是PC 上的点,且EF ⊥BC ,则PEEC=________.图1267【解析】 在三棱锥P ABC 中,因为PA ⊥底面ABC ,∠BAC =90°,所以AB ⊥平面APC . 因为EF ⊂平面PAC ,所以EF ⊥AB , 因为EF ⊥BC ,BC ∩AB =B , 所以EF ⊥底面ABC ,所以PA ∥EF , 因为F 是AC 的中点,E 是PC 上的点, 所以E 是PC 的中点,所以PE EC=1. 【答案】 17.如图1268所示,平面α⊥平面β,在α与β交线上取线段AB =4,AC ,BD 分别在平面α和β内,AC ⊥AB ,BD ⊥AB ,AC =3,BD =12,则CD =________.图1268【解析】 连接BC .∵BD ⊥AB ,α⊥β,α∩β=AB ,∴BD ⊥α.∵BC⊂α,∴BD ⊥BC ,∴△CBD 是直角三角形.在Rt△BAC 中,BC =32+42=5. 在Rt△CBD 中,CD =52+122=13. 【答案】 138.如图1269所示,在三棱锥P ABC 中,平面PAC ⊥平面ABC ,∠PCA =90°,△ABC 是边长为4的正三角形,PC =4,M 是AB 边上的一动点,则PM 的最小值为________.【导学号:45722060】图1269【解析】 连接CM ,则由题意知PC ⊥平面ABC ,可得PC ⊥CM ,所以PM=PC 2+CM 2,要求PM 的最小值只需求出CM 的最小值即可,在△ABC 中,当CM ⊥AB 时,CM 有最小值,此时有CM =4×32=23,所以PM 的最小值为27. 【答案】 27 三、解答题9.如图1270所示,三棱锥P ABC 中,已知△ABC 是等腰直角三角形,∠ABC =90°,△PAC 是直角三角形,∠PAC =90°,平面PAC ⊥平面ABC .求证:平面PAB ⊥平面PBC .图1270【证明】 ∵平面PAC ⊥平面ABC ,平面PAC ∩平面ABC =AC ,PA ⊥AC , ∴PA ⊥平面ABC .又BC ⊂平面ABC , ∴PA ⊥BC .又∵AB ⊥BC ,AB ∩PA =A ,AB ⊂平面PAB ,PA ⊂平面PAB ,∴BC ⊥平面PAB .又BC ⊂平面PBC , ∴平面PAB ⊥平面PBC .10.如图1271所示,△ABC 是边长为2的正三角形.若AE =1,AE ⊥平面ABC ,平面BCD ⊥平面ABC ,BD =CD ,且BD ⊥CD .图1271(1)求证:AE ∥平面BCD ; (2)求证:平面BDE ⊥平面CDE .【证明】 (1)取BC 的中点M ,连接DM ,因为BD =CD ,且BD ⊥CD ,BC =2.所以DM=1,DM⊥BC.又因为平面BCD⊥平面ABC,所以DM⊥平面ABC,又AE⊥平面ABC,所以AE∥DM.又因为AE⊄平面BCD,DM⊂平面BCD,所以AE∥平面BCD.(2)由(1)知AE∥DM,又AE=1,DM=1,所以四边形DMAE是平行四边形,所以DE∥AM.连接AM,易证AM⊥BC,因为平面BCD⊥平面ABC,所以AM⊥平面BCD,所以DE⊥平面BCD.又CD⊂平面BCD,所以DE⊥CD.因为BD⊥CD,BD∩DE=D,所以CD⊥平面BDE.因为CD⊂平面CDE,所以平面BDE⊥平面CDE.[能力提升]1.用a,b,c表示空间中三条不同的直线,γ表示平面,给出下列命题:①若a⊥b,b⊥c,则a∥c;②若a∥b,a∥c,则b∥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,b⊥γ,则a∥b.其中真命题的序号是( )A.①②B.②③C.①④D.②④【解析】对于①,正方体从同一顶点引出的三条直线a,b,c,满足a⊥b,b⊥c,但是a⊥c,所以①错误;对于②,若a∥b,a∥c,则b∥c,满足平行线公理,所以②正确;对于③,平行于同一平面的两条直线的位置关系可能是平行、相交或者异面,所以③错误;对于④,由垂直于同一平面的两条直线平行,知④正确.故选D.【答案】 D2.如图1272所示,在三棱锥DABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的是( )图1272A.平面ABC⊥平面ABDB.平面ABD⊥平面BCDC.平面ABC⊥平面BDE,且平面ACD⊥平面BDED.平面ABC⊥平面ACD,且平面ACD⊥平面BDE【解析】因为AB=CB,且E是AC的中点,所以BE⊥AC,同理有DE⊥AC,于是AC⊥平面BDE.因为AC⊂平面ABC,所以平面ABC⊥平面BDE.又AC⊂平面ACD,所以平面ACD⊥平面BDE.【答案】 C3.如图1273所示,边长为2a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED 是△AED绕DE旋转过程中的一个图形,现给出下列结论,其中正确的结论有________.(填上所有正确结论的序号)图1273①动点A′在平面ABC上的射影在线段AF上;②三棱锥A′FED的体积有最大值;③恒有平面A′GF⊥平面BCED;④异面直线A′E与BD不可能互相垂直.【解析】因为DE⊥A′G,DE⊥GF,A′G∩GF=G,所以DE⊥平面A′GF,又DE⊂平面BCED,所以平面A′GF⊥平面BCED,故③正确.过A′作A′H⊥AF,垂足为H,则A′H⊂平面A′GF,所以A′H⊥DE,又DE∩AF=G,所以A′H⊥平面ABC,故①正确.三棱锥A′FED的底面△FED的面积是定值,高是点A′到平面FED的距离.易证当A′G⊥平面FED时距离(即高)最大,三棱锥A′FED的体积最大,故②正确.易知BD∥EF,所以∠A′EF是异面直线A′E与BD所成的角.正△ABC的边长为2a,AE =a,EF=a,而A′F的长度的取值范围是(0, 3a),当A′F=2a时,A′E2+EF2=A′F2,∠A′EF=90°,此时直线A′E与BD互相垂直,故④错误.【答案】①②③4.如图1274所示,在正四棱柱ABCDA1B1C1D1中,E为AD的中点,F为B1C1的中点.(1)求证:A1F∥平面ECC1;(2)在CD上是否存在一点G,使BG⊥平面ECC1?若存在,请确定点G的位置,并证明你的结论;若不存在,请说明理由.【导学号:45722061】图1274【解】(1)如图,在正四棱柱ABCDA1B1C1D1中,取BC的中点M,连接AM,FM,所以B1F∥BM且B1F=BM,所以四边形B1FMB是平行四边形,所以FM∥B1B且FM=B1B.因为FM∥A1A且FM=A1A,所以四边形AA1FM是平行四边形,所以A1F∥AM.因为E为AD的中点,所以AE∥MC且AE=MC.所以四边形AMCE是平行四边形.所以CE∥AM,所以CE∥A1F.因为A1F⊄平面ECC1,EC⊂平面ECC1,所以A1F∥平面ECC1.(2)在CD上存在一点G,使BG⊥平面ECC1.取CD的中点G,连接BG,如图.在正方形ABCD中,DE=EC,CD=BC,∠ADC=∠BCD,所以△CDE≌△BCG,所以∠ECD=∠GBC.因为∠CGB+∠GBC=90°,所以∠CGB+∠DCE=90°,所以BG⊥EC.因为CC1⊥平面ABCD,BG⊂平面ABCD,所以CC1⊥BG.又EC∩CC1=C,所以BG⊥平面ECC1.故当G为CD的中点时,满足BG⊥平面ECC1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
1.2.2 第2课时 平面与平面平行
[学习目标] 1.通过对图形的观察,了解空间中不重合的两平面有平行和相交两种位置关
系.2.掌握平面与平面平行的判定定理和性质定理.
[知识链接]
1.直线与平面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,
那么这条直线和这个平面平行.
2.直线和平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个
平面相交,那么这条直线就和两平面的交线平行.
[预习导引]
1.空间两个平面的位置关系
位置关系 图形语言 符号语言 公共点个数
两平面平行 α∥β 无
两平面相交 α∩β=
a
无数个点有一条
公共直线
2.两个平面平行的判定定理
(1)定理:如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行.
(2)推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平
面平行.
3.两个平面平行的性质定理
如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
4.三个平面平行的性质
两条直线被三个平行平面所截,截得的对应线段成比例.
要点一 平面与平面的位置关系
例1 已知下列说法:
①若两个平面α∥β,a⊂α,b⊂β, 则a∥b;
②若两个平面α∥β,a⊂α,b⊂β,则a与b是异面直线;
2
③若两个平面α∥β;a⊂α,b⊂β,则a与b一定不相交;
④若两个平面α∥β;a⊂α,b⊂β,则a与b平行或异面;
⑤若两个平面α∩β=b,;a⊂α,则a与β一定相交.
其中正确的是________(将你认为正确的序号都填上).
答案 ③④
解析 ①错,a与b也可能异面;
②错.a与b也可能平行;
③对.∵α∥β,∴α与β无公共点,又∵a⊂α,b⊂β,∴a与b无公共点;
④对.由已知及③知:a与b无公共点,
那么a∥b或a与b异面;
⑤错.a 与β也可能平行.
规律方法 两个平面的位置关系有两种:平行和相交,没有公共点则平行,有公共点则相交,
熟练掌握这两种位置关系,并借助图形来说明,是解决本题的关键.
跟踪演练1 如果在两个平面内分别有一条直线,这两条直线互相平行,那么两个平面的位
置关系一定是( )
A.平行 B.相交
C.平行或相交 D.不能确定
答案 C
解析 如图所示,由图可知C正确.
要点二 平面与平面平行的判定
例2 在正方体ABCD-A1B1C1D1中,M,E,F,N分别是A1B1,B1C1,C1D1,D1A1的中点.
求证:(1)E,F,B,D四点共面;
(2)平面MAN∥平面EFDB.
证明 (1)如图,连接B1D1,
∵E,F分别是边B1C1,C1D1的中点,
∴EF∥B1D1,
而BD∥B1D1,∴BD∥EF.
3
∴E,F,B,D四点共面.
(2)易知MN∥B1D1,B1D1∥BD,∴MN∥BD.
又MN⊄平面EFDB,BD⊂平面EFDB,
∴MN∥平面EFDB.
连接DF,MF.∵M,F分别是A1B1,C1D1的中点,
∴MF∥A1D1,MF=A1D1,
∴MF∥AD,MF=AD.
∴四边形ADFM是平行四边形,∴AM∥DF.
又AM⊄平面BDFE,DF⊂平面BDFE,
∴AM∥平面BDFE.
又∵AM∩MN=M,∴平面MAN∥平面EFDB.
规律方法 证明两个平面平行的关键在于证明线面平行,在证明面面平行时,可利用面面平
行判定定理的推论:如果一个平面内的两条相交直线平行于另一个平面内的两条相交直线,
则这两个平面平行.即证一个平面内的两条相交直线与另一个平面的两条相交直线分别平行
即可.
跟踪演练2 如图,三棱锥P-ABC中,E,F,G分别是AB,AC,AP的中点.证明:平面GEF∥
平面PCB.
证明 因为E,F,G分别是AB,AC,AP的中点,
所以EF∥BC,GF∥CP.
因为EF,GF⊄平面PCB,
所以EF∥平面PCB,GF∥平面PCB.
又EF∩GF=F,
所以平面GFE∥平面PCB.
要点三 面面平行的性质定理的应用
例3 如图,平面四边形ABCD的四个顶点A、B、C、D均在平行四边形A′B′C′D′所确定
一个平面α外,且AA′、BB′、CC′、DD′互相平行.
4
求证:四边形ABCD是平行四边形.
证明 在▱A′B′C′D′中,A′B′∥C′D′.
∵A′B′⊄平面C′D′DC,C′D′⊂平面C′D′DC,
∴A′B′∥平面C′D′DC.
同理A′A∥平面C′D′DC.
又A′A∩A′B′=A′,∴平面A′B′BA∥平面C′D′DC.
∵平面ABCD∩平面A′B′BA=AB,
平面ABCD∩平面C′D′DC=CD,∴AB∥CD.
同理AD∥BC.∴四边形ABCD是平行四边形.
规律方法 1.利用面面平行的性质定理证明线线平行的关键是把要证明的直线看作是平面的
交线,往往需要有三个平面,即有两平面平行,再构造第三个面与两平行平面都相交.
2.面面平行⇒线线平行,体现了转化思想与判定定理的交替使用,可实现线线、线面及面面
平行的相互转化.
跟踪演练3 两条异面直线BA、DC与两平行平面α、β分别交于B、A和D、C,M、N分别
是AB、CD的中点.
求证:MN∥平面α.
证明 如图,过A作AE∥CD交α于E,取AE的中点P,
连接MP、PN、BE、ED.
∵AE∥CD,∴AE、CD确定平面AEDC.
则平面AEDC∩α=DE,平面AEDC∩β=AC,
∵α∥β,∴AC∥DE.
又P、N分别为AE、CD的中点,
∴PN∥DE.PN⊄α,DE⊂α,
∴PN∥α.
又M、P分别为AB、AE的中点,
∴MP∥BE,且MP⊄α,BE⊂α,
∴MP∥α,又MP∩PN=P,
∴平面MPN∥α.
又MN⊂平面MPN,∴MN∥α.
5
1.圆柱的两个底面的位置关系是( )
A.相交 B.平行
C.平行或异面 D.相交或异面
答案 B
解析 圆柱的两个底面无公共点,则它们平行.
2.下列说法正确的是( )
①一个平面内有两条直线都与另外一个平面平行,则这两个平面平行;
②一个平面内有无数条直线都与另外一个平面平行,则这两个平面平行;
③一个平面内任何直线都与另外一个平面平行,则这两个平面平行;
④一个平面内有两条相交直线与另外一个平面平行,则这两个平面平行.
A.①③ B.②④
C.②③④ D.③④
答案 D
解析 由两平面平行的判定定理知③④正确.
3.在正方体EFGHE1F1G1H1中,下列四对截面中,彼此平行的一对截面是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
答案 A
解析 EG∥E1G1,EG⊄平面E1FG1,E1G1⊂平面E1FG,∴EG∥面E1FG1,同理EH1∥平面E1FG1,且
EG∩EH1=E,∴平面EGH1∥平面E1FG
1
.
4.已知a和b是异面直线,且a⊂平面α,b⊂平面β,a∥β,b∥α,则平面α与β的
位置关系是________.
答案 平行
解析 在b上任取一点O,则直线a与点O确定一个平面γ,
设γ∩β=l,则l⊂β,∵a∥β,∴a与l无公共点,
∴a∥l,∴l∥α.又b∥α,根据面面平行的判定定理可得α∥β.
5.若平面α∥平面β,a⊂α,下列说法正确的是________.
①a与β内任一直线平行;②a与β内无数条直线平行;
③a与β内任一直线不垂直;④a与β无公共点.
6
答案 ②④
解析 ∵a⊂α,α∥β,∴a∥β,∴a与β无公共点,④正确;如图,在正方体中,令线
段B1C1所在的直线为a,显然a与β内无数条直线平行,故②正确;又AB⊥B1C1,故在β内
存在直线与a垂直,故①③错误.
常见的面面平行的判定方法:
(1)利用定义:两个平面没有公共点.
(2)归纳为线面平行.
①平面α内的所有直线(任一直线)都平行于β,则α∥β;
②判定定理:平面α内的两条相交直线a,b都平行于β.
a
⊂α
b
⊂α
a∩b=P
a
∥β
b
∥β
⇒α∥β,五个条件缺一不可.
应用时的关键是在α内找到与β平行的相交直线a,b.
(3)化归为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则
α∥β(证明后可用).
(4)利用平行平面的传递性:两个平面同时和第三个平面平行,则这两个平面平行.
