中职直线与圆的方程复习题
直线与圆的方程试题及答案 中职学校

直线与圆的方程试题及答案试题一给定直线的方程为 x + y = 2 和圆的方程为 x^2 + y^2 = 4,求直线与圆的交点坐标。
解答:首先,化简直线的方程可以得到 y = 2 - x。
将直线的方程 y = 2 - x 求根代入圆的方程中,即:x^2 + (2 - x)^2 = 4将上式展开求解,得到 x^2 - 4x + 4 + 4x - 4 = 0化简后得到 x^2 = 4通过求根公式,可以得到 x = 2 或 x = -2。
将 x 的值代入直线的方程 y = 2 - x 中,得到对应的 y 值。
当 x = 2 时,y = 2 - 2 = 0;当 x = -2 时,y = 2 - (-2) = 4。
因此,直线与圆的交点坐标为 (2, 0) 和 (-2, 4)。
试题二给定圆的方程为 (x - 3)^2 + (y + 4)^2 = 9 和直线的斜率为 -2,求直线与圆的交点坐标。
解答:首先,求出直线的方程为 y = -2x + c。
由圆的方程可知,圆心坐标为 (3, -4),半径为 3。
直线与圆相交时,直线上的点到圆心的距离等于半径。
将直线的方程 y = -2x + c 代入圆的方程 (x - 3)^2 + (y + 4)^2 = 9 中,得到:(x - 3)^2 + ((-2x + c) + 4)^2 = 9展开后,化简上式,得到:5x^2 + 10cx + c^2 - 36x + 48c - 72 = 0因为直线与圆相交,所以上式必有实数解。
根据二次方程的性质,上式的判别式必大于等于零。
即:(10c - 36)^2 - 4 * 5 * (c^2 + 48c - 72) >= 0通过求解不等式,可以得到c ∈ (-∞, 20)。
取 c = 10,将 c 的值代入直线的方程 y = -2x + c 中,得到直线的方程为 y = -2x + 10。
将直线的方程 y = -2x + 10 代入圆的方程 (x - 3)^2 + (y + 4)^2 = 9 中,求解 x 的值。
中职数学。第八章 直线和圆的方程复习题

中职数学。
第八章直线和圆的方程复习题第八章直线和圆的方程复题一、选择题:1.关于x轴、y轴对称的点的坐标分别为(B)(C)。
2.设直线l的方程为y-3=2(x-4),则直线l在y轴上的截距是(B)-5.3.已知直线l过点M(1,-1)和N(k,-2),且直线l的斜率为-1,则k的值是(D)-2.4.如果两条不重合直线的斜率都不存在,那么(D)无法判定。
5.若点(C)与圆的位置关系为相离。
6.直线:y=2x+3与直线x+y+m=0的距离为4,则m的值为(A)-5.7.已知l1:2x+y=5与l2:x-2y=4,则位置关系是(A)l1⊥l2.8.直线3x-y+6=0与x-3y=0的夹角的正切值为(B)1.9.若直线3x+6y+1=0与3x+6y+m=0平行,则m的值不为(D)10.10.若直线x+y+m=0(其中m为常数)经过圆(x+1)+(y-3)=25的圆心,则m的值为(B)2.11.圆x+y-10y=0的圆心到直线l:3x+4y-5=0的距离等于(C)5.12.半径为3,且与y轴相切于原点的圆的方程为(D)(x-3)^2+y^2=9 或 (x+3)^2+y^2=9.13.直线倾斜角α的取值范围是(B)0°<α<90°。
14.直线3x-y+5=0的倾斜角为(A)60°。
15.如果圆(x-2)^2+(y-3)^2=r^2和x轴相切,则r为(A)2.二、填空题:1.已知直线l的倾斜角为120°,则直线l的斜率k=tan(120°)=-√3.2.已知点A(4,3)、点B(6,-1),则以AB为直径的圆的方程为(x-5)^2+(y+1)^2=10.3.已知直线l斜率是2,且经过点(1,-2),则直线l方程点斜式是y+2=2(x-1)或2x-y-4=0.4.倾斜角为60°,在y轴上的截距为5的直线方程为y=√3x+5.5.已知直线l经过点(1,-2),且平行于直线3x+2y-6=0,则直线l的方程为什么?改写:已知直线l经过点(1,-2),且与直线3x+2y-6=0平行,求直线l的方程。
中职数学章节练习07直线与圆的方程
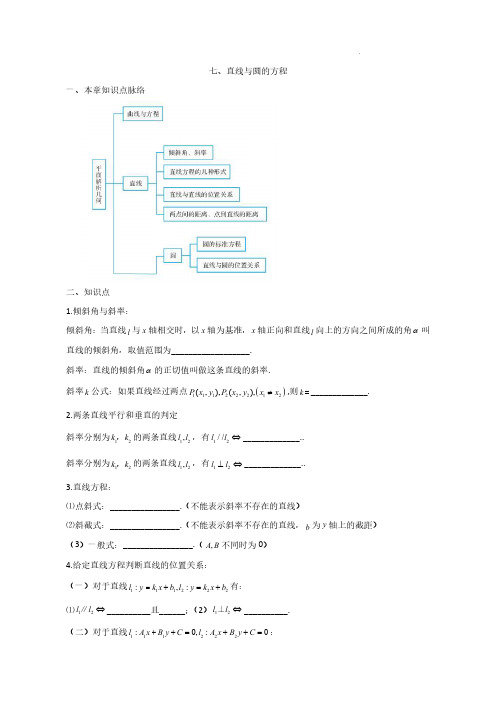
七、直线与圆的方程一、本章知识点脉络二、知识点 1.倾斜角与斜率:倾斜角:当直线l 与x 轴相交时,以x 轴为基准,x 轴正向和直线l 向上的方向之间所成的角 叫直线的倾斜角,取值范围为__________________. 斜率:直线的倾斜角 的正切值叫做这条直线的斜率.斜率k 公式:如果直线经过两点 11122212(,),(,),P x y P x y x x ,则=k _____________. 2.两条直线平行和垂直的判定斜率分别为12k k ,的两条直线12,l l ,有12//l l _____________.. 斜率分别为12k k ,的两条直线12,l l ,有12l l _____________.. 3.直线方程:⑴点斜式:________________.(不能表示斜率不存在的直线)⑵斜截式:________________.(不能表示斜率不存在的直线,b 为y 轴上的截距) (3)一般式:________________.(,A B 不同时为0) 4.给定直线方程判断直线的位置关系: (一)对于直线111222:,:l y k x b l y k x b 有:⑴12l l ∥__________且______;(2)12l l ⊥__________. (二)对于直线111222:0,:0l A x B y C l A x B y C :12//l l ________________且排除重合;;12l l ________________.5.直线的交点坐标与距离公式 (1)两点间距离公式:已知111222(,),(,)P x y P x y ,则12P P ________________.. (2)点到直线距离公式:00(,)P x y 到直线:0l Ax By C 的距离d 为:d ________________..(3)两平行线间的距离公式:1l :10Ax By C 与2l :20Ax By C 间的距离d 为:d ________________..6. 圆的方程 1.圆的方程:⑴标准方程:___________________ (其中圆心为_________,半径为r .)⑵一般方程:___________________.(2240D E F ).(其中圆心为_________,半径为_________.) 7.直线与圆的位置关系(1).直线0Ax By C 与圆222()()x a y b r 的位置关系:(d 表示圆心到直线的距离)d r 0 相离;d r 0 相切;d r 0 相交.(2)直线和圆相交弦长公式:l d 表示圆心到直线的距离) 三、练习【知识点1】两点间的距离公式与中点公式1.已知 3,6,2,4A B ,则A ,B 两点间的距离为( )A .5BC .3D2.已知 ,2,2,3,1,1A a B C 三点,且AB AC ,则a 的值为( ) A .72B .114C .32D .923.已知点(7,4),(4,)A B a ,且,A B 两点的距离为5,则a ( ) A .0B .8C .0或8D .44.已知 1,3A , 3,5B ,则线段AB 的中点坐标为( ) A .(1,4) B .(2,1)C .(2,8)D .(4,2)5.已知点(,2)A x 与(3,)B y 关于坐标原点对称,则x y 等于( ) A .5B .1C .5D .1【知识点2】直线的倾斜角与斜率6.直线30l y 的倾斜角 为( ) A .30B .60C .120D .1507.已知直线l 的倾斜角 10y 的倾斜角互补,则 ( ) A .30B .60C .120D .1508.已知直线:10l ax ,则a ( ) A .3B .3C .1D .19.已知直线l 经过两点 11,1P , 23,1P ,则直线l 的斜率是( ) A .12B .2C .12D .210.直线y 的倾斜角是 .11.若三点 2,3A , 3,2B ,1,2C m共线,则m .【知识点3】直线的点斜式与斜截式方程12.过点 2,1P ,且倾斜角为90 的直线方程为( ) A .1yB .2xC .2yD .=1x13.已知直线l ,在x 轴上的截距为3,则直线l 的方程为( )A .2yB .2yC .12yD .2y14.直线61y x 在y 轴上的截距b 是( ) A .1bB .1bC .6bD .6b15.已知直线l 的倾斜角60 ,在y 轴上的截距为2 ,则此直线方程为( )A .yB .2yC .yD .2y16.过点(2,3) 斜率为12的直线l 在y 轴上的截距为 .17.若直线l 的倾斜角α满足4sin α=3cos α,且它在x 轴上的截距为3,则直线l 的方程是 . 18.一条直线经过点 2,5,倾斜角为45 ,则这条直线的点斜式方程为 .19.已知直线l 经过点P 且倾斜角为α,求直线l 的点斜式方程. (1)P (2,3),4; (2)P (-2,-1),23;(3)P (-5,-1),2.20.根据下列条件分别写出直线的方程:(1),且经过点 5,3A ; (2)斜率为4,在y 轴上的截距为-2.【知识点4】直线的一般式方程21.若直线410mx y m 的斜率小于0,那么该直线不经过( ) A .第一象限B .第二象限C .第三象限D .第四象限22.过点(3,0) 和(0,4),的直线的一般式方程为( ) A .43120x yB .43120x yC .43120x yD .43120x y23.已知直线方程为sin30cos3050x y ,则该直线的倾斜角为( ) A .30B .60C .120D .15024.若0AB ,0BC ,则直线0Ax By C 不经过...的象限是( ) A .第一象限B .第二象限C .第三象限D .第四象限25.过点 1,P 与直线0x 平行的直线的一般式方程为 . 【知识点5】两条相交直线的交点26.直线1:3450l x y 与21:4303l x y 的交点坐标为( ) A .(2,3)B .7,33C .73,3D .3,3727.已知三条直线240,30,20x y kx y x y 交于一点,则实数k =( ) A .1B .1C .32D .1428直线220x y 与420ax y 互相垂直,则这两条直线的交点坐标为( ) A . 1,4B . 0,2C . 1,0D .0,1229.三条直线280,4310ax y x y 与210x y 相交于一点,则a 的值为 .30.直线l 经过原点,且经过直线3420x y 与220x y 的交点,则直线l 的斜率 . 31.直线1y x 与直线31y x 的交点组成的集合用列举法可以表示为 .【知识点6】两条直线平行的条件32.若直线210x y 与220mx y 平行,则实数m 的值为( ) A .3B .1C .1D .233.已知直线:40l x y ,则下列直线中与l 平行的是 A .12y xB .32y xC .30x yD .133y x34.下列四组直线中,互相平行的是 A .10x y 与10x y B .10x y 与1y x C .210x y 与10x yD .20x y 与2430x y35.过点 2,3A 且与直线30x y 平行的直线方程为 .36.若直线 22210a x a y 与直线270x y 平行,则a . 37.求过两条直线240x y 和20x y 的交点,且与3420x y+= 平行的直线方程 .【知识点7】两条直线垂直的条件38.直线0x 与直线0y 的位置关系是( ) A .垂直B .平行C .重合D .以上都不对39.直线30x y 与直线40x y 的位置关系为( ). A .垂直B .平行C .重合D .相交但不垂直40.已知直线1:(2)32l m x y m ,2:1l x my ,若12l l ,则实数m ( ) A .2B .3C .12D .241.直线4210x y 与直线40ax y 垂直,则a 等于( ) A .2B .2C .1D .142.过点 2,3A 且与直线260x y 垂直的直线方程是 .43.过直线240x y 与20x y 的交点,且垂直于直线210x y 的直线方程是 . 44.设a R ,若直线22x ay a 与直线1ax y a 垂直,则a 的值是 . 45.已知点(2,3),(3,1)M N ,则线段MN 的垂直平分线的一般式方程为 .46.经过点(2,1)P --和点CD 的直线与直线50x 垂直,则a . 【知识点8】点到直线的距离公式47.点(2,3)A 到直线:3430L x y 的距离为( )A .1B .2C .103D .9548.已知直线l 过点 2,3和 2,1 ,则原点到直线l 的距离为( )A B C D .349.已知点 2,1A ,点B 在直线30x y 上,则AB 的最小值为( )AB C .D .450.已知 2,4A , 4,6B 两点到直线:10l ax y 的距离相等,则a 的值为( ) A .1 或43B .3或4C .3D .451.已知点 1,4M 到直线:10l mx y 的距离等于1,则实数m 等于 . 52.点(1,2)P 到直线:23l x 的距离为 .53.已知点 1,P b 到直线210x y 的距离为2,则b . 【知识点9】圆的方程54.圆 22123x y 的圆心坐标和半径分别为( )A . 1,2B . 1,2C . 1,2 ,3D . 1,2,355.圆心为 1,1 ,半径为2的圆的方程为( ) A . 22114x yB . 22112x y C . 22114x yD . 22112x y56.若方程2220x y mx my 表示一个圆,则m 可取的值为( ) A .0B .1C .2D .357.若圆22:(2)2a C x y a与x 轴相切,则a ( )A .1BC .2D .458.圆心在y 轴,半径为1且过点(1,2)的圆的标准方程为: 59.已知圆C 的一般方程为2220x x y ,则圆C 的面积为 .60.已知M :22244x y x y 的圆心坐标为 ,a b ,半径为r ,则a b r . 61.写出下列圆的标准方程:①圆心为 3,4C ; ②圆心为 8,3C ,且经过点 5,3M .(2)求下列各圆的圆心坐标和半径: ①22250x y x ; ②222440x y x y .62.分别根据下列条件,求出圆的方程: (1)圆心在原点,半径为6;(2)圆心为点 3,4 ; (3)过点 6,3P ,圆心为 2,2C ; (4)过原点,圆心为点 1,2.【知识点10】直线与圆的位置关系63.直线:20l x y 与圆:C 22124x y 的位置关系是( )A .相切B .相离C .相交且l 过圆C 的圆心D .相交且l 不过圆C 的圆心64.直线320x my m 平分圆C :22220x x y y ,则m ( ) A .32B .1C .-1D .-365.直线30x y 被圆22240x y x y 所截得的弦长为( )AB .C .5D .1066.若直线:1l y kx 与圆22:1O x y 只有一个公共点,则k ( ) A .0B .1C .1D .267.以点 2,3P 为圆心,并且与y 轴相切的圆的标准方程是 .68.已知直线:l y x 被圆 222:310C x y r r 截得的弦长为2,则r69.已知圆222x y ,直线y x b ,当b 为何值时, (1)圆与直线有两个公共点; (2)圆与直线只有一个公共点; (3)圆与直线没有公共点.【知识点11】直线方程与圆的方程应用70.一座圆拱桥,当水面在如图所示位置时,拱顶离水面2米,水面宽12米,当水面下降2米后,水面宽是( )A .13米B .14米C .15米D .16米71.如图,某个圆拱桥的水面跨度是20米,拱顶离水面4米;当水面下降1米后,桥在水面的跨度为( )A .B .米C .D .米72.如图,圆弧形拱桥的跨度12m AB ,拱高4m CD ,则拱桥的直径为 m.73.某圆拱桥的水面跨度16m ,拱高4m ,现有一船,宽10m ,水面以上高3m ,问这条船能否通过?。
中职数学基础模块下册《直线与圆的方程的简单应用》word练习题

直线与圆的方程的应用_基础1.直线()()110a x b y +++=与圆222x y +=的位置关系是( ) A.相切 B.相离 C.相切或相交 D.相切或相离2.圆C 1:x 2+y 2+4x-4y+7=0与圆C 2:x 2+y 2-4x-10y+13=0的公切线有( )A.1条B.2条C.3条D.4条3.与圆x 2+(y-2)2=1相切,且在两轴上截距相等的直线有( )A.2条B.3条C.4条D.6条4.直线ax+by=c 与圆x 2+y 2=1相切,且a 、b 、c 均不为零,则以|a|、|b|、|c|为长度的线段能构成( )A.不等边锐角三角形B.等腰锐角三角形C.直角三角形D.钝角三角形5.点M 、N 在x 2+y 2+kx+2y -4=0上,且点M 、N 关于直线x -y+1=0对称,则该圆的半径等于( ).A .BC .1D .36.直线2x -y=0与圆C :(x -2)2+(y+1)2=9交于A 、B 两点,则△ABC (C 为圆心)的面积等于( ).A .B .C .D .7.圆(x -4)2+(y -4)2=4与直线y=kx 的交点为P 、Q ,原点为O ,则|OP|·|OQ|的值为( ).A .B .28C .32D .由k 确定8.点P 是直线2x+y+10=0上的动点,直线PA 、PB 分别与圆x 2+y 2=4相切于A 、B 两点,则四边形PAOB (O 为坐标原点)的面积的最小值等于( ).A .24B .16C .8D .49.已知圆C 的圆心是直线x -y+1=0与x 轴的交点,且圆C 与直线x+y+3=0相切,则圆C 的方程为________.10.过原点的直线与圆x 2+y 2-2x -4y+4=0相交所得弦的长为2,则该直线的方程为________.11.设圆22450x y x +--=的弦AB 的中点为(3,1)P ,则直线AB 的方程是 .12.直线0x m +-=与圆221x y +=在第一象限内有两个不同的交点,则实数m 的取值范围是.13.已知圆O 1:x 2+y 2+2x+6y+9=0与圆O 2:x 2+y 2―6x+2y+1=0.求圆O 1和圆O 2的公切线方程.14.求与y轴相切,且与圆A:x2+y2―4x=0也相切的圆P的圆心的轨迹方程.15.有弱、强两个喇叭在O、A两处,若它们的强度之比为1∶4,且相距60 m,问在什么位置听到两个喇叭传来的声音强度是相等的?【答案与解析】1.【答案】C直线过定点()1,1--.又()()22112-+-=,∴点在圆上,过圆上一点的直线与圆的位置关系有两种相切或相交.2. 【答案】C【解析】两圆公切线的条数取决于两圆的位置关系,相离:4条;外切:3条;相交:2条;内切:1条;内含:0条.C 1:(x+2)2+(y-2)2=1,C 2:(x-2)2+(y-5)2=16,C 1C 2=5=r 1+r 2,故两圆外切,公切线共3条.3. 【答案】C【解析】此题主要考查圆的切线及直线的截距的概念.过原点的有2条;斜率为-1的有2条.4. 【答案】C【解析】由圆心到直线的距离为圆的半径1,得22||b a c +=1,两边平方得a 2+b 2=c 2. 5.【答案】D【解析】 由M 、N 两点关于直线x -y+1=0对称,可知直线x -y+1=0过圆心,12k ⎛⎫-- ⎪⎝⎭,∴k=4,∴圆的方程即为(x+2)2+(y+1)2=9,∴r=3.6.【答案】A【解析】 ∵圆心到直线的距离d ==,∴||4AB ==,∴142ABC S ∆=⨯= 7.【答案】B【解析】 由平面几何知识可知|OP|·|OQ|等于过O 点圆的切线长的平方.8.【答案】C【解析】 ∵四边形PAOB 的面积12||||2S PA OA =⨯⨯==∴当直线OP 垂直直线2x+y+10=0时,其面积S 最小.9.【答案】(x+1)2+y 2=2【解析】 根据题意可知圆心坐标是(―1,0)=,故所求的圆的方程是(x+1)2+y 2=2.10.【答案】2x ―y=0【解析】 设所求直线方程为y=kx ,即kx ―y=0.由于直线kx ―y=0被圆截得的弦长等于2,圆的半径是10=,即圆心位于直线kx ―y=0上,于是有k ―2=0,即k=2,因此所求直线方程为2x ―y=0.11.【答案】40x y +-=【解析】12.2m <<【解析】结合图形,求出直线与圆在第一象限相切时的m 值为2,求出直线过(0,1)点时的mm 的取值范围.13.【答案】y+4=0或4x ―3y=0或3x+4y+10=0【解析】 圆O 1的圆心坐标为O 1(―1,―3),半径r 1=1,圆O 2的圆心坐标O 2(3,―1),半径r 2=3,则|O 1O 2|>r 1+r 2,∴ 1 3 ==①② 解得04k b =⎧⎨=-⎩ 或 430k b ⎧=⎪⎨⎪=⎩ 或 3452k b ⎧=-⎪⎪⎨⎪=-⎪⎩, 当斜率不存在时,x=0也和两圆相切,∴所求切线的方程为y+4=0或4x ―3y=0或3x+4y+10=0.14.【答案】y 2=8x (x >0)和y=0(x ≠0,x ≠2)【解析】把圆的方程配方得(x ―2)2+y 2=4.设P (x ,y )为轨迹上任意一点.(1)当圆P 与定圆A 外切时,不妨设两圆切点为B ,且圆P 与y 轴相切于点N ,则|PA|=|PN|+|AB|||2x =+.当x >0时,y 2=8x当x <0时,轨迹不存在;综上可知,动圆圆心的轨迹方程为y 2=8x (x >0)和y=0(x ≠0,x ≠2).【总结升华】由于两圆相切可以是外切,也可以是内切,所以情况(2)的讨论是必不可少的,这也是解答本题易忽视的地方,要引起重视.15.【答案】P 点的轨迹是以(-20,0)为圆心,40为半径长的圆周,也就是在此圆周上听到的声音强度相等【解析】以OA 为x 轴,O 为坐标原点建立如图所示的直角坐标系.设在P (x ,y )处听到O 、A 两处的喇叭声音强度相等. 由物理学知22||1||4OP PA =,即22221(60)4x y x y +=-+,整理得(x+20)2+y 2=402. 故P 点的轨迹是以(-20,0)为圆心,40为半径长的圆周,也就是在此圆周上听到的声音强度相等.。
(完整版)职高数学第八章直线和圆的方程及答案.docx

第 8 章直线和圆的方程练习 8.1两点间的距离与线段中点的坐标1.根据下列条件,求线段P P 的长度:1 2( 2) P ( -3, 1)、 P ( 2, 4)(1) P ( 0, -2)、P ( 3,0)121 2 (3) P ( 4, -2)、P ( 1,2)( 4) P ( 5, -2)、 P ( -1, 6)1 2122.已知 A(2,3) 、 B ( x , 1),且 |AB |= 13 ,求 x 的值。
3.根据下列条件,求线段 P 1P 2 中点的坐标:(1) P 1( 2, -1)、P 2( 3,4) ( 2) P 1( 0, -3)、P 2( 5,0) ( 3) P 1( 3, 2.5)、 P 2(4, 1.5)( 4) P 1( 6, 1)、P 2(3, 3)4.根据下列条件,求线段P 1P 2 中点的坐标:(1) P ( 3, -1)、P ( 3,5)( 2) P ( -3, 0)、 P ( 5,0)1 21 2(3) P 1( 3, 3.5)、 P 2(4, 2.5) ( 4) P 1( 5, 1)、 P 2(5, 3)参考答案:1.(1) 13 ;(2) 34 ;(3)5; (4)102.-1 或 53.(1) ( 5 , 3) ;(2) ( 5 ,3) ;(3) (7, 2) ; (4) (9, 2)222 222 4. (1)(3, 2) ;(2) (1,0) ;(3) (3.5,3) ; (4)(5, 2)练习 8.2.1 直线的倾斜角与斜率1.选择题(1)没有斜率的直线一定是()A. 过原点的直线B.垂直于 y 轴的直线C.垂直于 x 轴的直线D. 垂直于坐标轴的直线(2) 若直线 l的斜率为 -1,则直线 l 的倾斜角为( )A.90 B.0 C. 45D. 1352 已知直线的倾斜角,写出直线的斜率:(1) 30 , k ____ ( 2) (3)120 ,k____( 4)参考答案:1. ( 1) C( 2) D45 , k____150 , k____2. ( 1)3 3;(2) 1 ;(3) 3 ; (4)33练习 8.2.2 直线的点斜式方程与斜截式方程写出下列直线的点斜式方程(1)经过点 A (2,5),斜率是 4;(2)经过点 B ( 2,3),倾斜角为45;(3)经过点 C( -1,1),与 x 轴平行;(4)经过点 D (1,1),与 x 轴垂直。
中职直线与圆的方程复习

直线与圆的方程1、求直线的方程(1)定义法:点向式、点法式、点斜式【1】若ABC D 的顶点)2,3(),2,1(),1,0(C B A --,则BC 边上的高所在的直线方程为(边上的高所在的直线方程为( )。
A.01=-+y x B.01=+-y x C.03=++y x D.01=--y x【2】(2013年)已知点)2,3(),6,1(N M -,则线段MN 的垂直平分线线方程是(的垂直平分线线方程是( )。
A.04=--y x B.03=+-y x C.05=-+y x D.0174=-+y x【3】过点(3,-2)且平行于向量()0,1=v 的直线方程是(的直线方程是( )。
A .3=x B .2-=y C .023=-y x D .032=-y x【4】(2010年)若直线l 过两点(-2,0),(0,1),则直线l 的一般式方程是_______________. 【5】过点(1,2)且倾斜角的正弦值为54的直线方程为__________________________________. (2)待定系数法:点斜式、斜截式【1】(2013年)过)2,1(P 且与直线013=-+y x 平行的直线方程是(平行的直线方程是( )。
A.053=-+y x B.073=-+y x C.053=+-y x D.053=--y x【2】过点B(2,3)且在两坐标轴上有相等截距的直线的方程是且在两坐标轴上有相等截距的直线的方程是 ( )A.x+y-5=0 B.x+y+5=0 C.x+y-5=0或x+y+5=0 D.x+y-5=0或3x-2y=0 【3】(2010年)若直线l 过两点(-2,0),(0,1),则直线l 的一般式方程是_______________. 【4】已知圆的方程为1)1()2(2222=-+-y x ,P 点坐标为(3,4),求圆过P 点的切线方程.点的切线方程.【5】直线L 经过点P(5,5),且和圆O: 2522=+y x 相交于A,B 两点。
中职数学基础模块下册第六章直线和圆的方程习题答案

第六章 直线和圆的方程6.1两点间的距离公式和线段的中点坐标公式习题答案 练习6.11.M (-2,4);N(1,1); P(2,-2); Q(-1,-2).2.(1)AB =线段AB 的中点坐标(11,122);(2)5CD =,线段CD 的中点坐标(15,12);(3)5PQ =,线段PQ 的中点坐标(0,12).3.(1)中点D 的坐标(1,1);(2)中线AD .4.AB b =-,线段AB 的中点坐标(3333,22a b a b++). 习题6.1 A 组1.(1)AB =(2)5AB =,BC =AC =;(3)线段AB 的中点坐标(1,-1);(4)AB =线段AB 的中点坐标(111,122-).2.点P (2+)或P (2-).3.2PQ a=,线段PQ 的中点坐标(0,b ).4.点P 2的坐标为(6,1).5.2,AB AC BC ==,根据直角三角形判定定理,可知三角形是直角三角形. B 组 1. m=4,n=1.2.点B 的坐标(-4,5).3.顶点C 的坐标(0,0,.4.顶点A (6,5),顶点B (-2,3),顶点C (-4,-1). C 组 略.6.2直线的方程习题答案 练习6.2.1 1.2.(1)斜率为-1,倾斜角为4;(2)斜率为3;(3)斜率为56π.3.实数a =4.实数m=-1. 练习6.2.21.(1)1,4π;(23π;(3)2,3. 2.点A (2,3)在直线122y x =+上,点B (4,2)不在直线122y x =+上.3.(1)34(1)y x -=-;(2)55(2)y x +=-;(3)y x -=.4.(1)24y x =-+;(2)3y =+;(3)112y x =+;(4)1y x =-.5.4y -=;4y =+. 练习6.2.31.132y x =--.2.(1)2,230x y -+=;(2)23-,2340x y ++=.3.(1)A=0,B ≠0,C ≠0; (2)B=0,A ≠0,C ≠0.4.(1)37130x y +-=;(2)30y +=.5.30x y -+=,X 轴上的截距为-3,Y 轴上的截距为3. 习题6.21.(1)3-;(2)1,4π. 2.(1)210x y -+=;(2)3y =-;(3)430x y -+=. 3.(1)23,43;(2)1,3;(3)5,-12. 4.(1)A ≠0,B ≠0,C=0;(2)A=0,B ≠0,C=0;(3)A ≠0,B=0,C=0. 5.420x y +-=或420x y ++=. B 组1.实数52m =-.2.实数m=3,n=-8.3.(1)330x y +-=;(2)770x y -+=.4.(1)AB 边斜率为14,AC 边所在直线的斜率为1,BC 边所在直线的斜率为12-,AB 边所在直线的方程为470x y -+=;AC 边所在直线的方程为10x y -+=;BC 边所在直线的方程为2100x y +-=. (2)BC 边中线所在直线的斜率为12,AB 边中线所在直线的斜率不存在,AC 边中线所在直线的斜率为0,BC 边中线所在直线的方程为230x y -+=;AB 边中线所在直线的方程为3x =;AC 边中线所在直线的方程为3y =. C 组 略.6.3两条直线的位置关系习题答案 练习6.3.11. (1)平行;(2)重合;(3)重合;(4)平行.2.(1)12-;(2)20x y -+=;(3)360x y --=.练习6.3.21.(1)相交,交点坐标(194,3-);(2)相交,交点坐标(4,-5);(3)不相交.2.(1)不垂直;(2)垂直;(3)不垂直;(4)垂直.3.20x y +-=.4.32120x y +-=. 练习6.3.31.(1;(2)0;(3)5.2.m=-3或m=7.3.习题6.3 A 组1.(1)相交;(2)平行,重合;(3)垂直.2.(1)平行;(2)垂直;(3)相交;(4)垂直.3.(1)相交,交点坐标(18,58);(2)不相交,平行;(3)相交,交点坐标(14,14); (4)相交,交点坐标(315-,435).4.10x y -+=.390y ++-=.6.(1)95;(2)0;(3)25.7.2. B 组 1.实数32a =.2.实数m=-2或m=12. 3.实数m=4,n=2.6.4 圆习题答案 练习6.4.11.(1)221x y +=;(2)22(1)9x y +-=;(3)22(3)4x y -+=;(4)22(2)(1)45x y -++=.2.(1)圆心坐标为(0,0)半径为4;(2)圆心坐标为(1,0)半径为2;(3)圆心坐标为(0,-3)半径为3;(4)圆心坐标为(2,1;(5)圆心坐标为(-1,3)半径为5. 3.22(1)(3)25x y ++-=. 练习6.4.21.(1)圆心坐标为(2,0)半径为2;(2)圆心坐标为(0,-2)半径为3;(3)圆心坐标为(3,-1)半径为4;(4)圆心坐标为(-1,32.2284160x y x y +-++=.3.是圆的方程,圆心坐标为(2,-1),. 习题6.41.(1)22(3)(1)16x y -++=,226260x y x y +-+-=;(2)(-1,3.2.(1)(-3,2;(2)(2,0),2.3.22(3)(9x y -+-=.4.226670x y x y +-+-=.5.是圆的方程,圆心坐标为(4,-1),半径为1. B 组1.2220x y x y +--=.2.0a =或8a =.3.K <34,圆心坐标为(8,2),半径为√68−2k . C 组 略.6.5直线与圆的位置关系习题答案 练习6.51.(1)2;(2)1.2.(1)1,不存在;(2)2,不存在,0;(3)1,0.3.(1)相切;(2)相离;(3)相交.4.y =2,x =3.5.8. 习题6.5 A 组 1.1,2,0.2.224640x y x y +-++=.3.(1)相切;(2)相交;(3)相交.4.当1b =时,直线与圆相切;当11b <当1b >或1b <-. 5.4x -3y -25=0,34250x y +-=. B 组1.22(3)(4)8x y -+-=.2.当6k =±时,直线与圆相切;当6k <-6k >+时,直线与圆相交;当66k -<<+时,直线与圆相离.切线方程为(620x y +-+=和(620x y --+=.4.k <1或k >13. C 组 略.6.6直线与圆的方程应用举例习题答案 练习6.61.(12,03-).2.x 2+(y -20.19)2=12.992.3.建立直角坐标系,A (-10,0),B (10,0)D (-5,0),E (5,0).设圆的方程为222()()x a y b r -+-=,得a =0,b =-10.5,r =14.5,将D 点横坐标-5代入方程得3.1y =,因为3 m<3.1 m ,因此船可以通过. 习题6.6 A 组 1.M (4,0). 2.3240x y ++=.3. 第二根支柱的长度约为4.49 m. B 组1.10x y --=.2.入射光线所在的直线方程为12510x y +-=,反射光线所在的直线方程为12510x y --=.3.(1)会有触礁可能;(2)可以避免触礁. C 组 略. 复习题6 A 组一、1.B. 2.D. 3.B. 4.C. 5.B. 6.B. 7.D. 8.B. 二、9.5. 10.-1. 11.(0,0). 12.0. 13.2.三、14(1)(-2,-1);(210y -+=. 15.(1)20x y +-=;(2)22(2)2x y -+=. 16.x 2+(y -1)2=1.17.(1)(1,2),2;(2)34y x =,0x =. 18.2.19.是圆的方程,圆心坐标为(2.5,2),圆的半径为1.5. B 组1.(1)20x y +-=;(2)1.2.(1)m=4;(2)x 2+(y -4)2=16.3.(1)点A 的坐标(7,1),点B 的坐标(-5,-5);(2)15.4.解:我们以港口中心为原点O ,东西方向为x 轴,建立平面直角坐标系,圆的方程为22230x y +=,轮船航线所在的直线方程为472800x y +-=;如果圆O 与直线有公共点,则轮船有触礁危险,需要改变航向;如果圆O 与直线无公共点,则轮船没有触礁危险,无需改变航向.由于圆心O (0,0)到直线的距离为30d =>,所以直线与圆O 没有公共点,轮船没有触礁危险,不用改变航向.。
中职数学基础模块知识点、典型题目系列---直线与圆的方程(适合打印,经典

第八章 直线与圆的方程第1节 两点间的距离与线段中点的坐标一、两点间的距离及线段中点的坐标: 设()111,y x P ,()222,y x P ,则()()21221221y y x x P P -+-=. 中点()000,y x P 的坐标为121200,22++==x x y y x y【习题】1.已知()10,28A 和()22,12B ,求线段AB 的长度。
2.已知三角形的顶点分别为)6,2(A ,)3,4(-B ,()00,C ,求ABC ∆三条边长。
3.已知()4,1A ,()1,5B ,()1,1C 说明ABC ∆为∆Rt 。
【习题】1.已知)5,1(),3,1(---N M ,求线段MN 的长度,并求线段MN 的中点坐标。
2.已知ABC ∆的三个顶点为(1,0)A 、(2,1)B -、(0,3)C ,试求BC 边上的中线AD 的长度.第2 节 直线的倾斜角与斜率一、直线的倾斜角与斜率倾斜角∂:直线l 向上的方向与x 轴正方向所夹的最小正角。
范围:001800<≤α斜率k :1212tan x x y y k --=∂= 注:①当轴x l //或重合时,0=k ②当轴x l ⊥时,k 不存在③k 与两点的位置无关【习题】1.已知直线的倾斜角,求斜率。
(1)6π=∂(2) 135=∂(3) 90=∂2.已知直线的斜率,求倾斜角。
(1)3=k (2)33-=k (3)1=k 3.求经过下列两点的直线的斜率与倾斜角。
(1)()0,2-A 和()3,1B (2)()4,1M 和()2,3N *4.证明三点()1,0-A ,()1,3B ,()3,3--C 在同一条直线上。
作业布置:1.已知点()2,41P ,()y P ,52-且过1P ,2P 的直线的斜率是31,求y 的值。
2.已知三角形的三个顶点()1,0A ,()3,8B ,()1,1-C 分别求三角形三边所在的直线的斜率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《第八章 直线和圆的方程》复习题
一、选择题(每小题5分,共30分):
1、直线06=+-y x 与直线0=+y x 的交点坐标为( )
A 、 (-3,3)
B 、 (3,-3)
C 、(4,2)
D 、(3,3)
2、已知 A (-5,2)B (0,-3)则直线AB 斜率为( )
A 、 -1
B 、1
C 、 3
1 D 、0 3、经过点(1,2)且倾斜角为1350的直线方程为( )
A 、1+=x y
B 、x y 2=
C 、3+-=x y
D 、x y 2-=
4、直线013=--y x 的倾斜角为( )
A 、300
B 、 1500
C 、 60 0
D 、1200
5、已知直线ax-y+3=0与2x-3y=0平行,则a=( )
A 、 2
B 、 3
C 、 23
D 、 3
2 6、直线062=+-y x 与两坐标轴围成的三角形面积为( )
A 、12
B 、18
C 、 9
D 、6
二、填空(每小题5分,共20分):
7、经过点(1,3)、(5,11)的直线方程为
8、过点A (1,-1)且与x 轴平行的直线方程为
9、若直线l 垂直于直线012=+-y x 且它与直线042=+-y x 交于y 轴上同一点,则直线l 的方程为
10、点P (m ,-m+1)到直线0443=+-y x 的距离为7,则m 的值为_______________
三、解答题:(共40分)
11、已知直线l 经过点(-2,2)且垂直于直线x-y-2=0,求直线l 的方程。
12、求经过两条直线01032=+-y x 和0243=-+y x 的交点,且平行于直线0423=+-y x 的直线方程?
13、求两条平行直线0134=--y x 和0168=+-y x 的距离?
14、三角形的三个顶点是A(2,0),B(3,5),C(0,3)
求BC 边上的高所在的直线的方程;。
