三线八角 ppt课件
合集下载
5.2平行线(三线八角、判定、性质等共6课时的课件)

∵ ∠2=∠B (已知)
∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行)
例题
例2、如图,直线EF交直线AB、CD于点M、N, ∠EMB= ∠END,MG平分∠EMB ,NH平分 ∠END,试问:图中哪两条直线互相平行? E 为什么? G
A N F M H C D
2、下列推理正确的是( C )
A、因为a // d,b // c,所以c // d; B、因为a // c,b // d,所以c // d; C、因为a // b,a // c,所以b // c; D、因为a // b,c // d,所以a // c。
3、完成下列推理,并在括号内注明理由。 (1)如图1所示,因为AB // DE,BC // DE(已知)。所以 在同一直线上 A,B,C三点___________( 经过直线外一点,有且只有一 ) 条直线与这条直线平行 (2)如图2所示,因为AB // CD,CD // EF(已知),所以 AB EF ________ // _________( 如果两条直线都和第三条直线平行, ) 那么这两条直线也互相平行 A B C A B
B
考考你
1、如图,AF、CE、BD交于点B,且BE平分 ∠DBF,且∠1= ∠C,问BD与AC平行吗? 为什么? A
D E 1 B F C
考考你 2、如图,BC、DE分别平分ABD和BDF, 且1=2,请找出平行线,并说明理由。
A 1 B E
C
D 2 F
考考你 3、如图,AB、CD被EF所截,MG平分 ∠BMN,NH平分∠DNM,已知∠GMN+ ∠HNM=90°,试问:AB∥CD吗?请说明 理由。 E M A B H C F G N D
5.1.3 三线八角

2、
同位 内错
同旁内
根据图形按要求填空:
A
(1)∠1与∠2是直线
D
AB 和 DE 被直线
BC 所截而得的
同位角 .
1 B3
2 5
C
4
E
F
(2) ∠1与∠3是直
线 AB 和 DE 被直线
A D
BC所截而得的内错角. 1
B3
2 5
C
(3)∠3与∠4是直线
_B__C_和__E___F_____ 被直线
第五章 相交线与平行线 5.1.3 同位角、内错角、同旁内角
1.两条直线相交有几个角? (4个)
2.两条直线与第三条直线相交呢? (8个)
4.你能找出这8个角的关系吗? l3
21
∠1与∠3,∠2与∠4,
34
l1
∠5与∠7,∠6与∠8
65 7
分别是对顶角.
8
l2
5.这些角还有其它的关系吗
中国最早的风筝据说是由古代哲学家墨翟制作的,风 筝的骨架构成了多种关系的角.
(3)哪两条直线被哪一条所截,∠2与∠5是同位角?
C
4
E
F
找出图中与∠1构成同旁内角的角?
2
图中与∠1是同旁内角的角:
2
当堂反馈:
DA
1 4
5
E
23 F
B
C
(1)如果把图看成是直线AB,EF被直线CD所截,
那么∠1与∠2是一对什么角? (同位角)
∠3与∠4呢? (内错角)
∠ 2与∠4呢? (同旁内角)
当堂反馈:
DA
1 4
5
E
23 F
B
C
(2)如果把图看成是直线CD,EF被直线AB所截, 那么∠1与∠5是一对什么角? ∠4与∠5呢?
同位 内错
同旁内
根据图形按要求填空:
A
(1)∠1与∠2是直线
D
AB 和 DE 被直线
BC 所截而得的
同位角 .
1 B3
2 5
C
4
E
F
(2) ∠1与∠3是直
线 AB 和 DE 被直线
A D
BC所截而得的内错角. 1
B3
2 5
C
(3)∠3与∠4是直线
_B__C_和__E___F_____ 被直线
第五章 相交线与平行线 5.1.3 同位角、内错角、同旁内角
1.两条直线相交有几个角? (4个)
2.两条直线与第三条直线相交呢? (8个)
4.你能找出这8个角的关系吗? l3
21
∠1与∠3,∠2与∠4,
34
l1
∠5与∠7,∠6与∠8
65 7
分别是对顶角.
8
l2
5.这些角还有其它的关系吗
中国最早的风筝据说是由古代哲学家墨翟制作的,风 筝的骨架构成了多种关系的角.
(3)哪两条直线被哪一条所截,∠2与∠5是同位角?
C
4
E
F
找出图中与∠1构成同旁内角的角?
2
图中与∠1是同旁内角的角:
2
当堂反馈:
DA
1 4
5
E
23 F
B
C
(1)如果把图看成是直线AB,EF被直线CD所截,
那么∠1与∠2是一对什么角? (同位角)
∠3与∠4呢? (内错角)
∠ 2与∠4呢? (同旁内角)
当堂反馈:
DA
1 4
5
E
23 F
B
C
(2)如果把图看成是直线CD,EF被直线AB所截, 那么∠1与∠5是一对什么角? ∠4与∠5呢?
三线八角课件

c
1
2
4
a b
3 5 6
∠ 1与∠ 5在直线c的同一侧, 直线a、b的同一方。 ∠ 3与∠ 5在直线c的两侧, 直线a、b之间。
8
7
在图中∠ 3与∠ 5的位置和同位角∠ 1和∠ 5相比, 有什么一样?有什么不一样?
侧 ,直 线a、 ∠ 3与∠ 5处于直线c的 两 b 之 间 。这样的一对角就是内错角。 图中,内错角还有 ∠ 4与∠ 6 。
华东师范大学出版社七年级数学上册
第五章第三小节
同位角、内错角、同旁内角
主讲人:张英
C A2Βιβλιοθήκη 3 O14B
D
对顶角∠2与∠4 ,∠1与 ∠3 。 从位置关系看 :
补角∠1 与∠2,∠2与∠3, ∠3与∠4, ∠ 4与 ∠1.
从数量关系看: ∠1=∠3,∠2=∠4。 ∠1+∠2=180
∠2+∠3=180°∠3+∠4=180°∠4+∠1=180°
将左右手的大拇指和食指各组成一个角, 两食指相对成一条直线,两个大拇指反向的时 候,组成内错角;
两食指相对成一条直线,两个大拇指同向 的时候,组成同旁内角;
两手的拇指和食指如何组合得到同位角?
在一个平面内,一条直线c与两条直线a、b分别交 与点P、Q,这就可以说成“直线c分别截直线a、 a b与P、Q”. c c a
P Q P
a b b c
P Q (3)
R
b
Q
(2)
(1)
在(1)中,直线 a 和直线 b 被直线 c 所截。 在(2)中,直线 b 和直线 c 被直线 a 所截。 在(3)中,可以有几种说法?分别是什么?
a 2 1 c 3 4 b 5 8 6 7
七年级数学下册_三线八角_课件
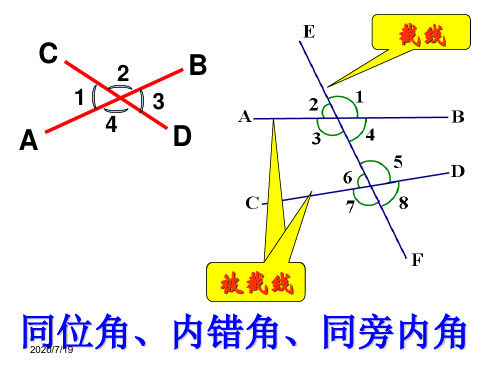
同旁内角
∠3和∠6 ∠4和∠5
分别位于被截线的( 内 )侧,位 于截线的( 同 )侧。
2020/7/19
指出下列各图中所有的同位角、内错角、同旁内角。
a
b
b
c
6
5
c
2187
4 3
2 34
a
2020/7/19
直线DE、BC被AB所截。 1、∠1与∠2、∠1与∠3、∠1与∠4各是什么角? 2、如果∠1=∠4,
A
E1 3D
B2
4
FC
(2)若ED,BC被AF所截,
则∠3与_∠_4___是内错角。
2020/7/19
看图填空
A
E1 3D
B2
4
FC
(3)∠1与∠3是AB和AF被 __D_E__所截构成的__内__错___角。
2020/7/19
看图填空
A
E1 3D
B2
4
FC
(4)∠2与∠4是_A__B__和__A_F__被 BC所截构成的__同__位__角。
1
1
2
()
2020/7/19
2 ()
A
D
31
4
2
E
B
C
(1)∠1和∠2是直线(AD)和(CB )被(AC)所截,构成(内错)角.
(2)∠3和∠4是直线( AB )和(DC)被( AC )所截,构( 内错角)。
(3)∠BAD与∠D是直线( AB ) 和(DC) 被(AD) 所截,构成
( 同旁内角 )。
(4)∠2与∠4是_同__位___角。
2020/7/19
∠1与哪个角是内错角,与哪个角是同旁 内角?它们分别是哪两条直线被哪一条直 线所截形成的?∠2呢?
【数学课件】三线八角

好好学习,天天向上。
19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱
心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
A 1 B 3 D 4
5 E
2
C
5、(1)DE和BC被AB截得∠ADE
和∠ B是什么角? (2)DE和BC被AC截得∠DEC 和∠ C是什么角?
D E B
A
C
小结
1、这节课研究的是两条直线被第三条直线所截形成的不同顶点 处的两个角之间的位置关系,即同位角、内错角、同旁内角。
2、同位角、内错角、同旁内角的特点:
与被截直线的关系
同位角 内错角
与截线的关系 截线的同旁 截线的两旁 截线的同旁
被截直线的同一方向 被截直线之间
同旁内角 被截直线之间
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基
新授
A
E
2
1
3 4 6
B
3、同旁内角的定义
如: ∠ 1和∠ 5
5
C 8 F 7
D
像 4与 6 分别在被截直线AB、CD之 间(内),截线EF的同侧(同旁)”,这样 的两个角叫做同旁内角。
巩固 1、指出下列各图中所有的同位角、内 错角、同旁内角。
a 5 2 3 1 8 4 b b c
6
7 c
1
2
新华师大版七年级上册初中数学 5-1-3 三线八角 教学课件

新课讲解
例2 如图,试找出图中与∠2是同位角、内错角的角.
导引:在AF和AG被DE所截的这个
基本图形中,可以看出∠6和 ∠2处于“同一个位置”,因 此,∠2的同位角为∠6,∠2和∠8是内错角. 解: ∠2的同位角为∠6,∠2的内错角为∠8.
新课讲解
归纳
寻找一个角的同位角、内错角,首先应该把这个角放在 一个“三线八角”的基本图形中,其次不管是同位角,还是 内错角,它们具有一个共同特征,这两个角有一对边在同一 直线上,这条直线就是定义中的“第三条直线”,而这两个 角剩下的两边所在的直线就是两条被截的直线 ;最后看这两 个角的位置特征是否满足同位角、内错角的位置特征:三边 成“F ” 、“Z ”形.
新课讲解
例1 如图,下列四个图形中,∠1和∠2不是同位角 的是( B )
新课讲解
导引:根据同位角的概念,找出“三线”之后再看是否为 “F”形即可判定.选项B中的∠1与∠2的边有四条,
分别为PA,PC,QB,QD,不满足“三线”的条
件,故选项B中的∠1与∠2不是同位角;其他A,C, D三项中的∠1,∠2均满足同位角的条件,故选B.
新课讲解
例4 如图,∠1 与∠2 ,∠ 3 与∠4分别是内错角,它 们分别是由哪两条直线被哪一条直线所截得到的?
错解:∠1 与∠2 是直线AD 与 BC 被直线 AC 所截得到 的,∠ 3 与∠4 是直线AB 与 DC 被直线BD所截
得到的.
新课讲解
错解分析:错解中没有分清∠1与∠2,∠3与∠4分别是 由哪两条直线被第三条直线所截得到的,而 导致错误. 应根据相关的概念来确定.
新课导入
新课导入
如图,两条直线a,b相交形成四个角∠1,∠2, ∠3,∠4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同位角
“F”型
三线八角
内错角
“Z”型
同旁内角
“U”型
2. 在图形中判断三线八角的方法:描图法: ①把两个角在图中描画出来;
②找到两个角的公共直线;③观察所描的角,判断所属“字母”类型,同
位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变
式(旋转、对称)也是符合的.
ppt课件
20
首页
课后作业
E
4
1O
A
2
B
3
5
6 7
8
C F
简称“三线八角” D
ppt课件
5
首页
合作探究
如图,形成的三线八角中上面四个角与下面四个角是不共
顶点的,这节课我们要学习其中没有公共顶点的两个角之
间的位置关系。
l3 截线
21 34
l1
65
l2
78
被截直线
ppt课件
6
首页
一 同位角
活动1:观察∠1与∠5的位置关系 ①在直线EF的同旁(右边)
①在直线EF的两侧 ②在直线AB、CD的之间
内错角
E
1
B
2
A
34
3
65
C
78 D
F
图中的内错角还有哪些?
∠4和∠6
ppt课件
5
9
首页
变式图形:图中的∠1与∠2都是内错角
1
1
2
2
12
2 1
图形特征:在形如“Z”的图形中有内错角。
ppt课件
10
首页
三 同旁内角
问题3:观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB、CD的同一侧(上方)
E
21
B
A
34
1
65
C
78 D
同位角 5
F
图中的同位角还有哪些? ∠2和∠6;∠3和∠7;∠4和∠8
ppt课件
7
首页
变式图形:图中的∠1与∠2都是同位角。
2
1
12
1
12
2
图形特征:在形如字母“F”的图形中有同位角。
ppt课件
8
首页
二 内错角
问题2:观察∠3与∠5的位置关系
ppt课件
21
首页
ppt课件
2
首页
情境引入
E 两条直线CD和EF相交,能形成些具有 什么关系的角?
具 有 邻
C
4 33 11 2
D
补
角
F
关
系
的
角
ppt课件
3
首页
E
两条直线AB和EF相交,能形成些具 有什么关系的角?
具 有 对
A
43 12
B
顶
角 关
F
系
的
角
ppt课件
4
首页
若再添加一条直线,即两条直线AB、EF被第三条直线 CD所截,构成了几个角?
A.同位角
B.同旁内角
C.内错角
D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是
(C ) (D )
ppt课件
17
首页
3.看图填空: (1)若ED,BF被AB所截,则∠1与_∠__2__是同位角。
(2)若ED,BC被AF所截,则∠3与_∠__4__是内错角。
A
A
E1 3D
E1 3D
B2
4
D
2 3
B
1 4
∠4与∠6.
A
58
67 E C
变式:∠A与∠8是哪两条直线被第哪条直线所截的角?它们是 什么关系的角?∠A与∠5呢?∠A与∠6呢?
ppt课件
14
首页
温馨提示:解题之前要明确哪两条直线被哪条直
线所截。
例2(教材P13例2) 如图:直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4, 那么∠1=∠2.因为∠3和∠4互补,即 ∠4+∠3=180°,又因为∠1=∠4,所以
A
D F4
E
23
∠4+∠3=180°,即∠1与∠3互补。
1
B
C
ppt课件
16
首页
当堂检测
1.如图,∠DAB和∠ABC是
21 34
l1 同位角
截线 被截线 同旁 同侧
结构 特征
F
65 78
内错角 两旁
l2 同旁内角 同旁
之间 之间
Z U
ppt课件
13
首页
例题学习
例1:如图,直线DE截AB ,AC,构成8个角,指出所有的同
位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,
所以8个角中,同位角:∠2与∠5,∠4与 ∠7,∠1与∠8, ∠6和∠3;内错角:∠4与 ∠5,∠1与∠6,;同旁内角:∠1与∠5,
F
C B2
ppt课件
4
FC
18
首页
(3)∠1与∠3是AB和AF被_D__E__所截构成的_内__错____角。
(4)∠2与∠4是__A_B__和_A__F__被BC所截构成的__同__位__角。
A
A
E1 3D
E1 3D
B2
4
F
B2 C
4
FC
ppt课件
19
首页
课堂小结
1.同位角、内错角、同旁内角的结构特征:
②在直线AB、CD的之间
E
2
1
B
A
34
65
同旁内角
4 5
C
78 D
图形特征:在形如“FU”的图形中有同旁内角。
图中还有哪些同旁内角? ∠3和∠6
ppt课件
11
首页
合作探究
变式图形:图中的∠1与∠2都是同旁内角。
1
1
2
2
12
12
图形特征:在形如“U”的图形中有同旁内角。
ppt课件
12
首页
要点归纳
l3
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?
为什么?
A
答:(1)∠1与∠2是内错角,∠1和
D F4 23
E
ቤተ መጻሕፍቲ ባይዱ
∠3同旁内角,∠1和∠4是同旁内角。
1
B
C
ppt课件
15
首页
例2:(教材P13例2) 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
第五章 相交线与平行线 5.1 相交线
5.1.3 同位角、内错角、同旁内角
情境引入
合作探究
当堂检测
ppt课件
课堂小结
1
学习目标
1.理解同位角、内错角、同旁内角的概念。
情境引入
2.结合图形识别同位角、内错角、同旁内角。(重点)
3.从复杂图形分解为基本图形的过程中,体会化繁为简,化难为易的化归
思想。(难点)
