c++第2讲
第2讲氧化还原反应的基本概念和规律_

第2讲 氧化还原反应【考点透视】1. 理解氧化还原反应的本质。
2. 了解氧化还原反应在生产、生活中的应用。
【知识网络】一、 氧化还原反应的判断及与四种基本反应类型的关系【例1】下列类型的反应,一定发生电子转移的是A .化合反应B .分解反应C .置换反应D .复分解反应二、 氧化还原反应的相关概念、电子转移表示法 1.相关概念在Fe 2O 3+3CO=====高温2Fe +3CO 2的反应中________是氧化剂,________是还原剂;________元素被氧化,________元素被还原;Fe 2O 3具有 ,CO 具有 ;________是氧化产物,________是还原产物。
【例2】被称为万能还原剂的NaBH 4溶于水并和水反应:NaBH 4+2H 2O===NaBO 2+4H 2↑,下列说法中准确的是(NaBH 4中H 为-1价)A .NaBH 4既是氧化剂又是还原剂B .NaBH 4是氧化剂,H 2O 是还原剂C .硼元素被氧化,氢元素被还原D .被氧化的元素与被还原的元素质量之比为1∶1【例3】标出下列反应中电子转移的方向和数目(1)2KClO 3=====MnO 2△2KCl +3O 2↑ (2)Cl 2+2NaOH===NaCl +NaClO +H 2O(3) 2FeI 2+3Cl 2 ===2FeCl 3+2I 2 (4)4HCl(浓)+MnO 2=====△MnCl 2+Cl 2↑+2H 2O氧化 还 原 反 应实质 有电子转移,且转移电子数相等 特征化合价有升有降,且升降总值相等基本概念 反应规律 ①优先反应原理;②强弱原理;③价态原理(邻位转化规律、歧化规律、归中规律)原则:①电子守恒;②电荷守恒(离子方程式);③原子守恒 方法:化合价升降法依据:电子守恒①部分氧化还原计算;②推断产物化合价; ③求氧化剂、还原剂或氧化产物、还原产物质量比氧化剂 + 还原剂 === 还原产物 + 氧化产物(强氧化性) (强还原性) (弱还原性) (弱氧化性)化合价降低,+ne -,被还原化合价升高,-ne -,被氧化单线桥法; 双线桥法。
第二讲 绝对值

第2讲 绝对值的性质与化简【例1】(1)若xy xy =,则必有……………………………………………………( ) A .x,y 异号 C.x,y 中至少有一个是0B .x,y 同号 D . x ,y 同号或x,y 中至少有一个是0.(2)已知a 、b 、c 在数轴上位置如图,化简:代数式|a |+|a +b |+|c -a |-|b -c |.(3)若ab≠0,则ab a b+的取值不可能是………… ..……………………..( ) A.0 B.1 C.2 D.-2注1:化简a a=__________ 【例2】如果a 、b 、c 是非零有理数,且a+b+c =0,那么求||a a +||b b +||c c +||abc abc 的所有可能的值.【例3】设a<0,且a x a ≤,试化简12x x +--.【例4】已知a 、b 、c 均不为0,且a +b +c =0,设x =|||a b c ++||b c a ++||c a b+| ,试求代数式x 19-99x +2018的值.【例5】化简: (1)12a a -+-; (2)123x x x ++-+-; (3)13x --.注2:零点分段法基本步骤:_______________________________.【例6】已知:z x <<0,0>xy ,且x z y >>, 化简:y x z y z x --+++【例7】点A 、B 在数轴上分别表示数a 、b ,则A 、B 两点之间的距离表示为|a -b |.回答下列问题:(1)数轴上表示1和-3的两点之间的距离是_____________;(2)数轴上表示x 和-1的两点之间的距离是_____________;(3)当代数式|x -1|+|x -3|取最小值时,求相应x 的取值范围?_____________________(4)试求出123x x x -+-+-的最小值?(5)试求出12...99100x x x x -+-++-+-的最小值?结论:____________________________________________________________.(6)满足341>+++x x 的x 的取值范围为 .(7)已知36)13)(12)(21(=++-++--++z z y y x x ,求z y x 32++的最大值和最小值.【例8】2020020,20y x b x x b b b x =-+-+--<<≤≤已知,其中求y 的最小值.【例9】若2x+|10-5x|+|1-3x|+4的值在某个范围内,恒为常数,求x的取值范围及此常数的值.【例10】若a,b为实数,则下列各式对吗?若不对,应附加什么条件?(1)|a-b|=|b-a|;(2)若|a|<|b|,则a<b;(3)|a+b|=|a|+|b|;(4)|a-b|=|a|-|b|;(5)|ab|=|a||b|注3:绝对值满足三角不等式:_______________________________.【例11】已知a 、b 、c 、d 是有理数,│a -b │≤9,│c -d │≤16,且│a -b -c +d │=25,那么请求出代数式:│b -a │-│d -c │的值.【例12】已知,,,,,a b c d e f 为实数,满足0ace ≠,已知||||||ax b cx d ex f +++=+对于任意x 都成立,求式子ad -bc 的值一.选择题1.a<0时,化简a a等于………………………………………………………………..( )A 、1B 、—1C 、0D 、1±2.已知数轴上的三点A 、B 、C 分别表示有理数a ,1,-1,那么│a+1│表示…………( ).A.A 、B 两点的距离B.A 、C 两点的距离C.A 、B 两点到原点的距离之和D.A 、C 两点到原点的距离之和3.已知z x <<0,0>xy ,且x z y >>那么y x z y z x --+++的值….( )A .是正数B .是负数C .是零D .不能确定符号4.不相等的有理数a ,b ,c 在数轴上的对应点分别为A ,B ,C ,如果|a-b |+|b-c |=|a-c |,那么B 点应为…………………………( ).(1)在A ,C 点的右边; (2)在A ,C 点的左边;(3)在A ,C 点之间; (4)以上三种情况都有可能.5.已知a 是任意有理数,则│-a │-a 的值是………………………………………( ).A.必大于零B.必小于零C.必不大于零D.必不小于零6.使代数式|3|||4x x x-的值为正整数的x 值是…………………………………………( ). A.正数 B.负数 C.零 D.不存在的二.填空题7.计算:214131412131---+-=______. 8.已知│a│=1,│b│=2,│c│=3,且a>b>c,那么a+b-c=_______9.若m,n,p 满足:1m n p m n p++=,则3____2mnp mnp = 10.若有理数x 、y 满足2002(x -1)2+│x -12y +1│=0,则x 2+y 2=________.11.非零整数m,n 满足50m n +-=,所有这样的整数组(m,n )共____组12.若a,b 为有理数,那么,下列判断中:(1)若│a │=b ,则一定有a=b ;(2)若│a │>│b │,则一定有a>b ;(3)若│a │>b ,•则一定有│a │>│b │;(4)若│a │=b ,则一定有a 2=(-b )2.正确的是________(填序号)13.若m m =-,化简12m m ---的结果是_______14.已知有理数a 、b 、c 在数轴上的对应位置如图所示:则│c -1│+│a -c │+│a -b │化简后的结果是_________.15.能够使不等式0)1)((<+-x x x 成立的x 的取值范围是 .c a16.设a+b+c=0,abc>0,则求||b c a ++||c a b ++||a b c +的值.17.(1)若a +b <0,化简|a +b -1|-|3-a -b |;(2)│x -1│-│x -3│;(3)若x<0,化简23x xx x ---.18.当b 为何值时,5-12-b 有最大值,最大值是多少?19.如果0<p<15,请求出代数式1515x p x x p -+-+--在p≤x≤15•时的最小值.20.已知a 为有理数,那么代数式│a -1│+│a -2│+│a -3│+│a -4│的取值有没有最小值?如果有,试求出这个最小值;如果没有,请说明理由.21.若a ,b ,c 为整数,且|a -b |19+|c -a |99=1,试计算|c -a |+|a -b |+|b -c |的值.。
C类第二讲

第二部分 中华人民共和国刑法修正案(六) ——2006年6月29日
2013-8-11
13
第一百三十四条:工厂、矿山、林场、建筑施 工企业或者其他企业、事业单位的职工,在生 产、作业中违反有关安全管理的规定,因而发 生重大伤亡事故或者造成其他严重后果的,处 3年以下有期徒刑或者拘役;情节特别恶劣的, 处3年以上7年以下有期徒刑。强令他人违章冒 险作业,因而发生重大伤亡事故或者造成其他 严重后果的,处5年以下有期徒刑或者拘役; 情节特别恶劣的,处5年以上有期徒刑。
2013-8-11
26
关于严格实施建筑施工企业安全生产许可制度的 通知
建质电[2005]46号
一、各级建设行政主管部门在审核发放建设工程施工 许可证时,要严格依法对已经确定的建筑施工企业是 否具有安全生产许可证进行审查。自2005年7月14日 起,对没有取得安全生产许可证的,按照《安全生产 许可证条例》第二条的要求,不得颁发施工许可证; 擅自颁发施工许可证的,发证机关的工作人员要依法 承担相应的责任。造成重大安全事故,构成犯罪的, 依法追究刑事责任。
第一节 安全生产管理形势
2004年1月13日开始对“五大高危企业”实施安全生产 许可制度。 未取得安全生产许可证,不得从事生产活动。 未取得安全生产许可证从事生产活动的,将受到处罚。 取得安全生产许可证,应当具备安全生产条件。 不具备安全生产条件的,不得颁发安全生产许可证。 取得安全生产许可证后,应当继续保持和完善安全生产 条件。 发生生产安全事故的,暂扣安全生产许可证,并对其安 全生产条件进行重新审核。 安全生产条件不再具备,将暂扣安全生产许可证。 安全生产条件严重不具备的,将吊销安全生产许可证。
三大规程、五项规定、安全生产方针 《建筑法》、《安全生产法》确立了“安 全第一,预防为主”的安全生产方针 党的十六届五中全会提出了坚持“安全第 一,预防为主,综合治理”的安全生产方 针。 “五大高危企业” ,占总死亡人数的80% 以上 2004年1月13日,实施安全生产许可制度。
第2讲 空间向量基本定理、坐标运算和应用一(学生版)

第2讲 空间向量基本定理、坐标运算及应用一1.空间向量基本定理如果空间中的三个向量a ,b ,c 不共面,那么对空间中的任意一个向量p ,存在唯一的有序实数组(x ,y ,z ),使得p =x a +y b +z c .特别地,当a ,b ,c 不共面时,可知x a +y b +z c =0时,x =y =z =0. 2.空间中向量的坐标一般地,如果空间向量的基底{e 1,e 2,e 3}中,e 1,e 2,e 3都是单位向量,而且这三个向量两两垂直,就称这组基底为单位正交基底,在单位正交基底下向量的分解称为向量的单位正交分解,而且,如果p =x e 1+y e 2+z e 3,则称有序实数组(x ,y ,z )为向量p 的坐标,记作p =(x ,y ,z ).其中x ,y ,z 都称为p 的坐标分量. 思考1:若a =x e 1+y e 2+z e 3,则a 的坐标一定是(x ,y ,z )吗?【名师提醒】 不一定,当e 1,e 2,e 3是单位正交基底时,坐标是(x ,y ,z ),否则不是. 3.空间向量的运算与坐标的关系假设空间中两个向量a ,b 满足a =(x 1,y 1,z 1),b =(x 2,y 2,z 2),则有以下结论: (1)a +b =(x 1+x 2,y 1+y 2,z 1+z 2);(2)若u ,v 是两个实数,u a +v b =(ux 1+vx 2,uy 1+vy 2,uz 1+vz 2); (3)a·b =x 1x 2+y 1y 2+z 1z 2;(4)|a |=a ·a(5)当a ≠0且b ≠0时,cos 〈a ,b 〉=a·b|a|·|b|=x 1x 2+y 1y 2+z 1z 2x 21+y 21+z 21x 22+y 22+z 22.4.空间向量的坐标与空间向量的平行、垂直(1)当a ≠0时,a ∥b ⇔b =λa ⇔(x 2,y 2,z 2)=λ(x 1,y 1,z 1)⇔⎩⎪⎨⎪⎧x 2=λx 1y 2=λy 1z 2=λz 1,当a 的每一个坐标分量都不为零时,有a ∥b ⇔x 2x 1=y 2y 1=z 2z 1.(2)a ⊥b ⇔a·b =0⇔x 1x 2+y 1y 2+z 1z 2=0.5.直线l 的方向向量为a =(a 1,b 1,c 1).平面α,β的法向量u =(a 3,b 3,c 3),v =(a 4,b 4,c 4) (1)线面平行:l ∥α⇔a ⊥u ⇔a ·u =0⇔a 1a 3+b 1b 3+c 1c 3=0 (2)线面垂直:l ⊥α⇔a ∥u ⇔a =k u ⇔a 1=ka 3,b 1=kb 3,c 1=kc 3 (3)面面平行:α∥β⇔u ∥v ⇔u =k v ⇔a 3=ka 4,b 3=kb 4,c 3=kc 4 (4)面面垂直:α⊥β⇔u ⊥v ⇔u ·v =0⇔a 3a 4+b 3b 4+c 3c 4=0【玩转典例】考点一 基底的判断【例1】(2020·全国高二课时练习)在正方体1111ABCD A B C D -中,可以作为空间向量的一组基底的是( ) A .AB AC AD ,, B .11AB AA AB ,, C .11111 D A DC D D ,,D .111AC AC CC ,,【玩转跟踪】1.(2020·全国高二课时练习)下列说法正确的是( ) A .任何三个不共线的向量可构成空间向量的一个基底 B .空间的基底有且仅有一个C .两两垂直的三个非零向量可构成空间的一个基底D .基底{}a b c ,,中基向量与基底{}e f g ,,基向量对应相等2.(2020·全国高二课时练习)设向量,,a b c 不共面,则下列可作为空间的一个基底的是( ) A .{,,}a b b a a +- B .{,,}a b b a b +- C .{,,}a b b a c +- D .{,,}a b c a b c +++考点二 基本定理的运用【例2】(2020·绵竹市南轩中学高二月考)如图,在平行六面体1111ABCD A B C D -中,以顶点A 为端点的三条棱长都是1,且它们彼此的夹角都是60︒,M 为11A C 与11B D 的交点.若AB a =,AD b =,1AA c =,(1)用,,a b c 表示BM ; (2)求对角线1AC 的长; (3)求1cos ,AB AC 【玩转跟踪】1.(2020·济南市历城第二中学高二月考)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为1的正方形,侧棱PA 的长为2,且PA 与AB 、AD 的夹角都等于60,M 是PC 的中点, 设,,AB a AD b AP c ===. (1)试用,,a b c 表示出向量BM ; (2)求BM 的长.2.(2020·陕西新城。
C语言第二讲(顺序结构)3_22

printf("%2d\n",254); printf("%f\n",1.25);
第 二 章
2 输出实型数: “%m.nf” ”%m.ne” m指定总的输出宽度,n指定小数部分的宽度。
#include <stdio.h> main() { printf("%f\n",1.25676); printf("%5.2f\n",1.25676); printf("%8.4f\n",1.25); printf("%e\n",125.676); }
顺 序 结 构
第 二 章
3
“%o” 八进制形式输出整数 “%x” 十六进制形式输出整数 “%u” 输出无符号数据整数 “%c” 输出字符
顺 序 结 构
main() { printf("%o\n",255); printf("%x\n",255); printf("%u\n",-1); printf("%c\n", 65); }
第 二 章
4 同时输出几个数值,一个变量(或数值)对应一个%
格式符,其他符号原样输出。
顺 序 结 构
#include <stdio.h> main() { int a=12,b=65; float c; c=1.892; printf(“%d %f %c”,a,c,b); printf(“\n”); printf (“%d*_*%f->%c”,a,c,b); }
顺 序 结构
}
第 二 章
顺 序 结 构
第 二 章
一
数据输出
printf()的格式: printf(输出控制,输出数据列表); printf格式说明: 1 “%md” 用来输出整数,控制输出数据所占的宽度,如果m指定的宽 度小于实际的宽度,则按实际输出;如果m指定的宽度大于实际 的宽度,则按右对齐方式,左边补空格。
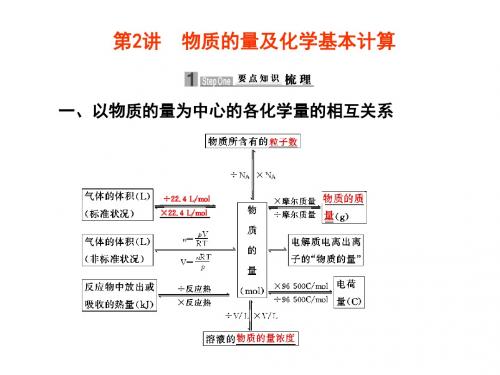
第2讲物质的量及化学基本计算
D项,
正确。
m (a b) g 1 000 ( a b) g/L ,因此只有选项C 3 V V 10 L V
答案 C
考点四
一定物质的量浓度的溶液的配制及误差 分析
【例4】 实验室配制500 mL 0.5 mol/L的NaCl溶 ①把称量的NaCl晶体放入小烧杯中, ②把①所得溶液小心转入500 mL容 ③继续向容量瓶中加蒸馏水至液面距刻度2~3 cm 处,改用胶头滴管小心滴加蒸馏水至溶液凹液面
(填“偏高”、“偏低”或
(5)若实验过程中出现如下情况应如何处理?加蒸
馏水时不慎超过了刻度 面 取。(3)根据c=
n ,V偏小,c V
。向容量 。
瓶中转移溶液时(操作步骤②)溶液流到容量瓶外
解析 (2)为防止仪器的遗漏,可根据步骤进行选
(4)加蒸馏水超过刻度,V偏大,c偏低这种情况
下配制的溶液浓度不是0.5 mol/L,因此要重配。 答案 (1)①②④③⑤ (2)500 mL容量瓶、托盘天
有关阿伏加德罗常数的应用问题,实质上是以 物质的量为中心的各物理量间的换算,需要特别注 1.状态问题,如标准状况下SO3为固态,戊烷为
液态。标准状况下的气体适用气体摩尔体积
(22.4 L/mol),相同状况下的气体适用阿伏加德罗 2.特殊物质的摩尔质量,如D2O、18O2 3.物质分子中的原子个数,如O3、白磷、稀有气 4.某些物质中的化学键,如SiO2、P4、CO2等。
24
如加入足量强碱并加热可得到c mol NH3,则原溶液
中的Al3+离子浓度(mol/L)为
2b c A. 2a
(
D. 2b c
6a
)
B. 2b c
第2讲 函数的单调性与最值
第2讲 函数的单调性与最值一、选择题1.下列函数中,既是偶函数又在(0,+∞)内单调递减的函数是( ).A .y =x 2B .y =|x |+1C .y =-lg|x |D .y =2|x | 解析 对于C 中函数,当x >0时,y =-lg x ,故为(0,+∞)上的减函数,且y =-lg |x |为偶函数.答案 C2.函数y =2x 2-(a -1)x +3在(-∞,1]内单调递减,在(1,+∞)内单调递增,则a 的值是( )A .1B .3C .5D .-1解析 依题意可得对称轴x =a -14=1,∴a =5. 答案 C3.若函数y =ax 与y =-b x 在(0,+∞)上都是减函数,则y =ax 2+bx 在(0,+∞)上是( )A .增函数B .减函数C .先增后减D .先减后增 解析 ∵y =ax 与y =-b x在(0,+∞)上都是减函数, ∴a <0,b <0,∴y =ax 2+bx 的对称轴方程x =-b 2a<0, ∴y =ax 2+bx 在(0,+∞)上为减函数.答案 B 4.设函数f (x )=⎩⎨⎧ 1,x >0,0,x =0,-1,x <0,g (x )=x 2f (x -1),则函数g (x )的递减区间是( ). A .(-∞,0] B .[0,1)C .[1,+∞)D .[-1,0]解析 g (x )=⎩⎨⎧x 2,x >1,0,x =1,-x 2,x <1.如图所示,其递减区间是[0,1).故选B. 答案 B 5.函数y =-x 2+2x -3(x <0)的单调增区间是( ) A .(0,+∞)B .(-∞,1]C .(-∞,0)D .(-∞,-1]解析 二次函数的对称轴为x =1,又因为二次项系数为负数,拋物线开口向下,对称轴在定义域的右侧,所以其单调增区间为(-∞,0).答案 C6.已知函数f (x )=x 2-2ax +a ,在区间(-∞,1)上有最小值,则函数g (x )=f x x 在区间(1,+∞)上一定( ).A .有最小值B .有最大值C .是减函数D .是增函数解析 由题意a <1,又函数g (x )=x +a x -2a 在[|a |,+∞)上为增函数,故选D. 答案 D二、填空题7.设函数y =x 2-2x ,x ∈[-2,a ],若函数的最小值为g (a ),则g (a )=________. 解析 ∵函数y =x 2-2x =(x -1)2-1,∴对称轴为直线x =1.当-2≤a <1时,函数在[-2,a ]上单调递减,则当x =a 时,y min =a 2-2a ;当a ≥1时,函数在[-2,1]上单调递减,在[1,a ]上单调递增,则当x =1时,y min =-1.综上,g (a )=⎩⎨⎧ a 2-2a ,-2≤a <1,-1,a ≥1. 答案 ⎩⎨⎧a 2-2a ,-2≤a <1-1,a ≥18.若f (x )为R 上的增函数,则满足f (2-m )<f (m 2)的实数m 的取值范围是________.解析 ∵f (x )在R 上为增函数,∴2-m <m 2.∴m 2+m -2>0.∴m >1或m <-2.答案 (-∞,-2)∪(1,+∞)9. 已知f (x )=⎩⎨⎧ 3a -1x +4a x <1,log a x x ≥1是(-∞,+∞)上的减函数,那么a 的取值范围是________.解析 ∵当x ≥1时,y =log a x 单调递减,∴0<a <1;而当x <1时,f (x )=(3a -1)x +4a 单调递减,∴a <13; 又函数在其定义域内单调递减,故当x =1时,(3a -1)x +4a ≥log a x ,得a ≤17, 综上可知,17≤a <13. 答案 .17≤a <1310.已知函数f (x )=⎩⎨⎧e -x -2,x ≤0,2ax -1,x >0(a 是常数且a >0).对于下列命题: ①函数f (x )的最小值是-1;②函数f (x )在R 上是单调函数;③若f (x )>0在⎣⎢⎡⎭⎪⎫12,+∞上恒成立,则a 的取值范围是a >1; ④对任意的x 1<0,x 2<0且x 1≠x 2,恒有f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2. 其中正确命题的序号是____________.解析 根据题意可画出草图,由图象可知,①显然正确;函在⎣⎢⎡⎭⎪⎫12,+∞数f (x )在R 上不是单调函数,故②错误;若f (x )>0上恒成立,则2a ×12-1>0,a >1,故③正确;由图象可知在f ⎝ ⎛⎭⎪⎫x 1+x 22(-∞,0)上对任意的x 1<0,x 2<0且x 1≠x 2,恒有<f (x 1)+f (x 2)2成立,故④正确. 答案 ①③④三、解答题11.已知函数f (x )=1a -1x(a >0,x >0). (1)求证:f (x )在(0,+∞)上是增函数;(2)若f (x )在⎣⎢⎡⎦⎥⎤12,2上的值域是⎣⎢⎡⎦⎥⎤12,2,求a 的值. 解 (1)证明:方法一:设x 2>x 1>0,则x 2-x 1>0,x 1x 2>0.∵f (x 2)-f (x 1)=⎝ ⎛⎭⎪⎫1a -1x 2-⎝ ⎛⎭⎪⎫1a -1x 1 =1x 1-1x 2=x 2-x 1x 1x 2>0, ∴f (x 2)>f (x 1),∴f (x )在(0,+∞)上是增函数.方法二:∵f (x )=1a -1x, ∴f ′(x )=⎝ ⎛⎭⎪⎫1a -1x ′=1x 2>0, ∴f (x )在(0,+∞)上为增函数.(2)∵f (x )在⎣⎢⎡⎦⎥⎤12,2上的值域是⎣⎢⎡⎦⎥⎤12,2, 又f (x )在⎣⎢⎡⎦⎥⎤12,2上单调递增, ∴f ⎝ ⎛⎭⎪⎫12=12,f (2)=2,∴a =25. 12.已知函数f (x )=x 2+a x (x ≠0,a ∈R ).(1)判断函数f (x )的奇偶性;(2)若f (x )在区间[2,+∞)上是增函数,求实数a 的取值范围.解 (1)当a =0时,f (x )=x 2(x ≠0)为偶函数;当a ≠0时,f (-x )≠f (x ),f (-x )≠-f (x ),∴f (x )既不是奇函数也不是偶函数.(2)设x 2>x 1≥2,则f (x 1)-f (x 2)=x 21+a x 1-x 22-a x 2=x 1-x 2x 1x 2[x 1x 2(x 1+x 2)-a ], 由x 2>x 1≥2,得x 1x 2(x 1+x 2)>16,x 1-x 2<0,x 1x 2>0.要使f (x )在区间[2,+∞)上是增函数,只需f (x 1)-f (x 2)<0,即x 1x 2(x 1+x 2)-a >0恒成立,则a ≤16.13.已知函数f (x )=a ·2x +b ·3x ,其中常数a ,b 满足ab ≠0.(1)若ab >0,判断函数f (x )的单调性;(2)若ab <0,求f (x +1)>f (x )时的x 的取值范围.解 (1)当a >0,b >0时,因为a ·2x ,b ·3x 都单调递增,所以函数f (x )单调递增;当a <0,b <0时,因为a ·2x ,b ·3x 都单调递减,所以函数f (x )单调递减.(2)f (x +1)-f (x )=a ·2x +2b ·3x >0.(i)当a <0,b >0时,⎝ ⎛⎭⎪⎫32x >-a 2b , 解得x >log 32⎝ ⎛⎭⎪⎫-a 2b ; (ii)当a >0,b <0时,⎝ ⎛⎭⎪⎫32x <-a 2b , 解得x <log 32⎝ ⎛⎭⎪⎫-a 2b . 14.函数f (x )对任意的a 、b ∈R ,都有f (a +b )=f (a )+f (b )-1,并且当x >0时,f (x )>1.(1)求证:f (x )是R 上的增函数;(2)若f (4)=5,解不等式f (3m 2-m -2)<3.解 (1)证明 设x 1,x 2∈R ,且x 1<x 2,则x 2-x 1>0,∴f (x 2-x 1)>1.f (x 2)-f (x 1)=f [(x 2-x 1)+x 1]-f (x 1)=f (x 2-x 1)+f (x 1)-1-f (x 1)=f (x 2-x 1)-1>0.∴f (x 2)>f (x 1).即f (x )是R 上的增函数.(2) ∵f (4)=f (2+2)=f (2)+f (2)-1=5,∴f (2)=3,∴原不等式可化为f(3m2-m-2)<f(2),∵f(x)是R上的增函数,∴3m2-m-2<2,解得-1<m<43,故解集为⎝⎛⎭⎪⎫-1,43.。
第2讲巧算与速算
(2)同上利用交换律,将13乘在最后。
(3)一个数连续除以几个数就等于这个数除以这几个数 的积,用100000除以32、125和25的积。 (4)可以将2600和25同时乘以4,利用“商不变”的性 质进行巧算。
解:(1)241×345÷678÷345×678÷241 =(241÷241)×(345÷345)×(678÷678) =1×1×1 =1
(2)(13×4×5×6)÷(4×5×6) =13×4×5×6÷4÷5÷6 =13×(4÷4)×5÷5×(6÷6) =13
(3)100000÷32÷125÷25 =100000÷(32×125×25) =1
(4)2600÷25 =2600×4÷(25×4) =104
【例2】用简便方法计算。 (1)6666×6666 (2)999×222+333×334 (3)999×999+1999
第2讲 巧算与速算(二)
凑整法;分组求和
乘法分配律:a×(b+c)=a×b+a×c或a×(bc)=a×b-a×c 乘法分配律逆运算:a×b+a×c=a×(b+c)或 a×b-a×c=a×(b-c)
课前测试
1. 187+63+37-87 2. 93+90+89+87+93+95+88+91
3. 163×175-163×34-163×41 4. 8888×125 5. 6544+8953-4544-5953 6. 995+994+993+…+3+2+1-2-3-4-…-993-994
1. 456÷123×798÷456÷798×123 2. (12×5×7×13×7)÷(7×7×13) 3. 45000÷8÷125 4. 1037000÷125 5. 1976÷19 6. 9999×2222+3333×3334 7. 28×36+48×54 8. 19999+9999×9999
第2讲 3-7节代数运算与三种运算律,一一映射
(1)由为双射,对a A,有且仅有一个a A使
(a)=a,即对a A, 在 -1下,有唯一的a A与之对应,
数运算.若⊙, ⊕对于B的任何元b,A的任何元 a1 , a2 都有
b (a1 a2 )=(b a1 ) (b a2 )
则说⊙, ⊕适合第一分配律.
定理
如果⊕适合结合律, ⊙, ⊕适合第一分配律,则
b B, a1, a2 ,an A, 都有
b (a1 a2 an ) =(b a1 ) (b a2 ) (b an )
(a1 a2 an )
(a1 a2 an ) a1 (a2 an )
(a1 a2 an )
是经过了一种加括号的步骤得出的结果,其中最后 总是对两个元进行运算: (a a a ) b b
1 2 n 1 2
其中b1是前面i个元加括号后所得结果,b2是其余n-i个 元加括号后所得结果,而i和n-i都不超过n-1,由归纳假 设: b1 a1 a2 ai
下哪些法则是给定集合上的代数运算? 1.
ab ab , Q上.
(不是,a=1,b=2) (不是,a=1,b=1)
2. A x x R且x 0 , a b a ln b
3. A n n Z and n 0 上,考虑数的减法
(不是,2-5=-3)
4. A n n Z and n 0 , a b a b
(a1 a2 an1 ) an a1 a2 an1 an
初三精英班第2讲勾股定理与三角函数
CF=DF+CD=41 3-10+40=41 3+3(0 米) EF=CF tan =41 3 30 41 1.7 99.7 100(米) 答:点E离地面的高度EF是100米
中考专练
1.(2014 年山东泰安)如图,∠ACB=90°,D 为 AB 的中点,连接 DC 并
延长到 E,使 CE= 1 CD,过点 B 作 BF∥DE,与 AE 的延长线交于点 F.若
3
AB=6,则 BF 的长为( )
A.6 B.7 C.8
D.10
解: ACB 90 ,D为AB的中点,AB 6
CD 1 AB 3.又CE 1 CD
2
3
CE 1
ED CE CD 4 又 BF DE,点D是AB的中点
2X
x
2X
x
3.(2015•牡丹江)在△ABC 中,AB=12 2 ,AC=13,cos∠B= 2 , 2
则 BC 边长为(
)
A.7 B.8
C.8 或 17
D.7 或 17
4. 如图,Rt△ABC 中,∠ACB=90º,AC=3,BC=4,将边 AC 沿 CE 翻折,使点 A 落在 AB 上的点 D 处;再将边 BC 沿 CF 翻折, 使点 B 落在 CD 的延长线上的点 B′处,两条折痕与斜边 AB 分 别交于点 E、F,则线段 B′F 的长为( )
锐角 A 的邻边与 斜边 的比叫做∠A 的余弦; 锐角 A 的对边与 邻边 的比叫做∠A 的正切。
即:
sinA
(斜对),cosA
=(斜邻),tanA
对
=( 邻)
2.特殊角的三角函数值
锐角 α
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.6 C++处理字符串的方法
例5.12 把一个班n个学生的简单资料(姓名和学号)输入计算 机保存。然后通过输入学生姓名查找与其相关资料。当输入一 个姓名后,查到输出姓名和学号,查不到输出“本班无此人” 。 string find_name; #include <iostream> cout << “please input #include <string> number of this class:”; using namespace std; cin >> n; input_date(); string name[50], num[50]; cout << “please input name int n; you want find:”; int main() cin >> find_name; { void input_date(); void search( string find_name); search(find_name); return 0; }
5.6 C++处理字符串的方法
5.6.2 字符串变量的运算
在以字符数组存放字符串时,字符串的运算要用字符串函 数,如strcat(连接)、strcmp(比较)、strcpy(复制),而对字 符串string类对象,可以不用函数,而直接用运算符。 (1) 字符串复制用赋值号 string1=string2; //作用同“strcpy(string1,string2);” (2) 字符串连接用加号 string string1=“C++”; string string2=“Language”; string1=string1+string2 ; (3) 字符串比较直接用关系运算符 可以直接用“==, >, <, !=, >=, <=”等关系运算符。
5.6 C++处理字符串的方法
字符串常量以‘\0‟作为结束符,但将字符串常量存放到字 符串变量中时,只存放字符串本身而不包括‘\0‟。
3. 字符串变量的输入输出
可以在输入输出语句中用字符串变量名输入输出字符串, 如: cin >> string1; //输入字符串给字符串变量string1 cout << string2; //输出字符串string2
5.6 C++处理字符串的方法
(4) 每一个字符串元素中只 包含字符串本身的字符而不包 含‘\0‟。
5.6.4 字符串运算举例
例5.11 输入3个字符串,要求将字母按由小到大的顺序输出。
#include <iostream> #include <string> using namespace std; int main()
第四章
内容提要:函数模板、有默认参数的函数
4.7
函数模板
上节介绍的函数重载可以实现一个函数名多用,在调用同 类函数时感到含义清楚,方法简单。但是在程序中仍然要 分别定义每一个函数。能否再简化呢? 为了解决问题,C++提供了函数模板(function template)。 所谓函数模板,实际上是建立一个通用函数,其函数类型 和形参类型不具体指定,用一个虚拟的类型来代表。 这个通用函数就称为函数模板。凡是函数体相同的函数都 可以用这个模板来代替,只需在模板中定义一次即可。在 调用函数时系统会根据实参的类型来取代模板中的虚拟类 型,从而实现了不同函数的功能。
double d1,d2,d3,d; cin>>d1>>d2 >>d3; d=max(d1,d2,d3); cout<<“d_max=”<<d<<endl; long g1,g2,g3,g; cin>>g1>>g2 >>g3; g=max(g1,g2,g3); cout<<“g_max=”<<g<<endl; return 0;
4.8 有默认参数的函数
在使用带有默认参数的函数时有两点要注意: (1)如果函数定义在函数调用之前,则应在函数定义 中给出默认值。如果函数定义在函数调用之后,则在 函数调用之前的函数声明中必须给出默认值,在函数 定义中可以不给默认值。默认值信息应在函数调用前 给出,否则出错。 (2)一个函数不能既作为重载函数,又作为有默认值的 函数。 例如:将例4.6中第4行改为 int max(int a, int b, int c=100); //max是重载函数 如果有一个函数调用“max(5,23)”,则系统无法 判定调用 哪一个函数,出错。
}
//输入语句 //函数调用 //输出语句 //输入语句 //函数调用 //输出语句
运行情况如下: 185 -76 567 i_max=567 56.78 90.23 -32.78 d_max=90.23 67854 -912456 673456 g_max=673456
4.7 函数模板
定义函数模板的一般形式为: template <typename T> 通用函数定义
4.8 有默认参数的函数
如果有多个形参,可以使每一个形参有一个默认值, 也可以只对一部分形参指定默认值,另一部分形参不 指定默认值。 实参与形参的结合是从左至右,第一个实参与第一个 形参结合,第二个实参与第二个形参结合……。因此 指定默认值的参数必须放在形参表列的最右端,否则 将出错。 如:void f1(float a, int b=0, int c, char d=„a‟); //不正确 void f2(float a, int c, int b=0, char d=„a‟); //正确 调用f2:f2(3.5, 5, 3, „x‟); //形参的值全部从实参得到 f2(3.5, 5, 3); //最后一个形参取默认值‘a‟ f2(3.5, 5); //最后两个形参取默认值b=0,d=„a‟
4.8 有默认参数的函数
一般情况下,在函数调用时形参从实参那里取得值, 因此实参的个数应与形参相同。有时多次调用同一函 数时用同样的实参,C++提供简单的处理办法,给形 参一个默认值,这样形参就不必一定要从实参那里取 值了。 如有一函数声明:float area(float r=6.5); 指定r的默认值为6.5,如果在调用此函数时,确认r的 值为6.5,则可以不必给出实参的值,如 area(); //相当 于area(6.5);如果不想使形参取此默认值,则通过实参 另行给出。如:area(7.5); //形参将得到7.5。
第五章
内容提要:C++处理字符串的方法
5.6 C++处理字符串的方法
C++提供了一种新的数据类型:字符串(string)类型。可以 用来定义变量,即字符串变量。 string并不是C++语言本身具有的基本类型,是在C++标准 库中声明的一个字符串类,用这种类可以定义对象。
5.6.1 字符串变量的定义和引用
ห้องสมุดไป่ตู้
例4.7
求3个数中最大的数
#include <iostream> //预处理命令 using namespace std; //使用命名空间std template <typename T> //模板声明,T为虚拟类型 T max(T a, T b, T c) //通用函数定义 { if (b>a) a=b; if (c>a) a=c; return a; } int main ( ) //主函数 { int i1,i2,i3,i; cin>>i1>>i2 >>i3; //输入语句 i=max(i1,i2,i3); //调用函数 cout<<“i_max=”<<i<<endl; //输出语句 //接下页
5.6 C++处理字符串的方法
5.6.3 字符串数组
不仅可以用string定义字符串变量,也可以用string定义字符 串数组。如 string name[5]={“Zhang”, “Li”, “Fun”, “Wang”, “Tan”} (1)在一个字符串数组中包含若干个元素,每个元素相当于一 个字符串变量。 (2)并不要求每个字符串元素具有相同的长度,即使对同一元 素而言,它的长度也是可以变化的,可赋不同值。 (3) 在字符串数组的每一个元素中存放一个字符串的地址,而 不是一个字符。
5.6 C++处理字符串的方法
void input_date() { int i; for (i=0; i<n; i++) { cout << “input name and number of student” << i+1 <<“:”<<endl; cin >> name[i] >> num[i];} } void search (string find_name) { int i; bool flag=false; for (i=0; i<n; i++) if (name[i]==find_name) { cout << name[i] << “has been found, his number is” << num[i] << endl; flag=true; break; } if (flag== false) cout << “can‟t find this name”; }
1.定义字符串变量:定义字符串变量要用类名string,如: string string1; string string2=“China”; 注意:要使用string类的功能时,必须包含头文件,即: #include<string>
