量子化学课程习题及标准答案
量子化学期末考试试卷及参考答案
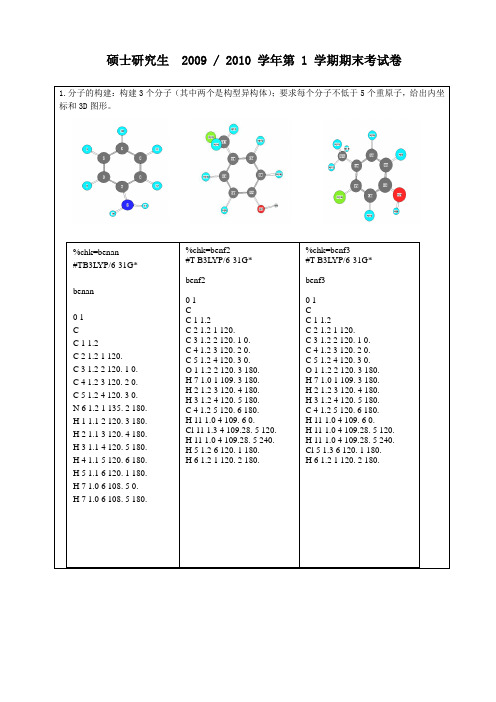
优化结构后的键长: C1-C2=1.399 C2-C3=1.388 C3-C4=1.407 C5-C6=1.398 C1-C6=1.395 C2-H9=1.085 C1-O7=1.366 O7-H8=0.970 C3-H10=1.088 C4-C11=1.511 C11-H12=1.091 C11-H13=1.097 C11-H14=1.097 C5-Cl15=1.786 C6-H16=1.086
3-氯代对甲基苯酚优化后的能量是:HF=-806.3769679 优化后的构型如下: HOMO
LUMO
各原子所带的电荷: Total atomic charges:
1 C 0.357296 2 C -0.150569 3 C -0.180892 4 C 0.171258 5 C -0.134553 6 C -0.194460 7 O -0.640742 8 H 0.410639 9 H 0.144774 10 H 0.133768 11 C -0.533938 12 H 0.180060 13 H 0.164373 14 H 0.164373 15 Cl -0.032464 16 H 0.141076 Sum of Mulliken charges= 0.00000
%chk=benf3 #T B3LYP/6-31G*
benf3
01 C C 1 1.2 C 2 1.2 1 120. C 3 1.2 2 120. 1 0. C 4 1.2 3 120. 2 0. C 5 1.2 4 120. 3 0. O 1 1.2 2 120. 3 180. H 7 1.0 1 109. 3 180. H 2 1.2 3 120. 4 180. H 3 1.2 4 120. 5 180. C 4 1.2 5 120. 6 180. H 11 1.0 4 109. 6 0. H 11 1.0 4 109.28. 5 120. H 11 1.0 4 109.28. 5 240. Cl 5 1.3 6 120. 1 180. H 6 1.2 1 120. 2 180.
chapter1 量子力学基础知识习题解答

在零点能;(4)没有经典运动轨道,只有概率分布;(5)存在节点,节点越多,
能量越高。以上这些特点是所以量子力学体系都有的特点。
2
乐山师范学院 化学与生命科学学院
本章习题解答
【1.1】将锂在火焰上燃烧,放出红光,波长λ=670.8nm,这是 Li 原子由电子组态 (1s)2(2p)1
→(1s)2(2s)1 跃迁时产生的,试计算该红光的频率、波数以及以 kJ ⋅ mol−1 为单位的能量。
描述,它包括体系的全部信息。这一函数称为波函数或态函数,简称态。
不含时间的波函数ψ (x, y, z) 称为定态波函数。在本课程中主要讨论定态波函
数。 由于空间某点波的强度与波函数绝对值的平方成正比,即在该点附近找到粒
子的几率正比于ψ *ψ ,所以通常将用波函数ψ 描述的波称为几率波。在原子、分 子等体系中,将ψ 称为原子轨道或分子轨道;将ψ *ψ 称为几率密度,它就是通常 所说的电子云;ψ *ψ dτ 为空间某点附近体积元 dτ 中电子出现的几率。
花粉: ∆x
=
h m∆v
=
6.626 ×10−34 J ⋅ s 10−13 kg ×1×10%m ⋅ s−1
=
6.63×10−20 m
5
乐山师范学院 化学与生命科学学院
电子: ∆x
=
h m∆v
=
6.626 ×10−34 J ⋅ s 9.1.0910−31kg ×1000 ×10%m ⋅ s−1
=
7.27 ×10−6 m
相反的两个电子。或者说:对于多电子体系,波函数对于交换任意两个电子是反
对称的。
三、箱中粒子的 Schrödinger 方程及其解
1. 一维无限势阱的 Schrödinger 方程:
量子力学课后习题答案

量子力学习题及解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ, (1)以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
结构化学练习之量子力学基础习题附参考答案

量子力学基础习题一、填空题(在题中的空格处填上正确答案)1101、光波粒二象性的关系式为_______________________________________。
1102、德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1104、测不准关系是_____________________,它说明了_____________________。
1105、一组正交、归一的波函数ψ1, ψ2, ψ3,…。
正交性的数学表达式为 ,归一性的表达式为 。
1106、│ψ (x 1, y 1, z 1, x 2, y 2, z 2)│2代表______________________。
1107、物理量xp y - yp x 的量子力学算符在直角坐标系中的表达式是_____。
1108、质量为 m 的一个粒子在长为l 的一维势箱中运动,(1)体系哈密顿算符的本征函数集为_______________________________ ;(2)体系的本征值谱为____________________, 最低能量为____________ ;(3)体系处于基态时, 粒子出现在0 ─ l /2间的概率为_______________ ;(4)势箱越长, 其电子从基态向激发态跃迁时吸收光谱波长__________ ;(5)若该粒子在长l 、宽为2l 的长方形势箱中运动, 则其本征函数集为____________,本征值谱为 _______________________________。
1109、质量为m 的粒子被局限在边长为a 的立方箱中运动。
波函数ψ211(x ,y ,z )= _________________________;当粒子处于状态ψ211时,概率密度最大处坐标是_______________________;若体系的能量为2247ma h ,其简并度是_______________。
结构化学 第一章 量子化学基础 习题

1029
y y y 设 体 系 处 在 状 态 =c1 211+ c2 210 中 , 角 动 量 M2 和 Mz 有 无 定 值 。其值为多少?若无 ,
则求其平均值。
1030
h¶
试 求 动 量 算 符 pˆ x=
的 本 征 函 数 (不 需 归 一 化 )。
i2p ¶x
1031
y 下 列 说 法 对 否 :” =cos x, px 有确 定 值 , p2x 没 有 确 定 值,只有平均值 。” ---------- ( )
(A) 16.5 × 10 -24? J (B) 9.5
× 10 -7 J (C) 1.9
× 10 (E) 1.75 × 10 -50? J
1039 一个在一维势箱中运动的粒子,
(1) 其 能 量 随 着 量 子 数 n 的 增 大 :------------------------ ( ) (A) 越 来 越 小 (B) 越 来 越 大 (C) 不变 (2) 其 能 级 差 En+1-En 随 着 势 箱 长 度 的 增大 : -------------------( ) (A) 越 来 越 小 (B) 越 来 越 大 (C) 不变
(A)
Aˆ U=λU, λ=常数
(B)
Bˆ U=U*
(C)
Cˆ U=U2
(D)
Dˆ U = dU
dx
(E)
Eˆ U=1/ U
1026 物 理 量 xp y- ypx
1027
_____ 。
某 粒 子 的 运 动 状 态 可 用波 函 数y =Ne-ix 来表 示 , 求 其 动 量 算符 pˆ x 的 本 征 值 。
1013
测 不 准 原 理 的 另一 种 形 式 为 Δ E·Δt≥h/2 π。当一个电子从 高能级向低能级跃迁 时,
量子力学教程课后习题答案

量子力学教程课后习题答案量子力学习题及解答第一章量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长与温度T成反比,即T=b(常量);并近似计算b的数值,准确到二位有效数字。
解根据普朗克的黑体辐射公式,(1)以及,(2),(3)有这里的的物理意义是黑体内波长介于λ与λ+dλ之间的辐射能量密度。
本题关注的是λ取何值时,取得极大值,因此,就得要求对λ的一阶导数为零,由此可求得相应的λ的值,记作。
但要注意的是,还需要验证对λ的二阶导数在处的取值是否小于零,如果小于零,那么前面求得的就是要求的,具体如下:如果令x= ,则上述方程为这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有把x以及三个物理常量代入到上式便知这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K附近,钠的价电子能量约为3eV,求其德布罗意波长。
解根据德布罗意波粒二象性的关系,可知E=h,如果所考虑的粒子是非相对论性的电子(),那么如果我们考察的是相对性的光子,那么E=pc 注意到本题所考虑的钠的价电子的动能仅为3eV,远远小于电子的质量与光速平方的乘积,即,因此利用非相对论性的电子的能量——动量关系式,这样,便有在这里,利用了以及最后,对作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
1.3 氦原子的动能是(k为玻耳兹曼常数),求T=1K时,氦原子的德布罗意波长。
鲁科版高中化学选择性必修2物质结构与性质课后习题 第1章 量子力学对原子核外电子运动状态的描述

分层作业2 量子力学对原子核外电子运动状态的描述A级必备知识基础练题组1.电子层与能级1.下列叙述正确的是( )A.同一多电子原子中,3s、2s、1s电子的能量逐渐增大B.同一多电子原子中,2s轨道的半径比3s的半径大C.能量高的电子在离核较近的区域运动,能量低的电子在离核较远的区域运动D.各电子层含有的能级数为n(n为电子层序数)2.下列能级符号不正确的是( )A.7sB.2fC.3dD.2p3.下列叙述正确的是( )A.每个电子层都是从s能级开始,f能级结束B.每个电子层所容纳的最多电子数为2n2C.基态Ca原子的最高能级为3sD.相同电子层中的np x、np y、np z能级的能量不同题组2.原子轨道与电子云4.在对电子运动状态的描述中,确定一个“轨道”应选择以下四项中的( )①电子层②能级③电子云的伸展方向④电子的自旋状态A.①②③④B.①②③C.①②D.②③④5.N电子层所含能级数、原子轨道数和最多容纳电子数分别为( )A.3、9、18B.4、16、32C.5、25、50D.2、4、86.下列能级中,轨道数为5的是( )A.3sB.4pC.3dD.5fB级关键能力提升练以下选择题中,有1~2个选项符合题意。
7.下列说法正确的是( )A.同一原子中,2s、3s、4s、5s电子能量逐渐升高B.能量高的电子在离核近的区域运动,能量低的电子在离核远的区域运动C.同一原子中,2p、3p、4p能级的轨道数依次增多D.各电子层含有的原子轨道数为n2(n为电子层序数)8.电子作为微观粒子,其运动特征与宏观物体的运动特征有着明显的区别,下列关于电子运动特征的叙述中正确的是( )A.电子在原子核周围的空间内围绕原子核做圆周运动,只不过每一个圆周的半径不同而已B.电子的运动存在固定的运动轨迹C.电子的运动速度特别快,运动范围特别小,不可能同时准确地测定其位置和速度D.电子的运动速度特别快,所以其能量特别大9.下列说法正确的是( )A.不同电子层的f能级最多容纳的电子数相同B.3d能级最多容纳10个电子C.第三电子层最多容纳8个电子D.第n电子层含有(n-1)个能级10.有两种气态单质A m和B n,已知2.4 g A m和2.1 g B n所含的原子个数相等,分子数之比为2∶3。
结构化学练习之量子力学基础习题附参考答案汇总

量子力学基础习题一、填空题(在题中的空格处填上正确答案)1101、光波粒二象性的关系式为_______________________________________。
1102、德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1104、测不准关系是_____________________,它说明了_____________________。
1105、一组正交、归一的波函数ψ1, ψ2, ψ3,…。
正交性的数学表达式为 ,归一性的表达式为 。
1106、│ψ (x 1, y 1, z 1, x 2, y 2, z 2)│2代表______________________。
1107、物理量xp y - yp x 的量子力学算符在直角坐标系中的表达式是_____。
1108、质量为 m 的一个粒子在长为l 的一维势箱中运动,(1)体系哈密顿算符的本征函数集为_______________________________ ;(2)体系的本征值谱为____________________, 最低能量为____________ ;(3)体系处于基态时, 粒子出现在0 ─ l /2间的概率为_______________ ;(4)势箱越长, 其电子从基态向激发态跃迁时吸收光谱波长__________ ;(5)若该粒子在长l 、宽为2l 的长方形势箱中运动, 则其本征函数集为____________,本征值谱为 _______________________________。
1109、质量为m 的粒子被局限在边长为a 的立方箱中运动。
波函数ψ211(x ,y ,z )= _________________________;当粒子处于状态ψ211时,概率密度最大处坐标是_______________________;若体系的能量为2247ma h ,其简并度是_______________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
量子化学习题及标准答案Chapter 011. A certain one-particle,one-dimensional system has/2bmx ibt e ae --=ψ,where a and b are constants and m is theparticle ’s mass. Find thepotential-energy function V for thissystem. (Hint : Use the time-dependentSchrodinger equation.)Solution :As (x,t) is known, we canderive the corresponding derivatives. ⎪⎪⎩⎪⎪⎨⎧ψ+ψ-=∂ψ∂ψ-=∂ψ∂⇒=ψ--222222/42),(),(),(2 x m b bm xt x ib t t x e ae t x bmx ibtAccording to time-dependentSchroedinger equation,substituting into the derivatives, weget222),(mx b t x V =2. At a certain instant of time, aone-particle, one-dimensional systemhas bx xe b /||2/13)/2(-=ψ, where b = 3.000 nm. If ameasurement of x is made at this time inthe system, find the probability thatthe result (a) lies between 0.9000 nm and0.9001 nm (treat this interval asinfinitesimal); (b) lies between 0 and2 nm (use the table of integrals, ifnecessary). (c) For what value of x isthe probability density a minimum?(There is no need to use calculus toanswer this.) (d) Verify that ψ isnormalized. 222(,)(,)2x t x t V i t m x∂ψ∂ψ=-+∂∂Solution :a) The probability of findingan particle in a space between x and x+dx is given by6/223210*29.32--==ψ=dx e x b dx P b x b) 0753.02910*20/223==⎰--dx e x bP b x c) Clearly, the minimum of probabilitydensity is at x=0, where the probabilitydensity vanishes. d)4220/223/223/2232===ψ=⎰⎰⎰⎰+∞-+∞∞--+∞∞--+∞∞-dx e x b dx e x b dx e x b dx P b x b x b x3. A one-particle, one-dimensionalsystem has the state function2222/4/16/4/12)/32)((cos )/2)((sin c x c x xe c at e c at --+=ψππwhere a is a constant and c = 2.000 Å.If the particle ’s position is measuredat t = 0, estimate the probability thatthe result will lie between 2.000 Å and2.001 Å.Solution :when t=0, the wavefunction is simplified as441610*158.2)32(),(22--==ψc x xec t x πChapter 021. Consider an electron in a one-dimensional box of length2.000Åwith the left end of the box at x = 0.(a) Suppose we have one million of these systems, each in the n= 1 state, and we measure the x coordinate of the electron in each system. About how many times will the electron be found between 0.600 Åand 0.601 Å? Consider the interval to be infinitesimal. Hint: Check whether your calculator is set to degrees or radians.(b) Suppose we have a large number of these systems, each in the n =1 state, and we measure the x coordinate of the electron in each system and find the electron between 0.700 Å and 0.701 Å in 126 of the measurements. In about how many measurements will the electron be found between 1.000 Å and 1.001 Å? Solution: a) In a 1D box, the energyand wave-function of a micro-system are given by)sin(2,22222x ln l ml n E πψπ== therefore, the probability density offinding the electron between 0.600 and0.601 Å is65510*545.6)(sin 242⇒==-dx x ln l P πb) From the definition of probability,the probability of finding an electron between x and x+dx is given bydx x l n l P )(sin 22π= As the number of measurements of findingthe electron between 0.700 and 0.701 Å is known, the number of system is1(sin 22*158712158712001.0)7.02*1(sin 2212612622=⇒===πP P N2. When a particle of mass 9.1*10-28 g ina certain one-dimensional box goes from the n = 5 level to the n = 2 level, itemits a photon of frequency 6.0*1014 s -1.Find the length of the box. Solution.lml h n n ml n n E lower up lower up 36222222222110*26646.18)(2)(-=-=-=∆ π3. An electron in a stationary state of a one-dimensional box of length 0.300 nmemits a photon of frequency 5.05*1015 s -1.Find the initial and final quantum numbers for this transition. Solution:2,388)(2)(22222222222===-⇒=-=-=∆lower upper lower up lower up lower up n n n n hv ml h n n ml n n E π4. For the particle in a one-dimensional box of length l , we could have put the coordinate origin at the center of the box. Find the wave functions and energylevels for this choice of origin.Solution: The wavefunction for a particle in a one-dimernsional box can be written as)2()2()(x mE BSin x mE ACos x+=ψ If the coordinate origin is defined at the center of the box, the boundary conditions are given as2()22(0)(2()22(0)(22mE BSin l mE ACos x mE BSin l mE ACos x l x lx +⇒=-⇒==-= ψψ Combining Eq1 with Eq2, we get)4(,0)22()3(,0)22(Eq l mE BSin Eq l mE ACos ==Eq3 leads to A=0, or )22(l mE Cos =0. We willdiscuss both situations in the following section.If A=0, B must be non-zero number otherwise the wavefunction vanishes.2220)22(02mlh n E n l mE l mE Sin B π=⇒=⇒=⇒≠If A ≠08)12()21(220)22(00)22(0)22(0222mlh n E n l mE l mE Cos B l mE Sin l mE Cos A ψπ⇒+=⇒+=⇒==⇒≠⇒=⇒≠5. For an electron in a certain rectangular well with a depth of 20.0 eV, the lowest energy lies 3.00 eV above the bottom of the well. Find the width of this well. Hint : Use tanθ = sin θ/cos θ Solution : For the particle in a certainrectangular well, the E fulfill with)2sin()2()2cos()(21010l mE V E l mE E E V ---=- Substituting into the V and E, we get1010011110*64.22)7954.0(7954.022)(2)2()2()2(-----=⇒+-=⇒+-=⇒-=--==lowest l mEn l n l mE V E E E V l mE Tan l mE Cos l mE Sin ππChapter 03 1. If A ˆf (x ) = 3x 2f (x ) + 2xd f /dx , givean expression for Aˆ. Solution :Extracting f(x) from the known equationleads to the expression of Adx d x x A 23ˆ2+=2. (a) Show that (Aˆ+Bˆ)2= (Bˆ+Aˆ)2for any two operators. (b) Under what conditionsis (A ˆ+B ˆ)2 equal to A ˆ2+2A ˆB ˆ+B ˆ2?Solution:a)2222ˆ()ˆˆ)(ˆˆ(ˆˆˆˆˆˆˆˆˆˆˆ)ˆˆ)(ˆˆ()ˆˆ(B A B A BA B A A B B A B B A A B A B A B A =++=+++=+++=++=+ b)B AA B A B B A A B A ˆˆ2ˆˆˆˆˆˆˆ)ˆˆ(2222++=+++=+If and only if A and B commute, (Aˆ+Bˆ)2equals to A ˆ2+2A ˆB ˆ+B ˆ2 3. If A ˆ = d 2/dx 2 and B ˆ = x 2, find (a) A ˆB ˆx 3; (b) B ˆA ˆx 3; (c) AˆB ˆf (x ); (d)B ˆA ˆf (x )Solution:a)3522320ˆˆx x dxd x B A == b)3322236ˆˆx x dxd x x A B == c))()(4)(2)]()(2[)]([)(ˆˆ2222222x f dxd x x f dx d x x f x f dxd x x xf dx d x f x dx d x f B A ++=+==d))()()(ˆˆ222222x f dxd x x f dx d x x f A B ==4. Classify these operators as linear ornonlinear: (a) 3x 2d 2/dx 2; (b) ( )2; (c) ∫dx ; (d) exp; (e) ∑=n x 1.Solution:Linear operator is subject to the following condition.f A c cf Ag A f A g f A ˆ)(ˆˆˆ)(ˆ=+=+ a) Linearb) Nonlinear c) Linear d) Nonlinear e) Linear5. The Laplace transform operator Lˆ is defined by⎰∞-=0)()(ˆdx x f e x f L px(a) Is L ˆ linear? (b) Evaluate L ˆ(1). (c)Evaluate L ˆe ax , assuming that p >a .Solution:a) L is a linear operatorb),1)1(ˆ0>==⎰∞-p p dx e L px c)pdx e dx e e e L x a p ax px ax ===⎰⎰∞--∞-)(ˆ0)(06. We define the translation operator hTˆ by hT ˆf (x ) = f (x + h ). (a) Is hT ˆ a linear operator? (b) Evaluate(2ˆ3ˆ121+-T T )x 2.Solution:a) The translation operator is linear operator2212212121(2ˆ3ˆ)2ˆ3ˆ(x x x T x T x T T +=+-=+-7. Evaluate the commutators (a) [xˆ,xp ˆ]; (b) [x ˆ,2ˆxp ]; (c) [x ˆ,y p ˆ]; (d) [x ˆ, ),,(ˆz y x V ]; (e)[xˆ,H ˆ]; (f) [z y x ˆˆˆ, 2ˆxp ]. Solution:a)i xx x x i x x i p xx =∂∂--∂∂-=∂∂-=)ˆ1ˆ(],ˆ[]ˆ,ˆ[b)xp i p p x p x p p xx x x x x x∂∂==+=222ˆ2)ˆ]ˆ,ˆ[]ˆ,ˆ[ˆ(]ˆ,ˆ[c)0)ˆˆ(],ˆ[]ˆ,ˆ[=∂∂-∂∂-=∂∂-=yx y x i y x i p xy0ˆ),,(ˆ),,(ˆˆ)],,(ˆ,ˆ[=-=x z y x V z y x V x z y x V xe)mxT x V T x H x ==+=21,ˆ[]ˆ,ˆ[]ˆˆ,ˆ[]ˆ,ˆ[f)xz y p z y xx∂∂=ˆˆ2]ˆ,ˆˆˆ[22Chapter 041:The one-dimensional harmonic-oscillator is at its first excited state and its wavefunction is given as)21exp()()(2)(24/14/31x x x βπβψ-=please evaluate the expectation values(average values) of kinetic energy (T), potential energy (V) and the total energy.Answer: 1) First of all, check the normalization property of the wavefunction.2) Evaluate the expectationvalue of kinetic energy.3) Evaluate the expectation valueof potential energy4) Total Energy = T + V 2. The one-dimensional harmonic-oscillator Hamiltonian is2222ˆ22ˆˆxm v mp H xπ+= The raising and lowering operators forthis problem are defined as]ˆ2ˆ[)2(1ˆ2/1x ivm p m A x π+=+, ]ˆ2ˆ[)2(1ˆ2/1x ivm p m A x π-=-Show thathv H A A 21ˆˆˆ-=-+, hv HA A21ˆˆˆ+=+-, hv A A-=-+]ˆ,ˆ[ ++=A hv A H ˆ]ˆ,ˆ[, ---=A hv A Hˆ]ˆ,ˆ[ Show that +Aˆ and -A ˆ are indeed ladder operators and that the eigenvalues are spaced at intervals of hv . Since both the kinetic energy and the potential energy are nonnegative, we expect the energy eigenvalues to be nonnegative. Hence there must be a state of minimum energy. Operate on the wave function for thisstate first with -A ˆ and then with +Aˆ and show that the lowest energy eigenvalueis hv 21. Finally, conclude that hvn E )21(+=, n = 0, 1, 2, …Answer:1) Write down the definition of operatordx di px -=ˆ2) Expand the operators in full form.]2[21]2[2122ˆ222222vmxi dx di mA vmxi dx d i mA mx v dx d m H πππ--=+-=+-=-+ 3) Evaluate the correspondingcombination of operators]22][2[21ˆ4222[21]2[2]2[2[21]2[21]22[ˆ21ˆ2122]4222[21]]2[2]2[[21]2[21]2[2121ˆ2122]42[21]4222[21]]2[2]2[[21]2[21]2[21222222332222222333222222222222222222222222222222222222222222222mx v dx d m vmxi dx d i mH A v dx d i mx v dx d ix v dx d i v dxd m i m vmxi dx d i mx v vmxi dx d i dxd m m vmxi dx d i mmx v dx d m A H hv H hv mx v dx d m x m v dxd vmx dx d x vm vm dx d m vmxi dxd i vmxi vmxi dx d i dx d i m vmxi dx d i mvmxi dx d i m A A hv H hv mx v dx d m x m v vm dxd m x m v dxd vmx dx d x vm vm dx d m vmxi dxd i vmxi vmxi dx d i dx d i m vmxi dx d i mvmxi dx d i m A A πππππππππππππππππππππππππππππππππ+-+-=+---=+-++--=+-+-=+=++-=+-++-=+--+--=+---=-=-+-=+--=++---=--+---=--+-=+++--++++=+-=+-=+-=-hvA vmxi m dx d i m hv vmxi m hv dxd i m hv mxi v dx d i v m H A A H ]22121[]221[]21[]42[21ˆˆ222ππππIn the same manner, we can get---=-hvA H A A H ˆˆ 4) Substituting the above communicatorsinto the Schroeidnger equation, we getψψψψψψψψψψψψ------++++++-=-=-=+=+=+==A hv E hvA E A hvA H A A H A hv E hvA E A hvA H A A H E H)(]ˆ[ˆ)(]ˆ[ˆˆThis shows that +Aˆ and -A ˆ are indeed ladder operators and that theeigenvalues are spaced at intervals ofhv . 5) Suppose that is the eigenfunctionwith the lowest eigenvalue. ψψlowest E H =ˆAccording to the definition of A_operator, we haveψψ---=A hv E A H )(ˆ As is the eigenfunction with thelowest eigenvalue, the above equation isfulfilled if and only if 0=-ψAOperating on the wave function for thisstate first with -Aˆ and then with +A ˆ leads to ψψψψhv H hv H A A 21ˆ]21ˆ[0=⇒-==-+Therefore, the lowest energy is 1/2 hv.3,2,1,0,)(21ˆ=+=n hv n H ψψChapter 051. For the ground state of theone-dimensional harmonic oscillator,compute the standard deviations x andp x and check that the uncertaintyprinciple is obeyed.Answer:1) The ground state wavefunction of theone-dimensional harmonic oscillator isgiven by2214141)(x e ααπψ--=2) The standard deviations x and p xare defined as222x x x -=∆222)∆∆-=p(p∆)(pThe product of x and p is given by2422122 ==∙=∆∆ααp xIt shows that the uncertainty principleis obeyed.2. (a) Show that the three commutationrelations [x L ˆ,y L ˆ] = z L i ˆ , [y L ˆ,z L ˆ] = x L i ˆ , [z L ˆ,x Lˆ] = y Li ˆ are equivalent to the single relation L L Lˆˆˆ i =⨯ (b) Find [2ˆx L ,y L ˆ] Answer:1): zy x y x z x z y z y x y x x z z y x y y x z x x z y z z y y z x z z y x y z x y x z y x z y x z y x L i L L L i L L L i L L k L j L i L i k L L j L L i L L k L L L L j L L L L i L L L L i L L j L L i L L k L L j L L k L L k L j L i L k L j L i L L L k L j L i L L ===⇒++=++=-+-+-=-++--=++⨯++=⨯++=],[],[],[)(],[],[],[)()()()()(ˆˆˆ2):)()()(],[],[],[2x z z x xz z x x y x y x x y x L L L L i L L i L i L L L L L L L L L +=+=+=3. Calculate the possible angles betweenL and the z axis for l = 2.Answer:The possible angles between L and thez axis are equivalent the angles betweenL and L z . Hence, the angles are given by:Lm Cos L z ==+=θ6)12(2 ︒︒︒︒=7.144,10.114,00.90,91.65,26.35θ 4. Complete this equation:m l m l z Y m Y L 333ˆChapter 061. Explain why each of the following integrals must be zero, where the functions are hydrogenlike wave functions: (a) <2p 1|z L ˆ|3p -1>; (b) <3p 0|z L ˆ|3p 0>Answer:Both 3p -1 and 3p 0 are eigenfunctions of L z , with eigenvalues of -1 and 0, respectively. Therefore, the above integrals can be simplified asa) due to orthogonalization properties of eigenfunctions03|213ˆ21111=-=--p p p L p z b) 02. Use parity to find which of the following integrals must be zero: (a)<2s |x |2p x >; (b) <2s |x 2|2p x >; (c)<2p y |x |2p x >. The functions in these integrals are hydrogenlike wave functions.Answer:1) b) and c) must be zero.3. For a hydrogen atom in a p state, the possible outcomes of a measurement of L z are – ħ, 0, and ħ. For each of the following wave functions, give the probabilities of each of these three results: (a)z p 2ψ; (b) y p 2ψ; (c) 12p ψ. Then find <L z > for each of these three wave functions.Answer:a) 022p p z ψψ=, therefore, the probabilities are: 0%, 100%, 0% )(2111222-+=p p p x ψψψ, the probabilities are 50%, 0%, 50%.12p ψ,the probabilities are 100%, 0%, 0% b) 0,0,14. A measurement yields 21/2ħ for themagnitude of a particle’s orbital angular momentum. If L x is now measured,what are the possible outcomes?Answer:1): Since the wavefunction is the eigenfunction of L2, a measurement of the magnitude of the orbital angular momentum should be+LLL=)1⇒21 (=,The possible outcomes when measure L x are-1, 0, 1Chapter 071. Which of the following operators areHermitian: d /dx , i (d /dx ), 4d 2/dx 2,i (d 2/d x 2)?Answer :An operator in one-D space is Hermitianif⎰⎰=dx A dx A **)ˆ(ˆψψψψ a)⎰⎰⎰⎰-=-=-=∞∞-dx dx d dx dx d dx dx d dx dxd *****)(ψψψψψψψψψψ b)⎰⎰⎰⎰=-=-=∞∞-dx dx d i dx d i dx dx d i i dx dx d i ****)(ψψψψψψψψψψc)⎰⎰⎰⎰⎰=+-=-=-=∞∞-∞∞-dxdxddxddxddxdxddxddxddxddxddxdxdψψψψψψψψψψψψψ2*22****22*44 444 44This operator can be written as a product of 1D kinetic operator and a constant. Hence, it’s Hermitian.d) As the third operator is Hermitian, this operator is not Hermitian.2. If Aˆ and Bˆ are Hermitian operators, prove that their product AˆBˆ is Hermitian if and only if Aˆ and Bˆcommute. (b) If Aˆ and Bˆ are Hermitian,prove that 1/2(A ˆB ˆ+B ˆA ˆ) is Hermitian. (c)Is x px ˆˆHermitian? (d) Is 1/2(x p x ˆˆ+x p xˆˆ) Hermitian?Answer:1)If operator A and B commute , we have⎰=-⇒=-⇒=0])ˆˆˆˆ[(0ˆˆˆˆˆˆˆˆˆ*τψψd A B B AA B B A A B B A ⎰⎰⎰=⇒=-⇒τψψτψψτψψd A B d B A d A B B A ***]ˆˆ[]ˆˆ[0])ˆˆˆˆ[( Operator A and B are Hermitian, we have⎰⎰⎰==⇒τψψτψψτψψd B A d B A d A B ˆˆ)ˆ()ˆ(]ˆˆ[***Therefore, when A and B commute, thefollowing equation fulfills. Namely, ABis also Hermitian.⎰⎰=τψψτψψd B A d B A ˆˆ]ˆˆ[** 2)]ˆˆˆˆ[21)]ˆˆˆˆ(21[***⎰⎰⎰+=+τψψτψψτψψd A B d B A d A B B AOperator A and B are Hermitian, we get⎰⎰⎰⎰⎰⎰⎰+=+⇒+=+=+τψψτψψτψψτψψτψψτψψτψψd A B B A d A B B A d B A A B d B A d A B d A B d B A *******])ˆˆˆˆ(21[)ˆˆˆˆ(21])ˆˆˆˆ(21[)ˆˆ()ˆˆ([21]ˆˆˆˆ[21The above equation shows that theoperator 1/2[AB+BA] is Hermitian.c) xp x is not Hermitian since both x andpx are Hermitian and do not commute.d) YesChapter 081. Apply the variation function cr e -=φtothe hydrogen atom; choose the parameterc to minimize the variational integral,and calculate the percent error in theground-state energy.Solution :1) The requirement of the variationfunction being a well-behaved functionrequires that c must be a positivenumber.2) check the normalization of the variation function.322*)(c d d Sin dr r e d cr πϕθθτφφ==⎰⎰⎰⎰- 3) The variation integral equals to)2(214])2[(2)1(21()121(ˆ32223*32*32*3**-=-∂∂+∂∂-=-∇-=-∇-==⎰⎰⎰⎰⎰⎰--c c c dr r e rr r e c d r c c d r c d d H w cr cr τφφπφπτφφπτφφτφφ4) The minimum of the variation integral is 21101-=⇒=⇒=-=∂∂w c c c w5) The percent error in the ground stateis 0%2. If the normalized variation functionx l 2/13)/3(=φ for 0 ≤ x ≤ l is applied tothe particle-in-a-one-dimensional-boxproblem, one finds that the variationintegral equals zero, which is less thanthe true ground-state energy. What is wrong?Solution:The correct trail variation function must be subject to the same boundary condition of the given problem. For the particle in a 1D box problem, the correct wavefunction must equal to zero at x=0 and x=l. However, the trial variation function x l 2/13)/3(=φ does not fulfill these requirement. The variation integral based on this incorrect variation function does not make any sense.3. Application of the variation function 2cx e -=φ(where c is a variationparameter) to a problem with V = af (x), where a is a positive constant and f (x ) is a certain function of x , gives thevariation integral as W = c ħ2/2m+15a /64c 3. Find the minimum value of Wfor this variation function.Solution:23434123434141min 4141413272598.03)25(23)25(0)64152(m a m a w m a c dc c a m c d c w ==⇒±=⇒=+=∂∂4. In 1971 a paper was published that applied the normalized variationfunction N exp(-br 2a 02-cr /a 0) to thehydrogen atom and stated that minimization of the variation integral with respect to the parameters b and c yielded an energy 0.7% above the true ground-state energy for infinite nuclear mass. Without doing any calculations, state why this result must be wrong. Solution:From the evaluation of exercise 1, we know that the variation function exp(-cr) gives no error in the ground state of hydrogen atom. This function is a special case of the normalized variationfunction N exp(-br 2a 02-cr /a 0) when bequals to zero. Therefore, adopting the normalized variation function as a trial variation function should also have no error in the ground state energy for hydrogen atom.5. Prove that, for a system with anondegenerate ground state, 0*ˆE d H >⎰τφφ, ifφ is any normalized, well-behaved function that is not equal to the true ground-state wave function. (E 0 is thelowest-energy eigenvalue of H ˆ) Solution:As the eigenfunctions of the Hermitian operator H form a complete set, any well-behaved function which is subjectto the same boundary condition can be expanded as a linear combination of the eigenfunction of the Hermitian operator, namely,∑∞==0i i i c ψφ, where i s are eigenfunctions of Hermitian operator H, c i s are constant.The expectation valueof with respect to the Hermitian operator is0201020201020020*00**00*0*0*ˆˆ)(ˆE c E E c E c c E c E c E c c E c cH c c d c H c d H i i i i i i i i i i i i i ij j j j i i i j j i i j j j i i i ==+>+======∑∑∑∑∑∑∑⎰∑∑⎰∑∑⎰∞=∞=∞=∞=∞=∞=∞=∞=∞=∞=∞=δψψτψψτφφChapter 09, 101. For the anharmonic oscillator with Hamiltonian43222212ˆdx cx kx dx d m H +++-= , evaluate E (1) for the first excited state, taking the unperturbed system as the harmonic oscillator.Solution:The wavefunction of the first excited state of the harmonic oscillator is241312)4(x xe απαψ-=Hence, the first order correct to energy of the first excited state is given by6213422134134324131'*1415)4()4()4)(()4(ˆ222απαπαπαπαψψαααd dx e x d dx x d e x xe x d x c xe dx H x x x ==∙=∙+∙=---⎰⎰⎰⎰2. Consider the one-particle, one-dimensional system withpotential-energyV = V 0 for l x l 4341<<, V = 0 for l x 410≤≤ and l x l ≤≤43and V = ∞ elsewhere, where V 0 = 22/ml .Treat the system as a perturbed particle in a box. (a) Find the first-order energy correction for the general stationary state with quantum number n . (b) Find the first-order correction to the wave function of the stationary state with quantum number n .Solution:The wavefunction of a particle in 1D box is given by)(2)0(x ln Sin l n πψ= Take this as unperturbed wavefunction, and the perturbation H ’ is given by V. a) The first-order energy correction forn is])23[]2[(224]2[4[2)()(2)()(2ˆ00004341)0('*)0()1(πππππππππψψn Sin n Sin n V V n S n Sin l l V dx V x l n Sin x l n Sin l dx x ln VSin x l n Sin l dx H E l ln n -+=-+====⎰⎰⎰b) The first correction to the wavefunction is given by)0()0()0()0()0()1(2)0()0(222)0('(818mn m mn nm n mn n E E H n E E ml h n E ψψψψ∑∞≠-==-⇒=3. For an anharmonic oscillator with3222212ˆcx kx dx d m H ++-= , take 'ˆH as cx 3. (a) Find E (1) for the state with quantum number v .(b) Find E (2) for the state with quantumnumber v . You will need the following integral:3,'2/13)0(3)0('2/)1[(3]8/)3)(2)(1[(||++++++>=<v v v v v v v v x αδαψψ1,'2/38/)2)(1([)2/(3---++v v v v v v αδα Solution: a) As the potential of the unperturbed is a even function, the eigenfunctions of the unperturbed system are either even or odd. The perturbation is an odd function with respect to x. Hence, thefirst order energy correction is zero.b) The second order energy correction is given by)51212(8]38)2)(1(838)1(338)3)(2)(1([()2(3)21(38)3)(2)(1((''2323333332)0()0(1,2/31,2/33,32)0()0(2)0(3)0()0()0()0()0()0()0()2(++-=--++-++-+++=-+++++++=-=-=∑∑∑∞≠-++∞≠∞≠n n hvc hvn n n hv n hv n hv n n n c E E n n n n n n n c E E cx E E H H E n m mn n n n n n n n m mn m n n m m n m n nm n αααααδαδαδαψψψψψψ4. Calculate the angle that the spin vector S makes with the z axis for an electron with spin function α.Solution:For an electron, both S and S z equal to one half. The magnitude of S is74.54]31[23)1(===+=ArcCos S S S θ5. (a) Show that 12ˆP and 23ˆP do not commutewith each other. (b) Show that 12ˆPand 23ˆP commute when they are applied to antisymmetric functions. Solution:a) Set the wavefunction to be)1()3()2()2()1()3(321321φφφφφφ≠b) When the function is antisymmetric, we haveψψψψψψψ2312121223231223ˆˆ)(ˆˆˆ)(ˆˆˆP P P P P P P P =-=-==-=-=6. Which of the following functions are (a) symmetric? (b) antisymmetric?(1) )2()1()2()1(ααg f ; (2) )]2()1()2()1()[2()1(αββα-f f ;(3) )3()2()1()3()2()1(βββf f f ; (4) )(21r r a e --;(5) )]1()2()2()1()][2()1()2()1([βαβα--f g g f ; (6) )(21221r r a e r +-. Solution:(2) is antisymmetric(3), (5) and (6) are symmetricChapter 11, 131. How many electrons can be put in each of the following: (a) a shell with principal quantum number n ; (b) a subshell with quantum numbers n and l ; (c) an orbital; (d) a spin-orbital? Solution:a) 2n 2, b) 2*(2l+1), c) 2, d) 12. Give the possible values of the total-angular-momentum quantum number J that result from the addition of angular momentum with quantum numbers (a) 3/2 and 4; (b) 2, 3, and 1/2 Solution:Coupling between two angular momentums with quantum number j 1 and j 2 gives the possible quantum number J of the total angular momentum as:2121j j J j j +<<-a) The possible values are 11/2, 9/2, 7/2,5/2b) The possible values are:11/2, 9/2, 9/2, 7/2, 7/2, 5/2, 5/2, 3/2, 3/2, 1/23. Find the terms that arise from each of the following electron configurations: (a) 1s22s22p63s23p5g; (b) 1s22s22p3p3d (c) 1s22s22p24dSolution:As fully-filled sub-shells do not contribution the total orbital and spin angular momentum, we can ignore the electrons in these sub-shells while considering the atomic terms. Hence, a) The atomic terms can be:3H, 1H, 3G, 1G, 3F, 1Fb) The atomic terms can be:4G, 2G, 4F, 2F, 4D, 2D, 4P, 2P, 4S, 2S4F 2F, 4D, 2D, 4P, 2P4D, 2D, 4P, 2P, 4S, 2Sc) The atomic terms can be:。
