拟合威布尔随机寿命S-N曲线的新算法
合集下载
结合S-N曲线和断裂力学的焊接结构疲劳寿命分析
基金项 目： 国家 自然科学基金 资助项 目（ ５ １ ５ ７ ５ ４ ０ ８ ） ； 湖北省 自 然 科 学基金资助项 目（ ２ ０ １ ４ Ｃ Ｆ Ｂ ８ ０ ３ ） ； 武汉工程大学化 工装 备 强 化 与 本 质 安 全 湖 北 省 重 点 实 验 室 开 放 课 题
提 出一 种 新 此外 ， 一些 学者 基于 断裂力 学理 论 ， 将 焊 接结 构 的寿 裂 纹萌 生和扩 展 ２个 不 同 阶段 的寿 命 ， 命定义为初始裂纹扩展至临界尺寸 的循环次数 ， 采 的疲劳寿命分析方法．
用Ｐ ａ ｒ ｉ ｓ 模型进行积分求解．这种方 法在描述焊接 结构裂纹萌生和短裂纹断裂行为方面还存在许多不 完善 的地方．首先不同学者对焊缝初始裂纹长度给 出了不 同的假设 （ 覆盖 ０ ． １—０ ． ５ ｍ ｍ） Ｊ ， 这 给疲 劳
问题 ．
制参量 ， 提 出了一 种 统 一 的跨 尺度 裂 纹 模 型 及 其 求
常用 的疲 劳评 定 方 法 有 名 义应 力 法 、 热 点 应 力 解 算法 ． 与 文献 中较 常 出现 的焊 接 接 头 不 同 ， 工 程 实 践 法、 结构应 力法 等 － ４ Ｊ ， 这 些方 法都 基 于特 定 焊接 接
第３ ８ 卷 第２ 期
２ ０ １ ７年 ２ 月
焊 接 学 报
Ｔ ＲＡＮ Ｓ ＡＣ Ｔ Ｉ ＯＮ Ｓ ＯＦ Ｔ ＨＥ Ｃ ＨＩ ＮＡ ＷＥ Ｌ ＤＩ Ｎ Ｇ Ｉ ＮＳ Ｔ Ｉ Ｔ Ｕ Ｔ Ｉ Ｏ Ｎ
Ｖ ｏ １ ． ３ ８ Ｎ 。 ． ２
Ｆ ｅ ｂ ｒ ｕ ａ ｒ ｙ ２ ０ １ ７
裂纹 的萌 头类 型 的 Ｓ ． Ｎ 曲线 ， 没有 考 虑 焊 缝 细 节几 何 形 貌 尤 中焊接结构的构造和应力状况更为复杂 ， 采 用 上 述 方 法 进 行 疲 劳 其是初始裂纹状态的影响．彭凡 等人 基于 Ｔ ａ ｙ ｌ ｏ ｒ 生 和扩 展模式 有 很 大不 同 ，
利用EXCE的规划求解进行求解威布尔分布参数
于产品寿命有γ ≥ 0 ,γ =0 时退化为二参数 威布尔分布； t 是产品的工作时间， t ≥ γ 。
当m<1 时， 由式( 3 ) 给出的失效率是递减型的，适合于 建模早期失效；当m=1 时， 失效率为常数，即退化为指 数分布，适合于建
模随机失效；当m>1 时，失效率是递增的， 适合于建模磨耗或老 化失效。
设有n 个产品进行寿命试验数据，按失效时间先后得到的寿 命数据
失效时间(顺序统计 量)为 n t ≤ t ≤Λ ≤ t 1 2 ，对应 的累计失效概率(经验分布函数)为( ) ( ) ( )
1 2 n F t ≤ F t ≤Λ ≤ F t 。
其中到第i 个产品失效时的累计失效概率F(ti )可用中 位秩算
2）使用“规划求解”功能估计位置参数γ ⑴ 选择“工具→规划求解”功能打开规划求
解参数对话框，目标单元格设为$I$10，目 标值设为0， 可变单元格设为$I$8:$B$2。
⑵ 对于产品寿命有1 0 ≤&gamma
; < t ，故单击约束条件“添加”按钮，添加约束条件： $I$8<=$B$2 和$I$8>=0；
i x ⋅ y ； ⑼ 在C7 单元格中输入公式 “=AVERAGE(C2:C6)”，C7 单元格的值为x ； ⑽ 在C8 单元 格中
输入公式“=SUM(D2:D6)”，C8 单元格的值为Σ= n i i x ` 2 ； ⑾ 在C9 单元格中输入公式“=AVER
AGE(F2:F6)”，C9 单元格的值为y ； ⑿ 在C10 单元格中输 入公式“=SUM(G2:G6)”，C10 单元格的值为&Sigma
焊接结构主s-n曲线拟合方法及软件开发
(1)厚度修正
∆S s
=
∆σs t(2−m)/2m
(6)
N = (∆S s/Cd)1/h
(5)
式 中 ： Cd， h为 通 过 试 验 数 据 拟 合 的 主 S-N 曲 线
(2)弯曲比修正
∆S s
=
∆σs I(r)1/m
(7)
常数.
(3) 多轴应力修正
∆S s
=
F
1 (δ)
(
t
2−m 2m
)
∆σk
针对上述原始试验数据，建立了数据库，并开 发了专用的主 S-N 曲线拟合软件，以该软件提供的 数据库为基础，开发了计算结构应力、等效结构应
收稿日期：2019 − 10 − 18 基金项目：辽宁省自然科学基金项目 (20170520162)；大连市高层次人才
计划项目 (2017RQ132)
力、等效剪切结构应力及等效多轴结构应力的算法 程序；采用最小二乘法原理，开发了主 S-N 曲线拟 合程序. 通过对比不同拟合算法的标准差，得到主 S-N 曲线方程各参数，提高了主 S-N 曲线的拟合精 度. 另外，所开发的软件还具有完备的数据分析功 能，其专用数据分类模块，可对不同的焊接工艺、不 同的焊后处理方法及不同的板厚等参数进行对比 分类，还可用于研究不同分类形式及不同拟合算法 的主 S-N 曲线方程. 该软件为研究焊接结构疲劳寿 命的影响因素及计算方法提供了高效分析工具，并 取得了良好的应用效果.
Fig. 1
σx
σb
σm
σn
σs = σb + σm
式中：a为裂纹长度；N 为循环次数；C为试验常数； n，m 由典型裂纹的试验数据确定；∆K为应力强度
图 1 焊趾处应力分布及结构应力定义 Stress distribution and structural stress definition
S-N疲劳曲线的数学表达式处理方法探讨
S-N疲劳曲线的数学表达式处理方法探讨
张亚军
【期刊名称】《理化检验-物理分册》
【年(卷),期】2007(043)011
【摘要】介绍了S-N曲线的一般数学表达形式.将最常用的幂函数表达式Sm·N=C变换成了标准幂函数形式S=C1/m·N-1/m,用该式和标准幂函数式
S=C·Nm拟合处理了三种材料焊接接头的疲劳试验数据.对处理结果的比较发现,拟合处理方法不同,得到的S-N曲线的具体表达式也完全不同.按前式拟合得到标准离差比后者普遍偏大,根据该曲线方程确定的条件疲劳强度比后者普遍偏小.为工程应用中进行疲劳设计时,对S-N曲线方程拟合方法的选择提供了依据.
【总页数】3页(P563-565)
【作者】张亚军
【作者单位】西安交通大学,西安,710049;洛阳船舶材料研究所,洛阳,471039【正文语种】中文
【中图分类】O346.2
【相关文献】
1.轴承用20CrMoH钢S-N疲劳曲线的拟合 [J], 郑程;黄旭东
2.标称应力法中构件S-N疲劳曲线的预测 [J],
3.燃机传动系统17CrNiMo6齿轮材料不同热处理R-S-N疲劳曲线测试研究 [J], 刘韶峰;胡云波;邹俊伟;郑学斌
4.工业测控软件中的字符型数学表达式处理 [J], 方志宏;方路平
5.科技论文中过长数学表达式的处理 [J], 姜丰辉
因版权原因，仅展示原文概要，查看原文内容请购买。
第三讲 P-S-N曲线,疲劳统计学
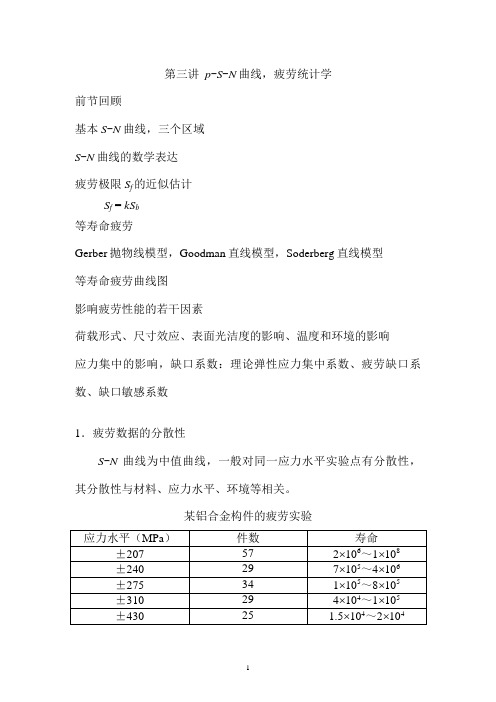
第三讲p-S-N曲线，疲劳统计学前节回顾基本S-N曲线，三个区域S-N曲线的数学表达疲劳极限S f的近似估计S f = kS b等寿命疲劳Gerber抛物线模型，Goodman直线模型，Soderberg直线模型等寿命疲劳曲线图影响疲劳性能的若干因素荷载形式、尺寸效应、表面光洁度的影响、温度和环境的影响应力集中的影响，缺口系数：理论弹性应力集中系数、疲劳缺口系数、缺口敏感系数1．疲劳数据的分散性S-N曲线为中值曲线，一般对同一应力水平实验点有分散性，其分散性与材料、应力水平、环境等相关。
某铝合金构件的疲劳实验应力水平低则寿命 长，分散性也大，在同 样应力水平下，疲劳寿 命可以相差几十到几百 倍。
2．p -S -N 曲线p -S -N 曲线是组成不同成活率p 下的S -N 曲线集，这一曲线集给出了：1）在给定应力水平下失效循环次数N 的分布数据；2）在给定的有限寿命下疲劳强度S 的分布数据；3）无限寿命或N > N L 的疲劳强度－疲劳极限的分布数据。
p -S -N 曲线由成组实验获得。
p -S -N 曲线在有限寿命段（103 < N <106）在双对数坐表系上近似为直线。
3．疲劳寿命与疲劳强度 概率分布之间的关系疲劳破坏是疲劳损伤 逐渐累积的结果，材料中 宏观或微观的不可逆变形 是疲劳损伤的主要形式。
lg NSlg NS疲劳寿命概率分布：在给定疲劳强度下构件的疲劳寿命概率分布形式。
一般可由疲劳实验获得。
疲劳强度概率分布：在给定疲劳寿命下构件的疲劳强度概率分布形式。
设在一疲劳荷载作用下，构件在给定疲劳强度S *下的疲劳寿命N 的概率分布密度为f (n |S *)，而在给定疲劳寿命N *下的疲劳强度S 的概率分布密度为g (s |N *)，则可以证明ds N s g dn S n f S N )()(***0*⎰⎰=即在给定的疲劳强度S *下 疲劳寿命N 小于或等于N *的 概率与在给定的疲劳寿命N * 下疲劳强度S 小于或等于S * 的概率相等。
强度理论-应力寿命法2
2. 尺寸效应
一样可用高应力区体积旳不同来解释。 应力水平相同步，试件尺寸越大，高应力 区域体积越大。 疲劳发生在高应力区材料最单薄处，体积 越大，存在缺陷或单薄处旳可能越大。
尺寸效应能够用一种修正因子Csize体现为：
Csize=1.189d-0.097
8mmd250mm
当直径d<8mm时，Csize=1。
N=C/Sm=1.536×1025/568.47.314=1.09×105 (次)
影响疲劳性能旳若干原因
1. 载荷形式旳影响
Sf（弯）＞Sf（拉）
疲劳破坏主要取决于 作用应力旳大小和材料抵 抗疲劳破坏旳能力。
拉压循环高应力区体积大，存在缺陷并引起裂 纹萌生旳可能大、机会多。所以，一样应力水平作 用下，拉压循环载荷时寿命比弯曲短；或者说，一 样寿命下，拉压循环时旳疲劳强度比弯曲情况低。
Goodman 0
1 Sm/Su
对于其他给定旳N，只需将S-1换成Sa(R=-1)即可。 利用上述关系，已知Su和基本S-N曲线，即可估计 不同Sm下旳Sa 或SN。
例2.1: 构件受拉压循环应力作用，Smax=800 MPa, Smin=80 MPa。 若已知材料旳极限强度为 Su=1200 MPa，试估算其疲劳寿命。
S=A+B lg N
（半对数线性关系）
S
Sf 3 4 5 6 7 Lg N
3) 三参数式 (S-Sf)m.N=C
考虑疲劳极限Sf，且当S趋近于Sf时，N。
最常用旳是幂函数式。 高周应力疲劳，适合于 N>104-107。
3. S-N曲线旳近似估计
1)疲劳极限Sf与极限强度Su之关系
斜线OA+水平线AB R=-1，旋转弯曲时有：
基于疲劳强度分布假设的P-S-N曲线模型
PSN
关键词： 疲劳强度; - 中图分类号院0211
P S N 曲线； 极大似然法； 正态分布 文 献 标 志 码 :A 文章编号院2095-2945 (2017)27-0020-02
1 概述 由于不确定因素的影响，材料的疲劳性能数据存在很大的 分散性。概率疲劳性能曲线是结构疲劳寿命预测和可靠性分析 的重要基础。P-S - N 曲线拟合问题已有大量研究， 常用的是最小 二乘法和极大似然法。 傅惠民等™对疲劳寿命和疲劳强度的百分位值进行最小二乘 法拟合得到三参数的 P- S - N 曲线。文献[2]中的双加权最小二乘 法考虑了样本容量和试验结果分散性的影响， 可以处理包含成组 法和升降法在内的疲劳试验数据。 N e lson 假设疲劳寿命服从对数正态分布，提出了一种拟合 包含截尾数据的极大似然法。Pascual等基于极大似然法原理提 出了一个随机疲劳极限(R F L M ) 模型。 最小二乘法在拟合 P- S - N 曲线时没有考虑疲劳寿命分散性 的变化规律， 数据有限时会出现曲线对数寿命标准差为负或应力 水平越高对数标准差越大的反常情况。 此外， 若疲劳试验没有按照成组法或升降法来进行， 最小二 乘法也会失效。 上述的几种极大似然法模型对升降法试验数据的处理无能 为力。一般认为疲劳寿命服从对数正态分布或威布尔分布， 但是 当应力水平趋于疲劳极限时， 这一假设不再合理， 传统的疲劳寿 命分布假设无法描述低应力水平的P- S - N 曲线。 本文以疲劳强度的分布假设为基础提出了一个新的极大似 然法模型，该模型合理地描述了中长寿命区和疲劳极限附近的 P- S - N 曲线， 同时对试验方法没有限制， 可以处理包含单点法、 成 组法、 升降法和截尾数据在内的疲劳试验数据。 2 疲劳强度分布假设 2.1 传统极大似然法 大量的金属材料疲劳性能曲线的研究表明，中长寿命区的 P_S - N 曲线可采用三参数公式来描述
几种有效的P_S_N曲线的数据处理方法
个 对 应 关 系, 不 同 的 质 量 对 应 不 同 的 u p , u p 符 合 由此得出的结果可以推广到其 N ( 0, 1) 标准正态分布。 他对称分布。
lg N = c + m lg S + u p ΡN ΡN = a + b lg S 式中 c, m , a , b ——与材料和结构有关的系数 ΡN ——对数寿命标准差 211 母体分布参数的选取 21111 给定应力试验 给定应力试验时, 将应力水平 ( 1)
为本文通过计算机模拟试验对以上问题进行了较详细的讨论和分析提出了一些切实可用的数据处理方2模拟试验的基础大量的疲劳试验得出材料或简单结构的疲劳寿命符合对数正态分布因此模拟试验中采用了对数正态分布模型即认为试样的质量与up通过式1个对应关系不同的质量对应不同的upup符合标准正态分布
第21卷第1期
1999 年 3 月
L F10M nSiT i1111242 5 - 361849 8 81457 4 20C r2N i4A 241989 0 - 71413 0 ZG25 19114 - 5184
对焊接头 丁字接头
141298 9 - 31632 0 121748 6 - 21946 9
01464 4 - 01086 99 01273 9
机 械 强 度
JOU RNAL O F M ECHAN ICAL STR EN GTH
. 21 Vol M a rch
N o. 1 1999
几种有效的 P —S —N 曲线的数据处理方法
Ξ
SEVERAL USEFUL STAT IST ICAL M ETHOD S USED FO R D EAL ING W ITH P —S —N CURVE
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3. G20CrNi2Mo 轴承钢的 S-N 曲线
3.1. G20CrNi2Mo 轴承钢疲劳寿命的威布尔分布
赵永翔和梁红琴的疲劳寿命数据见表 1。
212
王桂金 Table 1. Fatigue life of G20CrNi2Mo steel under four levels of cyclic stress 表 1. G20CrNi2Mo 轴承钢在四种交变应力下的疲劳寿命，107 cycles
2. 两参数威布尔分布的拟合
2.1. 极大似然法
设已知一组失效寿命序列(时间或转数) t1 , t2 , , tn ， 分别对应于累计失效率 f ( t1 ) , f ( t2 ) , , f ( tn ) 。 对
211
王桂金
下述极大似然法公式(2)进行迭代计算可获得两参数威布尔分布的最佳参数 κ ，然后将所得参数 κ 代入式 (3)算出尺寸参数 λ 。为保证结果可靠，本文计算进行到式(2)左边绝对值小于 10−5 后停止[7]，
1 + ∑ ln ( t ) − ∑ t ln ( t ) κ N 1
N N k N k i i i 1= i 1 i= i 1 i =
0 (∑ t ) =
(2)
1 N λ = ∑ i=1 tik N
为了评价威布尔分布参数拟合的优劣，本文建议采用如下拟合指数 η ：
= η
(η1 + η2 )
2
(6)
式中 η1 = κ ( γ 1 ) κ ， η2 = κ ( γ 2 ) κ 并且 κ ( γ 1 ) ， κ ( γ 2 ) 分别是试验数组内禀斜度和峭度的形状参数， κ 是 拟合的威布尔形状参数。显然，当 η1 和 η2 皆为 1 或接近 1 时威布尔形状参数 κ 拟合结果最佳。两参数威 布尔分布难以达到最佳拟合，这样就需要引入非零位置参数 to (三参数威布尔分布)以及名义全失效寿命
origin 0.588 0.943 1.460 2.90 3.41 3.42 3.67 4.10 6.57 7.42 7.51 8.50 13.50 21.10
norm* 0.0916 0.1469 0.2274 0.4517 0.5312 0.5327 0.5717 0.6387 1.0234 1.1558 1.1698 1.3204 2.1029 3.1154
origin 0.877 1.50 2.48 5.40 6.49 6.52 7.07 8.02 13.70 15.80 16.00 18.40 31.20 52.00
2
norm* 0.0645 0.1104 0.1825 0.3974 0.4776 0.4798 0.5202 0.5901 1.0081 1.1626 1.1773 1.3539 2.2958 3.9735
2.2. 威布尔分布的斜度和峭度
已知形状参数为 κ 的威布尔分布具有斜度 skewness：
3 2 γ1 = Γ3 − 3Γ 2 Γ1 + 2Γ1 Γ 2 − Γ1 32
(4)
而过盈峭度 excess kurtosis (以下简称峭度)是[6]：
γ2 =
{( Γ − 4Γ Γ + 6Γ Γ − 3Γ ) ( Γ − Γ ) } − 3
th th th
Abstract
This paper presents a new approach to build up S-N curve by first fitting fatigue datasets to three parameter Weibull distribution under the scheme of adjusting location parameter and maximum fatigue life to match the shape parameter of skewness and kurtosis from sample fatigue data with that of fitted Weibull distribution. Thereafter, the dimensional parameter of the Weibull distribution under various cyclic stresses can be used to calculate S-N curve, its expected standard deviation and accumulated failure life rate L10, L63, L90. This new approach has been justified due to available experimental data of Zhao etc.
New Approach for S-N Curve after Fitting Random Fatigue Life Data to Weibull Distribution
Guijin Wang
Alloy Steels Department, Central Iron & Steel Research Institute, Beijing Received: Jun. 9 , 2017; accepted: Jun. 24 , 2017; published: Jun. 28 , 2017
王桂金
为各组试样数据已符合威布尔分布，可以根据尺寸参数随应力的变化计算S-N曲线并计算标准差及预期 寿命L10，L63和L90。本文以赵永翔等人的数据为例，说明如何应用这种新算法。
关键词
S-N曲线，威布尔分布，斜度和峭度，拟合指数
Copyright © 2017 by author and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). /licenses/by/4.0/
*
origin 2.25 3.88 6.42 14.1 17.0 17.0 18.5 21.0 36.1 41.6 42.1 48.6 82.9 139.0
norm* 0.0628 0.1083 0.1793 0.3937 0.4747 0.4747 0.5166 0.5864 1.0081 1.1617 1.1756 1.3572 2.3150 4.0491
origin 0.163 0.288 0.372 0.438 0.598 0.799 1.39 1.83 5.07 5.73 6.61 7.07 10.3 17.9
norm* 0.2114 0.2342 0.2495 0.2615 0.2906 0.3271 0.4346 0.5146 1.1037 1.2237 1.3837 1.4673 2.0546 3.6364
Open Access
1. 引言
自从 Wohler 在 1870 年提出材料疲劳寿命和所加交变应力存在一定关系之后，各国科学家一直寻求 其最合适的表达式[1] [2] [3] [4]。然而，由于疲劳样本容量以及试验机运行时间的限制，常常得不到满意 结果。后来美国 ASTM 提出可由定幅交变应力(应变)下 N 个疲劳数据先求出平均值及标准差，如果对数 平均寿命和对数应力(应变)之间存在线性关系， 则可认为各组疲劳命数据服从对数正态分布或者威布尔分 布[1] [3] [4]。但是由于样本小没能合理验证寿命数据的分布函数，结果不理想。为了改进威布尔寿命数 据拟合精度，本作者发展一种新算法，通过调整位置参数和名义最大寿命数据(99%)使得三参数威布尔形 状参数 κ 和疲劳数据内禀斜度/峭度形状参数一致[5]。在这个基础上，就可以计算 S-N 曲线及其标准差和 预期寿命 L10，L63 和 L90。
Statistics and Application 统计学与应用, 2017, 6(2), 210-218 Published Online June 2017 in Hans. /journal/sa https:///10.12677/sa.2017.62024
1κ
(3)
由于威布尔分布只在 t 趋近无限大时才等于 100%，为了方便，本文设定满足 f ( t f ) = 99% 的 t f 为名 义全失效寿命。极大似然法能够保证似然函数极大，但不能保证拟合威布尔曲线和试验寿命的分布形状 也一致。因此有必要对试验寿命以及拟合分布曲线的斜度和峭度进行计算和比较。
f (t ) = 1 − exp ( t λ ) ( λ, t,κ ) > 0
κ
{
}
(1-2)
进一步令 t 以 λ 为单位计数，则得到归一化单参数威布尔分布：
f (t ) = 1 − exp −t κ
( ) (t,κ ) > 0
(1-3)
威布尔失效密度分布就是上述诸式对时间 t 的导函数。威布尔分布参数的各种估算方法已经被详细 研究过了[6] [7]。现在广为应用的是极大似然法。
Keywords
S-N Curve, Weibull Distribution, Skewness and Kurtosis, Fitting Indicator
拟合威布尔随机寿命S-N曲线的新算法
王桂金
原钢铁研究总院合金钢室，北京
收稿日期：2017年6月9日；录用日期：2017年6月24日；发布日期：2017年6月28日
摘
要
本文对不同定幅交变应力下的疲劳寿命数据， 采取调整位置参数和最大寿命值的方法使其数据内禀斜度/ 峭度的形状参数与极大似然法拟合的三参数威布尔分布的形状参数一致，进而建立相应的S-N曲线。因
文章引用: 王桂金. 拟合威布尔随机寿命 S-N 曲线的新算法[J]. 统计学与应用, 2017, 6(2): 210-218. https:///10.12677/sa.2017.62024