高等数学第八章多元函数积分学优秀课件

《高等数学》第八章(上)多元函数微积分简介

第一节空间解析几何简介
在空间任取一点 M，过点 M 分别作与坐标轴垂直的平面，交 x 轴、y 轴和 z 轴于点 P，Q，R，如图所示．点 P， Q，R 称为点 M 在三条坐标轴上的投影．设点 P，Q，R 在三条坐标轴上的坐标分别记为 x，y，z，于是点 M 确定了唯一的有序数组 (x ，y ，z) ；反之，给定一个有序数组 (x ，y ，z) ，总能在 x 轴、y 轴和 z 轴上分别确定以 x，y，z 为坐标的三个点 P，Q，R，过这三个点分别作垂直于 x 轴、 y 轴和 z 轴的平面，这三个平面必相交于唯一一点 M．
第一节空间解析几何简介
一、空间直角坐标系
三个坐标面把空间分成八个部分，每一部分称为卦限，含有三个正半轴的卦限称为第一卦限，它位于 xOy 面的上方．在 xOy 面的上方，按逆时针方向排列着第二卦限、第三卦限和第四卦限．在 xOy 面的下方，与第一卦限对应的是第五卦限，按逆时针方向还排列着第六卦限、第七卦限和第八卦限．八个卦限分别用字母Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、 Ⅵ、Ⅶ、Ⅷ表示，如图所示．
第一节空间解析几何简介
2．常见曲面的方程
1）球面在空间中到定点的距离等于定值的点的轨迹称为球面，定点称为球心，定值称为半径．例 3 建立球心在点 M0 (x0 ，y0 ，z0 ) 、半径为 R 的球面的方程．
特别地，球心在原点 O(0，0，0) 、半径为 R 的球面的方程为 x2 y2 z2 R2 ．
由于 M2M3 M1M3 ，所以原结论成立．
第一节空间解析几何简介
例 2 设点 P 在 x 轴上，它到点 P1(0 ， 2 ，3) 的距离为到点 P2 (0，1，1) 的距离的两倍，求点 P 的坐标．

第八章多元函数积分学.

第八章多元函数积分学基本课题：8 1 二重积分的概念与性质目的要求：理解二重积分的概念与性质重点：二重积分的性质难点：8 1 二重积分的概念教学方法：讲授与讨论结合教学手段：电子课件、黑板教参：《高等数学》(人大理工类本科教材) 教学环节及组织：复习并引入新课

一、二重积分的概念 1 曲顶柱体的体积设有一立体 它的底是xOy面上的闭区域D 它的侧面是以D的边界曲线为准线而母线平行于z轴的柱面 它的顶是曲面zf(x y) 这里f(x y)0且在D上连续 这种立体叫做曲顶柱体 现在我们来讨论如何计算曲顶柱体的体积 首先 用一组曲线网把D分成n个小区域：  1  2      n  分别以这些小闭区域的边界曲线为准线 作母线平行于z轴的柱面 这些柱面把原来的曲顶柱体分为n个细曲顶柱体 在每个 i中任取一点( i   i) 以f ( i   i)为高而底为 i的平顶柱体的体积为： f ( i   i) i (i1 2     n )

这个平顶柱体体积之和：iiinifV),(1 可以认为是整个曲顶柱体体积的近似值 为求得曲顶柱体体积的精确值 将分割加密 只需取极限 即 iiinifV),(lim10 其中是个小区域的直径中的最大值 定义设f(x y)是有界闭区域D上的有界函数 将闭区域D任意分成n个小闭区域  1  2      n  其中 i表示第i个小区域 也表示它的面积 在每个 i上任取一点( i i) 作和

iiinif),(1

如果当各小闭区域的直径中的最大值趋于零时 这和的极限总存在 则称此极限为函数f(x y)在闭区域D上的二重积分 记作dyxfD),( 即

《高等数学》第八章(上)

第一节空间解析几何简介
设点 M1(x1 ，y1 ，z1) 和 M2 (x2 ，y2 ，z2 ) 是空间两点，如图所示，则根据立体几何知识可知，长方体的各棱长分别为
| x2 x1 | ， | y2 y1 | ， | z2 z1 | ．长方体对角线的平方等于三条棱长的平方和，即
M1M2 (x2 x1)2 (y2 y1)2 (z2 z1)2 ．特别地，如果一点是原点 O(0，0，0) ，另一点是点 M (x ，y ，z) ，则
坐标面上和坐标轴上的点，其坐标各有一定的特征．例如，点 M 在 yOz 面上，则 x 0 ；在 zOx 面上的点，y 0 ；在 xOy 面上的点，z 0 ．如果点 M 在 x 轴上，则有 y z 0 ；在 y 轴上，有 z x 0 ；在 z 轴上，有 x y 0 ．如果点 M 为原点，则 x y z 0 ．
例如，方程 y2 2x 表示母线平行于 z 轴的柱面，它的准线是 xOy 面上的抛物线 y2 2x ，该柱面称为抛物柱面，如图所示．
第一节空间解析几何简介
又如，方程 x y 0 表示母线平行于 z 轴的柱面，其准线是 xOy 面的直线 x y 0 ，所以它是过 z 轴的平面，如图所示．
第一节空间解析几何简介
例 7 将 zOx 坐标面上的双曲线 x2 z2 1和 x2 z2 1 分别绕 z 轴旋转
a2 c2
c2
一周，求所生成的旋转曲面的方程．
解双曲线 x2 z2 1绕 z 轴旋转所得的旋转曲面的 a2 c2
方程为
x2 y2 a2
z2 c2
1，称此曲面为旋转双叶双曲面，如
所示．
第一节空间解析几何简介
2．一般二次曲面

高等数学_第八章_多元微分_第五节_隐函数求导

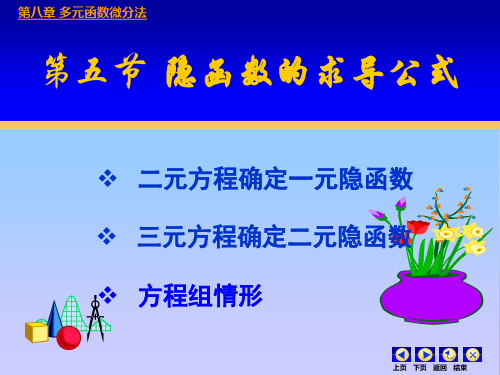
Fx F v Gx Gv
课本P34课本P34-P35 P34
Fy F v GyGv
F Fx u Gu Gx F u Gu
参见二元线性方程组的求解公式
Fy Gy
上页下页返回结束
例4. 设 x = e
u+v
, y =e
u+v
u−v
, z = uv , 求
u−v
解现在 z = uv , 式中 u = u(x, y), v = v(x, y)由方程由方程
z
z
F′⋅ 1 1 z
∂z =− y ∂y ′ F′⋅ (− x ) + F2 ⋅ (− 2 ) 1 2
z z
F′ ⋅ 1 2 z
′ z F2 = ′ x F′ + y F2 1
故
Fx ∂z ∂z ∂z z dz = dx + dy = =− (F′dx + F′dy) 1 2 ∂x ∂y x F′ + y F′ ∂x Fz 1 2
再对 x 求导
2+
∂z 2 1+ ( ) ∂x
∂2z −4 2 = 0 ∂x
上页
下页
返回
结束
解二利用隐函数求导公式设则
F(x, y, z) = x2 + y2 + z2 − 4z
Fx = 2x,
Fz = 2z − 4
∴
x x Fx ∂z = =− =− z −2 2− z ∂x Fz
两边对 x 求偏导
上页下页返回结束
微分法. 解二微分法对方程
两边求微分: 两边求微分
x y F′⋅ d( ) + F′ ⋅ d( ) = 0 2 1 z z zdx − xdz zdy − ydz F′⋅ ( ) + F′ ⋅( ) =0 1 2 z2 z2 ′ xF′+ yF2 F′dx +F′ dy 1 2 整理得 dz = 1 2 z z z dz = (F′dx + F′dy) 解得 1 2 x F′ + y F′ 1 2

同济版高数下册第八章课件

1 2
直角坐标系下的二重积分计算
通过将二重积分转化为累次积分，逐一计算x和y 方向的积分，得到最终结果。
极坐标系下的二重积分计算
利用极坐标与直角坐标的转换关系，将二重积分转化为极坐标形式，简化计算。
3
区域的可加性和可数性
利用二重积分的性质，将被积区域划分为若干个子区域，分别计算后再求和或求极限。
由矢量构成的场，每个点对应一个矢量。
标量场
由标量构成的场，每个点对应一个标量。
流场
由流线与矢量构成的场，描述流体运动状态。
梯度与散度
梯度
表示标量场中某点处函数增量的方向和大小，即函数在该点的变化率。
散度
表示矢量场在某点处发散的程度，即矢量场流入或流出的程度。
01
多重积分
二重积分的概念与性质
二重积分的定义
01
二重积分是定积分在二维平面上的扩展，表示二维曲顶柱体的
体积。
二重积分的性质
02
二重积分具有可加性、可交换性、可数性等性质，这些性质有
助于简化计算和证明。
二重积分的几何意义
03
二重积分在几何上表示二维曲顶柱体的体积，其中被积函数表
示曲顶的函数值。
二重积分的计算方法
曲面积分性质
曲面积分具有一些重要性质，如线性性质、可加性、奇偶性等，这些性质在计算和证明中具有重要作用。
曲面积分的应用
曲面积分在物理学、工程学等领域有广泛的应用，如计算曲面质量、面密度、通量等。
ห้องสมุดไป่ตู้ 01
场论初步
场论的基本概念
场
在空间中定义点的集合，每个点具有一个或多个与之相关的数或量。
矢量场
知识结构

《高数下第八章》课件

高数下第八章
引言知识重点与难点公式与定理习题解答章节总结
目录
CONTENTS
引言
01
02
重点掌握这些概念的定义、性质和计算方法，以及它们在实际问题中的应用。
本章主要介绍高数下第八章的基本概念和主要知识点，包括极限、导数、积分等。
掌握高数下第八章的基本概念和知识点。
理解极限、导数、积分等概念的定义和性质，能够熟练计算和应用。
掌握情况4
01
02
04
03
感谢您的观看
THANKS
02
涉及知识点：本章节的全部重点和难点，包括但不限于极限、连续、导数、积分等。
03
解题方法：需要学生根据题目要求，灵活运用所学知识进行解答，往往需要构造反例或进行深入讨论。
04
难度：较高。
章节总结
知识点1
知识点2
知识点3
知识点4
01
02
03
04
极限的定义与性质
函数的连续性与间断点
导数的概念与计算
了解这些概念在实际问题中的应用，提高解决实际问题的能力。
知识重点与难点
理解极限的四则运算法则，掌握处理极限运算中的一些常见技巧，如等价无穷小替换、洛必达法则等。
极限的运算技巧
理解微分中值定理（如拉格朗日中值定理、柯西中值定理）的证明过程，掌握其在解决实际问题中的应用。
微分中值定理的应用
理解定积分与二重积分的几何意义，掌握定积分在解决实际问题（如求面积、体积等）中的应用。
积分的几何意义与物理意义
理解多元函数的偏导数概念，掌握复合函数、隐函数的求导法则，理解方向导数和梯度的几何意义。
多元函数的微分法则
公式与定理
اپ=1n∑n−1k=0Zk+12Xk+12Zk+12Xk+12