基于曲率保持PDE的非线性结构张量
求解高维黎曼流形上的黎曼曲率张量积分问题

求解高维黎曼流形上的黎曼曲率张量积分问题下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!求解高维黎曼流形上的黎曼曲率张量积分问题引言在微分几何中,黎曼流形是一种具有局部欧几里德空间结构的空间。
曲面度量张量与曲率张量

锡 1.1 曲面第一基本形式及曲面度量张量
定义 1.1 (曲面第一基本形式). 由 gij(xΣ) = (gi(xΣ), gj(xΣ))Rm+1 构成的 m × m 矩阵
谢 G(xΣ)
=
g11(xΣ ...
)
···
g1m (xΣ ) ...
=
DΣT(xΣ
)DΣ (xΣ )
∈
Rm×m,
STAS STBS
= =
Im, λ1
...
. λm
锡麟
式中, Im 为 m 阶单位矩阵, λi 满足 det(B − λiA) = 0, i = 1, · · · , m.
证明 由于 A 是对称矩阵, 因此一定唯一存在一个正交矩阵 QA, 使得
表达式中, 则有 ∆ij ̸= 0; 并且如果 g 的表达式不包含 gij, 则有 ∆ij = 0. 随后, 可作以下推导:
∂g ∂xlΣ
∑ =
包含gij
∂g ∂gij
∂gij ∂xlΣ
(xΣ )
=
∑
包含gij
∆ij
∂gij ∂xlΣ
(xΣ
)
=
∑ m
p,q=1
∆pq
∂gpq ∂xlΣ
(xΣ )
=
ggpq
稿 gm1(xΣ) · · · gmm(xΣ)
讲 称为曲面 Σ(xΣ) 的第一基本形式. 性质 1.1 (曲面第一基本形式的对称性、正定性). 曲面的第一基本形式矩阵 G 是对称矩阵; 在曲面的正则点处, 曲面的第一基本形式矩阵 G 是对称正定矩阵.
析 证明 由内积的对称性, 矩阵 G 的对称性是显然的. 下面证明正定性.
非线性薛定谔方程 runge-kutta

非线性薛定谔方程 runge-kutta
非线性薛定谔方程 runge-kutta
非线性薛定谔方程,即非线性常微分方程,是用于描述物理系统的状
态变化的重要方程,可用于描述各种物理系统的动力学和稳定性问题。
Runge-Kutta方法是一种常用的数值解决非线性薛定谔方程的方法。
Runge-Kutta方法可以求解一阶非线性薛定谔方程,也可以求解多阶非线性薛定谔方程,不需要求解方程的精确解,而是对方程的近似解。
它的基本思想是:将时间区间[t0,t1]划分为若干小的时间步长,将每
次步长的解看作是一个函数,再用多项式拟合这个函数,从而得到方
程的近似解。
Runge-Kutta方法的特点是求解精度高,计算量少,但它也有一定的局限性,即要求解的方程必须是可以求导的,对于非线性或不可导的方程,Runge-Kutta方法就不能使用了。
另外,Runge-Kutta方法只能求
解单变量的非线性薛定谔方程,而多变量的非线性薛定谔方程则无能
为力。
总之,Runge-Kutta方法是一种有效的解决非线性薛定谔方程的方法,它的优点是求解精度高,计算量少,但也有一定的限制,不能解决某
些复杂的问题。
应用PDE讲义03_特征线

把偏微分方程可以重新表示为 ,, · , , 1 0
几何上, , , 落在解曲面每一点的切平面上。因此,如果通过 求解常微分方程组(特征方程组)
,, ,, ,, 来构造曲线 , , ,其中 为参数,那么对于所有的 , 这条曲线就落在解曲面上。另外,如果在 0上要求
的上方
和下方的,虽然是 , 的连续函数,且沿此抛物线取相同的值
,
,
3
但在此抛物线上
,
,
也就是说,偏微分方程的一个连续合成解的一阶导数沿特征线产生间 断,是不连续的。
对于所有的标量拟线性方程,解的定义域至少是被通过边界曲线 投影端点的特征投影所限制,另一个限制是系数 , 均为零,或者沿
14
特征线积分时破裂,即解及其导数出现奇性,或者是在 , 平面的
, 处的 值。
如果把 ,0
看成初始扰动,那么上述结果就表明,这
个扰动以速度| |传播,波形保持不变;当 0,是向右移动;当 0,
是向左移动。
1.3 定义域和破裂
虽然已经得到解的局部存在性结果,但是在远离特征线 的地方,
解仍然可能产生奇性,尤其当方程不是线性的时候极其容易发生。在
线性方程中
,,
, , ,,
某些曲线上 Jacobi 行列式 这些曲线上不能再延拓。
, / , 为零所致,解的定义域在
§2 线性波动方程的初值问题
高阶偏微分方程,常可以通过引入新的未知函数的方法,化为一 个一阶偏微分方程组。特别指出,一个一阶偏微分方程组未必能化为 一个高阶偏微分方程。例如可压缩流体动力学方程组。
2.1 一阶线性偏微分方程组
2
在绪论里面,建立了种群演化密度偏微分方程构成定解问题:
传统经典断层识别实战——相干、曲率
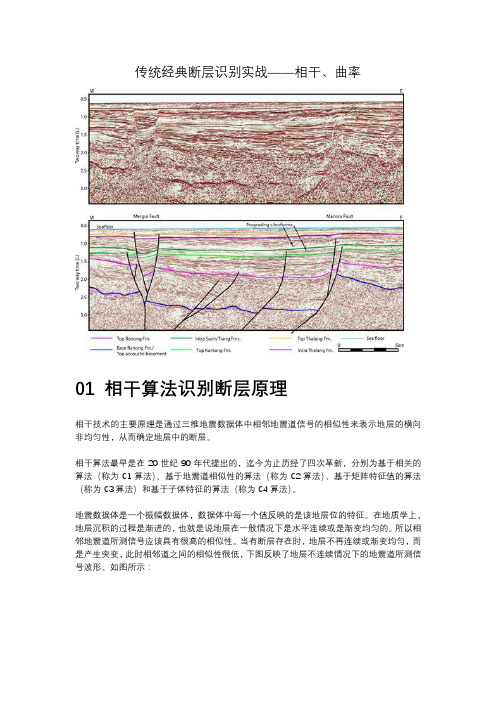
传统经典断层识别实战——相干、曲率01 相干算法识别断层原理相干技术的主要原理是通过三维地震数据体中相邻地震道信号的相似性来表示地层的横向非均匀性,从而确定地层中的断层。
相干算法最早是在20世纪90年代提出的,迄今为止历经了四次革新,分别为基于相关的算法(称为C1算法)、基于地震道相似性的算法(称为C2算法)、基于矩阵特征值的算法(称为C3算法)和基于子体特征的算法(称为C4算法)。
地震数据体是一个振幅数据体,数据体中每一个值反映的是该地层位的特征。
在地质学上,地层沉积的过程是渐进的,也就是说地层在一般情况下是水平连续或是渐变均匀的。
所以相邻地震道所测信号应该具有很高的相似性。
当有断层存在时,地层不再连续或渐变均匀,而是产生突变,此时相邻道之间的相似性很低,下图反映了地层不连续情况下的地震道所测信号波形。
如图所示:通过计算横向和纵向相邻道之间的相关值得到三维相干值数据体,从而将三维地震振幅数据体转换成相干数据体。
相干切片是相干数据体的水平切片,体现某一时间深度不同相干值的点构成的平面。
断层线是该平面上相干值小的点连成的线,通常是断层的所在位置。
用三维相干算法计算地震相干数据体突出了不相干的数据,其相干体水平切片表现了断层线所在位置,为油气储层评价提供了理论依据。
02 曲率识别断层原理曲率用来反映几何体的弯曲程度,描述的是曲线上任意一点的弯曲程度,表明曲线偏离直线的程度。
曲率越大,表示曲线的弯曲程度越大。
地震曲率断层检测技术由A.Roberts首先提出的,在构造解释中,我们可以根据层位的解释数据计算其曲率,从而可以定量描述其构造特征。
图给出了背单斜、向斜和断层曲率描述,其中背斜的曲率为正,向斜的曲率为负,而且褶皱越厉害,曲率值越大,平层和单斜层的曲率为零,断层在平滑后可近似认为其曲率由正到负或由负到正的变化。
显然,上述曲率对于单斜和水平地层的区分是无能为力的,对于平行断层,水平面上或沿层面上有方向变化的复杂构造,也是无能为力的,必须要借助于以二维曲面分析为基础的曲率属性。
基于曲率驱动的类双线性图像快速插值方法

f .ntue fO ts n l t n sC iee c dm S i csC eg u6 0 , hn ; Isi to pi d e r i , hns a e yo ce e, hn d 12 9 C ia 1 t ca E co c A f n 0
2 Sh o polc o iI omain U i ri Eet nc cec n cn lg , h nd 0 4 C ia .c o lfO t et n f r t , nv syo l r iS i e dT h ooy C eg u6 5 , hn ; o e r cn o e t f co n a e 1 0
A s m a eEnl r e e tM e h d Ba e n Fa tI g a g m n t o sd o
Cu v t r—rv nQu s bl e r n ep lt n r au ed ie ai in a tr oai - i I o
基于结构相似度的图像修补算法
基于结构相似度的图像修补算法作者:许凯等来源:《计算机时代》2015年第10期摘要:提出了一种基于Criminisi算法的改进的图像修补算法。
引入了图像质量评价标准SSIM定义的结构相似度,结合结构相似度进行图像修补过程中的模板匹配,从而减少了模板匹配时错误匹配的情况,提高了图像修补的质量。
仿真结果显示,改进的算法对于图像修补有不错的效果,优于原有的Criminisi修补算法。
关键词:图像修补;结构相似度; Criminisi算法;模板匹配中图分类号:TP391 文献标志码:A 文章编号:1006-8228(2015)10-07-03Abstract: A new inpainting algorithm based on the Criminisi algorithm is proposed in this paper. The new algorithm combines with the structural similarity, which comes from image quality evaluation criteria SSIM, to carry out the template matching in the image inpainting process. The algorithm can reduce the probability of error matching and improve the quality of image inpainting. The simulation results show that the improved algorithm has a good effect on the image inpainting,and is superior to the original Criminisi algorithm.Key words: image inpainting; structural similarity; Criminisi algorithm; template matching0 引言图像修补是对图像缺失区域或者被破坏的地方进行修复,在手工修复图像时,容易破坏图像且需要大量的时间[1]。
第五章引力场方程
它是1个2阶的对称张量,方程的左端应当是1个表示时空弯曲的2阶对称张量,由度规的2阶偏导数组成.
曲率张量表示时空的弯曲,由度规及其1,2阶偏导数组成,然而它是1个4阶张量. 很自然会想到用曲率
张量来构造1个对称的2阶张量. 将曲率张量 Rµναβ 的上下指标缩并1次就可以得到1个2阶张量. 从曲率张量对前2个指标的反对称
附录A中指出方括号内任何1对指标都是反对称指标,而克氏符号的2个下指标是对称指标,唯一的可能 是上式恒等于零. 在§4.4中我们用过同样的逻辑.
Bianchi恒等式需要对曲率张量求协变导数,在LGS中变成求普通偏导数,问题在于这时曲率张量 Rµναβ 是否还能用(5.4)式表示. 注意虽然在LGS中克氏符号的导数不一定为零,克氏符号本身全为零.
显然,性质(5.5),(5.6)和(5.7)是相互关联的. 例如,只要证明了后2式,第1式就不证自明了. 先来证明性质(5.6). 注意 Rµν(αβ) 是1个张量,为证明它是1个零张量,只需在1个特殊坐标系里证明 就可以了,今后将经常采用这种方法. 在LGS里,根据(5.4)式,有
Rµναβ = ηµρ −Γρνα,β + Γρνβ,α .
性,容易证明
Rµµαβ ≡ 0.
(5.11)
曲率张量对后2个指标的反对称性表明和第3或第4指标的缩并只差1个符号. 定义Ricci张量为曲率张量第1和第3个指标的缩并:
Rαβ = Rραρβ .
(5.12)
有一些广义相对论的书籍和文献中将Ricci张量定义为第1和第4个指标的缩并,结果会和这里差符号. Ricci张量是1个对称张量,证明如下:
果是否与路径有关. 关于这一点在§4.2中已有比较详尽的讨论. (2)由3条测地线组成的三角形的内角和是
大挠度空间梁的静、动力学建模、分析与计算
综合以上文献的研究埘以看出,建模是基于Hamilton原理或者牛顿第二运动定 律,在考虑到电子大变形掰雩{超稿位移一应变韵鞯线镶菸盛保留撵瞧粱在弯曲变形 黠熬夸熬辫率瓣嚣绞篷磺翡肇疆上接导爨寒豹粱懿丈挠度运动凌力学徽分方程。~ 系列实验和实践表明,保留到二阶或者量阶非线性项的影响所建立的梁的大挠度送 嬲微分方程是瀵怒工程或麓装求豹。
1.2.1静力学方程的求解方法概述
对于大挠度梁结构来说,位移和应变之间的已经不再表示为线性关系。而且由 于梁结构的大挠度变形,位移和应变之间呈非线性关系,刚度矩阵也不再是常数矩 阵,而是单元位移的矩阵函数。几何非线性有限元是在传统方法的基础上,引入了
大挠度空间梁的静、动力学建模、分析与计算
应变与位移之间的几何非线性关系,然后再将系统动力学方程中的非线性项作’近 似变换,非线性项就可以表示为与节点位移有关的几何刚度矩阵㈣㈣,即
influence of the nonlinearity is obvious,the conclusion drawn from the present method is
same the
to the conclusion ofthe other correlative literatures。
广义结构张量
广义结构张量
广义结构张量主要应用在分析图像、数据流、形状等的方向、大小、偏转、纹理以及与这些对象有关的动态变化的描述上。
以下是有关它的特点的更具体的说明:
1. 独立于基的几何对象:广义结构张量是一个几何对象,它与坐标基无关。
这意味着在不同的基下,广义结构张量有不同的代数表示,但这些代数表示之间有明确的转换规则。
2. 线性函数:更严格地说,表示直线、平面等“线性”几何对象的余向量是广义结构张量的一种。
如果给行向量一个符号,比如α=[2 1],那么余向量实际上代表了所有平行的直线。
3. 方向和大小:广义结构张量可以用来描述方向和大小的变化。
例如,在图像处理中,它可以用来检测边缘的方向和强度。
4. 动态变化:广义结构张量还可以用于描述动态变化的形状,例如在视频处理中,它可以用来检测物体的运动方向和速度。
总的来说,广义结构张量是一种强大的工具,可用于描述和解释各种复杂的几何现象。
更多信息建议咨询数学或物理学专家或查阅相关文献资料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
156 2010,46(18) Computer Engineering and Applw ̄ions计算机工程与应用 基于曲率保持PDE的非线性结构张量 郑钰辉1,潘瑜2,孙权森2,韦志辉2,夏德深2 ZHENG Yu—hui ,PAN Yu ,SUN Quan—sen2,WEI Zhi-hui ,XIA De-shen
1.南京信息工程大学计算机与软件学院,南京210044 2.南京理工大学计算机科学与技术学院,南京210094 1.Computer and Software Institute,Nanjing University of Information Science&Technology,Nanjing 210044,China 2.School of Science,Nanjing University of Science&Technology,Nanjing 210094,China
ZHENG Yu—hlli。PAN Yu。SUN Quan-sen。et a1.Curvature preserving PDE-based nonlinear structure tensor.Computer Engineering and Applications,2010,46(18):156-159.
Abstract:A new curvature—preserving diffusion based nonlinear structure tensor calculation method is proposed.At first,three re- quirements of nonlinear structure tensor algorithms are presented,based on which the defects of the divergence—based nonlinear structure tensor and the trace—based nonlinear structure tensor,in comer information extraction,are pointed out.After that,this paper smoothes the structure tensor with an extended curvature—preserving PDE method and gets the new nonlinear structure tensor,which is capable of structure estimation.Experimental results show that the method can produce better local structure estimation results. Key words:matrix-valued data field;nonlinear structure tensor;structure information;curvature preserving
摘要:提出了一种基于曲率保持扩散方程的非线性结构张量计算方法。在讨论了非线性结构张量算法必须满足3个条件的基础 上,指出了基于散度的非线性结构张量与基于迹的非线性结构张量在提取图像二维结构信息时的不足;将曲率保持正则化方法用 于平滑结构张量,使得新的非线性结构张量具有更好的结构估计能力。实验结果表明:该文方法对噪声图像仍能取得较好地局部 结构估计结果。 关键词:矩阵值数据场;非线性结构张量;结构信息;曲率保持 DOI:10.3778/j.issn.1002—8331.2010.18.049 文章编号:1002—8331(2010)18~0156—04 文献标识码:A 中图分类号:TP391.41
1引言 随着计算机技术与新型医学成像技术的发展,一种新的数 据集——矩阵值数据集越来越多地受到人们的重视。目前,围 绕这类数据集的处理与分析成为了这一领域的研究热点。该工 作主要在三个方面展开:(1)弥散核磁共振影像的处理、分割及 三维重建技术;(2)非线性结构张量(NonLinear Structure Ten— sor,NLST)的计算方法;(3)张量场数据可视化技术。值得注意 的是这三个方向的研究成果可相互借鉴与吸收。 众所周知,线性结构张量Linear Structure Tensor,LST)【 作为传统的局部结构分析工具,已被广泛地应用在图像处理、 分割、特征检测与光流场计算等计算机视觉领域。遗憾的是由 于LST对结构张量(Structure Tensor,ST)数据采用了线性平滑 技术,因此由其得到的局部结构估计结果精度不高。在人们对 定量数据精度越来越高的要求下,NEST计算方法引起了众多 学者的广泛关注 。 许多学者在各种应用背景下构建了不同的自适应sT平滑
方法,得到了不同的NEST。Nagel等 计算光流场时利用自适 应高斯核平滑sT得到了NEST。Kothe 为了准确提取图像的特 征点,设计了一种类似于沙漏形的滤波器与原始ST做卷积,得 到了相应的NLST。Weijier等同在估计纹理方向时指出传统的 局部方向最小二乘估计等价于LST,这与方向误差度量函数的 选取有关,并在此基础上设计一种合理的鲁棒估计器,通过迭 代的方法计算得到了NLST。借助于迅速发展的扩散PDE图像 滤波方法,Brox等f7】将散度型张量驱动PDE图像滤波方法 扩 展到张量场,建立了相应的散度型张量驱动PDE张量场平滑方 法,然后用该方法平滑sT得到了基于散度的NLST(Divergence— based NLST,DNLST)。郑等[。指出DNEST对纹理丰富的图像区 域不能得到较好的局部结构估计结果,随后将迹型张量驱动 PDE图像滤波方法Ⅱ 展到张量场,用其平滑sT得到了基于 迹的NEST(Trace—based NLST,TNLST)。 该文将继续深入研究基于PDE的NLST计算方法。各向异 性PDE正则化方法的发展为NLST计算方法的丰富与发展提
基金项目:国家自然科学基金(the National Natural Science Foundation of China under Grant No.60773172)。 作者简介:郑钰辉(1982一),男,博士,讲师,主要研究方向为偏微分方程图像处理与分析、模式识别与人工智能;潘瑜(1984一),女,博士研究生,主 要研究方向图像处理、模式识别与人工智能;孙权森(1965一),男,博士,教授,博士生导师,主要研究方向为图像处理、模式识别与人工 智能;韦志辉(1963一),男,博士,教授,博士生导师,主要研究方向为变分偏微分方程图像处理、模式识别;夏德深(1941一),男,博士,教 授,博士生导师,主要研究方向为图像处理、卫星遥感、模式识别。 收稿日期:2009—02—27 修回日期:2009—11-04 郑钰辉,潘瑜,孙权森,等:基于曲率保持PDE的非线性结构张量 2010。46(18) 157 供了理论和技术上的保障。此类滤波算子不仅结合了局部数据 的跳变信息,而且考虑了局部数据的方向信息,从而使得到的 NLST对图像局部结构估计较为准确。针对已有的NLST算法不 能较好地保持张量场二维结构信息的不足,将文献[11]方法推 广到矩阵场,通过平滑张量场,得到了一种新的NLST,称为基 于曲率保恃的NEST(Curvature preserving-based NLST,CPNLST)。 最后实验分析了CPNLST对图像局部信息的提取能力。 2 NLST相关知识 对于图像,,其在某点x=( ,Y)的梯度Vlx=(L,/y) ,则在 该点的sT为: G:f - z 1 (1) \,, //\Ml2/ ̄22/ 由于sT容易受噪声影响,可采用滤波技术平滑该张量场 数据。平滑方法的统一表达式为: p(G) U12 1 \UI2 / ̄22/ 当P(・)为线性滤波方法时,P(G)为LST;当P(・)为基于散 度的PDE正则化方法时,P(G)为DNLST,见下式: =div(TVu ̄)(i,j=l,2) (2) 其中, 为张量场条件下的扩散张量(91。由于DNLST计算方法 存在一干扰项,因而影响了这种NLST的结构估计结果。在前 期工作 中,提出了一种TNLST计算方法,公式如下: =tr(珊)(i =l,2) (3) 其中,日=(; ;:)为海森矩阵。TN T运用了基于迹的 PDE正则化方法,因此能取得比DNLST更好地估计结果。需要 指出得的式(3)可改写为: t“o exp\X'r4  ̄x) 卢1,2) 其中,u:表示点X处初始ST的第( J)通道值; 表示点X处 时刻ST的第( , )通道值; 表示卷积运算。由上式可以发现, 式(3)可以理解为通过自适应各向异性高斯核与初始sT做卷 积,因此这种方法与文献[5]方法等价。 当得到NLST后,对其进行谱分解可用于估计图像局部结 构和方向。p(G)特征值计算公式为: Ai,2= (/Lll+/ ̄22+V/(/.Lll-/Z22) ::) (4) 两个特征值对应的特征向量 , 为: 『 / 2u : \ IU22--Ull+ 』 (5) 【V2Iv1 A 与A 分别反映了v 与 方向上图像灰度变化的大小。 NEST在分析局部几何结构时,依据的分类规则为:(1)对于 图像平坦区域,两个特征值有A, , O;(2)对于图像边缘,因 为沿v,(边缘方向)方向图像灰度几乎没有变化,而跨越边缘 的方向v ,图像灰度有较大变化,因此其对应的特征值有A > A  ̄--0;(3)对于图像角点,因为图像灰度值在 和 方向上都 有变化,则有A1>A >0。
3 NLST算法评价 利用优良的NLST能得到准确的结构分析结果,这本质上 取决于NLST的计算方法。至今,尽管学者们提出了各种NLST 算法,但均未给出对这类方法的评判准则。为此,提出了NLST 计算方法必须具备的3个基本条件:(1)去噪。排除噪声对张量 场的影响,提高分析结果的可靠性;(2)保边。保持张量场的一 维各向异性信息,以便得到较好地图像边缘估计结果;(3)保 角。保持张量场的二维曲率信息,以得到准确的图像二维结构 分析结果。 基于上述3个条件,考察了LST与已有的NLST计算方法, 其结果见表1。对于LST,因为使用了线性高斯滤波技术,虽然 能较好地去除噪声,但不能保持张量场的间断信息;在基于统 计的NLST计算方法方面,文献【4—6]提出的方法均不能保持局 部角点结构,这是因为这些算法在设计时只考虑了保持一维各 向异性信息;在基于PDE的NLST计算方法方面,DNLST与 TNLST在计算时,均通过扩散张量 综合各个通道的信息,使 得各个通道数据沿着跳变小的方向扩散。需要指出的是这种各 向异性扩散仍然是一维方向扩散,因此不能很好地保持张量场 的二维结构信息。
