2012年北京市中考二模压轴题分类之24题汇总
2012年北京市各区二模试题分类解析【数学文】(14):空间几何体.pdf

1.运用多种修辞方法,表达思想感情,增强气势。
2.品味语言,理解语言中所包含的深意。
教学时数:一课时。
教学过程 一、预习 1.给下列加点字注音。
(多媒体显示) 伫立(zhu4) 睥睨(pi4 ni4) 咆哮(xiao4) 波澜(lan2) 污秽(hui4) 犀利(xi1) 劈开(pi1) 稽首(qi3) 驰骋(cheng3)虐待(nüe4) 2.解释下列词语。
睥睨:眼睛斜着看,形容高傲的样子。
污秽:不干净。
犀利:(武器、言语等)锋利;锐利。
播弄:摆布。
虐待:用残暴狠毒的手段待人。
雷霆:雷暴;霹雳。
踌躇:犹豫。
鞭挞:鞭打。
比喻抨击。
祈祷:一种宗教仪式,信仰宗教的人向神默告自己的愿望。
忏悔:认识了过去的错误或罪过而感觉痛心。
罪孽:迷信的人认为应受到报应的罪恶。
拖泥带水:比喻说话、写文章不简洁或做事不干脆。
二、导入 介绍历史尉《屈原》写作的时代背景。
郭沫若历史剧《屈原》写于1942年1月。
当时是抗日战争后期,日本帝国主义侵占了中国的半壁河山。
1942年1月,时值“皖南事变,,以后,郭沫若在重庆创作了《屈原》,借古讽今,揭露国民党统治下的黑暗现实。
他借屈原的独自,鞭挞蒋介石的反动统治,抒发了人民的愤恨。
《雷电颂>出现在《屈原》第五幕第二场。
屈原被囚禁在东皇太一庙。
他手足带着刑具,颈上系着长链,散发披肩,独身徘徊。
这时,狂风咆哮,电闪雷鸣。
面对这黑暗的世界,他想到祖国就要沦亡,听着风吼、雷鸣,看着闪电劈空,他感到了大自然的伟大力量,他激愤的心情发展到极点,他的心像火一样燃烧起来,铸成了这大气磅礴,动人心魄的独自——《雷电颂》。
它是屈原斗争精神的最集中、最突出的表现。
是全剧高潮中最强力的一个音符。
三、朗读课文 课文在形式上并不押韵,但节奏分明,声调铿锵有力,要求学生反复朗读,品味文章语言,体会文章气势,并谈感受。
四、再读课文,理清思路 学生讨论、交流。
明确: 《雷电颂》这段独白,大致包含两方面的内容:一是对风、雷、电的期待与歌颂,一是对光明的渴望与追求。
3个技巧 9道经典题 24个几何模型 拿下几何中考最难题资料
-8-
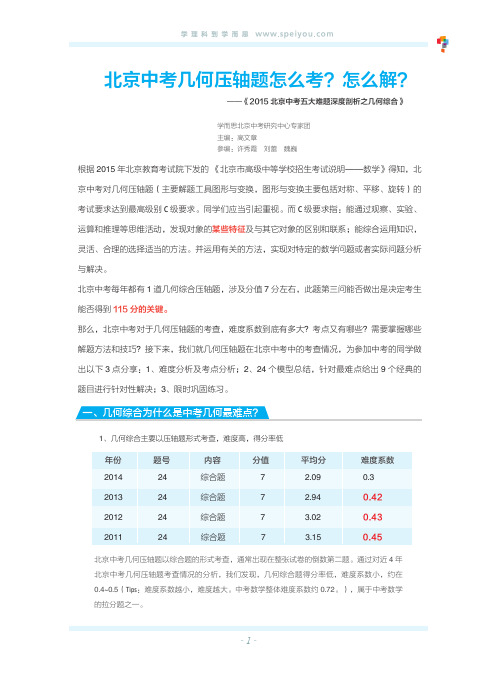
二:利用几何变换造等腰 1、利用轴对称造等腰(边)三角形 【模型 12】角平分线 + 垂线,等腰三角形必呈现(角分垂等腰归); 解释:角是天然的轴对称图形,角平分线所在的直线就是其对称轴。所以如果向角平分线作了垂线, 则延长该垂线段,必出对称全等,必出等腰三角形!
II. 最后 1 问(有时 2 问)的正确率在 30% 以下,得分率低,难度大,这是几何压轴题的核心,也 是整张试卷中起到中考选拔作用的题目,所以建议要参加中考的同学专项训练几何压轴题最后 1 问或 2 问的典型题目,总结归纳对应的解题方法和技巧。 那么怎么才能把几何压轴题的分数收入囊中呢?为帮助同学们顺利解决几何压轴题,学而思北京 中考研究中心团队通过数百道真题分析,提炼 3 重要考点,24 个重要模型,9 道经典练习题,为 初三同学们带来权威、实用的解题秘籍。
-1-
2、几何综合,综合性强,考查几何模型、辅助线添加技巧、倒角能力等,区分度大
真题考查
主要考点
几何变换
中考要求
分值 难度
2014 中考 24 题(1)问 作图
轴对称 B
1 分 易
为等边三角形
A
D
E
B
(3)∵
C
,
∴ 又∵ ∴
为等腰直角三角形
A
D E
B
C
考点1. 利用旋转构造了等边 三角形 ABE:主考考查模型 18
- 14 -
(1)如图 1,直接写出∠ ABD 的大小(用含 的式子表示); (2)如图 2,∠ BCE=150°,∠ ABE=60°,判断△ ABE 的形状并加以证明; (3)在(2)的条件下,连结 DE,若∠ DEC=45°,求 的值。
2012年北京市各区二模试题分类解析【数学理】(5)三角函数
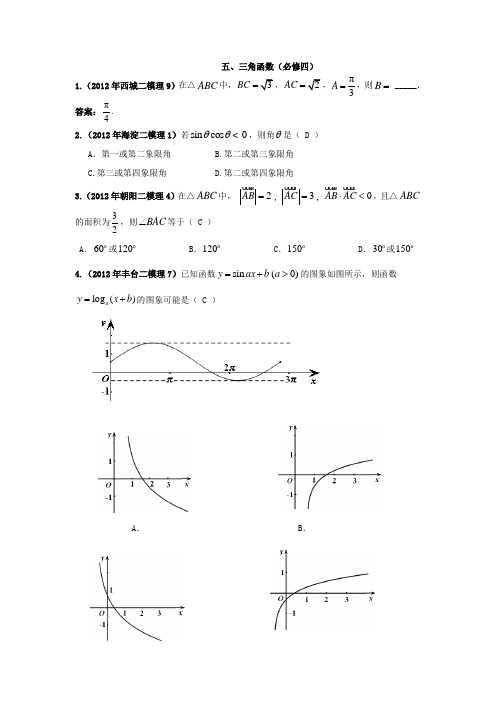
五、三角函数(必修四)1.(2012年西城二模理9)在△ABC 中,BC =,AC =,π3A =,则B = _____. 答案:π4. 2.(2012年海淀二模理1)若sin cos 0θθ<,则角θ是( D ) A .第一或第二象限角 B.第二或第三象限角 C.第三或第四象限角 D.第二或第四象限角3.(2012年朝阳二模理4)在△ABC 中, 2AB =,3AC =,0AB AC ⋅<,且△ABC 的面积为32,则BAC ∠等于( C ) A .60或120 B .120 C .150 D .30或150 4.(2012年丰台二模理7)已知函数sin (0)y ax b a =+>的图象如图所示,则函数log ()a y x b =+的图象可能是( C )A .B .C .D .5.(2012年昌平二模理9)在∆ABC 中,4,2,2π===A b a 那么角C =_________.答案:127π。
6.(2012年东城二模理11)在平面直角坐标系xOy 中,将点A 绕原点O 逆时针旋转90到点B ,那么点B 的坐标为____,若直线OB 的倾斜角为α,则sin2α的值为 .答案:)3,1(-2-7.(2012年海淀二模理11)在ABC ∆中,若120=∠A ,5c =,ABC ∆的面积为,则a = .。
8.(2012年西城二模理15)已知函数22π()cos ()sin 6f x x x =--.(Ⅰ)求π()12f 的值; (Ⅱ)若对于任意的π[0,]2x ∈,都有()f x c ≤,求实数c 的取值范围. 解:(Ⅰ)22ππππ()cos ()sin cos 12121262f =--==. ………………5分 (Ⅱ) 1π1()[1cos(2)](1cos 2)232f x x x =+--- ………………7分1π13[cos(2)cos 2]2cos 2)2322x x x x =-+=+ ………………8分π)3x =+. ………………9分 因为 π[0,]2x ∈,所以 ππ4π2[,]333x +∈, ………………10分所以当 ππ232x +=,即 π12x =时,()f x 取得最大值2. ………………11分所以 π[0,]2x ∀∈,()f x c ≤ 等价于c ≤.故当 π[0,]2x ∀∈,()f x c ≤时,c的取值范围是)+∞. ………………13分 9.(2012年朝阳二模理15) 已知函数()2cos cos f x x x x m =-+()R m ∈的图象过点π(,0)12M .(Ⅰ)求m 的值;(Ⅱ)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c .若cos +cos =2cos c B b C a B ,求()f A 的取值范围.解:(Ⅰ)由()12(cos 21)2f x x x m =-++π1sin(2)62x m =--+.…3分因为点π(,0)12M 在函数()f x 的图象上, 所以ππ1sin(2)01262m ⋅--+=,解得12m =. …5分 (Ⅱ) 因为cos +cos =2cos c B b C a B ,所以sin cos sin cos C B B C +=2sin cos A B ,所以sin(+)2sin cos B C A B =,即sin 2sin cos A A B =. ……7分 又因为(0,A ∈π),所以sin 0A ≠,所以1cos 2B =. ……8分 又因为(0,B ∈π),所以π3B =,2π3A C +=. ……10分所以2π03A <<, ππ7π2666A -<-<,所以πsin(2)6A -∈1(,1]2-.…12分所以()f A 的取值范围是1(,1]2-. ……13分10.(2012年丰台二模理15)已知函数()cos sin )f x x x x =-(Ⅰ)求()3f π的值;(Ⅱ)求函数()y f x =在区间[0,]2π上的最小值,并求使()y f x =取得最小值时的x 的值. 解:因为()cos sin )f x x x x =-2sin cos x x x -=1cos 21)sin 222x x +--12sin 22x x -=cos(2)6x π+(Ⅰ)()cos(2)336f πππ=⨯+==7分 (Ⅱ)因为 [0,]2x π∈, 所以2666x ππ7π≤+≤.当 26x π+=π,即512x π=时,函数()y f x =有最小值是12--. 当512x π=时,函数()y f x =有最小值是12--. …13分 11.(2012年昌平二模理15)已知向量a (cos ,sin ),θθ= b = (13-,), 22π≤θ≤π-.(Ⅰ)当b a ⊥时,求θ的值;(Ⅱ)求||b a +的取值范围.解:(Ⅰ) a ⊥b ∴b a ⋅0sin cos 3=-=θθ ……… 2分 得3tan =θ 又∵22π≤θ≤π-……… 4分 即:θ=3π……6分 (Ⅱ)||b a +=4)sin cos 3(21||2||22+-+=+⋅+θθb b a a )3sin(45π--=θ ……… 9分22π≤≤π-θ 6365π≤π-≤π-∴θ … 11分 21)3sin(1≤π-≤-∴θ 4)3sin(42≤π--≤-∴θ∴33≤+≤||b a … 13分12.(2012年东城二模理15)已知函数()sin()f x A x =+ωϕ(其中∈R x ,0A >,ππ0,22ωϕ>-<<)的部分图象如图所示.(Ⅰ)求函数()f x 的解析式;(Ⅱ)已知在函数()f x 的图象上的三点,,M N P 的横坐标分别为-解:(Ⅰ)由图可知,1A =,最小正周期428T =⨯=.由2π8T ==ω,得4π=ω. ………3分又π(1)sin()14f ϕ=+= ,且ππ22ϕ-<<,所以ππ42+=ϕ, 即4π=ϕ . ………5分 所以π()sin()sin (1)444f x x x =+=+ππ. ………6分(Ⅱ)因为(1)0,(1)1,f f -==π(5)sin (51)1,4f =+=-所以(1,0),(1,1),(5,1)M N P --. …………7分所以MN PN MP ===由余弦定理得3cos5MNP ∠==-. ………11分因为[)0,MNP ∠∈π, 所以4sin 5MNP ∠=. ……13分。
2012年北京市丰台区中考二模数学试题及答案

丰台区2012年初三统一练习(二)数 学 试 卷学校 姓名 准考证号 考生须知 1.本试卷共6页,共五道大题,25道小题,满分120分.考试时间120分钟. 2.在试卷和答题卡上准确填写学校名称、姓名和准考证号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,将本试卷、答题卡和草稿纸一并交回.一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.2-的绝对值是A .12-B .12 C .2 D .2-2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000 002 5米,把0.000 002 5用科学记数法表示为A .62.510⨯ B .50.2510-⨯ C . 62.510-⨯ D .72510-⨯ 3.如图,在△ABC 中, DE ∥BC ,如果AD =1, BD =2,那么DEBC的值为 A .12 B .13 C .14 D .194.在4张完全相同的卡片上分别画有等边三角形、矩形、菱形和圆,在看不见图形的情况下随机抽取1张,卡片上的图形是中心对称图形的概率是 A .14 B .12C .34D .1 5.若230x y ++-=则 y x 的值为A .-8B .-6C .6D .8 6.下列运算正确的是 A .222()a b a b +=+B .235a b ab +=C .632a a a ÷=D .325a a a ⋅=7.小张每天骑自行车或步行上学,他上学的路程为2 800米,骑自行车的平均速度是步行的平均速度的4倍,骑自行车上学比步行上学少用30分钟.设步行的平均速度为x 米/分.根据题意,下面列出的方程正确的是EDCBAA .30428002800=-xx B .30280042800=-x xC .30528002800=-x xD .30280052800=-xx8.如图1是一个小正方体的侧面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上..一面的字是 A .北 B .京C .精D .神二、填空题(本题共16分,每小题4分)9.如果二次根式1x -有意义,则x 的取值范围是 . 10.分解因式:=+-b ab b a 25102.11.如图, ⊙O 的半径为2,点A 为⊙O 上一点,OD ⊥弦BC 于点D ,如果1OD =,那么BAC ∠=________︒. 12.符号“f ”表示一种运算,它对一些数的运算如下:2(1)11f =+,2(2)12f =+,2(3)13f =+,2(4)14f =+,…, 利用以上运算的规律写出()f n = (n 为正整数) ;(1)(2)(3)(100)f f f f ⋅⋅⋅= .三、解答题(本题共30分,每小题5分) 13.计算:()︒⎪⎭⎫ ⎝⎛+45sin 4-211-3-272-03.14.已知2230a a --=,求代数式2(1)(2)(2)a a a a --+-的值.15.解分式方程:21124x x x -=--.16.如图,在△ABC 与△ABD 中, BC 与AD 相交于点O ,∠1=∠2,CO = DO .求证:∠C =∠D .DOCBA 21DOC17.已知:如图,在平面直角坐标系xOy 中,一次函数y =-x 的图象与反比例函数ky x的图象交于A 、B 两点. (1)求k 的值; (2)如果点P 在y 轴上,且满足以点A 、B 、P 为顶点的三角形是直角三角形,直接写出点P 的坐标.18.为了增强居民的节约用电意识,某市拟出台居民阶梯电价政策:每户每月用电量不超过230千瓦时的部分为第一档,按每千瓦时0.49元收费;超过230千瓦时且不超过400千瓦时的部分为第二档,超过的部分按每千瓦时0.54元收费;超过400千瓦时的部分为第三档,超过的部分按每千瓦时0.79元收费.(1)将按阶梯电价计算得以下各家4月份应交的电费填入下表:4月份总用电量/千瓦时 电费/元小刚 200 小丽300(2)设一户家庭某月用电量为x 千瓦时,写出该户此月应缴电费y (元)与用电量x (千瓦时)之间的函数关系式.四、解答题(本题共20分,每小题5分)19.已知:如图,菱形ABCD 中,过AD 的中点E 作AC 的垂线EF ,交AB 于点M ,交CB 的延长线于点F .如果FB 的长是2,求菱形ABCD 的周长.20.已知:如图,点A 、B 在⊙O 上,直线AC 是⊙O 的切线,联结AB 交O C 于点D ,AC =CD . (1)求证:OC ⊥OB ;(2)如果OD =1,tan ∠OCA =52,求AC 的长.OD C BAMFEBCDA21.某课外小组为了解本校八年级700名学生每学期参加社会实践活动的时间,随机对该年级50名学生进行了调查,根据收集的数据绘制了如下的频数分布表和频数分布直方图(各组数据包括最小值,不包括最大值).(1)补全下面的频数分布表和频数分布直方图:(2)可以估计这所学校八年级的学生中,每学期参加社会实践活动的时间不少于8小时的学生大约有多少人?22.小杰遇到这样一个问题:如图1,在□ABCD中,AE⊥BC于点E,AF⊥CD于点F,连结EF,△AEF 的三条高线交于点H,如果AC=4,EF=3,求AH的长.小杰是这样思考的:要想解决这个问题,应想办法将题目中的已知线段与所求线段尽可能集中到同一个三角形中.他先后尝试了翻折、旋转、平移的方法,发现可以通过将△AEH平移至△GCF的位置(如图2),可以解决这个问题.请你参考小杰同学的思路回答:(1)图2中AH的长等于.(2)如果AC=a,EF=b,那么AH的长等于.BA DCEFHGHFE CDAB图1 图2分组/时频数频率6~8 2 0.04 8~10 0.12 10~1212~14 1814~16 10 0.20 合计50 1.00五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的一元二次方程242(1)0x x k -+-=有两个不相等的实数根. (1)求k 的取值范围;(2)如果抛物线242(1)y x x k =-+-与x 轴的两个交点的横坐标为整数,求正整数k 的值;(3)直线y =x 与(2)中的抛物线在第一象限内的交点为点C ,点P 是射线OC 上的一个动点(点P 不与点O 、点C 重合),过点P 作垂直于x 轴的直线,交抛物线于点M ,点Q 在直线PC 上,距离点P 为2个单位长度,设点P 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.24.在△ABC 中,D 为BC 边的中点,在三角形内部取一点P ,使得∠ABP =∠ACP .过点P 作PE ⊥AC 于点E ,PF ⊥AB 于点F .(1)如图1,当AB =AC 时,判断的DE 与DF 的数量关系,直接写出你的结论; (2)如图2,当AB ≠AC ,其它条件不变时,(1)中的结论是否发生改变?请说明理由. 12345–1–2–3–412345–1–2xy OCE BAD FP 图1AEFPBD C图225.如图,将矩形OABC 置于平面直角坐标系xOy 中,A (32,0),C (0,2). (1) 抛物线2y x bx c =-++经过点B 、C ,求该抛物线的解析式;(2)将矩形OABC 绕原点顺时针旋转一个角度α(0°<α<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标; (3)如图(2),将矩形OABC 绕原点顺时针旋转一个角度θ(0°<θ<180°),将得到矩形OA’B’C’,设A ’C’的中点为点E ,联结CE ,当θ= °时,线段CE 的长度最大,最大值为 .北京市丰台区2011_2012学年第二学期初三综合练习(二)参考答案一、选择题(本题共32分,每小题4分) 题号 1 2 3 4 5 6 7 8 答案 CCBCADAA二、填空题(本题共16分,每小题4分)题号 9 1011 12答案x ≥12)5(-a b 60°21n+;5151 三、解答题(本题共30分,每小题5分)13.解:原式=3-1+4-422⨯……4分=6-22….5分14.解:2(1)(2)(2)a a a a --+-=22224a a a --+……1分.=224aa -+. ……2分2230a a --=, ∴223a a -=.…3分∴原式=224347aa -+=+=.….….5分15.21124x x x -=-- 解:2(2)(4)1x x x +--=.……1分22241x x x +-+=.……2分 23x =-.…… 3分32x =-.…….4分 检验:经检验,32x =-是原方程的解.∴原方程的解是32x =-.……5分 16.证明: ∠1=∠2, ∴OA=OB .…1分 在△COA 和△DOB 中 , OA=OB ,∠AOC =∠BOD , CO=DO .∴△COA ≌△DOB .……….4分∴∠C =∠D . …………….5分17.解:(1)反比例函数ky x=的图象经过点A (-1,1) , ∴-11-1k =⨯=.…………1分 (2)P 1(0,2)、 P 2(0,-2)、P 3(0,2)、 P 4(0,-2) ……5分18.解:(1)……2分4月份总用电量/千瓦时 电费/元小刚20098小丽300 150.5 (2)当0230x ≤≤时,0.49y x =;……3分当230400x <≤时,0.54-11.5y x =;……4分当400x >时,0.79-111.5y x =.……5分 四、解答题(本题共20分,每小题5分) 19.解:联结BD . ∵在菱形ABCD 中, ∴AD ∥BC ,AC ⊥BD .……1分又∵EF ⊥AC , ∴BD ∥EF .∴四边形EFBD 为平行四边形.……2分 ∴FB = ED =2.……3分 ∵E 是AD 的中点. ∴AD =2ED =4.……4分 ∴菱形ABCD 的周长为4416⨯=.……5分20.(1)证明:∵OA =OB , ∴∠B =∠4. ∵CD =AC , ∴∠1=∠2.∵∠3=∠2,∴∠3=∠1. ∵AC 是⊙O 的切线, ∴OA ⊥AC .……1分∴∠OAC =90°.∴∠1+∠4=90°. ∴∠3+∠B =90°. ∴OC ⊥OB .……2分(2)在Rt △OAC 中 ,∠OAC =90°, ∵tan ∠OCA =52,∴52OA AC =.……3分 ∴设AC =2x ,则AO =5x .由勾股定理得,OC =3x .∵AC =CD , ∴AC =CD =2x . ∵OD =1, ∴OC =2x +1. ∴2x +1=3x .……4分∴x =1. ∴AC =21⨯=2.……5分21.解:(1)……3分(注:错一空扣1分,最多扣3分)…4分(2)700⨯(1-0.04)=672.……5分答:这所学校每学期参加社会实践活动的时间不少于8小时的学生大约有672人. 22.解:(1)7;……3分(2)22a b -.……5分分组/时 频数 频率 6~8 2 0.04 8~10 6 0.12 10~12 14 0.28 12~14 18 0.36 14~16 10 0.20 合 计501.00五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.解:(1)由题意得△>0. ∴△=2(4)4[2(1)]8240k k ---=-+>.……1分 ∴解得3<k .……2分(2)∵3<k 且k 为正整数,∴1=k 或2.……3分当1=k 时,x x y 42-=,与x 轴交于点(0,0)、(4,0),符合题意;当2=k 时,242+-=x x y ,与x 轴的交点不是整数点,故舍去. 综上所述,1=k .……4分432ABCD O1(3)∵2,4y x y x x =⎧⎨=-⎩,∴点C 的坐标是(5,5).∴OC 与x 轴的夹角为45°.过点Q 作QN ⊥PM 于点N ,(注:点Q 在射线PC 上时,结果一样,所以只写一种情况即可)∴∠NQP =45°,NQ PM S ⋅=21. ∵PQ =2,∴NQ =1.∵P (t t ,),则M (t t t 4,2-),∴PM =t t t t t 5)4(22+-=--.……5分 ∴t t S 5212+-=. ∴当50<<t 时,t t S 25212+-=;……6分 当5>t 时,t t S 25212-=.……7分24.解:(1)DE =DF .……1分(2)DE =DF 不发生改变.……2分理由如下:分别取BP 、CP 的中点M 、N ,联结EM 、DM 、FN 、DN .∵D 为BC 的中点,∴BP DN BP DN //,21=.……3分 ∵,AB PE ⊥∴BP BM EM 21==.∴21,∠=∠=EM DN .∴12213∠=∠+∠=∠.…4分同理,524,//DM FN MD PC =∠=∠. ∴四边形MDNP 为平行四边形.……5分∴67∠=∠.∵,41∠=∠∴35∠=∠. ∴EMD DNF ∠=∠.……6分 ∴△EMD ≌△DNF . ∴DE =DF .……7分25.解:(1)∵矩形OABC ,A (32,0),C (0,2),∴B (32,2).∴抛物线的对称轴为x =3.∴b =3.……1分 ∴二次函数的解析式为:2232y x x =-++.……2分(2)①当顶点A 落在对称轴上时,设点A 的对应点为点A ’,联结OA ’, 设对称轴x =3与x 轴交于点D ,∴OD =3.∴OA ’ = OA =32.7654321NMCD BPFEACA B yxB'C'DA'O在Rt△OA’D中,根据勾股定理A’D =3.∴A’(3,-3) .……4分②当顶点落C对称轴上时(图略),设点C的对应点为点C’,联结OC’,在Rt△OC’D中,根据勾股定理C’D =1.∴C’(3,1).……6分(3) 120°,4.……8分。
2012北京中考数学二模方程不等式分类

延庆2012.615.(本题满分5分)解方程: 542332xx x +=--石景山2012.614.解分式方程123482---=-x x x . 解:顺义2012.616.解分式方程:32322x x x -=+-. 丰台2012.615.解分式方程:21124x x x -=--. 通州2012.614.解方程:x x 211=-朝阳2012.614.解方程:53412-=+x x .昌平2012.614.解方程:211x x x+=-. 大兴2012.6 14.解分式方程:451+=x x 燕山2012.614. 解方程 2x 1x 2142x 3++=-+.房山2012.614.解方程:2132+=+-a a a解:东城2012.6 14. 解方程组212x y x y +=⎧⎨-=⎩,.朝阳2012.611.在平面直角坐标系中,点P (k -2,k )在第二象限,且k 是整数,则k 的值为 .顺义2012.614.解不等式2(2)x +≤4(1)6x -+,并把它的解集在数轴上表示出来.门头沟2012.614.解不等式组:()⎪⎩⎪⎨⎧<-+≤+321234x x x x密云2012.6 10.不等式组211,1(6)2x x x -≥⎧⎪⎨-⎪⎩ 的解集是 . 密云2012.614.用配方法解方程:01632=--x x .平谷2012.614.用配方法解方程:0242=--x x门头沟2012.67.关于x 的一元二次方程032=-+m x x 有两个不相等的实数根,则m 的取值范围是A. B. C. D.密云2012.611.已知关于x 的一元二次方程22410x x k ++-=有实数根,则的最大值是 . 燕山2012.616.已知方程4x 2+12x +k=0有两个相等的实数根,求k 的值和方程的解.丰台2012.67.小张每天骑自行车或步行上学,他上学的路程为2 800米,骑自行车的平均速度是步行 的平均速度的4倍,骑自行车上学比步行上学少用30分钟.设步行的平均速度为x 米/分.根据题意,下面列出的方程正确的是A .30428002800=-xx B .30280042800=-x x 121>m 121<m 121->m 121-<mC .30528002800=-x xD .30280052800=-xx石景山2012.618.列方程(组)解应用题:如图是一块长、宽分别为60 m 、50 m 的矩形草坪,草坪中有宽度均为x m 的一横两纵的甬道.(1)用含x 的代数式表示草坪的总面积S ;(2)当甬道总面积为矩形总面积的4.10%时,求甬道的宽.解:平谷2012.618.列方程(组)解应用题:夏季里某一天,离供电局30千米远的郊区发生供电故障,抢修队接到通知后,立即前去抢修.维修工骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果两车同时到达抢修点.已知抢修车的速度是摩托车速度的1.5倍,求这两种车的速度.门头沟2012.618. 列方程或方程组解应用题某中学库存960套旧桌凳,修理后捐助贫困山区学校.现有甲、乙两个木工小组都想承揽这项业务.经协商后得知:甲小组单独修理这批桌凳比乙小组多用20天;乙小组每天修的桌凳套数是甲小组的1.5倍.求甲、乙两个木工小组每天各修桌凳多少套?通州2012.618.某纺织厂有纺织工人300名,为增产创收,该纺织厂又增设了制衣车间,准备将这300名纺织工人合理分配到纺织车间和制衣车间.现在知道工人每人每天平均能织布30米或制4件成衣,每件成衣用布1.5米,若使生产出的布匹刚好制成成衣,求应有多少人去生产成衣?大兴2012.618.某小型超市购进了两批相同品种的水果,第一批用了200元,第二批用了550元,第二批购进水果的重量是第一批的2.5倍,且进价比第一批每千克多1元.求第一批购进水果多少千克?密云2012.618.列方程解应用题:某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?昌平2012.618.列方程(组)解应用题:李明同学喜欢自行车和长跑两项运动,在某次训练中,他骑自行车的平均速度为每分钟600米,跑步的平均速度为每分钟200米,自行车路段和长跑路段共5000米,用时15分钟.求自行车路段和长跑路段的长度.燕山2012.617. 列方程或方程组解应用题:某石化工程公司第一工程队承包了铺设一段输油管道的工程,原计划用9天时间完成;实际施工时,每天比原计划平均多铺设50米,结果只用了7天就完成了全部任务. 求实际施工时,平均每天铺设多少米?这段输油管道有多长?东城2012.617.列方程或方程组解应用题:小明家有一块长8m、宽6m的矩形空地,现准备在该空地上建造一个十字花园(图中阴影部分),并使花园面积为空地面积的一半,小明设计了如图的方案,请你帮小明求出图中的x值。
2012北京中考数学二模全等分类
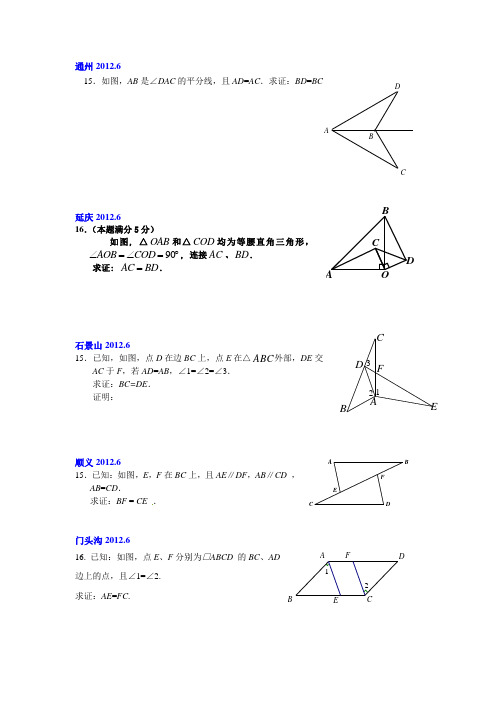
DABC 15.如图,AB是∠DAC的平分线,且AD=AC.求证:BD=BC延庆2012.616.(本题满分5分)如图, △OAB和△COD均为等腰直角三角形,90AOB COD∠=∠=︒, 连接AC、BD.求证: AC BD=.石景山2012.615.已知,如图,点D在边BC上,点E在△ABC外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.求证:BC=DE.证明:顺义2012.615.已知:如图,E,F在BC上,且AE∥DF,AB∥CD ,AB=CD.求证:BF = CE .门头沟2012.616.已知:如图,点E、F分别为□ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.F EDCB A21FEDCBA16.如图,在△ABC 与△ABD 中, BC 与AD 相交于点O ,∠1=∠2,CO = DO .求证:∠C =∠D .密云2012.615.已知:如图,∠C =∠CAF =90°,点E 在AC 上,且AE =BC ,EF ⊥AB 于点D .求证:AB =FE . ,请直接写出△AOB 的面积.朝阳2012.616.已知:如图,点D 、E 分别在AB 、AC 上,BE 与CD 相交于点F ,BD=CE ,∠B =∠C .求证:BE =CD .昌平2012.616.如图:已知在等边三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD =CE .求证:DC =EA .西城2012.615.如图,点F ,G 分别在△ADE 的AD ,DE 边上,C ,B 依次21DOCBAA DCEB为GF 延长线上两点,AB=AD ,∠BAF =∠CAE ,∠B=∠D . (1)求证:BC=DE ;(2)若∠B=35°,∠AFB =78°,直接写出∠DGB 的度数.大兴2012.615.已知:如图,∠ABC=90°,DC ⊥BC ,E ,F 为BC 上两点,且BE CF =,AB DC =. 求证:ABF DCE △≌△;燕山2012.615. 已知:如图, P 是线段AB 的中点,线段MN 经过 点P ,MA ⊥AB ,NB ⊥AB .求证:AM=BN.东城2012.615. 已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB的平分线. 求证:AB =DC ..平谷2012.6 16.如图,BE ⊥CE 于E ,AD ⊥ED 于D ,∠ACB =90°,AC =BC . 求证:AD =CE .房山2012.616.如图,在△ABC 中,AD 是中线,分别过点B 、C 作AD 及其延长线的垂线BE 、CF ,垂足分别为点E 、F .求证:BE =CF . 证明:ABPMN。
2012年北京朝阳中考二模数学
2012年北京朝阳中考二模数学一、选择题(共8小题;共40分)1. 的算术平方根是______A. B. C. D.2. 2012 年1 月21 日,北京市环保监测中心开始在其官方网站上公布的研究性监测数据.是指大气中直径小于或等于米即微米的颗粒物,也称为可入肺颗粒物.把用科学记数法表示为______A. B. C. D.3. 掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有到的点数,掷得朝上一面的点数小于的概率为______A. B. C. D.4. 如图,直线,直角三角板的顶点在直线上,则等于______A. B. C. D.5. 有一组数据:,,,,,这组数据的方差是______A. B. C. D.6. 如图,在中,直径弦于点,是上的点,若,则的度数为______A. B. C. D.7. 下面由个完全相同的小正方体组成的几何体的主视图是______A. B.C. D.8. 如图,在平面直角坐标系中,是反比例函数图象上的一个动点,点在轴上,且,是中边上的高.设,,则下列图象中,能表示与的函数关系的图象大致是______A. B.C. D.二、填空题(共4小题;共20分)9. 若分式有意义,则的取值范围是______.10. 分解因式: ______.11. 在平面直角坐标系中,点在第二象限,且是整数,则的值为______.12. 如图,在平面直角坐标系中,是以为圆心,为半径的圆与过点且平行于轴的直线的一个交点;是以为圆心,为半径的圆与过点且平行于轴的直线的一个交点;是以为圆心,为半径的圆与过点且平行于轴的直线的一个交点;是以为圆心,为半径的圆与过点且平行于轴的直线的一个交点;,且点,,,,都在轴右侧,按照这样的规律进行下去,点的坐标为______,点的坐标为______(用含的式子表示,是正整数).三、解答题(共13小题;共169分)13. 计算:.14. 解方程:.15. 已知,求的值.16. 已知:如图,点,分别在,上,与相交于点,,.求证:.17. 如图,点是反比例函数的图象上的一点.(1)求该反比例函数的解析式;(2)设直线与双曲线的两个交点分别为和,当时,直接写出的取值范围.18. 如图,四边形是矩形,,,把矩形沿直线折叠,点落在点处,连接,与相交于点,求的长和的面积.19. 如图, , 分别是 的直径和弦,弦 与 , 分别相交于点 , ,过点 的切线 与 的延长线相交于点 ,且 .(1)求证: ;(2)若, ,求 的半径长.20. 2012 年 4 月北京国际汽车展览会期间,某公司对参观本次车展的观众进行了随机调查. ① 根据调查结果,将受访者购置汽车的意愿情况整理后,制成如图统计图;② 将有购买家庭用汽车意愿的受访者的购车预算情况整理后,作出相应的统计表和频数分布直方图:(注:每组包含最小值不包含最大值)购车预算 万元 频数频率合计请你根据以上信息,回答下列问题: (1)统计表中的 ______, ______; (2)补全频数分布直方图;(3)这次调查中一共调查了______位参观者.21. 如图,港口 在港口 的东北方向,上午 时,一艘轮船从港口 出发,以 海里/时的速度向正东方向航行,同时一艘快艇从港口 出发也向正东方向航行.上午 时轮船到达 处,同时快艇到达 处,测得 处在 处的北偏东 的方向上,且 , 两地相距海里,求快艇每小时航行多少海里?(结果精确到海里/时,参考数据:,,)22. 已知二次函数.(1)当时,求出该二次函数的图象与轴的交点坐标;(2)若时,该二次函数的图象与轴有且只有一个交点,求的取值范围.23. 正方形的边长为,点是边上的动点,点在边上,且,沿翻折得到,是边上一点,沿翻折得到,使点落在射线上.(1)如图,当时,四边形的面积为______;(2)若,则四边形的面积为______(要求:用含的代数式表示,并写出的取值范围).24. 如图,是中边的中点,和都是等边三角形,,分别是,的中点.(1)求证:是等边三角形;(2)连接,是中点,于点.求证:.同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路做为参考:小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.25. 在平面直角坐标系中,抛物线经过,两点,且与轴交于点,点在轴的负半轴上,且,有一动点从点出发,沿线段以每秒个单位长度的速度向点移动,同时另一个动点从点出发,沿线段以某一速度向点移动.(1)求该抛物线的解析式;(2)若经过秒的移动,线段被垂直平分,求此时的值;(3)该抛物线的对称轴上是否存在一点,使的值最小?若存在,求出点的坐标;若不存在,请说明理由.答案第一部分1. A2. C3. B4. D5. B6. C7. D8. A第二部分9.10.11.12. ;第三部分13. 原式.14. 检验:当时,.是原方程的解.15. 原式.,.原式.16. 在和中,.,...17. (1)点在反比例函数的图象上,由得,反比例函数的解析式为.(2)或.18. ,,.,...,即.设.则,.在中,.即.解得.即...19. (1)如图,连接,是的切线,.即.,.,.,....(2)如图,连接.,分别是的直径和弦,,即..在中,.的半径长为.20. (1);(2)(3)21. 分别过点,作的垂线,交的延长线于点,.中,,,,..,,,四边形是矩形..在中,,,....答:快艇的速度约为海里/时.22. (1)由题意,得当时,,解得该二次函数的图象与轴的交点坐标为,.(2)抛物线的对称轴为.(i)若抛物线与轴只有一个交点,则交点为.有,解得.(ii)若抛物线与轴有两个交点,且满足题意,则有:当时,,,解得.当时,,,解得..综上所述,的取值范围是或.23. (1)(2)四边形四边形24. (1)取的中点,连接,.,,为等边三角形,,.,.,..,..是等边三角形.(2)连接,..中,,.,,.,.....25. (1)抛物线经过两点,解得所求抛物线的解析式为.(2)如图,依题意知,连接,,,,可得,,.,垂直平分,,.,......,解得..线段被垂直平分时,的值为.(3)设抛物线的对称轴与轴交于点.,关于对称轴对称,连接交该对称轴于点,则,即.当时,最小,此时,...,解得..即在抛物线的对称轴上存在一点,使得的值最小.第11页(共11 页)。
【物理】2012年北京中考物理二模力学综合题汇编
【关键字】物理2012年北京中考物理二模力学综合题[丰台二模]39. 图20是某科技小组设计的滑轮组模型装置。
滑轮组由电动机提供动力,在实验室中小明和他的同学进行了如下实验:在底面积为500cm2的圆柱形玻璃筒中倒入一定量的液体。
长方体金属块A的底面积为100cm2。
在0-7s内,金属块A以0.1m/s的速度在液体中匀速竖直上升,当金属块A浸没在液体中上升时滑轮组的机械效率为7/12。
金属块A全部露出液面后以另一速度匀速竖直上升。
细绳的质量、滑轮与轴的摩揩、液体对金属块A的阻力均忽略不计,金属块A的密度为3×103kg/m3,这个过程中电动机工作的功率随时间变化的规律如图22所示,g取10N/kg。
求:(1) 金属块露出液面前电动机所提供的拉力F1;(2) 金属块A从上表面接触液面到下表面离开一共用时2秒,离开液面前后,液体对容器底部的压强变化量。
[延庆二模]38.如图23所示,置于水平桌面的物体A的质量为,悬挂在滑轮组下的物体B 的质量为。
在物体B的作用下,A恰能沿水平桌面向左匀速直线运动。
现在用水平向右的拉力F1 拉动物体A以/s的速度沿水平桌面向右匀速直线运动,在此过程中,物体A通过绳子拉动滑轮组的力为T1,T1提升物体B的机械效率为η1。
当用此装置以相同的速度提升物体C时,水平向右拉物体A的力为F2 ,物体A通过绳子拉动滑轮组的力为T2,T2提升物体C的机械效率为η2。
已知η1:η2=16:15,T1:T2=5:4,不计绳重及滑轮的摩揩,求(1)A与桌面间的滑动摩揩力(2)拉力F2的功率[顺义二模]38.图22甲是某科技小组设计的滑轮组模型装置。
在底面积为2的圆柱形容器中装有密度为的液体,边长为的正立方体物块M完全浸没在液体中匀速竖直上升时,滑轮组的机械效率为;密度为的物块M全部露出液面后匀速竖直上升时,滑轮组的机械效率为,与之比为8:9。
滑轮的质量、且,细绳的质量、滑轮与轴之间的摩揩、液体对物块M的阻力均忽略不计,液体与物块M的质量与体积关系的图像如图22乙示。
2012年北京市各区二模试题分类解析【数学理】(7):不等式.pdf
教学课时:一课时 教学步骤:一.导入新课: 北方冬天的雪,纷纷扬扬地飘落,它覆盖着原野、山村、村庄、道路。
漫天皆白,玉龙飞舞,引得古往今来无数文人墨客诗兴大发。
毛泽东同志既是一位伟大的革命家,同时也是一位杰出的诗人,他的词作《沁园春.雪》就是咏雪的名篇。
(板书课题) 1936年2月,抗日战争爆发前,在陕北的清涧县,毛泽东同志登上海拔千米、白雪覆盖的塬上视察地形,观赏风光。
面对苍茫大地,胸中豪情激荡,过后写下了这首词。
1945年8月,抗战胜利后,为了国家的前途的人民的利益,毛泽东同志亲赴重庆与国民党谈判。
其间,民主人士、诗人柳亚子先生请他写诗,毛泽东同志就把这首《沁园春.雪》抄给他,随后《新民晚报》公开发表,引起了极大的轰动。
二.教学新课 (一)明确教学目标及重点:(投影)1.正音:分娆逊数汗 解词:惟余竞折腰红装素裹风骚 (二)整体感知 1.范读全词,学生想象词作所描绘的景象,初步体会词作所表达的感情。
2.齐读一遍。
3.教师讲解:这首词分上下两阕。
上阕写景,实景有飞雪、冰封、长城、黄河、群山、高原;虚景有雪晴后的红装素裹,大气包举,气象雄伟。
下阕议论、抒情,评论古代英雄的不足,赞美当代革命英雄,充满对革命前途的必胜信念。
(三)重点学习与训练1.学习上阕。
指名学生朗读,提问,上阕分几层意思?理出写景顺序。
解题思路:分三层。
前三句概写,极目万里,动静结合;中间七名具体写,气势磅礴,生机盎然;后三句写想象中的景色,红白交映,艳丽多姿。
2.逐层分析上阕结构: ①前三句从哪个角度写雪景?所写景物有何特点?解题思路:总写北国雪景,“千里”“万里”是互文,千万里冰封,千万里雪飘,写也视野的辽阔。
“封”写地面,凝然安静;“飘”写天空,雪姿轻盈。
一静一动,动静结合,相映成趣。
②“望”字统领到哪一句?“山舞银蛇,原驰蜡象”,山脉怎会像银蛇在舞动,高原怎么像白象在奔跑? 解题思路:字统领到“欲与天公试比高”。
2012年北京各区初三物理二模23题12题汇总
2012二模23题汇总东城23.如图11所示电路,滑动变阻器的最大阻值为R 2=30Ω,灯上标有“3V 3W ”字样,电源电压及灯L 的电阻保持不变。
当S 1、S 2闭合S 3断开、且滑片滑到a 端时,电流表A 1、A 2的示数之比是3:1;当S 1、S 2断开S 3闭合,且滑片P 置于变阻器的中点时,灯刚好正常发光。
通过调节开关的通断和变阻器滑片的位置,可使整个电路消耗的电功率最小,此最小电功率值是 W 。
(保留两位小数)西城23.如图10所示,顶面带有光滑凹槽的轻质杠杆AB 可以绕支点O 转动,杠杆的A 端用细线沿竖直方向连接在地板上,OB =0.5m ,在杠杆的B 端悬挂一个密度为0.8×103kg/m 3的圆柱体M 。
地板上有一个盛满水的容器。
在圆柱体M 体积的1/3浸入水中时,从容器内溢出0.4N 的水,杠杆在水平位置平衡。
此时让一个质量为200g 的小球从B 点沿凹槽向A 端匀速运动,经过4s 的时间,系在A 端细线的拉力恰好等于0N 。
若整个过程中杠杆始终保持水平平衡,则小球的运动速度为 m/s 。
(g 取10N/kg )海淀23.将一轻质弹簧的两端分别固定在正方体物体A 、B 表面的中央,把正方体物体B 放在水平桌面上,当物体A 、B 静止时,弹簧的长度比其原长缩短了5cm ,如图7甲所示。
现将物体A 、B 上下倒置,并将它们放入水平桌面上的平底圆柱形容器内,使物体A 与容器底接触(不密合),再向容器中缓慢倒入一定量的某种液体,待物体A 、B 静止时,物体B 上表面与液面平行,且有14体积露出液面,此时容器底对物体A 的支持力为1 N 。
已知物体A 、B 的边长分别为5cm 、10cm ,物体A 、B 的密度之比为16:1,圆柱形容器的底面积为150cm 2,弹簧原长为10cm ,弹簧所受力F 的大小与弹簧的形变量Δx (即弹簧的长度与原长的差值的绝对值)的关系如图7乙所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
密云
24. 如图,在直角坐标系xoy中,以y轴为对称轴的抛物线经过直线323yx与y轴的交点A和点
M
(32,0).
(1)求这条抛物线所对应的二次函数的解析式;
(2)将这条抛物线沿x轴向右平移,使其经过坐标原点.
①在题目所给的直角坐标系xoy中,画出平移后的
抛物线的示意图;
②设平移后的抛物线的对称轴与直线AB(B是直线323yx与x轴的交点)相交于C点,判断以
O
为圆心、OC为半径的圆与直线AB的位置关系,并说明理由;
(3)P点是平移后的抛物线的对称轴上的点,求P点的坐标,使得以O、A、C、P四点为顶点的四边
形是平行四边形.
燕山
24. 如图,已知点M(-3,2)和抛物线y=2x31,O为直角坐标系的原点.
(1)若直线y=kx+3经过点M,且与x轴交于点A,
求∠MAO的度数;
(2)在(1)的条件下,将图中的抛物线向右平移,
设平移后的抛物线与y轴交于点E,与直线AM
的一个交点记作F,当EF∥x轴时, 求抛物线
的顶点坐标.
y
M
O · x
海淀
平谷
24. 如图,在直角坐标系中,O为原点.点A在x轴的正半轴上,点B在y轴的正半轴上,2OABtan.二
次函数22yxmx的图象经过点A,B,顶点为D.
(1)求这个二次函数的解析式;
(2)将OAB△绕点A顺时针旋转90后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下
平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为1B,顶点为1D.点P在平移后的二次函数图象上,
且满足1PBB△的面积是1PDD△面积的2倍,求点P的坐标.
x
y
O
A
B
通州
房山
25.如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒1个单位长的速度运动t(t>0)
秒,抛物线y=x2+bx+c经过点O和点P.已知矩形ABCD的三个顶点为A(1,0)、B(1,-5)、D(4,0).
⑴求c、b(可用含t的代数式表示);
⑵当t>1时,抛物线与线段AB交于点M.在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,
说明理由;若不变,求出∠AMP的值;
⑶在矩形ABCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分
成数量相等的两部分,请直接..写出t的取值范围.
解:⑴
⑵
⑶
B C A
x y F O
D
E
东城
25. 如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴
上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两
边分别交y轴的正半轴、x轴的正半轴于点E和F.
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ的周长最小,求
出P、Q两点的坐标.
朝阳
25. 在平面直角坐标系xOy中,抛物线42bxaxy经过A(-3,0)、B(4,0)两点,且与y轴交于点
C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB
以每秒1个单位长度的速
度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)求该抛物线的解析式;
(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
(3)该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请
说明理由.
y
x
-1-3-2-4-512345
-1
-2
-3
-4
1
2
3
4
5
O
昌平
24.如图所示,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴和x轴的正半轴
上,抛物线y=ax2+bx+c经过点A、B和D(4,32).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找到点M,使得M到D、B的距离之和最小,求出点M的坐标;
(3)如果点P由点A出发沿线段AB以2cm/s的速度向点B运动,同时点Q由点B出发沿线段BC以1cm/s
的速度向点C运动,当其中一点到达终点时,另一点也随之停止运动.设S=PQ2(cm2).
①求出S与运动时间t之间的函数关系式,并写出t的取值范围;
②当S=54时,在抛物线上存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形, 求出点R的
坐标.
顺义
25.如图,在平面直角坐标系xOy中,二次函数212yxbxc的图象经过点A(-3,6),并与x轴交于
点B(-1,0)和点C,顶点为P.
(1)求二次函数的解析式;
(2)设D为线段OC上的一点,若DPCBAC,求点D的坐标;
(3)在(2)的条件下,若点M在抛物线212yxbxc上,点N在y轴上,要使以M、N、B、D为顶点
的四边形是平行四边形,这样的点M、N是否存在,若存在,求出所有满足条件的点M的坐标;若不
存在,说明理由.
y
B
A
O
x
1221-1-1
C
丰台
25.如图,将矩形OABC置于平面直角坐标系xOy中,A(32,0),C(0,2).
(1) 抛物线2yxbxc经过点B、C,求该抛物线的解析式;
(2)将矩形OABC绕原点顺时针旋转一个角度(0°<<90°),在旋转过程中,当矩形的顶点落在(1)
中的抛物线的对称轴上时,求此时这个顶点的坐标;
(3)如图(2),将矩形OABC绕原点顺时针旋转一个角度(0°<<180°),将得到矩形OA’B’C’,设
A’C’的中点为点E,联结CE,当 °时,线段CE
的长度最大,最大值为 .
石景山
25.已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线
y=2x交于点B、C(B在右、C
在左).
(1)求抛物线的解析式;
(2)设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得BFECFE,若存在,求出点
F
的坐标,若不存在,说明理由;
(3)射线OC上有两个动点P、Q同时从原点出发,分别以每秒5个单位长度、每秒25个单位长度的速
度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运
动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
解:
y
x
O
西城
25.在平面直角坐标系xOy中,抛物线21124yx的顶点为M,直线2yx,点0Pn,为x轴上的一个动
点,过点P作x轴的垂线分别交抛物线21124yx和直线2yx于点A,点B.
⑴直接写出A,B两点的坐标(用含n的代数式表示);
⑵设线段AB的长为d,求d关于n的函数关系式及d的最小值,并直接写出此时线段OB与线段PM的位置
关系和数量关系;
(3)已知二次函数2yaxbxc(a,b,c为整数且0a),对一切实数x恒有
x≤y≤2124x,求a,b,c
的值.
