债券价格与收益率的Matlab实现
《高级债券投资分析与Matlab》 -- 详细介绍及大纲

2015年第二期《高级债券投资分析与Matlab》培训邀请函6月16 – 21 云南大理【中国债券俱乐部财讯金融培训】联合举办随着债券市场的发展,债券品种、债券投资策略、债券组合管理也在不断创新,收益率曲线的波动性与动力学也越发丰富。
如何掌握复杂债券片中的定价,设计合理的债券投资策略与组合管理一直是债券专业人士面临挑战。
为了结合高级债券培训,我们推出Matlab金融应用与高级债券分析的套餐培训计划。
Matlab在金融建模、金融计算中应用广泛,是金融定量分析不可或缺的工具。
第一模块:提供专门的Matlab培训(大纲见附录一)第二模块:提供高级债券培训(大纲见附录二)。
可参选任一模块,需要全面掌握债券高级分析理论与实施方法的学员我们建议参加第一与第二模块。
《高级债券投资分析》培训项目简介:我们强调系统的分析能力与分析工具的使用,真正教会每个学员的实际分析能力。
在完成基础债券分析模块后,就可以进一步深入学习高级债券分析。
该模块针对一些债券投资中的一些主要课题进行深入的研究,根据成熟的理论和实践经验,是债券专门人士管理债券投资组合、挖掘债券价值必不可少的重头课程。
我们的主要的分析工具是Matlab,你将不仅学习到债券高级分析方法,还能掌握实施这些方法的高级工具与软件。
所涉及的主要内容包括收益率曲线拟合技术、浮息债券分析、收益率曲线动力学与主因子分析、内置期权债券分析、收益率曲线的构成、可转债定价技术、高级债券交易与投资策略以及债券与利率金融产品的创新等等。
培训后每个学员能够从高级分析人员的角度,独立进行债券投资策略的制定与风险管理。
所有案例的源程序全部赠送。
(详细内容见附录)培训对象:参加人员:证券,基金,保险,信托,商业银行等机构投资部经理,投资策略师,债券高级分析人员,交易员。
预备知识:证券数量分析方法基础。
Matlab知识强烈推荐。
课程目标:学员通过本门课程的强化培训,应能达到以下学习目标✧掌握研究中国债券品种的先进方法,进行债券定量分析。
matlab实验报告--证券的投资选择

Matlab上机实验报告一.题目设有三种证劵S1,S2,S3,期望收益率分别为10%,15%和40%,风险分别是10%,5%和20%。
假定投资总风险用最大一种投资股票的风险来度量,且同期银行存款利率为r0=5%,无风险,为投资者建议一种投资策略(投资比例),使其尽可能获得最大收益。
二.问题分析本题是一种投资问题,可以转化为具有约束条件的线性函数的极值求解问题。
根据各种投资方式的收益率,列出总收益与投资比例(各种投资方式的投资数目)的方程。
以总投资数为1,各种投资方式的的风险不大于最大投资风险,各种投资方式投资数大于0为约束条件,建立含约束条件的线性函数。
通过求极值解决问题。
三.假设约定假设投资三种证劵的资金分别为s1,s2,s3,投资银行存款的资金为s0,总投资金额为S,投资的风险度为a,设这三种证劵之间是相互独立的,且在投资的同一时期内,证劵收益率,风险度及银行的利率都不发生变化。
四.模型建立由题目的已知条件可以知道投资后获得的各项收益为0.05s0,0.1s1,0.15s2,0.4s3,投资三种证劵的风险度分别为0.1s1/S, 0.05s2/S, 0.2s3/S,为使投资者获得最大收益,在总风险不超过a的情况下,可以建立如下模型:max 0.05s0+0.1s1+0.15s2+0.4s3且:s0+s1+s2+s3=S0.1s1/S<=a0.05s2/S<=a0.2s3/S<=as1>=0,s2>=0,s3>=0五.模型简化令xi=si/S,则原模型可以简化为:min f=-0.05x0-0.1x1-0.15x2-0.4x3其中:x1+x2+x3+x4=10.1x1<=a0.05x2<=a0.2x3<=ax1>=0,x2>=0,x3>=0 六.程序代码使用MATLAB编写的程序如下所示:a=0;c=[-0.05,-0.1,-0.15,-0.4];A=[0,0.1,0,0,;0,0,0.05,0;0,0,0,0.2];aeq=[1,1,1,1];beq=[1];vlb=[0,0,0,0];vub=[0];for a=0:0.01:0.3b=[a,a,a,a];[x,val]=linprog(c,A,b,aeq,beq,vlb,vub);ax=x’Q=-valplot(a,Q,’.’)hold onend七.实验结果程序运行后所得的结果如下所示原始数据如下:a =0.1990x =0 0.0000 0.0050 0.9950Q =0.3987a =0.2000x = 0 0.0000 0.0000 1.0000 Q = 0.4000a =0.2010x =0 0.0000 0.0000 1.0000Q = 0.4000a = 0.2020x =0 0.0000 0.0000 1.0000Q = 0.4000a =0.2030x =0 0.0000 0.0000 1.0000Q = 0.4000八.结果分析(1)风险越大,收益也越大,但不承线性分布。
CAPM模型计算的MATLAB实现

CAPM模型中beta系数的MATLAB实现CAPM模型中两条重要的线分别是资本市场线和证券市场线,资本市场线研究的是在无风险利率存在的条件下,有效资产组合的预期收益与风险的关系,而证券市场线研究的是在无风险利率存在的条件下,单个证券的预期收益与风险的关系。
均衡的单个证券的预期收益率定价公式如下:E(r i)=r f+[E(r M)−r f]∙βi是单个证券的风险调整系数。
下面编写Matlab 其中,βi=Cov(r i,r M)σM2程序,计算单只证券的β系数。
在此所用软件为MATLAB R2014a。
根据CAPM模型公式中的β系数的计算方法,可编写函数式M 文件,计算单个证券或证券组合的beta系数。
该函数如下function beta=portbeta(portReturn,marketReturn)% 函数目的:利用CAPM模型公式,计算beta系数% 输入参数:% portReturn: 单个证券或证券组合的收益率序列% marketReturn:市场或基准的收益率序列% 输出参数:% beta:基于CAPM模型的beta值temp_cov=cov(portReturn,marketReturn); % 计算协方差矩阵beta=temp_cov(1,2)/temp_cov(2,2); % beta=组合与市场的协方差/市场的方差end一、不同类型证券的β系数假设我们考察的证券为:股票型基金—诺安高端制造股票(001707)、混合型基金—嘉实主题新动力混合(070021)、债券型基金—博时裕瑞纯债债券(001578),用沪深300收益率(或者日涨跌幅)代表市场组合的收益率,时间为2018年5月-2019年4月。
各收益率数据如下:下面首先画出证券收益率和市场收益率(沪深300)的图形,直观观察证券与市场的相对波动程度大小,画图代码如下:% 载入数据load data.txt% 数据列顺序为:诺安高端制造股票、嘉实主体新动力混合、博时裕瑞纯债债券x=1:size(data,1);plot(x,data(:,1),'m-o',x,data(:,2),'g-', x, data(:,3), 'r:', x, data(:,4),'b--')legend('诺安高端','嘉实主体','博时裕瑞','沪深300')图1 基金收益率与沪深300收益率(单位:%)从上图可见,诺安高端制造股票的波动幅度大于沪深300,嘉实主体新动力混合的波动幅度裕沪深300接近,而博时裕瑞纯债债券的波动幅度远远小于沪深300,故此可初步判断出,诺安高端制造股票的beta系数大于1、嘉实主体新动力混合的beta系数接近1,而博时裕瑞纯债债券的beta系数远小于1。
MATLAB程序设计 资产收益率分布的拟合与检验
资产收益率分布的拟合与检验在统计推断中,通常假定总体服从一定的分布(例如正态分布),然后在这个分布的基础上,构造相应的统计量,根据统计量的分布作出一些统计推断,而统计量的分布通常依赖于总体分布的假设,也就是说总体所服从的分布在统计推断中是至关重要的,会影响到结果的可靠性。
从这个意义上来说,由样本观测数据去推断总体所服从的分布是非常必要的。
指数与基金的收益率,介绍根据样本观测数据拟合总体的分布,并进行分布的检验。
本章主要内容包括:数据的描述性统计,分布的检验,核密度(kernel density)估计。
其中数据的描述性统计又包括均值、标准差、最大值、最小值、极差、中位数、众数、变异系数、偏度和峰度等描述性统计量,以及箱线图、经验分布函数图、频率直方图和正态概率图等统计图;分布的检验主要介绍chi2gof、jbtest、kstest、kstest2、lillietest等函数的用法。
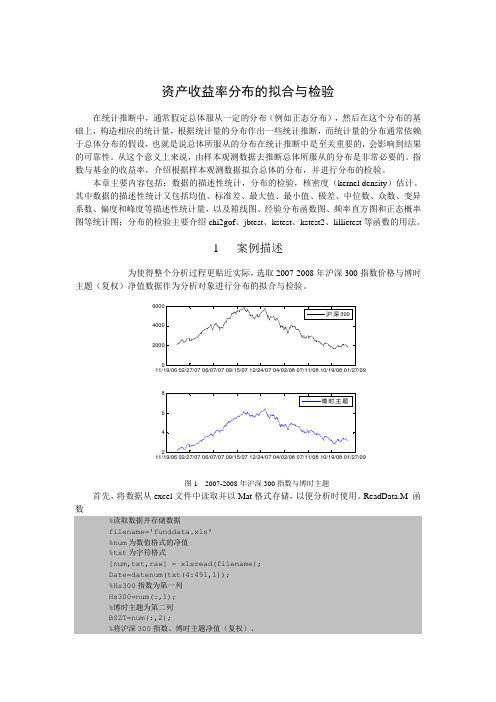
1 案例描述为使得整个分析过程更贴近实际,选取2007-2008年沪深300指数价格与博时主题(复权)净值数据作为分析对象进行分布的拟合与检验。
图1 2007-2008年沪深300指数与博时主题首先,将数据从excel文件中读取并以Mat格式存储,以便分析时使用。
ReadData.M 函数%读取数据并存储数据filename='funddata.xls'%num为数值格式的净值%txt为字符格式[num,txt,raw] = xlsread(filename);Date=datenum(txt(4:491,1));%Hs300指数为第一列Hs300=num(:,1);%博时主题为第二列BSZT=num(:,2);%将沪深300指数、博时主题净值(复权)、%日期数据存储在TestData 中save TestData Hs300 BSZT Date %画图subplot(2,1,1)plot(Date,Hs300,'k');%将时间轴的 数值日期转变为 月/年 格式 dateaxis('x',2) legend('沪深300') subplot(2,1,2)plot(Date,BSZT,'b--');%将时间轴的 数值日期转变为 月/年 格式 dateaxis('x',2) legend('博时主题')2 数据的描述性统计2.1 描述性统计量在进行数据分析之前,先从几个特征数字上认识一下它们,也就是说计算几个描述性统计量,包括均值、标准差、最大值、最小值、极差、中位数、众数、变异系数、偏度和峰度。
Matlab在货币金融学可视化教学中的运用_—_—以“利息的计算与运用”为例

2022年第2期总第554期No.2,2022SumNo.554 Journal of Science and Education1引言货币金融学是高等院校经济类专业的核心课程和金融学专业的基础必修课程,课程内容涉及利率、金融工具、金融衍生品等的计算。
近年来,我国高校金融计算类课程的开设已逐渐普及[1]。
因此,在金融学课程中有必要培养学生处理和解决金融计算中的实际问题,提高学生解决实际问题的能力。
传统课堂利用公式推导、演算等手段进行金融计算内容的教学,学生普遍反映内容理论性太强,概念抽象,计算过程复杂,得到的结果难以理解。
因此,需要构建可视化的教学模式和方法,将难以理解的概念、模型及公式具象化。
利息的计算与运用是本科货币金融学课程中重要的教学内容之一,同时为后续金融衍生工具等内容的学习打下良好的基础[2]。
利息的概念容易理解,但是利息的计算及其应用处理起来相当烦琐,导致学生很难理解相关概念,对图像的认知也不清晰。
本文使用Matlab的APP Designer功能,以利息的计算与运用为例,通过图形用户界面的布局设计及回调函数的程序编写,解决传统教学方式在可视化教学上的问题,将学生从复杂的数学计算中解放出来,加深学生对概念的认知和理解,增强学生的直观感性认识,激发学生的学习兴趣。
2图形用户界面设计利用Matlab APP Designer建立空白的APP后,对图形用户界面进行控件布局和编程,通过图形界面来控制相关性能的可视化过程。
货币金融学可视化教学图形界面主要包括三个选项卡组,分别对应单利与复利、现值、到期收益率三个子界面。
每个子界面按照需要分为参数区、控制区、公式区、结果区、示例区、显示区等,在用户界面控件的Callback回调函数下输入相应的控制程序实现交互性。
通过设定参数,点击相关按钮,会执行相应按钮回调函数下的程序,并将图形化的结果在显示区呈现,或者给出案例示例。
2.1单利与复利单利(simpleinterest),是指以本金为基数计算利息,而借贷期内所生利息不再加入本金计算下期利息的一种利息计算方法,即在当期产生的利息不作为下一期的本金,只是把每一期产出的利息累加到投资期末。
第二讲 固定收益证券的matlab计算

ans = 32
例2:请分别用30E/360,ISDA,PSA,SIA法计算例1 中的应计天数。 解:
30E/360,ISDA,PSA,SIA对basis代码分别是: E_Days=daysdif('2/27/2007','3/31/2007',6) E_Days = 33 >> ISDA_Days=daysdif('2/27/2007','3/31/2007',5) ISDA_Days = 34 >> PSA_Days=daysdif('2/27/2007','3/31/2007',4) PSA_Days = 34 >> SIA_Days=daysdif('2/27/2007','3/31/2007',1) SIA_Days = 34
D = daysdif(D1, D2) D = daysdif(D1, D2, Basis) Optional Inputs: Compounding, Basis Inputs: D1 - [Scalar or Vector] of dates. D2 - [Scalar or Vector] of dates.
如一张10年期国债被剥离成20张半年期债券,每 张都可视为零息票,它们到期日从6个月到10年不 等,最后本多支付是另一张零息证券,所有的支付 都单独计算,并配有自己的CUSIP号码
由于这种债券息票被“剥离”了,因此被称为本 息剥离式国债STRIPS(separate trading of registered interest and principal of securities).
债券久期与凸度的Matlab实现

案例分析:债券久期与凸度的Matlab实现一、计算公式(一)债券久期麦考利久期(Macaulay duration)是利用加权平均数的形式计算债券的平均到期时间。
它是债券在未来产生现金流的时间的jia全平均,其权重是各期现金值在债券价格中所占的比重。
普通债券的久期如下式所示:D=∑PV(c t)×t Tt=1P式中,D是麦考利久期;P是债券的当前市场价格;PV(c t)是债券未来第t期现金流(利息或面值)的现值;T是债券的到期时间。
(二)债券凸度由于债券价格与收益率之间的关系曲线存在凸向原点的非线性特征,当收益率大幅波动时,久期不能准确地描述债券价格对利率变动的敏感性。
为纠正久期的这种不足,引入凸度或凸性的概念。
与久期一样,凸度也是度量债券价格波动性的方法。
凸度越大,债券价格曲线弯曲程度越大,用修正久期度量债券的利率风险所产生的误差越大。
凸度的计算公式如下:d2p dy2=∑t(t+1)c t(1+y)t+2凸度的性质如下:第一,凸度随久期的增加而增加。
若收益率、久期不变,则票面利率越大,凸度越大。
利率下降时,凸度增加。
第二,对于没有隐含期权的债券来说,凸度总大于0,即利率下降,债券价格将以加速度上升;当利率上升时,债券价格以减速度下降。
第三,含有隐含期权的债券的凸度一般为负,即价格随着利率的下降以减速度上升,或债券的有效持续期随利率的下降而缩短,随利率的上升而延长。
二、Matlab实现(一)债券久期1、根据价格计算久期Matlab的Financial Toolbox提供了给定债券期限与价格计算久期的函数为bnddurp。
常用调用格式如下:[ModDuration, YearDuration] = bnddurp(Price, CouponRate, Settle, Maturity, Period, Basis)主要输入参数:➢Price:债券净价➢CouponRate:票面利率➢Settle:结算日➢Maturity:到期日➢Period:年付息次数,默认值为2,可选0、1、2、3、4、6、12。
固定收益证券的matlab计算

5. 美国CD存单 美国CD存单(certificate deposit): 由银行等金
融机构向存款人发行的证券,存单上标有一个到期 日和利率,并且以任意面值发行,可以买卖, 偿还期 限小于1年. 6. 回购协议(repurchase agreement)
是短期抵押贷款. 指一方向另一方出售证券的同 时,承诺在未来的某一天按协定的价格将相同的证 券买回,通常由借款方发起并贷出证券,回购中涉及 的证券通常具有较高的信用质量.
美国的固定收益证券可以分为以下几个品种:
1. (短期)国库券(Treasury bills, T-bills) 期限小于一年,贴现发行,面值usu. 1~10万美元.是流
动性最高的债券品种,违约风险小,其利率usu当作无 风险利率。 2.政府票据(Treasury notes, T-notes)
即美国中期国债,期限1~10年,是coupon. 3. 长期国债(Treasury bonds, T-bonds)
第二讲 固定收益证券的 matlab计算
吴义能 TEL: 15387002178 QQ: 294808610 E-mail: wuyineng2003@
第一节 固定收益基本知识
固定收益证券: 一组稳定现金流的证券.广义上还包括
了债券市场上的衍生产品及优先股.以债券为 主.
一. 固定收益的品种 国债是固定收益的重要形式,以贴现债券 (discount security)与息票债券(coupon bonds)两种形式发行.
如一张10年期国债被剥离成20张半年期债券,每 张都可视为零息票,它们到期日从6个月到10年不 等,最后本多支付是另一张零息证券,所有的支付 都单独计算,并配有自己的CUSIP号码
由于这种债券息票被“剥离”了,因此被称为本 息剥离式国债STRIPS(separate trading of registered interest and principal of securities).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例分析:债券定价与收益率的Matlab实现一、计算公式(一)债券价格计算1、一次还本付息债券的定价公式P=P T(1+r c)T (1+r)T其中,P T为债券面值,r c为票面利率,r为必要收益率/到期收益率/贴现率,T是债券期限。
2、附息债券的定价公式P=∑r c×P T (1+rn)tT×nt=1+P T (1+rn)T×n=r c×P Tr[1−1(1+r/n)]+P T(1+r/n)其中,P T为债券面值,r c为票面利率,r为必要收益率/到期收益率/贴现率,T是债券期限(以年为单位),n为年付息次数。
实际上,附息债券的定价包括两类:其一,付息日的债券定价;其二,付息日之间的债券定价。
上面的定价公式适用于情况一。
当投资者在两个付息日之间购买债券时,债券发行人通常将在下一个付息日将本期利息支付给债券购买者,债券出售者无法获得本期利息。
但是,由于出售者是在两个付息日之间卖出债券,他对本期利息也享有部分权利。
故此,债券购买者必须将下次利息支付的一部分付给出售者作为补偿,这部分利息被称为应计利息(Accrued interest)。
美国的中长期国债按照“实际天数/实际天数”原则计算利息,即上一期付息日至交割日之间的实际天数除以上一期付息日至下一期付息日之间的实际天数。
根据财政部、中国人民银行和中国证券监督管理委员会《关于试行国债净价交易有关事宜的通知》(财库[2001]12号),中国的附息国债采用净价交易制度,应计利息=面值×票面利率×应计息天数÷365(天)。
其中,应计息天数是指上一期付息日至交割日的实际日历天数(1年按365天计算,闰年2月29日不计算利息),计息原则是“算头不算尾”,即付息日当天计算利息,到期日当天不计算利息。
债券报价通常不包含应计利息,即净价,而投资者购买债券支付的金额是包括应计利息的价格,即全价,全价=净价+应计利息。
下面介绍债券全价和应计利息的常用计算方法:P=1(1+r/n)T1/T2[∑r cn×P T(1+r/n)t−1Tt=1+P T(1+r/n)T−1]应计利息=P T×r cn×T3T2式中,T1表示交割日至下一期付息日之间的实际天数,T2表示上一期付息日至下一期付息日(即两个付息日)之间的实际天数,T3表示上一期付息日至交割日之间的实际天数,T表示交割日至清偿日或到期日之间的付息次数,P表示债券全价,P T表示债券面值,r c表示票面利率,r表示市场利率或贴现率,n表示年付息次数。
(二)到期收益率计算在衡量债券收益率的指标中,到期收益率(Yield to maturity,YTM)是应用最广泛的指标。
到期收益率是指使得债券未来现金流的现值正好等于债券当前的市场价格的贴现率。
它是按复利计算的收益率,考虑了货币的时间价值,能够较好地反映债券的实际收益。
1、零息债券的到期收益率零息债券只有一笔现金流,它的到期收益率计算公式为:P=P T(1+r YTM)T式中,T是距离到期日的年数,r YTM是到期收益率,P T和P分别为债券面值和债券的市场价格。
2、附息债券的到期收益率计算附息债券的到期收益率是计算债券价值的逆过程,可以将式(16-4)和(16-8)中的r替换为到期收益率r YTM得到。
第一,在付息日购买的债券的到期收益率计算方法,如下所示:P=∑r cn×P T (1+r YTM/n)tTt=1+P T(1+r YTM/n)T上式也适用于n=1,即每年支付一次利息的情形。
第二,在付息日之间购买的债券的到期收益率计算方法,如下所示:P=1(1+r YTM/n)[∑r cn×P T(1+r YTM/n)Tt=1+P T(1+r YTM/n)]二、Matlab实现(一)债券价格计算Matlab的Financial Toolbox提供了计算债券价格的bndprice 函数,该函数既可用于在付息日交割的债券定价,也适用于在两个付息日之间交割的债券定价。
常用调用格式:[Price, AccruedInt] = bndprice(Yield, CouponRate, Settle, Maturity, Period, Basis)主要输入参数:➢Yield:到期收益率➢CouponRate:票面利率➢Settle:结算日➢Maturity:到期日➢Period:年付息次数,默认值为2,可选0、1、2、3、4、6、12。
➢Basis:(可选项)债券的天数计算方法,默认值为0(实际值/实际值),常见选项具体如下:◼0:实际值/实际值◼1:30/360◼2:实际值/360◼3:实际值/365输出参数:➢Price:价格(净价),全价=净价+交割日利息➢AccruedInt:交割日的利息注意:银行间债券市场于2001年7月开始实行净价交易,沪深交易所市场也于2002年开始实行净价交易。
在净价交易条件下,由于交易价格不含有应计利息,所以其价格形成及变动能够更加准确地体现债券的内在价值、供求关系及利率的变动趋势。
通过净价交易,有利于投资者对市场利率走势和债券交易决策做出更为理性的判断。
【算例1】债券A:到期收益率为3%,票面利率4%,年付息2次,面值为100,交割日为2016年6月1日,到期日为2018年6月1日。
交割日在付息日。
债券B:到期收益率为3%,票面利率4%,年付息2次,面值为100,交割日为2016年3月1日,到期日为2018年6月1日。
交割日在多于1个付息期的两次付息日之间。
债券C:到期收益率为3%,票面利率4%,年付息2次,面值为100,交割日为2018年3月1日,到期日为2018年6月1日。
交割日在不足1个付息期的两次付息日之间。
计算代码如下:% 到期收益率Yield=0.03;% 票面利率CouponRate=0.04;% 交割日Settle_A='01-Jun-2016';Settle_B='01-Mar-2016';Settle_C='01-Mar-2018';% 到期日Maturity='01-Jun-2018';% 债券A的净价和应计利息[Price_A,Accured_A]=bndprice(Yield,CouponRate,Settle_A, Maturity);% 债券B的净价和应计利息[Price_B,Accured_B]=bndprice(Yield,CouponRate,Settle_B, Maturity);% 债券C的净价和应计利息[Price_C,Accured_C]=bndprice(Yield,CouponRate,Settle_C, Maturity);% 计算结果输出Price=[Price_A;Price_B;Price_C]Accured=[Accured_A;Accured_B;Accured_C]计算结果如下:Price =101.9272102.1577100.2462Accured =0.99450.9890(二)到期收益率计算Matlab的Financial Toolbox提供了债券到期收益率的计算函数bndyield。
该函数既可用于在付息日交割的债券到期收益率计算,也适用于在两个付息日之间交割的债券到期收益率计算。
常用调用格式:Yield = bndyield(Price, CouponRate, Settle, Maturity, Period, Basis)主要输入参数:➢Price:债券净价➢CouponRate:票面利率➢Settle:结算日➢Maturity:到期日➢Period:年付息次数,默认值为2,可选0、1、2、3、4、6、12。
➢Basis:(可选项)债券的天数计算方法,默认值为0(实际值/实际值),常见选项具体如下:◼0:实际值/实际值◼1:30/360◼2:实际值/360◼3:实际值/365输出参数:➢Yield:到期收益率【算例2】债券A:票面利率为5%,面值为100元,每年付息两次(6月底和12月底),交割日为1997年12月31日,到期日为2002年6月30日,净价为104.8106元。
债券B:票面利率为5%,面值为100元,每年付息两次(6月底和12月底),交割日为1997年12月31日,到期日为2002年6月30日,净价为95.4384元。
债券C:票面利率为5%,面值为100元,每年付息两次(6月底和12月底),交割日为1998年1月20日,到期日为2002年6月30日,净价为99.9951元。
计算代码如下:% 票面利率都为5%CouponRate=0.05;% 债券净价Price_A=104.8106;Price_B=95.4384;Price_C=99.9951;% 交割日Settle_AB='31-Dec-1997';Settle_C ='20-Jan-1998';% 到期日都是2002年6月30日Maturity='30-Jun-2002';% 调用bndyield函数Yield_A=bndyield(Price_A,CouponRate,Settle_AB,Maturity) Yield_B=bndyield(Price_B,CouponRate,Settle_AB,Maturity) Yield_C=bndyield(Price_C,CouponRate,Settle_C ,Maturity)计算结果如下:Yield_A =0.0383Yield_B =0.0618Yield_C =0.0500本案例分析中所有代码均在MatlabR2014a环境下运行。
参考资料:[1]郑志勇、王洪武. 金融数量分析—基于MATLAB编程[M]. 北京:北京航空航天出版社, 2018.[2]张志涌、杨祖樱. Matlab教程[M]. 北京:北京航空航天大学出版社, 2017.。
