现代控制理论习题集
胡寿松《现代控制理论》习题集部分解答

胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
非 卖 品
ROnei(李荣辉)完成,仅供参考
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
品 卖 非
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
ROnei(李荣辉)完成,仅供参考
非 卖 品
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
非 卖 品
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
非 卖 品
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
非 卖 品
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
非 卖 品
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
非 卖 品
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
品 卖 非
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
非 卖 品
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
非 卖 品
ROnei(李荣辉)完成,仅供参考
胡寿松《自动控制原理习题集》第九章现代控制理论B部分习题解答
ROnei(李荣辉)完成,仅供参考
《现代控制理论》课后习题答案1.pdf

《现代控制理论》第一章习题解答1.1 线性定常系统和线性时变系统的区别何在? 答:线性系统的状态空间模型为:xAx Bu y Cx Du=+=+线性定常系统和线性时变系统的区别在于:对于线性定常系统,上述状态空间模型中的系数矩阵A ,B ,C 和中的各分量均为常数,而对线性时变系统,其系数矩阵D A ,B ,C 和中有时变的元素。
线性定常系统在物理上代表结构和参数都不随时间变化的一类系统,而线性时变系统的参数则随时间的变化而变化。
D 1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别? 答: 传递函数模型与状态空间模型的主要区别如下:传递函数模型(经典控制理论)状态空间模型(现代控制理论) 仅适用于线性定常系统 适用于线性、非线性和时变系统用于系统的外部描述 用于系统的内部描述基于频域分析基于时域分析1.3 线性系统的状态空间模型有哪几种标准形式?它们分别具有什么特点?答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对角线标准型。
对于阶传递函数n 1212101110()n n n n n n n b s b s b s b G s d s a s a s a −−−−−−++++=+++++"",分别有[]012101210100000100000101n n n xx ua a a a yb b b b x du−−−⎧⎡⎤⎪⎢⎥⎪⎢⎥⎪⎢⎥=+⎪⎢⎥⎨⎢⎥⎪⎢⎥⎪−−−−⎣⎦⎪=+⎪⎩"" ###%##"""⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⑴ 能控标准型:[]0011221100010********001n n n b a b a xa x ub a b y xdu −−−⎧−⎡⎤⎡⎤⎪⎢⎥⎢⎥−⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=−+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎢⎥⎢⎥⎪−⎣⎦⎣⎦⎪=+⎪⎩"" "######""⑵ 能观标准型:[]1212001001001n n p p x x up y c c c x du⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥⎪⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎨⎢⎥⎢⎥⎪⎣⎦⎣⎦⎪⎪=+⎩"" ##%##""⑶ 对角线标准型: 式中的和可由下式给出,12,,,n p p p "12,,,n c c c "12121012111012()n n n n n n n n nb s b s b s bc c c G sd d s a s a s a s p s p s p −−−−−−++++=+=++++++−−−"""++能控标准型的特点:状态矩阵的最后一行由传递函数的分母多项式系数确定,其余部分具有特定结构,输出矩阵依赖于分子多项式系数,输入矩阵中的元素除了最后一个元素是1外,其余全为0。
现代控制理论基础(习题)
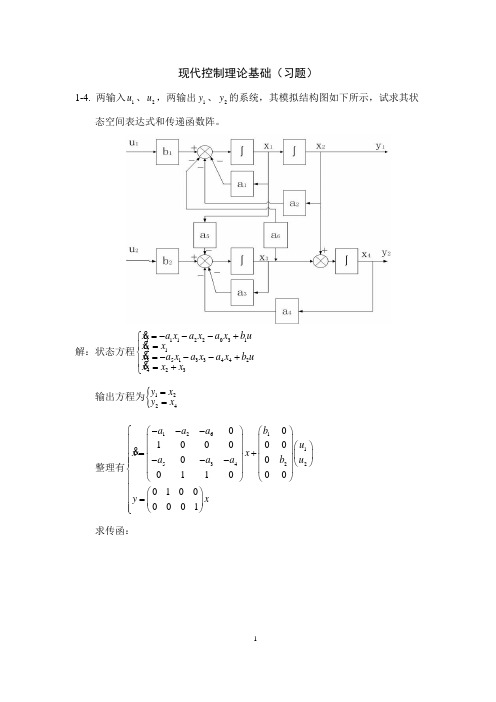
现代控制理论基础(习题)1-4. 两输入1u 、2u ,两输出1y 、2y 的系统,其模拟结构图如下所示,试求其状态空间表达式和传递函数阵。
解:状态方程111220312135133442423x a x a x a x b u x x x a x a x a x b u xx x =---+⎧⎪=⎨=---+⎪=+⎩输出方程为{1224y xy x ==整理有1261125342001000000001100001000001a a a b u x x u a a a b y x ⎧---⎛⎫⎛⎫⎪⎪ ⎪⎛⎫⎪ ⎪ ⎪=+ ⎪⎪ ⎪ ⎪---⎪⎝⎭⎪ ⎪⎨⎝⎭⎝⎭⎪⎪⎛⎫⎪= ⎪⎪⎝⎭⎩求传函:1121126153420010000()()00010000001001000000010001100b G s sI A b s a a a b s a s a a b s --⎛⎫ ⎪⎛⎫ ⎪=-⎪ ⎪⎝⎭ ⎪⎝⎭+⎛⎫⎛⎫ ⎪ ⎪-⎛⎫ ⎪ ⎪=⎪⎪ ⎪+⎝⎭⎪ ⎪--⎝⎭⎝⎭125342616122234534213415622346242260100det()det 001100(1)(1)det 0(1)det 1101()()()()s a a a s sI A a s a a s a a s a a s a a s a s a a s s a s s a a a a a s s a s a a s a s a a sa s a +++⎛⎫ ⎪- ⎪-= ⎪+ ⎪--⎝⎭+⎛⎫⎛⎫ ⎪ ⎪=-⋅-⋅++-⋅⋅+ ⎪ ⎪⎪ ⎪---⎝⎭⎝⎭=+-++++++-=+432222346241313441564221313562414232446()()()()a s a a a a s a a s a a s a s a a s a a s s a a s a a a a a a s a a a a s a a a a -+++++++-=+++-+++++-121223141243()b a b a G s b a b a ⎛⎫= ⎪⎝⎭322134a s a s a s =++ 4153(1)a a s a=-+ 236a a s =- 243126a s a s a a =++- 213141622511321222621()det()(1)b s a b s a b a b s G s sI A a b s b a b s a b s a b a b ⎛⎫++-= ⎪--+++-⎝⎭1-5. 系统的动态特性由下列微分方程描述(1)5732y y y y u u +++=+(2)57332y y y y u u u +++=++列写其相应的状态空间表达式,并画出相应的模拟结构图。
现代控制理论习题

《现代控制理论》练习题判断题1. 由一个状态空间模型可以确定惟一一个传递函数。
3. 对一个给定的状态空间模型,若它是状态能控的,则也一定是输出能控的。
4. 对系统Ax x= ,其Lyapunov 意义下的渐近稳定性和矩阵A 的特征值都具有负实部是一致的。
5. 对一个系统,只能选取一组状态变量;6. 由状态转移矩阵可以决定系统状态方程的系统矩阵,进而决定系统的动态特性;7. 状态反馈不改变系统的能控性。
8. 若传递函数B A sI C s G 1)()(--=存在零极相消,则对应状态空间模型描述的系统是不能控的;9. 若线性系统是李雅普诺夫意义下稳定的,则它是大范围渐近稳定的;10. 相比于经典控制理论,现代控制理论的一个显著优点是可以用时域法直接进行系统的分析和设计。
11. 传递函数的状态空间实现不唯一的一个主要原因是状态变量选取不唯一。
12. 状态变量是用于完全描述系统动态行为的一组变量,因此都是具有物理意义。
13. 等价的状态空间模型具有相同的传递函数。
14. 互为对偶的状态空间模型具有相同的能控性。
15. 一个系统的平衡状态可能有多个,因此系统的李雅普诺夫稳定性与系统受扰前所处的平衡位置无关。
16. 若一线性定常系统的平衡状态是渐近稳定的,则从系统的任意一个状态出发的状态轨迹随着时间的推移都将收敛到该平衡状态。
17. 反馈控制可改变系统的稳定性、动态性能,但不改变系统的能控性和能观性。
18. 如果一个系统的李雅普诺夫函数确实不存在,那么我们就可以断定该系统是不稳定的。
填空题l .系统状态完全能控是指 。
2.系统状态的能观性是指 。
3.系统的对偶原理: 。
4.对于一个不能控和不能观的系统,按系统结构标准分解为 、 、 、 、的四个子系统。
5.对于单输入单输出系统,系统能控、能观的充要条是 是 。
7.系统平衡状态的渐近稳定性的定义为: 。
10.受控系统∑),,(C B A ,采用状态反馈能镇定的充分必要条件是 。
现代控制理论习题及答案

现代控制理论习题及答案现代控制理论习题及答案现代控制理论是控制工程领域的重要分支,它研究如何设计和分析控制系统,以实现对动态系统的稳定性、响应速度、精度等方面的要求。
在学习现代控制理论过程中,习题是一个非常重要的环节,通过解答习题可以帮助我们巩固理论知识,提高问题解决能力。
本文将介绍一些常见的现代控制理论习题及其答案,希望对读者有所帮助。
1. 题目:给定一个开环传递函数 G(s) = 10/(s+5),求其闭环传递函数 T(s) 和稳定性判断。
解答:闭环传递函数 T(s) 可以通过公式 T(s) = G(s) / (1 + G(s)) 计算得到。
代入G(s) 的表达式,得到 T(s) = 10/(s+15)。
稳定性判断可以通过判断开环传递函数G(s) 的极点是否在左半平面来进行。
由于 G(s) 的极点为 -5,位于左半平面,因此系统是稳定的。
2. 题目:给定一个系统的状态空间表达式为 dx/dt = Ax + Bu,其中 A = [[-1, 2], [0, -3]],B = [[1], [1]],求系统的传递函数表达式。
解答:系统的传递函数表达式可以通过状态空间表达式进行求解。
首先,计算系统的特征值,即矩阵 A 的特征值。
通过求解 det(sI - A) = 0,可以得到系统的特征值为 -1 和 -3。
然后,将特征值代入传递函数表达式的分母,得到传递函数的分母为 (s+1)(s+3)。
接下来,计算传递函数的分子,可以通过求解 C = D(sI - A)^(-1)B 得到,其中 C 和 D 分别为输出矩阵和输入矩阵。
代入给定的 A、B 矩阵,计算得到 C = [1, 0] 和 D = [0]。
因此,系统的传递函数表达式为 G(s) = C(sI - A)^(-1)B = [1, 0] * [(s+1)^(-1), -2(s+3)^(-1); 0, (s+3)^(-1)] * [1; 1] =(s+1)^(-1) + 2(s+3)^(-1)。
现代控制理论1-8三习题库
信息工程学院现代控制理论课程习题清单正确理解线性系统的数学描述,状态空间的基本概念,熟练掌握状态空间的表达式,线性变换,线性定常系统状态方程的求解方法。
重点内容:状态空间表达式的建立,状态转移矩阵和状态方程的求解,线性变换的基本性质,传递函数矩阵的定义.要求熟练掌握通过传递函数、微分方程和结构图建立电路、机电系统的状态空间表达式,并画出状态变量图,以及能控、能观、对角和约当标准型。
难点:状态变量选取的非唯一性,多输入多输出状态空间表达式的建立.预习题1.现代控制理论中的状态空间模型与经典控制理论中的传递函数有何区别?2。
状态、状态空间的概念?3。
状态方程规范形式有何特点?4。
状态变量和状态矢量的定义?5.怎样建立状态空间模型?6。
怎样从状态空间表达式求传递函数?复习题1.怎样写出SISO系统状态空间表达式对应的传递函数阵表达式2.若已知系统的模拟结构图,如何建立其状态空间表达式?3.求下列矩阵的特征矢量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=2510221-1A4.(判断)状态变量的选取具有非惟一性。
5.(判断)系统状态变量的个数不是惟一的,可任意选取。
6.(判断)通过适当选择状态变量,可将线性定常微分方程描述其输入输出关系的系统,表达为状态空间描述。
7.(判断)传递函数仅适用于线性定常系统;而状态空间表达式可以在定常系统中应用,也可以在时变系统中应用。
8.如果矩阵A 有重特征值,并且独立特征向量的个数小于n ,则只能化为模态阵。
9.动态系统的状态是一个可以确定该系统______(结构,行为)的信息集合。
这些信息对于确定系统______(过去,未来)的行为是充分且必要的。
10.如果系统状态空间表达式中矩阵A,B, C,D中所有元素均为实常数时,则称这样的系统为______(线性定常,线性时变)系统。
如果这些元素中有些是时间t 的函数,则称系统为______(线性定常,线性时变)系统.11.线性变换不改变系统的______特征值,状态变量)。
现代控制理论1-8三习题库
信息工程学院现代控制理论课程习题清单3.有电路如图1-28所示。
以电压U(t)为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻 R 2上的电压作为输出量的输出方程。
4.建立图P12所示系统的状态空间表达式。
M 21 f(t)5.两输入u i ,U 2,两输出y i ,y 的系统,其模拟结构图如图1-30所示,练习题 ,输出为,试自选状态变量并列写出其状2.有电路如图所示,设输入为 态空间表达式。
Cri _ l- ------- sR 2 U i U ciL uA------—2R i试求其状态空间表达式和传递函数阵。
6.系统的结构如图所示。
以图中所标记的 x 1、x 2、x 3作为状态变量,推导其状态空间表达式。
其中,u 、y 分别为系统的输入、 输出,1、2试求图中所示的电网络中,以电感L i 、L 2上的支电流x i 、X 2作为状态变量的状态空间表达式。
这里 u 是恒流源的电流值,输出 y 是R 3上的 支路电压。
8.已知系统的微分方程y y 4y 5y 3u ,试列写出状态空间表达式。
9.已知系统的微分方程2y 3y u u , 试列写出状态空间表达式。
10. 已知系统的微分方程y2y 3y 5y5u 7u ,试列写出状态空间表达式。
7.3均为标量。
11.系统的动态特性由下列微分方程描述y 5 y 7 y 3y u 3u 2u列写其相应的状态空间表达式,并画出相应的模拟结构图。
12. 已知系统传递函数 W(s) 坐 卫 2 ,试求出系统的约旦标准型s(s 2)(s 3)的实现,并画出相应的模拟结构图13. 给定下列状态空间表达式X 1 0 1 0 X 10 X 2 2 30 X 2 1 u X 31 13 X 32X 1y 00 1 x 2X 3(1)画出其模拟结构图;(2)求系统的传递函数14. 已知下列传递函数,试用直接分解法建立其状态空间表达式,并画出状 态变量图。
《现代控制理论》课后习题答案(完整版)
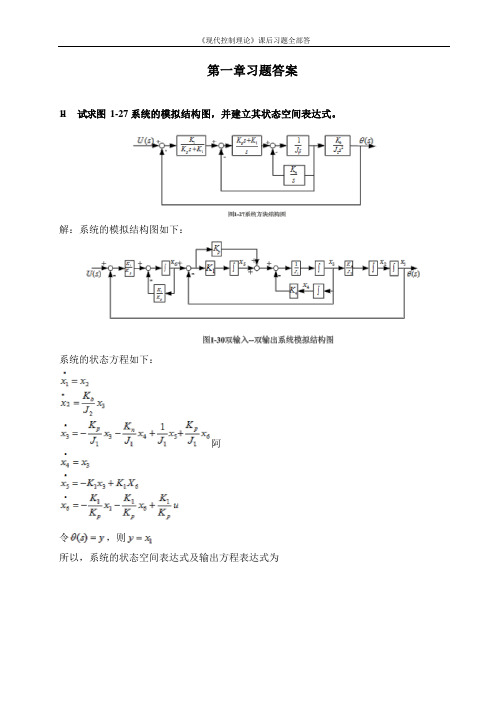
1-1
解:系统的模拟结构图如下:
系统的状态方程如下:
阿
令 ,则
所以,系统的状态空间表达式及输出方程表达式为
1-2
解:由图,令 ,输出量
有电路原理可知:既得
写成矢量矩阵形式为:
1-4 两输入 , ,两输出 , 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
(1)
解法1:
解法2:
求T,使得得所以
解:系统的状态空间表达式如下所示:
1-5
列写其相应的状态空间表达式,并画出相应的模拟结构图。解:令 ,则有
相应的模拟结构图如下:
1-6
解:
1-7
‘
(1)画出其模拟结构图
(2) 求系统的传递函数解:
(2)
1-8
(3)(3)
解:A的特征方程
解得: 令得
(或令 ,得)
当 时,
解得: 令 得
1-9
(2)
解:A的特征方程
当时,
解之得 令 得
当时,
解之得 令 得
当 时,
解之得令得
约旦标准型
1-10
试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果解:(1)串联联结
(2)并联联结
1-11
求系统的闭环传递函数解:
求系统的闭环传递函数解:
1-12已知差分方程为
试将其用离散状态空间表达式表示,并使驱动函数u的系数b(即控制列阵)为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定义状态变量为
利用状态反馈控制律 ,要求闭环极点为 (i=1,2,3),其中
试确定必需的状态反馈增益矩阵K。
5.5试用MATLAB求解习题4.6。
5.6给定线性定常系统
式中
试设计一个全维状态观测器。该观测器的期望特征值为 。
5.7考虑习题4.8定义的系统。假设输出y是可以准确量测的。试设计一个最小阶观测器,该观测器矩阵所期望的特征值为 ,即最小阶观测器所期望的特征方程为 。
11122100021x?xux?x??????????????????????????21122100011x?xux?x????????????????????????31122010011x?xux?x????????????????????????试分别研究有无最优控制使下列性能指标21222012jxxudt?取极小值
3.5给定线性定常系统
式中
试将该状态方程化为能观测标准形。
第四章
4.1试确定下列二次型是否为正定的。
4.2试确定下列二次型是否为负定的。
4.3试确定下列非线性系统的原点稳定性。
考虑下列二次型函数是否可以作为一个可能的Lyapunov函数:
4.4试写出下列系统的几个Lyapunov函数
并确定该系统原点的稳定性。
试求最优控制 ,使下列性能指标
取最小值。
6.2求从 到直线 之间距离最短的曲线及最优终端时间。
6.3系统状态方程及边界条件为:
试求最优控制使下列指标取极值并求最优轨线。
6.4设系统状态方程及初始条件为
未给定,试求最有控制及 使下列指标取极值,并求出最优轨线。
6.5设系统状态方程及初始条件为:
中断状态受如下约束
试求该齐次状态方程的解x(t)。
2.4已知系统方程如下
求输入和初值为以下值时的状态响应和输出响应。
1) ;2)
3) ;4)
2.5验证下列矩阵是否满足状态转移矩阵的条件,若满足,求相应的状态系数矩阵A。
2.6对线性定常系统 ,已知
求系统矩阵A。
2.7已知线性时变系统的系统矩阵如下,计算状态转移矩阵 。
4.5试确定下列线性系统平衡状态的稳定性
4.6试确定下列线性系统平衡状态的稳定性。
第五章线性系统的综合
5.1给定线性定常系统
式中
采用状态反馈控制律 ,要求该系统的闭环极点为s=-2±j4,s=-10。试确定状态反馈增益矩阵K。
5.2试用MATLAB求解习题4.3。
5.3给定线性定常系统
试证明无论选择什么样的矩阵K,该系统均不能通过状态反馈控制 来稳定。
6.9设系统状态方程为
试确定最优控制 ,使下列性能指标
取极小值。
6.10设有下列受控系统状态方程:
1. 2.
3.
试分别研究有无最优控制使下列性能指标
取极小值?是否存在正定矩阵 ?分析受控系统状态可控性、稳定性与最优解的关系。
5.11考虑图4.17所示的I型闭环伺服系统。图中的矩阵A、B和C为
试确定反馈增益常数 和 ,使得闭环极点为 。试利用计算机对所设计的系统进行仿真,并求该系统单位阶跃响应的计算机解,绘出y(t)对t的曲线。
图4.17I型闭环伺服系统
5.12考虑4.4节讨论的倒立摆系统。参见图4.2所示的原理图。假设
式中
试求其传递函数Y(s)/U(s)。
1.5考虑下列矩阵:
试求矩阵A的特征值λ1,λ2,λ3和λ4。再求变换矩阵P,使得
第二章
2.1用三种方法计算下列矩阵A的矩阵指数函数 。
1) ;2)
2.2计算下列矩阵的矩阵指数函数 。
1) ;2) ;3) ;4)
5) ;6) ;7)
2.2给定线性定常系统
式中
且初始条件为
3.1考虑由下式定义能观测。该系统是输出能控的吗?
3.2下列能控标准形
式中
是状态能控和状态能观测的吗?
3.3考虑如下系统
式中
除了明显地选择 外,试找出使该系统状态不能观测的一组 , 和 。
3.4给定线性定常系统
式中
试将该状态空间表达式化为能控标准形和能观测标准形。
的响应,并比较这两种系统的响应。
5.14考虑4.7节讨论的倒立摆系统。设计一个状态反馈增益矩阵K,其中已知 和积分增益常数 。假设该系统的期望闭环极点为 。试利用MATLAB确定增益矩阵K和积分增益常数 。再求当单位阶跃输入作用于小车位置时的阶跃响应曲线。
第六章最优控制
6.1设系统状态方程及边界条件为:
5.13考虑4.4节讨论的倒立摆系统。假设M、m和l的值与4.4节中的相同。对于该系统,状态变量定义为
试求该系统的状态空间表达式。
假设采用状态反馈控制律 ,试设计一个稳定的控制系统。考虑以下两种情况下的期望闭环极点
情况1: ;
情况2:
试确定在这两种情况下的状态反馈增益矩阵K。再求设计出的系统对初始条件
M=2千克,m=0.5千克,l= 1米
定义状态变量为
输出变量为
试推导该系统的状态空间表达式。
若要求闭环极点为
试确定状态反馈增益矩阵K。
利用已被求出的状态反馈增益矩阵K,用计算机仿真检验该系统的性能。试写出一个MATLAB程序,以求出该系统对任意初始条件的响应。对一组初始条件
米/秒
试求x1(t),x2(t),x3(t)和x4(t)对t的响应曲线。
1) ;2)
2.8给定系统 和其伴随方程 ,其状态转移矩阵分别用 和 表示,证明: 。
2.9求解下列系统的状态响应。
2.10已知如下离散时间系统, , 是从单位斜坡函数t采样得到的,求系统的状态响应。
2.11已知如下离散时间系统,试求 ,使系统能在第二个采样时刻转移到原点。
第三章线性系统的能控性与能观性
《现代控制理论》习题
第一章控制系统的状态空间模型
1.1考虑以下系统的传递函数:
试求该系统状态空间表达式的能控标准形和可观测标准形。
1.2考虑下列单输入单输出系统:
试求该系统状态空间表达式的对角线标准形。
1.3考虑由下式定义的系统:
式中
试将该系统的状态空间表达式变换为能控标准形。
1.4考虑由下式定义的系统:
5.8给定线性定常系统
式中
假设该系统的结构与图4.5所示的相同。试设计一个全维状态观测器,该观测器的期望特征值为 。
5.9给定线性定常系统
该观测器增益矩阵的一组期望的特征值为 。试设计一个全维观测器。
5.10考虑习题4.11给出的同一系统。假设输出y可准确量测。试设计一个最小阶观测器。该最小阶观测器的期望特征值为 。
试求最优控制是下列性能指标
取极小值,且求出最优轨线。
6.6设一阶离散系统方程为
边界条件为: 。试求最优控制序列,使下列性能指标
取极小值,并求出状态序列。
6.7设系统状态方程及边界条件为:
; ,
试求最优控制是指标 取极值,并求出最优轨线及最优性能指标。
6.8设系统状态方程及边界条件为:
; ,
试求最有控制及 使 取极值。
