组合数学课程介绍
最经典同等考辅_离散数学与组合数学讲义
同等学力申硕离散数学与组合数学讲义主讲：单志勇博士目录引言 (1)第一章 (9)1.1 命题及其符号化 (9)1.2 合式公式和真值赋值 (14)第二章 (20)2.1等值关系及联结词全功能集 (20)2.3 范式 (25)第三章命题逻辑自然推理 (30)第四章 (37)4.1~2谓词和量词、一阶语言 (37)4.3一阶等值演算 (43)4.4一阶逻辑形式推理 (48)第五章集合 (55)5.1~5.3集合的概念及其表示、运算、定律 (55)5.4 有限集计数问题 (62)第六章关系 (68)6.1~3二元关系及其表示、性质、运算 (68)6.4特殊关系及性质 (75)第七章函数 (81)7.1~7.3函数的基本概念、合成、反函数 (81)7.4～5特殊函数及集合的基数 (85)引言一、课程内容·数理逻辑：是计算机科学的基础，应熟练掌握将现实生活中的条件化成逻辑公式，并能做适当的推理，这对程序设计等课程是极有用处的。
·集合论：数学的基础，对于学习程序设计、数据结构、编译原理等几乎所有计算机专业课程和数学课程都很有用处。
熟练掌握有关集合、函数、关系等基本概念。
·代数结构：对于抽象数据类型、形式语义的研究很有用处。
培养数学思维，将以前学过的知识系统化、形式化和抽象化。
熟练掌握有关代数系统的基本概念，以及群、环、域等代数结构的基本知识。
·图论：对于解决许多实际问题很有用处，对于学习数据结构、编译原理课程也很有帮助。
要求掌握有关图、树的基本概念，以及如何将图论用于实际问题的解决，并培养其使用数学工具建立模型的思维方式。
·讲课时间为两个学期，第一学期讲授数理逻辑与集合论，第二学期讲授代数结构和图论。
考试内容限于书中的内容和难度，但讲课内容不限于书中的内容和难度。
二、数理逻辑发展史1. 目的·了解有关的背景，加深对计算机学科的全面了解，特别是理论方面的了解，而不限于将计算机看成是一门技术或工程性的学科。
组合数学 第二章 容斥原理
500 5
100,|A
B|
500 15
33
根据容斥原理，从1到500的整数中被3或5除尽的数的个数为
|A B| |A|+|B||A B| 233
§2.1 容斥原§理2例.41 容斥原理
2.1.3 容斥原理
例题
例4、求有a,b,c,d四个字符构成的n位符 号串中，a,b,c至少出现一次的符号串的 数目。
A BA B
A BA B
注：De Morgan定律可推广到n个有限子集。
S
A
S AB
§§22..11容容斥原斥理原定理理1-1
2.1.2 计数定理
定理 2.1
|A B| |A||B||A B|
可用Venn图说明该定理的正确性。 或通过组合分析法，若A代表具有性质a的元素集合，B代表具有 性质b的元素集合，等式左端表示至少具有性质a、b之一的元素 个数，|A|表示具有性质a的元素个数，|B|表示具有性质b的元素个 数，但二者相加时，同时具有性质a、b的元素计数重复加了一次， 故需要减去重复的数|A∩B|。 注：加法法则相当于该等式A∩B=Φ的一个特例。
解：设S为26个字母的全排列集，令Ai分别为出现dog, god, gum, depth, thing的排列集，i=1,2,3,4,5。出现dog的排列，可把dog作 为一个元素看，|A1|=24!，同理|A2|=|A3|=24!，|A4|=|A5|= 22!。因 dog, god不可能同时出现，故|A1∩A2|=0，同理|A2∩A3|=|A1∩A4|= |A1∩A5|= 0，gum, dog可以在dogum中同时出现，故|A3∩A1|=22!， 同理|A2∩A4|=|A3∩A4|=|A5∩A2|=|A5∩A3|=20!, |A4∩A5|=19!。同理 |A1∩A2∩A3|=|A1∩A2∩A4|=|A1∩A2∩A5| =|A2∩A3∩A4|=|A2∩A3∩A5|=|A1∩A4∩A5|=|A1∩A3∩A4| =|A1∩A3∩A5|=|A2∩A4∩A5|= 0，|A3∩A4∩A5|=17!，其他4个、5 个子集的交集均为空集。 根据容斥原理，所求的排列数为
抽屉原理优秀教案
抽屉原理优秀教案
简介
抽屉原理（Pigeonhole Principle）是一种非常基础的组合数学原理，也是解决问题的常用思路。
在高中数学的课程中，抽屉原理也是非常重要的一部分。
下面将介绍一份优秀的抽屉原理教案，帮助老师更好地让学生掌握该原理。
教材准备
•白板、白板笔、橡皮擦、教材
•尺子、铅笔、草稿纸
教学目标
•理解抽屉原理的概念和应用条件；
•运用抽屉原理解决实际问题；
•提高学生的组合数学思维和解决问题的能力。
教学过程
1. 引入
1.1 翻译和解释抽屉原理的概念。
1.2 提示学生，抽屉原理能够帮助解决哪些问题，引出本课核心内容。
2. 案例练习
2.1 由老师出题，引导学生使用抽屉原理解决有关组合数学的实际问题。
2.2 根据题目难易程度逐步提高练习难度，帮助学生逐步掌握使用抽屉原理的方法。
3. 归纳
3.1 学生归纳抽屉原理的应用范围和方法，并在白板上进行讲解。
3.2 带领学生解决课堂上未完成的案例，检测学生对抽屉原理的掌握程度。
4. 课后练习
4.1 布置课后练习，让学生巩固抽屉原理的应用。
4.2 课后批改作业，对学生掌握程度进行检测和评价。
教学评估
•课堂互动表现
•课堂练习和课后作业完成情况
•学生对课程知识点的掌握和理解
小结
本教案针对高中生，以案例练习为主，教师通过引入案例和逐步讲解抽屉原理的方法，帮助学生掌握该原理的应用方法，提高学生的组合数学思维和解决问题的能力。
同时，通过课堂互动和课后练习等方式进行评估，帮助学生巩固和深化所学知识，从而达到提高教学质量的目的。
清华大学计算机研究生课程表
清华大学计算机研究生课程表清华大学计算机研究生课程表计算机系研究生课程介绍课程名称：组合数学课程编号：60240013 课学时：48 开课学期：秋任课教师：黄连生【主要容】主要介绍组合数学的基本容，包括基本记数方法、母函数与递推关系、容斥原理与鸽巢原理、Burnside引理与Polya定理、区组设计与编码的初步概念、线性规划问题的单纯形算法。
课程名称：数据结构课程编号：60240023 课学时：48 开课学期：春秋任课教师：严蔚敏【主要容】线性表、树、图等各种基本类型数据结构的结构特性、存储表示及基本操作实现的算法；查找表的各种表示方法；各种排序算法的设计与分析；文件组织方法的简单介绍。
课程名称：软件工程技术和设计课程编号：60240033 课学时：48 开课学期：春任课教师：周之英【主要容】1、软件开发技术发展史；2、软件工程技术方法的基本原则；3、软件过程改进；4、需求工程；5、软件体系结构；6、面向对象设计方法；7、Design Pattern；8、分布式系统对象模型：CORBA及DCOM/COM(OLE)等；9、实例分析（实时系统的设计）等。
课程名称：专家系统课程编号：60240043 课学时：48 开课学期：春任课教师：艾海舟【主要容】讲解专家系统的基本原理、构造方法、应用实例、开发工具和发展趋势，介绍人工智能原理和知识工程的相关容，包括产生式系统、搜索技术、知识表示、知识获取、推理机、不确定推理方法等容。
课程名称：人工智能课程编号：60240052 课学时：32 开课学期：秋任课教师：群秀【主要容】人工智能的定义、发展历史及研究的课题；人工智能的典型系统结构--产生式系统；搜索技术（盲目搜索、启发式搜索、博奕树搜索）；谓词演算（知识表示）；人工智能语言程序设计。
课程名称：微型计算机系统接口技术课程编号：60240063 课学时：48 开课学期：春任课教师：芬【主要容】本课程是全部用PC机控制的以硬件为主的软硬件结合的综合接口技术。
3、组合数学第三章排列组合(1)
P（5，3）
（2）同（1），若不限制每天考试的次数，问有多 少种排法？
53
例3.8 排列26个字母，使得在a 和 b之间正好有7个 字母，问有多少种排法？
例3 用26个字母排列，是元音 a,e,i,o,u 组不相继 出现，有多少种排法？
（1）排列所有辅音：P(21,21)=21！ （2）在辅音前后的22个空档中排元音:
n2 +... + nk .
2若r=n,则N= n! ; n1 !n2 !...nk !
3若r < n且对一切i,i =1, 2,..., k,有ni ? r,则N=kr ; 4若r < n,且存在着某个ni < r,则对N没有一般的求解公式。
§3.5 多重集的组合
多重集S中r个元素进行无序选择，构成一个多重 集的r-组合。 篮子里有2个苹果，1个桔子，3个香蕉，篮子里 的水果构成“多重集”。
解1 (1)任意坐： n=9! (2)不相邻：A先就坐，B不相邻：7 其余8人排序：8！ m=7*8！ (3) P=m/n=7*8!/9!=7/9
例6 10个人为圆桌任意就坐，求指定的两个人 A与B不相邻的概率。
解2 (1)任意坐： n=9! (2)A,B相邻：A先就坐，B左右相邻：2 其余8人排序：8！ k=2*8！ (3)不相邻：m=9!-2*8! (4) 两人不相邻的概率 P=m/n=（9!-2*8!)/9!=1-2/9=7/9
证明
(1) 从{ 1,2,…,n }中选出2-组合有
C
2 n
(2) 另一种选法：
最大数为k的2-组合共有k-1个，k=1,2,…,n
有加法原理，共有 0+1+2+…+(n-1) 个2-组合
专业大类教育平台课程教学大纲-湖南大学数学与计量经济学院
数学与计量经济学院本科教育课程教学大纲Syllabus for Undergraduate Programs专业大类教育平台课程2005．03专业大类教育平台课程A组课程《高等代数》课程教学大纲《空间解析几何》课程教学大纲《概率论与数理统计》课程教学大纲《计算方法》课程教学大纲《最优化原理》课程教学大纲《运筹学》课程教学大纲《现代数学选讲》课程教学大纲B组课程《数学模型》课程教学大纲《组合数学》课程教学大纲《偏微分方程》课程教学大纲《专业英语》课程教学大纲《高等代数》课程教学大纲课程编号：10115，10124课程名称：高等代数英文名称：Higher Algebra学时：160学分：10适用专业：数学与应用数学专业，信息与计算科学专业课程类别: 专业大类A组先修课程：初等数学一、课程的性质及教学目标高等代数是数学类专业三大重要基础理论课程之一。
通过高等代数课程的学习，使学生掌握高等代数的基本概念，基本定理及它的思想方法和运算技能，为学生进一步学习后继及相关课程，进一步深入各领域的研究等奠定必要的代数与几何基础。
通过高等代数的整个教学过程提高学生的数学素质与能力特别是培养提高逻辑推理的能力，抽象思维能力，观察分析概括类比能力，学习理解能力及各种解题技能等。
充分开发学生的自学、创新潜能，以利于他们今后进一步地学习新知识，开发研究新问题。
二、课程的教学内容及基本要求1．多项式理论掌握一元多项式的整除，最大公因式、互素多项式、不可约多项式、多项式的因式分解，重因式等基本概念及其性质，理解多项式的根（重根）与它的一次因式（重因式）间的关系，掌握多项式的是否有重因式的判别法，实、复系数多项式的不可约多项式的形式及标准分解式的形式及有理系数多项式的不可约充分判别法，掌握求多个多项式的最大公因式，求整系数多项式的有理根等基本方法，了解多元多项式的基本概念其主要性质。
2．行列式理解、掌握n级排列的逆序数，对换，奇偶性及n级行列式的概念，熟悉、掌握行列式的性质及按行列展开定理，能熟练综合运用行列式性质及展开定理计算、讨论行列式，能运用克兰姆法则求解某些特殊的线性方程组。
“组合数学”课程教学规律探索
旦 皇
‘ ‘ 组合数 Байду номын сангаас’ 果 ’ｉ 程教学规律搽索
文０ 孙侠 殷志祥 张家秀 许峰 （ 安徽理工 大学 淮南）
摘要 ： 文介 绍 了 者 在 “ 本 作 组合 数 学” 以 解决 第 三章 中容 斥原 理 的 一些 问题 ，还 教 学过 程 中的 经验 ，希 望 学生 能 在合 适 的 可 以求 解 第 四章 中的递 推 关 系 。讲 清 这些 教 学方 法 下提 高学 习积 极性 ， 牢 固的 掌握 知 识 点之 间 的联 系 ，让学 生 有 一 个整 体 的 了解和 认 识 ，比单 纯 、孤 立 的 讲 解效 果要 该课 程 的知 识 。 关键 词 ：组合 数 学 ；教 学 ；认 知 特 点 好 得 多 。另 外 ，课 堂 教学 中不 能一 直 处于 现 代 数学 可 以分 为 两大 类 ：一 类是 研 教 师 “ 独 角戏 ” 的 状 态 ，每 个 知识 点 在 唱 究 连续 对 象的 ，如 分析 ，方程 等 ；另一 类 教 授 时 不妨 就 它 的特 点和 方 法 与 学生 进 行 是研 究 离 散对 象 的组 合 数学 。组 合 数学 是 交 流 。要 允 许学 生 大 胆 质疑 ，结 合学 生 的 计算 机 、应 用数 学 等专 业 的一 门 重要 的 基 疑 点讲 解 课 程并 把 它 带到 后 面 的 习题 教学 础 理论 课 ，它的 发 展改 变 了 传统 数 学 中分 中予 以 更 深 刻 的 剖 析 。 析 和代 数 占统 治 地 位的 局 面 。本 课 程 各部 （ ） 教 学 模 式 合 理 化 ， 创 造 良 好 三 分 内容 既 相对 独 立 又彼 此联 系 ，课 程 中既 的 教 学 氛 围 很 多 人 对 组 合 数 学 的 认 识 就 是 一 个 字 有 重要 的 原 理 ，又 有针 对 不 同 问题 的技 巧 和 方 法 ，大 量 学 生 感 到 学 习 的 困难 较 大 。 难 ，如 果 老 师 只求把 内容 讲 完 ， 完成 下 面就 本 人 的教 学 经验 谈 谈 怎样 教 授该 课 教 学 任 务 ，那 么学 生 很 难 会 有 学 习兴 趣 ， 程。 当然 更 谈不 ｊ学 好这 门 课程 了 。我 们 不能 二 把 学 生 当成 是 在 教与 学 的过 程 中一种 被 动 课 堂教 学 （ ） 教 学 手 段 合 理 化 一 的认 知 信息 的 接 受者 ，要 充分 认 识 到学 生 数 学 往 往 需 要 大 量 严 密 的 逻 辑 推 理 ， 的认 知 特 点 ， 进行 “ 味 ” 教学 。 比如 ： 趣 所 以 很 多数 学 老 师 都 选 择 传 统 的 板 书 教 幻方 是 一 个很 难 的知 识 点 ，为 了提 高 学生 学 。板 书 是 传 统的 教 学媒 体 ，体 现 在 课 堂 的兴 趣 ，我 们 可以 从 介 绍 它 的 起 源 讲 起 。 教 学 中 ，就 是 大 量 使 用 黑 板讲 解知 识 点 。 其 实 ，对于 幻 方 我们 都 不 陌生 ，最 早接 触 使 用 板 书教 学 的好 处 是 符合 大 多数 学 生 的 它是 在 电视 剧 《 雕英 雄 传 》 里面 ，神算 射 习惯 ，便 于 讲 解学 生 随 机提 出 的 问题 ，但 子瑛 姑 苦 苦研 究 数十 载 ，后 被 黄蓉 一 语道 板 书 往往 又 让 人感 到 枯燥 死 板 ，这 也 是 很 破 天 机的就 是 三阶 幻方 。 射雕英 雄 传》每 ‘ 多学 生 不喜 欢 上数 学 课 的原 因 之一 。组 合 个人 都 看 过 ，但 很 少有 人 知 道瑛 始 专研 的 数学 课 程 中的 许 多知 识 源于 生 活 中的 数 学 就是 组 合 数 学 中的 幻方 。如 果这 样 引入幻 游 戏 ，老师 在 教授 这 门 课程 时要 抓 住 它 的 方的 知 识 ，相信 很 多 同学 都会 感 兴 趣 ，很 趣 味 性 ，如 果 大量 使 用 板书 教学 ，课 堂 气 多 人都 会 感叹 ：数 学 真 的 无 处 不 在 呀 ！ 氛 必然 沉 闷压 抑 ，而 适 当地 使 用 多媒 体 教 二 、 习题 教 学 学方 式 ，会 大 大 改变 这 种现 象 。 比 如鸽 巢 “ 合 数 学 ”是 一 门技 巧性 很 强 的课 组 原 理 的 引入 ，可 以利 用 多媒 体 先 介绍 《 晏 程 ，习题 教学具 有 不可 替代 的作 用 。 目前 ， 子春秋 里晏子 “ 二桃杀三 士”的故事 ，用 “ 合数 学 ”课 程一 般安排 ５０ 个学 时 ，老 组 故 事 开 头 ， 必然 会提 高 学 生 的 学 习 兴 趣 ， 师 有 充分 的时 间实 施 习 题 教学 。 活 跃课 堂 气 氛 。 （ ） 习 题 教 学 应 该 以 课 堂 内 容 为 一 多 媒体 教 学的 特 点 是 图文 并 茂 、形 象 起 点 ， 以 学 生 为 主 体 逼 真和 容 易体 现 教学 要 求 ，但 是 很 多 人容 安 排 的 习题 要 以 教学 内 容为 基 准 ， 从 易 把 电子讲 稿 做 成 教材 的 翻版 ，认 为把 教 教授 的基 本 内 容人 手 ，熟 悉 主 要概 念 和 原 学 内 容 简单 堆 砌 在 一 起 就 是 电子 讲 稿 了 。 理 ，掌 握 重 要 的技 巧 和方 法 。 对于 基 本题 这 是一 个 很严 重 的 认识 误 区 。在 使 用 多媒 型 ，一般 都 有 简单 的 示例 ，通 过老 师的 分 体 教学 的过 程 中 ，我们 要 坚持 “ 媒体 围 多 析 讲 解 ，要 让 学 生 明 白用 到 哪 个 知 识 点 ， 绕 教师 ，多媒 体 服 务教 学 ” 的原 则 。 电予 怎 样 使用 的 ，并且 能 在此 基 础 上解 决 简单 讲 稿要 求 教 师要 准 确把 握 课程 的 重 点和 难 的题 目。 比如鸽 巢原 理 ，在具体 的 题 目中 ， 点 ，有 目的 、有 层 次 的组 织 讲稿 内 容 ，抓 如何 构造 “ 巢” 鸽 ，将 什么视 为 “ 鸽子 ” ，这 住 学生 心 理 ，但 是 在 实 际的 教学 过 程 中要 些 都 需要 在 习 题 中不 断体 会 理 解 。要 以 学 做 到这 些 ，需 要 对 课程 的 精 心组 织 和大 量 生 为 主体 ，重 视学 生 的 心理 特 点和 认 知 规 教 学 经 验 的 积 累 ，不 是 一 朝一 夕 的事 情 ， 律 ，教 师应 该 合 理的 编 排指 导 书 ， 突破 陈 需 要 长 期 的 实践 摸 索 。 规 ， 灵活 安 排 习题 。 （ ） 概 念 系 统 化 ， 避 免 知 识 点 孤 二 （ ） 在 习 题 教 学 中 突 出 自学 二 立 化 习题 教 学 不是 单 纯 的讲 题 目， 课本 对 组 合 数学 主 要 研究 一 组 离散 对象 满 足 知 识 点的 介 绍 有 深 有 浅 ，有 细 致 有 粗 略 ， 定 条件 的 安排 的 存 在性 ，以及 这 种 安排 在 教 学 中有 时 候 会发 现 书本 上 没有 介 绍 到 的构 造 、枚 举计 数 和 优化 等 问题 。所 有这 的知识 ，此 时 可以合 理 引导学 生深 入学 习 ， 些 不是 孤 立 的 ， 它们 最终 还 是要 放 到 一个 全 面 掌握 相 关 知 识 。 同时 ，可以 有 意识 的 系统 中去 使 用 。 比如 ：生 成 函数 法 是 组合 留下 相 当 的知 识 在课 堂 上 不做 讲授 ，在 习 数 学 中的 一 种重 要 方 法 ，其 思想 是 将 欲求 题 课 开始 的时 候 提 出来 ，让学 生 结 合课 本 序 列 “ 着 ”在 幂级 数 上 ，使之 能 够 用纯 与其 它 资料 ，掌 握相 应 的 知识 。比 如 幻方 附 代 数 或数 学 分析 的 方 法解 决 。利 用这 种 方 的构 造 ，课 本 只 简单 介 绍 了奇 数 阶 幻方 的 法 ，可以 解 决第 二 章 中集 合 的排 列 与组 合 构 造 方 法 ，老 师 可 以 引导 学生 探 索 偶数 阶 问题 （ 论 是普 通 集合 ，还是 多 重集 合 ） 幻方 的 存 在性 以 及构 造 方 法 。这 种 学 生 自 无 、 第二类 Ｓｔｒｉ ｉ ｌｎｇ数以及正整数的分拆 数 ，可 主型 的学 习更 能 牢 固的掌 握 相 关知 识 。
组合数学在计算机研究中的作用
组合数学在计算机研究中的作用1 组合数学简介现代数学可以分为两大类：一类是研究连续对象的，如分析、方程等；另一类就是研究离散对象的组合数学。
广义的组合数学就是离散数学，也有人认为离散数学是狭义的组合数学和图论、代数结构、数理逻辑等的总称。
但这只是不同学者在叫法上的区别。
总之，组合数学是一门研究离散对象的科学。
狭义的组合数学主要研究满足一定条件的组态（也称组合模型）的存在、计数以及构造等方面的问题。
计算机出现以后，由于离散对象的处理是计算机科学的核心，研究离散对象的组合数学得到迅猛发展。
与传统的数学课程相比，组合数学研究的是一些离散的事物之间存在的数学关系，包括存在性问题、计数性问题、构造性问题以及最优化问题等，其主要内容是计数和枚举。
计数问题是组合学中研究得最多的内容，它出现在所有的数学分支中。
2 组合数学在计算机科学方面的作用对离散对象的处理是计算机科学的核心，而研究离散量的科学是组合数学。
组合数学的发展奠定了20世纪计算机革命的基础，而计算机的出现又促进了组合数学本身的大发展。
组合数学的萌芽可以溯源至公元前两千多年中国的大禹治水时代，尽管它所涉及的有些问题最初是以数学游戏的形式出现的，但在后来实际背景的影响下，获得了新的生命。
随着计算机科学的发展，组合数学也在迅猛发展，而组合数学在理论方面的推进也促进计算机科学的发展。
计算机软件空前发展的今天要求有相应的数学基础，组合数学作为大多数计算机软件设计的理论基础，它的重要性也就不言而喻。
组合数学在计算机方面的应用极其广泛。
计算机软件与各种算法的研究分不开，为了衡量一个算法的效率，必须估计用此算法解答具有给定长的输入(问题) 时需要多少步(例如算术运算、二进制比较、程序调用等的次数) 。
这要求对算法所需的计算量及存储单元数进行估算，这就是计数问题的内容，而组合数学分析主要研究内容就是计数和枚举的方法和理论。
当今计算机科学界的最权威人士很多都是研究组合数学出身的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
12
• 斯坦福数学系的教授研究了这个问题， 设立了一个小小的奖项来征集答案， 100美金.
• 数学家和计算机学者都来参与了 • 谁赢了呢？
– 伊利诺大学计算机系的比尔.卡特勒借助计算机 得出的答案是17152种拼法
– 数学家用纸和笔对排列进行分类，共24个基本 族，基本解法是536种，考虑旋转32种，答案 也是17152种。
大禹(2205BC -2105BC)
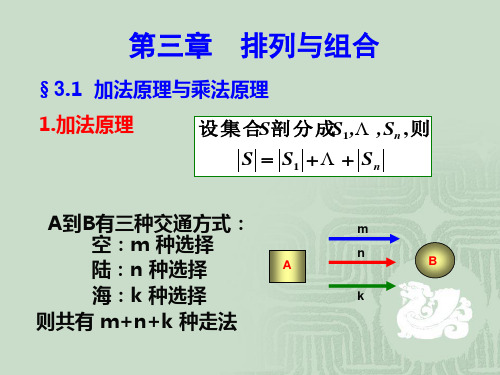
492 357 816
10
• 组合数学中有许多象幻方这样精巧的结构。
• 1977年美国旅行者1号、2号宇宙飞船就带 上了幻方以作为人类智慧的信号。
2200BC
4 9 2神 3 5 7农
幻
8 1 6方
15世纪
1 15 14 4 ４ 12 6 7 9 阶
幻 8 10 11 5 方
31
• “6度分离” —对每个人来说，平均大约只需要通过６ 个人就能将信寄到目的地。
• 研究无尺度网络，对于防备黑客攻击、防治流行病、和 开发新药等，都具有重要的意义。
• 在1999年，Barab´asi et al.发现在因特网上，任意两个 网页间的链接即网页之间的“距离”平均为18.59 。从 任意一个网页出发， 原则上可以通过不超过19次链接到 达互联网中的任何网页。 (Nature 401, 1999)
/zh-cn/%E7%BB%84%E5%90%88%E6%95%B0%E5%AD%A6
Combinatorics: Combinatorics is a branch of pure mathematics concerning the study of discrete (and usually finite) objects. It is related to many other areas of mathematics, such as algebra, probability theory, ergodic theory and geometry, as well as to applied subjects in computer science and statistical physics.
7
• 组合数学研究的是事物按照某种规则的安排，主 要有：存在性问题、计数性问题和对已知安排的 研究 —— Richard A. BrualDi 所著 《Introductory Combinatorics》
• 组合数学就是对给定描述的事物有多少种或者某 种事物发生的途径有多少种的研究 ——Daniel I. A. Cohen 所著《Basic Techniques of Combinatorial Theory》
• 此后数学家 Heawood 花费了毕生的精力致力于四色研 究，于1890年证明了五色定理（每个平面图都是5顶点 可着色的）。
• 直到1976年6月，美国数学家 K. Appel与 W. Haken， 在3台不同的电子计算机上，用了1200小时，才终于完 成了“四色猜想”的证明，从而使“四色猜想”成为了四 色定理。
• 1967年一家航空公司申请要求贝尔公司增加一些 服务点，而这些服务点恰恰位于构造该公司各分 部的斯坦纳最小树需增加的斯坦纳顶点上。
–不仅要拉新线，增加服务网点， –而且还要减少收费。 –这一意外事件迫使贝尔公司自此以后便采用了斯坦纳
最小树原则 。
28
29
• “<数学年刊>就是发表了，也不能说就是正确的 ，1991年堵丁柱与黄光明证明斯坦纳比猜想，获 得国内外大奖，被美国列为十大科学进展，1996 年发现是错误的。”
/wiki/Combinatorics
5
• 狭义的组合数学主要研究满足一定条件的组态（ 也称组合模型）的存在、计数以及构造等方面的 问题。
– 组合数学的主要内容有组合计数、组合设计、组合矩 阵、组合优化等。
• 离散数学(Discrete mathematics)是数学的几个分支 的总称，以研究离散量的结构和相互间的关系为 主要目标，其研究对象一般是有限个或可数无穷 个元素；因此它充分描述了计算机科学离散性的 特点。一切推理和发现，不管是否
亚里士多德。和牛顿先后独立 发明了微积分。
用语言描述，都能归结为如数，
字，声，色这些元素经过某种组
合的有序集合。
17
• 组合数学不仅在基础数学研究中具有极其重要的 地位，在其它的学科如计算机科学、编码和密码 学、物理、化学、生物等学科中，甚至在企业管 理，交通规划，战争指挥，金融分析，城市物流 等领域均有重要应用。
• 如果不允许增加任何额外的点作为网络的 顶点，这种最短网络称为最小生成树。
• 在前面的例子中Steiner最小树的长为 3 而最小生成树的长为2。
26
3 2
27
• Pollak－Gilbert猜想起源于在美国贝尔电话公司 发生的一个富有戏剧性的事件。
• 1967年前，贝尔公司按照连结各分部的最小生成 树的长度来收费。
组合数学课程介绍
3
4 组合数学
Combinatorics
组合数学:有人认为广义的组合数学就是离散数学，也有人认 为离散数学是狭义的组合数学和图论、代数结构、数理逻辑 等的总称。但这只是不同学者在叫法上的区别。 总之，组合数学是一门研究离散对象的科学。 随着计算机科学的日益发展，组合数学的重要性也日渐凸显 ，因为计算机科学的核心内容是使用算法处理离散数据。
• 埃尔德什数：保罗·埃尔德什就是随机图理论的开创者之 一。与他一起发表过论文的学者的“埃尔德什数”是1， 与这些学者合作发表过论文的学者的“埃尔德什数”是2， 以此类推。美国数学会的数据库中记录的超过40万名数 学家们的“埃尔德什数”平均是4.65，最大的是13。
• “1996年，堵丁柱的老师越民义在《运筹学杂志 》发表论文，否定了堵丁柱和黄光明的工作。”
30
• 20世纪20年代，由Karinthy提出。 • 1950年， Pool 和 Kochen提出这样一个问题：
“两个毫无关系的人，要让他们互相认识，至少 要经过多少人？” • 美国哈佛大学社会心理学家S. Milgram在1967年 做过一项有趣的实验，据说他从内布拉斯加州的 奥马哈随机选了300人，然后请他们每个人尝试 寄一封信到波士顿的一位证券业务员。寄信的规 则很简单，就是任何收信者只能把信寄给自己熟 识的人。 • 平均只需要5次转发，就能够到达目标。也就是说， 在社会网络中，任意两个人之间的“距离”是6
P
B
C
|PA|+|PB|+|PC| = 3
25
• 由于最短网络在运输、通讯和计算机等现 代经济与科技领域中都有重要的应用，对 这个问题的研究也越来越深入。问题的对 象已由三个点扩展到任意有限个点集。
• 斯坦纳（Steiner）最小树是可以在给定的 点之外再增加若干个点(称为斯坦纳点)， 然后将所有这些点连起来。
8.1 加法法则和乘法法则 8.2 基本排列组合的计数方法 8.3 递推方程的求解与应用 8.4 题例分析
第9章 代数系统简介 第10章 形式语言和自动机初步
第1章 第2章 第3章 第4章 第5章 第6章 第7章 第8章
排列与组合 递推关系与母函数 容斥原理与鸽巢原理 Burnside引理与Polya定理 区组设计 线性规划 编码简介 组合算法简介
13 3 2 16
11
• 阿基米德
– 公元前287年-公元前212年
• 希腊文写在羊皮纸上的阿基米德手稿 副本，距今约1000年
• 2003年，科学家借助现代科技手段 初步破译了这篇论文, 结论是这篇论 文解决的是组合数学问题《十四巧板》 (stomachion)。
• 在论文中阿基米德是在计算把14条 不规则的纸带拼成正方形一共能有多 少种不同的拼法。这在现在被称为 tiling问题。
的路线（称为网络）。这种网络有许多个，其中最短路线 者显然是二边之和（如AB∪AC）。
A
B
C
|AB|+|AC| = 2
24
• 但若增加一个周转站（新点P），连接4点的新网络的最 短路线为PA＋PB＋PC。最短新路径之长N比原来只连三 点的最短路径O要短。
• 这样得到的网络不仅比原来节省材料，而且稳定性也更 好。 A
•
四色定理是第一个主要由电脑证明的著名数学定理。
• 1979年，逻辑哲学和数学哲学家托马斯·蒂莫兹佐在《四色定理 及其哲学意义》一文中提出，四色定理与其证明能否称之为“ 定理”和“证明”，尚有疑问。
• 1986年，哈肯和阿佩尔应《数学情报》杂志的邀请写了一篇短 文，用清晰易懂的语言总结了他们的证明工作。1989年，最终 的定稿以单行本的形式出版，超过400页。
• 在美国有一家公司用组合数学的方法来提高企业 管理的效益，这家公司办得非常成功。
• 在美国已有专门的公司用组合设计的方法开发软 件，来解决工业界中的试验设计问题。
• 德国一位著名组合数学家利用组合数学方法研究 药物结构，为制药公司节省了大量的费用，引起 了制药业的关注。
18
• 著名的组合数学家 Thomas Tutte(1917-2002) 在组合数学界 是泰斗级的大师。直到最近人们 才知道，原来他对提前结束“二 战”有着突出贡献。
2004年9月，数学家乔治·龚提尔使用Coq对四 色定理的机器证明进行了机器验证。
22
网络可靠性问题
• 一个通讯网络怎样布局稳定性最好，而且 费用最节省？
• 美国的贝尔实验室和IBM公司都有世界一流 的组合数学家在研究这个问题，这个问题 直接关系到巨大的经济利益。
23
最短网络问题
• 如何用最短的线路将三部电话连起来？ • 此问题可抽象为设△ABC为等边三角形，，连接三顶点
15
组合数学的历史
1666年莱布尼兹所著《论
组合的艺术》一书问世， 这是组合数学的第一部专