高中数学 2-3-1,2-3-2幂函数的概念 幂函数的图象和性质课件 湘教版必修1(共33张PPT)
湘教版高考总复习一轮数学精品课件 第三章 函数与基本初等函数 第四节 幂函数与二次函数

求二次函数解析式,一般运用待定系数法,选择规律如下:
考点三
二次函数的图象与性质(多考向探究预测)
考向1二次函数的图象
例题(多选)(2023·湖南岳阳高三检测)如图,二次函数y=ax2+bx+c(a≠0)的图
象与x轴交于A,B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0),
则下列结论正确的是(
= 7.
= 8,
4
故 f(x)=-4x2+4x+7.
(方法 2 利用二次函数的顶点式)设 f(x)=a(x-m)2+n(a≠0).
2+(-1)
因为 f(2)=f(-1),所以二次函数 f(x)图象的对称轴为直线 x= 2
又根据题意函数有最大值 8,所以 n=8,
所以 y=f(x)=a
1 2
x- +8.
( 1 )-( 2 )
x1≠x2,都有 - >1,不妨令 x1>x2,则
1 2
( 1 )-( 2 )
2
>1⇔f(x
1)-x1>f(x2)-x2,令 g(x)=f(x)-x=ax -2x+1,则函数 g(x)在[1,+∞)上
所以a<0,且f(x)max=f(-1)=-a=8,所以a=-8,
所以f(x)=-8x(x+2)=-8x2-16x.
引申探究2将本例中条件变为二次函数f(x)的图象经过点(4,3),在x轴上截得
的线段长为2,且∀x∈R,都有f(2+x)=f(2-x),试确定f(x)的解析式.
解 因为f(2+x)=f(2-x)对任意的x∈R恒成立,所以f(x)的对称轴为直线x=2.
幂函数课件(优质课)(共20张PPT)

③y x 2 x 否
⑤y x 0 是
2 2
⑥y 1 否
2、若函数 f ( x) (a 3a 3) x 是幂函数,求a的值。 -1或4 规律
x 的系数是1
底数是单一的x 指数是常数
总结
幂函数的定义 幂函数的定义:一般地函数 y 其中x是自变量,α是常数。
上是增函数,0.5< 3 ∴ ∴ ( )2 (
3 2 3 ∴( ) ( ) 底数相同,若指数相同利用幂函数的
9 10
9 10
1.40.5 1.4 3
5
) 2∴ ( ) 2 ( ) 3 10 5 10
课堂练习 1、下列函数不是幂函数的是( c )
3 1 A y x B y x C y 2x D y x
定义域
y x2
R
(0,+∞)
O
x
值域
奇偶性
偶
单调性(-∞,0)减
(0,+∞)增
y
y x3
函数
y x3
定义域 R
O
x
值域
R
奇偶性 奇
单调性 增
y
1 x2
y
函数
y
1 x2
定义域 [0,+∞)
O
x
值域
[0,+∞)
奇偶性 非奇非偶
单调性
增
幂函数的性质
函数 定义域 值域 奇偶性
yx
yx
5
(
9 10
1 )3
9 2 (4)取中间量 ( ) ,∵函数 9 x 10 y ( ) 在R 上是增函数
2024-2025学年高一数学必修第一册(湘教版)配套课件第4章-4.1.3幂函数

【以下各个函数有什么共同的特征?】
【探究】(1)如果卢老师以1元/kg的价格购买了某种蔬菜千克,那么他需要支付
的钱数 = 元,这里是的函数;
(2)如果正方形的边长为,那么正方形的面积 = 2,这里是的函数;
(3)如果立方体的棱长为,那么立方体的体积 = 3,这里是的函数;
第4章
4.1.3
幂函数
高中数学
必修第一册
湖南教育版
学习目标
1.通过具体实例,结合函数
变化规律.
1
y x, y , y x 2 , y x , y x 3
x
2.了解幂函数的概念.
核心素养:数学抽象、数学建模、直观想象
的图象,理解幂函数图象的
高中数学
必修第一册
幂函数的概念
湖南教育版
整数次幂函数:
实数次幂函数൝
分数次幂函数: = − ( ≠ 0, ∈ N ∗ )
高中数学
必修第一册
湖南教育版
幂函数的图像
【说明】对于幂函数,特别地研究
在同一坐标系中画出函数
的图像:
【总结】①只有
时图像才是直线;
②图像一定会出现在第一象限,
一定不会出现在第四象限;
③图像一定经过 (1,1) 这个定点;
A.5-a<5a<0.5a
C.0.5a<5-a<5a
解析
1
a
=5 ,因为
-a
5
1
且5<0.5<5,
所以5a<0.5a<5-a.
√
B.5a<0.5a<5-a
D.5a<5-a<0.5a
a<0 时,函数 y=x 在(0,+∞)上单调递减,
2018版高考数学专题指数函数对数函数和幂函数2.3.1幂函数的概念2.3.2幂函数的图象和性质学案湘教版
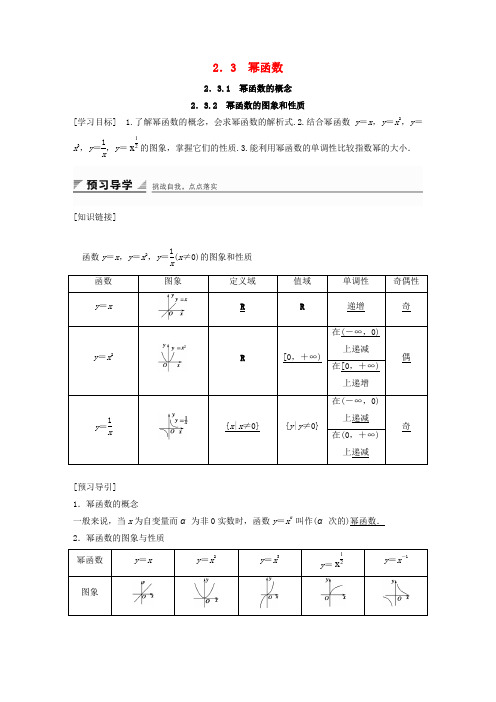
2.3 幂函数2.3.1 幂函数的概念 2.3.2 幂函数的图象和性质[学习目标] 1.了解幂函数的概念,会求幂函数的解析式.2.结合幂函数y =x ,y =x 2,y =x 3,y =1x,y =12x 的图象,掌握它们的性质.3.能利用幂函数的单调性比较指数幂的大小.[知识链接]函数y =x ,y =x 2,y =1x(x ≠0)的图象和性质[预习导引] 1.幂函数的概念一般来说,当x 为自变量而α为非0实数时,函数y =x α叫作(α次的)幂函数. 2.幂函数的图象与性质要点一 幂函数的概念 例1 函数f (x )=(m 2-m -1)x m 2+m -3是幂函数,且当x ∈(0,+∞)时,f (x )是增函数,求f (x )的解析式.解 根据幂函数定义得,m 2-m -1=1,解得m =2或m =-1,当m =2时,f (x )=x 3,在(0,+∞)上是增函数,当m =-1时,f (x )=x -3,在(0,+∞)上是减函数,不合要求. ∴f (x )的解析式为f (x )=x 3.规律方法 1.本题在求解中常因不理解幂函数的概念而找不出“m 2-m -1=1”这一等量关系,导致解题受阻.2.幂函数y =x α(α∈R )中,α为常数,系数为1,底数为单一的x .这是判断一个函数是否为幂函数的重要依据和唯一标准.幂函数与指数函数的解析式形同而实异,解题时一定要分清,以防出错.跟踪演练1 已知幂函数f (x )=x α的图象经过点(9,3),则f (100)=________. 答案 10解析 由题意可知f (9)=3,即9α=3, ∴α=12,∴f (x )=12x ,∴f (100)=12100=10.要点二 幂函数的图象例2 如图所示,图中的曲线是幂函数y =x n在第一象限的图象,已知n 取±2,±12四个值,则相应于c 1,c 2,c 3,c 4的n 依次为( )A .-2,-12,12,2B .2,12,-12,-2C .-12,-2,2,12D .2,12,-2,-12答案 B解析 考虑幂函数在第一象限内的增减性.注意当n >0时,对于y =x n ,n 越大,y =x n增幅越快,n <0时看|n |的大小.根据幂函数y =x n的性质,在第一象限内的图象当n >0时,n 越大,y =x n递增速度越快,故c 1的n =2,c 2的n =12,当n <0时,|n |越大,曲线越陡峭,所以曲线c 3的n =-12,曲线c 4的n =-2,故选B.规律方法 幂函数图象的特征:(1)在第一象限内,直线x =1的右侧,y =x α的图象由上到下,指数α由大变小;在第一象限内,直线x =1的左侧,y =x α的图象由上到下,指数α由小变大.(2)当α>0时,幂函数的图象都经过(0,0)和(1,1)点,在第一象限内,当0<α<1时,曲线上凸;当α>1时,曲线下凸;当α<0时,幂函数的图象都经过(1,1)点,在第一象限内,曲线下凸.跟踪演练2 如图是幂函数y =x m与y =x n在第一象限内的图象,则( )A .-1<n <0<m <1B .n <-1,0<m <1C .-1<n <0,m >1D .n <-1,m >1 答案 B解析 在(0,1)内取同一值x 0,作直线x =x 0,与各图象有交点,如图所示.根据点低指数大,有0<m <1,n <-1.要点三 比较幂的大小例3 比较下列各组数中两个数的大小:(1)⎝ ⎛⎭⎪⎫1312与⎝ ⎛⎭⎪⎫1412;(2)⎝ ⎛⎭⎪⎫-23-1与⎝ ⎛⎭⎪⎫-35-1; (3)0.2514-与6.2514;(4)0.20.6与0.30.4.解 (1)∵y =12x 是[0,+∞)上的增函数,且13>14,∴⎝ ⎛⎭⎪⎫1312>⎝ ⎛⎭⎪⎫1412. (2)∵y =x -1是(-∞,0)上的减函数,且-23<-35,∴⎝ ⎛⎭⎪⎫-23-1>⎝ ⎛⎭⎪⎫-35-1. (3)0.2514-=⎝ ⎛⎭⎪⎫1414-=212,6.2514-=2.512. ∵y =x 12是[0,+∞)上的增函数,且2<2.5, ∴212<2.512,即0.2514-<6.2514.(4)由幂函数的单调性,知0.20.6<0.30.6,又y =0.3x 是减函数,∴0.30.4>0.30.6,从而0.20.6<0.30.4.规律方法 1.比较幂值的大小,关键在于构造适当的函数:(1)若指数相同而底数不同,则构造幂函数;(2)若指数不同而底数相同,则构造指数函数.2.若指数与底数都不同,需考虑是否能把指数或底数化为相同,是否可以引入中间量. 跟踪演练3 比较下列各组数的大小:(1)⎝ ⎛⎭⎪⎫230.5与⎝ ⎛⎭⎪⎫350.5;(2)-3.143与-π3; (3)⎝ ⎛⎭⎪⎫1234与⎝ ⎛⎭⎪⎫3412. 解 (1)∵y =x 0.5在[0,+∞)上是增函数且23>35,∴⎝ ⎛⎭⎪⎫230.5>⎝ ⎛⎭⎪⎫350.5. (2)∵y =x 3是R 上的增函数,且3.14<π, ∴3.143<π3,∴-3.143>-π3.(3)∵y =⎝ ⎛⎭⎪⎫12x 是减函数,∴⎝ ⎛⎭⎪⎫1234<⎝ ⎛⎭⎪⎫1212. y =12x 是[0,+∞)上的增函数,∴⎝ ⎛⎭⎪⎫3412>⎝ ⎛⎭⎪⎫1212.∴⎝ ⎛⎭⎪⎫3412>⎝ ⎛⎭⎪⎫1234.1.下列函数是幂函数的是( ) A .y =5xB .y =x 5C .y =5xD .y =(x +1)3答案 B解析 函数y =5x是指数函数,不是幂函数;函数y =5x 是正比例函数,不是幂函数;函数y =(x +1)3的底数不是自变量x ,不是幂函数;函数y =x 5是幂函数. 2.下列函数中,其定义域和值域不同的函数是( ) A .y =13x B .y =x12-C .y =53xD .y =x 23答案 D解析 y =x 23=3x 2,其定义域为R ,值域为[0,+∞),故定义域与值域不同.3.设α∈⎩⎨⎧⎭⎬⎫-1,1,12,3,则使函数y =x α的定义域为R 且为奇函数的所有α值为( )A .1,3B .-1,1C .-1,3D .-1,1,3答案 A解析 可知当α=-1,1,3时,y =x α为奇函数,又∵y =x α的定义域为R ,则α=1,3. 4.若a =(12)35,b =(15)35,c =(-2)3,则a 、b 、c 的大小关系为________.答案 a >b >c解析 ∵y =x 35在(0,+∞)上为增函数. ∴(12)35>(15)35,即a >b >0.而c =(-2)3=-23<0,∴a >b >c . 5.幂函数f (x )=(m 2-m -1)·x m 2-2m -3在(0,+∞)上是减函数,则实数m =________.答案 2解析 ∵f (x )=(m 2-m -1)xm 2-2m -3为幂函数,∴m 2-m -1=1,∴m =2或m =-1.当m =2时,f (x )=x -3在(0,+∞)上是减函数, 当m =-1时,f (x )=x 0=1不符合题意. 综上可知m =2.1.幂函数y =x α的底数是自变量,指数是常数,而指数函数正好相反,底数是常数,指数是自变量.2.幂函数在第一象限内指数变化规律在第一象限内直线x =1的右侧,图象从上到下,相应的指数由大变小;在直线x =1的左侧,图象从下到上,相应的指数由大变小. 3.简单幂函数的性质(1)所有幂函数在(0,+∞)上都有定义,并且当自变量为1时,函数值为1,即f (1)=1. (2)如果α>0,幂函数在[0,+∞)上有意义,且是增函数. (3)如果α<0,幂函数在x =0处无意义,在(0,+∞)上是减函数.一、基础达标1.已知幂函数f (x )的图象经过点⎝ ⎛⎭⎪⎫2,22,则f (4)的值为( ) A .16 B.116C.12D .2答案 C解析 设f (x )=x α,则有2α=22,解得α=-12,即f (x )=x 12-,所以f (4)=412-=12.2.下列命题中正确的是( )A .当α=0时,函数y =x α的图象是一条直线 B .幂函数的图象都经过(0,0)(1,1)两点C .若幂函数y =x α的图象关于原点对称,则y =x α在定义域上是增函数 D .幂函数的图象不可能在第四象限 答案 D解析 当α=0时,函数y =x α的定义域为{x |x ≠0,x ∈R },其图象为两条射线,故A 选项不正确;当α<0时,函数y =x α的图象不过(0,0)点,故选项B 不正确;幂函数y =x -1的图象关于原点对称,但其在定义域内不是增函数,故选项C 不正确;当x >0,α∈R 时,y =x α>0,则幂函数的图象都不在第四象限,故选项D 正确.3.下列幂函数中①y =x -1;②y =x 12;③y =x ;④y =x 2;⑤y =x 3,其中在定义域内为增函数的个数为( ) A .2B .3C .4D .5 答案 B解析 由幂函数性质知②③⑤在定义域内为增函数.4.当0<x <1时,f (x )=x 2,g (x )=x 12,h (x )=x -2的大小关系是( ) A .h (x )<g (x )<f (x ) B .h (x )<f (x )<g (x ) C .g (x )<h (x )<f (x )D .f (x )<g (x )<h (x )答案 D解析 在同一坐标系中,画出当0<x <1时,函数y =x 2,y =x 12,y =x -2的图象,如图所示.∴当0<x <1时,有x -2>x 12>x 2, 即f (x )<g (x )<h (x ).5.下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数是( ) A .y =x -2B .y =x -1C .y =x 2D .y =13x答案 A解析 由于y =x -1和y =13x 都是奇函数,故B 、D 不合题意.又y =x 2虽为偶函数,但在(0,+∞)上为增函数,故C 不合题意.y =x -2=1x2在(0,+∞)上为减函数,且为偶函数,故A满足题意.6.幂函数y =f (x )的图象经过点(2,18),则满足f (x )=-27的x 值等于________.答案 -13解析 设f (x )=x α,由题意可知2α=18,α=-3,即f (x )=x -3.由x -3=-27可知x =-13.7.比较下列各组中两个值的大小: (1)1.535与1.635;(2)0.61.3与0.71.3; (2)3.523-与5.323-;(4)0.18-0.3与0.15-0.3.解 (1)∵幂函数y =x 35在(0,+∞)上单调递增,且1.5<1.6,∴1.535<1.635. (2)∵幂函数y =x 1.3在(0,+∞)上单调递增,且0.6<0.7,∴0.61.3<0.71.3. (3)∵幂函数y =x 23-在(0,+∞)上单调递减,且3.5<5.3,∴3.523->5.323-.(4)∵幂函数y =x -0.3在(0,+∞)上单调递减,且0.18>0.15,∴0.18-0.3<0.15-0.3二、能力提升8.设a =⎝ ⎛⎭⎪⎫2535,b =⎝ ⎛⎭⎪⎫2525,c =⎝ ⎛⎭⎪⎫3525,则a ,b ,c 的大小关系是( ) A .a >b >c B .c >a >b C .a <b <cD .b >c >a答案 C解析 ∵函数y =⎝ ⎛⎭⎪⎫25x在R 上是减函数,又35>25,∴⎝ ⎛⎭⎪⎫2535<⎝ ⎛⎭⎪⎫2525,即a <b .又∵函数y =x 25在R 上是增函数,且35>25,∴⎝ ⎛⎭⎪⎫3525>⎝ ⎛⎭⎪⎫2525,即c >b , ∴a <b <c . 9.函数y =x -2x -1的图象是( )答案 B解析 方法一 代入选项验证即可. 方法二 y =x -2x -1=x -1-1x -1=-1x -1+1,利用函数图象的变换可知选B. 10.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”.那么函数解析式为f (x )=x 2,值域为{1,4}的“同族函数”共有( ) A .7个B .8个C .9个D .无数个 答案 C解析 值域为{1,4},∴其定义域由1,-1,2,-2组成,∴有{1,2},{1,-2},{-1,2},{-1,-2},{1,-1,-2},{1,-1,2},{1,2,-2},{-1,2,-2},{1,-1,2,-2},共有9种情况.11.已知幂函数f (x )的图象过点(25,5). (1)求f (x )的解析式;(2)若函数g (x )=f (2-lg x ),求g (x )的定义域、值域. 解 (1)设f (x )=x a ,则由题意可知25a=5, ∴a =12,∴f (x )=x 12.(2)∵g (x )=f (2-lg x )=2-lg x , ∴要使g (x )有意义,只需2-lg x ≥0, 即lg x ≤2,解得 0<x ≤100.∴g (x )的定义域为(0,100], 又2-lg x ≥0,∴g (x )的值域为[0,+∞). 三、探究与创新12.已知幂函数y =f (x )=x -2m 2-m +3,其中m ∈{x |-2<x <2,x ∈Z },满足: (1)是区间(0,+∞)上的增函数;(2)对任意的x ∈R ,都有f (-x )+f (x )=0.求同时满足(1),(2)的幂函数f (x )的解析式,并求x ∈[0,3]时f (x )的值域. 解 因为m ∈{x |-2<x <2,x ∈Z }, 所以m =-1,0,1.因为对任意x ∈R ,都有f (-x )+f (x )=0, 即f (-x )=-f (x ),所以f (x )是奇函数.当m =-1时,f (x )=x 2只满足条件(1)而不满足条件(2); 当m =1时,f (x )=x 0条件(1)、(2)都不满足.当m =0时,f (x )=x 3条件(1)、(2)都满足,且在区间[0,3]上是增函数. 所以x ∈[0,3]时,函数f (x )的值域为[0,27].13.已知幂函数f (x )=xm 2-2m -3(m ∈N )的图象关于y 轴对称,且在(0,+∞)上函数值随着x 的增大而减小,求满足(a +1)-m 3<(3-2a )-m3的a 的取值范围.解 ∵函数f (x )在(0,+∞)上的函数值随着x 的增大而减小,∴m 2-2m -3<0, 利用二次函数的图象可得-1<m <3. 又∵m ∈N ,∴m =0,1,2. 又∵函数的图象关于y 轴对称, ∴m 2-2m -3是偶数,故m =1, ∴(a +1)-13<(3-2a )-13.又∵y =x -13在(-∞,0)和(0,+∞)上均单调递减,∴有以下三种情况:①当⎩⎪⎨⎪⎧a +1<0,3-2a >0,即a <-1时,不等式的左边为负数,右边为正数,不等式成立;②当⎩⎪⎨⎪⎧ a +1>0,3-2a >0时,必有a +1>3-2a ,即⎩⎪⎨⎪⎧a +1>0,3-2a >0,a +1>3-2a ,解得23<a <32;③当⎩⎪⎨⎪⎧a +1<0,3-2a <0时,必有a +1>3-2a ,即⎩⎪⎨⎪⎧ a +1<0,3-2a <0,a +1>3-2a ,此不等式组无解,综上可得a 的取值范围是(-∞,-1)∪⎝ ⎛⎭⎪⎫23,32.。
高中数学 2.3.1幂函数的概念教学设计 湘教版必修1

幂函数的概念教学目标:知识与技能通过具体实例了解幂函数的概念、图象和性质,并能进行简单的应用.过程与方法能够类比研究一般函数、指数函数、对数函数的过程与方法,来研究幂函数的图象和性质.情感、态度、价值观体会幂函数的变化规律及蕴含其中的对称性.教学重难点:重点从五个具体幂函数中认识幂函数的概念和一些性质.难点画五个具体幂函数的图象并由图象概括其性质,体会图象的变化规律.教学程序与环节设计:问题引入,得出幂函数的概念。
幂函数性质的初步应用.教学过程与操作设计:材料三:幂函数性质归纳.观察图象,总结填写下表:师:引导学生应用画函数的性质画图象,如:定义域、奇偶性.师生共同分析,强调画图象易犯的错误.环节教学内容设计师生双边互动组织探究xy=2xy=3xy=21xy=1-=xy定义域值域奇偶性单调性定点师:引导学生观察图象,归纳概括幂函数的的性质及图象变化规律.生:观察图象,分组讨论,探究幂函数的性质和图象的变化规律,并展示各自的结论进行交流评析,并填表.材料四:总结常见幂函数的某些共同性质(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);(2)13,,-===xyxyxy是奇函数,2xy=是偶函数(3)在区间(0,+∞)上函数2132,,,xyxyxyxy====是增函数,1-=xy是减函数。
(4)在第一象限中,函数1-=xy的图像向上与y轴无限接近,向右与x轴无限接近。
材料五:例题[例1](教材例题) 证明幂函数x x f =)(在(0,+∞)上是增函数(重点分析分子有理化的理由,化简的方向和最后的化简结果形式)师:引导学生回顾讨论函数性质的方法,规范解题格式与步骤.并指出函数单调性是判别大小的重要工具,幂函数的图象可以在单调性、奇偶性基础上较快描出. 生:独立思考,给出解答,共同讨论、评析.环节 呈现教学材料师生互动设计 尝试 练 习证明:幂函数2)(x x f =在(0, +∞)上是增函数;在(-∞,0)上是减函数学生板演师:评价反馈情况,并重点强调化简的方法,化简的方向和最终结果的保留形式,探究 与 发 现 1.如图所示,曲线是幂函数αx y =在第一象限内的图象,已知α分别取2,21,1,1-四个值,则相应图象依次为: .规律1:在第一象限,作直线)1(>=a a x ,它同各幂函数图象相交,按交点从下到上的顺序,幂指数按从小到大的顺序排列.环节呈现教学材料师生互动设计则有:且任取证明,),,0(,:2121x x x x <+∞∈))(()()(2121222121x x x x x x x f x f +-=-=-,0,0,0212121>+<-<≤x x x x x x 所以因为.),0()()((0)()(22121上是增函数在幂函数)即所以+∞∈=∴<<-x x x f x f x f x f x f ,0,0,0434343<+<-<<x x x x x x 所以因为.)0,()()((0)()(24343上是减函数在幂函数)即所以-∞∈=∴>>-x x x f x f x f x f x f 则且同理任取,),0,(,4343x x x x <-∞∈))(()()(4343242343x x x x x x x f x f +-=-=-。
高中数学 2.3.1幂函数的图像、性质及应用课件 新人教A版必修1

点评:比较两个幂的大小的关键是搞清楚底数与指数是否相同,若
底数相同,利用指数函数的性质比较大小;若指数相同,利用幂函
栏 目
链
数的性质比较大小;若底数指数均不同,考虑利用中间值来比较大 接
小.
►跟踪训练
2.比较下列各组数的大小:
11 (1)1.53,1.73,1;
(2)-
22-32,-17023,1.1-43;
例1
函数f(x)=(m2-m-1)xm2+m-3是幂函数,且当
x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.
解析:根据幂函数定义得
m2-m-1=1,解得m=2或m=-1,
栏
当m=2时,f(x)=x3在(0,+∞)上是增函数,
目 链
当m=-1时,f(x)=x-3在(0,+∞)上是减函数,不合要求,故接
解析:∵f(x)为幂函数,∴2m2+m=1,得m=21或m=-1.
栏
当m=12时,f(x)=x-41=
1 4
,
目 链 接
x
定义域为x>0,显然不具有奇偶性;
当m=-1时,f(x)=x-1=x1是奇函数.
答案:-1
题型2 利用你幂函数的性质比较大小
例2 比较下列各组中两个数的大小:
6
6
(1)0.611与0.711;
f(x)=x3.
点评:幂函数y=xα(α∈R)其中α为常数,其本质特征是以幂的
底x为自变量,指数α为常数(也可以为0).这是判断一个函数是否为
幂函数的重要依据和唯一标准.对例1来说,还要根据单调性验
根,以免增根.
►跟踪训练
1.已知函数f(x)=(2m2+m)xm2+m-1为幂函数且是奇函数,
幂函数是什么意思有什么特性及性质
幂函数是什么意思有什么特性及性质例如函数y=x0、y=x1、y=x2、y=x-1注:y=x-1=1/xy=x0时x≠0等都是幂函数。
当α取非零的有理数时是比较容易理解的,而对于α取无理数时,初学者则不大容易理解了。
因此,在初等函数里,我们不要求掌握指数为无理数的问题,只需接受它作为一个已知事实即可,因为这涉及到实数连续性的极为深刻的知识。
幂函数的图像必须出现在第一象限,而不是第四象限。
它是否出现在第二和第三象限取决于函数的奇偶性;幂函数图像最多只能出现在两个象限;如果幂函数图像与坐标轴相交,则交点必须是原点取正值当α>0时,幂函数y=Xα它具有以下性质:a、图像都经过点1,10,0;b、函数的映像是[0,+∞;c、在第一象限内,α>1时,导数值逐渐增大;α=1时,导数为常数;0<α<1时,导数值逐渐减小,趋近于0;取负值当α<0时,幂函数y=xα有下列性质:a、所有图像都通过点1,1;b、图像在区间0,+∞上是减函数;内容补充:若为x-2,易得到其为偶函数。
利用对称性,对称轴是y轴,可得其图像在区间-∞,0上单调递增。
其余偶函数亦是如此c、在第一象限中,有两条渐近线,即坐标轴。
自变量接近0,函数值接近+∞, 自变量接近+∞, 函数值接近0。
取零当α=0时,幂函数y=XA具有以下特性:a、y=x0的图像是直线y=1去掉一点0,1。
它的图像不是直线。
x=0时,函数值没意义关于α,的值是一个非零有理数。
有必要在几种情况下讨论它们的特点:首先我们知道如果α=p/q,且p/q为既约分数即p,q互质,q和p都是整数,则x^p/q=q次根号下x的p次方,如果q是奇数,函数的定义域是r,如果q是偶数,函数的定义域是[0,+∞。
当指数α是负整数时,设α=-k,则y=1/x^k,显然x≠0,函数的定义域是-∞,0∪0,+∞。
因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道:α小于0时,X不等于0;α的分母为偶数时,x不小于0;α当的分母为奇数时,X取R。
4.1.1有理数指数幂(课件)-高一数学(湘教版2019必修第一册)
算法则进行运算,而引入分数指数的概念就可以大大简化根式运算.
当 > 0,, ∈ 且 ≥ 2时,规定 = ,
这样就有
24
4
2
= 2 = 4, 6
1
33
=3
3
−6
=3
1
2
−
=
1
3
=
1
=
−
.
3
,方便多了.
1
−2
= 5,求下列各式的值:
(1) + −1 ;(2)2 + −2 ;(2)
1
2
解:将 +
1
−2
3
3
−
2 − 2
1
1
−
2 − 2
.
= 5两边同时平方,得: + −1 + 2 = 5.
(1) + −1 = 5 − 2 = 3;
(2)将 + −1 两边同时平方,得:2 + −2 + 2 = 9.∴2 + −2 = 7.
∙ = + ,( ) = ,() = .
下面,我们把整数指数幂推广到有理数指数幂.
新知探索——根式
若一个(实)数的次方( ∈ , ≥ 2)等于,即 = ,则称是的次
方根.
当是奇数时,数的次方根记作 .
当 > 0时, > 0;当 = 0时, = 0;当 < 0时, < 0.
1
−2
1 −3
125 −2
;(3)( ) ;(4)( ) 3 .
4.1.3幂函数(课件)-高一数学(湘教版2019必修第一册)
,则2
= 2
∴=2.即() = 2 .
同理可得,() = −2 .
画出() = 2 和() = −2 的函数图象,
则由图象可知:当 < −1或 > 1时,() > () ;
当 = ±1时,() = ();
当−1 < < 1时,() < ().
由于底数1.5 < 1.6,所以1.51.4 < 1.61.4 .
(2)1.50.4 ,1.60.4 可看作幂函数 = 0.4 的两个函数值.该函数在[0, +∞)上递增,由
于底数1.5 < 1.6,所以1.50.4 < 1.60.4 .
(3)1.5−1.5 ,1.6−1.5 可看作幂函数 = −1.5 的两个函数值.该函数在(0, +∞)上递减,
新知探索
上面的讨论中用到的自变量, 2 和 3 ,都是自变量的函数.这三种函数我
们已经很熟悉了.
一般来说,当为自变量而为非零实数时,函数 = 叫作(次)幂函数.上
面提到的1,2,3次幂函数,都是正整数次幂函数 = ( ∈ , ∈ + )的例子.
注:幂函数的表达式 = 中,的系数必须为“1”.
练习
变3.比较下列各题中两个幂的值的大小.
1
1
−2
−2
(1)1.5 与1.4 ;
(2)2
−
3
−4
1
2
3 3
与( )4 .
2
解:(1)∵幂函数 = 在(0, +∞)上是单调递减的,
又1.5 > 1.4,∴1.5
(2)∵2
1
高中数学 231,232幂函数的概念 幂函数的图象和性质课件 湘教版必修1
2
3
(4)y=x-5; (5)y=x-3; (6)y=x-4.
解 (1)y=x6 的定义域是 R,值域是[0,+∞).
(2)y=x35=5 x3的定义域是 R,值域是 R.
(3)y=x14=4 x的定义域是[0,+∞),值域是[0,+∞).
(4)y=x-5=x15的定义域是{x|x∈R 且 x≠0},值域是{y|y∈R,
幂函数.
第十四页,共33页。
【变式1】 下列函数中哪些是幂函数:
(1)y=x12;
4
(4)y=(x-2)5;
(2)y=21x; (3)y=32x; (5)y=1; (6)y=x0;
(7)y=-2·4x; (8)y= 1 . 5 x2
解 (1)是幂函数,因为 y=x12=x-2; (2)不是幂函数,它是指数函数 y=12x; (3)不是幂函数,y=32x=9x 是指数函数;
第十页,共33页。
α=qp
α<0
0<α<1
α>1
p、q都 是奇数
q是偶数 p是奇数
q是奇数 p是偶数
第十一页,共33页。
当α>0时,幂函数的图象都经过原点和点(1,1),在第一象限内, 当0<α<1时,曲线上凸;当α>1时,曲线下凸. (3)幂函数的增减性 在区间(0,+∞)上,当α>0时,y=xα是递增(dìzēng)函数;当α<0 时,y=xα是递减函数. (4)幂函数的奇偶性
∴23-23<π6 -23,即(-23)-23<-π6 -23.
22
22
3
(4)4.15>15=1,0<3.8-3<1-3=1,(-1.9)5<0,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数.
预习测评
1.下列函数为偶函数的是
1
( B.y=x2 D.y=x3
).
A.y=x-1 C.y=x2
答案
C
1
2. 当 0<x<1 时, f(x)=x2, g(x)=x2, h(x)=x 2 的大小关系是(
-
).
A.h(x)&lf(x) 答案 D
B.h(x)<f(x)<g(x)
2.3
2.3.2
【课标要求】
1.掌握幂函数的概念.
幂函数
2.3.1 幂函数的概念
幂函数的图象和性质
1 2.熟悉 α= 1,2,3, ,- 1,- 2 时幂函数 y= xα 的图象与性质. 2 3.能利用幂函数的性质来解决一些实际问题.
自学导引
1.一般来说,当x为自变量而α为非0实数时,函数y=xα叫作 幂函数 (α次的)_________(power function). 一般说来,我们只考虑定义域为[0,+∞)的分数次幂函数
的幂函数 . _________
幂函数: 2.
1 1 y=x,y=x ,y=x ,y= x,y= ,y= 2. x x
2 3
代表了幂函数的各种不同类型. x>0 时才能都有 对于一般的非0实数α,幂函数y=xα只在______ 3. 意义.对于整数次的幂函数,由于图象的对称性,把它们 (0,+∞) 上的图象和性质说清楚了,其他部分的情形 在__________ 也就很容易了解.
名师点睛
幂函数 (1)幂函数的有关概念与性质
①幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的
底x为自变量,指数α为常数.y=x+1,y=x2-2x等都不是 幂函数.②在(0,1)上,幂函数中指数愈大,函数图象愈靠 近x轴(简记为“指大图低”),在(1,+∞)上,幂函数中指数越 大,函数图象越远离x轴.③幂函数的图象一定会出现在第 一象限内,一定不会出现在第四象限,至于是否出现在第 二、三象限内,要看函数的奇偶性;
q是偶数 p是奇数
q是奇数 p是偶数
当α>0时,幂函数的图象都经过原点和点(1,1),在第一象限
内,当0<α<1时,曲线上凸;当α>1时,曲线下凸.
(3)幂函数的增减性 在区间(0,+∞)上,当α>0时,y=xα是递增函数;当α<0时,y= xα是递减函数. (4)幂函数的奇偶性
q 令 α= (其中 p,q 互素, p 和 q∈N). p
(0,0) 和______ (1,1) ,即0α=0,1α=1; ①都经过两个点______
增 函数; ②是递___
③图象与直线y=x有如下关系:
0<x<1 α>1 0<α<1 在y=x下方 __________ 在y=x上方 __________
x>1
在y=x上方 __________
在y=x下方 __________
eαlnx ,可见幂函数 注意到当x>0时,有等式xα=(eln x)α=_____
的性质都可以归结到指数函数和对数函数的性质.例如,
递增 ;α<0时,xa 由ex和ln x的递增性立刻得知:α>0时xα _____ xα>0 . 递减 ,由ex恒为正可知x>0时_____ _____
4.定义在非负数范围内的幂函数y=xα的定义域只有两种可能: [0,+∞) ,当α<0时是__________ (0,+∞) . 当α>0时是__________ 5.(1)当α>0时,幂函数在区间[0,+∞)上有如下性质:
幂函数的图象最多只能同时出现在两个象限内;
如果幂函数图象与坐标轴相交,则交点一定是原点. (2)幂函数的图象
当指数α=1时,y=x的图象是直线;当α=0时,y=xα=
x0=1是直线(不包括(0,1)点).除上述特例外,幂函数的 图象都是曲线,如下表.
q α= p
α<0
0<α<1
α>1
p、q都 是奇数
p
y=xq ,这里p是不为0的整数,q是大于1的正整数,并且p ______
互素 . 和q_____
1 y= n ,叫作负整数次的幂函数. 正整数次幂函数的倒数_____ x y=x-n ,这里n是正整数,x≠0. 一般写成________
整数次 负整数次的幂函数和正整数次的幂函数,统称为________
D.f(x)<g(x)<h(x)
3.当x∈(0,1)时,y=xp (p∈R)的图象在y=x的上方,则p的 范围是________.
答案
(-∞,1)
4.已知函数y=(a2-3a+3)xa(a为常数)为幂函数,则a= ________. 解析 答案 由幂函数定义知a2-3a+3=1,解得a=1或2. 1或2
函数.
解 (1)若
2 m + m- 1= 1, f(x)为正比例函数,则 2 ⇒ m= 1. m + 2m≠ 0
(2)若 f(x)为反比例函数,
2 m + m- 1=- 1, 则 2 ⇒ m=- 1. m + 2m≠ 0
(3)若
2 m + m- 1= 2, f(x)为二次函数,则 2 m + 2m≠ 0
-1± 13 ⇒ m= . 2 (4)若 f(x)为幂函数,则 m2+2m=1⇒ m=-1± 2.
(2)当α<0时,幂函数在区间(0,+∞)上有如下性质:
(1,1) ,即1α=1; ①图象都过点_______ 减 函数; ②是递___ y轴 正向无限接近,向右与____ x轴 正向无限接 ③图象向上与____
近.
自主探究
1.y=1和y=x0(x≠0)一样吗?它们都是幂函数吗? 提示 提示 不一样,y=1不是幂函数,y=x0(x≠0)是幂函数. 指数函数y=ax(a>0且a≠1)的底数a为常数,指数为 幂函数与指数函数有什么区别? 2. 变量;幂函数y=xα(α∈R)以幂的底为自变量,指数α为常
q
①若 p 是奇数,则 y=xp的奇偶性取决于 q 是奇数或偶数.当 q 是奇 q 数时,则 y=xp是奇函数;当 q 是偶数时,则 y=x 是偶函数.②若 p p
q q
是偶数,则 q 必是奇数,此时 y=xp既不是奇函数,也不是偶函数.
典例剖析
题型一 幂函数的概念
xm2+m-1,m为何值时, 【例1】 已知函数f(x)=(m2+2m)· f(x)是(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂
