流体静力学4
流体静力学实验报告
一、实验目的1.掌握用液式测压计测量流体静压强的技能。
2.验证不可压缩流体静力学基本方程,加深对位置水头、压力水头和测压管水头的理解。
3.观察真空度(负压)的产生过程,进一步加深对真空度的理解。
4.测定油的相对密度。
5.通过对诸多流体静力学现象的实验分析,进一步提高解决静力学实际问题的能力。
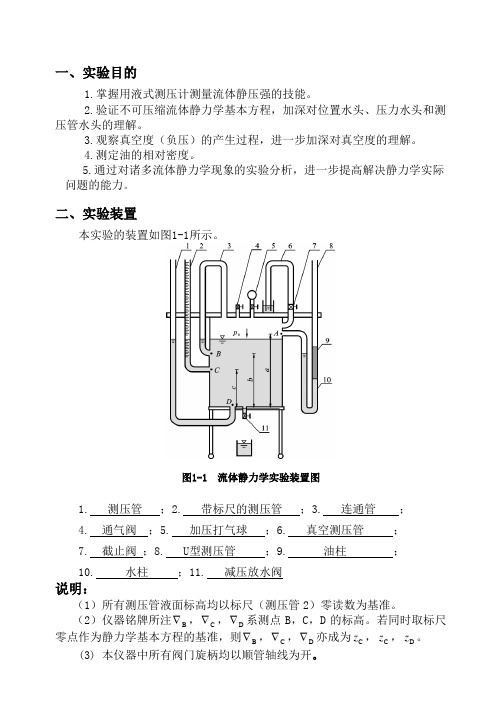
二、实验装置本实验的装置如图1-1所示。
图1-1 流体静力学实验装置图1. 测压管 ;2. 带标尺的测压管 ;3. 连通管 ;4. 通气阀 ;5. 加压打气球 ;6. 真空测压管 ;7. 截止阀 ;8. U 型测压管 ;9. 油柱 ; 10. 水柱 ;11. 减压放水阀说明:(1)所有测压管液面标高均以标尺(测压管2)零读数为基准。
(2)仪器铭牌所注B ∇,C ∇,D ∇系测点B ,C ,D 的标高。
若同时取标尺零点作为静力学基本方程的基准,则B ∇,C ∇,D ∇亦成为C z ,C z ,D z 。
(3) 本仪器中所有阀门旋柄均以顺管轴线为开。
三、实验原理1.在重力作用下不可压缩流体静力学基本方程。
形式一:pz γ+=const (1-1-1a )形式二:P=P 。
+γ (1-1-1b ) 式中 z---测点在基准面以上的位置高度;P —测点的静水压强(用相对压强表示,一下同); P 。
--水箱中液面的表面压强; γ--液体的重度; h —测点的液体深度; 2.油密度测量原理。
当u 形管中水面与油水界面齐平(见图1-1-2),取油水界面为等压面时,有:P01=w γ=0γH (1-1-2) 另当U 形管中水面与油面平齐(见图1-1-3),取油水界面为等压面时,有:P02+W γH=0γH即P02=-w γh2=0γH-W γH (1-1-3)图1-2 图1-3四、实验要求1.记录有关常数 实验装置编号No. 12 各测点的标尺读数为:B ∇= 2.1 -210m ⨯;C ∇= -2.9 -210m ⨯;D ∇= -5.9 -210m ⨯; 基准面选在 测压管的0刻度线处 ; C z = -2.3 -210m ⨯;D z = -5.9 -210m ⨯;2.分别求出各次测量时,A 、B 、C 、D 点的压强,并选择一基准验证同一静止液体内的任意二点C 、D 的(pz γ+)是否为常数. 3.求出油的重度。
流体静力学

结论: 1)仅在重力作用下,静止流体中某一点的静水压强随 深度按线性规律增加。 2)仅在重力作用下,静止流体中某一点的静水压强等 于表面压强加上流体的容重与该点淹没深度的乘积。
3)自由表面下深度h相等的各点压强均相等—只有重力 作用下的同一连续连通的静止流体的等压面是水平面。 4)推广:已知某点的压强和两点间的深度差,即可求另 外一点的压强值。
3-3-2 静止流体平衡的微分方程式
欧拉运动方程
V 1 (V )V F grad p t F 1
V=0
grad p
一、流体平衡微分方程——欧拉平衡方程
图示,在平衡流体中取一微元六面体,边长分别为dx, dy,dz,设中心点的压强为p(x,y,z)=p,对其进行受力 分析,以y方向为例
2008年01月07日08:45
液压机械的工作原理液压机Leabharlann 液力倍压器液压千斤顶
二、液体静压强分布的基本规律
1、重力作用下,静止液体中等压面是一个水平面。
2、两种液体的分界面既是水平面,又是等压面。
3、静止的非均质液体,水平面既是等压面,又是等 密度面和等温面。 4、液体静压强的大小与容器的形状无关。
绝对静止 相对静止 流动的理想流体 (流体质点间可能有相对运动) 理想流体动压强呈静水压强分布特性, 即:px=py=pz=pn=p p表示静止流体中作用在该点任意取向的面积元上压应力的大 小,叫做流体静力学压强,简称压强. 压强是流体力学中—个很重要的参数.在国际单位制中压 强的单位是帕(Pa),这是为了纪念法国数学家帕斯卡(Pascal) 对流体静力学的贡献而命名的.1Pa=1N/m2.
p1 pa 3332 Pa
p 2 pa p1 水g h水 3332 1000 9.8 0.09 4214 Pa
流体静力学实验教程

流体静力学实验教程一、引言流体静力学是研究静止流体中压力分布和力的平衡关系的学科。
它在物理、工程、地球科学等领域具有广泛的应用。
本实验教程将介绍流体静力学实验的基本原理、仪器设备、实验操作步骤以及实验数据处理方法,帮助读者深入理解和掌握该领域的知识。
二、实验原理1. 海氏定律海氏定律是流体静力学中最基本的定律之一,它表明在静止流体中,单位面积上的压力仅与液体的深度有关,与池底形状、容器的大小和液体的密度无关。
2. 压力的测量压力是流体静力学实验中重要的物理量之一,常用的测量方法有U型压力计、气压法、压力传感器等。
3. 力的平衡条件流体静力学中,液体受到的压力形成一个平衡系统,对液体的任何一个小体积,受到的合力为零。
这是力的平衡条件,用于分析液体静力学问题的基本原理。
三、实验仪器设备1. 液压台:用于放置实验装置和测量液体的压力。
2. U型压力计:用于测量液体的压力。
3. 液体容器:用于储存液体并提供压力。
4. 压力传感器:用于测量液体的压力并将信号转化为电信号。
5. 数据采集系统:用于记录和处理实验数据。
四、实验步骤1. 准备实验装置:将液压台放置在平稳的地面上,安装好U型压力计、液体容器和压力传感器。
2. 调整仪器:根据实验要求调整U型压力计和压力传感器的零位,确保测量准确。
3. 测量压力:将液体注入液体容器,打开压力传感器记录压力值,并用U型压力计进行验证。
4. 改变液体深度:改变液体容器中液体的深度,记录对应的压力值并进行分析。
5. 实验数据记录和处理:将实验数据导入数据采集系统,进行数据处理和分析。
五、实验注意事项1. 实验过程中要保持实验环境的整洁,确保实验数据的准确性。
2. 操作仪器时要仔细、轻柔,避免对实验装置造成损坏。
3. 实验结束后要及时清洁实验装置,并归位储存,保持设备的良好状态。
六、实验结果与讨论通过实验可以得到不同液体深度下的压力值,并进行数据处理和分析。
借助实验结果,可以验证海氏定律在静止流体中的适用性,并深入理解流体静力学的原理。
1.2 流体静力学

m 1 y1 2 y2 n yn
Mm p 或 m RT
Mm y1 M1 y2 M2 ym Mm
9
五、比体积(比容) 单位质量的流体所具有的体积。
V m
六、相对密度d
m3/kg
d
ρ ρ 4C H2O
ρ 1000
10
[例1-1]已知干空气的组成为:O221%、N278%和Ar1%(均为体积 %)。试求干空气在压力为9.81×104Pa、温度为100℃时的密度。 解: 首先将摄氏度换算成开尔文: 100℃=273+100=373K 求干空气的平均分子量:Mm = M1y1 + M2y2 + M3y3
解:已知水的密度0=1000kg/m3 ,40%的酒精密度
a=920kg/m3 , 煤油的密度b=850kg/m3 可得:p1- p2 =0 gR=(a - b)gR'
已知 R=10mm 于是 R'= 0R/(a - b )=1000×10/(920-850)=143mm 则放大的倍数为 R'/R= 0 /(a - b )=14.3
气体
6
三、纯物质的密度
查取:查教材P328-335附录三-九 ,查化工手册(注 意查共线图的方法)
注意:查g 须注意温度、压力。 计算:气体为可压缩性的流体,通常(压力不太 高,温度不太低)时可按理想气体处理,否则按 真实气体状态方程处理。
m pM ρ V RT
0T0 p
Tp0
21
讨论:
1.U形压差计可测系统内两点的压差,当将U形管一端与被测点 连接、另一端与大气相通时,也可测得流体的表压或真空度; p1 p1
p0 压差 表压 真空度
化工原理2.2.2流体静力学基本方程

2)积分形式
南京工业大学
p2 p1 g(z1 z2 )
压力形式
p1
z1 g
p2
z2 g
能量形式
南京工业大学
3)引伸:
修正压强 pm (Modified Pressure)
pm p gz const.
静止、连通、恒密度流体在重力场中, 不同位置的流体质点间的修正压强不变。
2.静力学基本方程的应用
1) 压力及压力差的测量
南京工业大学
pa
a)简单测压管 p A
pA pB pa gR pA pa gR
R
AB
b)U形压差计:
pmA pm3 , pmB pm4 pmA pmB pm3 pm4 p3 p4
p1 p2 , p1 p3 gR, p2 p4 i gR pmA pmB p3 p4 (i )gR
南京工业大学
任意放置管:
pA
pmA pmB (i )gR
U型压差计测得的是修正压强
南京工业大学
pB
m
水平管
ZA ZB
pA pB (i )
R 12
c)微差压差计
南京工业大学
d 2 R / 4 D2h / 4
h R(d / D)2
p1 p2 (i )gR gR(d / D) 2
A
液封高度: h p pa g
b)化简得到微分形式:
z方向
dp gdz 0
x和y方向
dp / dx 0 dp / dy 0
c)通过对微分形式进行分析,得到结论:
①水平面为等压面:同一连续静止的流体中间,同一水平面上 静压相同。
第二章流体静力学

当四面体的体积趋于零时,可证得px= py=pz=pn
即
p=p(x,y,z)
§2-2 流体的平衡微分方程及积分
一、流体的平衡微分方程
在平衡流体中取如图所示微小正交六面体。分析六面
体在x、y、z方向所受外力,列平衡方程,整理化简得
fx
1
p x
0
fy
1
p y
0
1 p
fz z 0
上式也可用矢量方程表示:
虚压力体:压力体和液体在受压曲面的异侧, Pz向上。
A
A
B
B
例4:试绘制图中abc曲面上的压力体。如已知曲面abc为半圆 柱面,宽度为1m,d=3m,试求abc柱面所受静水压力的水平分 力Px和竖直分力Pz 。
a
d d/2
b 水
水 c
[解] 因abc曲面左右两侧均有水的作用,故应分别考虑。
考虑左侧水的作用
故得欧拉平衡微分方程综合式(即全微分形式)
dp ( f xdx f ydy f z dz)
四.等压面
1.定义: p=C或dp=0的平面或曲面。
2.等压面微分方程
f xdx f y dy f z dz 0
或
f•
ds
0
3.等压面的性质
(1)等压面与等势面重合;
(2)等压面恒与质量力正交。
其作用点为通过体积重心所引出的水平线与受压面的交点D。 当相对压强分布图为三角形时,D点位于自由液面下(2h)/3处。
对于相对压强分布图为梯形情况,可将其分解成三角形和矩 形两部分进行计算后,最后利用合力矩定理求总压力作用点。
例3.铅垂放置的矩形平板闸门,面板后布置三根横梁,各横梁受 力相等,已知闸门上游水头H=4m,试求: (1)每根横梁所受静水总压力的大小; (2)各横梁至水面的距离。
工程流体力学公式
工程流体力学公式1.流体静力学公式:(1) 压强公式:P = ρgh,其中P为压强,ρ为流体密度,g为重力加速度,h为液面高度。
(2)压力公式:P=F/A,其中P为压力,F为作用力,A为受力面积。
2.流体力学基本方程:(1)质量守恒方程:∂(ρ)/∂t+∇·(ρv)=0,其中ρ为密度,t为时间,v为速度矢量。
(2) 动量守恒方程:∂(ρv)/∂t + ∇·(ρvv) = -∇P + ∇·τ +ρg,其中P为压力,τ为应力张量,g为重力加速度。
(3) 能量守恒方程:∂(ρe)/∂t + ∇·(ρev) = -P∇·v +∇·(k∇T) + ρg·v,其中e为单位质量的总能量,T为温度,k为热传导系数。
3.流体动力学方程:(1)欧拉方程:∂v/∂t+(v·∇)v=-∇(P/ρ)+g,其中v为速度矢量,P为压力,ρ为密度,g为重力加速度。
(2)再循环方程:∂v/∂t+(v·∇)v=-∇(P/ρ)+g+F/M,其中F为体积力,M为质量。
4.流体阻力公式:(1) 粘性流体的阻力公式:F = 6πμrv,其中F为阻力,μ为粘度,r为流体直径,v为速度。
(2)粘性流体在管道中的流量公式:Q=(π/8)ΔP(R^4)/(Lμ),其中Q为流量,ΔP为压差,R为半径,L为管道长度,μ为粘度。
5.流体力学定律:(1) Pascal定律:在封闭的液体容器中,施加在液体上的外力将均匀传递到液体的每一个点。
(2) Bernoulli定律:沿着流体流动方向,速度增大则压力减小,速度减小则压力增大。
除了上述公式之外,还有许多与特定问题相关的公式,如雷诺数、流体阻力系数、泵和液力传动公式等。
这些公式是工程流体力学研究和设计的基础,可以帮助工程师分析和解决与流体运动和相互作用有关的问题。
流体静力学基本方程式
第一节 流体静力学基本方程式流体静力学是研究流体在外力作用下达到平衡的规律。
在工程实际中,流体的平衡规律应用很广,如流体在设备或管道内压强的变化与测量、液体在贮罐内液位的测量、设备的液封等均以这一规律为依据。
1-1-1流体的密度一、密度单位体积流体所具有的质量,称为流体的密度,其表达式为:Vm =ρ (1-1) 式中 ρ——流体的密度,kg/m 3;m ——流体的质量,kg ;V ——流体的体积,m 3。
不同的流体密度不同。
对于一定的流体,密度是压力P 和温度T 的函数。
液体的密度随压力和温度变化很小,在研究流体的流动时,若压力和温度变化不大,可以认为液体的密度为常数。
密度为常数的流体称为不可压缩流体。
流体的密度一般可在物理化学手册或有关资料中查得,本教材附录中也列出某些常见气体和液体的密度值,可供查用。
二、气体的密度气体是可压缩的流体,其密度随压强和温度而变化。
因此气体的密度必须标明其状态,从手册中查得的气体密度往往是某一指定条件下的数值,这就涉及到如何将查得的密度换算为操作条件下的密度。
但是在压强和温度变化很小的情况下,也可以将气体当作不可压缩流体来处理。
对于一定质量的理想气体,其体积、压强和温度之间的变化关系为将密度的定义式代入并整理得'''Tp p T ρρ= (1-2) 式中 p ——气体的密度压强,Pa ;V ——气体的体积,m 3;T ——气体的绝对温度,K ;上标“'”表示手册中指定的条件。
一般当压强不太高,温度不太低时,可近似按下式来计算密度。
RTpM =ρ (1-3a ) 或 000004.22Tp p T Tp p T M ρρ== (1-3b ) 式中 p ——气体的绝对压强,kPa 或kN/m 2;M ——气体的摩尔质量,kg/kmol ;T ——气体的绝对温度,K ;R ——气体常数,8.314kJ/(kmol ·K )下标“0”表示标准状态(T 0=273K ,p 0=101.3kPa )。
第二章 流体静力学
§2-4 液柱测压计
一、测压管
若被测流体的压强较高时,用一个U形管则过长,可以 采用串联的U形管组成多U形管测压计。通常采用双U形 管或三U形管测压计。若为n个串联U形管测压计,则被 测容器A中的相对压强计算通式为
p gh 1g hi 1 g h j
i 1 j 1
流体静压强的分布规律
静力学基本方程的另一种形式
如右图所示,选取如图所示基准 面,则静力学基本方程可写为:
z1
或:
p1
z2
p2
z0
p0
z
p
C
§2-2 流体静压强的分布规律
物理意义:在重力作用下,静止 的不可压缩流体中单位重量流体 的总势能保持不变
p p
z
z hp hp
P 、P 、G ldA 1 p1dA 2 p2 dA
将上式代入平衡方程得
p2 p1 h
§2-2 流体静压强的分布规律
如果液面的压强为p0 ,则液面以下深度h点处的压强为:
p p0 h ---------液体静力学基本方程式
结论:1)仅在重力作用下,静止流体中某一点的静水压强随深 度按线性规律增加。 2)仅在重力作用下,静止流体中某一点的静水压强等于 表面压强加上流体的容重与该点淹没深度的乘积。 3)自由表面下深度h相等的各点压强均相等——只有重力 作用下的同一连续连通的静止流体的等压面是水平面。 帕斯卡定律:静止液体任一边界面上面上的压强变化,将 等值的传到其他各点。 即: p p0
§2-4 液柱测压计
一、测压管
3、U型测压管 1)p>pa p1=p2 p1=p+ρ 1gh1 p2=pa+ρ 2gh2 所以 p+ρ 1gh1=pa+ρ 2gh2 M点的绝对压强为 pabs=pa+ρ 2gh2-ρ 1gh1 M点的相对压强为 p=p-pa=ρ 2gh2-ρ 1gh1 由右图知 而
1.2_流体静力学基本方程解析
3 液封高度的计算
例:如图示。(P24 例题1-8)
已知:炉内p≤10.7kpa(表压)
求:h=? 解:如图等压面0-0´。 p1=炉内压力=pa+10.7×103Pa p2= pa+gh
b
pa h
0´
a
0
1
2
由 p2= p1
a-乙炔发生炉
b-液封管
解得: h=1.09 m 为了安全起见,实际应略小于1.09 m 。
F=ma=Va
2
表面力
表面力是由与流体表面相接触的物质(包括相邻流体)
施加给该流体的作用力,其大小与作用面积成正比。 垂直于表面的力
作用于流体上的表面力 平行于表面的力
(1)压力是垂直作用于表面的力,作用在流体单位面积上的 压力称为压强。 (2)剪切力是平行作用于表面的力,作用在流体单位面积上 的剪切力称为剪应力。 压强和剪应力的单位均为N/m2或Pa。
p
或
+ gz = 常数
p1 p + gz1= 2+ gz2
p0 …(2) 1-15a …(3) 1-15b p h
p2=p1+g(z1-z2)
p=p0+gh
(1)(2)(3)三式为流体静力学基本方程式
静力学方程的讨论:
1 适用范围:仅适用于静止的、不可压缩性流体在重力场
中的情况,且为连续的同一流体。如气体, p 变化不大,
因为p0=p0´, 所以
pa pb = R( A B ) g
注意: (1) 静压强也有基准, 在同一计算中,应注意用统一的压强基准;
(2) 压力基准可以任意选取,但选定后计算中通常不能随意改变;
