长沙理工大学水力学考研复习资料第八章 明槽恒定非均匀流1
第九章 明渠恒定非均匀流

dh ( ) = = Fr 3 ds 2g gA ds ds
2
3.dhw/ds为单位距离的水头 3.dhw/ds为单位距离的水头 损失,即水力坡度.近似用 谢才公式计算:
dhw Q =J = 2 ds K
2
将以上三个关系式代入式(9.1),有 将以上三个关系式代入式(9.1),有
dh dh Q2 i + Fr2 + 2 = 0 ds ds K
M1 型水面曲线两端的趋势: 型水面曲线两端的趋势: 上游: 上游: 水深减小,h→ho,则K→K0,1水深减小,h→ho,则K→K0,1-(K0/K)2 0; h>hc,1- >0,所以dh/ds→ h>hc,1-Fr2>0,所以dh/ds→ 0 . 这表明 M1 型水面线上游以 N-N 线为渐近线.在理论 上,Ml 型水面曲线上端与正常水深线在无穷远处重合,但 型水面曲线上端与正常水深线在无穷远处重合, 在实践中,可假定在有限距离内与正常水深线相重合, 在实践中,可假定在有限距离内与正常水深线相重合,一般 认为在 h =(1.01~1.05 )ho处重合. ho处重合. 下游: 下游: h→∞,则K→∞,1 h→∞,则K→∞,1-(K0/K)2 1; Fr2 0,1- Fr2 1,所以dh/ds→i. 0,11,所以dh/ds→ 这表明 MI 型水面线下游以水平线为渐近线. Ml型水面线是上,下游分别以正常水深线和水平线为渐 Ml型水面线是上,下游分别以正常水深线和水平线为渐 近线,水深沿程增加的一条下凹形的曲线, 近线,水深沿程增加的一条下凹形的曲线,见图 9.7(a). 9.7(a). 在缓坡明渠上修建闸,坝挡水, 在缓坡明渠上修建闸,坝挡水,如闸,坝前水深被抬高至 正常水深以上, 正常水深以上,则闸,坝上游明渠中将形成 Ml 型水面线. 如图 9.7(b) 所示.
水力学辅导材料6

水力学辅导材料6:一、第6章明槽恒定流动(1)【教学基本要求】1、了解明槽水流的分类和特征,了解棱柱体渠道的概念,掌握明槽底坡的概念和梯形断面明渠的几何特征和水力要素。
2、了解明槽均匀流的特点和形成条件,熟练掌握明槽均匀流公式,并能应用它来进行明渠均匀流水力计算。
3、理解水力最佳断面和允许流速的概念,掌握水力最佳断面的条件和允许流速的确定方法,学会正确选择明渠的糙率n值。
4、掌握明槽均匀流水力设计的类型和计算方法,能进行过流能力和正常水深的计算,能设计渠道的断面尺寸。
5、掌握明渠水流三种流态(急流、缓流、临界流)的运动特征和判别明渠水流流态的方法,理解佛汝德数Fr的物理意义。
6、理解断面比能、临界水深、临界底坡的概念和特性,掌握矩形断面明渠临界水深h k 的计算公式和其它形状断面临界水深的计算方法。
【内容提要和学习指导】这一章是工程水力学部分内容最丰富也是实际应用最广泛的一章。
本章有4个重点:明渠均匀流水力计算;明渠水流三种流态的判别;明渠恒定非均匀渐变流水面曲线分析和计算,这部分也是本章的难点;水跃的特性和共轭水深计算。
学习中应围绕这4个重点,掌握相关的基本概念和计算公式。
这一讲我们讨论前2个问题,后面2个问题将放在第7讲讨论。
明渠水流的复杂性在于有一个不受边界约束的自由表面,自由表面能随上下游的水流条件和渠道断面周界形状的变化而上下变动,相应的水流运动要素也发生变化,形成了不同的水面形态。
6.1 明槽和明槽水流的几何特征和分类(1)明槽水流的分类明槽恒定均匀流明槽恒定非均匀流明槽非恒定非均匀流明槽非恒定均匀流在自然界是不可能出现的。
明槽非均匀流根据其流线不平行和弯曲的程度,又可以分为渐变流和急变流。
(2)明槽梯形断面水力要素的计算公式:水面宽度 B = b +2 mh (6—1) 过水断面面积 A =(b + mh )h (6—2) 湿周 (6—3) 水力半径 (6—4) 式中:b 为梯形断面底宽,m 为梯形断面边坡系数,h 为梯形断面水深。
水力学专题 明渠非恒定流

z z z z zw zw udz vdz u w v w w u b v b w 0 z z x b y b y y x z z w x z zb
结合边界条件:
z w (hu ) (hv ) 0 t x y
三、水波的分类 明渠非恒定流是一种具有自由水面的波动 (一)按主要作用力分 重力波(gravitational wave) :主要恢复力为重力――洪水波 表面张力波(capillary wave) :风波成长初期的涟波 压力波(compression wave) : (少见――水下爆破引起等) (二)按质点运动方式分 振动波:波运动时,其水质点沿封闭的轨迹运动――海洋波浪 运行波:波运动时,水质点不断行进――洪水波
u
z zw
u
v
w
z zw udz u w z x b x
dw
zb x
z zb
z zw vdz v w z y b y
v
z zw
zb y
z zb
zw
zb
w dz 0 z
w w w dx dy dz x y z
这里,我们只给出了两个方向的动量方程,z 方向的动量方程省去了。事实 上,由于垂向上的加速度和重力加速度相比可以忽略,垂向的速度 w 很小,所以
w 亦可以忽略。因此,垂向上的重力加速度和压力梯度平衡:
p g z
直接积分得: p g ( z w z )
一般地,河道中的水流均为紊流,所以要研究河流中的平均运动,就要用 雷诺时均方程,雷诺时均方程和 NS 方程相比,只是增加了紊动切应力项。 由于脉动流速在各方向上具有相同的数量级,所以雷诺应力在各方向上也 具有相同的数量级。但只是他们的梯度出现在方程中,而雷诺应力在垂向变化的 距离比纵向和横向上的小得多,故垂向上的梯度变化是最重要的。 鉴于此,描述自由表面流动的雷诺方程可简化为:
SHL8水力学

作用在控制面液体上的力只有∑F,则
F y1 A1 y2 A2
在单位时间内,控制面ABDCA内的液体动量增量为
Q
g (v2 v1)
按恒定总流的动量方程,则有
Q
g
v2
v1
y1 A1
y2
A2
整理后得
Q 2
gA1
y1 A1
Q 2
gA2
y2 A2
棱柱形渠道完整水跃基本方程
明渠均匀流和非均匀流
当i , n及d一定,无压圆管均匀流的平均流速最大值vmax在 θ=257º30’处,相应的水深h=0.81d(即充满度α=0.81)。
明渠均匀流和非均匀流
2、无压管道的计算问题
过流断面面积:A d 2 ( sin )
8
湿周: d
2
水力半径:R
d 4
1
s in
充满度: h sin2
水流在无压圆管中的充满度
r
h d
h d
无压圆管水力最优状况计算, 就是求其输水性能最优时的水流 充满度可根据水力最优条件导出
明渠均匀流和非均匀流
当水深h超过半径时,过水能力最强,据均匀流的计算
公式有
Q
Av
A
1
2
R3
J
1 2
n
5
i n
A3
2
3
过流断面积:A d 2 ( sin )
8
湿周: d
结论:
1) Rmax
h 2
明渠均匀流和非均匀流
A (b mh)h R
b 2h 1 m2
b 2( 1 m2 m) h
Rmax
h 2
2) 矩形最优水力断面 b 2h
流体力学第8章 明渠流动

产生明渠均匀流的条件: 水流应为恒定流。流量应沿程不变,即无支流。 渠道必须是长而直的棱柱体顺坡明渠,粗糙系数沿
程不变。另外渠道中无水工建筑物的局部干扰。
明渠均匀流的特性
加速运动 均速运动 Ff < Gs 加速运动 Ff = Gs
d 2
θ
h
d
采用曼宁公式计算谢才系数,则当i,n和d一定时,得
Q f ( A, ) f ( )
说明流量Q仅为充满角的函数。
dQ d i A5/ 3 d ( sin )5/ 3 0 2/ 3 d d n d 从而 1 5 cos 2 sin 0 解得 308 3 3
acri2121aabhbmhh212212121bmhhmh因为所以存在极小值此时最优梯形断面的宽深比最优梯形断面的水力半径渠道的允许流速是根据渠道所担负的生产任务如通航水电站引水或灌溉渠槽表面材料的性质水流含沙量的多少及运行管理上的要求而确定的技术上可靠经济上合理的流速
主要内容: 明渠的几何特性 明渠均匀流的特性 明渠均匀流的计算公式 明渠均匀流的水力计算 水力最佳断面及允许流速 圆管中无压均匀流的水力计算
b 2( 1 m2 m) 2( 1 1.252 1.25) 0.702 h0
A (b mh0 )h0 (0.702 1.25) h02
1 1 1 2 h0 1/2 8/3 Q 1.952h0 i 2/3 1.952 i1/2 h0 n n 2 2 3/8 2/3 2 Qn h0 1.486m 1/ 2 1.952 i
水力学教学课件ppt作者裴国霞唐朝春7,8,9章第九章明渠恒定非均..
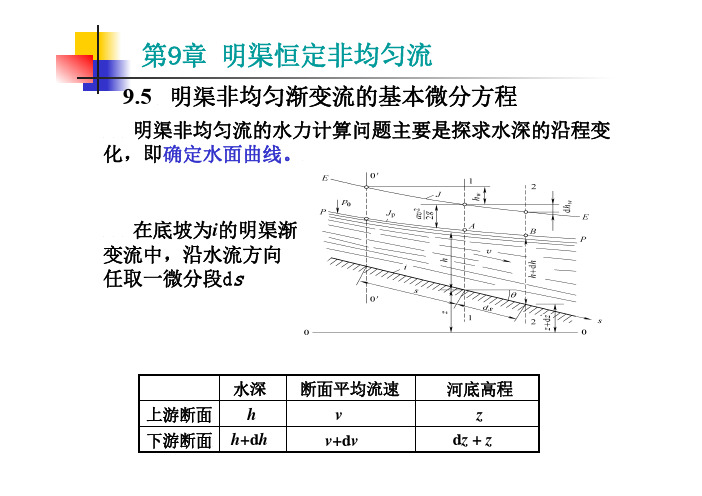
9.5 的明渠渐 d z + zv+d vzv河底高程断面平均流速对微小流段建立能量方程idsdz -=1)θsin =i dsdzds z z -=-=219.6 明渠非均匀渐变流水面曲线分析区号1:h cr 2:h cr 3:h cr各区编号M 1M 2M 3N CNcrh 0h cri i < 陡坡上均匀流K K NNcrh 0h 1s 2s 3s CC N N cri i >i = i crN N ,C C,N crh h 03c 1c 平坡渠道i = 0crh 3h逆坡渠道i < 0Ccrh 2A 3A 2A 水面曲线形式9.6.1⒈S 3S 1S 2NC C cri i > ⒉ 陡坡渠道( )cr i i >表 陡坡水面线类型及特性h h →h h →控制水深壅水急流降水 水平线壅水 缓流急流 下游趋向上游趋向 水面形态 流态 水跃 控制水深、水跌i=2H3i = 0表 平坡水面线类型及特性A 2i < 0CC A 30<i 表 逆坡水面线类型及特性当h→ 时,与C-C线有成垂直的趋势;cr h 9.6.4 水面曲线的共性与绘制步骤 ⒈ 水面曲线的共性1、3区为壅水曲线;2区为降水曲线当h→h 0时,以N-N线为渐近线;当h→∞时,以水平线为渐近线每一区域内只有相应的一条水面曲线● 渠道水面线总结⏹ 1 区水面线均为壅水曲线⏹ 2 区水面线均为降水曲线⏹ 3 区水面线均为壅水曲线⏹ 水面线通过 C-C线产生水跃或水跌⏹ 水面线:起始:N-N线,或水库水面⏹ 回落:N-N线,或水库水面,或临界水深⏹ 中间:符合12种水面曲线的变化规律⏹画水面线必须表明水面的类型号例9.7 明渠非均匀渐变流水面曲线的计算Wh 渐变流水头损失仅考虑沿程水头损失fW h h ∆≈∆明渠均匀流l∆Ji g e l -∆=∆/这就是分段计算水面曲线的有限差式,称为分段求和法公式。
分段求和法计算水面曲线的步骤:9.7.23)由控制断面向下游(或上游)取给定的 ,便可定出断。
第九章(明渠恒定非均匀流)
第九章 明渠恒定非均匀流一.明渠非均匀流的特征:◆1.重力在流动方向的分力与阻力不平衡。
◆2.流速与水深沿程发生变化。
◆3.水面线一般为曲线 。
◆4.水力坡度J 、水面坡度Jp 和渠道底坡i 互不相等。
二.明渠非均匀流的几种流动现象:1.壅水现象:水深沿程增加,流速沿程减小,这种现象称为壅水现象。
相应的水面曲线 称为壅水曲线。
2.降水现象:水深沿程减小,流速沿程增大,这种现象称为降水现象。
相应的水面曲线称为降水曲线。
三.本章主要研究的问题:在明渠恒定非均匀流中,确定断面水深和水面曲线。
§9-1 明渠水流的三种流态、佛汝德数一.微小扰动波的波速C :在平底(i=0)棱柱形明渠中,液体静止,外界引起的干扰微波向左右传波。
现以随波峰向左移动、速度为C 的运动作标系来看:相对于这个坐标系,水流以速度C 向右运动(波峰固定不动),流动为恒定流,如图所示。
对相距很近的1—1和2—2断面列伯努利方程(不计损失),有:g V αγp h h g V αγp h a a 22222211++∆+'=++'C V αα===1210.1注意到:取又,由连续性方程,有: ()dA A V A V A V +==122211dAA A CdA A A V V +=+=∴111112 ()212212212121212212122222222B dAA B A B A g C h dAA A A g C h dA A A g C h g C ++∆=++∆=++∆=∴即为渠中水深。
)(显然,对于矩形断面。
为过流断面的平均水深引入:m m h BA h 1=hh h h g C h g C m m m ∆++∆=∴2222222 h g gh C m ∆+=22整理得:m gh C h =→∆20有:时,当mgh C =∴二.明渠水流的三种流态:1.当V>C 时,液体所遇到的扰动不能向上游传播,这种流动,称为急流。
水力学第八讲
渐进关系: 渐进关系: h → 0 ⇒ A → 0 ⇒
αQ 2
2 gA
2
→ ∞ ⇒ ES → ∞
h→∞⇒ A→∞⇒
αQ 2
2 gA
2
→ 0 ⇒ ES → h
比能随水深增加而增加; 上半枝 dE S / dh > 0 ,比能随水深增加而增加; 比能随水深减小而增加; 下半枝 dE S / dh < 0 ,比能随水深减小而增加;
Hale Waihona Puke 在 n < 0.020 和 R < 0.5m 应 用
1 16 效果较好, C = R n
在水深较大或宽阔水域时,
1 16 C= h n
§ 8-3恒定均匀流基本公式 恒定均匀流基本公式 • 3巴甫洛夫斯基 巴甫洛夫斯基(H. H. aВЛОВСКИЙ) 公式 巴甫洛夫斯基
1 y C= R n
y = 2.5 n − 0.13 − 0.75 R ( n − 0.1)
dE S = 0 :即 E S min 对应的 hK 满足临界水深的条件是 dh
3 dE S αQ 2 αQ 2 AK = 1− B = 0得 = 由 3 dh g BK gA
①矩形断面临界水深: BK = b , AK = bhK 得 hK = 3 矩形断面临界水深: 临界水深 ②梯形断面临界水深: AK = (b + mhK ) hK , BK = 梯形断面临界水深: 临界水深
§ 8-6无压圆管均匀流的水力计算 无压圆管均匀流的水力计算 • 1无压圆管的水力要素 无压圆管的水力要素 • 充满度:水深与管径的比值; 充满度:水深与管径的比值;
h α= d
• 充满角:湿周所对的圆心角; 充满角:湿周所对的圆心角;
明渠恒定流(均匀流与非均匀流)之欧阳治创编
水力学教案第六章明槽恒定流动【教学基本要求】1、了解明槽水流的分类和特征,了解棱柱体渠道的概念,掌握明槽底坡的概念和梯形断面明渠的几何特征和水力要素。
2、了解明槽均匀流的特点和形成条件,熟练掌握明槽均匀流公式,并能应用它来进行明渠均匀流水力计算。
3、理解水力最佳断面和允许流速的概念,掌握水力最佳断面的条件和允许流速的确定方法,学会正确选择明渠的糙率n值。
4、掌握明槽均匀流水力设计的类型和计算方法,能进行过流能力和正常水深的计算,能设计渠道的断面尺寸。
5、掌握明渠水流三种流态(急流、缓流、临界流)的运动特征和判别明渠水流流态的方法,理解佛汝德数Fr的物理意义。
6、理解断面比能、临界水深、临界底坡的概念和特性,掌握矩形断面明渠临界水深h k的计算公式和其它形状断面临界水深的计算方法。
7、了解水跃和水跌现象,掌握共轭水深的计算,特别是矩形断明渠面共轭水深计算。
8、能进行水跃能量损失和水跃长度的计算。
9、掌握棱柱体渠道水面曲线的分类、分区和变化规律,能正确进行水面线定性分析,了解水面线衔接的控制条件。
10、能进行水面线定量计算。
11、了解缓流弯道水流的运动特征。
【内容提要和教学重点】这一章是工程水力学部分内容最丰富也是实际应用最广泛的一章。
本章有4个重点:明渠均匀流水力计算;明渠水流三种流态的判别;明渠恒定非均匀渐变流水面曲线分析和计算,这部分也是本章的难点;水跃的特性和共轭水深计算。
学习中应围绕这4个重点,掌握相关的基本概念和计算公式。
明渠水流的复杂性在于有一个不受边界约束的自由表面,自由表面能随上下游的水流条件和渠道断面周界形状的变化而上下变动,相应的水流运动要素也发生变化,形成了不同的水面形态。
6.1 明槽和明槽水流的几何特征和分类(1) 明槽水流的分类明槽恒定均匀流明槽恒定非均匀流(包括渐变流和急变流)明槽非恒定流明槽非恒定流一定是非均匀流。
明槽非均匀流根据其流线不平行和弯曲的程度,又可以分为渐变流和急变流。
明渠非均匀流计算公式
明渠非均匀流计算公式
明渠非均匀流是指在明渠水流中,由于底坡、流量、水深等因素的变化,导致流速分布不均匀,水力要素(如水深、流速、压强等)沿程发生变化的流动。
这种流动状态在水力学中是很常见的,特别是在天然河流和人工渠道中。
明渠非均匀流的计算公式主要是用来描述这种流动的水力要素沿流程的变化规律。
这些公式通常基于水力学的基本原理,如伯努利方程、连续性方程等,并结合明渠的具体条件进行推导。
下面给出两个明渠非均匀流的计算公式示例:
1.水深沿程变化公式:
2.当明渠中的水流受到阻力作用时,水深会沿流程减小。
这个变化可以用以
下公式描述:
3.$\frac{dh}{dx} = -\frac{Q}{A}\left(\frac{1}{\sqrt{1+S^2}} +
\frac{f}{1+S}\right)$
4.其中,$h$ 是水深,$Q$ 是流量,$A$ 是过水面积,$S$ 是底坡,$f$ 是
阻力系数。
这个公式可以帮助我们了解水流的水深如何随着流程而变化。
5.断面平均流速公式:
6.在明渠非均匀流中,断面平均流速是重要的水力要素。
这个量可以用以下
公式计算:
7.$\bar{v} = \sqrt{\frac{Q}{\pi r^2 h}}$
8.其中,$\bar{v}$ 是断面平均流速,$r$ 是水力半径(即过水面积与湿周之
比),$h$ 是水深。
这个公式可以帮助我们了解水流的速度是如何分布的。
以上两个公式只是明渠非均匀流计算中的一部分,实际上还有许多其他的公式和模型可以用来描述这种流动。
这些公式和模型的选择取决于具体问题的条件和要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2
(b) 流速v < c
c=
gh
边随水流向下游运动。
棱柱形平坡渠道静止水体中的微幅波波速
v
v
(c) v > c
(d) v = c
波动不能向上游传播。 明槽中,其微幅波与两侧壁面的反射波叠加,在远处近似为平面波。
假设波速、波高保持不变,取一运动惯性参考系随波峰一起移 动,相对运动呈恒定非均匀流动 水深 过水断面面积 相对流速 断面1 h A v1=c 断面2 h+Δh A+ΔA v2 = cA/(A+ΔA) 能量方程
15
临界坡度的计算式 i K =
gχ K Q2 = 2 2 2 AK CK R K αC K BK
若用曼宁公式计算CK ,得
iK =
gn 2 χ K 13 αR K BK
(长度单位均为m,g单位为m·s-2)
iK的大小与流量、糙率和断面形状及尺寸有关: 其它条件相同,糙率n越大,iK越大; 流量增加, iK是增是减,与断面形状、流量和临界水深的大小有关。
第八章
明槽恒定流动
第三节 明槽恒定渐变流
单一波源在等深度无穷大静止水域中产生的微幅扰动波以波源为 圆心呈同心圆状向四周扩展
一、微幅扰动波与明槽流态
c
使水流偏离均匀流的因素:流量、断面、底坡 和糙率的沿程变化,水流中的建筑物和障碍物 = 对水流的干扰
c c
(a) 静水中
c
v
c- v
c+v
扰动以重力表面波的形式向上、下游ห้องสมุดไป่ตู้播 ――扰动波,所到之处 使水深、流速等发生变化。 微幅波:水深波幅Δh << 原水深h; 有限幅度波(断波):其波幅与原水深为同一数量级或更大。 在流速为v的动水中,固定波源产生的圆形波面一边扩展,一 浅水长波理论: 大水体中微幅波传播速度
v v = = Fr c gA B
c≈ g
A B
(3)v = c ,即Fr =1时,称为临界流(Critical flow),逆行波 停驻在波源,急流、缓流的分界点。 弗劳德数代表水流惯性力与重力作用之比,缓流时,重力作用大 于惯性力作用;急流时,惯性力作用则占上风。
为一弗劳德数。
Fr =
5
矩形断面明槽
例 8 -5
一梯形断面渠道,b =10 m, m =1.0,当Q = 12 m3/s时, h0 =1.0 m,问该渠道是缓坡渠道还是陡坡渠道?
解: 均匀流时 A =(b + mh0)h0 = (10 + 1×1)×1 = 11 m2 B=b+2mh0= 10 + 2×1×1 = 12 m, 则
Fr =
v = Q / A = 1.09 m/s
v = 1.09 / 9.8 × 11 / 12 = 0.364 < 1 gA B
陡坡、缓坡,只与均匀流的急、缓流有对应关系,与非均匀流流态无关
17
均匀流流态为缓流,所以i < iK,为缓坡。
18
不是小底坡的情况下的有关方程和表达式 dES αQ 2B = cos θ − ≈ 1 − Fr 2 cos θ dh gA 3
16
五.小结
明槽水流(均匀流或非均匀流)流态的判别
判别指标 水深 h Fr 流速 v 缓流 h > hK Fr < 1 v<c 临界流 h = hK Fr = 1 v = 微幅波波速 c 急流 h < hK Fr > 1 v>c
例8-4 一矩形断面渠道,宽度b =5 m,流量Q =30 m3/s,水深h =1.0 m,判断此时明槽流动的流态。 Q 30 v 解: Fr = = = = 1.917 > 1 gh bh gh 5 × 1× 9.8 × 1 或 急流
当ES一定时,求极值
g (2E S − 3h ) gh dq = 2g (E S − h ) / α − = =0 dh 2g (E S − h )α 2g (E S − h )α
得
h = 2ES /3 = hK (极大值点)。
在断面形状尺寸一定时,Q越大,hK越大; 当流量一定时,断面越宽,临界水深越小。
v gh
6
二.明槽恒定流动的基本方程与断面比能 明槽恒定非均匀流 J≠i,不能用明槽均匀流的基本公式。 明槽恒定渐变流总水头 = 水面高程(水位)z +αv2/2g 明槽恒定流动的能量方程
ES = h cos θ +
αv 2 αQ 2 = h cos θ + 2g 2gA 2
断面比能形式的明槽恒定流动能量方程
v
c-v
c+v
h+
c2 c2 ⎛ A ⎞ = h + Δh + ⎜ ⎟ 2g 2g ⎝ A + ΔA ⎠
4
2
3
ΔA≈BΔh,得
微幅扰动波向上游传播(逆行波)的绝对波速= c - v
2
c= g
A B
(1 + ΔA / A )
(1)v < c,即Fr <1时,这种流态称为缓流(Subcritical flow), 下游的扰动可以影响上游,水力要素受下游水流条件影响;
10
ES = h +
αv 2 αQ 2 =h + 2g 2gA 2
存在一个极小值点hK
棱柱形明槽A=A(h), 当流量给定时ES =ES (h)
dE S dE S dh = =i− j ds dh ds
dES αQ dA αQ B = 1− = 1− dh gA 3 dh gA 3
2 2
αQ B αv = ≈ Fr 2 gA / B gA 3
7
h zb
hcosθ
dE S =i −J ds
均匀流: i = J , dES /ds = 0 ,ES 沿程不变; 非均匀流:i > J 时 ES 沿程增加;i < J 时ES 沿程减少。
8
以下分析和推导仅限于棱柱形明槽和小底坡的情况。 小底坡时,cosθ≈1,
三.临界水深
h ~ ES曲线图 临界水深(Critical depth) = 给定流量,同一个断面 上断面比能为最小值的水 深。 (1)h > hK时(曲线上支), dES /dh > 0,Fr <1,明 槽流态为缓流; (2)h < hK时(曲线下支),dES /dh < 0,Fr>1,流态为急流; (3)h = hK时(极值点),dES /dh = 0,Fr =1,流态为临界流。 ◆一个ES值对应缓流、急流两个水深: 交替水深(Alternate depths)
2 2
棱柱形明槽恒定渐变流的基本微分方程式
9
dh i−J = ds 1 − Fr 2
hK满足方程
1−
αQ 2 B K =0 或 3 gA K
3 AK αQ 2 = BK g
(4)矩形断面 B = b,A = hb (单宽流量q = Q / b) 且 h = hK时
得
hK = 3
αq 2 g
( AK=A(hK),BK=B(hK) ) 已知Q、断面形状尺寸、α,求解hK (1)迭代法或二分法,计算机程序(第六节)或Excel (2)试算法(手算) (3)梯形断面的情况,迭代计算式可用(手算或Excel)
13
14
四.临界坡度 已知流量、糙率和断面形状尺寸,正 常水深h0随着底坡i的增大而减小。
当i=iK时,h0=hK ,A=AK、C=CK、R=RK、χ=χK、B=BK , 同时满足
Q = AK C K R K i K
3 AK αQ 2 = BK g
顺坡渠道(i > 0)的底坡有三种情况: (1)临界坡(Critical slope): i = iK,此时h0=hK ,均匀流流态 为临界流。 (2)缓坡(Mild slope):i < iK,此时h0>hK ,均匀流流态为缓流; (3)陡坡(Steep slope):i > iK,此时h0<hK ,均匀流流态为急流;
h K = 3 αq 2 g = 3 1.0 × (30 5) 9.8 = 1.543 m > h
2
顺 坡 明 槽 ( i > 0) 的 底 坡 类 型 与 流 态
判别指标 正 常 水 深 h0 底坡 i 均匀流流态 非均匀流流态 缓坡 h0 > hK i < iK 缓流 临界坡 h0 = hK i = iK 临界流 均有可能 陡坡 h0 < hK i > iK 急流
(
)
Fr =
dh 1 i −J = ⋅ ds cos θ 1 − Fr 2
cos θ − αQ 2 B k
3 gAk
v A cos θ g B
临界水深满足的关系式
=0
矩形断面临界水深
hK = 3
αq 2 g cos θ
19
ES = ES min = h K +
αv 2 αq 2 h3 3 = hK + = h K + K2 = h K 2 2g 2gh K 2h K 2
2 E S min 3
所以矩形断面明槽 h K = 反之
hK
(n +1)
⎡ αQ 2 (n ) ⎤ =⎢ b + 2mh K ⎥ g ⎣ ⎦
(
)
1
3
1 (n ) b + mh K
z
z1 +
αv αv = z 2 + 2 + h w1− 2 2g 2g
2 1 1 2 2
可以用来求解水位z的沿程变化。 两个断面应是渐变流断面,但断面1、2之间可以有急变流段。 z = z b + h cosθ 定义:断面比能 ( Specific energy) ES = 总水头-zb (槽底为基准面的总水头)
