2016-2017年广东省揭阳市普宁市华侨中学高一上学期期中数学试卷带答案
广东省普宁市华侨中学2016-2017学年高一上学期第二次月考数学试题 含答案

普宁市华侨中学2016—2017学年度上学期第二次月考高一数学试题注意事项:1.本试题共4页,满分150分,考试时间90分钟.2.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号等相关信息填写在答题卷密封线内,并在“座位号"栏内填写座位号。
3。
所有题目必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷上各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.)1.在“①高一数学课本中的难题;②所有的正三角形;③方程的实数解"中,能够表示成集合的是()A.②B.③C.②③D.①②③2。
设集合,为实数,为整数集,则()A.B.C.D.3.已知,则() A.B.C.D.4.以下六个关系式:①,②,③,④,⑤,⑥是空集,其中错误的个数是()A.4 B.3 C。
2 D.15.集合,,,且,,则有()A.B.C。
D.不属于中的任意一个6。
已知集合,则的子集个数为()A.8 B.2 C。
4 D.77。
已知全集,则集合中元素的个数为()A.2 B.3 C.4 D.58。
设全集,集合,,则下列图中的阴影部分表示集合的是( )A.B.C。
D.9。
定义在上的偶函数满足:对任意的,有,且,则不等式的解集是()A.B.C.D.10。
若函数,且对实数,则()A.B.C.D.与的大小不能确定11。
函数对任意正整数满足条件,且,则()A.B.C.D.12.在上定义的函数是偶函数,且.若在区间上的减函数,则()A.在区间上是增函数,在区间上是增函数B.在区间上是减函数,在区间上是减函数C.在区间上是减函数,在区间上是增函数D.在区间上是增函数,在区间上是减函数二、填空题(本大题共4小题,每小题5分,共20分. 把答案填在答题卡内.)13.已知集合M={0,x},N={1,2},若M∩N={1},则M∪N=______.14.若函数f(x)=是奇函数,则a+b=______.15.已知函数f(x)=x2+4mx+n在区间上是减函数,求实数m的取值范围________.16.如果函数f(x)=是奇函数,则a=__________.三、解答题(本大题共6小题,17题10分,18—22题12分.解答时应写出必要的文字说明、证明过程或演算步骤)17.已知函数f(x)=ax+(其中a,b为常数)的图象经过(1,2),(2,)两点.(1)求函数f(x)的解析式;(2)判断f(x)的奇偶性.18.已知圆心为C的圆过点A(0,﹣6)和B(1,﹣5),且圆心在直线l:x﹣y+1=0上.(1)求圆心为C的圆的标准方程;(2)过点M(2,8)作圆的切线,求切线方程.19.斜三棱柱A1B1C1﹣ABC中,侧面AA1C1C⊥底面ABC,侧面AA1C1C 是菱形,∠A1AC=60°,AC=3,AB=BC=2,E、F分别是A1C1,AB 的中点.(1)求证:EF∥平面BB1C1C;(2)求证:CE⊥面ABC.(3)求四棱锥E﹣BCC1B1的体积.20.已知函数f(x)=1﹣在R上是奇函数.(1)求a;(2)对x∈(0,1],不等式s•f(x)≥2x﹣1恒成立,求实数s的取值范围;(3)令g(x)=,若关于x的方程g(2x)﹣mg(x+1)=0有唯一实数解,求实数m的取值范围.21.已知函数(1)若函数在的单调递减区间(—∞,2],求函数在区间上的最大值.(2)若函数在在单区间(—∞,2]上是单调递减,求函数的最大值.22.已知函数.(1)求证:函数在R上为增函数;(2)当函数为奇函数时,求函数在上的值域.21。
广东省普宁市华侨中学高一数学上学期期中试题

普宁华侨中学2016-2017学年度第一学期期中考试高一数学试题一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{}1,2,3,4,5U =,集合{}1,4M =,{}1,3,5N =,则()UN M ⋂=( ). A.{}1,3 B. {}3,5 C. {}1,3,5 D. {}4,5 2.下列四组函数中,表示相等函数的一组是( ).2.(),()A f x x g x x ==22.(),()()B f x x g x x == 21.(),()11x C f x g x x x -==+- 2.()11,()1D f x x x g x x =+-=-3.函数22)(2+-=x x x f 在区间(0,4]的值域为( ).A 、]10,2(B 、 ]10,1[C 、]10,1(D 、]10,2[4.已知函数8)(35+++=cx bx ax x f ,且10)2(=-f ,则函数)2(f 的值是( ). A 、2- B 、6- C 、6 D 、8 5. 若()x x g21-=,()21log 1f g x x =⎡⎤⎣⎦+,则()1f -=( ). A . 1- B .0 C .1 D .2 6.已知()5412-+=-x x x f ,则()x f 的表达式是( ).A .x x 62+B .782++x xC .322-+x xD .1062-+x x 7.设)(x f 是R 上的偶函数,且在[)+∞,0上单调递增,则(2)f -,(3)f ,()f π-的大小顺序是( ).A .)()2()3(π->->f f fB .)3()2()(f f f >->-πC .)()3()2(π->>-f f fD .)2()3()(->>-f f f π 8.设集合{}1,0A =,集合{}2,3B =,集合{}(),,M x x b a b a A b B ==+∈∈,则集合M 的真子集的个数为( ).A.7个B. 12个C. 16个D.15个 9.已知()x f x a =(0,a >且)1a ≠在[]1,2上的最大值和最小值之和为12,则a 的值为( ). A .3 B .4 C .4- D .4-或310.定义在()1,1-上的函数()f x 是奇函数,且函数()f x 在()1,1-上是减函数,则满足()()2110f a f a -+-<的实数a 的取值范围是( ). A .[]0,1 B .()2,1- C .[]2,1- D .()0,1 11. 定义在R 上的函数)(x f 满足:①0)0(=f ,②1)1()(=-+x f x f ,③)(21)3(x f xf =,且当1021≤<≤x x 时,)()(21x f x f ≤,则)81()31(f f +等于( ). A .1 B .43 C .32 D .21 12.对于函数2()f x ax bx =+,存在一个正数b ,使得()f x 的定义域和值域相同,则非零实数a 的值为( )A . 2B .-2C .-4D .4二、填空题:本大题共4小题,每小题5分,满分20分。
广东省普宁市第一中学高一数学上学期期中试题

普宁市第一中学2016-2017学年度上学期期中考试高一数学试题一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确答案......填涂..在答题...卷.上.). 1.设集合{}101M =-,,,{}2N x x x =≤,则M N =( )A .{}0B .{}01,C .{}11-,D .{}101-,,2.设全集为R ,函数()f x 的定义域为M ,则R C M 为( )A .()2,+∞B .(),2-∞C .(],2-∞D .[)2,+∞ 3.函数2()log f x x =在区间[1,2]上的最小值是( )A .1-B .0C .1D .2 4.指数函数()(1)xf x a =-在R 上是增函数,则a 的取值范围是( )A .1a >B .2a >C .01a <<D .12a << 5.已知0.43a =,30.4b =,0.4log 3c =,则( )A .b a c <<B .c a b <<C .c b a <<D .a c b << 6. 函数()f x 是R 上的偶函数,且在[0,)+∞上单调递增,则下列各式成立的是( )A . )1()0()2(f f f >>-B .)0()1()2(f f f >->-C .)2()0()1(->>f f fD . )0()2()1(f f f >->7. 已知函数2log ,0,()2,0.x x x f x x >⎧=⎨≤⎩若1()2f a =,则a =( )A .1-BC .1-D .1或 8.若函数()y f x =是函数3xy =的反函数,则12f ⎛⎫⎪⎝⎭的值为( )A.2log 3-B.3log 2-C.199.已知212()log (2)f x x x =-的单调递增区间是( )A.(1,)+∞B.(2,)+∞C.(,0)-∞D.(,1)-∞ 10.函数1()4x f x a-=+(0a >,且1a ≠)的图像过一个定点,则这个定点坐标是( )A .(5,1)B .(1,5)C .(1,4)D .(4,1) 11.幂函数()y f x =经过点,则()f x 是( )A .偶函数,且在(0,)+∞上是增函数B .偶函数,且在(0,)+∞上是减函数C .奇函数,且在(0,)+∞上是减函数D .非奇非偶函数,且在(0,)+∞上是增函数12.已知函数12log ,0,()2,0,x x x f x x >⎧⎪=⎨⎪≤⎩若关于x 的方程()f x k =有两个不等的实根,则实数k 的取值范围是 ( )A .(0,)+∞B .(,1)-∞C .(1,)+∞D .(0,1] 一、填空题(20分,每题5分) 13.函数y =的定义域是___________.14.函数()21log 23xy x ⎛⎫=-+ ⎪⎝⎭在[]1,1-上最大值为____________.15.若函数()12x f x x=-的零点为a ,则log 2a 与log 3a 的大小关系为________________. 16.已知()f x 为R 上的奇函数,当0x >时,2()4f x x x =-.则不等式()f x x <解集用区间表示为_______________.三、解答题:本大题共6小题,满分70分。
广东省普宁英才华侨中学2016-2017学年高一上学期期中

普宁英才华侨中学2016-2017学年度上学期期中考试高一化学试题可能用到的相对原子质量:H-1C-12 N-14O-16Na—23 Mg-24 Al-27S-32 Cl-35.5K-39 Fe-56 Ca-40 Cu-64 Zn-65第Ⅰ卷选择题(共45分)一、选择题(本题包括15小题,每小题3分,共45分。
每小题只有一个选项符合题意。
)1.10月11日早上7点30分,万众瞩目的神舟十一号飞船发射成功。
其运载火箭点火后,偏二甲肼与四氧化二氮发生剧烈的氧化还原反应:(CH3)2NNH2 + 2N2O4 == 2CO2 + 4H2O + 3N2,该反应中四氧化二氮属于A.还原剂B.氧化剂C.还原产物D.氧化产物2.下列操作中溶液的导电能力变化不大的是A. Ba(OH)2溶液中滴入H2SO4溶液至过量B.向盐酸中滴加氨水C.澄清石灰水中通入CO2至恰好完全沉淀 D.NH4Cl溶液中逐渐加入NaOH固体3.下列生产、生活中的事例不属于氧化还原反应的是A.金属冶炼B.燃放鞭炮C.食物腐败D.点制豆腐4.下列有关CuSO4·5H2O的叙述正确的是A.1 mol CuSO4·5H2O的质量为250g/molB.125g CuSO4·5H2O的物质的量为0.5 molC. CuSO4·5H2O的摩尔质量为250gD.配制100mL 0.1mol/L 硫酸铜溶液需要CuSO4·5H2O 1.6g5.下列物质的水溶液能导电,但属于非电解质的是A.CH3COOH B.Cl2C.NH4HCO3D.CO26.下列不存在丁达尔效应的分散系是A.有尘埃的空气 B.纯水C.食盐水 D.向沸水中滴入FeCl3饱和溶液所得液体7.下列离子方程式正确的是:A.向氨水中滴入盐酸:OH- + H+ = H2OB.石灰乳与Na2CO3溶液反应:Ca2+ + CO32- = CaCO3↓C.向澄清石灰水中通入少量二氧化碳:Ca2++ 2OH- + CO2=CaCO3↓+ H2O△D.向沸水中逐滴滴加FeCl3饱和溶液:Fe3+ + 3H2O === Fe(OH)3↓+ 3 H+8.下列物质分类全部正确的是①纯碱②食盐水③石灰水④NaHSO4⑤液态氧⑥NaOHA.盐——①④ B.碱——①⑥ C.纯净物——③④⑤ D.混合物——②⑤9.用N A表示阿伏加德罗常数的数值,下列叙述正确的是A.等质量的O2和O3中所含分子数相等B.常温常压下,14g N2含有质子数为7N AC.标准状况下,22.4L H2含有的原子数为N AD.等质量的CO与CO2中所含碳原子数之比为7:1110.工业上制取ClO2的化学反应:2NaClO3 + SO2 + H2SO4 = 2ClO2 + 2NaHSO4,下列说法正确的是A.1mol氧化剂在反应中得到1mol电子 B.SO2在反应中被还原C.H2SO4 在反应中作氧化剂 D.NaClO3在反应中失去电子11.下列各组中的离子能在强酸性的无色溶液中大量共存的是A.Mg2+、Cl-、Al3+、SO42- B.Ba2+、Na+、SO42-、MnO4-C.K+、Cl-、HCO3-、CH3COO- D.Cu2+、NH+4、NO-3、K+12.在6KOH + 3Cl2 == KClO3 + 5KCl + 3H2O的反应中,下列说法中正确的是A.Cl2是氧化剂,KOH是还原剂B.KOH是氧化剂,Cl2是还原剂C.KCl是还原产物,KClO3是氧化产物D.被氧化的氯原子与被还原的氯原子数之比为5∶113.有下列三个反应:①3Cl2 + 2FeI2==2FeCl3 + 2I2②2Fe2+ + Br2 == 2Fe3+ + 2Br-③Co2O3 + 6HCl== 2CoCl2 + Cl2↑+ 3H2O,下列说法正确的是A.①②③中氧化产物分别是FeC12、Fe3+、C12B.根据以上方程式可以得到氧化性C12 > Co2O3 > Fe3+C.在反应③中生成1molCl2时,有2molHC1被氧化D.根据反应①②一定可以推理得到C12 + FeBr2 == FeC12+Br214.对下列实验过程的评价,正确的是A.验证烧碱溶液中是否含有Cl-,先加稀硝酸除去OH-,再加入AgNO3溶液,有白色沉淀,证明含有Cl-B.某溶液中先滴加稀硝酸酸化,再滴加几滴Ba(NO3)2溶液,生成白色沉淀,证明一定含有SO42-C.某无色溶液滴入紫色石蕊试液显红色,该溶液一定显碱性D.某固体中加入稀盐酸,产生了无色气体,证明该固体中一定含有碳酸盐15.已知常温下,在溶液中发生如下反应:①16H+ + 10Z- + 2XO4- = 2X2+ + 5Z2 + 8H2O②2A2+ + B2 = 2A3+ + 2B-;③2B- + Z2 = B2 + 2Z-。
2016-2017年广东省揭阳市普宁市华美实验学校高一上学期期中数学试卷带答案

15. (5 分)设 f(x)=ax2+bx+2 是定义在[1+a,2]上的偶函数,则 f(x)的值域 是 . (x≠0,x∈R)有下列命题:
16. (5 分)关于函数 f(x)=lg
①函数 y=f(x)的图象关于 y 轴对称; ②在区间(﹣∞,0)上,函数 y=f(x)是减函数; ③函数 f(x)的最小值为 lg2; ④在区间(1,+∞)上,函数 f(x)是增函数. 其中正确命题序号为 .
【解答】解:因为 N={x|x2≤x}={x|0≤x≤1},M={﹣1,0,1}, 所以 M∩N={0,1}. 故选:B.
2. (5 分)设全集为 R,函数
的定义域为 M,则∁RM 为(
)
A. (2,+∞) B. (﹣∞,2) C. (﹣∞,2] D.[2,+∞) 【解答】解:要使函数 则 2﹣x≥0 即 x≤2. ∴M={x|x≤2}. 则∁RM=(2,+∞) . 故选:A. 有意义,
5. (5 分)已知 a=30.4,b=0.43,c=log0.43,则( A.b<a<c B.c<a<b C.c<b<a D.a<c<b
6. (5 分)函数 f(x)是 R 上的偶函数,且在[0,+∞)上单调递增,则下列各 式成立的是( )
A.f(﹣2)>f(0)>f(1) B.f(﹣2)>f(﹣1)>f(0)C. f (1) >f (0) >f(﹣2) D.f(1)>f(﹣2)>f(0) 7. (5 分)已知函数 f(x)= A.﹣1 B. C.﹣1 或 D.1 或 ) 若 f(a)= ,则 a=( )
②2lg5+lg4+ln
19. (12 分)已知函数 f(x)=2x2﹣4x+a,g(x)=logax(a>0 且 a≠1) . (Ⅰ)若函数 f(x)在[﹣1,2m]上不具有单调性,求实数 m 的取值范围; (Ⅱ)若 f(1)=g(1) . (ⅰ)求实数 a 的值; (ⅱ)设 t3 的大小. 20. (12 分)已知函数 f(x)=log2(x+1) ,g(x)=log2(3x+1) . (1)求出使 g(x)≥f(x)成立的 x 的取值范围; (2)当 x∈[0,+∞)时,求函数 y=g(x)﹣f(x)的值域. 21. (12 分)已知函数 f(x)=loga , (a>0 且 a≠1) . ,t2=g(x) , ,当 x∈(0,1)时,试比较 t1,t2,
普宁华侨中学2016届高中毕业班文科数学第一学期期中考试试卷与参考答案
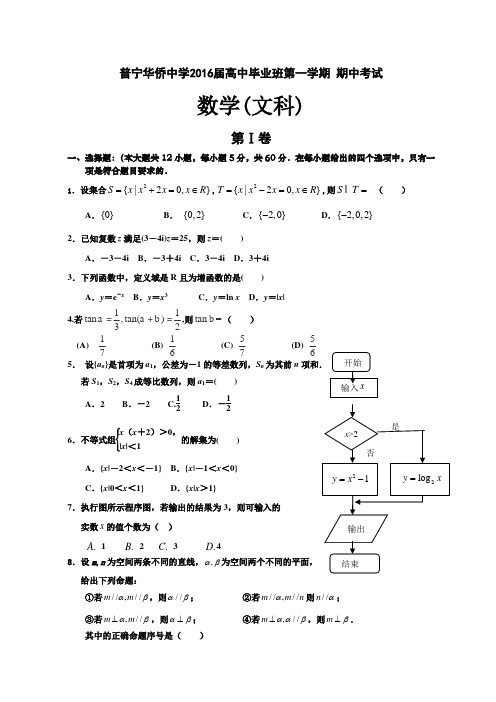
普宁华侨中学2016届高中毕业班第一学期 期中考试数学(文科)第Ⅰ卷一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|20,}Sx x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T = ( )A .{0}B . {0,2}C .{2,0}-D .{2,0,2}-2.已知复数z 满足(3-4i)z =25,则z =( )A .-3-4iB .-3+4iC .3-4iD .3+4i 3.下列函数中,定义域是R 且为增函数的是( )A .y =e -x B .y =x 3 C .y =ln x D .y =|x |4.若11tan ,tan()32a ab =+=,则tan =b ( ) (A) 17 (B) 16 (C) 57 (D) 565. 设{a n }是首项为a 1,公差为-1的等差数列,S n 为其前n 项和.若S 1,S 2,S 4成等比数列,则a 1=( ) A .2 B .-2 C.12 D .-126.不等式组⎩⎪⎨⎪⎧x (x +2)>0,|x |<1的解集为( )A .{x |-2<x <-1}B .{x |-1<x <0}C .{x |0<x <1}D .{x |x >1}7.执行图所示程序图,若输出的结果为3,则可输入的 实数x 的值个数为( ).A 1 .B 2 .C 3 .D 48.设m ,n 为空间两条不同的直线,,αβ为空间两个不同的平面,给出下列命题:①若//,//m m αβ,则//αβ; ②若//,//m m n α则//n α; ③若,//m m αβ⊥,则αβ⊥; ④若,//m ααβ⊥,则m β⊥.其中的正确命题序号是( )A .③④B .②④C .①②D . ①③9.某几何体三视图如图所示,则该几何体的体积为( )A .8-π4B .8-π2 C .8-π D .8-2π10. 已知圆C :(x -3)2+(y -4)2=1和两点A (-m ,0),B (m ,0)(m >0).若圆C 上存在点P ,使得∠APB =90°, 则m 的最大值为( )A .7B .4C .5D .611.已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F .短轴的一个端点为M ,直线:340l x y -=交椭圆E 于,A B 两点.若4AF BF +=,点M 到直线l 的距离不小于45,则椭圆E 的离心率的取值范围是( )A .B .3(0,]4C .D .3[,1)412.定义区间()[],,(,],[,),,a b a b a b a b 的长度均为d b a =-,用[]x 表示不超过x 的最大整数,记{}[],x x x x R =-∈,设[]{}()f x x x =⋅,()1g x x =-,若用d 来表示()()f x g x <的解集区间的长度,则当03x ≤≤时,有( ).A 1d = .B 2d = .C 3d = .D 4d = 第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.13. 若x ,y 满足⎩⎪⎨⎪⎧y ≤1,x -y -1≤0,x +y -1≥0,则z =3x +y 的最小值为________.14.函数y =32sin 2x +cos 2x 的最小正周期为________. 15. 已知单位向量e 1,e 2的夹角为α,且cos α=13.若向量a =3e 1-2e 2,则|a |=________.16.已知定义在R 上的奇函数 ()f x 满足 (4)()f x f x +=-,且 []0,2x ∈时,2()log (1)f x x =+,给出下列结论:① (3)1f =;②函数 ()f x 在 []6,2--上是增函数;③函数 ()f x 的图像关于直线x=1对称;④若 ()0,1m ∈,则关于x 的方程 ()0f x m -=在[-8,8]上的所有根之和为-8.则其中正确的命题为_________。
2015-2016学年广东省普宁市华侨中学高一上学期期中考试数学试卷(带解析)
绝密★启用前2015-2016学年广东省普宁市华侨中学高一上学期期中考试数学试卷(带解析)试卷副标题考试范围:xxx ;考试时间:138分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、函数上的最大值和最小值之和为,则的值为( )A .B .C .D .2、函数的零点所在的大致区间是( ) A .B .C .D .3、若指数函数在上是增函数, 则实数的取值范围是( )A .B .C .D .4、函数的图象可能是()5、若函数在上是单调函数,则的取值范围是()A. B.C. D.6、三个数大小的顺序是()A. B. C. D.7、设则()A.0 B.1 C.2 D.38、下列所给出的函数中,是幂函数的是()A. B. C. D.9、函数的定义域为()A.(,)B.,1)C.(,4)D.()(10、下列四个图形中,不是以x为自变量的函数的图象是()A. B. C.Array D.11、已知全集,集合,则为()A. B. C. D.12、若偶函数在上是增函数,则下列关系式中成立的是()A.B.C.D.第II卷(非选择题)二、填空题(题型注释)13、设,且,则____ ______.14、的值是_____ ______.15、已知,则= .16、函数的定义域是.三、解答题(题型注释)17、(本小题14分)已知函数;(1)求证:无论为何实数总是增函数;(2)确定的值,使为奇函数;(3)当为奇函数时,求的值域.18、(本题12分)已知是定义在R上的偶函数,当时,(1)求的值;(2)求的解析式并画出简图;(3)讨论方程的根的情况。
19、(本小题12分)已知函数(1)证明:函数在上是增函数;(2)求在上的值域。
2016-2017年广东省揭阳市普宁一中高一(上)期中数学试卷及参考答案
2016-2017学年广东省揭阳市普宁一中高一(上)期中数学试卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确答案填涂在答题卷上)1.(5分)设集合M={﹣1,0,1},N={x|x2≤x},则M∩N=()A.{0}B.{0,1}C.{﹣1,1}D.{﹣1,0,1}2.(5分)设全集为R,函数的定义域为M,则∁R M为()A.(2,+∞)B.(﹣∞,2)C.(﹣∞,2]D.[2,+∞)3.(5分)函数f(x)=log2x在区间[1,2]上的最小值是()A.﹣1 B.0 C.1 D.24.(5分)指数函数f(x)=(a﹣1)x在R上是增函数,则a的取值范围是()A.a>1 B.a>2 C.0<a<1 D.1<a<25.(5分)已知a=30.4,b=0.43,c=log0.43,则()A.b<a<c B.c<a<b C.c<b<a D.a<c<b6.(5分)函数f(x)是R上的偶函数,且在[0,+∞)上单调递增,则下列各式成立的是()A.f(﹣2)>f(0)>f(1)B.f(﹣2)>f(﹣1)>f(0)C.f(1)>f(0)>f(﹣2)D.f(1)>f(﹣2)>f(0)7.(5分)已知函数f(x)=若f(a)=,则a=()A.﹣1 B.C.﹣1或D.1或8.(5分)若函数y=f(x)是函数y=3x的反函数,则f()的值为()A.﹣log23 B.﹣log32 C.D.9.(5分)已知f(x)=log(x2﹣2x)的单调递增区间是()A.(1,+∞)B.(2,+∞)C.(﹣∞,0)D.(﹣∞,1)10.(5分)函数f(x)=a x﹣1+4(a>0,且a≠1)的图象过一个定点,则这个定点坐标是()A.(5,1) B.(1,5) C.(1,4) D.(4,1)11.(5分)幂函数y=f(x)经过点(3,),则f(x)是()A.偶函数,且在(0,+∞)上是增函数B.偶函数,且在(0,+∞)上是减函数C.奇函数,且在(0,+∞)是减函数D.非奇非偶函数,且在(0,+∞)上是增函数12.(5分)已知函数f(x)=,若关于x的方程f(x)=k有两个不等的实根,则实数k的取值范围是()A.(0,+∞)B.(﹣∞,1)C.(1,+∞)D.(0,1]二、填空题(20分,每题5分)13.(5分)函数y=的定义域是.14.(5分)函数y=x﹣log2(x+2)在[﹣1,1]上的最大值为.15.(5分)若函数f(x)=2x﹣的零点为a,则log a2与log a3的大小关系为.16.(5分)已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2﹣4x,则不等式f(x)<x的解集用区间表示为.三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.17.(10分)设全集U=R,集合A={y|﹣1<y<4},B={y|0<y<5},试求∁U B,A ∪B,A∩B,A∩(∁U B),(∁U A)∩(∁U B).18.(12分)设y1=a3x+1,y2=a﹣2x(a>0,a≠1),确定x为何值时,有:(1)y1=y2 ;(2)y1>y2.19.(10分)(1)解方程4x﹣2x﹣2=0.(2)求不等式log2(2x+3)>log2(5x﹣6);(3)求函数y=(),x∈[0,5)的值域.20.(12分)已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,并根据(1)写出函数f(x)(x∈R)的增区间;(2)写出函数f(x)(x∈R)的解析式;(3)若函数g(x)=f(x)﹣2ax+2(x∈[1,2]),求函数g(x)的最小值.21.(14分)已知二次函数f(x)=ax2+bx+c,(a,b,c∈R)满足,对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤(x+2)2成立.(1)证明:f(2)=2;(2)若f(﹣2)=0,求f(x)的表达式;(3)在(2)的条件下,设g(x)=f(x)﹣x,x∈[0,+∞),若g(x)图象上的点都位于直线y=的上方,求实数m的取值范围.22.(12分)已知函数f(x)=log a(x+1),g(x)=log a,(a>0且a≠1).记F(x)=2f(x)+g(x).(1)求函数F(x)的零点;(2)若关于x的方程F(x)﹣2m2+3m+5=0在区间[0,1)内仅有一解,求实数m的取值范围.2016-2017学年广东省揭阳市普宁一中高一(上)期中数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确答案填涂在答题卷上)1.(5分)设集合M={﹣1,0,1},N={x|x2≤x},则M∩N=()A.{0}B.{0,1}C.{﹣1,1}D.{﹣1,0,1}【解答】解:因为N={x|x2≤x}={x|0≤x≤1},M={﹣1,0,1},所以M∩N={0,1}.故选:B.2.(5分)设全集为R,函数的定义域为M,则∁R M为()A.(2,+∞)B.(﹣∞,2)C.(﹣∞,2]D.[2,+∞)【解答】解:要使函数有意义,则2﹣x≥0即x≤2.∴M={x|x≤2}.则∁R M=(2,+∞).故选:A.3.(5分)函数f(x)=log2x在区间[1,2]上的最小值是()A.﹣1 B.0 C.1 D.2【解答】解:∵函数f(x)=log2x在区间[1,2]上为增函数,∴当x=1时,函数f(x)取最小值0,故选:B.4.(5分)指数函数f(x)=(a﹣1)x在R上是增函数,则a的取值范围是()A.a>1 B.a>2 C.0<a<1 D.1<a<2【解答】解:∵指数函数f(x)=(a﹣1)x在R上是增函数,∴a﹣1>1,即a>2.故选:B.5.(5分)已知a=30.4,b=0.43,c=log0.43,则()A.b<a<c B.c<a<b C.c<b<a D.a<c<b【解答】解:∵a=30.4>30=1,b=0.43=0.064,c=log0.43<log0.41=0,∴c<b<a.故选:C.6.(5分)函数f(x)是R上的偶函数,且在[0,+∞)上单调递增,则下列各式成立的是()A.f(﹣2)>f(0)>f(1)B.f(﹣2)>f(﹣1)>f(0)C.f(1)>f(0)>f(﹣2)D.f(1)>f(﹣2)>f(0)【解答】解:∵f(x)是R上的偶函数,且在[0,+∞)上单调递增,∵f(﹣2)=2,且2>1>0∴f(2)>f(1)>f(0)即f(﹣2)>f(1)>f(0)∵f(﹣1)=f(1)∴f(﹣2)>f(﹣1)>f(0)故选:B.7.(5分)已知函数f(x)=若f(a)=,则a=()A.﹣1 B.C.﹣1或D.1或【解答】解:令f(a)=则或,解之得a=或﹣1,故选:C.8.(5分)若函数y=f(x)是函数y=3x的反函数,则f()的值为()A.﹣log23 B.﹣log32 C.D.【解答】解:∵函数y=f(x)是函数y=3x的反函数,∴y=f(x)=log3x,∴f()=log3=﹣log32故选:B.9.(5分)已知f(x)=log(x2﹣2x)的单调递增区间是()A.(1,+∞)B.(2,+∞)C.(﹣∞,0)D.(﹣∞,1)【解答】解:令t=x2﹣2x>0,求得x<0,或x>2,故函数的定义域为(﹣∞,0)∪(2,+∞),且f(x)=log(x2﹣2x)=g(t)=log t.根据复合函数的单调性,本题即求函数t=x2﹣2x在定义域内的减区间.再利用二次函数的性质可得函数t=x2﹣2x在定义域内的减区间为(﹣∞,0),故选:C.10.(5分)函数f(x)=a x﹣1+4(a>0,且a≠1)的图象过一个定点,则这个定点坐标是()A.(5,1) B.(1,5) C.(1,4) D.(4,1)【解答】解:令x﹣1=0,解得x=1,则x=1时,函数y=a0+4=5,即函数图象恒过一个定点(1,5).故选:B.11.(5分)幂函数y=f(x)经过点(3,),则f(x)是()A.偶函数,且在(0,+∞)上是增函数B.偶函数,且在(0,+∞)上是减函数C.奇函数,且在(0,+∞)是减函数D.非奇非偶函数,且在(0,+∞)上是增函数【解答】解:设幂函数的解析式为:y=xα,将(3,)代入解析式得:3α=,解得α=,∴y=,故选:D.12.(5分)已知函数f(x)=,若关于x的方程f(x)=k有两个不等的实根,则实数k的取值范围是()A.(0,+∞)B.(﹣∞,1)C.(1,+∞)D.(0,1]【解答】解:画出函数f(x)=的图象,和直线y=k,关于x的方程f(x)=k有两个不等的实根等价于f(x)的图象与直线有且只有两个交点.观察得出:(1)k>1,或k<0有且只有1个交点;(2)0<k≤1有且只有2个交点.故实数k的取值范围是(0,1].故选:D.二、填空题(20分,每题5分)13.(5分)函数y=的定义域是[﹣3,1] .【解答】解:由3﹣2x﹣x2≥0得:x2+2x﹣3≤0,解得:x∈[﹣3,1],故答案为:[﹣3,1]14.(5分)函数y=x﹣log2(x+2)在[﹣1,1]上的最大值为3.【解答】解:因为单调递减,y=log2(x+2)单调递增,所以函数y=﹣log2(x+2)在区间[﹣1,1]上是单调递减函数,所以函数的最大值是f(﹣1)=3.故答案为:3.15.(5分)若函数f(x)=2x﹣的零点为a,则log a2与log a3的大小关系为log a2>log a3.【解答】解:∵函数f(x)=2x﹣,∴g(x)=2x,k(x)=,k(1)=1,g(1)=2,g(x)增函数,k(x)为减函数.∴函数f(x)=2x﹣的零点为a,0<a<1∵y=log a x单调递减∴log a2>log a3故答案为:log a2>log a316.(5分)已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2﹣4x,则不等式f(x)<x的解集用区间表示为(﹣∞,﹣5)∪(0,5).【解答】解:作出f(x)=x2﹣4x(x>0)的图象,如图所示,∵f(x)是定义在R上的奇函数,∴利用奇函数图象关于原点对称作出x<0的图象,不等式f(x)<x表示函数y=f(x)图象在y=x下方,∵f(x)图象与y=x图象交于P(5,5),Q(﹣5,﹣5),则由图象可得不等式f(x)<x的解集为(﹣∞,﹣5)∪(0,5)故答案为:(﹣∞,﹣5)∪(0,5)三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.17.(10分)设全集U=R,集合A={y|﹣1<y<4},B={y|0<y<5},试求∁U B,A ∪B,A∩B,A∩(∁U B),(∁U A)∩(∁U B).【解答】解:由条件得B={y|0<y<5},从而C U B={y|y≤0或y≥5},A∪B={y|﹣1<y<5},A∩B={y|0<y<4},A∩(C U B)={y|﹣1<y≤0},(C U A)∩(C U B)={y|y≤﹣1或y≥5}18.(12分)设y1=a3x+1,y2=a﹣2x(a>0,a≠1),确定x为何值时,有:(1)y1=y2 ;(2)y1>y2.【解答】解:(1)∵y1=y2 ,∴3x+1=﹣2x,解之得:(2)因为a>1,所以指数函数为增函数.又因为y1>y2,所以有3x+1>﹣2x,解得;若0<a<1,指数函数为减函数.因为y1>y2,所以有3x+1<﹣2x,解得综上:.19.(10分)(1)解方程4x﹣2x﹣2=0.(2)求不等式log2(2x+3)>log2(5x﹣6);(3)求函数y=(),x∈[0,5)的值域.【解答】解:(1)解:原方程可化为(2x)2﹣2x﹣2=0.令2x=t,则t>0,所以t2﹣t﹣2=0,解得t=2或t=﹣1(舍).由2x=2解得x=1;(2)原不等式等价于,解得<x<3,∴原不等式的解集为();(3)令u=x2﹣4x,x∈[0,5),则﹣4≤u<5,则,即.即值域为(].20.(12分)已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,并根据(1)写出函数f(x)(x∈R)的增区间;(2)写出函数f(x)(x∈R)的解析式;(3)若函数g(x)=f(x)﹣2ax+2(x∈[1,2]),求函数g(x)的最小值.【解答】解:(1)如图,根据偶函数的图象关于y轴对称,可作出f(x)的图象,(2分),则f(x)的单调递增区间为(﹣1,0),(1,+∞);(5分)(2)令x>0,则﹣x<0,∴f(﹣x)=x2﹣2x∵函数f(x)是定义在R上的偶函数,∴f(x)=f(﹣x)=x2﹣2x∴解析式为f(x)=(10分)(3)g(x)=x2﹣2x﹣2ax+2,对称轴为x=a+1,当a+1≤1时,g(1)=1﹣2a为最小;当1<a+1≤2时,g(a+1)=﹣a2﹣2a+1为最小;当a+1>2时,g(2)=2﹣4a为最小;∴g(x)=.(16分)21.(14分)已知二次函数f(x)=ax2+bx+c,(a,b,c∈R)满足,对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤(x+2)2成立.(1)证明:f(2)=2;(2)若f(﹣2)=0,求f(x)的表达式;(3)在(2)的条件下,设g(x)=f(x)﹣x,x∈[0,+∞),若g(x)图象上的点都位于直线y=的上方,求实数m的取值范围.【解答】解:(1)由条件知:f(2)=4a+2b+c≥2成立,又另取x=2时,成立,∴f(2)=2;(2)∵,∴,4a+c=1,又f(x)≥x恒成立,即ax2+(b﹣1)x+c≥0在R上恒成立,∴a>0且△=(b﹣1)2﹣4ac≤0,,解得:,所以,(3)由题意可得:g(x)=+在[0,+∞)时必须恒成立,即x2+4(1﹣m)x+2>0在[0,+∞)时恒成立,则有以下两种情况:①△<0,即16(1﹣m)2﹣8<0,解得②,解得:,综上所述:.22.(12分)已知函数f(x)=log a(x+1),g(x)=log a,(a>0且a≠1).记F(x)=2f(x)+g(x).(1)求函数F(x)的零点;(2)若关于x的方程F(x)﹣2m2+3m+5=0在区间[0,1)内仅有一解,求实数m的取值范围.【解答】解:(1)F(x)=2f(x)+g(x)=(a>0且a≠1),要使函数F(x)有意义,则必须,解得﹣1<x<1,∴函数F(x)的定义域为D=(﹣1,1).令F(x)=0,则…(*)方程变为,∴(x+1)2=1﹣x,即x2+3x=0解得x1=0,x2=﹣3,经检验x=﹣3是(*)的增根,∴方程(*)的解为x=0,∴函数F(x)的零点为0.(2)函数在定义域D上是增函数,可得:①当a>1时,F(x)=2f(x)+g(x)在定义域D上是增函数,②当0<a<1时,函数F(x)=2f(x)+g(x)在定义域D上是减函数.因此问题等价于关于x的方程2m2﹣3m﹣5=F(x)在区间[0,1)内仅有一解.①当a>1时,由(2)知,函数F(x)在[0,1)上是增函数,∴F(x)∈[0,+∞),∴只需2m2﹣3m﹣5≥0,解得:m≤﹣1,或.②当0<a<1时,由(2)知,函数F(x)在[0,1)上是减函数,∴F(x)∈(﹣∞,0],∴只需2m2﹣3m﹣5≤0解得:,综上所述,当0<a<1时:;当a>1时,m≤﹣1,或.。
广东省普宁英才华侨中学2016-2017学年高一上学期期中考试数学试题解析(解析版)
广东省普宁英才华侨中学2016-2017学年高一上学期期中考试数学试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.在平面直角坐标系xOy 中,设直线2y x =-+与圆222(0)x y r r +=>交于,A B 两点,O 为坐标原点,若圆上一点C 满足5344OC OA OB =+,则r =A .B .5C .3 D【答案】D【解析】 试题分析:由题意可得,OA OB OC r ===设<,OA OB >=θ,θ∈[0,π]则2cos cos OA OB OA OB r θθ==∵5344OC OA OB =+ 两边同时平方可得,2222591516168OC OA OB OA OB =++即222225915cos 16168r r r r θ=++⨯∴cos θ=−35∵2cos 2cos 1,0,222θθπθ⎡⎤=-∈⎢⎥⎣⎦∴且cos 2θ>0∴cos 2θ=设圆心O 到直线x+y-2=0的距离为d ,则cos 2d r θ==r ==考点:直线与圆的位置关系2.满足的集合的个数为( )A .15B .16C .31D .32【答案】C【解析】试题分析:集合有5个元素,所以子集个数为5232=个,真子集有31个考点:集合的子集3.下列每组函数是同一函数的是( )A. 0()f x x =1)(=x f 与 B.1)(2-=x x f 与)(x f =1||-x C.24)(2+-=x x x f 2)(-=x x f 与 D.)2)(1()(--=x x x f 与 21)(--=x x x f【答案】B【解析】试题分析:A 中两函数定义域不同;B 中两函数定义域相同,对应关系相同,是同一函数;C 中两函数定义域不同;D 中两函数定义域不同考点:函数的概念4.已知函数23)13(2++=+x x x f ,则=)10(f ( )A.30B.6C.9D.20【答案】D【解析】试题分析:令3110x +=得3x =()210333220f ∴=+⨯+= 考点:函数求值5.下列各图中,不是函数图象的是( )【答案】C【解析】试题分析:由函数的概念可知每一个自变量x 值只能对应1个函数值y ,因此不能出现一对多的情况,所以C 中不能表示函数考点:函数概念及函数图像6.下列集合中,表示31x y x y +=⎧⎨-=⎩集合的是( ) A . B .C .D . 【答案】C【解析】试题分析:方程31x y x y +=⎧⎨-=⎩的解为21x y =⎧⎨=⎩,所以解集为(){}2,1 考点:集合的表示方法7.计算()2333)2(ππ-+-的值为( )A.5B. 1-C.52-πD.π25-【答案】B考点:根式运算8.若241log -=a ,则=a ( ) A.2 B.4 C.21 D.41 【答案】A 【解析】试题分析:221111log 22444a a a a -=-∴=∴=∴= 考点:指数式与对数式的转化9.计算20log 10log 25lg 2lg 55-++的值为( )A.21B.20C.2D.1【答案】C 【解析】试题分析:()255510lg 2lg 52log 10log 20lg 2lg 5log lg101220++-=++=+=考点:对数式运算10.下列图象中可作为函数)(x f y =图象的是( )A. B.C.D.【答案】C【解析】 试题分析:由函数的概念可知每一个自变量x 值只能对应1个函数值y ,因此不能出现一对多的情况,所以C 中图像能表示函数考点:函数概念及图像11.已知a =20.2,b =0.40.2,c =0.40.6,则( )A .a >b >cB .a >c >bC .c >a >bD .b >c >a【答案】A【解析】试题分析:()()0.20.20.621,0.40,1,0.40.1a b c =>=∈=∈,结合指数函数0.4x y =单调性可知b c >,所以a >b >c考点:函数性质比较大小12.函数x x f x -+=-25)(11的定义域为( )A . }21{≤<x x B.}21{≤≤x x C.}12{≠≤x x x 且 D.}10{≠≥x x x 且【答案】C【解析】试题分析:要使函数有意义,需满足10220x x x -≠⎧∴≤⎨-≥⎩且1x ≠,所以定义域为}12{≠≤x x x 且 考点:函数定义域 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.不等式1)12(log 3≤-x 的解集为 . 【答案】1(,2].2【解析】试题分析:3log (21)1x -≤化为331log (21)log 3021322x x x -≤∴<-≤∴<≤ 考点:对数不等式解法14.函数2()(1)2f x x =--的递增区间是___________________ .【答案】[1,+∞)【解析】试题分析:2()(1)2f x x =--的对称轴为1x =,函数开口向上,所以增区间为[1,+∞)考点:函数单调性15.设2()2f x ax bx =++是定义在[1,2]a +上的偶函数,则()f x 的值域是_______.【答案】[]10,2-【解析】试题分析:由偶函数性质可知()()()23320120a f x f x f x xb a ⎧=--=⎧∴∴=-+⎨⎨=++=⎩⎩,定义域为[]2,2-,所以函数最大值为()02f =,最小值为()210f =-,所以值域为[]10,2-考点:函数奇偶性及函数值域16.关于函数f(x)=lg 21x x+(x 不为0,x ∈R),下列命题正确的是________.(填序号) ①函数y =f(x)的图象关于y 轴对称;②在区间(-∞,0)上,函数y =f(x)是减函数;③函数y =f(x)的最小值为lg2;④在区间(1,+∞)上,函数y =f(x)是增函数.【答案】①③④考点:函数单调性奇偶性及函数最值三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分)已知集合A B {17},{210},{}A x x B x x C x x a =≤<=<<=<,R 为实数集。
广东省普宁市华侨中学高一数学上学期期中试题
普宁华侨中学2015-2016学年度第一学期期中考试 高一数学试卷注意事项:答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号等相关信息填写在答题卷密封线内,并在“座位号”栏内填写座位号。
所有题目必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷上各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
一、选择题:(本大题共12小题,每小题5分,共60分)1.已知全集{}0,1,2,3,4U =,集合{}{}1,2,3,2,4A B ==,则U C A B U 为( )A .{}1,2,4B .{}2,3,4C .{}0,2,4D .{}0,2,3,42.下列四个图形中,不.是.以x 为自变量的函数的图象是( ).A B C D 3.函数()()34log 1xf x x -=++的定义域为( ) A.(1-,+∞) B. [1-,1)(1,4]U C.(1-,4) D.(1,1-)U (1,4] 4.下列所给出的函数中,是幂函数的是( )A. 3-=x yB. 3x y -=C.32x y =D.13-=x y5.设()()⎪⎩⎪⎨⎧≥-<=-.2,1log ,2,2231x x x e x f x 则=))2((f f ( ) A.0 B.1 C.2 D.3 6.若偶函数)(x f 在(]1,-∞-上是增函数,则下列关系式中成立的是( ) A .)2()1()23(f f f <-<- B .)2()23()1(f f f <-<-C .)23()1()2(-<-<f f fD .)1()23()2(-<-<f f f 7. 三个数0.377,0.3,ln 0.3a b c ===大小的顺序是 ( )A .a b c >> B. a c b >> C .b a c >> D. c a b >>8.若函数2()48f x x kx =--在[5,8]上是单调函数,则k 的取值范围是( ) A .(],40-∞ B .[40,64] C .(][),4064,-∞+∞U D .[)64,+∞ 9.函数1(0,1)xy a a a a=->≠的图象可能是 ( )10. 若指数函数(23)xy a =-在R 上是增函数, 则实数a 的取值范围是( ) A. (,2)-∞ B. (,2]-∞ C. (2,)+∞ D. [2,)+∞ 11.函数2()ln(1)f x x x=+-的零点所在的大致区间是( ) A .(3,4) B .(2,)e C . (1,2) D . (0,1)12.函数]1,0[)1(log )(在++=x a x f a x上的最大值和最小值之和为a ,则a 的值为( ) A .41 B .21C .2D .4 二、填空题:(本大题共4小题,每小题5分,共20分) 13.函数1()xf x -=的定义域是 14.已知x x x f 2)12(2-=+,则)3(f = . 15. 5lg 20的值是_____ ______.16. 设25ab m ==,且,111=+ba 则m =三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步) 17.(本小题满分10分)设全集{}1,2,3,4,5,6,7,8U =,{}1,2,3A =,{}3,4,5,6B =. (1)求A B ⋃,A B ⋂,()U C A B ⋃,()U C A B ⋂; (2)求U C A , U C B .18.(本题满分10分,每小题各5分)计算下列各式 (Ⅰ)5lg )4lg 3(lg 24lg ++-(Ⅱ) 460.250382005+--)()19. (本小题12分)已知2)0(,22)(=+=f mx f x x且 ⑴ 求m 的值; ⑵ 判断)(x f 的奇偶性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11. (5 分)定义在 R 上的函数 f(x)满足:①f(0)=0,②f(x)+f(1﹣x)=1, ③f( )= f(x)且当 0≤x1<x2≤1 时,f(x1)≤f(x2) ,则 f( )+f( )等 于( A.1 ) B. C. D. ,存在一个正数 b,使得 f(x)的定义域 )
12. (5 分)对于函数 f(x)= 和值域相同,则非零实数 a 的值为( A.2 B.﹣2 C.﹣4 D.4
)
,g(x)=x+1
【解答】解:A.函数 g(x)= 相等函数. B.函数 f(x)= 是相等函数.
第 2 页(共 15 页)
19. (12 分)数列{an}的前 n 项和记为 Sn,a1=t,an+1=2Sn+1(n∈N*) . (1)当 t 为何值时,数列{an}为等比数列? (2)在(1)的条件下,若等差数列{bn}的前 n 项和 Tn 有最大值,且 T3=15,又 a1+b1,a2+b2,a3+b3 成等比数列,求 Tn. 20. (12 分)已知函数 f(x)=log2(x+1) ,g(x)=log2(3x+1) . (1)求出使 g(x)≥f(x)成立的 x 的取值范围; (2)当 x∈[0,+∞)时,求函数 y=g(x)﹣f(x)的值域. 21. (12 分)已知函数 f(x)=loga , (a>0 且 a≠1) .
4. (5 分)已知 f(x)=ax5+bx3+cx+8,且 f(﹣2)=10,则 f(2)=( A.﹣2 B.﹣6 C.6 D.8 ,则 f(﹣1)=( )
)
5. (5 分)若 g(x)=1﹣2x,f[g(x)]=log2 A.﹣1 B.0 C.1 D.2
6. (5 分)已知 f(x﹣1)=x2+4x﹣5,则 f(x)的表达式是( A.x2+6x B.x2+8x+7 C.x2+2x﹣3 D.x2+6x﹣10
二、填空题:本大题共 4 小题,每小题 5 分,满分 20 分. 13. (5 分)设 f(x﹣1)=3x﹣1,则 f(x)= 14. (5 分)函数 f(x)= 15. (5 分)化简 16. (5 分)化简(log43+log83) (log32+log92)= + 的定义域为 . (用集合或区间表示) . 的结果是 . .
2016-2017 学年广东省揭阳市普宁市华侨中学高一(上)期中数 学试卷
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选 项中,只有一项是符合题目要求的. 1. (5 分)设全集 U={1,2,3,4,5},集合 M={1,4},N={1,3,5},则 N∩ (∁UM)等于( )
(1)判断 f(x)的奇偶性,并加以证明; (2)是否存在实数 m 使得 f(x+2)+f(m﹣x)为常数?若存在,求出 m 的值; 若不存在,说明理由. 22. (12 分)已知二次函数 g(x)=mx2﹣2mx+n+1(m>0)在区间[0,3]上有最 大值 4,最小值 0. (Ⅰ)求函数 g(x)的解析式; (Ⅱ)设 f(x)= 的取值范围. .若 f(2x)﹣k•2x≤0 在 x∈[﹣3,3]时恒成立,求 k
第 3 页(共 15 页)
2016-2017 学年广东省揭阳市普宁市华侨中学高一(上) 期中数学试卷
参考答案与试题解析
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选 项中,只有一项是符合题目要求的. 1. (5 分)设全集 U={1,2,3,4,5},集合 M={1,4},N={1,3,5},(5 分)设 f(x)是 R 上的偶函数,且在[0,+∞)上单调递增,则 f(﹣2) , f(3) ,f(﹣π)的大小顺序是( A.f(3)>f(﹣2)>f(﹣π) ) B.f(﹣π)>f(﹣2)>f(3) C. ( f ﹣
2)>f(3)>f(﹣π) D.f(﹣π)>f(3)>f(﹣2) 8. (5 分)设集合 A={1,0},集合 B={2,3},集合 M={x|x=b(a+b) ,a∈A,b ∈B},则集合 M 的真子集的个数为( A.7 个 B.12 个 C.16 个 D.15 个 )
A.{1,3} B.{1,5} C.{3,5} D.{4,5} 【解答】解:全集 U={1,2,3,4,5},集合 M={1,4},N={1,3,5}, ∴∁UM={2,3,5}, ∴则 N∩(∁UM)={3,5}. 故选:C.
2. (5 分)下列四组函数中,表示相等函数的一组是( A.f(x)=|x|, C. B. D. , ,
A.{1,3} B.{1,5} C.{3,5} D.{4,5} 2. (5 分)下列四组函数中,表示相等函数的一组是( A.f(x)=|x|, C. B. D. , , ) )
,g(x)=x+1
3. (5 分)函数 f(x)=x2﹣2x+2 在区间(0,4]的值域为( A. (2,10] B.[1,10] C. (1,10] D.[2,10]
三.解答题(70 分) 17. (10 分)已知函数 f(x)=b•ax(a>0,且 a≠1,b∈R)的图象经过点 A(1, 6) ,B(3,24) . (1)设 g(x)= ﹣ ,确定函数 g(x)的奇偶性;
(2)若对任意 x∈(﹣∞,1],不等式( )x≥2m+1 恒成立,求实数 m 的取 值范围. 18. (12 分)已知全集 U={不大于 10 的非负偶数},A={0,2,4,6},B={x|x∈ A,且 x<4},求集合∁UA 及 A∩(∁UB) .
9. (5 分)已知 f(x)=ax(a>0,且 a≠1)在[1,2]上的最大值和最小值之和
第 1 页(共 15 页)
为 12,则 a 的值为( A.3 B.4
)
C.﹣4 D.﹣4 或 3
10. (5 分)定义在(﹣1,1)上的函数 f(x)是奇函数,且函数 f(x)在(﹣1, 1)上是减函数,则满足 f(1﹣a)+f(1﹣a2)<0 的实数 a 的取值范围是( A.[0,1] B. (﹣2,1) C.[﹣2,1] D. (0,1) )
