关于刚体绕瞬心的转动方程
刚体绕定轴转动及运动方程_工程力学_[共5页]
![刚体绕定轴转动及运动方程_工程力学_[共5页]](https://img.taocdn.com/s3/m/2218c6be25c52cc58ad6be38.png)
刚体的简单运动 180 第12章 由此可知
a b r r BA =+ 对时间t 求导得 d d d d d d A B r r BA t t t =+ 由于BA 是常矢量,因此d 0d BA t
= ,于是
A B v v = (12.1) 再对时间t 求一次导数得
A B a a = (12.2)
综上所述,可以得到如下结论:当刚体做平动时,其上所有点的轨迹相同;在每一瞬时,各点的速度相同、加速度也相同。
因此,刚体上任意一点的运动就可以代表整个刚体的运动,即刚体的平动可以归纳为点的运动来研究。
12.2 刚体绕定轴转动及运动方程
皮带轮、齿轮、车床上的工件等的运动都具有一个共同的特点,即在运动的过程中,体内有一条直线始终固定不动,而其余各点均绕此点做圆周运动,这种运动称刚体绕定轴的转动。
该固定不动的直线称为转轴,至于行驶的车辆的轮子,钻床的钻头的运动则不是定轴转动,因为它们的转轴并不固定,而是在运动。
12.2.1 转动方程
取转轴为z 轴。
通过轴线作一固定平面Ⅰ,
此外,通过轴线作一与刚体固连的动平面Ⅱ,如
图12-3所示。
这两个平面间的夹角用ϕ 表示,称
为刚体的转角。
转角ϕ 是一个代数量,它确定了刚体的位置,
它的符号规定为:从z 轴正向往下看,逆时针为正,
反之为负。
并用弧度(rad )表示,当刚体转动时,
转角ϕ 是时间t 的单值连续函数,即
()f t
ϕ= (12.3)
式(12.3)称为刚体的转动方程,它反映转
动刚体任一瞬时在空间的位置,即刚体的转动规律。
图12-3 刚体的移动。
刚体的简单运动—刚体绕定轴的转动(理论力学)

主轴转动两圈后停止 0
2 02 2
0 10π2 2 4π
负号表示 的转向与主轴转动方向相反,故为减速运动。
小结
1.刚体绕定轴转动 刚体运动时,有上或其扩展部分有两点保持不动,这种运动
为刚体的绕定轴转动。通过两点的直线称为转轴,不在转轴上 的各点都在垂直于转轴的平面内做圆周运动。
2.角速度
三、定轴转动的角速度和角加速度
1、角速度
lim
Δt 0
Δ Δt
d
dt
代数量 正负与转角相同
若已知转动方程 f (t)
f (t)
刚体转动的快慢和方向 单位为 rad/s
2、角加速度
设当t 时刻为 , t +△t 时刻为 +△
角加速度
lim
t 0
t
d
dt
d2
dt2
f (t)
表征角速度变化的快慢 单位:rad/s2 (代数量)
§6-2 刚体绕定轴的转动
一、刚体绕定轴转动
刚体运动时,其上或其扩展部分有两点保持不动, 这种运动为刚体的绕定轴转动。通过两点的直线称为 转轴,不在转轴上的各点都在垂直于转轴的平面内做 圆周运动。
二、转角和转动方程
____ 转角,单位弧度(rad)
=f(t)
转动方程
方向规定: 从Z轴正向看
逆时针为正
f (t) 刚体转动的快慢和方向 单位为 rad/s (代数量)
3.角加速度
f (t)
如果与同号,则转动是加速的;如果与异号,则转动是减
速的。
如果与同号,则转动是加速的; 如果与异号,则转动是减速的。
与同号,转动加速
与异号,转动减速
O
刚体的定轴转动定理和方程

Mg
TR J
T
a at R
y
J 1 MR2
mg
2
(mmM2)Rg
a 2m g T Mm g
2mM
2mM
例. 物体 m1>m2,滑轮(R,m)。阻力
矩Mf , 绳子质量忽略,不伸长、不打滑。
求重物的加速度及绳中张力
R
解: m1gT1m1a
T2m2gm2a
T1RT2RJ
aat R
JO
1 MR2 2
N
N
N
F irisin i firisiin ( m iri2)
i 1
i 1
i 1
根据内力性质(每一对内力等值、反向、共 线,对同一轴力矩之代数和为零),得:
N
firi sini 0
i1
N
N
得到: Firisini (miri2)
i1
i1
上式左端为刚体所受外力的合外力矩,以M 表
示;右端求和符号内的量与转动状态无关,称为刚
理论计算 J
miri2(分立)单位:
r2dm(连续)kg m2
例:
mr
O
dm
一质点对O点:J = m r 2
同样质量做成半径r 的圆环,对中心轴
J r2dmm 2r
m
决定转动惯量 的大小的因素
转动惯量与转轴位置有关 转动惯量与质量分布有关 转动惯量与材料性质有关
转动惯量是描述刚体对轴转动惯性大小的物理量
A1 2M d1 2J221 2J12
刚体定轴转动的动能定理:总外力矩对 刚体所做的功等于刚体转动动能的增量。
五.刚体的重力势能
对于一个不太大的质量m 为 的物体,它
刚体转动欧拉方程

刚体转动欧拉方程
【实用版】
目录
1.欧拉方程的定义
2.刚体转动的概述
3.刚体转动欧拉方程的推导过程
4.刚体转动欧拉方程的应用
5.总结
正文
1.欧拉方程的定义
欧拉方程,又称为欧拉角方程,是用来描述刚体三维旋转的数学方程。
它由三个方程组成,可以描述刚体的三维旋转,无论旋转的轴是绕哪个坐
标轴。
欧拉方程是描述刚体旋转最常用的方程。
2.刚体转动的概述
刚体转动是指在三维空间中,一个刚体围绕某个固定点或固定轴进行的旋转。
在物理学和工程学中,刚体转动是一个重要的研究对象。
对于刚体的转动,我们需要描述其旋转的速度和方向,这就需要用到欧拉方程。
3.刚体转动欧拉方程的推导过程
刚体转动欧拉方程的推导过程较为复杂,需要涉及到三维空间的旋转矩阵和角速度等概念。
在此,我们简单描述一下推导过程:首先,我们假
设刚体围绕原点旋转,旋转矩阵由三个旋转角速度组成,然后通过求导得
到欧拉方程。
4.刚体转动欧拉方程的应用
刚体转动欧拉方程在实际应用中具有广泛的应用,例如在机械工程中,
可以用来分析和设计旋转机械的动态性能;在航空航天领域,可以用来研究飞行器的飞行姿态等。
5.总结
刚体转动欧拉方程是描述刚体在三维空间中旋转的重要方程,它可以描述刚体的旋转速度和方向,被广泛应用于物理学、工程学等领域。
刚体的平面运动 解释瞬心3

研究内容 1.刚体平面运动的特性 2.刚体平面运动各点速度的计算
10.1平面运动的概念
1.刚体平面运动:刚体内各点分别保持在与某一 固定平面平行的平面内运动
如图: 2. 刚体的平面运动可以简化为 : S 为刚体上任一平行于 根据平面运动的定义: 平面图形 S在其所 S平动 →Ⅰ A的平面 A 固定平面 1 2平动, → Ⅱ 在平面内的运动 → A A2上各点运动情况 A1A2 1 为任一垂直于固定 相同 .所以 S上a,点代表 (即 :只要知道了平面图形 1A 平面 Ⅰ 的直线 并交SA 于 a2 点 上各点运动平面 S上各点 S的运动 ,就可以知道整个 代表整个刚体的运动 刚体的运动 ) Ⅰ
vevr3由于b点为滑动连接轮与摇杆相互接触的两点的速度不相等应用点的合成运动的方法分析vavrvavevr动坐标放在插杆o上则所求摇杆的角速度就是牵连运动的角速度将速度合成公式向x轴投影得vaxcos60ve0ve0866vo摇杆oo1aveob0688vo2rcos3002rads107如图传动机构当oa绕o轴转动时可使圆轮轴转动
[例10.8]轮O在水平面内滚动而不滑动,轮缘上 有一固定销钉B,此销钉在摇杆O1A的槽内滑 动并带动摇杆绕O1轴转动.已知轮的半径R= o.5m,在图所示位置时AO1是轮的切线,轮 心的速度VO=o.2m/s,摇杆与水平面的交角 α=60°,求摇杆的角速度. Vr VB Ve
[解] (1)机构由轮和摇杆 Vr O1A组成。 VB 轮子作平面运动, 摇杆O1A作定轴转动; Ve 连接点B对摇杆有相对 滑动。 (2)求平面运动轮子的 速度瞬心和角速度. 只滚不滑的轮子速度瞬心为与地面的接触 点C,其角速度为:
上面方程组共同决定S的位置, 称为平面运动方程
理论力学7—刚体的平面运动2
vC
vC C C 2 w BC
3 rw 3
习题7-12 图示小型精压机的传动机构,OA= O1B=r=0.1m,EB=BD=AD=l=0.4 m,在 图示瞬时OA⊥AD,O1B⊥ED,O1D在水平位 置,OD和EF在铅直位置。已知曲柄OA的转速 n=120 rpm,求此时压头F 的速度。
a C O r r
t
w
O
vO
n aCO
aO aO
aO r
vO r
aO
2
t aCO
C
aCO rw
n 2
r(
)
2
vO r
w
vO r
,
aO r
a C O a O , a C O vO / r
t n 2
取如图的投影轴, 将各矢量 投影到投影轴上得
y
aCx aO aCO 0
A2 A4
vA2
A1
v A 3 2 rw 2 v
2 rw 2v
例7-7 曲柄肘杆式压床如图。已知曲柄OA长r, 以匀角速度w 转动,AB = BC = BD = l,当曲柄 与水平线成30º 角时,连杆AB处于水平位置,而 肘杆DB与铅垂线也成30º 角。试求图示位置时, 杆AB、BC的角速度以及冲头C 的速度。 解:连杆AB作平面运动,瞬 D 30º 心在点C1,则
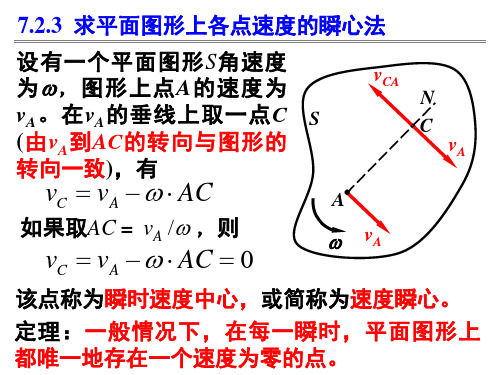
7.2.3 求平面图形上各点速度的瞬心法
设有一个平面图形S角速度 vCA 为 w ,图形上点A的速度为 N vA 。在vA 的垂线上取一点C S C (由vA 到AC的转向与图形的 vA 转向一致),有 vC v A w A C A 如果取AC= vA /w ,则 w vA vC v A w A C 0
3.刚体定点转动的运动方程

令 I3s2 ,cos x
I1
x&2
I12
x 2
2
I3
1 x2
2 E mglx 1 x2
与 &也相同。
&
J x J sin sin I1x
&
J y J sin cos I1y
J z J cos I3x J y J sin cos I1y
J z J cos I3z I3
x 0 cos nt y 0 sin nt
B点的加速度为:
ar B
ar A
dr
dt
rr r r rr
dr
dt
1
r dj dt
1, 0
r j
1V
R
r i
vr A
r Vj
r
r
1 j
V R
r k
rr
l
sin
r i
l
cos
r k
ar
aA
dr
dt
rr
r
r
rr
V 2
r i
1V
r i
r
r
l sin i l cos k
I2yx
d ( T ) T
dt &
Mz
I3&z (I1 I2 )yx M z
这就是z分量的欧拉动力学方程。由于把哪一个主轴作为z轴 是完全任意的,因此我们可以通过轮换下标的方法写出沿其 它两个方向的欧拉动力学方程。对所有轴的方程为
I1&x I 2&y
(I2 (I3
I3 I1
刚体定轴转动定理

注意点:
定轴转动定律是合外力矩对归纳刚体的瞬时作用 规律,公式中各量均需是同一时刻对同一刚体、 同一转体而言,否则是没有意义的。在定轴转动 中,由于合外力矩Mz和角加速度β的方向均在转术语
刚体定轴转动定律是指刚体所受的对于某定轴的 合外力矩等于刚体对此定轴的转动惯量与刚体在 此合外力矩作用下所获得的角加速度的乘积。
名称:刚体定轴转动定律(law of rotation)
公式:Mz=Jβ
其中Mz表示对于某定轴的合外力矩,J表示刚体 绕给定轴的转动惯量,β表示角加速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于刚体绕瞬心的转动方程
一、刚体围绕瞬心的转动方程
1.什么是刚体武绕瞬心的转动方程
刚体绕瞬心的转动方程,也叫刚体转动方程,是指一个刚体以某点为中心,以一个恒定角速度沿角位移变化的运动过程。
它用数学公式描述了刚体旋转中形变的动力学,是刚体动力学的基本方程。
2.刚体绕瞬心的转动方程的基本公式
刚体绕瞬心的转动方程的基本公式为:
ω ̇= τ/I
其中,ω是角速度,τ是外力的作用所产生的力矩,I是转动惯量。
3.在转动过程中的推导
设刚体以ω初值旋转,它的力矩为τ,则
τdφ = I dω
令静止情况下的角位移量φ = 0;
即δω = (τ/I)δt
解得,ω = ω 0 + (τ/I)t
即ω = ω 0 + τ t
τ为转动惯量。
4、刚体绕瞬心的转动方程的物理意义
刚体绕瞬心的转动方程不仅表示了刚体转动的物理过程,它还解释了与转动有关的力矩和动量守恒。
其中τ代表的是外力作用所产生的力矩,而I代表的是转动惯量。
因此,可以看到,只要力矩恒定,则角速度就会随时间的增加而增加;反之,只要力矩逐渐减小,则角速度也会随之减小。
二、结论
刚体绕瞬心的转动方程的基本公式为:ω ̇=τ/I,这一方程不仅反映了刚体的转动过程,也解释了力矩和动量的守恒,只要外力的作用恒定,角速度就会随时间变化而变化。
