立体几何近12年全国真题(及答案文科)
2012-2017全国高考立体几何题

2012-2017全国高考立体几何题 (2012年)19.(本小题满分12分) 如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,90ACB ∠=︒,AC=BC=21AA 1,D 是棱AA 1的中点。
(1)证明:平面BDC 1⊥平面BDC ;(2)平面BDC 1分此棱柱为两部分,求这两部分体积的比。
【解析】(1)在Rt DAC ∆中,AD AC =, 得:45ADC ︒∠=,同理:1114590A DC CDC ︒︒∠=⇒∠=, 得:1DC DC ⊥。
由题设知BC ⊥CC 1,BC ⊥AC ,1CC AC C =所以BC ⊥平面11ACC A 。
又1DC ⊂平面11ACC A ,所以1DC BC ⊥ 而DC BC C = ,所以1DC ⊥平面BDC 。
又1DC ⊂平面1BDC ,故平面BDC 1⊥平面BDC 。
(2)由已知AC=BC=21AA 1,D 是棱AA 1的中点, 设12AA a =,AC BC AD a ===,则11123122ABC A B C V a a a -=⋅=。
由(1),BC ⊥平面11ACC A ,所以BC 为四棱锥1B ACC D -的高, 所以13111(3)322B ACCD V a a a a -=⨯⨯⨯⨯=。
因此平面BDC 1分此棱柱为两部分体积的比为11111333112112ABC A B C B ACC DB ACC Da a V V V a -----==。
2013.19.如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠= 。
(Ⅰ)证明:1AB AC ⊥;(Ⅱ)若2AB CB ==,1AC =111ABC A B C -的体积。
19.【答案】(I )取AB 的中点O ,连接OC O 、1OA O 、1A B ,因为CA=CB ,A 1所以OC AB ⊥,由于AB=A A 1,∠BA A 1=600,故,A A B ∆为等边三角形,所以OA 1⊥AB.因为OC ⨅OA 1=O ,所以AB ⊥平面OA1C.又A 1CC 平面OA 1C ,故AB ⊥AC 。
高考全国卷Ⅰ文科数学立体几何专题复习(附详细解析)

2012-2018年新课标全国卷Ⅰ文科数学汇编立 体 几 何一、选择题【2017,6】如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是( )【2016,7】如图所示,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3,则它的表面积是( ) A .17π B . 18π C . 20π D . 28π【2016,11】平面α过正方体1111ABCD A B C D -的顶点A ,α∥平面11CB D ,α平面ABCD m =,α平面11ABB A n =,则,m n 所成角的正弦值为( )A .32 B .22 C .33 D .13【2015,6】《九章算术》是我国古代内容极为丰富的数学名著,书 中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各位多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( ) A .14斛 B .22斛 C .36斛 D .66斛【2015,11】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为16+20π,则r =( ) B A .1 B .2 C .4 D .8【2015,11】 【2014,8】 【2013,11】 【2012,7】【2014,8】如图,网格纸的各小格都是正方形,粗实线画出的一个几何体的三视图,则这个几何体是( ) A .三棱锥 B .三棱柱 C .四棱锥 D .四棱柱【2013,11】某几何体的三视图如图所示,则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π【2012,7】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为A .6B .9C .12D .15【2012,8】平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A .6πB .43πC .46πD .63π【2018,5】已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,该圆柱的表面积为A. 12πB. 12πC. 8πD. 10π【2018,9】某圆柱的高为2,底面周长为16,其三视图如右图,圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A. 2B.C. 3D.2【2018,10】在长方形ABCD-A 1B 1C 1D 1中,AB=BC=2,AC 1与平面BB 1C 1C 所成的角为30°,则该长方体的体积为A. 8B. 6C. 8D.8二、填空题【2017,16】已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA SCB ⊥平面,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为_______. 【2013,15】已知H 是球O 的直径AB 上一点,AH ∶HB =1∶2,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为______.三、解答题【2017,18】如图,在四棱锥P ABCD -中,AB ∥CD ,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.【2016,18】如图所示,已知正三棱锥P ABC -的侧面是直角三角形,6PA =,顶点P 在平面ABC 内的正投影为点D ,D 在平面PAB 内的正投影为点E .连结PE 并延长交AB 于点G . (1)求证:G 是AB 的中点;(2)在题图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.PABD CGE【2015,18】如图四边形ABCD 为菱形,G 为AC 与BD 交点,BE ⊥平面ABCD ,(Ⅰ)证明:平面AEC ⊥平面BED ; (Ⅱ)若∠ABC =120°,AE ⊥EC , 三棱锥E - ACD 6【2014,19】如图,三棱柱111C B A ABC -中,侧面C C BB 11为菱形,C B 1的中点为O ,且⊥AO 平面C C BB 11.(1)证明:;1AB C B ⊥(2)若1AB AC ⊥,,1,601==∠BC CBB 求三棱柱111C B A ABC -的高.【2013,19】如图,三棱柱ABC -A 1B 1C 1中,CA =CB ,AB =AA 1,∠BAA 1=60°.(1)证明:AB ⊥A 1C ;(2)若AB =CB =2,A 1C 6,求三棱柱ABC -A 1B 1C 1的体积.【2012,19】如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,90ACB ∠=︒,AC=BC=21AA 1,D 是棱AA 1的中点.(1)证明:平面BDC 1⊥平面BDC ; (2)平面BDC 1分此棱柱为两部分,求这两部分体积的比.【2018,18】如图,在平行四边形ABCM 中,AB=AC=3,∠ACM=90°,以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB ⊥DA 。
2007-2017全国1卷文科数学立体几何配答案汇总
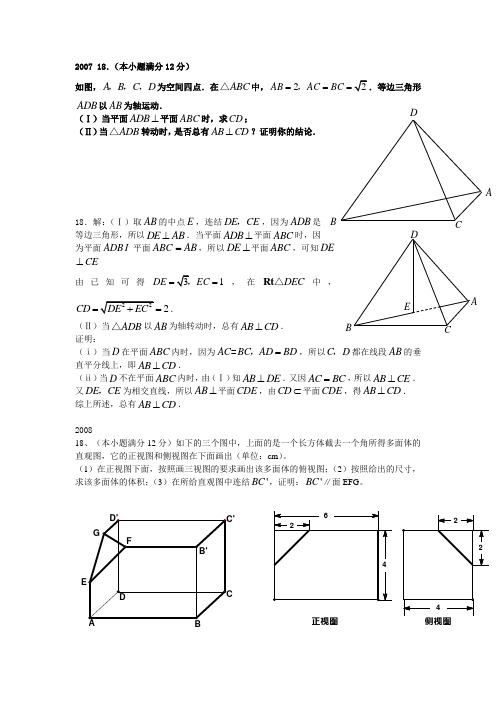
2007 18.(本小题满分12分)如图,AB C D ,,,为空间四点.在ABC △中,2AB AC BC ===,ADB 以AB 为轴运动.(Ⅰ)当平面ADB ⊥平面ABC 时,求CD ; (Ⅱ)当ADB △转动时,是否总有AB CD ⊥?证明你的结论.18.解:(Ⅰ)取AB 的中点E ,连结DE CE ,,因为ADB 是等边三角形,所以DE AB ⊥.当平面ADB ⊥平面ABC 时,因为平面ADB 平面ABC AB =,所以DE ⊥平面ABC ,可知DE CE ⊥由已知可得1DE EC ==,在DEC Rt △中,2CD =.(Ⅱ)当ADB △以AB 为轴转动时,总有AB CD ⊥. 证明:(ⅰ)当D 在平面ABC 内时,因为AC BC AD BD ==,,所以C D ,都在线段AB 的垂直平分线上,即AB CD ⊥.(ⅱ)当D 不在平面ABC 内时,由(Ⅰ)知A B D E ⊥.又因AC BC =,所以AB CE ⊥.又DE CE ,为相交直线,所以AB ⊥平面CDE ,由CD ⊂平面CDE ,得AB CD ⊥. 综上所述,总有AB CD ⊥. 200818、(本小题满分12分)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm )。
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连结'BC ,证明:'BC ∥面EFG 。
DBAEDB CA正视图18.【试题解析】(1)如图(2)所求多面体的体积()311284446222323V V V cm ⎛⎫=-=⨯⨯-⨯⨯⨯⨯= ⎪⎝⎭正长方体三棱锥 (3)证明:如图,在长方体''''ABCD A B C D -中,连接'AD ,则'AD ∥'BC 因为E,G分别为''',AA A D 中点,所以'AD ∥EG ,从而EG ∥'BC ,又'B C E F G ⊄平面, 所以'BC∥平面EFG; 2009(19)(本小题满分12分)如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,AD =,2DC SD ==,点M 在侧棱SC 上,∠ABM=60。
2012年高考试题:文科数学(全国卷)——含答案及解析

2012年普通高等学校招生全国统一考试文科数学(必修+选修Ⅰ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
考试结束后,将本卷和答题卡一并交回。
第Ⅰ卷注意事项:1、答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2、每小题选出答案后,用2B 铅笔把答题卡上对应题目答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
3、第Ⅰ卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
一、选择题(1)已知集合{|}{|}{|}{|}A x xB x xC x xD x x ==是平行四边形,是矩形,是正方形,是菱形,则( ).()()()()A A B B C B C D C D A D⊆⊆⊆⊆【考点】集合【难度】容易【点评】本题考查集合之间的运算关系,即包含关系。
在高一数学强化提高班上学期课程讲座1,第一章《集合》中有详细讲解,在高考精品班数学(文)强化提高班中有对集合相关知识的总结讲解。
(2)函数1(1)y x x =+-≥的反函数为( ). 2()1(0)A yx x =-≥ 2()1(1)B yx x =-≥ 2()1(0)C yx x =+≥ 2()1(1)D yx x =+≥ 【考点】反函数【难度】容易【点评】本题考查反函数的求解方法,注意反函数的定义域即为原函数的值域。
在高一数学强化提高班上学期课程讲座1,第二章《函数与初等函数》中有详细讲解,在高考精品班数学(文)强化提高班中有对函数相关知识的总结讲解。
(3)若函数()s i n [0,2]3x fx ϕϕ+=∈(π)是偶函数,则ϕ=( ).()2A π 2()3B π 3()2C π 5()3D π 【考点】三角函数与偶函数的结合【难度】中等【点评】本题考查三角函数变换,及偶函数的性质。
文科数学立体几何历年高考解答题

图 4GEF ABCD图 5DGBFCAE文科数学立体几何历年高考解答题1、(2013)如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中2BC =. (1) 证明:DE //平面BCF ; (2) 证明:CF ⊥平面ABF ; (3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -.2、 (2012)如图5所示,在四棱锥P ABCD -中,AB ⊥平面PAD ,//,AB CD PD AD =,E 是PB 中点,F 是DC 上的点,且12DF AB =,PH 为PAD ∆中AD 边上的高。
(1)证明:PH ⊥平面ABCD ;(2)若1,2,1PH AD FC ===,求三棱锥E BCF -的体积; (3)证明:EF ⊥平面PAB .3、(2011)如图所示,将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面水平向右平移得到的,,,,A A B B ''分别为,,,,CD C D DE D E ''''的中点,1122,,,'O O O O '分别为,,,CD C D DE D E ''''的中点.(Ⅰ)证明:12',,,O A O B '四点共面; (Ⅱ)设G 为AA '中点,延长1''A O 到H ',使得11''O H A O ''=,证明: 2'BO ''⊥面H B G .4、(2010)如图4,弧AEC 是半径为a 的半圆,AC 为直径,点E 为弧AC 的中点,点B 和点C 为线段AD 的三等分点,平面AEC 外一点F 满足FC ⊥平面BED,FB=a 5 (1)证明:EB ⊥FD(2)求点B 到平面FED 的距离.5、(2009)某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P - EFGH,下部分是长方体ABCD - EFGH. 图5和图6分别是该标识墩的正(主)视图和俯视图.(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积;(3)证明: 直线BD 平面PEG.6、(2008)如图5所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.(1)求线段PD的长;(2)若PCR,求三棱锥P-ABC的体积.侧视图4 图5 图6 E7、 (2007) 已知某几何体的俯视图是如图5所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视 图)是一个底边长为6、高为4的等腰三角形. (1)求该几何体的体积V ; (2)求该几何体的侧面积S 8、(本小题满分12分)在棱长为1的正方体1111ABCD A B C D -中,,,,E F G H 分别是棱1111,,,AB CC D A BB 的中点. (1)证明://FH 平面1A EG ; (2)证明:AH EG ⊥; (3)求三棱锥1A EFG -的体积.ABCDA 1B 111EFG H。
高考立体几何文科大题及答案

(Ⅱ)求二面角A— —B的大小。
14.(2009宁夏海南卷文)如图,在三棱锥 中,⊿ 是等边三角形,∠PAC=∠PBC=90(Ⅰ)证明:AB⊥PC
(Ⅱ)若 ,且平面 ⊥平面 ,
求三棱锥 体积。
15.(2009福建卷文)如图,平行四边形 中, , 将
沿 折起到 的位置,使平面 平面
(I)求证:
又底面ABCD是正方形, CD AD,又SD AD=D, CD 平面SAD。
过点D在平面SAD内做DF AE于F,连接CF,则CF AE,
故 CFD是二面角C-AE-D的平面角,即 CFD=60°
在Rt△ADE中, AD= , DE= ,AE= 。
于是,DF=
在Rt△CDF中,由 cot60°=
得 ,即 =3
【解法2】如图,以D为原点建立空间直角坐标系 ,
设
则 ,
(Ⅰ)∵ ,
∴ ,
∴AC⊥DP,AC⊥DB,∴AC⊥平面PDB,
∴平面 .
(Ⅱ)当 且E为PB的中点时, ,
设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∵ ,
∴ ,
∴ ,即AE与平面PDB所成的角的大小为 .
由 得2AD= ,解得AD= 。
故AD=AF。又AD⊥AF,所以四边形ADEF为正方形。
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF。
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD。
连接CH,则∠ECH为 与平面BCD所成的角。
因ADEF为正方形,AD= ,故EH=1,又EC= =2,
(Ⅰ)设 ,则
2013-2018全国新课标1.2卷文科数学立体几何题(附答案)
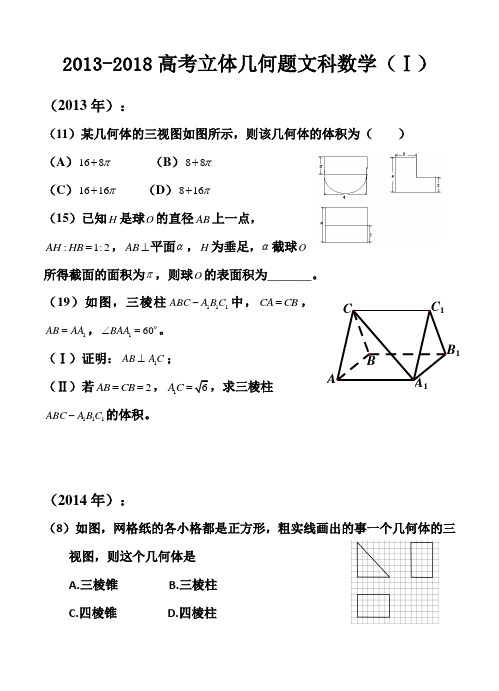
2013-2018高考立体几何题文科数学(Ⅰ)(2013年):(11)某几何体的三视图如图所示,则该几何体的体积为( ) (A )168π+ (B )88π+ (C )1616π+ (D )816π+ (15)已知H 是球O 的直径AB 上一点,:1:2AH HB =,AB ⊥平面α,H 为垂足,α截球O所得截面的面积为π,则球O 的表面积为_______。
(19)如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠=o 。
(Ⅰ)证明:1AB A C ⊥;(Ⅱ)若2AB CB ==,16AC =,求三棱柱111ABC A B C -的体积。
(2014年):(8)如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是 A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱C 1B 1AA B C(19)如图,三棱柱111C B A ABC -中,侧面C C BB 11为菱形,C B 1的中点为O ,且⊥AO 平面C C BB 11.(Ⅰ)证明:证明:;1AB C B ⊥(Ⅱ)若1AB AC ⊥,,1,601==∠BC CBB ο求三棱柱111C B A ABC -的高.(2015年):6、《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛11、圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( )(A )1 (B )2 (C )4 (D )816、已知F 是双曲线22:18y C x -=的右焦点,P 是C 左支上一点,()0,66A ,当APF ∆周长最小时,该三角形的面积为 . 18. (本小题满分12分)如图四边形ABCD 为菱形,G 为AC 与BD 交点,BE ABCD ⊥平面, (I )证明:平面AEC ⊥平面BED ; (II )若120ABC ∠=o ,,AE EC ⊥ 三棱锥E ACD -的体积为63,求该三棱锥的侧面积.(2016年):7.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是283π,则它的表面积是A . 17πB . 18πC . 20πD . 28π11.平面α过正方体ABCD —A 1B 1C 1D 1的顶点A ,,ABCD m α⋂=平面, 11ABB A n α⋂=平面,则m ,n 所成角的正弦值为A .32 B . 22 C . 33 D . 1318.如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于G(Ⅰ)证明:G是AB的中点;(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.(2017年):6.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是A. B. C. D.16.已知三棱锥SABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥SABC的体积为9,则球O 的表面积为________.18.如图,在四棱锥P ABCD -中, AB CD P ,且90BAP CDP ∠=∠=︒. (1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===, 90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.(2018年):5.已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .B .C .D .9某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为 A.B.C. D. 210. 在长方体中,,与平面所成的角为,则该长方体的体积为 A. B. C.D.18.如图,在平行四边形中,,,以为折痕将△折起,使点到达点的位置,且.(1)证明:平面平面;(2)为线段上一点,为线段上一点,且,求三棱锥的体积.2013-2018高考立体几何题文科数学(Ⅱ)(2013年):9、一个四面体的顶点在空间直角坐标系O xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为()(A) (B) (C) (D)(15)已知正四棱锥O ABCD -32,3则以O 为球心,OA 为半径的球的表面积为________。
新课标全国卷历年高考立体几何真题(含答案)

2.(2012年全国卷)如图,直三棱柱 中, , 是棱 的中点, .
(Ⅰ)证明: ;(Ⅱ)求二面角 的大小.
3.(2013年全国Ⅱ卷)如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= AB.
新课标全国卷历年高考立体几何真题(含答案)
班别:______________________姓名:___________________
题号
1
2
3
4
5
6
7
8
9
10
11
总分
得分
1.(2011年全国卷)如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
由(1)可得 , , , ,
所以 , .故 .
所以直线 与直线 所成角的余弦值为
9.【解析】⑴∵ 为正方形∴ ∵ ∴ ∵ ∴ 面 面 ∴平面 平面 ⑵由⑴知 ∵ 平面 平面 ∴ 平面 平面 ∵面 面 ∴ ,∴ ∴四边形 为等腰梯形以 为原点,如图建立坐标系,设
, , 设面 法向量为 . ,即 ,
设面 法向量为 .即 ,
7.【解析】(1)交线围成的正方形EHGF如图:
(2)作EM⊥AB,垂足为M,则AM=A1E=4,EM=AA1=8.
因为四边形EHGF为正方形,所以EH=EF=BC=10.
于是MH= =6,所以AH=10.以D为坐标原点, 的方向为x轴的正方向,建立如图所示的空间直角坐标系D-xyz,则
A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8), =(10,0,0), =(0,-6,8).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
综上所述,总有 .
15.【解析】(Ⅰ)如图:
…………… 3分
(Ⅱ)所求多面体体积
.
(Ⅲ)证明:在长方体 中,
连结 ,则 .
因为 分别为 , 中点,所以 ,
从而 .又 平面 ,所以 面 .
16.【解析】(Ⅰ)因为 是等边三角形, ,
所以 ,
可得 .
如图,取 中点 ,连结 , ,
37.(2018年全国Ⅰ卷第18题)如图,在平行四边形 中, , ,以 为折痕将△ 折起,使点 到达点 的位置,且 .
(1)证明:平面 平面 ;
(2) 为线段 上一点, 为线段 上一点,且 ,求三棱锥 的体积.
38.(2018年全国Ⅱ卷第19题)如图,在三棱锥 中, ,
, 为 的中点.
(1)证明: 平面 ;
26.(2017年全国Ⅰ卷第16题)已知三棱锥 的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥 的体积为9,则球O的表面积为________.
27.(2015年全国Ⅰ卷第18题)如图四边形ABCD为菱形,G为AC与BD交点, .
( )证明:平面 平面 ;
9.(2013年全国Ⅱ卷第16题)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周
都在同一个球面上.若圆锥底面面积是这个球面面积的 ,则这两个圆锥中,体积较小者
的高与体积较大者的高的比值为______________.
10.(2017年全国Ⅰ卷第6题)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是
( )若 ,
三棱锥 的体积为 ,
求该三棱锥的侧面积.
28.(2016年全国Ⅰ卷第18题)如图,在已知正三棱锥 的侧面是直角三角形,
,顶点 在平面 内的正投影为点 , 在平面 内的正投影为 ,连接 并延长交 于点 .
( )证明 是 的中点;
( )在答题卡第(18)题图中作出点 在
平面 内的正投影 (说明作法及理由),
17.(2010年全国卷第18题)如图,已知四棱锥 的底面为等腰梯形, ∥ , ,垂足为 , 是四棱锥的高.
(Ⅰ)证明:平面 平面;
(Ⅱ)若 , ,求四棱锥 的体积.
18.(2011年全国卷第18题)如图,四棱锥 中,底面 为平行四边形,
, , 底面 .
(Ⅰ)证明: ;
(Ⅱ)设 ,求棱锥 的高.
19.(2014年全国Ⅱ卷第18题)如图,四棱锥 中,底面 为矩形, 平面 , 是 的中点.
35.(2017年全国Ⅱ卷第18题)如图,四棱锥 中,侧面 为等边三角形且垂直于底面 , .
(Ⅰ)证明:直线 平面 ;
(Ⅱ)若 面积为 ,求四棱锥 的体积.
36.(2017年全国Ⅲ卷第19题)如图,四面体ABCD中,△ABC是正三角形,AD=CD.
(Ⅰ)证明:AC⊥BD;
(Ⅱ)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
(Ⅰ)证明: 平面 ;
(Ⅱ)设 ,三棱锥 的体积 ,求 到平面 的距离.
20.(2013年全国Ⅱ卷第18题)如图,直三棱柱 中, 分别是 的中点.
(Ⅰ)证明: 平面 ;
(Ⅱ)设 ,
求三棱锥 的体积.
21.(2015年全国Ⅱ卷第19题)如图,长方体 中, ,点 分别在 、 上, .过 的平面 与此长方体的面相交,交线围成一个正方形.
又 平面 , 平面 .
所以 平面 .
(Ⅱ)
由 ,可得 .作 交 于 .
由题设知 ,所以 .
故 ,又 ,所以 到平面 的距离为 .
20.【解析】(Ⅰ)连结 交 于点 ,
则 为 中点.又 是 中点,连结 ,则 .
因为 平面 , 平面 ,
所以 平面 .
(Ⅱ)因为 是直三棱柱,所以 .
由已知 , 为 的中点,所以 .
又 , 平面 , 平面 ,且 .
所以 平面 ,而 平面 ,故平面 平面 .
(Ⅱ)因为四边形 为等腰梯形,
所以 , , , .
因为 ,所以 , .可得 .
所以等腰梯形 的面积为 .
所以四棱锥的体积为 .
18.【解析】(Ⅰ)因为 , ,
由余弦定理得 ,从而 ,故 .
又 平面 , 平面 ,故 .
由 可得 平面 .
而 平面 ,故 .
(Ⅱ)如图,作 ,垂足为 .
已知 平面 , 平面 ,故 .
由(Ⅰ)知 ,又 ,所以 .
由 可得 平面 .
而 平面 ,故 .
另由 ,得 平面 .
由题设知, ,则 ,
根据 ,得 ,
即棱锥 的高为
19.【解析】(Ⅰ)设 交 于点 ,连结 .
因为 为矩形,所以 为 的中点.
又 为 的中点,所以 .
26.
27.【解析】(Ⅰ) 四边形 为菱形, ,
而 平面 ,
平面 , ,
而 , 平面 , 平面 .
又 平面 , 平面 平面 .
(II)设 ,在菱形 中,又 ,
可得 , .
, 在 中,可得 .
平面 , 平面 , , ,
三棱锥 的体积 = ,解得 =2,
从而可得 .
所以 的面积为 , 的面积与 的面积均为 ,
空间点、线、面的位置关系(文科)
考纲要求
常考知识点
能力要求
命题规律
理解点、直线、平面之间的位
置关系;
证明平行或垂直;
求锥体或柱体的高或体积.
考查考生空间想象能力,运算求解能力与
推理论证能力.
通常都会有一道选填题与一道解答题,选填题难度中等,而解答题则位于第18题与第19题之间。
【十年真题】
(A)组
1.(2016年全国Ⅱ卷第4题)边长为 的正方体顶点都有同一球面上,则该球的表面积为
(2)若点 在棱 上,且 ,求点 到平面 的距离.
39.(2018年全国Ⅱ卷第19题) 如图,矩形 所在平面与半圆弧 所在平面垂直, 是 上异于 , 的点.
(1)证明:平面 平面 ;
(2)在线段 上是否存在点 ,使得 平面 ?说明理由.
空间点、线、面的位置关系(文科)
(A)组
1.A 2.B 3.B 4.B 5.C 6.D 7. 8. 9. 10.A
(A) 斛(B) 斛
(C) 斛(D) 斛
3.(2010年全国卷第7题)设长方体的长、宽、高分别为 、 、 ,其顶点都在一个球面上,则该球的表面积为
(A) (B) (C) (D)
4.(2012年全国卷第8题)平面 截球 的球面所得圆的半径为 ,球心 到平面 的距离为 ,则此球的体积为
(A) (B) (C) (D)
(A) (B) (C) (D)
14.(2007年海南宁厦卷第18题)如图, 为空间四点.在 中, .等边三角形 以 为轴运动.
(Ⅰ)当平面 平面 时,求 ;
(Ⅱ)当 转动时,是否总有 ?证明你的结论.
15.(2008年海南宁厦卷第18题)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图.它的正视图
所以 ,选D.
23.【解析】由题意得 , ,所以 正确,当 时, 不垂直于 .
24.【解析】如图在正方体的前面补一个相同的正方体,由题意得 , ,由正方体的性质易知 与 所成的角为 ,所以 与 所成的角为 .正弦值为 .
25.【解析】在三边长为6,8,10的直角三角形中,
它的内切圆的半径 ,
因为 ,所以当 时球的体积最大, .
(A) (B) (C) (D)
2.(2015年全国Ⅰ卷第6题)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有
31.(2014年全国Ⅰ卷第19题)如图,三棱柱 中,侧面 为菱形, 的中点为 ,且 平面 .
(Ⅰ)证明:
(Ⅱ)若 , , ,
求三棱柱 的高.
32.(2016年全国Ⅱ卷第19题)如图,菱形 的对角线 与 交于点 ,点 、 分别在 , 上, , 交 于点 ,将 沿 折到 的位置.
(I)证明: ;
(II)若 ,求五棱锥 体积.
11.(2017年全国Ⅱ卷第15题)长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为.
12.(2017年全国Ⅲ卷第9题)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为
(A) (B) (C) (D)
13.(2017年全国Ⅲ卷第10题)在正方体 中,E为棱CD的中点,则
(I)在图中画出这个正方形(不必说明画法和理由);
(II)求平面 把该长方体分成的两部分体积的比值.
(B)组
22.(2007年海南宁厦卷第11题)已知三棱锥 的各顶点都在一个半径为 的球面
上,球心 在 上, 底面 , ,则球的体积与三棱锥体积之比是
(A) (B) (C) (D)
23.(2008年海南宁厦卷第11题)已知平面 平面 , ,点 , ,直线 ,直线 ,直线 ,则下列四种位置关系中,不一定成立的是
33.(2016年全国Ⅲ卷第19题)如图,四棱锥 中, 底面 , , , , 为线段 上一点, , 为 的中点.
(I)证明: 平面 ;
(II)求四面体 的体积.
34.(2017年全国Ⅰ卷第18题)
如图,在四棱锥P-ABCD中,AB//CD,且
(Ⅰ)证明:平面PAB⊥平面PAD;
