近三年高考全国卷政治科立体几何真题

合集下载

近九年高考全国卷空间立体几何真题汇编答案

近九年高考全国卷空间立体几何真题汇编参考答案2018年全国普通高等学校招生考试(全国卷Ⅲ)19．【解析】(1)由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ．因为M 为 CD上异于C ，D 的点，且DC 为直径，所以DM ⊥CM ．又BC CM =C ，所以DM ⊥平面BMC ．而DM ⊂平面AMD ，故平面AMD ⊥平面BMC ．(2)以D 为坐标原点，DA 的方向为x 轴正方向，建立如图所示的空间直角坐标系D xyz -．当三棱锥M ABC -体积最大时，M 为 CD的中点．由题设得(0,0,0)D ，(2,0,0)A ，(2,2,0)B ，(0,2,0)C ，(0,1,1)M ，(2,1,1)AM =- ，(0,2,0)AB = ，(2,0,0)DA = 设(,,)x y z =n 是平面MAB 的法向量，则0,0.AM AB ⎧⋅=⎪⎨⋅=⎪⎩ n n 即20,20.x y z y -++=⎧⎨=⎩可取(1,0,2)=n ．DA 是平面MCD 的法向量，因此5cos ,5||||DA DA DA ⋅== n n n ，5sin ,5DA = n ，所以面MAB 与面MCD 所成二面角的正弦值是255．2018年全国普通高等学校招生考试(全国卷Ⅱ)20．【解析】(1)因为4AP CP AC ===，O 为AC 的中点，所以OP AC ⊥，且3OP =连结OB ．因为22AB BC AC ==，所以ABC △为等腰直角三角形，且OB AC ⊥，122OB AC ==．由222OP OB PB +=知PO OB ⊥．由⊥OP OB ，⊥OP AC 知PO ⊥平面ABC ．(2)如图，以O 为坐标原点，OB uu u r 的方向为x 轴正方向，建立空间直角坐标系O xyz -．由已知得(0,0,0)O ，(2,0,0)B ，(0,2,0)-A ，(0,2,0)C ，(0,0,3)P ，(0,2,23)=AP uu u r ，取平面PAC 的法向量(2,0,0)OB =uu u r ．设(,2,0)(02)-<≤M a a a ，则(,4,0)AM a a =-uuu r．设平面PAM 的法向量为(,,)x y z =n ．由0,0AP AM ⋅=⋅=uu u r uuu r n n 得230(4)0y z ax a y ⎧+=⎪⎨+-=⎪⎩，可取(3(3,)a a a =--n ，所以2223(cos ,23(4)3OB a a a =-++uu u rn ．由已知得3|cos ,|2OB =uu u r n ．22233223(4)3a a a -++．解得4a =-（舍去），43a =．所以83434(,,)333=--n ．又(0,2,23)PC =-uu u r ，所以3cos ,4PC =uu u r n ．所以PC 与平面PAM 所成角的正弦值为34．2018年全国普通高等学校招生考试(新课标全国Ⅰ卷)18．【解析】(1)由已知可得，BF ⊥PF ，BF ⊥EF ，所以BF ⊥平面PEF ．又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD ．(2)作PH ⊥EF ，垂足为H ．由(1)得，PH ⊥平面ABFD ．以H 为坐标原点，HF 的方向为y 轴正方向，||BF 为单位长，建立如图所示的空间直角坐标系-H xyz．由(1)可得，DE ⊥PE ．又DP =2，DE =1，所以PE又PF =1，EF =2，故PE ⊥PF ．可得2=PH ,32=EH ．则(0,0,0)H，(0,0,2P ，3(1,,0)2--D，3(1,,)22= DP ，3(0,0,)2HP = 为平面ABFD 的法向量．设DP 与平面ABFD 所成角为θ，则334sin ||4||||HP DP HP DP θ⋅===⋅ ．所以DP 与平面ABFD 所成角的正弦值为34．18．【解析】（1）由已知90BAP CDP ∠=∠=︒，得AB ⊥AP ，CD ⊥PD ．由于AB ∥CD ，故AB ⊥PD ，从而AB ⊥平面PAD ．又AB ⊂平面PAB ，所以平面PAB ⊥平面PAD ．（2）在平面PAD 内做PF AD ⊥，垂足为F ，由（1）可知，AB ⊥平面PAD ，故AB PF ⊥，可得PF ⊥平面ABCD ．以F 为坐标原点，FA 的方向为x 轴正方向，||AB 为单位长，建立如图所示的空间直角坐标系F xyz -．由（1）及已知可得2,0,0)2A ，2(0,0,2P ，2,1,0)2B ，2(,1,0)2C -．所以22(,1,22PC =-- ，2,0,0)CB = ，2222PA =- ，(0,1,0)AB = ．设(,,)x y z =n 是平面PCB 的法向量，则00PC CB ⎧⋅=⎪⎨⋅=⎪⎩ n n ，即2202220x y z ⎧-+-=⎪=，可取(0,1,2)=--n ．设(,,)x y z =m 是平面PAB 的法向量，则00PA AB ⎧⋅=⎪⎨⋅=⎪⎩ m m ，即220220x z y -=⎨⎪=⎩，可取(1,0,1)=n ．则3cos ,||||3⋅==-<>n m n m n m ，所以二面角A PB C --的余弦值为33-．19．【解析】（1）取PA 的中点F ，连结EF ，BF ．因为E 是PD 的中点，所以EF AD ∥，12EF AD =．由90BAD ABC ∠=∠= 得BC AD ∥，又12BC AD =，所以EF BC ∥，四边形BCEF 是平行四边形，CE BF ∥，又BF ⊂平面PAB ，CE ⊄平面PAB ，故CE ∥平面PAB ．（2）由已知得BA AD ⊥，以A 为坐标原点，AB 的方向为x 轴正方向，||AB 为单位长，建立如图的空间直角坐标系A xyz -，则(0,0,0)A ，(1,0,0)B ，(1,1,0)C ，3)P ，(1,0,3)PC = ，(1,0,0)AB = ．设(,,)M x y z (01)x <<，则(1,,)BM x y z =- ，(,1,3)PM x y z =-- ．因为BM 与底面ABCD 所成的角为45，而(0,0,1)=n 是底面ABCD 的法向量，所以|cos ,|sin 45BM <>= n 22222(1)x y z =-++，即222(1)0x y z -+-=．①又M 在棱PC 上，设PM PC λ= ，则x λ=，1y =，33z λ=．②由①，②解得212162x y z ⎧=+⎪⎪⎪=⎨⎪⎪=-⎪⎩（舍去），212162x y z ⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩所以26(1,1,)22M -，从而26(1,1,22AM =- ．设000(,,)x y z =m 是平面ABM 的法向量，则0=0AM AB ⎧⋅=⎪⎨⋅⎪⎩ m m ，即0000(22)2600x y z x ⎧++=⎪⎨=⎪⎩，所以可取(0,6,2)=m ，于是10cos ,||||5⋅<>==m n m n m n ．因此二面角M AB D --的余弦值为105．2017年普通高等学校统一招生考试·丙卷(新课标Ⅲ)19．【解析】（1）由题设可得，ABD CBD ∆≅∆，从而AD DC =．又ACD ∆是直角三角形，所以0=90ACD ∠取AC 的中点O ，连接DO ，BO ，则DO AC ⊥，DO AO =．又由于ABC ∆是正三角形，故BO AC ⊥．所以DOB ∠为二面角D AC B --的平面角．在Rt AOB ∆中，222BO AO AB +=．又AB BD =，所以222222BO DO BO AO AB BD +=+==，故90DOB ∠= ．所以平面ACD ⊥平面ABC ．（2）由题设及（1）知，OA,OB,OD 两两垂直，以O 为坐标原点，OA 的方向为x 轴正方向，OA 为单位长，建立如图所示的空间直角坐标系O xyz -，则(1,0,0)A ，3,0)B ，(1,0,0)C -，(0,0,1)D ．由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得31(0,)22E ．故(1,0,1)AD =- ，(2,0,0)AC =- ，31(1,,)22AE =- 设()=x,y,z n 是平面DAE 的法向量，则AD AE ⎧=⎪⎨=⎪⎩ 0，0，n n 即x z x y z -+=⎧⎪⎨-++=⎪⎩031022可取3(1,,1)3=n 设m 是平面AEC 的法向量，则0，0，AC AE ⎧=⎪⎨=⎪⎩ m m 同理可得(0,3)=-m 则cos ,== 77n m n m n m 所以二面角D AE C --的余弦值为77．（18）【解析】：（Ⅰ）由已知可得F DF A ⊥，F F A ⊥E ，所以F A ⊥平面FDC E ．又F A ⊂平面F ABE ，故平面F ABE ⊥平面FDC E ．（Ⅱ）过D 作DG F ⊥E ，垂足为G ，由（Ⅰ）知DG ⊥平面F ABE ．以G 为坐标原点，GF 的方向为x 轴正方向，GF 为单位长度，建立如图所示的空间直角坐标系G xyz -．由（Ⅰ）知DF ∠E 为二面角D F -A -E 的平面角，故DF 60∠E = ，则2DF =，DG =，可得()1,4,0A ，()3,4,0B -，()3,0,0E -，(D ．由已知，//F AB E ，所以//AB 平面FDC E ．又平面CD AB 平面FDC DC E =，故//CD AB ，CD//F E ．由//F BE A ，可得BE ⊥平面FDC E ，所以C F ∠E 为二面角C F -BE -的平面角，C F 60∠E =．从而可得(C -．所以(C E = ，()0,4,0EB =，(C 3,A =-- ，()4,0,0AB =- ．设(),,n x y z =是平面C B E 的法向量，则C 00n n ⎧⋅E =⎪⎨⋅EB =⎪⎩，即040x y ⎧+=⎪⎨=⎪⎩，所以可取(3,0,n = ．设m 是平面CD AB 的法向量，则C 00m m ⎧⋅A =⎪⎨⋅AB =⎪⎩ ，同理可取()4m =．则cos ,19n m n m n m ⋅==- ．故二面角C E -B -A的余弦值为19-．（19）【解析】（I ）证明：∵54AE CF ==，∴AE CF AD CD =，∴EF AC ∥．∵四边形ABCD 为菱形，∴AC BD ⊥，∴EF BD ⊥，∴EF DH ⊥，∴EF D H '⊥．∵6AC =，∴3AO =；又5AB =，AO OB ⊥，∴4OB =，∴1AE OH OD AO=⋅=，∴3DH D H '==，∴222'OD OH D H '=+，∴'D H OH ⊥．又∵OH EF H =I ∴'D H ⊥面ABCD ．（Ⅱ）建立如图坐标系H xyz -．()500B ，，，()130C ，，，()'003D ，，，()130A -，，，()430AB =uu u r ，，，()'133AD =-uuur ，，，()060AC =uuu r ，，，设面'ABD 法向量()1n x y z =，，u r ，由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩ 得430330x y x y z +=⎧⎨-++=⎩，取345x y z =⎧⎪=-⎨⎪=⎩，∴()1345n =-u r ，，．同理可得面'AD C 的法向量()2301n =u u r ，，，∴121275cos 25n n n n θ⋅==u r u u r u r u u r ，∴sin 25θ=．2016年普通高等学校招生全国统一考试·丙卷（新课标Ⅲ）（19）【解析】（Ⅰ）由已知得232==AD AM ，取BP 的中点T ，连接TN AT ,．由N 为PC 中点知BC TN //，221==BC TN .又BC AD //，故TN 平行且等于AM ，四边形AMNT 为平行四边形，于是AT MN //.因为⊂AT 平面PAB ，⊄MN 平面PAB ，所以//MN 平面PAB .（Ⅱ）取BC 的中点E ，连结AE ，由AC AB =得BC AE ⊥，从而AD AE ⊥，且5)2(2222=-=-=BC AB BE AB AE .以A 为坐标原点，AE 的方向为x 轴正方向，建立如图所示的空间直角坐标系xyz A -，由题意知，)4,0,0(P ，)0,2,0(M ，)0,25(C ，)2,1,25(N ，)4,2,0(-=PM ，)2,1,25(-=PN ，)2,1,25(=AN .设(,,)x y z = n 为平面PMN 的法向量，则00PM PN ⎧⋅=⎪⎨⋅=⎪⎩ n n ，即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ，可取)1,2,0(=，于是2558|||||||,cos |==><AN n AN n AN n.2015年全国高考试题独家解析(新课标全国卷Ⅱ)19．【解析】（Ⅰ）交线围成的正方形EHGF如图：（Ⅱ）作EM AB ⊥，垂足为M ，则14AM A E ==，18EM AA ==，因为EHGF 为正方形，所以10EH EF BC ===．于是6MH ==，所以10AH =．以D 为坐标原点，DA 的方向为x 轴的正方向，建立如图所示的空间直角坐标系D xyz -，则(10,0,0)A ，(10,10,0)H ，(10,4,8)E ，(0,4,8)F ，(10,0,0)FE = ，(0,6,8)HE =- ．设(,,)n x y z = 是平面EHGF 的法向量，则0,0,n FE n HE ⎧⋅=⎪⎨⋅=⎪⎩ 即100,680,x y z =⎧⎨-+=⎩所以可取(0,4,3)n = ．又(10,4,8)AF =- ，故cos ,15n AF n AF n AF⋅<>==⋅ ．所以直线AF 与平面α所成角的正弦值为4515．2015年全国高考试题独家解析(新课标卷Ⅰ)18．【解析】（Ⅰ）连接BD ，设BD AC G = ，连接,,EG FG EF ．在菱形ABCD 中，不妨设1GB =，由120∠= ABC ，可得AG GC ==，由⊥BE 平面ABCD ，AB BC =可知，AE EC =，又∵⊥AE EC ，∴EG =，⊥EG AC ，在Rt EBG D 中，可得BE =2DF =．在Rt FDG D 中，可得2FG =．在直角梯形BDFE 中，由2BD =，BE =22DF =，可得322EF =，∴222EG FG EF +=，∴EG ⊥FG ，∵AC ∩FG =G ，∴EG ⊥平面AFC ，∵EG ⊂面AEC ，∴平面AFC ⊥平面AEC ．（Ⅱ）如图，以G 为坐标原点，分别以,GB GC 的方向为x 轴，y 轴正方向，||GB为单位长度，建立空间直角坐标系G-xyz ，由（Ⅰ）可得A (0，0），E )，F(－1,0，2)，C (0，0)，∴AE =(1)，CF =(-1，，2)．故cos ,3||||<>==-AE CF AE CF AE CF .所以直线AE 与CF 所成的角的余弦值为3．2014年普通高等学校招生全国统一考试(全国大纲卷)19．【解析】：解法一：(1)1A D ^平面ABC ，1A D Ì平面11AA C C ，故平面11AA C C ^平面ABC ．又BC AC ^，BC \^平面11AA C C ．连结1A C ，∵侧面11AA C C 为菱形，故11AC A C ^，由三垂线定理得11AC A B ^；(2)BC ^平面11AA C C ，BC Ì平面11BCC B ，故平面11AA C C ^平面11BCC B ．作11,A E CC E ^为垂足，则1A E ^平面11BCC B ．又直线1AA ∥平面11BCC B ，因而1A E 为直线1AA 与平面11BCC B的距离，1A E =∵1A C 为1ACC Ð的角平分线，故11A D A E ==．作,DF AB F ^为垂足，连结1A F ，由三垂线定理得1A F AB ^，故1A FD Ð为二面角1A AB C --的平面角．由1AD ==得D 为AC 的中点，111tan ,2A D AC BC DF A FD AB DF´=´=Ð==∴二面角1A AB C --的大小为．解法二：以C 为坐标原点，射线CA 为x 轴的正半轴，以CB 长为单位长，建立如图所示的空间直角坐标系C xyz -．由题设知1A D 与z 轴平行，z 轴在平面11AA C C 内．(1)设()1,0,A a c ，由题设有()()2,2,0,0,0,1,0,a A B £则1(2,1,0),(2,0,0),(2,0,)AB AC AA a c=-=-=-111(4,0,),(,1,)AC AC AA a c BA a c=+=-=-由12AA =2，即2240a a c -+=①．于是22111140,AC BA a a c AC A B ×=-+=\^．(2)设平面11BCC B 的法向量(,,),m x y z=则1,,m CB m BB ^^即10,0m CB m BB ×=×= ．()0,1,0,CB = ()112,0,,BB AA a c ==-故0y =，且()20a x cz -+=．令x c =，则()2,,0,2z a m c a =-=-，点A 到平面11BCC B 的距离为cos ,CA m CA CA c m××==．又依题设，点A 到平面11BCC B的距离为c \=．代入①解得3a =（舍去）或1a =．于是1(1,0,AA=-．设平面1ABA 的法向量(),,n p q r =，则1,n AA n AB ^^，即10,0,0n AA n AB p ×=×=\-+= ，故且20p q -+=．令p =，则1,q r ==)n =．又()0,0,1p =为平面ABC 的法向量，故1cos ,4n p n p n p ⋅==⋅，∴二面角1A AB C --的大小为1arccos 4．2014年全国高考试题独家解析(新课标卷Ⅱ)18．【解析】（I ）连接BD 交AC 于点O ，连结EO 。

历年高考真题专题04立体几何

专题04 立体几何【2020年】1.（2020·新课标Ⅰ）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（）A. 51-B. 51-C. 51+D. 51+ 【解析】如图，设,CD a PE b ==，则22224a PO PE OEb =-=-，由题意212PO ab =，即22142a b ab -=，化简得24()210b b a a -⋅-=，解得15b a +=（负值舍去）.2.（2020·新课标Ⅰ）已知A 、B 、C 为球O 球面上的三个点，⊙1O 为ABC 的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为（）A. 64πB. 48πC. 36πD. 32π【解析】设圆1O 半径为r ，球的半径为R ，依题意，得24,2r r ππ=∴=，由正弦定理可得2sin 6023AB r =︒=，123OO AB ∴==，根据圆截面性质1OO ⊥平面ABC ， 222211111,4OO O A R OA OO O A OO r ∴⊥==+=+=，∴球O 的表面积2464S R ππ==.3.（2020·新课标Ⅱ）如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M，在俯视图中对应的点为N，则该端点在侧视图中对应的点为（）A. EB. FC. GD. H【解析】根据三视图，画出多面体立体图形，图中标出了根据三视图M点所在位置，可知在侧视图中所对应的点为E。

4.（2020·新课标Ⅲ）下图为某几何体的三视图，则该几何体的表面积是（）2233【解析】根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDBS S S===⨯⨯=△△△根据勾股定理可得：22AB AD DB===∴ADB△是边长为2根据三角形面积公式可得：2113sin 60(22)23222ADB S AB AD =⋅⋅︒=⋅=△ ∴该几何体的表面积是：2362332=⨯++.5.（2020·北京卷）某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为（）． A . 63+ B. 623+C. 123+D. 1223+ 【解析】由题意可得，三棱柱的上下底面为边长为2的等边三角形，侧面为三个边长为2的正方形，则其表面积为：()1322222sin 6012232S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+⎪⎝⎭. 6.（2020·山东卷）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为（）A. 20°B. 40°C. 50°D. 90°【解析】画出截面图如下图所示，其中CD 是赤道所在平面的截线；l 是点A 处的水平面的截线，依题意可知OA l ⊥；AB 是晷针所在直线.m 是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直，根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与点A 处的水平面所成角为40BAE ∠=︒.7.（2020·天津卷）若棱长为23的正方体的顶点都在同一球面上，则该球的表面积为（） A. 12π B. 24π C. 36π D. 144π【解析】这个球是正方体的外接球，其半径等于正方体的体对角线的一半，即()()()22223232332R ++==，所以，这个球的表面积为2244336S R πππ==⨯=.8.（2020·浙江卷）某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm 3）是（）A. 73B. 143C. 3D. 6【解析】由三视图可知，该几何体是上半部分是三棱锥，下半部分是三棱柱，且三棱锥的一个侧面垂直于底面，且棱锥的高为1，棱柱的底面为等腰直角三角形，棱柱的高为2，所以几何体的体积为：11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+= ⎪ ⎪⎝⎭⎝⎭. 9.（2020·山东卷）已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1D 为球心，5为半径的球面与侧面BCC 1B 1的交线长为________．【解析】如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为BAD ∠=60°，直四棱柱1111ABCD A B C D -的棱长均为2，所以△111D B C 为等边三角形，所以1D E 3=，111D E B C ⊥，又四棱柱1111ABCD A B C D -为直四棱柱，所以1BB ⊥平面1111D C B A ，所以111BB B C ⊥，因为1111BB B C B =，所以1D E ⊥侧面11B C CB ，设P 为侧面11B C CB 与球面的交线上的点，则1D E EP ⊥，因为球的半径为5，13D E =，所以2211||||||532EP D P D E =-=-=，所以侧面11B C CB 与球面的交线上的点到E 的距离为2，因为||||2EF EG ==，所以侧面11B C CB 与球面的交线是扇形EFG 的弧FG ，因为114B EF C EG π∠=∠=，所以2FEG π∠=，所以根据弧长公式可得2222FG ππ=⨯=. 10.（2020·浙江卷）已知圆锥展开图的侧面积为2π，且为半圆，则底面半径为_______．【解析】设圆锥底面半径为r ，母线长为l ，则21222r l r l ππππ⨯⨯=⎧⎪⎨⨯⨯=⨯⨯⨯⎪⎩，解得1,2r l ==. 11.（2020·江苏卷）如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半轻为0.5 cm ，则此六角螺帽毛坯的体积是____cm.【解析】正六棱柱体积为23622=123⨯；圆柱体积为21()222ππ⋅=；所求几何体体积为1232π 12.（2020·新课标Ⅲ）已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．2【解析】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，其中2,3BC AB AC ===，且点M 为BC 边上的中点，设内切圆的圆心为O ，由于223122AM =-=，故1222222S =⨯⨯=△ABC ，设内切圆半径为r ，则： ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯ ()1332222r =⨯++⨯=，解得：22r ，其体积：34233V r ππ==. 【2019年】1．【2019·全国Ⅰ卷】已知三棱锥P −ABC 的四个顶点在球O 的球面上，P A =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是P A ，AB 的中点，∠CEF =90°，则球O 的体积为( )A ．68πB ．64πC ．62πD ．6π 【解析】,PA PB PC ABC ==△为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CEAC C EF =∴⊥平面PAC ，∴PB ⊥平面PAC ，2APB PA PB PC ∴∠=90︒,∴===，P ABC ∴-为正方体的一部分，22226R =++=，即364466,π62338R V R =∴=π=⨯=π，故选D ．2．【2019·全国Ⅱ卷】设α，β为两个平面，则α∥β的充要条件是( )A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ∥的充分条件，由面面平行性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ∥的必要条件，故选B ．3．【2019·全国Ⅲ卷】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则( )A ．BM =EN ，且直线BM ，EN 是相交直线；B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM ，EN 是异面直线；D ．BM ≠EN ，且直线BM ，EN 是异面直线【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线.过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知3,12EO ON EN ===,，35,,722MF BF BM ==∴=，BM EN ∴≠，故选B ．4．【2019·浙江卷】祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V 柱体=Sh ，其中S 是柱体的底面积，h 是柱体的高．若某柱体的三视图如图所示（单位：cm ），则该柱体的体积（单位：cm 3）是( )A ．158B ．162C ．182D ．324 【解析】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为264633616222++⎛⎫⨯+⨯⨯=⎪⎝⎭. 故选B.5．【2019·浙江卷】设三棱锥V –ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P –AC –B 的平面角为γ，则( ) A ．β<γ，α<γ B ．β<α，β<γ C ．β<α，γ<α D ．α<β，γ<β 【解析】如图，G 为AC 中点，连接VG ，V 在底面ABC 的投影为O ，则P 在底面的投影D 在线段AO 上，过D 作DE 垂直于AC 于E ，连接PE ，BD ，易得PE VG ∥，过P 作PF AC ∥交VG 于F ，连接BF ，过D 作DH AC ∥，交BG 于H ，则,,BPF PBD PED αβγ=∠=∠=∠，结合△PFB ，△BDH ，△PDB 均为直角三角形，可得cos cos PF EG DH BD PB PB PB PBαβ===<=，即αβ>；在Rt △PED 中，tan tan PD PD ED BD γβ=>=，即γβ>，综上所述，答案为B.6．【2019·全国Ⅲ卷】学生到工厂劳动实践，利用3D 打印技术制作模型.如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，16cm 4cm AB =BC =, AA =，3D 打印所用原料密度为0.9 g/cm 3，不考虑打印损耗，制作该模型所需原料的质量为___________g.【解析】由题意得，214642312cm 2EFGH S =⨯-⨯⨯⨯=四边形，∵四棱锥O −EFGH 的高为3cm ， ∴3112312cm 3O EFGH V -=⨯⨯=．又长方体1111ABCD A B C D -的体积为32466144cm V =⨯⨯=，所以该模型体积为3214412132cm O EFGH V V V -=-=-=，其质量为0.9132118.8g ⨯=．7．【2019·北京卷】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__________．【解析】如图所示，在棱长为4的正方体中，三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体，则几何体的体积()3142424402V =-⨯+⨯⨯=.8．【2019·北京卷】已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ； ②m ∥α； ③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．【解析】将所给论断，分别作为条件、结论，得到如下三个命题：（1）如果l ⊥α，m ∥α，则l ⊥m ，正确；（2）如果l ⊥α，l ⊥m ，则m ∥α，不正确，有可能m 在平面α内；（3）如果l ⊥m ，m ∥α，则l ⊥α，不正确，有可能l 与α斜交、l ∥α.故答案为：如果l ⊥α，m ∥α，则l ⊥m.9．【2019·天津卷】已知四棱锥的底面是边长为2的正方形，侧棱长均为5．若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为_____________．【解析】由题意，四棱锥的底面是边长为2的正方形，侧棱长均为5，借助勾股定理，可知四棱锥的高为512-=.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，一个底面的圆心为四棱锥底面的中心，故圆柱的高为1，圆柱的底面半径为12，故圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭. 10．【2019·江苏卷】如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD 的体积是 ▲ .【解析】因为长方体1111ABCD A B C D -的体积为120，所以1120AB BC CC ⋅⋅=，因为E 为1CC 的中点，所以112CE CC =，由长方体的性质知1CC ⊥底面ABCD ，所以CE 是三棱锥E BCD -的底面BCD 上的高，所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=. 【2018年】1．【2018·全国Ⅰ卷】某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为A ．172B ．52C ．3D ．2【答案】B2．【2018·全国Ⅰ卷】已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为 A ．33 B ．23 C ．324D ．3【解析】根据相互平行的直线与平面所成的角是相等的，所以在正方体1111ABCD A B C D -中，平面11AB D 与线11111,,AA A B A D 所成的角是相等的，所以平面11AB D 与正方体的每条棱所在的直线所成角都是相等的，同理，平面1C BD 也满足与正方体的每条棱所在的直线所成角都是相等的，要求截面面积最大，则截面的位置为夹在两个面11AB D 与1C BD 中间，且过棱的中点的正六边形，且边长为22，所以其面积为232336424S ⎛⎫=⨯⨯= ⎪ ⎪⎝⎭，故选A. 3．【2018·全国Ⅲ卷】中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是【解析】本题主要考查空间几何体的三视图.由题意知，俯视图中应有一不可见的长方形，且俯视图应为对称图形.故选A ．4．【2018·浙江卷】某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是俯视图正视图2211A ．2B ．4C ．6D ．8【解析】根据三视图可得几何体为一个直四棱柱，高为2，底面为直角梯形，上、下底分别为1，2，梯形的高为2，因此几何体的体积为()112226,2⨯+⨯⨯=故选C. 5．【2018·全国Ⅲ卷】设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为93，则三棱锥D ABC -体积的最大值为 A ．123B ．183C ．243D ．543【解析】如图所示，设点M 为三角形ABC 的重心，E 为AC 中点，当点D 在平面ABC 上的射影为M 时，三棱锥D ABC -的体积最大，此时，4OD OB R ===，2393ABC S AB ==△，6AB ∴=,点M 为三角形ABC 的重心，2233BM BE ∴==，Rt OBM ∴△中，有222OM OB BM =-=，426DM OD OM ∴=+=+=，()max 19361833D ABC V -∴=⨯⨯=，故选B.6．【2018·全国Ⅱ卷】在长方体1111ABCD A B C D -中，1AB BC ==，13AA =，则异面直线1AD 与1DB 所成角的余弦值为 A ．15B ．5C ．5 D ．2 【解析】方法一：用一个与原长方体相同的长方体拼到原长方体的前面，如图，则11B P AD ∥，连接DP ，易求得1=5DB DP =，12B P =，则1DB P ∠是异面直线1AD 与1DB 所成的角，由余弦定理可得222111115cos 2545DB B P DP DB P DB PB +-∠===⋅.故选C.方法二：以D 为坐标原点，DA ,DC ,DD 1所在直线分别为x ,y ,z 轴建立空间直角坐标系，则()()((110,0,0,1,0,0,3,3D A B D ,所以()(111,0,3,3AD DB =-=, 因为1111115cos ,25AD DB AD DB AD DB ⋅===⨯，所以异面直线1AD 与1DB 所成角的余弦值为55，故选C. 7．【2018·浙江卷】已知四棱锥S −ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S −AB −C 的平面角为θ3，则A ．θ1≤θ2≤θ3B ．θ3≤θ2≤θ1C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ1【解析】设O 为正方形ABCD 的中心，M 为AB 中点，过E 作BC 的平行线EF ，交CD 于F ，过O 作ON 垂直EF 于N ，连接SO ，SN ，SE ，SM ，OM ，OE ，则SO 垂直于底面ABCD ，OM 垂直于AB ，因此123,,,SEN SEO SMO ∠=∠=∠=θθθ 从而123tan ,tan ,tan ,SN SN SO SOEN OM EO OM====θθθ 因为SN SO EO OM ≥≥，，所以132tan tan tan ,≥≥θθθ即132≥≥θθθ，故选D.8．【2018·江苏卷】如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．【答案】439．【2018·全国II 卷】已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45°，若SAB △的面积为515__________．【解析】因为母线SA ，SB 所成角的余弦值为78，所以母线SA ，SB 所成角的正弦值为158，因为SAB △的面积为515,l 所以22115515,802l l ⨯=∴=，因为SA 与圆锥底面所成角为45°，所以底面半径为π2cos ,42r l ==因此圆锥的侧面积为22ππ402π.2rl l == 【2017年】1．【2017·全国Ⅱ卷】已知直三棱柱111ABC A B C -中，120ABC ∠=︒，2AB =，11BC CC ==，则异面直线1AB 与1BC 所成角的余弦值为A 3B 15C 10D 3【答案】C【解析】如图所示，补成直四棱柱1111ABCD A B C D -，则所求角为21111,2,21221cos603,5BC D BC BD C D AB ∠==+-⨯⨯⨯︒===，易得22211C D BD BC =+，因此111210cos 55BC BC D C D ∠===，故选C ． 2．【2017·全国Ⅰ卷】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A ．10B ．12C ．14D ．16【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为12(24)2122⨯+⨯⨯=，故选B ． 3．【2017·北京卷】某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为A ．2B ．3C ．2D ．2【解析】几何体是四棱锥P ABCD -，如图.最长的棱长为补成的正方体的体对角线，即该四棱锥的最长棱的长度为22222223l =++=，选B ． 4．【2017·全国Ⅱ卷】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A ．90πB ．63πC ．42πD ．36π【解析】由题意，该几何体是一个组合体，下半部分是一个底面半径为3，高为4的圆柱，其体积213436V =π⨯⨯=π，上半部分是一个底面半径为3，高为6的圆柱的一半，其体积221(36)272V =⨯π⨯⨯=π，故该组合体的体积12362763V V V =+=π+π=π．故选B ．5．【2017·全国Ⅲ卷】已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为 A ．πB ．3π4 C ．π2D ．π4【解析】绘制圆柱的轴截面如图所示：由题意可得：11,2AC AB ==，结合勾股定理，底面半径2213122r ⎛⎫=-= ⎪⎝⎭，由圆柱的体积公式，可得圆柱的体积是2233ππ1π24V r h ⎛⎫==⨯⨯= ⎪ ⎪⎝⎭，故选B. 6．【2017·浙江卷】某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是A ．12π+ B ．32π+ C ．312π+ D ．332π+ 【解析】根据所给三视图可还原几何体为半个圆锥和半个棱锥拼接而成的组合体，所以，几何体的体积为21113(21)13222V π⨯π=⨯⨯+⨯⨯=+，故选A ．7．【2017·浙江卷】如图，已知正四面体–D ABC （所有棱长均相等的三棱锥），P ，Q ，R 分别为AB ，BC ，CA 上的点，AP=PB ，2BQ CRQC RA==，分别记二面角D –PR –Q ，D –PQ –R ，D –QR –P 的平面角为αβγ,,，则A ． γαβ<<B ．αγβ<<C ．αβγ<<D ．βγα<<【解析】设O 为三角形ABC 中心，则O 到PQ 距离最小，O 到PR 距离最大，O 到RQ 距离居中，而三棱锥的高相等，因此αγβ<<，所以选B ．8．【2017·全国I 卷】如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O 上的点，△DBC ，△ECA ，△F AB 分别是以BC ，CA ，AB 为底边的等腰三角形.沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△F AB ，使得D ，E ，F 重合，得到三棱锥.当△ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为 .【解析】如下图，连接DO 交BC 于点G ，设D ，E ，F 重合于S 点，正三角形的边长为x (x >0)，则133OG x =⨯3x =.∴35FG SG x ==-， 222233566SO h SG GO x x ⎛⎫⎛⎫==-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭3553x ⎛⎫=- ⎪ ⎪⎝⎭， ∴三棱锥的体积2113355333ABC V S h x x ⎛⎫=⋅=⨯⨯- ⎪ ⎪⎝⎭△451535123x x =-. 设()4535n x x x =-，x >0，则()345320n x x x '=-，令()0n x '=，即43403x -=，得43x =，易知()n x 在43x =处取得最大值. ∴max 154854415V =⨯⨯-=.9．【2017·山东卷】由一个长方体和两个14圆柱体构成的几何体的三视图如图，则该几何体的体积为.【解析】由三视图可知,长方体的长、宽、高分别为2,1,1,圆柱的高为1,底面圆的半径为1,所以2π1π21121242V⨯=⨯⨯+⨯⨯=+.10．【2017·天津卷】已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为___________．【解析】设正方体的边长为a，则26183a a=⇒=，其外接球直径为233R a==，故这个球的体积34π3V R==4279ππ382⨯=．11．【2017·江苏卷】如图，在圆柱12O O内有一个球O，该球与圆柱的上、下底面及母线均相切．记圆柱12O O的体积为1V，球O的体积为2V，则12VV的值是.【解析】设球半径为r，则213223423V r rV rπ⨯==π．故答案为32．12．【2017·全国Ⅲ卷】a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：①当直线AB与a成60°角时，AB与b成30°角；②当直线AB与a成60°角时，AB与b成60°角；③直线AB与a所成角的最小值为45°；④直线AB与a所成角的最大值为60°.其中正确的是________.（填写所有正确结论的编号）【解析】设1AC BC ==.由题意，AB 是以AC 为轴,BC 为底面半径的圆锥的母线，由,AC a AC b ⊥⊥，又AC ⊥圆锥底面，所以在底面内可以过点B ，作BD a ∥，交底面圆C 于点D ，如图所示，连接DE ，则DE ⊥BD ，DE b ∴∥，连接AD ，等腰ABD △中，2AB AD ==,当直线AB 与a 成60°角时，60ABD ∠=，故2BD =，又在Rt BDE △中，2,2BE DE =∴=，过点B 作BF ∥DE ，交圆C 于点F ，连接AF ，由圆的对称性可知2BF DE ==,ABF ∴△为等边三角形，60ABF ∴∠=，即AB 与b 成60°角，②正确，①错误.由图可知③正确；很明显，可以满足平面ABC ⊥直线a ，则直线AB 与a 所成角的最大值为90°，④错误.故正确的是②③.【2016年】1. 【2016高考新课标1卷】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是（）（A ）17π （B ）18π （C ）20π （D ）28π【解析】该几何体直观图如图所示：是一个球被切掉左上角的18,设球的半径为R ,则37428V R 833ππ=⨯=,解得R 2=,所以它的表面积是78的球面面积和三个扇形面积之和2271=42+32=1784S πππ⨯⨯⨯⨯故选A ． 2.【2016高考新课标2理数】下图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（）（A ）20π （B ）24π （C ）28π （D ）32π【解析】由题意可知，圆柱的侧面积为12π2416πS =⋅⋅=，圆锥的侧面积为2π248πS =⋅⋅=，圆柱的底面面积为23π24πS =⋅=，故该几何体的表面积为12328πS S S S =++=，故选C.3.【2016年高考北京理数】某三棱锥的三视图如图所示，则该三棱锥的体积为（）A.16B.13C.12D.1 【解析】分析三视图可知，该几何体为一三棱锥P ABC -，其体积111111326V =⋅⋅⋅⋅=，故选A. 4.【2016高考新课标3理数】如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为（）（A ）18365+（B ）54185+（C ）90 （D ）81【解析】由三视图该几何体是以侧视图为底面的斜四棱柱，所以该几何体的表面积236233233554185S =⨯⨯+⨯⨯+⨯⨯=+，故选B ．5.【2016高考山东理数】一个由半球和四棱锥组成的几何体，其三视图如图所示.则该几何体的体积为（）（A ）1233+π （B ）1233+π （C ）1236+π （D ）216+π 【解析】由三视图可知,2的半球,体积为31142223V =⨯π⨯=）,下面是底面积为1,高为1的四棱锥,体积2111133V =⨯⨯=,故选C. 6.【2016高考浙江理数】已知互相垂直的平面αβ，交于直线l .若直线m ，n 满足,m n αβ∥⊥，则（）A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n【解析】由题意知,l l αββ=∴⊂，,n n l β⊥∴⊥．故选C ． 7.【2016年高考四川理数】已知三棱锥的四个面都是腰长为2的等腰三角形，该三棱锥的正视图如图所示，则该三棱锥的体积是 .正视图331【解析】由三棱锥的正视图知，三棱锥的高为1，底面边长为232,2，所以，该三棱锥的体积为113322132V =⨯⨯⨯=.8.【2016高考浙江理数】某几何体的三视图如图所示（单位：cm ），则该几何体的表面积是 cm 2，体积是 cm 3.【解析】几何体为两个相同长方体组合，长方体的长宽高分别为4,2,2，所以体积为2(224)32⨯⨯⨯=，由于两个长方体重叠部分为一个边长为2的正方形，所以表面积为2(222244)2(22)72⨯⨯+⨯⨯-⨯=9.【2016高考新课标2理数】 ,αβ是两个平面，,m n 是两条直线，有下列四个命题：（1）如果,,//m n m n αβ⊥⊥，那么αβ⊥.（2）如果,//m n αα⊥，那么m n ⊥.（3）如果//,m αβα⊂，那么//m β.（4）如果//,//m n αβ，那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有． (填写所有正确命题的编号）【解析】对于①，,,//m n m n αβ⊥⊥，则,αβ的位置关系无法确定，故错误；对于②,因为//n α，所以过直线n 作平面γ与平面β相交于直线c ，则//n c ，因为,,m m c m n α⊥∴⊥∴⊥，故②正确；对于③，由两个平面平行的性质可知正确；对于④，由线面所成角的定义和等角定理可知其正确，正确的有②③④.10.【2016高考浙江理数】如图，在△ABC 中，AB =BC =2，∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ，满足PD =DA ，PB =BA ，则四面体PBCD 的体积的最大值是 .【解析】ABC △中，因为2,120AB BC ABC ==∠=，所以30BAD BCA ∠=∠=.由余弦定理可得2222cos AC AB BC AB BC B =+-⋅2222222cos12012=+-⨯⨯=，所以AC =设AD x =，则0x <<DC x =.在ABD ∆中，由余弦定理可得2222cos BD AD AB AD AB A =+-⋅22222cos30x x =+-⋅24x =-+.故BD =在PBD ∆中，PD AD x ==，2PB BA ==.由余弦定理可得222cos 2PD PB BD BPD PD PB +-∠===⋅，所以30BPD ∠=. 由此可得，将△ABD 沿BD 翻折后可与△PBD 重合，无论点D 在任何位置，只要点D 的位置确定，当平面PBD ⊥平面BDC 时，四面体PBCD 的体积最大（欲求最大值可不考虑不垂直的情况）.EDC B A P过P 作直线BD 的垂线，垂足为O .设PO d =，则11sin 22PBD S BD d PD PB BPD =⨯=⋅∠△，12sin 302d x =⋅，解得d = 而△BCD的面积111sin )2sin 30(2)222S CD BC BCD x x=⋅∠=⋅=.当平面PBD ⊥平面BDC 时：四面体PBCD 的体积111)332BCD V S d x=⨯=⨯△=.观察上式，易得)2x x x x +≤，当且仅当x x -，即x 时取等号，同时我们可以发现当x x PBCD 的体积最大，为1.211.【2016高考新课标1卷】平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α//平面CB 1D 1,α平面ABCD =m ,α平面AB B 1A 1=n ,则m 、n 所成角的正弦值为 (A)2(B )2(C)3 (D)13【解析】设平面11CB D 平面ABCD ='m ，平面11CB D 平面11ABB A ='n ，因为α∥平面11CB D ，所以','m m n n ∥∥，则,m n 所成的角等于','m n 所成的角.过1D 作11D E B C ∥，交AD 的延长线于点E,连接CE ，则CE 为'm .连接1A B ，过B 1作111B F A B ∥，交1AA 的延长线于点1F ，则11B F 为'n .连接BD ，则111,BD CE B F A B ∥∥，则','m n 所成的角即为1,A B BD 所成的角，为60︒，故,m n 所成角的正弦值为32，选A.12.【2016高考新课标3理数】在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，13AA =，则V 的最大值是（）（A ）4π （B ）92π （C ）6π （D ）323π 【解析】要使球的体积V 最大，必须球的半径R 最大．由题意知球的与直三棱柱的上下底面都相切时，球的半径取得最大值32，此时球的体积为334439()3322R πππ==，故选B ． 13.【2016高考天津理数】已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图所示（单位：m ），则该四棱锥的体积为_______m 3.【解析】由三视图知四棱锥高为3，底面平行四边形的一边长为2，其对应的高为1，因此所求四棱锥的体积1(21)323V =⨯⨯⨯=．故答案为2．。

近九年高考全国卷空间立体几何真题汇编

近九年高考全国卷空间立体几何真题汇编2018年全国普通高等学校招生考试(全国卷Ⅲ)19．（12分）如图，边长为2的正方形ABCD 所在的平面与半圆弧 CD所在平面垂直，M 是 CD 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；(2)当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．2018年全国普通高等学校招生考试(全国卷Ⅱ)20．（12分）如图，在三棱锥-P ABC 中，==AB BC 4====PA PB PC AC ，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且二面角--M PA C 为30︒，求PC 与平面PAM 所成角的正弦值．2018年全国普通高等学校招生考试(新课标全国Ⅰ卷)18．（12分）如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥．(1)证明：平面PEF ⊥平面ABFD ；(2)求DP 与平面ABFD 所成角的正弦值．2017年普通高等学校统一招生考试·乙卷(新课标Ⅰ)18．（12分）如图，在四棱锥P ABCD -中，AB ∥CD ，且90BAP CDP ∠=∠=．(1)证明：平面PAB ⊥平面PAD ；(2)若PA PD AB DC ===，90APD ∠=，求二面角A PB C --的余弦值．2017年普通高等学校招生统一考试·甲卷（新课标Ⅱ）19．（12分）如图，四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面三角形ABCD ，12AB BC AD ==，90BAD ABC ∠=∠= ，E 是PD 的中点．(1)证明：直线CE ∥平面PAB ；(2)点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45，求二面角M AB D --的余弦值2017年普通高等学校统一招生考试·丙卷(新课标Ⅲ)19．（12分）如图，四面体ABCD 中，ABC ∆是正三角形，ACD ∆是直角三角形，ABD CBD ∠=∠，AB BD =．(1)证明：平面ACD ⊥平面ABC ；(2)过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D AE C --的余弦值．（18）（本小题满分12分）如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF =2FD ，90AFD ∠=，且二面角D -AF -E 与二面角C -BE -F 都是60．（I ）证明：平面ABEF ⊥平面EFDC ；（II ）求二面角E -BC -A 的余弦值．2016年普通高等学校招生全国统一考试·甲卷(全国卷Ⅱ)（19）（本小题满分12分）如图，菱形ABCD 的对角线AC 与BD 交于点O ，5AB =，6AC =，点E ，F 分别在AD ，CD 上，54AE CF ==，EF 交BD 于点H ．将ΔDEF 沿EF 折到ΔD EF '的位置，OD '=（Ⅰ）证明：D H '⊥平面ABCD ；（Ⅱ）求二面角B D A C '--的正弦值．（19）（本小题满分12分）如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，AD BC ，=3AB AD AC ==，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（Ⅰ）证明MN 平面PAB ；（Ⅱ）求直线AN 与平面PMN 所成角的正弦值．2015年全国高考试题独家解析(新课标全国卷Ⅱ)19．(本小题满分12分）如图，长方体ABCD -A 1B 1C 1D 1中AB =16，BC =10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E =D 1F =4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．（Ⅰ）在图中画出这个正方形（不必说出画法和理由）；（Ⅱ）求直线AF 与平面α所成角的正弦值．2015年全国高考试题独家解析(新课标全国卷Ⅰ)18．如图，四边形ABCD 为菱形，120ABC ∠=，,E F 是平面ABCD 同一侧的两点，BE⊥平面ABCD ，DF ⊥平面ABCD ，BE =2DF ，AE ⊥EC ．（Ⅰ）证明：平面AEC ⊥平面AFC ；（Ⅱ）求直线AE 与直线CF 所成角的余弦值．2014年全国高考试题独家解析(新课标卷Ⅱ)18．（本小题满分12分）如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．（Ⅰ）证明：PB ∥平面AEC ；（Ⅱ）设二面角D AE C --为60°，AP =1，AD ，求三棱锥E ACD -的体积．19．(本小题满分12分)如图三棱锥111ABC A B C -中，侧面11BB C C 为菱形，1AB B C ⊥．(Ⅰ)证明：1AC AB =；(Ⅱ)若1AC AB ⊥，o160CBB ∠=，AB BC =，求二面角111A A B C --的余弦值．2014年普通高等学校招生全国统一考试(全国大纲卷)19．（本小题满分12分）如图，三棱柱111ABC A B C -中，点1A 在平面ABC 内的射影D 在AC 上，090ACB ∠=，11,2BC AC CC ===．(1)证明：11AC A B ⊥；(2)设直线1AA 与平面11BCC B 1A AB C --的大小．（18）如图，直三棱柱111ABC A B C -中，,D E 分别是1,AB BB 的中点，122AA AC CB AB ===(Ⅰ)证明：1BC //平面1A CD ；(Ⅱ)求二面角1D A C E --的正弦值．2013年全国高考试题独家解析(新课标卷Ⅰ)18．（本小题满分12分）如图，三棱柱ABC-A 1B 1C 1中，CA =CB ，AB =AA 1，∠BA A 1=60°．(Ⅰ)证明AB ⊥A 1C ；(Ⅱ)若平面ABC ⊥平面AA 1B 1B ，AB=CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值．19．（本小题满分12分）如图，四棱锥P-ABCD 中，090ABC BAD ∠=∠=，2BC AD =，PAB ∆和PAD ∆都是等边三角形．(1)证明：;PB CD ⊥(2)求二面角.A PD C --的大小2012年普通高等学校招生全国统一考试（新课标全国卷）19．（本小题满分12分）如图，直三棱柱111C B A ABC -中，112AC BC AA ==，D 是棱1AA 的中点，BD DC ⊥1．（Ⅰ）证明：BC DC ⊥1；（Ⅱ）求二面角11C BD A --的大小．AC B1B 1A D1C18．如图，四棱锥P ABCD -中，底面ABCD 为菱形，PA ⊥底面ABCD ，AC =，PA =2，E 是PC 上的一点，2PE EC =．(Ⅰ)证明：PC ⊥平面BED ；(Ⅱ)设二面角A PB C --为90°，求PD 与平面PBC 所成角的大小．2011年普通高等学校招生全国统一考试(新课标全国卷)18．（本小题满分12分）如图，四棱锥P ABCD -中，底面ABCD 为平行四边形，60DAB ∠=︒，2AB AD =，PD ⊥底面ABCD ．(Ⅰ)证明：PA BD ⊥；(Ⅱ)若PD AD =，求二面角A PB C --的余弦值．19．（本小题满分12分）如图，四棱锥S ABCD -中，AB CD ⊥，BC CD ⊥，侧面SAB 为等边三角形，2,1AB BC CD SD ====．(Ⅰ)证明：SD SAB ⊥平面；(Ⅱ)求AB 与平面SBC 所成角的大小．2010年普通高等学校招生全国统一考试(新课标全国卷)18．（本小题满分12分）如图，已知四棱锥P ABCD -的底面为等腰梯形，AB CD ∥，AC BD ⊥，垂足为H ，PH 是四棱锥的高，E 为AD 中点．(Ⅰ)证明：PE BC ⊥；(Ⅱ)若60APB ADB ∠=∠=，求直线PA 与平面PEH 所成角的正弦值．19．（本小题满分12分）如图，直三棱柱111ABC A B C -中，AC BC =，1AA AB =，D 为1BB 的中点，E 为1AB 上的一点，13AE EB =．(1)证明：DE 为异面直线1AB 与CD 的公垂线；(2)设异面直线1AB 与CD 的夹角为45°，求二面角111A AC B --的大小．2010年普通高等学校招生全国统一考试(全国大纲Ⅰ卷)19．(本小题满分12分)如图，四棱锥S ﹣ABCD 中，SD ⊥底面ABCD ，AB ∥DC ，AD ⊥DC ，AB =AD =1，DC =SD =2，E 为棱SB 上的一点，平面EDC ⊥平面SBC ．(1)证明：SE =2EB ；(2)求二面角A ﹣DE ﹣C 的大小．。

2021-2023三年新高考立体几何大题-含答案

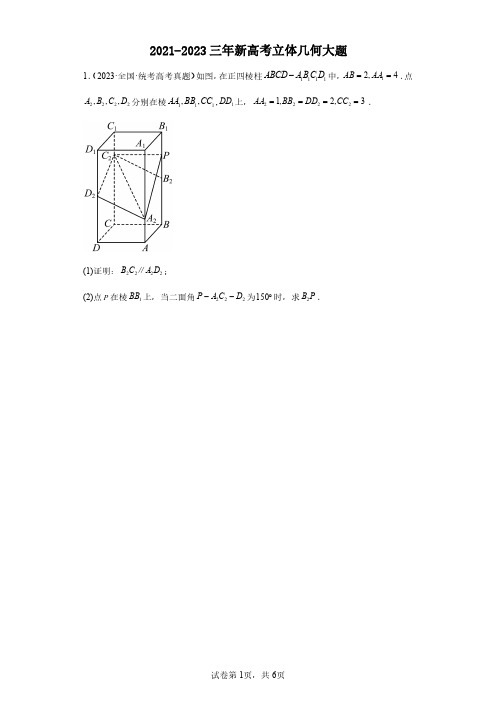
2021-2023三年新高考立体几何大题1．（2023·全国·统考高考真题）如图，在正四棱柱1111ABCD A B C D -中，12,4AB AA ==．点2222,,,A B C D 分别在棱111,,AA BB CC ,1DD 上，22221,2,3AA BB DD CC ====．(1)证明：2222B C A D ∥；(2)点P 在棱1BB 上，当二面角222P A C D --为150︒时，求2B P ．2．（2023·全国·统考高考真题）如图，三棱锥A BCD -中，DA DB DC ==，BD CD ⊥，60ADB ADC ∠=∠= ，E 为BC 的中点．(1)证明：BC DA ⊥；(2)点F 满足EF DA = ，求二面角D AB F --的正弦值．(1)求A 到平面1A BC 的距离；(2)设D 为1AC 的中点，1AA AB =，平面弦值．4．（2022·全国·统考高考真题）如图，PO 是三棱锥-P ABC 的高，PA PB =，AB AC ⊥，E 是PB 的中点．(1)证明：//OE 平面PAC ；(2)若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --的正弦值．5．（2021·全国·统考高考真题）如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.（1）证明：OA CD ⊥；（2）若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积.（1）证明：平面QAD⊥--（2）求二面角B QD A参考答案：答案第1页，共1页2021-2023三年新高考立体几何大题1．（2023·全国·统考高考真题）如图，在正四棱柱1111ABCD A B C D -中，12,4AB AA ==．点2222,,,A B C D 分别在棱111,,AA BB CC ,1DD 上，22221,2,3AA BB DD CC ====．(1)证明：2222B C A D ∥；(2)点P 在棱1BB 上，当二面角222P A C D --为150︒时，求2B P ．【答案】(1)证明见解析；(2)1【分析】（1）建立空间直角坐标系，利用向量坐标相等证明；（2）设(0,2,)(04)P λλ≤≤，利用向量法求二面角，建立方程求出λ即可得解.【详解】（1）以C 为坐标原点，1,,CD CB CC 所在直线为,,x y z 轴建立空间直角坐标系，如图，则2222(0,0,0),(0,0,3),(0,2,2),(2,0,2),(2,2,1)C C B D A ，2222(0,2,1),(0,2,1)B C A D ∴=-=- ，设(2,0,0),(0,0,2),(0,2,0),D A B 设平面DAB 与平面ABF 的一个法向量分别为二面角D AB F --平面角为θ,而AB 因为()2,0,2EF DA ==- ，所以1111220220x z y z ⎧-+=⎪∴⎨-=⎪⎩，取11x =，所以22222020y z x ⎧-=⎪⎨-=⎪⎩，取21y =，所以n(1)求A 到平面1A BC 的距离；(2)设D 为1AC 的中点，1AA AB =，平面弦值．【答案】(1)2(2)32【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得BC 间向量法即可得解.【详解】（1）在直三棱柱111ABC A B C -中，设点则11112233A A BC A A ABC BC V S h h V --=⋅===由（1）得2AE =，所以12AA AB ==，1A B =则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以AC 则()1,1,1BD = ，()()0,2,0,2,0,0BA BC == ,设平面ABD 的一个法向量(),,m x y z = ，则m BD m BA ⎧⋅⎨⋅⎩可取()1,0,1m =- ，设平面BDC 的一个法向量(),,n a b c = ，则n BD n BC ⎧⋅⎨⋅⎩可取()0,1,1n =-r ，则11cos ,222m n m n m n ⋅===⨯⋅ ，所以二面角A BD C --的正弦值为21122⎛⎫-= ⎪⎝⎭(1)证明：//OE 平面PAC ；(2)若30ABO CBO ∠=∠=︒，3PO =，【答案】(1)证明见解析(2)1113【分析】（1）连接BO 并延长交AC 于点再根据直角三角形的性质得到AO DO =即可得证；（2）建立适当的空间直角坐标系，利用空间向量法求出二面角的余弦的绝对值，再根据同角三角函数的基本关系计算可得【详解】（1）证明：连接BO 并延长交因为PO 是三棱锥-P ABC 的高，所以所以PO AO ⊥、PO BO ⊥，又PA PB =，所以POA POB ≅△△，即又AB AC ⊥，即90BAC ∠=︒，所以∠所以ODA OAD∠=∠所以AO DO =，即AO DO OB ==，所以又OE ⊄平面PAC ，PD ⊂平面PAC 所以//OE 平面PAC（2）解：过点A 作//Az OP ，如图建立空间直角坐标系，13-中，平面ABD⊥5．（2021·全国·统考高考真题）如图，在三棱锥A BCD=，O为BD的中点.AB AD（1）证明：OA CD ⊥；所以42(0,,),33EB m BC =--= 设(),,n x y z =r 为平面EBC 的法向量，因为OA ⊥平面BCD ，所以EG EFG ∠为二面角E BC D --的平面角．因为45EFG ∠=︒，所以EG =由已知得1OB OD ==，故OB如图可知π(0,)2α∈，即有tan根据三角形相似知，点G为OD 结合α的正切值，可得2,1EG OA==从而可得三棱锥（1）证明：平面QAD⊥（2）求二面角B QD A--【答案】（1）证明见解析；【分析】（1）取AD的中点为QAD⊥面ABCD.（2）在平面ABCD内，过【详解】AD 的中点为O ，连接,QO CO QD =，OA OD =，则QO ⊥2,5QA =，故51QO =-=ABCD 中，因为2AD =，故3=，故222QC QO OC =+，故AD O = ，故QO ⊥平面ABCD ⊂平面QAD ，故平面QAD ⊥）在平面ABCD 内，过O 作//OT CD ）中的QO ⊥平面ABCD ，故可建如图所示的空间坐标系则()()()0,1,0,0,0,2,2,1,0D Q B -，故设平面QBD 的法向量(),,n x y z = ，则00n BQ n BD ⎧⋅=⎨⋅=⎩ 即220220x y z x y -++=⎧⎨-+=⎩，取故11,1,2n ⎛⎫= ⎪⎝⎭ .而平面QAD 的法向量为()1,0,0m = ，故二面角B QD A --的平面角为锐角，故其余弦值为。

2016年-2019年立体几何大题全国卷高考真题及答案

1、（2015年1卷18题）如图，四边形ABCD 为菱形，∠ABC=120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE=2DF ，AE ⊥EC.试题解析：（Ⅰ）连接BD ，设BD∩AC=G，连接EG ，FG ，EF ，在菱形ABCD 中，不妨设GB=1，由∠ABC=120°，可得AG=GC=3. 由BE ⊥平面ABCD ，AB=BC 可知，AE=EC ，又∵AE ⊥EC ，∴EG=3，EG ⊥AC ，在Rt △EBG 中，可得BE=2，故DF=22. 在Rt △FDG 中，可得FG=62. 在直角梯形BDFE 中，由BD=2，BE=2，DF=22可得EF=322， ∴222EG FG EF +=，∴EG ⊥FG ， ∵AC∩FG=G，∴EG ⊥平面AFC ，∵EG ⊂面AEC ，∴平面AFC ⊥平面AEC.（Ⅱ）如图，以G 为坐标原点，分别以,GB GC 的方向为x 轴，y 轴正方向，||GB 为单位长度，建立空间直角坐标系G-xyz ，由（Ⅰ）可得A （030），E （2），F （－1,0，22），C （030），∴AE =（132），CF =（-1，3，22）.…10分故cos ,3||||AE CF AE CF AE CF ⋅<>==-. 所以直线AE 与CF 所成的角的余弦值为3. 2、（2016年1卷18题）如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60．（I ）证明：平面ABEF ⊥平面EFDC ；（II ）求二面角E -BC -A 的余弦值．试题解析：（I ）由已知可得F DF A ⊥,F F A ⊥E ,所以F A ⊥平面FDC E ．又F A ⊂平面F ABE ,故平面F ABE ⊥平面FDC E ．（II ）过D 作DG F ⊥E ,垂足为G ,由（I ）知DG ⊥平面F ABE ．以G 为坐标原点,GF 的方向为x 轴正方向,GF 为单位长度,建立如图所示的空间直角坐标系G xyz -．由（I ）知DF ∠E 为二面角D F -A -E 的平面角,故DF 60∠E =,则DF 2=,DG 3=,可得()1,4,0A ,()3,4,0B -,()3,0,0E -,(D ．由已知,//F AB E ,所以//AB 平面FDC E ．又平面CDAB 平面FDC DC E =,故//CD AB ,CD//F E ．由//F BE A ,可得BE ⊥平面FDC E ,所以C F ∠E 为二面角C F -BE -的平面角,C F 60∠E =．从而可得(C -．所以(C E =,()0,4,0EB =,(C 3,A =--,()4,0,0AB =-．设(),,n x y z =是平面C B E 的法向量,则C 00n n⎧⋅E =⎪⎨⋅EB =⎪⎩,即40x y ⎧+=⎪⎨=⎪⎩, 所以可取(3,0,n =．CABDEF设m 是平面CD AB 的法向量,则C 00m m ⎧⋅A =⎪⎨⋅AB =⎪⎩,同理可取()0,3,4m =．则219cos ,19n m n m n m ⋅==-．故二面角C E -B -A 的余弦值为21919-．3（2016年2卷19题）（本小题满分12分）如图，菱形ABCD 的对角线AC 与BD 交于点O ，5AB =，6AC =，点E ，F 分别在AD ，CD 上，54AE CF ==，EF 交BD 于点H .将△DEF 沿EF 折到△D EF '的位置10OD '=.（I ）证明：D H '⊥平面ABCD ；（II ）求二面角B D A C '--的正弦值.【解析】⑴证明：∵54AE CF ==，∴AE CF AD CD=，∴EF AC ∥． ∵四边形ABCD 为菱形，∴AC BD ⊥，∴EF BD ⊥，∴EF DH ⊥，∴EF DH'⊥．∵6AC =，∴3AO =；又5AB =，AO OB ⊥， ∴4OB =，∴1AE OH OD AO=⋅=，∴3DH D H '==，∴222'OD OH D H '=+， ∴'D H OH ⊥．又∵OH EF H =，∴'D H ⊥面ABCD ．⑵建立如图坐标系H xyz -．()500B ，，，()130C ，，，()'003D ，，，()130A -，，， ()430AB =，，，()'133AD =-，，，()060AC =，，，设面'ABD 法向量()1n x y z =，，，由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩，取345x y z =⎧⎪=-⎨⎪=⎩， ∴()1345n =-，，．同理可得面'AD C 的法向量()2301n =，，， ∴12129575cos 255210n n n n θ⋅+===⋅，∴295sin 25θ=4、（2017年1卷18题）如图，在四棱锥P ABCD -中，AB CD ∥中，且90BAP CDP ∠=∠=︒．（1）证明：平面PAB ⊥平面PAD ；（2）若PA PD AB DC ===，90APD ∠=︒，求二面角A PB C --的余弦值．【解析】（1）证明：∵90BAP CDP ∠=∠=︒∴PA AB ⊥，PD CD ⊥又∵AB CD ∥，∴PD AB ⊥又∵PD PA P =，PD 、PA ⊂平面PAD ∴AB ⊥平面PAD ，又AB ⊂平面PAB ∴平面PAB ⊥平面PAD（2）取AD 中点O ，BC 中点E ，连接PO ，OE ∵AB CD∴四边形ABCD 为平行四边形 ∴OE AB由（1）知，AB ⊥平面PAD∴OE ⊥平面PAD ，又PO 、AD ⊂平面PAD ∴OE PO ⊥，OE AD ⊥ 又∵PA PD =，∴PO AD ⊥ ∴PO 、OE 、AD 两两垂直∴以O 为坐标原点，建立如图所示的空间直角坐标系O xyz - 设2PA =，∴()002D -，，、()220B ，，、()002P ，，、()202C -，，， ∴()022PD =--，，、()222PB =-，，、()2200BC =-，，设()n x y z =,,为平面PBC 的法向量由00n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩，得2220220x y z x ⎧+-=⎪⎨-=⎪⎩令1y =，则2z =，0x =，可得平面PBC 的一个法向量()012n =,, ∵90APD ∠=︒，∴PD PA ⊥又知AB ⊥平面PAD ，PD ⊂平面PAD ∴PD AB ⊥，又PA AB A = ∴PD ⊥平面PAB即PD 是平面PAB 的一个法向量，()022PD =--,, ∴23cos 323PD n PD n PD n⋅-===-⋅, 由图知二面角A PB C --为钝角，所以它的余弦值为33-5．（2018年1卷18题）如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥． ⑴证明：平面PEF ⊥平面ABFD ； ⑵求DP 与平面ABFD 所成角的正弦值．解答：（1）,E F 分别为,AD BC 的中点，则//EF AB ，∴EF BF ⊥，又PF BF ⊥，EF PF F ⋂=，∴BF ⊥平面PEF ， BE ⊂平面ABFD ，∴平面PEF ⊥平面ABFD . （2）PF BF ⊥，//BF ED ，∴PF ED ⊥，又PF PD ⊥，ED DP D ⋂=，∴PF ⊥平面PED ，∴PF PE ⊥，设4AB =，则4EF =，2PF =，∴23PE =，过P 作PH EF ⊥交EF 于H 点，由平面PEF ⊥平面ABFD ，∴PH ⊥平面ABFD ，连结DH ，则PDH ∠即为直线DP 与平面ABFD 所成的角，由PE PF EF PH ⋅=⋅，∴23234PH ⋅==，而4PD =，∴3sin 4PH PDH PD ∠==， ∴DP 与平面ABFD 所成角的正弦值34. 6.(2018年新课标Ⅱ理)如图,在三棱锥P -ABC 中,AB ＝BC ＝22,P A ＝PB ＝PC ＝AC ＝4,O 为AC 的中点.（1）求证:PO ⊥平面ABC ；（2）若点M 在棱BC 上,且二面角M -P A -C 为30°,求PC 与平面P AM 所成角的正弦值.【解析】（1）证明:∵AB ＝BC ＝22,AC ＝4,∴AB 2＋BC 2＝AC 2,即△ABC 是直角三角形. 又O 为AC 的中点,∴OA ＝OB ＝OC . ∵P A ＝PB ＝PC ,∴△POA ≌△POB ≌△POC . ∴∠POA ＝∠POB ＝∠POC ＝90°.∴PO ⊥AC ,PO ⊥OB ,OB ∩AC ＝0,∴PO ⊥平面ABC .（2）以O 坐标原点,OB ,OC ,OP 所在直线分别为x ,y ,z 轴建立空间直角坐标系如图所示.易知A (0,－2,0),P (0,0,23),C (0,2,0),B (2,0,0),BC →＝(－2,2,0). 设BM →＝λBC →＝(－2λ,2λ,0),0＜λ＜1,则AM →＝BM →－BA →＝(－2λ,2λ,0)－(－2,－2,0)＝(2－2λ,2λ＋2,0), 则平面P AC 的一个法向量为m ＝(1,0,0).设平面MP A 的法向量为n ＝(x ,y ,z ),则PA →＝(0,－2,23), 则n ·PA →＝－2y －23z ＝0,n ·AM →＝(2－2λ)x ＋(2λ＋2)y ＝0. 令z ＝1,则y ＝－3,x ＝(λ＋1)31－λ,即n ＝⎝ ⎛⎭⎪⎫(λ＋1)31－λ，－3，1.∵二面角M -P A -C 为30°,∴cos 30°＝m ·n |m ||n |＝32,即(λ＋1)3λ－1⎝ ⎛⎭⎪⎫(λ＋1)31－λ2＋1＋3×1＝32,解得λ＝13或λ＝3(舍去). ∴n ＝(23,－3,1),PC →＝(0,2,－23).PC 与平面P AM 所成角的正弦值sin θ＝|cos 〈PC →,n 〉|＝⎪⎪⎪⎪⎪⎪－23－2316·16＝4316＝34.18．（2019年1卷18题）（12分）如图，直四棱柱ABCD ﹣A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．（1）证明：MN ∥平面C 1DE ；（2）求二面角A ﹣MA 1﹣N 的正弦值．解答】（1）证明：如图，过N作NH⊥AD，则NH∥AA1，且，又MB∥AA1，MB＝，∴四边形NMBH为平行四边形，则NM∥BH，由NH∥AA1，N为A1D中点，得H为AD中点，而E为BC中点，∴BE∥DH，BE＝DH，则四边形BEDH为平行四边形，则BH∥DE，∴NM∥DE，∵NM⊄平面C1DE，DE⊂平面C1DE，∴MN∥平面C1DE；（2）解：以D为坐标原点，以垂直于DC得直线为x轴，以DC所在直线为y轴，以DD1所在直线为z轴建立空间直角坐标系，则N（，，2），M（，1，2），A1（，﹣1，4），，，设平面A1MN的一个法向量为，由，取x＝，得，又平面MAA1的一个法向量为，∴cos＜＞＝＝＝．∴二面角A﹣MA1﹣N的正弦值为．8．（12分）(2019年新课标Ⅱ理）如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1. （1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，求二面角B –EC –C 1的正弦值.解：（1）由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ，故11B C ⊥BE ．又1BEEC ⊥，所以BE ⊥平面11EB C ．（2）由（1）知190BEB ∠=︒．由题设知11Rt Rt ABE A B E ≅△△，所以45AEB ∠=︒，故AE AB =，12AA AB =．以D 为坐标原点，DA 的方向为x 轴正方向，||DA 为单位长，建立如图所示的空间直角坐标系D -xyz ，则C （0，1，0），B （1，1，0），1C （0，1，2），E （1，0，1），(1,1,1)CE =-，1(0,0,2)CC =．设平面EBC 的法向量为n =（x ，y ，x ），则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x x y z =⎧⎨-+=⎩ 所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =（x ，y ，z ），则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩m m 即20,0.z x y z =⎧⎨-+=⎩ 所以可取m =（1，1，0）．于是1cos ,||||2⋅<>==-n m n m n m ．所以，二面角1B EC C --3．。

新课标全国卷历年高考立体几何真题

1 1.（2012年全国卷）如图，直三棱柱111ABC A B C -中，112AC BC AA ==，D 是棱1AA 的中点，BD DC ⊥1.（Ⅰ）证明：BC DC ⊥1；（Ⅱ）求二面角11C BD A --的大小.2.（2013年全国Ⅱ卷）如图，直棱柱ABC-A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点，AA 1AB. （Ⅰ）证明：BC 1//平面A 1CD ，（Ⅱ）求二面角D-A 1C-E 的正弦值3.（2013年全国Ⅰ卷）如图，三棱柱111C B A ABC -中，CB CA =，1AA AB =， 601=∠BAA . （Ⅰ）证明C A AB 1⊥；（Ⅱ）若平面ABC ⊥平面AA 1B 1B ，AB=CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值.24.（2014年全国Ⅱ卷）如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ；(Ⅱ)设二面角D-AE-C 为60°，AP=1，求三棱锥E-ACD 的体积.5.（2015年全国Ⅱ卷）如图，长方体ABCD-A 1B 1C 1D 1中，AB=16，BC=10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E=D 1F=4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形. (Ⅰ)在图中画出这个正方形(不必说出画法和理由)；(Ⅱ)求直线AF 与平面α所成角的正弦值.6.（2016年全国Ⅱ卷）如图，菱形ABCD 的对角线AC 与BD 交于点O ，5,6AB AC ==，点,E F 分别在,AD CD 上，54AE CF ==，EF 交BD 于点H ．将DEF ∆沿EF 折到'D EF ∆位置，OD '=（Ⅰ）证明：D H '⊥平面ABCD ；（Ⅱ）求二面角B D A C '--的正弦值．。

2018-2022五年全国高考数学立体几何真题分类汇编(试卷版)

2018-2022五年全国各省份高考数学真题分类汇编专题21 立体几何解答题一、解答题1. (2022高考北京卷·第17题)如图, 在三棱柱中, 侧面为正方形, 平面平面, , M, N分别为, AC的中点.(1)求证: 平面；(2)再从条件①、条件②这两个条件中选择一个作为已知, 求直线AB与平面BMN所成角的正弦值．条件①: ；条件②: .注：如果选择条件①和条件②分别解答, 按第一个解答计分．2. (2022年高考全国甲卷数学(理)·第18题)在四棱锥中, 底面.(1)证明: ；(2)求PD与平面所成的角的正弦值.3. (2022年浙江省高考数学试题·第19题)如图, 已知和都是直角梯形, , , , , , , 二面角的平面角为. 设M, N分别为的中点.(1)证明: ；(2)求直线与平面所成角的正弦值.4. (2022新高考全国II卷·第20题)如图, 是三棱锥的高, , , E是的中点.(1)证明: 平面；(2)若, , , 求二面角/正弦值．5. (2022新高考全国I卷·第19题)如图, 直三棱柱的体积为4, 的面积为.(1)求A到平面1A BC的距离；(2)设D为的中点, , 平面平面, 求二面角的正弦值.6. (2022年高考全国乙卷数学(理)·第18题)如图, 四面体中, , E为的中点.(1)证明: 平面平面；(2)设, 点F在上, 当的面积最小时, 求与平面所成的角的正弦值．7. (2021年高考浙江卷·第19题)如图, 在四棱锥中, 底面是平行四边形, , M, N分别为的中点, .(1)证明: ；(2)求直线与平面所成角的正弦值.8. (2021年新高考全国Ⅱ卷·第19题)在四棱锥中, 底面是正方形, 若.(1)证明: 平面平面；(2)求二面角/平面角的余弦值.9. (2021年新高考Ⅰ卷·第20题)如图, 在三棱锥中, 平面平面, , 为的中点.(1)证明: ；(2)若是边长为1/等边三角形, 点在棱上, , 且二面角的大小为, 求三棱锥的体积．10. (2021年高考全国乙卷理科·第18题)如图, 四棱锥的底面是矩形, 底面, , 为的中点,且.(1)求BC；(2)求二面角的正弦值.11. (2021年高考全国甲卷理科·第19题)已知直三棱柱中, 侧面为正方形, , E, F分别为和/中点, D为棱上的点.(1)证明: ；(2)当为何值时, 面与面所成的二面角的正弦值最小?12. (2021高考北京·第17题)如图: 在正方体中, 为中点, 与平面交于点.(1)求证: 为的中点；(2)点是棱上一点, 且二面角的余弦值为, 求的值．13. (2020年高考课标Ⅰ卷理科·第18题)如图, 为圆锥的顶点, 是圆锥底面的圆心, 为底面直径, . 是底面的内接正三角形, 为上一点, .(1)证明: 平面；(2)求二面角的余弦值.14. (2020年高考课标Ⅱ卷理科·第20题)如图, 已知三棱柱ABC-A1B1C1的底面是正三角形, 侧面BB1C1C是矩形, M, N分别为BC, B1C1的中点, P为AM上一点, 过B1C1和P 的平面交AB于E, 交AC于F.(1)证明: AA1∥MN, 且平面A1AMN⊥EB1C1F；(2)设O为△A1B1C1的中心, 若AO∥平面EB1C1F, 且AO=AB, 求直线B1E与平面A1AMN 所成角的正弦值.15．(2020年高考课标Ⅲ卷理科·第19题)如图, 在长方体中, 点分别在棱上, 且, ．(1)证明: 点/平面内；(2)若, , , 求二面角的正弦值．16. (2020年新高考全国Ⅰ卷(山东)·第20题)如图, 四棱锥P-ABCD的底面为正方形, PD⊥底面ABCD. 设平面PAD与平面PBC的交线为l.(1)证明: l⊥平面PDC；(2)已知PD=AD=1, Q为l上的点, 求PB与平面QCD所成角的正弦值的最大值．17. (2020年新高考全国卷Ⅱ数学(海南)·第20题)如图, 四棱锥P-ABCD的底面为正方形,PD底面ABCD. 设平面PAD与平面PBC的交线为.(1)证明: 平面PDC；(2)已知PD=AD=1, Q为上的点, QB=, 求PB与平面QCD所成角的正弦值．18. (2020年浙江省高考数学试卷·第19题)如图, 三棱台DEF—ABC中, 面ADFC⊥面ABC, ∠ACB=∠ACD=45°, DC =2BC.(I)证明: EF⊥DB；(II)求DF与面DBC所成角的正弦值.19. (2020天津高考·第17题)如图, 在三棱柱中, 平面, , 点分别在棱和棱上, 且为棱的中点.(Ⅰ)求证: ；(Ⅱ)求二面角1B B E D --的正弦值；(Ⅲ)求直线与平面所成角的正弦值.20. (2020江苏高考·第24题)在三棱锥中, 已知,, 为的中点, 平面, , 为的中点.(1)求直线AB 与DE 所成角的余弦值；(2)若点在上, 满足, 设二面角的大小为, 求的值.21. (2020江苏高考·第15题)在三棱柱中, , 平面, 分别是的中点.(1)求证: 平面；(2)求证：平面平面.22. (2020北京高考·第16题)如图, 在正方体中, 为的中点.(Ⅰ)求证: 平面；(Ⅱ)求直线与平面所成角的正弦值.23. (2019年高考浙江·第19题)如图, 已知三棱柱, 平面平面, , , , , 分别是, 的中点．(Ⅰ)证明: ；(Ⅱ)求直线与平面所成角的余弦值.24. (2019年高考天津理·第17题)如图, 平面, , . (Ⅰ)求证: 平面；(Ⅱ)求直线CE 与平面BDE 所成角的正弦值；(Ⅲ)若二面角的余弦值为, 求线段的长.25. (2019年高考上海·第17题)如图, 在长方体中, 为上一点, 已知, , , . (1)求直线1A C 与平面ABCD 的夹角； (2)求点A 到平面1A MC 的距离.FE C 1A 1B 1CBAABCDEF26. (2019年高考全国Ⅲ理·第19题)图1是由矩形ADEB, Rt △ABC 和菱形BFGC 组成的一个平面图形, 其中AB=1, BE=BF=2, ∠FBC=60°, 将其沿AB, BC 折起使得BE 与BF 重合, 连结DG, 如图2.(1)证明: 图2中的A, C, G, D 四点共面, 且平面ABC ⊥平面BCGE ；(2)求图2中的二面角B −CG −A 的大小.27. (2019年高考全国Ⅱ理·第17题)如图, 长方体的底面是正方形, 点在棱上, . 证明: 平面；若, 求二面角的正弦值．图2图1D A28. (2019年高考全国Ⅰ理·第18题)如图, 直四棱柱的底面是菱形, 分别是, , 的中点.(1)证明: 平面；(2)求二面角的正弦值.29. (2019年高考江苏·第16题)如图, 在直三棱柱中, 分别为, 的中点, .求证：(1)平面；(2).30. (2019年高考北京理·第16题)如图, 在四棱锥P–ABCD中, PA⊥平面ABCD, AD ⊥CD, AD∥BC, PA=AD=CD=2, BC=3. E为PD的中点, 点F在PC上, 且.(Ⅰ)求证: CD⊥平面PAD；(Ⅱ)求二面角F–AE–P的余弦值；(Ⅲ)设点G在PB上, 且. 判断直线AG是否在平面AEF内, 说明理由.31. (2018年高考数学江苏卷·第25题)(本小题满分10分)如图, 在正三棱柱ABC-A1B1C1中, AB=AA1=2, 点P, Q分别为A1B1, BC的中点.(1)求异面直线BP与AC1所成角的余弦值；(2)求直线CC1与平面AQC1所成角的正弦值.32. (2018年高考数学江苏卷·第15题)(本小题满分14分)在平行六面体中, .求证: (1)；(2).33. (2018年高考数学浙江卷·第19题)(本题满分15分)如图, 已知多面体, 均垂直于平面,, , , ．(1)证明: 平面；(2)求直线与平面所成角的正弦值.34. (2018年高考数学上海·第17题)(本题满分14分, 第1小题满分6分, 第2小题满分8分)已知圆锥的顶点为, 底面圆心为, 半径为2, (1)设圆锥的母线长为4, 求圆锥的体积；(2)设, 是底面半径, 且, 为线段的中点, 如图, 求异面直线与所成的角的大小．35. (2018年高考数学天津(理)·第17题)(本小题满分13分)如图, 且, , 且, , 且, 平面, . (1)若为的中点, 为的中点, 求证：平面； (2)求二面角E BC F --的正弦值；(3)若点在线段上, 且直线与平面所成的角为, 求线段的长.ACA 1C 1B 136. (2018年高考数学课标Ⅲ卷(理)·第19题)(12分)如图, 边长为的正方形所在平面与半圆弧所在的平面垂直, 是弧上异于的点. (1)证明: 平面平面；(2)当三棱锥体积最大时, 求面与面所成二面角的正弦值．37. (2018年高考数学课标Ⅱ卷(理)·第20题)(12分) 如图, 在三棱锥中, , , 为的中点． (1)证明: 平面；(2)若点在棱上, 且二面角为, 求与平面所成角的正弦值．ABC DEFG MN38. (2018年高考数学课标卷Ⅰ(理)·第18题)(12分)如图, 四边形为正方形, 分别为的中点, 以为折痕把折起, 使点到达点的位置, 且. (1)证明:平面PEF ⊥平面ABFD ； (2)求与平面所成角的正弦值.39. (2018年高考数学北京(理)·第16题)(本小题14分)如图, 在三棱柱中, 平面,分别为的中点, , . (Ⅰ)求证: 平面；(Ⅱ)求二面角1B CD C --的余弦值； (Ⅲ)证明: 直线与平面相交.PABMCO。

五年(2019-2023)年高考真题专题04 立体几何(解析版)

五年（2019-2023）年高考真题分项汇编专题04立体几何考点精析：考点一空间几何体的侧面积和表面积1．（2021()A ．2B ．C ．4D ．【解析】由题意，设母线长为l ，因为圆锥底面周长即为侧面展开图半圆的弧长，圆锥的母线长即为侧面展开图半圆的半径，则有2l ππ=⋅，解得l =所以该圆锥的母线长为故选：B ．2．（2022•上海）已知圆柱的高为4，底面积为9π，则圆柱的侧面积为．【解析】因为圆柱的底面积为9π，即29R ππ=，所以3R =，所以224S Rh ππ==侧．故答案为：24π．3．（2021•上海）已知圆柱的底面圆半径为1，高为2，AB 为上底面圆的一条直径，C 是下底面圆周上的一个动点，则ABC ∆的面积的取值范围为．【解析】如图1，上底面圆心记为O ，下底面圆心记为O '，连接OC ，过点C 作CM AB ⊥，垂足为点M ，则12ABC S AB CM ∆=⨯⨯，根据题意，AB 为定值2，所以ABC S ∆的大小随着CM 的长短变化而变化，如图2所示，当点M 与点O 重合时，CM OC ===此时ABC S ∆取得最大值为122⨯=；如图3所示，当点M 与点B 重合，CM 取最小值2，此时ABC S ∆取得最小值为12222⨯⨯=．综上所述，ABC S ∆的取值范围为．故答案为：．4．（2021•上海）已知圆柱的底面半径为1，高为2，则圆柱的侧面积为．【解析】圆柱的底面半径为1r =，高为2h =，所以圆柱的侧面积为22124S rh πππ==⨯⨯=侧．故答案为：4π．5．（2019•上海）一个直角三角形的两条直角边长分别为1和2，将该三角形分别绕其两个直角边旋转得到的两个圆锥的体积之比为()A ．1B ．2C ．4D ．8【解析】如图，则21142133V ππ=⨯⨯=，22121233V ππ=⨯⨯=，∴两个圆锥的体积之比为43223ππ=．故选：B ．6．（2020•浙江）已知圆锥的侧面积（单位：2)cm 为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：)cm 是．【解析】圆锥侧面展开图是半圆，面积为22cm π，设圆锥的母线长为acm ，则2122a ππ⨯=，2a cm ∴=，∴侧面展开扇形的弧长为2cm π，设圆锥的底面半径OC rcm =，则22r ππ=，解得1r cm =．故答案为：1cm ．7．（2022•新高考Ⅱ）已知正三棱台的高为1，上、下底面边长分别为3343，其顶点都在同一球面上，则该球的表面积为()A ．100πB ．128πC ．144πD ．192π【解析】当球心在台体外时，由题意得，上底面所在平面截球所得圆的半径为3332sin 60=︒4=，如图，设球的半径为R 1=，解得5R =，∴该球的表面积为24425100R πππ=⨯=．当球心在台体内时，如图，1=，无解．综上，该球的表面积为100π．故选：A ．8．（2021•新高考Ⅱ）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步轨道卫星的轨道位于地球赤道所在平面，轨道高度为36000km （轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O ，半径r 为6400km 的球，其上点A 的纬度是指OA 与赤道平面所成角的度数．地球表面上能直接观测到的一颗地球静止同步轨道卫星点的纬度最大值为α，该卫星信号覆盖地球表面的表面积22(1cos )S r πα=-（单位：2)km ，则S 占地球表面积的百分比约为()A ．26%B ．34%C ．42%D ．50%【解析】由题意，作出地球静止同步卫星轨道的左右两端的竖直截面图，则36000640042400OP =+=，那么64008cos 4240053α==；卫星信号覆盖的地球表面面积22(1cos )S r πα=-，那么，S 占地球表面积的百分比为222(1cos )4542%4106r r παπ-=≈．故选：C ．考点二空间几何体的体积9．（2022•新高考Ⅰ）已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上．若该球的体积为36π，且3l，则该正四棱锥体积的取值范围是()A ．[18，81]4B ．27[4，814C ．27[4，64]3D ．[18，27]【解析】如图所示，正四棱锥P ABCD -各顶点都在同一球面上，连接AC 与BD 交于点E ，连接PE ，则球心O 在直线PE 上，连接OA ，设正四棱锥的底面边长为a ，高为h ，在Rt PAE ∆中，222PA AE PE =+，即2222221(22l h a h =+=+，球O 的体积为36π，∴球O 的半径3R =，在Rt OAE ∆中，222OA OE AE =+，即2222(3))2R h =-+，∴221602a h h +-=，∴22162a h h +=，26l h ∴=，又3l∴3922h ，∴该正四棱锥体积2232112()(122)4333V h a h h h h h h ==-=-+，2()282(4)V h h h h h '=-+=- ，∴当342h <时，()0V h '>，()V h 单调递增；当942h <时，()0V h '<，()V h 单调递减，()max V h V ∴=（4）643=，又327(24V = ，981()24V =，且278144<，∴2764()43V h ，即该正四棱锥体积的取值范围是27[4，643，故选：C ．10．（2022•新高考Ⅰ）南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库．已知该水库水位为海拔148.5m 时，相应水面的面积为2140.0km ；水位为海拔157.5m 时，相应水面的面积为2180.0km ．将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m 上升到157.5m 时，增加的水量约为(7 2.65)(≈)A ．931.010m ⨯B ．931.210m ⨯C ．931.410m ⨯D ．931.610m ⨯【解析】26214014010km m =⨯，26218018010km m =⨯，根据题意，增加的水量约为666614010180101401018010(157.5148.5)3⨯+⨯⨯⨯⨯⨯-6(140180607)109++⨯=6693(32060 2.65)103143710 1.410m ≈+⨯⨯⨯=⨯≈⨯．故选：C ．11．（2021•新高考Ⅱ）正四棱台的上、下底面的边长分别为2，4，侧棱长为2，则其体积为()A ．203+B ．282C ．563D ．2823【解析】解法一：如图1111ABCD A B C D -为正四棱台，2AB =，114A B =，12AA =．在等腰梯形11A B BA 中，过A 作11AE A B ⊥，可得14212A E -==，2211413AE AA A E =--=．连接AC ，11A C ，4422AC =+=，11161642A C =+，过A 作11AG A C ⊥，142222A G -==，AG ===，∴正四棱台的体积为：V h=22243++=2823=．解法二：作出图形，连接该正四棱台上下底面的中心，如图，该四棱台上下底面边长分别为2，4，侧棱长为2，∴该棱台的记h =下底面面积116S =，上底面面积24S =，则该棱台的体积为：1211282((164333V h S S =++=⨯++=．故选：D ．12．【多选】（2023•新高考Ⅰ）下列物体中，能够被整体放入棱长为1（单位：)m 的正方体容器（容器壁厚度忽略不计）内的有()A ．直径为0.99m 的球体B ．所有棱长均为1.4m 的四面体C ．底面直径为0.01m ，高为1.8m 的圆柱体D ．底面直径为1.2m ，高为0.01m 的圆柱体【解析】对于A ，棱长为1的正方体内切球的直径为10.99>，选项A 正确；对于B ，如图，正方体内部最大的正四面体11D A BC - 1.4=>，选项B 正确；对于C ，棱长为1 1.8<，选项C 错误；对于D ，如图，六边形EFGHIJ 为正六边形，E ，F ，G ，H ，I ，J 为棱的中点，高为0.01米可忽略不计，看作直径为1.2米的平面圆，六边形EFGHIJ 棱长为2米，30GFH GHF ∠=∠=︒，所以62FH ===米，故六边形EFGHIJ 内切圆半径为62米，而223(1.2) 1.442=>=，选项D 正确．故选：ABD ．13．【多选】（2022•新高考Ⅱ）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，//FB ED ，2AB ED FB ==．记三棱锥E ACD -，F ABC -，F ACE -的体积分别为1V ，2V ，3V ，则()A ．322V V =B ．31V V =C ．312V V V =+D ．3123V V =【解析】设22AB ED FB ===，114||33ACD V S ED ∆=⨯⨯=，212||33ABC V S FB ∆=⨯⨯=，如图所示，连接BD 交AC 于点M ，连接EM 、FM ，则3FM =6EM =，3EF =，故1323622EMF S ∆==，3113222332EMF V S AC ∆=⨯=⨯，故C 、D 正确，A 、B 错误．故选：CD ．14．【多选】（2021•新高考Ⅰ）在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+ ，其中[0λ∈，1]，[0μ∈，1]，则()A ．当1λ=时，△1AB P 的周长为定值B ．当1μ=时，三棱锥1P A BC -的体积为定值C ．当12λ=时，有且仅有一个点P ，使得1A P BP ⊥D ．当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P 【解析】对于A ，当1λ=时，1BP BC BB μ=+ ，即1CP BB μ= ，所以1//CP BB ，故点P 在线段1CC 上，此时△1AB P 的周长为11AB B P AP ++，当点P 为1CC 的中点时，△1AB P ，当点P 在点1C 处时，△1AB P 的周长为1，故周长不为定值，故选项A 错误；对于B ，当1μ=时，1BP BC BB λ=+ ，即1B P BC λ= ，所以1//B P BC ，故点P 在线段11B C 上，因为11//B C 平面1A BC ，所以直线11B C 上的点到平面1A BC 的距离相等，又△1A BC 的面积为定值，所以三棱锥1P A BC -的体积为定值，故选项B 正确；对于C ，当12λ=时，取线段BC ，11B C 的中点分别为M ，1M ，连结1M M ，因为112BP BC BB μ=+ ，即1MP BB μ= ，所以1//MP BB ，则点P 在线段1M M 上，当点P 在1M 处时，1111A M B C ⊥，111A M B B ⊥，又1111B C B B B = ，所以11A M ⊥平面11BB C C ，又1BM ⊂平面11BB C C ，所以111A M BM ⊥，即1A P BP ⊥，同理，当点P 在M 处，1A P BP ⊥，故选项C 错误；对于D ，当12μ=时，取1CC 的中点1D ，1BB 的中点D ，因为112BP BC BB λ=+ ，即DP BC λ= ，所以//DP BC ，则点P 在线的1DD 上，当点P 在点1D 处时，取AC 的中点E ，连结1A E ，BE ，因为BE ⊥平面11ACC A ，又1AD ⊂平面11ACC A ，所以1AD BE ⊥，在正方形11ACC A 中，11AD A E ⊥，又1BE A E E = ，BE ，1A E ⊂平面1A BE ，故1AD ⊥平面1A BE ，又1A B ⊂平面1A BE ，所以11A B AD ⊥，在正方体形11ABB A 中，11A B AB ⊥，又11AD AB A = ，1AD ，1AB ⊂平面11AB D ，所以1A B ⊥平面11AB D ，因为过定点A 与定直线1A B 垂直的平面有且只有一个，故有且仅有一个点P ，使得1A B ⊥平面1AB P ，故选项D 正确．故选：BD ．15．（2023•新高考Ⅱ）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为．【解析】如图所示，根据题意易知△11SO A SOA ∆∽，∴11121222SO O A SO OA ===，又13SO =，6SO ∴=，13OO ∴=，又上下底面正方形边长分别为2，4，∴所得棱台的体积为1(416416)3283⨯++⨯⨯=．故答案为：28．16．（2023•新高考Ⅰ）在正四棱台1111ABCD A B C D -中，2AB =，111A B =，12AA =，则该棱台的体积为．【解析】如图，设正四棱台1111ABCD A B C D -的上下底面中心分别为M ，N ，过1A 作1A H AC ⊥，垂足点为H ，由题意易知122A M HN ==，又2AN =22AH AN HN ∴=-=，又1AA =，1A H MN ∴==∴该四棱台的体积为1(14326⨯++⨯=．故答案为：766．17．（2020•海南）已知正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，则三棱锥1A NMD -的体积为．【解析】如图，正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，∴111122ANM S ∆=⨯⨯=，∴111112323A NMD D AMN V V --==⨯⨯=．故答案为：13．18．（2022•上海）如图所示三棱锥，底面为等边ABC ∆，O 为AC 边中点，且PO ⊥底面ABC ，2AP AC ==．（1）求三棱锥体积P ABC V -；（2）若M 为BC 中点，求PM 与面PAC 所成角大小．【解析】（1）在三棱锥P ABC -中，因为PO ⊥底面ABC ，所以PO AC ⊥，又O 为AC 边中点，所以PAC ∆为等腰三角形，又2AP AC ==．所以PAC ∆是边长为2的为等边三角形，3PO ∴=，三棱锥体积2113231334P ABC ABC V S PO -∆=⋅=⨯⨯，（2）以O 为坐标原点，OB 为x 轴，OC 为y 轴，OP 为z轴，建立空间直角坐标系，则(0P ，03)，(3B 0，0)，(0C ，1，0)，3(2M ，12，0)，3(2PM = ，12，3)-，平面PAC 的法向量(3OB = 0，0)，设直线PM 与平面PAC 所成角为θ，则直线PM 与平面PAC 所成角的正弦值为332sin ||4||||32PM OB PM OB θ⋅===⋅⨯ ，所以PM 与面PAC 所成角大小为319．（2020•上海）已知四棱锥P ABCD -，底面ABCD 为正方形，边长为3，PD ⊥平面ABCD ．（1）若5PC =，求四棱锥P ABCD -的体积；（2）若直线AD 与BP 的夹角为60︒，求PD 的长．【解析】（1）PD ⊥ 平面ABCD ，PD DC ∴⊥．3CD = ，5PC ∴=，4PD ∴=，2134123P ABCD V -∴=⨯⨯=，所以四棱锥P ABCD -的体积为12．（2）ABCD 是正方形，PD ⊥平面ABCD ，BC PD ∴⊥，BC CD⊥又PD CD D= BC ∴⊥平面PCDBC PC∴⊥ 异面直线AD 与PB 所成角为60︒，//BC AD∴在Rt PBC ∆中，60PBC ∠=︒，3BC =故33PC =在Rt PDC ∆中，3CD =32PD ∴=考点三空间中直线与直线之间的位置关系20．（2022•上海）如图正方体1111ABCD A B C D -中，P 、Q 、R 、S 分别为棱AB 、BC 、1BB 、CD 的中点，联结1A S ，1B D ．空间任意两点M 、N ，若线段MN 上不存在点在线段1A S 、1B D 上，则称MN 两点可视，则下列选项中与点1D 可视的为()A ．点PB ．点BC ．点RD ．点Q【解析】线段MN 上不存在点在线段1A S 、1B D 上，即直线MN 与线段1A S 、1B D 不相交，因此所求与1D 可视的点，即求哪条线段不与线段1A S 、1B D 相交，对A 选项，如图，连接1A P 、PS 、1D S ，因为P 、S 分别为AB 、CD 的中点，∴易证11//A D PS ，故1A 、1D 、P 、S 四点共面，1D P ∴与1A S 相交，A ∴错误；对B 、C 选项，如图，连接1D B 、DB ，易证1D 、1B 、B 、D 四点共面，故1D B 、1D R 都与1B D 相交，B ∴、C 错误；对D 选项，连接1D Q ，由A 选项分析知1A 、1D 、P 、S 四点共面记为平面11A D PS ，1D ∈ 平面11A D PS ，Q ∉平面11A D PS ，且1A S ⊂平面11A D PS ，点11D A S ∉，1D Q ∴与1A S 为异面直线，同理由B ，C 选项的分析知1D 、1B 、B 、D 四点共面记为平面11D B BD ，1D ∈ 平面11D B BD ，Q ∉平面11D B BD ，且1B D ⊂平面11D B BD ，点11D B D ∉，1D Q ∴与1B D 为异面直线，故1D Q 与1A S ，1B D 都没有公共点，D ∴选项正确．故选：D ．21．（2021•浙江）如图，已知正方体1111ABCD A B C D -，M ，N 分别是1A D ，1D B 的中点，则()A ．直线1A D 与直线1DB 垂直，直线//MN 平面ABCDB ．直线1A D 与直线1D B 平行，直线MN ⊥平面11BDD B C ．直线1A D 与直线1D B 相交，直线//MN 平面ABCDD ．直线1A D 与直线1D B 异面，直线MN ⊥平面11BDD B 【解析】连接1AD ，如图：由正方体可知11A D AD ⊥，1A D AB ⊥，1A D ∴⊥平面1ABD ，11A D D B ∴⊥，由题意知MN 为△1D AB 的中位线，//MN AB ∴，又AB ⊂ 平面ABCD ，MN ⊂/平面ABCD ，//MN ∴平面ABCD ．A ∴对；由正方体可知1A D 与平面1BDD 相交于点D ，1D B ⊂平面1BDD ，1D D B ∉，∴直线1A D 与直线1D B 是异面直线，B ∴、C 错；//MN AB ，AB 不与平面11BDD B 垂直，MN ∴不与平面11BDD B 垂直，D ∴错．故选：A ．22．（2020•上海）在棱长为10的正方体1111ABCD A B C D -中，P 为左侧面11ADD A 上一点，已知点P 到11A D的距离为3，P 到1AA 的距离为2，则过点P 且与1A C 平行的直线交正方体于P 、Q 两点，则Q 点所在的平面是()A ．11AAB BB ．11BBC C C ．11CCD D D ．ABCD 【解析】如图，由点P 到11A D 的距离为3，P 到1AA 的距离为2，可得P 在△1AA D 内，过P 作1//EF A D ，且1EF AA 于E ，EF AD 于F ，在平面ABCD 中，过F 作//FG CD ，交BC 于G ，则平面//EFG 平面1A DC ．连接AC ，交FG 于M ，连接EM ，平面//EFG 平面1A DC ，平面1A AC ⋂平面11A DC A C =，平面1A AC ⋂平面EFM EM =，1//EM A C ∴．在EFM ∆中，过P 作//PQ EM ，且PQ FM 于Q ，则1//PQ A C ．线段FM 在四边形ABCD 内，Q 在线段FM 上，Q ∴在四边形ABCD 内．∴则Q 点所在的平面是平面ABCD ．故选：D ．23．（2023•上海）如图所示，在正方体1111ABCD A B C D -中，点P 为边11A C 上的动点，则下列直线中，始终与直线BP 异面的是()A ．1DDB ．AC C ．1AD D ．1B C【解析】对于A ，当P 是11A C 的中点时，BP 与1DD 是相交直线；对于B ，根据异面直线的定义知，BP 与AC 是异面直线；对于C ，当点P 与1C 重合时，BP 与1AD 是平行直线；对于D ，当点P 与1C 重合时，BP 与1B C 是相交直线．故选：B ．考点四异面直线及其所成的角24．【多选】（2022•新高考Ⅰ）已知正方体1111ABCD A B C D -，则()A ．直线1BC 与1DA 所成的角为90︒B ．直线1BC 与1CA 所成的角为90︒C ．直线1BC 与平面11BBD D 所成的角为45︒D ．直线1BC 与平面ABCD 所成的角为45︒【解析】如图，连接1B C ，由11//A B DC ，11A B DC =，得四边形11DA B C 为平行四边形，可得11//DA B C ，11BC B C ⊥ ，∴直线1BC 与1DA 所成的角为90︒，故A 正确；111A B BC ⊥ ，11BC B C ⊥，1111A B B C B = ，1BC ∴⊥平面11DA B C ，而1CA ⊂平面11DA B C ，11BC CA ∴⊥，即直线1BC 与1CA 所成的角为90︒，故B 正确；设1111A C B D O = ，连接BO ，可得1C O ⊥平面11BB D D ，即1C BO ∠为直线1BC 与平面11BB D D 所成的角，1111sin 2OC C BO BC ∠== ，∴直线1BC 与平面11BB D D 所成的角为30︒，故C 错误；1CC ⊥ 底面ABCD ，1C BC ∴∠为直线1BC 与平面ABCD 所成的角为45︒，故D 正确．故选：ABD ．考点五空间中直线与平面之间的位置关系25．（2019•上海）已知平面α、β、γ两两垂直，直线a 、b 、c 满足：a α⊆，b β⊆，c γ⊆，则直线a、b、c不可能满足以下哪种关系()A．两两垂直B．两两平行C．两两相交D．两两异面【解析】如图1，可得a、b、c可能两两垂直；如图2，可得a、b、c可能两两相交；如图3，可得a、b、c可能两两异面；故选：B．26．【多选】（2021•新高考Ⅱ）如图，下列正方体中，O为底面的中心，P为所在棱的中点，M，N为正方体的顶点，则满足MN OP⊥的是()A．B．C．D．【解析】对于A，设正方体棱长为2，设MN与OP所成角为θ，则12tan12θ==，∴不满足MN OP⊥，故A错误；对于B，如图，作出平面直角坐标系，设正方体棱长为2，则(2N ，0，0)，(0M ，0，2)，(2P ，0，1)，(1O ，1，0)，(2MN = ，0，2)-，(1OP = ，1-，1)，0MN OP ⋅= ，∴满足MN OP ⊥，故B 正确；对于C ，如图，作出平面直角坐标系，设正方体棱长为2，则(2M ，2，2)，(0N ，2，0)，(1O ，1，0)，(0P ，0，1)，(2MN =- ，0，2)-，(1OP =- ，1-，1)，0MN OP ⋅= ，∴满足MN OP ⊥，故C 正确；对于D ，如图，作出平面直角坐标系，设正方体棱长为2，则(0M ，2，0)，(0N ，0，2)，(2P ，1，2)，(1O ，1，0)，(0MN = ，2-，2)，(1OP = ，0，2)，4MN OP ⋅= ，∴不满足MN OP ⊥，故D 错误．故选：BC ．考点六直线与平面所成的角27．（2020•山东）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为)O ，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40︒，则晷针与点A 处的水平面所成角为()A ．20︒B ．40︒C ．50︒D ．90︒【解析】可设A 所在的纬线圈的圆心为O '，OO '垂直于纬线所在的圆面，由图可得OHA ∠为晷针与点A 处的水平面所成角，又OAO '∠为40︒且OA AH ⊥，在Rt OHA ∆中，O A OH '⊥，40OHA OAO '∴∠=∠=︒，另解：画出截面图，如下图所示，其中CD 是赤道所在平面的截线．l 是点A 处的水平面的截线，由题意可得OA l ⊥，AB 是晷针所在直线．m 是晷面的截线，由题意晷面和赤道面平行，晷针与晷面垂直，根据平面平行的性质定理可得//m CD ，根据线面垂直的定义可得AB m ⊥，由于40AOC ∠=︒，//m CD ，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与A 处的水平面所成角为40BAE ∠=︒，故选：B ．28．（2021•上海）如图，在长方体1111ABCD A B C D -中，已知2AB BC ==，13AA =．（1）若P 是棱11A D 上的动点，求三棱锥C PAD -的体积；（2）求直线1AB 与平面11ACC A的夹角大小．【解析】（1）如图，在长方体1111ABCD A B C D -中，1112322332C PAD PAD C PAD V S h -∆-⎛⎫=⋅=⨯⨯⨯⨯= ⎪⎝⎭平面；（2）连接1111A C B D O = ，AB BC = ，∴四边形1111A B C D 为正方形，则11OB OA ⊥，又11AA OB ⊥，111OA AA A = ，1OB ∴⊥平面11ACC A ，∴直线1AB 与平面11ACC A 所成的角为1OAB ∠，∴221122122262sin 23OB OAB AB +∠===+∴直线1AB 与平面11ACC A 所成的角为261329．（2021•浙江）如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，120ABC ∠=︒，1AB =，4BC =，15PA =M ，N 分别为BC ，PC 的中点，PD DC ⊥，PM MD ⊥．（Ⅰ）证明：AB PM ⊥；（Ⅱ）求直线AN 与平面PDM 所成角的正弦值．【解析】（Ⅰ）证明：在平行四边形ABCD 中，由已知可得，1CD AB ==，122CM BC ==，60DCM ∠=︒，∴由余弦定理可得，2222cos60DM CD CM CD CM =+-⨯⨯︒11421232=+-⨯⨯⨯=，则222134CD DM CM +=+==，即CD DM ⊥，又PD DC ⊥，PD DM D = ，CD ∴⊥平面PDM ，而PM ⊂平面PDM ，CD PM ∴⊥，//CD AB ，AB PM ∴⊥；（Ⅱ）解：由（Ⅰ）知，CD ⊥平面PDM ，又CD ⊂平面ABCD ，∴平面ABCD ⊥平面PDM ，且平面ABCD ⋂平面PDM DM =，PM MD ⊥ ，且PM ⊂平面PDM ，PM ∴⊥平面ABCD ，连接AM ，则PM MA ⊥，在ABM ∆中，1AB =，2BM =，120ABM ∠=︒，可得2114212(72AM =+-⨯⨯⨯-=，又PA =Rt PMA ∆中，求得PM ==，取AD 中点E ，连接ME ，则//ME CD ，可得ME 、MD 、MP 两两互相垂直，以M 为坐标原点，分别以MD 、ME 、MP 为x 、y 、z 轴建立空间直角坐标系，则(A 2，0)，(0P ，0，，1,0)C -，又N 为PC的中点，31(22N ∴-，335(22AN =- ，平面PDM 的一个法向量为(0,1,0)n = ，设直线AN 与平面PDM 所成角为θ，则5||2sin |cos ,|||||AN n AN n AN n θ⋅=<>==⋅ ．故直线AN 与平面PDM 所成角的正弦值为156．30．（2020•海南）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知1PD AD ==，Q 为l上的点，QB =，求PB 与平面QCD所成角的正弦值．【解析】（1）证明：过P 在平面PAD 内作直线//l AD ，由//AD BC ，可得//l BC ，即l 为平面PAD 和平面PBC 的交线，PD ⊥ 平面ABCD ，BC ⊂平面ABCD ，PD BC ∴⊥，又BC CD ⊥，CD PD D = ，BC ∴⊥平面PCD ，设m 为平面PCD 中任意一条直线，则BC m ⊥，//l BC ，l m ∴⊥，由线面垂直的定义是l ⊥平面PCD ；（2）解：如图，以D 为坐标原点，直线DA ，DC ，DP 所在的直线为x ，y ，z 轴，建立空间直角坐标系D xyz -，1PD AD == ，Q 为l上的点，QB =，PB ∴=，1QP =，则(0D ，0，0)，(1A ，0，0)，(0C ，1，0)，(0P ，0，1)，(1B ，1，0)，作//PQ AD ，则PQ 为平面PAD 与平面PBC 的交线为l，因为QB =，QAB ∆是等腰直角三角形，所以(1Q ，0，1)，则(1DQ = ，0，1)，(1PB = ，1，1)-，(0DC = ，1，0)，设平面QCD 的法向量为(n a = ，b ，)c ，则00n DC n DQ ⎧⋅=⎪⎨⋅=⎪⎩ ，∴00b a c =⎧⎨+=⎩，取1c =，可得(1n =- ，0，1)，|cos n ∴<，6||||3||||n PB PB n PB ⋅>=== ，PB ∴与平面QCD所成角的正弦值为3．31．（2020•上海）已知ABCD 是边长为1的正方形，正方形ABCD 绕AB 旋转形成一个圆柱．（1）求该圆柱的表面积；（2）正方形ABCD 绕AB 逆时针旋转2π至11ABC D ，求线段1CD 与平面ABCD 所成的角．【解析】（1）该圆柱的表面由上下两个半径为1的圆面和一个长为2π、宽为1的矩形组成，221214S πππ∴=⨯⨯+⨯=．故该圆柱的表面积为4π．（2）正方形11ABC D ，1AD AB ∴⊥，又12DAD π∠=，1AD AD ∴⊥，AD AB A = ，且AD 、AB ⊂平面ADB ，1AD ∴⊥平面ADB ，即1D 在面ADB 上的投影为A ，连接1CD ，则1D CA ∠即为线段1CD 与平面ABCD 所成的角，而1126cos 33AC D CA CD ∠==，∴线段1CD 与平面ABCD 所成的角为6arccos3．32．（2020•山东）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知1PD AD ==，Q 为l 上的点，求PB 与平面QCD所成角的正弦值的最大值．【解析】（1）证明：过P 在平面PAD 内作直线//l AD ，由//AD BC ，可得//l BC ，即l 为平面PAD 和平面PBC 的交线，PD ⊥ 平面ABCD ，BC ⊂平面ABCD ，PD BC ∴⊥，又BC CD ⊥，CD PD D = ，BC ∴⊥平面PCD ，设平面PCD 中有任一直线l '，则BC ⊥直线l '，//l BC ，l ∴⊥直线l '，∴由线面垂直的定义得l ⊥平面PCD ；（2）如图，以D 为坐标原点，直线DA ，DC ，DP 所在的直线为x ，y ，z 轴，建立空间直角坐标系D xyz -则(0D ，0，0)，(1A ，0，0)，(0C ，1，0)，(0P ，0，1)，(1B ，1，0)，设(Q m ，0，1)，(DQ m = ，0，1)，(1PB = ，1，1)-，(0DC = ，1，0)，设平面QCD 的法向量为(n a = ，b ，)c ，则00n DC n DQ ⎧⋅=⎪⎨⋅=⎪⎩ ，∴00b am c =⎧⎨+=⎩，取1a =-，可得(1n =- ，0，)m ，cos n ∴< ，2||||31n PB PB n PB m⋅>==⋅⋅+ ，PB ∴与平面QCD 2223123131m m m m ++=+⋅+2323261131323m m =++=+1m =取等号，PB ∴与平面QCD 所成角的正弦值的最大值为63．33．（2020•浙江）如图，在三棱台ABC DEF -中，平面ACFD ⊥平面ABC ，45ACB ACD ∠=∠=︒，2DC BC =．（Ⅰ）证明：EF DB ⊥；（Ⅱ）求直线DF 与平面DBC 所成角的正弦值．【解析】（Ⅰ）证明：作DH AC ⊥，且交AC 于点H ，面ADFC ⊥面ABC ，DH ⊂面ADFC ，DH BC ∴⊥，∴在Rt DHC ∆中，2cos 452CH CD =⋅︒=，2DC BC = ，2222CH BC BC ∴===，∴22BC CH =，即BHC ∆是直角三角形，且90HBC ∠=︒，HB BC ∴⊥，BC ∴⊥面DHB ，BD ⊂ 面DHB ，BC BD ∴⊥，在三棱台DEF ABC -中，//EF BC ，EF DB ∴⊥．（Ⅱ）设1BC =，则1BH =，2HC =在Rt DHC ∆中，2DH =2DC =，在Rt DHB ∆中，22213DB DH HB =+=+=，作HG BD ⊥于G ，BC HG ⊥ ，HG ∴⊥面BCD ，GC ⊂ 面BCD ，HG GC ∴⊥，HGC ∴∆是直角三角形，且90HGC ∠=︒，设DF 与面DBC 所成角为θ，则θ即为CH 与面DBC 的夹角，且sin sin 2HG HCG HC θ=∠== 在Rt DHB ∆中，DH HB BD HG ⋅=⋅，2633DH HB HG BD ⋅∴===，633sin 322θ∴===．34．（2019•上海）如图，在长方体1111ABCD A B C D -中，M 为1BB 上一点，已知2BM =，3CD =，4AD =，15AA =．（1）求直线1A C 和平面ABCD 的夹角；（2）求点A 到平面1A MC 的距离．【解析】（1）依题意：1AA ⊥平面ABCD ，连接AC ，则1A C 与平面ABCD 所成夹角为1A CA ∠，15AA = ，5AC =，∴△1A CA 为等腰三角形，14A CA π∴∠=，∴直线1A C 和平面ABCD 的夹角为4π，（2）（空间向量），如图建立坐标系，则(0A ，0，0)，(3C ，4，0)，1(0A ，0，5)，(3M ，0，2)，∴(3AC = ，4，0)，1(3A C = ，4，5)-，(0MC = ，4．2)-，设平面1A MC 的法向量(n x = ，y ，)z ，由13450420n A C x y z n MC y z ⎧⋅=+-=⎪⎨⋅=-=⎪⎩ ，可得(2n = ，1，2)，∴点A 到平面1A MC的距离||10||3AC n d n ⋅== ．35．（2019•浙江）如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ，90ABC ∠=︒，30BAC ∠=︒，11A A A C AC ==，E ，F 分别是AC ，11A B 的中点．（Ⅰ）证明：EF BC ⊥；（Ⅱ）求直线EF 与平面1A BC所成角的余弦值．【解析】方法一：证明：（Ⅰ）连接1A E ，11A A A C = ，E 是AC 的中点，1A E AC ∴⊥，又平面11A ACC ⊥平面ABC ，1A E ⊂平面11A ACC ，平面11A ACC ⋂平面ABC AC =，1A E ∴⊥平面ABC ，1A E BC ∴⊥，1//A F AB ，90ABC ∠=︒，1BC A F ∴⊥，111A F A E A = ，BC ∴⊥平面1A EF ，EF BC ∴⊥．解：（Ⅱ）取BC 中点G ，连接EG 、GF ，则1EGFA 是平行四边形，由于1A E ⊥平面ABC ，故1A E EG ⊥，∴平行四边形1EGFA 是矩形，由（Ⅰ）得BC ⊥平面1EGFA ，则平面1A BC ⊥平面1EGFA ，EF ∴在平面1A BC 上的射影在直线1A G 上，连接1A G ，交EF 于O ，则EOG ∠是直线EF 与平面1A BC 所成角（或其补角），不妨设4AC =，则在Rt △1A EG中，1A E =，EG =，O 是1A G的中点，故12A G EO OG ===2223cos 25EO OG EG EOG EO OG +-∴∠==⨯⨯，∴直线EF 与平面1A BC 所成角的余弦值为35．方法二：证明：（Ⅰ）连接1A E ，11A A A C = ，E 是AC 的中点，1A E AC ∴⊥，又平面11A ACC ⊥平面ABC ，1A E ⊂平面11A ACC ，平面11A ACC ⋂平面ABC AC =，1A E ∴⊥平面ABC ，如图，以E 为原点，在平面ABC 中，过E 作AC 的垂线为x 轴，EC ，1EA 所在直线分别为y ，z 轴，建立空间直角坐标系，设4AC =，则1(0A ，0，，B，1B，33(22F ，(0C ，2，0)，33(22EF =，(BC = ，由0EF BC = ，得EF BC ⊥．解：（Ⅱ）设直线EF 与平面1A BC 所成角为θ，由（Ⅰ）得(BC = ，1(0A C = ，2，-，设平面1A BC 的法向量(n x = ，y ，)z ，则100BC n y A C n y ⎧=+=⎪⎨==⎪⎩ ，取1x =，得n = ，||4sin 5||||EF n EF n θ∴== ，∴直线EF 与平面1A BC35=．考点七二面角的平面角及求法36．（2022•浙江）如图，已知正三棱柱111ABC A B C -，1AC AA =，E ，F 分别是棱BC ，11A C 上的点．记EF 与1AA 所成的角为α，EF 与平面ABC 所成的角为β，二面角F BC A --的平面角为γ，则()A ．αβγB ．βαγC ．βγαD ．αγβ【解析】正三棱柱111ABC A B C -中，1AC AA =，∴正三棱柱的所有棱长相等，设棱长为1，如图，过F 作FG AC ⊥，垂足点为G ，连接GE ，则1//A A FG ，EF ∴与1AA 所成的角为EFG α∠=，且tan GE GE FGα==，又[0GE ∈，1]，tan [0α∴∈，1]，EF ∴与平面ABC 所成的角为FEG β∠=，且1tan [1GF GE GEβ==∈，)+∞，tan tan βα∴，...①，再过G 点作GH BC ⊥，垂足点为H ，连接HF ，又易知FG ⊥底面ABC ，BC ⊂底面ABC ，BC FG ∴⊥，又FG GH G = ，BC ∴⊥平面GHF ，∴二面角F BC A --的平面角为GHF γ∠=，且1tan GF GH GHγ==，又[0GH ∈，32，tan γ∴∈)+∞，tan tan γα∴，...②，又GE GH ，tan tan βγ∴，...③，由①②③得tan tan tan αβγ，又α，β，[0γ∈，)2π，tan y x =在[0，2π单调递增，αβγ∴，故选：A．37．（2019•浙江）设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P AC B --的平面角为γ，则()A ．βγ<，αγ<B ．βα<，βγ<C ．βα<，γα<D ．αβ<，γβ<【解析】方法一、如图G 为AC 的中点，V 在底面的射影为O ，则P 在底面上的射影D 在线段AO 上，作DE AC ⊥于E ，易得//PE VG ，过P 作//PF AC 于F ，过D 作//DH AC ，交BG 于H ，则BPF α=∠，PBD β=∠，PED γ=∠，则cos cos PF EG DH BD PB PB PB PB αβ===<=，可得βα<；tan tan PD PD ED BDγβ=>=，可得βγ<，方法二、由最小值定理可得βα<，记V AC B --的平面角为γ'（显然)γγ'=，由三正弦定理可得βγγ'<=；方法三、（特殊图形法）设三棱锥V ABC -为棱长为2的正四面体，P 为VA 的中点，易得12cos α==sin α=，sin β=sin 3γ==，当23AP =时，由余弦定理可得273PB ==，281628999cos 27433α+-==sin α=，可得αγ<，故C 错误．故选：B．38．【多选】（2023•新高考Ⅱ）已知圆锥的顶点为P ，底面圆心为O ，AB 为底面直径，120APB ∠=︒，2PA =，点C 在底面圆周上，且二面角P AC O --为45︒，则()A ．该圆锥的体积为πB．该圆锥的侧面积为C．AC =D ．PAC ∆【解析】取AC 中点D ，则OD AC ⊥，PD AC ⊥，由二面角的定义可知，二面角P AC O --的平面角即为45PDO ∠=︒，对于A ，PAB ∆中，由于2PA PB ==，120APB ∠=︒，则1PO =，AO =，则1OD =，1313V ππ=⋅⋅=，选项A 正确．对于B，2S π==侧，选项B 错误．对于C，AC ==，选项C 正确．对于D，PD =122PAC S ∆==，选项D 错误．故选：AC ．39．（2023•上海）已知直四棱柱1111ABCD A B C D -，AB AD ⊥，//AB CD ，2AB =，3AD =，4CD =．（1）证明：直线1//A B 平面11DCC D ；（2）若该四棱柱的体积为36，求二面角1A BD A --的大小．【解析】（1）证明：根据题意可知//AB DC ，11//AA DD ，且1AB AA A = ，∴可得平面11//A ABB 平面11DCC D ，又直线1A B ⊂平面11A ABB ，∴直线1//A B 平面11DCC D ；（2）设1AA h =，则根据题意可得该四棱柱的体积为1(24)3362h ⨯+⨯⨯=，4h ∴=，1A A ⊥ 底面ABCD ，在底面ABCD 内过A 作AE BD ⊥，垂足点为E ，则1A E 在底面ABCD 内的射影为AE ，∴根据三垂线定理可得1BD A E ⊥，故1A EA ∠即为所求，在Rt ABD ∆中，2AB =，3AD =，BD ∴==，AB AD AE BD ⨯∴==，又14A A h ==，114tan 6A A A EA AE ∴∠===∴二面角1A BD A --的大小为213arctan3．40．（2023•新高考Ⅱ）如图，三棱锥A BCD -中，DA DB DC ==，BD CD ⊥，60ADB ADC ∠=∠=︒，E为BC 中点．（1）证明BC DA ⊥；（2）点F 满足EF DA = ，求二面角D AB F --的正弦值．【解析】证明：（1）连接AE ，DE ，DB DC = ，E 为BC 中点．DE BC ∴⊥，又DA DB DC == ，60ADB ADC ∠=∠=︒，ACD ∴∆与ABD ∆均为等边三角形，AC AB ∴=，AE BC ∴⊥，AE DE E = ，BC ∴⊥平面ADE ，AD ⊂ 平面ADE ，BC DA ∴⊥．（2）解：设2DA DB DC ===，∴BC =DE AE ==2AD =，2224AE DE AD ∴+==，AE DE ∴⊥，又AE BC ⊥ ，DE BC E = ，AE ∴⊥平面BCD ，以E 为原点，建立如图所示空间直角坐标系，(2,0,0)D ，2)A ，2,0)B ，(0E ，0，0)，EF DA = ，∴(2,0,2)F -，∴(2,0,2)DA =- ，2,2)AB = ，(2,0,0)AF = ，设平面DAB 与平面ABF 的一个法向量分别为1111(,,)n x y z = ，2222(,,)n x y z = ，则1111220220x z z ⎧-+=⎪⎨-=⎪⎩，令11x =，解得111y z ==，22222020z -==⎪⎩，令21y =，解得20x =，21z =，故1(1n = ，1，1)，2(0n = ，1，1)，设二面角D AB F --的平面角为θ，则1212||26|cos |3||||32n n n n θ⋅==⨯ ，故3sin 3θ=，所以二面角D AB F --33．41．（2023•新高考Ⅰ）如图，在正四棱柱111ABCD A B C D -中，2AB =，14AA =．点2A ，2B ，2C ，2D 分别在棱1AA ，1BB ，1CC ，1DD 上，21AA =，222BB DD ==，23CC =．（1）证明：2222//B C A D ；（2）点P 在棱1BB 上，当二面角222P A C D --为150︒时，求2B P ．【解析】（1）证明：根据题意建系如图，则有：2(0B ，2，2)，2(0C ，0，3)，2(2A ，2，1)，2(2D ，0，2)，∴22(0,2,1)B C =- ，22(0,2,1)A D =- ，∴2222B C A D = ，又2B ，2C ，2A ，2D 四点不共线，2222//B C A D ∴；（2）在（1）的坐标系下，可设(0P ，2，)t ，[0t ∈，4]，又由（1）知2(0C ，0，3)，2(2A ，2，1)，2(2D ，0，2)，∴22(2,2,2)C A =- ，2(0,2,3)C P t =- ，22(0,2,1)A D =- ，设平面22PA C 的法向量为(,,)m x y z = ，则22222202(3)0m C A x y z m C P y t z ⎧⋅=+-=⎪⎨⋅=+-=⎪⎩ ，取(1,3,2)m t t =-- ，设平面222A C D 的法向量为(,,)n a b c = ，则2222222020n C A a b c n A D b c ⎧⋅=+-=⎪⎨⋅=-+=⎪⎩ ，取(1,1,2)n = ，∴根据题意可得|cos150||cos m ︒=< ，|||||||m n n m n ⋅>= ，∴22362(1)(3)46t t =-+-+⨯，2430t t ∴-+=，又[0t ∈，4]，∴解得1t =或3t =，P ∴为12B B 的中点或2B B 的中点，21B P ∴=．42．（2022•浙江）如图，已知ABCD和CDEF都是直角梯形，//EF=，AB=，3DC=，1DC EF，5AB DC，//--的平面角为60︒．设M，N分别为AE，BC的中点．∠=∠=︒，二面角F DC B60BAD CDE（Ⅰ）证明：FN AD⊥；（Ⅱ）求直线BM与平面ADE所成角的正弦值．【解析】证明：()I由于CD CB⊥，⊥，CD CF平面ABCD⋂平面CDEF CD=，CF⊂平面CDEF，CB⊂平面ABCD，所以FCB--的平面角，∠为二面角F DC B则60⊥．∠=︒，CD⊥平面CBF，则CD FNFCB又3()3,3()3=-==-=CF CD EF CB AB CD则BCF⊥，∆是等边三角形，则CB FN，FC⊂平面FCB，BC⊂平面FCB，因为DC FC⊥，DC BC⊥，FC BC C=所以DC⊥平面FCB，因为FN⊂平面FCB，所以DC FN⊥，，DC⊂平面ABCD，CB⊂平面ABCD，又因为DC CB C=所以FN⊥平面ABCD，因为AD⊂平面ABCD，故FN AD⊥；解：（Ⅱ）由于FN⊥平面ABCD，如图建系：于是3,0),3,0),(0,0,3),(1,0,3),(3,3,0)B A F E D -，则33)22M ，33(3,),3,0),(2,3,3)22BM DA DE =-==- ，设平面ADE 的法向量(n x = ，y ，)z ，则00n DA n DE ⎧⋅=⎪⎨⋅=⎪⎩ ，∴2302330x x z ⎧+=⎪⎨-++=⎪⎩，令3x =，则1y =-，3z =∴平面ADE 的法向量(3,3)n =- ，设BM 与平面ADE 所成角为θ，则||57sin 14||||BM n BM n θ⋅== ．43．（2022•新高考Ⅱ）如图，PO 是三棱锥P ABC -的高，PA PB =，AB AC ⊥，E 为PB 的中点．（1）证明：//OE 平面PAC ；（2）若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --的正弦值．【解析】（1）证明：连接OA ，OB ，依题意，OP ⊥平面ABC ，又OA ⊂平面ABC ，OB ⊂平面ABC ，则OP OA ⊥，OP OB ⊥，90POA POB ∴∠=∠=︒，又PA PB =，OP OP =，则POA POB ∆≅∆，OA OB ∴=，延长BO 交AC 于点F ，又AB AC ⊥，则在Rt ABF ∆中，O 为BF 中点，连接PF ，在PBF ∆中，O ，E 分别为BF ，BP 的中点，则//OE PF ，OE ⊂/ 平面PAC ，PF ⊂平面PAC ，//OE ∴平面PAC ；（2）过点A 作//AM OP ，以AB ，AC ，AM 分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，由于3PO =，5PA =，由（1）知4OA OB ==，又30ABO CBO ∠=∠=︒，则AB =∴3(0,0,0),)2P B A E ，又tan 6012AC AB =︒=，即(0C ，12，0)，设平面AEB 的一个法向量为(,,)n x y z =，又3)2AB AE == ，则0302n AB n AE y z ⎧⋅==⎪⎨⋅=++=⎪⎩ ，则可取(0,3,2)n =- ，设平面AEC 的一个法向量为(,,)m a b c =，又3(0,12,0),2AC AE == ，则120302m AC b m AE b c ⎧⋅==⎪⎨⋅=++=⎪⎩，则可取(m = ，设锐二面角C AE B --的平面角为θ，则cos |cos ,|||||||13m n m n m n θ⋅=<>== ，∴11sin 13θ==，即二面角C AE B --正弦值为1113．44．（2022•新高考Ⅰ）如图，直三棱柱111ABC A B C -的体积为4，△1A BC的面积为（1）求A 到平面1A BC 的距离；（2）设D 为1A C 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值．【解析】（1）由直三棱柱111ABC A B C -的体积为4，可得11111433A ABC ABC ABC V --==，设A 到平面1A BC 的距离为d ，由11A ABC A A BC V V --=，∴11433A BC S d ⋅= ，∴14233d ⨯=，解得2d =．（2）连接1AB 交1A B 于点E ，1AA AB = ，∴四边形11ABB A 为正方形，11AB A B ∴⊥，又平面1A BC ⊥平面11ABB A ，平面1A BC ⋂平面111ABB A A B =，1AB ∴⊥平面1A BC ，1AB BC ∴⊥，由直三棱柱111ABC A B C -知1BB ⊥平面ABC ，1BB BC ∴⊥，又111AB BB B = ，BC ∴⊥平面11ABB A ，BC AB ∴⊥，以B 为坐标原点，BC ，BA ，1BB所在直线为坐标轴建立如图所示的空间直角坐标系，1AA AB = ，12222BC ∴⨯=，又1142AB BC AA ⨯⨯=，解得12AB BC AA ===，则(0B ，0，0)，(0A ，2，0)，(2C ，0，0)，1(0A ，2，2)，(1D ，1，1)，则(0BA = ，2，0)，(1BD = ，1，1)，(2BC = ，0，0)，设平面ABD 的一个法向量为(n x = ，y ，)z ，则200n BA y n BD x y z ⎧⋅==⎪⎨⋅=++=⎪⎩，令1x =，则0y =，1z =-，∴平面ABD 的一个法向量为(1n = ，0，1)-，设平面BCD 的一个法向量为(m a = ，b ，)c ，200m BC a m BD a b c ⎧⋅==⎪⎨⋅=++=⎪⎩ ，令1b =，则0a =，1c =-，平面BCD 的一个法向量为(0m = ，1，1)-，cos n <，12m >== ，二面角A BD C --32=．45．（2021•新高考Ⅱ）在四棱锥Q ABCD -中，底面ABCD 是正方形，若2AD =，QD QA ==3QC =．（Ⅰ）求证：平面QAD ⊥平面ABCD ；（Ⅱ）求二面角B QD A --的平面角的余弦值．【解析】（Ⅰ）证明：QCD ∆中，2CD AD ==，QD =，3QC =，所以222CD QD QC +=，所以CD QD ⊥；又CD AD ⊥，AD QD D = ，AD ⊂平面QAD ，QD ⊂平面QAD ，所以CD ⊥平面QAD ；又CD ⊂平面ABCD ，所以平面QAD ⊥平面ABCD ．（Ⅱ）解：取AD 的中点O ，在平面ABCD 内作Ox AD ⊥，以OD 所在直线为y 轴，OQ 所在直线为z 轴，建立空间直角坐标系O xyz -，如图所示：则(0O ，0，0)，(2B ，1-，0)，(0D ，1，0)，(0Q ，0，2)，因为Ox ⊥平面ADQ ，所以平面ADQ 的一个法向量为(1α= ，0，0)，设平面BDQ 的一个法向量为(x β= ，y ，)z ，由(2BD =- ，2，0)，(0DQ = ，1-，2)，得00BD DQ ββ⎧⋅=⎪⎨⋅=⎪⎩ ，即22020x y y z -+=⎧⎨-+=⎩，令1z =，得2y =，2x =，所以(2β= ，2，1)；所以cos α<，23||||αββαβ⋅>===⋅ ，所以二面角B QD A --的平面角的余弦值为23．46．（2021•新高考Ⅰ）如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点．（1）证明：OA CD ⊥；（2）若OCD ∆是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积．【解析】（1）证明：因为AB AD =，O 为BD 的中点，所以AO BD ⊥，又平面ABD ⊥平面BCD ，平面ABD ⋂平面BCD BD =，AO ⊂平面ABD ，所以AO ⊥平面BCD ，又CD ⊂平面BCD ，所以AO CD ⊥；（2）方法一：取OD 的中点F ，因为OCD ∆为正三角形，所以CF OD ⊥，过O 作//OM CF 与BC 交于点M ，则OM OD ⊥，所以OM ，OD ，OA 两两垂直，以点O 为坐标原点，分别以OM ，OD ，OA 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系如图所示，则(0B ，1-，0)，1,0)2C ，(0D ，1，0)，。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

近三年高考全国卷政治科立体几何真题
1. 2019年高考全国卷政治科真题
选择题：
1. 立体几何中，以下哪一条件不足以判定两个立体图形全等？
A. 有一对相等的正视图的对应边相等
B. 有一对相等的正视图的对应角相等
C. 有一对相等的平面角的对应边相等
D. 有对应边相等的对应面有一对角相等
2. 设立体立方体ABCDA'B'C'D'，以下哪一种将该立方体剖分的方法不正确？
A. 用一平面将立方体的后侧面与下侧面分离
B. 用一平面将立方体的前侧面与右侧面分离
C. 用一平面将立方体的下侧面与右侧面分离
D. 用一平面将立方体的上侧面与后侧面分离
填空题：
3. 立体几何中，已知两个立体图形的正视图和侧视图全等，则这两个立体图形 __相等__。

2. 2018年高考全国卷政治科真题
选择题：
1. 若已知一个平面图形的两个平面角都等于60°，则这个平面图形可能是 __正三角形__。

填空题：
2. 平面直角坐标系中，图像x^2+x^2=16 是圆x对于y轴的镜像图形的方程是 __x^2+x^2=x^2__。

2. 2017年高考全国卷政治科真题
选择题：
1. 根据下列作图过程，选择中能得到正方形的方案是 __作正方形内切于给定⚪x__
填空题：
2. 解下列方程：xxx^2x+xxxx=1的解的个数是 __6__。

以上是近三年高考全国卷政治科的立体几何真题的部分题目和答案。