信号与系统 实验指导1 矩形脉冲信号的分解与合成(2020·东北大学秦皇岛分校)
矩形脉冲信号的分解实验注意事项

矩形脉冲信号的分解实验注意事项矩形脉冲信号是实验中常见的一种信号形式,通过对矩形脉冲信号的分解实验,可以更好地理解信号的频谱特性。
在进行这个实验之前,有一些注意事项需要注意,以确保实验的顺利进行。
首先,为了获得准确的实验结果,我们需要使用高质量的信号发生器。
信号发生器应该能够产生高稳定性、低噪声的矩形脉冲信号。
此外,信号发生器的频率范围要足够广泛,以满足不同频率的矩形脉冲信号的需求。
其次,实验中使用的电路连接需要尽量简洁、稳定。
在将信号发生器与示波器连接时,确保连接线路的插头和插孔是干净的,并且牢固地连接在一起。
此外,为了避免干扰,应将电路放置在远离电源和其他干扰源的地方。
在准备实验样品时,我们应该选择适当的负载电阻。
负载电阻应该与信号发生器的输出阻抗相匹配,以确保信号的正确传输。
此外,实验样品的尺寸和材料也需要仔细选择,以满足实验的要求。
在实验过程中,我们还应该注意示波器的设置。
示波器的触发设置应该适当调整,以便捕捉到期望的矩形脉冲信号。
同时,示波器的时间和电压尺度也需要相应设置,以确保信号的完整显示。
在进行实验测量时,我们应该尽量减小误差。
可以通过多次测量和取平均值的方法来减小随机误差。
此外,还应注意测量仪器的精确度,并对实验结果进行合理的误差分析。
最后,在实验结束后,我们应该对实验过程和结果进行总结和分析。
我们可以将实验结果与理论计算结果进行比较,以验证实验的准确性。
同时,我们还可以探讨实验中遇到的问题和挑战,并提出改进的建议。
通过遵守以上注意事项,我们可以更好地进行矩形脉冲信号的分解实验,并获得准确、可靠的实验结果。
这将有助于我们更深入地了解信号处理和频谱分析的原理,为未来的研究奠定基础。
矩形脉冲信号的分解实验报告

矩形脉冲信号的分解实验报告矩形脉冲信号的分解实验报告引言在现代通信领域,信号的分解与合成是一项重要的技术。
矩形脉冲信号是一种常见的信号形式,它具有方波的特点,被广泛应用于数字通信、雷达、计算机网络等领域。
本实验旨在通过实际操作,探究矩形脉冲信号的分解原理与方法。
实验装置与步骤实验装置主要包括信号发生器、示波器以及信号分析仪。
首先,将信号发生器与示波器连接,调节信号发生器的频率和幅度,以产生一定的矩形脉冲信号。
然后,将示波器与信号分析仪连接,通过信号分析仪对矩形脉冲信号进行频谱分析,获取信号的频谱成分。
实验结果与讨论通过实验操作,我们得到了矩形脉冲信号的频谱图。
从频谱图中可以看出,矩形脉冲信号主要由基波和谐波组成。
基波对应于矩形脉冲信号的最低频率成分,而谐波则是基波频率的整数倍。
这是因为矩形脉冲信号具有周期性的特点,其频谱成分正好对应于周期性信号的谐波分布。
进一步分析矩形脉冲信号的频谱特性,我们发现谐波成分的幅度逐渐衰减。
这是由于矩形脉冲信号的边缘陡峭性导致高频成分的衰减速度较快。
因此,在实际应用中,我们常常需要对矩形脉冲信号进行滤波处理,以消除谐波成分的干扰。
除了频谱分析,我们还可以通过时域分析来研究矩形脉冲信号的特性。
通过示波器观察矩形脉冲信号的波形,我们可以发现其具有快速上升和下降的特点。
这是因为矩形脉冲信号的边缘陡峭性导致信号的变化速度较快。
同时,我们还可以通过示波器测量矩形脉冲信号的占空比,即高电平时间与周期的比值。
占空比的变化可以影响信号的平均功率和能量分布,对于某些应用场景具有重要意义。
结论通过本次实验,我们深入了解了矩形脉冲信号的分解原理与方法。
矩形脉冲信号主要由基波和谐波组成,谐波成分的幅度逐渐衰减。
矩形脉冲信号具有快速上升和下降的特点,其占空比的变化对信号的特性有着重要影响。
在实际应用中,我们需要根据具体需求对矩形脉冲信号进行滤波处理,以消除谐波成分的干扰。
总结矩形脉冲信号作为一种常见的信号形式,其分解与合成技术对于现代通信领域具有重要意义。
矩形脉冲信号的分解实验报告

一、实验目的1. 理解矩形脉冲信号的基本特性及其分解原理。
2. 掌握利用傅里叶级数对矩形脉冲信号进行分解的方法。
3. 通过实验验证傅里叶级数在信号分解中的应用。
二、实验原理矩形脉冲信号是一种典型的非正弦周期信号,其波形呈矩形,具有快速上升和下降的边缘。
在信号处理领域,矩形脉冲信号的分解对于理解信号的结构和特性具有重要意义。
根据傅里叶级数理论,任何周期信号都可以分解为一系列正弦波和余弦波的叠加。
对于矩形脉冲信号,其分解过程如下:1. 将矩形脉冲信号表示为傅里叶级数的形式,即:\[ f(t) = \frac{A}{2} + \sum_{n=1}^{\infty} \frac{4A}{\pi n}\sin(n\omega_0 t) \]其中,A为矩形脉冲信号的幅度,\( \omega_0 \) 为基波频率。
2. 通过滤波器将矩形脉冲信号分解为基波和各次谐波分量。
3. 利用示波器或频谱分析仪观察和分析分解后的信号。
三、实验仪器与设备1. 信号发生器2. 示波器3. 频谱分析仪4. 滤波器5. 矩形脉冲信号发生电路四、实验步骤1. 搭建矩形脉冲信号发生电路,调节信号发生器输出矩形脉冲信号,其幅度为A,周期为T。
2. 将矩形脉冲信号输入滤波器,滤波器应能分别通过基波和各次谐波分量。
3. 将滤波器输出的各次谐波分量分别接入示波器,观察和分析分解后的信号。
4. 利用频谱分析仪测量各次谐波分量的幅度和频率,并与理论值进行比较。
5. 记录实验数据,分析实验结果。
五、实验结果与分析1. 实验结果:通过实验,成功分解了矩形脉冲信号,得到了基波和各次谐波分量。
示波器显示的分解波形与理论分析一致,频谱分析仪测量的各次谐波分量幅度和频率也与理论值基本相符。
2. 分析:实验结果表明,傅里叶级数在矩形脉冲信号的分解中具有重要作用。
通过滤波器将信号分解为基波和各次谐波分量,有助于理解信号的结构和特性。
六、实验结论1. 矩形脉冲信号可以通过傅里叶级数进行分解,分解后的信号包括基波和各次谐波分量。
脉冲实验报告

一、实验目的1. 理解脉冲信号的基本特性;2. 掌握脉冲信号的分解与合成方法;3. 熟悉脉冲信号在信号处理中的应用。
二、实验原理脉冲信号是一种离散时间信号,具有快速上升和下降的波形。
脉冲信号在通信、控制、信号处理等领域具有广泛的应用。
本实验主要研究脉冲信号的分解与合成方法,以及脉冲信号在信号处理中的应用。
三、实验内容1. 脉冲信号的分解(1)实验目的:了解脉冲信号的分解方法,掌握使用示波器观察脉冲信号分解过程。
(2)实验原理:通过观察不同频率、不同幅度、不同脉冲宽度的脉冲信号,了解脉冲信号的分解特性。
(3)实验步骤:① 准备示波器、脉冲信号发生器、衰减器等实验设备;② 设置脉冲信号发生器的参数,如频率、幅度、脉冲宽度等;③ 将脉冲信号输入示波器,观察脉冲信号的波形;④ 逐渐改变脉冲信号的参数,观察脉冲信号分解过程。
2. 脉冲信号的合成(1)实验目的:掌握脉冲信号的合成方法,了解脉冲信号合成后的特性。
(2)实验原理:利用傅里叶级数将分解后的脉冲信号重新合成,观察合成后的脉冲信号波形。
(3)实验步骤:① 将分解后的脉冲信号分别通过不同频率、不同幅度、不同脉冲宽度的滤波器;② 将滤波后的信号分别输入加法器,合成新的脉冲信号;③ 观察合成后的脉冲信号波形,分析其特性。
3. 脉冲信号在信号处理中的应用(1)实验目的:了解脉冲信号在信号处理中的应用,掌握脉冲信号滤波、调制等方法。
(2)实验原理:脉冲信号在信号处理中具有重要作用,如滤波、调制、解调等。
(3)实验步骤:① 使用脉冲信号对原始信号进行滤波处理,观察滤波效果;② 使用脉冲信号对原始信号进行调制处理,观察调制效果;③ 使用脉冲信号对调制信号进行解调处理,观察解调效果。
四、实验结果与分析1. 脉冲信号的分解实验结果表明,脉冲信号的分解与参数设置密切相关。
随着频率、幅度、脉冲宽度的改变,脉冲信号的分解特性也随之变化。
2. 脉冲信号的合成实验结果表明,通过分解后的脉冲信号合成新的脉冲信号,可以观察到合成后的脉冲信号波形与原始脉冲信号具有相似性。
信号的分解与合成
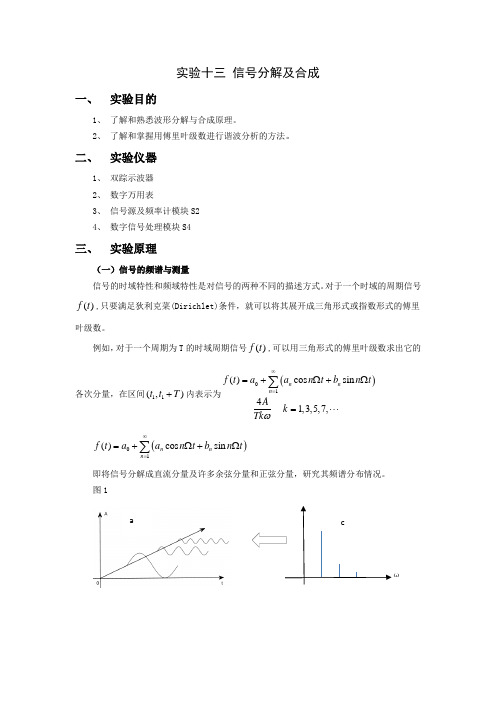
实验十三 信号分解及合成一、 实验目的1、 了解和熟悉波形分解与合成原理。
2、 了解和掌握用傅里叶级数进行谐波分析的方法。
二、 实验仪器1、 双踪示波器2、 数字万用表3、 信号源及频率计模块S24、 数字信号处理模块S4三、 实验原理(一)信号的频谱与测量信号的时域特性和频域特性是对信号的两种不同的描述方式。
对于一个时域的周期信号()f t ,只要满足狄利克菜(Dirichlet)条件,就可以将其展开成三角形式或指数形式的傅里叶级数。
例如,对于一个周期为T 的时域周期信号()f t ,可以用三角形式的傅里叶级数求出它的各次分量,在区间11(,)t t T +内表示为()01()cos sin 41,3,5,7,n n n f t a a n t b n t Ak Tk ω∞==+Ω+Ω=⋅⋅⋅∑()01()cos sin n n n f t a a n t b n t ∞==+Ω+Ω∑即将信号分解成直流分量及许多余弦分量和正弦分量,研究其频谱分布情况。
图1ωca信号的时域特性和频域特性信号的时域特性与频域特性之间有着密切的内在联系,这种联系可以用图13-1来形象地表示。
其中图(a)是信号在幅度—时间—频率三维坐标系统中的图形;图(b)是信号在幅度一时间坐标系统中的图形即波形图:把周期信号分解得到的各次谐波分量按频率的高低排列,就可以得到频谱图。
反映各频率分量幅度的频谱称为振幅频谱。
图(c)是信号在幅度—频率坐标系统中的图形即振幅频谱图。
反映各分量相位的频谱称为相位频谱。
在本实验中只研究信号振幅频谱。
周期信号的振幅频谱有三个性质:离散性、谐波性、收敛性。
测量时利用了这些性质。
从振幅频谱图上,可以直观地看出各频率分量所占的比重。
测量方法有同时分析法和顺序分析法。
同时分析法的基本工作原理是利用多个滤波器,把它们的中心频率分别调到被测信号的各个频率分量上。
当被测信号同时加到所有滤波器上,中心频率与信号所包含的某次谐波分景频率-致的滤波器便有输出。
信号与系统实验_矩形信号的分解

学号: 姓名:实验三、矩形信号的分解一、实验目的1、分析典型的矩形脉冲信号,了解矩形脉冲信号谐波分量的构成;2、观察矩形脉冲信号分解出各谐波分量的情况。
二、预备知识1.学习“周期信号的傅里叶级数分析”一节;2.复习matlab 软件的使用方法。
3.信号的滤波知识三、实验原理1、信号的频谱与测量信号的时域特性和频域特性是对信号的两种不同的描述方式。
对于一个时域的周期信号)t (f ,只要满足狄利克莱(Dirichlet)条件,就可以将其展开成三角形式或指数形式的傅里叶级数。
例如,对于一个周期为T 的时域周期信号)t (f ,可以用三角形式的傅里叶级数求出它的各次分量,在区间)T t ,t (11+内表示为)sin cos ()(10t n b t n a a t f n n n Ω+Ω+=∑∞=即将信号分解成直流分量及许多余弦分量和正弦分量,研究其频谱分布情况。
AA(c)图3-1 信号的时域特性和频域特性信号的时域特性与频域特性之间有着密切的内在联系,这种联系可以用图3-1来形象地表示。
其中图3-1(a)是信号在幅度--时间--频率三维座标系统中的图形;图3-1(b)是信号在幅度--时间座标系统中的图形即波形图;把周期信号分解得到的各次谐波分量按频率的高低排列,就可以得到频谱图。
反映各频率分量幅度的频谱称为振幅频谱。
图3-1(c)是信号在幅度--频率座标系统中的图形即振幅频谱图。
反映各分量相位的频谱称为相位频谱。
在本实验中只研究信号振幅频谱。
周期信号的振幅频谱有三个性质:离散性、谐波性、收敛性。
测量时利用了这些性质。
从振幅频谱图上,可以直观地看出各频率分量所占的比重。
测量方法有同时分析法和顺序分析法。
2、 矩形脉冲信号的频谱一个幅度为E ,脉冲宽度为τ,重复周期为T 的矩形脉冲信号,如图10-3所示。
图3-2 周期性矩形脉冲信号其傅里叶级数为:t n Tn Sa T E T E t f n i ωπτττcos )(2)(1∑=+= 该信号第n 次谐波的振幅为:Tn T n T E T n Sa T E a n /)/sin(2)(2τπτπττπτ== 由上式可见第n 次谐波的振幅与E 、T 、τ有关。
矩形脉冲信号的分解与合成实验报告

基波,它的频率与基波频率相同;当 k = 2 时,即为 c2 cos(2ω0t + ϕ2 ) ,称此为二次
-1-
谐波,它的频率是基波频率的二倍;依次类推, ck cos(kω0t + ϕk ) 称为 k 次谐波, 而相应的 ck 为 k 次谐波分量的振幅;ϕk 为 k 次谐波分量的初始相位。
利用式(2)可以将信号分解成直流分量及许多余弦分量,研究其频谱分布 情况。
∞
∑ x(t) = a0 + (ak cos kω0t + bk sin kω0t) k =1
(1)
∫ ∫ 式
中
,
ω0
=
2π T
称
为
基
波
频
率
,
a0
=
1 T
t0 +T x(t)dt
t0
,
ak
=2 T
t0 t0
+T
x(t)
cos
kω0tdt
,
∫ bk
=
2 T
t0 t0
+T
x(t)
sin
kω0tdt
。 a0、 ak、bk
-5-
波形合成时为合成波形的输出。 S2:复位开关。 SW1:4 位拨码开关。
图 6 数字信号处理模块的主要器件
3.2 双踪示波器 一台 本实验采用 GDS-1102 100MHz 数字存储示波器,可以直接利用示波器的
“save”按键存储当前示波器的显示内容至 SD 卡内。 四、实验内容
(1)方波信号的分解。调整“信号源及频率计模块”各主要器件,通过 TP1~TP8 观察 500Hz 方波信号的各次谐波,并记录各次谐波的峰峰值。
东北大学秦皇岛分校 信号与系统实验报告三 抽样定理实验 2020.04.30

2K
2K 正弦波
4K
2K
2K 正弦波
8K
2K
2K 正弦波
16K
2K
1K 三角波
16K
2K
1K 三角波
16K
6K
自己尝试设计某种组合进行扩展
说明 1.5 倍抽样脉冲 2 倍抽样脉冲 4 倍抽样脉冲 8 倍抽样脉冲 复杂信号恢复 复杂信号恢复
3. 频谱混叠现象验证
(1) 设置各信号参数 设置原始信号为:“正弦”,频率:1KHz,幅度设置指示为 50;设置抽样脉冲频率: 8KHz,占空比:4/8(50%);恢复滤波器截止频率:2K;
m(t) T (t) 的傅立叶变换是M() 和T () 的卷积:
M () = 1 M () () = 1
M (− n) s
T
s
2
T n =−
该式表明,已抽样信号 ms(t) 的频谱 需要注意,若抽样间隔 T 变得大于
Ms1
() 是无穷多个间隔为 ωs 的 M () 相迭加而成。 , 则 M () 和 () 的卷积在相邻的周期内存在
(5) 抽样信号时域观测 用四通道示波器,在 2P1 可观测原始信号,在 2P2 可观测抽样脉冲信号,在 2P7 可观测PAM 取
样信号;
(6) 抽样信号频域观测 使用示波器的 FFT 功能或频谱仪,分别观测 2P1,2P2,2P7 测量点的频谱;
(7) 恢复信号观察 鼠标点击框图上的“恢复滤波器”按钮,设置恢复滤波器的截止频率为 3K(点击截止频率数
3. 当模拟信号为 2KHz 正弦波、抽样频率为 8KHz、恢复滤波器为 2KHz 时: 原始信号波形、抽样脉冲波形、抽样输出波形、恢复信号波形
4. 当模拟信号为 2KHz 正弦波、抽样频率为 16KHz、恢复滤波器为 2KHz 时: 原始信号波形、抽样脉冲波形、抽样输出波形、恢复信号波形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验1 矩形脉冲信号的分解与合成
一、实验目的
掌握矩形脉冲信号时域特性及矩形脉冲信号谐波分量的构成;
验证组成矩形脉冲简单信号的存在;
验证谐波的齐次、离散、收敛特性;
理解各次谐波在合成信号中的作用;
观察矩形脉冲信号分解出的各谐波分量可以通过叠加合成出原矩形脉冲信号。
二、实验原理
1.信号的频谱与测量
信号的时域特性和频域特性是对信号的两种不同的描述方式。
对于一个时域的周期信号f ( t ) ,只要满足狄利克莱(Dirichlet)条件,就可以将其展开成三角形式或指数形式的傅里叶
级数。
例如,对于一个周期为 T 的时域周期信号f(t) ,可以用三角形式的傅里叶级数求出它的各次分量,在区间(t1,t1+T ) 内表示为:
即将信号分解成直流分量及许多余弦分量和正弦分量,研究其频谱分布情况。
A
0 Ω3Ω
A
5Ωω
(c)
图1-1 信号的时域特性和频域特性
信号的时域特性与频域特性之间有着密切的内在联系,这种联系可以用图1-1 来形象地表示。
其中图1-1(a)是信号在幅度——时间——频率三维座标系统中的图形;图1-1(b)是信号在幅度——时间座标系统中的图形即波形图;把周期信号分解得到的各次谐波分量按频率的高低排列,就可以得到频谱图。
反映各频率分量幅度的频谱称为振幅频谱。
图1-1(c)是信号在幅度——频率座标系统中的图形即振幅频谱图。
反映各分量相位的频谱称为相位频谱。
在本实验中只研究信号振幅频谱。
周期信号的振幅频谱有三个性质:离散性、谐波性、收敛性。
测
量时利用了这些性质。
从振幅频谱图上,可以直观地看出各频率分量所占的比重。
测量方法有同
时分析法和顺序分析法。
同时分析法的基本工作原理是利用多个滤波器同时取出复杂信号中的各次谐波,滤波器的中心频率分别设置在各次谐波上。
实验平台基于数字信号处理技术,在FPGA 中同时设计了8 个滤波器,如图1-2 所示。
图1-2 用同时分析法解析信号频谱
2.矩形脉冲信号的频谱
一个幅度为E,脉冲宽度为τ,重复周期为T 的矩形脉冲信号,如图1-3 所示。
T
其傅里叶级数为:
图1-3 周期性矩形脉冲信号
该信号第n 次谐波的振幅为:
a =
2EτSa( nτπ) =2Eτsin(nτπ/ T )
n T T T nτπ/ T
由上式可见第n 次谐波的振幅与E 、T 、τ有关。
3.信号的分解提取
对复杂进行信号分解或谐波提取是滤波系统的一项基本任务。
当我们仅对信号的某些分量感兴趣时,可以利用选频滤波器,提取其中有用的部分,而将其它部分滤去。
目前数字滤波器已基本取代了传统的模拟滤波器,数字滤波器与模拟滤波器相比具有许多优点。
数字滤波器具有灵活性高、精度高和稳定性高,体积小、性能高,便于实现等优点。
因此在这里我们选用了数字滤波器来实现信号的分解。
实验平台的“数字信号与语音信号处理模块”上,设计了 8 个滤波器(一个低通、六个带通、一个高通),可以同时提取基波、1 次谐波 。
7 次谐波及 8 次以上的频率分量。
分解输出的 8 路信号可以用示波器观察。
4. 周期性的矩形信号可分解成各次谐波,因此,按傅里叶级数分解出的谐波信号合成应
该能还原矩形信号。
本实验的信号合成部分内容就是通过加法器,验证各次谐波叠加后能合成原始信号;
四、实验内容及步骤
1、在实验列表中选择“信号的合成与分解”实验
2、调节信号源,使 DDS1 输出方波,f=4KHz,幅度输出 2Vpp 。
3、示波器可分别在各个谐波输出上观测信号各次谐波的波形;
4、根据表 1-1 中给定的数值进行实验,并记录实验获得的数据填入表中。
表 1-1
21=τ
的矩形脉冲信号的频谱
5、按表1-2 的要求,组合图 1-2 中的开关,观测占空比为 1/2 的方波各次谐波合成结果。
表 1-2 矩形脉冲信号的各次谐波之间的合成
六、实验报告要求
1.总结谐波特性;
2.分析各次谐波对合成信号的影响;
3.矩形脉冲信号为例,总结周期信号的分解与合成原理.
4.要完整的恢复出原始矩形脉冲信号,各次谐波幅度要成什么样的比例关系。
