与圆有关的位置关系 (1)
圆与圆的位置关系 (1)

练习:判断下列两圆的位置关系:
2 ( x 2) 2 ( y 2) 2 1与(x 2) ( y 5) 2 16 2 2 2 2 (2) x y 6 x 7 0与x y 6 y 27 0 解(1):两圆的圆心坐标为(-2 , 2), (2 , 5),两圆的圆心距
x
列表如下:
外 离 外 切 相 交 内 切 内 含
d r1 r2 d r1 r2 r1 r2 d r1 r2 d r1 r2 d r1 r2
r1
d
r1
d
r1
r2
d
r1
d r2
r1
d r2
r2
r2
观察:当两圆相切(外切、内切)时,切点与两圆的连心线 有什么关系? (切点在两圆的连心线上).
( x 3)2 ( y 3 3)2 16. 解得:
例6.求以圆C1∶x2+y2-12x-2y-13=0和 圆C2:x2+y2+12x+16y-25=0的公共弦为直径的圆方程. 解法 相减得公共弦所在直线方程为4x+3y-2=0.
∵所求圆以AB为直径,
于是圆的方程为(x-2)2+(y+2)2=25 .
6.圆系方程:
①设圆C1∶x2+y2+D1x+E1y+F1=0和
圆C2∶x2+y2+D2x+E2y+F2=0. 若两圆相交,则过交点的圆系方程为 x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ为 参数,圆系中不包括圆C2,λ=-1为两圆的公共弦 所在直线方程). ②设圆C∶x2+y2+Dx+Ey+F=0与直线l: Ax+By+C=0,若直线与圆相交,则过交点的圆 系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0 (λ为参 数).
《与圆有关的位置关系(第1课时)》公开课教案 (省一等奖)2022年人教版

24.2 与圆有关的位置关系教学内容1.设⊙O的半径为r,点P到圆心的距离OP=d,那么有:点P在圆外⇔d>r;点P在圆上⇔d=r;点P在圆内⇔d<r.2.不在同一直线上的三个点确定一个圆.3.三角形外接圆及三角形的外心的概念.4.反证法的证明思路.教学目标1.理解并掌握设⊙O的半径为r,点P到圆心的距离OP=d,那么有:点P在圆外⇔d>r;点P在圆上⇔d=r;点P在圆内⇔d<r及其运用.2.理解不在同一直线上的三个点确定一个圆并掌握它的运用.3.了解三角形的外接圆和三角形外心的概念.4.了解反证法的证明思想.复习圆的两种定理和形成过程,并经历探究一个点、两个点、•三个点能作圆的结论及作图方法,给出不在同一直线上的三个点确定一个圆.接下去从这三点到圆心的距离逐渐引入点P•到圆心距离与点和圆位置关系的结论并运用它们解决一些实际问题.重难点、关键1.•重点:点和圆的位置关系的结论:不在同一直线上的三个点确定一个圆其它们的运用.2.难点:讲授反证法的证明思路.3.关键:由一点、二点、三点、•四点作圆开始导出不在同一直线上的三个点确定一个圆.教学过程一、复习引入〔学生活动〕请同学们口答下面的问题.1.圆的两种定义是什么?2.你能至少举例两个说明圆是如何形成的?3.圆形成后圆上这些点到圆心的距离如何?4.如果在圆外有一点呢?圆内呢?请你画图想一想.老师点评:〔1〕在一个平面内,线段OA绕它固定的一个端点O旋转一周,•另一个端点A所形成的图形叫做圆;圆心为O,半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形.〔2〕圆规:一个定点,一个定长画圆.〔3〕都等于半径.〔4〕经过画图可知,圆外的点到圆心的距离大于半径;•圆内的点到圆心的距离小于半径.二、探索新知由上面的画图以及所学知识,我们可知:设⊙O的半径为r,点P到圆心的距离为OP=d那么有:点P在圆外⇒d>r点P在圆上⇒d=r点P在圆内⇒d<r反过来,也十清楚显,如果d>r⇒点P在圆外;如果d=r⇒点P在圆上;如果d<r⇒点P在圆内.因此,我们可以得到:这个结论的出现,对于我们今后解题、判定点P是否在圆外、圆上、圆内提供了依据.下面,我们接下去研究确定圆的条件:〔学生活动〕经过一点可以作无数条直线,经过二点只能作一条直线,那么,经过一点能作几个圆?经过二点、三点呢?请同学们按下面要求作圆.〔1〕作圆,使该圆经过点A,你能作出几个这样的圆?〔2〕作圆,使该圆经过点A、B,你是如何做的?你能作出几个这样的圆?其圆心的分布有什么特点?与线段AB有什么关系?为什么?〔3〕作圆,使该圆经过点A、B、C三点〔其中A、B、C三点不在同一直线上〕,•你是如何做的?你能作出几个这样的圆?老师在黑板上演示:〔1〕无数多个圆,如图1所示.〔2〕连结A、B,作AB的垂直平分线,那么垂直平分线上的点到A、B的距离都相等,都满足条件,作出无数个.其圆心分布在AB的中垂线上,与线段AB互相垂直,如图2所示.lBA(1) (2) (3)〔3〕作法:①连接AB、BC;②分别作线段AB、BC的中垂线DE和FG,DE与FG相交于点O;③以O为圆心,以OA为半径作圆,⊙O就是所要求作的圆,如图3所示.在上面的作图过程中,因为直线DE与FG只有一个交点O,并且点O到A、B、C•三个点的距离相等〔中垂线上的任一点到两边的距离相等〕,所以经过A、B、C三点可以作一个圆,并且只能作一个圆.也就是,经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆.外接圆的圆心是三角形三条边垂直平分线的交点,叫做这个三角形的外心.下面我们来证明:经过同一条直线上的三个点不能作出一个圆.证明:如图,假设过同一直线L上的A、B、C三点可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线L1,又在线段BC的垂直平分线L2,•即点P为L1与L2点,而L1⊥L,L2Alm BAC ED OF ⊥L ,这与我们以前所学的“过一点有且只有一条直线与直线垂直〞矛盾. 所以,过同一直线上的三点不能作圆.上面的证明方法与我们前面所学的证明方法思路不同,它不是直接从命题的得出结论,而是假设命题的结论不成立〔即假设过同一直线上的三点可以作一个圆〕,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到命题成立.这种证明方法叫做反证法. 在某些情景下,反证法是很有效的证明方法.例1.某地出土一明代残破圆形瓷盘,如以下图.为复制该瓷盘确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.分析:圆心是一个点,一个点可以由两条直线交点而成,因此,只要在残缺的圆盘上任取两条线段,作线段的中垂线,交点就是我们所求的圆心. 作法:〔1〕在残缺的圆盘上任取三点连结成两条线段; 〔2〕作两线段的中垂线,相交于一点. 那么O 就为所求的圆心. 三、稳固练习教材P100 练习1、2、3、4. 四、应用拓展例2.如图,梯形ABCD 中,AB ∥CD ,AD=BC ,AB=48cm ,CD=30cm ,高27cm ,求作一个圆经过A 、B 、C 、D 四点,写出作法并求出这圆的半径〔比例尺1:10〕分析:要求作一个圆经过A 、B 、C 、D 四个点,应该先选三个点确定一个圆,•然后证明第四点也在圆上即可.要求半径就是求OC 或OA 或OB ,因此,•要在直角三角形中进行,不妨设在Rt △EOC 中,设OF=x ,那么OE=27-x 由OC=OB 便可列出,•这种方法是几何代数解. 作法分别作DC 、AD 的中垂线L 、m ,那么交点O 为所求△ADC 的外接圆圆心. ∵ABCD 为等腰梯形,L 为其对称轴 ∵OB=OA ,∴点B 也在⊙O 上 ∴⊙O 为等腰梯形ABCD 的外接圆 设OE=x ,那么OF=27-x ,∵OC=OB222215(27)24x x +=-+ 解得:x=20∴221520+=25,即半径为25m .五、归纳总结〔学生总结,老师点评〕 本节课应掌握:点和圆的位置关系:设⊙O 的半径为r ,点P 到圆心的距离为d ,那么;;.P d r P d r P d r ⇔>⎧⎪⇔=⎨⎪⇔<⎩点在圆外点在圆上点在圆内 2.不在同一直线上的三个点确定一个圆. 3.三角形外接圆和三角形外心的概念.4.反证法的证明思想.5.以上内容的应用.六、布置作业1.教材P110 复习稳固 1、2、3. 2.选用课时作业设计.第一课时作业设计一、选择题.1.以下说法:①三点确定一个圆;②三角形有且只有一个外接圆;•③圆有且只有一个内接三角形;④三角形的外心是各边垂直平分线的交点;⑤三角形的外心到三角形三边的距离相等;⑥等腰三角形的外心一定在这个三角形内,其中正确的个数有〔• 〕A.1 B.2 C.3 D.42.如图,Rt△ABC,∠C=90°,AC=3cm,BC=4cm,那么它的外心与顶点C的距离为〔〕.A.2.5 B.2.5cm C.3cm D.4cmB ACBACDO3.如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平分∠ACB,那么弦AD长为〔〕A.522 B.52C.2 D.3二、填空题.1.经过一点P可以作_______个圆;经过两点P、Q可以作________•个圆,•圆心在_________上;经过不在同一直线上的三个点可以作________个圆,•圆心是________的交点. 2.边长为a的等边三角形外接圆半径为_______,圆心到边的距离为________.3.直角三角形的外心是______的中点,锐角三角形外心在三角形______,钝角三角形外心在三角形_________.三、综合提高题.1.如图,⊙O是△ABC的外接圆,D是AB上一点,连结BD,并延长至E,连结AD,•假设AB=AC,∠ADE=65°,试求∠BOC的度数.B AC O2.如图,通过防治“非典〞,人们增强了卫生意识,大街随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中,如图24-49所示,A、B、C•为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,•要使得回收站建在三个小区都相等的某处,请问如果你是工程师,你将如何选址.BAC3.△ABC 中,AB=1,AC 、BC 是关于x 的一元二次方程〔m+5〕x 2-〔2m-5〕x+12=0两个根,外接圆O 的面积为4π,求m 的值.答案:一、1.B 2.B 3.A二、1.无数,无数,线段PQ 的垂直平分线,一个,三边中垂线 2.33 a 36a 3.斜边 内 外 三、1.100°2.连结AB 、BC ,作线段AB 、BC 的中垂线,两条中垂线的交点即为垃圾回收站所在的位置. 3.∵πR 2=4π,∴R=12,∵AB=1,∴AB 为⊙O 直径,∴AC 2+BC 2=1,即〔AC+BC 〕2-2AC ·BC=1, ∴〔255m m -+〕2-•2·125m +=1,m 2-18m-40=0,∴m=20或m=-2, 当m=-2时,△<0〔舍去〕, ∴m=20.[教学反思]学生对展开图通过各种途径有了一些了解,但仍不能把平面与立体很好的结合;在遇到问题时,多数学生不愿意自己探索,都要寻求帮助。
与圆有关的几种位置关系

圆与圆的位置关系有五种:外离、外切、相交、内切、内含。
设两个圆的半径为R和r,圆心距为d。
则有以下五种关系:
1、d>R+r两圆外离;两圆的圆心距离之和大于两圆的半径之和。
2、d=R+r两圆外切;两圆的圆心距离之和等于两圆的半径之和。
3、d=R-r两圆内切;两圆的圆心距离之和等于两圆的半径之差。
4、d<R-r两圆内含;两圆的圆心距离之和小于两圆的半径之差。
5、d<R+r两园相交;两圆的圆心距离之和小于两圆的半径之和。
扩展资料
圆的性质:
1、圆是轴对称图形,其对称轴是任意一条通过圆心的直线。
圆也是中心对称图形,其对称中心是圆心。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的2条弧。
垂径定理的逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的2条弧。
2、有关圆周角和圆心角的性质和定理。
在同圆或等圆中,如果两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其余各组量都分别相等。
在同圆或等圆中,相等的弧所对的圆周角等于它所对的圆心角的一半(圆周角与圆心角在弦的同侧)。
圆和圆的位置关系(1)k

若设两圆的半径分别为R和r两圆的圆心距为d 则两圆的位置关系可用d与R和r之间的关系表示 两圆的位置关系 外离 外切 相交 内切 内含 d与R和r的关系
d>R+r d = R+r
R - r<d<R+r
d=R-r d<R - r
练习:
R
3 2 5 3 4
1, 填表
r
1 4 3 4 3
5 2 8 0 .5 2
哇!天怎么突然黑了?
原来是发生日食了!
如果把月亮和太阳抽象成两个圆,在发生 日食过程中,这两个圆具有不同的位置关系。 今天我们就来学习——
24.2.3圆和圆的位置关系
现在我们通过以下的演示观察一下 两圆有几种位置关系?
两圆共有五种位置关系
(1)
(2)
(3)
(4)
(5)
你有什么办法来区分这五种位置呢 两圆公共点的个数。
· 0
r
1
r
R d
R
02
·
r R
01
· 0
r
1
r
R
R
02
·
(1)两圆外离
d > R+r
(2)两圆外切
d = R+r
R
· ·
01 02
(3)两圆相交
R- r<d<R+r (R≥r)
r
R
.·
02
d = R- r (R>r)
r
. 0·
01
2
(4)两圆内切
(5)两圆内含
d<R- r (R>r)
注意:“ ”的含义是:由两圆的位置关系可以得到圆心距与两圆半径的数量关系; 反之由圆心距与两圆半径的数量关系也可以确定两圆的位置关系。
与圆有关的位置关系
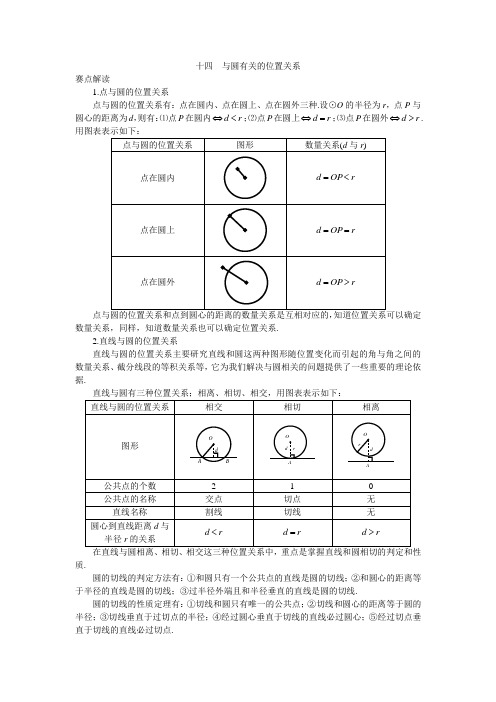
十四 与圆有关的位置关系赛点解读1.点与圆的位置关系点与圆的位置关系有:点在圆内、点在圆上、点在圆外三种.设⊙O 的半径为r ,点P 与圆心的距离为d ,则有:⑴点P 在圆内r d <⇔;⑵点P 在圆上r d =⇔;⑶点P 在圆外r d >⇔.用图表表示如下:点与圆的位置关系图形数量关系(d 与r )点在圆内r OP d <=点在圆上r OP d ==点在圆外r OP d >=点与圆的位置关系和点到圆心的距离的数量关系是互相对应的,知道位置关系可以确定数量关系,同样,知道数量关系也可以确定位置关系.2.直线与圆的位置关系直线与圆的位置关系主要研究直线和圆这两种图形随位置变化而引起的角与角之间的数量关系、截分线段的等积关系等,它为我们解决与圆相关的问题提供了一些重要的理论依据.直线与圆有三种位置关系;相离、相切、相交,用图表表示如下:直线与圆的位置关系相交相切相离图形dBOAr dOArd OA公共点的个数 2 1 0 公共点的名称 交点 切点 无 直线名称 割线切线 无 圆心到直线距离d 与半径r 的关系 r d <r d =r d >在直线与圆相离、相切、相交这三种位置关系中,重点是掌握直线和圆相切的判定和性质.圆的切线的判定方法有:①和圆只有一个公共点的直线是圆的切线;②和圆心的距离等于半径的直线是圆的切线;③过半径外端且和半径垂直的直线是圆的切线.圆的切线的性质定理有:①切线和圆只有唯一的公共点;②切线和圆心的距离等于圆的半径;③切线垂直于过切点的半径;④经过圆心垂直于切线的直线必过圆心;⑤经过切点垂直于切线的直线必过切点.涉及切线的重要性质还有切线长定理和弦切角定理,其中切线长定理及其对应的基本图形、以及圆的外切三角形、外切四边形所存在的线段之间的关系也是解决问题常用的依据和方法,弦切角定理更是转化圆中相关角的重要定理.和圆有关的比例线段定理包括相交定理、切割定理及其推论,统称圆幂定理,它揭示了直线与圆相交后所存在的线段间的比例关系.相交弦定理:圆内的两条相交弦被交点分成的两条线段的积相等. 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆的交点的两条线段的比例中项.割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.概括圆幂定理其内容为:过定点圆的弦被该点内分(或外分)成的两条线段的积为定值,如图14-3.()22r OP PB AP -=⋅定值PBAO BP AO3.圆与圆的位置关系两圆的位置关系共分为五种:外离、外切、相交、内切、内含(同心圆是内含的特例).用图表表示如下:两圆的位置关系 图形 公共点的个数 数量关系(d 与R 、r)外离dO 2O 1rR0个 r R d +>外切dO 2O 1r R1个r R d +=相交dO 2O 1r R2个r R d r R +<<-内切Td O 2O 1rR1个r R d -=关于圆和圆的位置关系的性质,判定: ⑴设两圆的半径分别为R 、r ,圆心距为d ,则: ①r R d +>⇔⇔两圆外离条公切线4 ②r R d +=⇔⇔两圆外切条公切线3③()r R r R d r R ≥+<<-⇔⇔两圆相交条公切线2 ④()r R r R d >-=⇔⇔两圆内切条公切线1⑤()r R r R d >-<⇔⇔两圆内含无公切线 ⑵相切两圆的性质:如果两圆相切,那么连心线必过切点. ⑶相交两圆的性质:相交两圆的连心线垂直平分公共弦.由圆的对称性知,若两圆有两条外(内)公切线,那么这两条外(内)公切线长相等;若两条外(内)公切线相交,则交点必在连心线上,并且连心线平分两条切线所夹的角.运用直线与圆、圆与圆的有关知识解决问题,既是圆的有关知识综合应用,同时又是重要的数学方法的体现.本节常用的解题方法有:⑴切线的判定常用的两种方法: ①若待证的切线与圆有一个公共点,则连线过该点的半径,证这条直线与所连半径垂直,即为圆的切线;②当直线与圆的公共点不明确,要证该直线是圆的切线时,常过圆心作该直线的垂线,证圆心到直线的距离等于圆的半径,即为圆的切线.⑵切线应用方法与技巧:遇到条件中有切线时,常用如下途径思考: ①连过切点的半径——利用切线的性质定理; ②将切点与圆上的点相连,构造弦切角——利用弦切角定理; ③应用切割线定理. ⑶利用和圆有关的比例线段定理,可直接进行线段的等积式的转换,或比例线段的转化. ⑷求两圆外(或内)公切线的长或求公切线与连心线的夹角的常规方法是通过构造直角三角形,将两圆半径、圆心距、公切线集中起来解决.如图(14-4(1)(2))2()1()⑸遇到两圆相交的问题,常作公共弦或连心线,尤其是公共弦,它是联系两圆关系的重要纽带.⑹遇到两圆相切的问题,常过切点作公切线,构造弦切角,可进行有关角的转化. 本节涉及到的热门赛点有:内含d O 2O 1r R0个r R d -<1.圆中有关计算.2.证线段相等.3.证等积、等比及其他有关线段的等式. 赛题详解赛点1:圆中有关计算例1 在平行四边形ABCD 中,过A 、B 、C 三点的圆交AD 于E ,且与CD 相切,若4=AB ,5=BE ,则DE 的长为( )A.3B.4C.415 D.516 BEDCA例2 如图14-6,在半径为r 的⊙O 中,AB 为直径,C 为弧AB 的中点,D 为弧CB 的三分之一等分点,且弧DB 的长等于两倍的弧CD 的长;连接AD 并延长交⊙O 的切线CE 于点E (C 为切点),求AE 的长.DEC BOA例3 如图14-7,7根圆形筷子的横截面圆的半径为r ,则捆扎这7根筷子一周的绳子的长度为 .CB AO 2O 1例4 已知:如图14-8,P A 、PB 分别切⊙O 于点A 、B ,PO 交AB 于点M ,C 是MB 上的一点,OC 的延长线交⊙O 于点E ,OE PD ⊥,垂足为D ,且3=OC ,8=OD ,求⊙O 的半径.PD EC MOBA例5 如图14-9,D 、E 是△ABC 边上BC 上的两点,F 是BA 延长线上一点,CAF DAE ∠=∠.⑴判断△ABD 的外接圆与△ACE 的外接圆的位置关系,并证明你的结论. ⑵若△ABD 的外接圆半径是△ACE 的外接圆半径的2倍,6=BC ,4=AB ,求BE 的长.E D CFB A赛点2:证线段相等例6 如图14-10,已知BC 是⊙O 的切线,OC 平行弦AD ,过点D 作AB DE ⊥于点E ,连接AC ,与DE 交于点P ,问:EP 与PD 是否相等?证明你的结论.CDPB OE A例7 如图14-11,已知AB 为⊙O 的直径,C 为⊙O 上一点,延长BC 至D ,是BC CD =,AD CE ⊥,垂足为E ,BE 交⊙O 于F ,AF 交CE 于P ,求证:PC PE =.BOF CP EDA赛点3:证等积、等比及其他有关线段的等式 例8 如图14-12,P 是⊙O 外一点,P A 与⊙O 切于A ,P AC 是⊙O 的割线,PO AD ⊥于D ,求证:CD PC BD PB ::=.COD BPA例9 如图14-13,已知点P 是⊙O 外一点,PS 、PT 是⊙O 的两条切线,过点P 作⊙O 的割线P AB ,交⊙O 于A 、B 两点,与ST 交于点C .求证:⎪⎭⎫ ⎝⎛+=PB PA PC 11211. H ACOTPBS实战演练赛点整合,步步为营1.如图14-14,在△ABC 中,︒=∠70A ,⊙O 截△ABC 的三条边所得的三条弦都相等,则BOC ∠的度数是 .CB AO2.如图14-15,正方形ABCD 的边长为4,E 点在BC 上,以E 为圆心,EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则EC = .EC BDA3.如图14-16,⊙O 1和⊙O 2内切于点P ,⊙O 2的弦AB 经过⊙O 1的圆心,交⊙O 1于点C 、D .若2:4:1::=DB CD AC ,则点O 2与⊙O 1的位置关系是( )A.O 2在⊙O 1内B.O 2在⊙O 1外C.O 2在⊙O 1上D.以上情况都有可能O 2O 1PDC BA4.直角三角形△ABC 的三条边长分别为3,4,5,若将其内切圆挖去,则剩下部分的面积等于 .5.在平面上,如果点A 和点B 到点C 的距离分别为3和4,那么A 、B 两点的距离d 应该是( )A.1=dB.2=dC.7=dD.71≤≤d 6.如图14-17,等边△ABC 中,边AB 与⊙O 相切于点H ,边BC 、CA 分别与⊙O 交于点D 、E 、F 、G .已知2=AG ,6=GF ,1=FC ,则DE = .DEFGHCOBA7.如图14-18,大圆O 的直径acm AB =,分别以OA 、OB 为直径作⊙O 1和⊙O 2,并在⊙O 与⊙O 1和⊙O 2的空隙间作两个等圆⊙O 3和⊙O 4,这些圆互相内切或外切,则四边形O 1O 2O 3O 4的面积为 cm 2.O 3O 4O 2O 1OBA8.如图14-19,ABCD 是边长为a 的正方形,以D 为圆心,DA 为半径的圆弧与以BC 为直径的半圆交于另一点P ,延长AP 交BC 于点N ,则=NCBN. NPCBDA9.如图14-20所示,AB 是⊙O 1的直径,AO 1是⊙O 2的直径,弦MN ∥AB ,且MN 与⊙O 2相切点C .若⊙O 1的半径为2,则由O 1B 、弧BN 、NC 、弧CO 1围成的图形的面积等于 .O 2O 1N M CBA10.如图14-21,⊙O 是正方形ABCD 的外接圆,O 为圆心,点P 在劣弧AB 上,DP 交AO 于点Q .若QO PQ =,则AQQC等于( )A.132-B.23+C.23+D.32PQ OD BCA11.如图14-22,在等腰三角形△ABC 中,O 为底边BC 的中点,以O 为圆心作半圆与AB 、AC 相切,切点分别为D 、E .过半圆上一点F 作半圆的切线,分别交AB 、AC 于M 、N ,那么2BC CN BM ⋅的值等于( )A.81B.41C.21D.1 ED FN M CABO12.如图14-23所示,A 为弧BC 的中点,过点C 的切线交BA 的延长线于D ,G 为DC的中点,AC DE ⊥于E ,求证:EC BD 2=.ECGDBA13.如图14-24,已知AB 是半圆O 的直径,过A 、B 作弦AC 与BD 交于点E ,过C 、D 作圆的切线交于点P .求证:BA PE ⊥.OPDCBEA智能升级,链接赛题14.已知线段AB 的中点为C ,以点A 为圆心、AB 的长为半径作圆,在线段AB 的延长线上取点D ,使得AC BD =;再以点D 为圆心、DA 的长为半径作圆,与⊙A 分布相交于F 、G 两点,连接FG 交AB 于点H ,则BHAH的值为 . 15.图14-25中的三块阴影部分由两个半径为1的圆及其外公切线分割而成.如果中间一块阴影的面积等于上下两块阴影的面积之和,则这两圆的公共弦长是( )A.25 B.26 C.22521π- D.21621π- PNMQ 2Q 1CBDA 16.如图14-26,正方形ABCD 的对角线AC 、BD 交于点M ,且分正方形为四个三角形,⊙O 1、⊙O 2、⊙O 3、⊙O 4分别为△AMB 、△BMC 、△CMD 、△DMA 的内切圆,已知1=AB ,则⊙O 1、⊙O 2、⊙O 3、⊙O 4所夹的中心(阴影)部分的面积为( )A.()()162234--π B.()4223π- C.()()42234--π D.164π-MO 2O 4O 3O 1CDBA17.如图14-27,已知圆心为A 、B 、C 的三个圆彼此相切,且均与直线l 相切,若⊙A 、⊙B 、⊙C 的半径分别为a 、b 、c (0<c<a<b ),则a 、b 、c 一定满足的关系式为( )A.c a b +=2B.c a b +=2C.b a c 111+= D.ba c 111+=CBAl18.如图14-28有五个圆顺次相外切,且又都与直线a 、b 相切.如果其中最小圆与最大圆的直径分别为18和32,那么⊙O 3的直径为 .O 5O 4O 3O 2O 119.已知直角梯形ABCD 的四条边长分别为2=AB ,10==CD BC ,6=AD ,过B 、D 两点作圆,与BA 的延长线交于点E ,与CB 的延长线交于点F ,则BF BE -的值为 .20.如图14-29,点C 是半径为1的半圆弧AB 的一个三等分点,分别以弦AC 、BC 为直径向外侧作4个半圆,则图中阴影部分(4个新月形)的面积是 .EDCBA21.8月8日,第29届奥运会在北京举行,奥运五环旗象征着全世界人民的大团结,五环旗中,五个大小相等的环环环相扣,三个环在上,两个环在下,五个环的中心连接成等腰梯形,构成一个喜庆、和谐、优美的轴对称图形.如图14-30,假设a O O =42,a O O 221=,a O =∠1,则等腰梯形O 1O 2O 4O 5的对角线O 1O 4的长为 .O 5O 4O 3O 2O 122.宏远广告公司要为某企业的一种产品设计商标图案,给出了如下几种初步方案,供继续设计选用(设图中圆的半径均为r )(图14-31). ⑴如图14-31(1),分别以线段O 1O 2的两个端点为圆心,以这条线段的长为半径作出两个互相交错的圆的图案,试求两圆相交部分的面积. ⑵如图14-31(2),分别以等边△O 1O 2O 3的三个顶点为圆心,以其边长为半径,作出三个两两相交的相同的圆,这时这三个圆相交部分的面积又是多少呢? ⑶如图14-31(3),分别以正方形O 1O 2O 3O 4的四个顶点为圆心,以其边长为半径作四个相同的圆,则这四个圆的相交部分的面积又是多少呢?图3()图(2)图1()O 1O 2O 3O 2O 1O 4O 3O 2O 123.如图14-32,已知△ABC 内接于⊙O ,AD 、BD 为⊙O 的切线,作DE ∥BC ,交AC 于E ,连接EO 并延长交BE 于F ,求证:BF=FC .OFE DCBA24.如图14-33,△ABC 是锐角三角形,以BC 为直径作⊙O ,AD 是⊙O 的切线,从AB 上一点E 作AB 的垂线交AC 的延长线于点F ,若ACAEAF AB =,求证:AE AD =. OFE DCBA25.如图14-34,△ABC 为等腰三角形,AP 是底边BC 上的高,点D 是线段PC 上的一点,BE 和CF 分别是△ABD 和△ACD 的外接圆直径,连接EF .求证:BCEF PAD =∠tan . CD P EFB A26.已知等腰三角形△ABC 中,AC AB =,∠C 的平分线与AB 边交于点P ,M 为△ABC 的内切圆⊙I 与BC 边的切点,作MD ∥AC ,交⊙I 于点D ,证明:PD 是⊙I 的切线.C M I DPB A。
圆与圆的位置关系

图1扇形、圆与圆的位置关系一、圆和圆的位置关系.1、外离、外切、相交、内切、内含(包括同心圆)这五种位置关系的定义.(1)外离: 两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离.(2)外切: 两个圆有惟一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时, 叫做这两个圆外切.这个惟一的公共点叫做切点.(3)相交: 两个圆有两个公共点,此时叫做这个两个圆相交.(4)内切: 两个圆有惟一的公共点,并且除了这个公共点以外,一个圆上的都在另一个圆的内部时,叫做这两个圆内切.这个惟一的公共点叫做切点.(5)内含: 两个圆没有公共点, 并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.两圆同心是两圆内的一个特例. 2、相切两圆的性质:如果两个圆相切,那么切点一定在连心线上. 3、 相交两圆的性质:相交两圆的连心线垂直平分公共弦. 二、弧长及扇形的面积1、圆周长公式: 圆周长C=2πR (R 表示圆的半径)2. 弧长公式: 弧长180R n l π= (R 表示圆的半径, n 表示弧所对的圆心角的度数)3、扇形定义:一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.4、弓形定义:由弦及其所对的弧组成的图形叫做弓形. 弓形弧的中点到弦的距离叫做弓形高. 5、圆的面积公式.2R S π= (R 表示圆的半径) 6、扇形的面积公式:扇形的面积3602R n S π=扇形 (R 表示圆的半径, n 表示弧所对的圆心角的度数)※弓形的面积公式:(如图5) (1)当弓形所含的弧是劣弧时, 三角形扇形弓形S S S -= (2)当弓形所含的弧是优弧时, 三角形扇形弓形S S S += (3)当弓形所含的弧是半圆时, 扇形弓形S R S ==221π提高试题1、如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为( )A. (4+cm B. 9 cmC. D.cm第1题 第2题2、如图,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,B 为AN 弧的中点,点P 是直径MN 上一个动点,则PA+PB 的最小值为( )A .22B .2C .1D .23、已知两圆的半径为R,r 分别是方程X 2-5X+6=0两根,两圆的圆心距为1,两圆的位置关系是( ) A.外离 B.外切 C.内切 D.相交4、已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于 ( )A .8πB .9πC .10πD .11π 5、一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是 ( ).A .1B .34C .12D .136、 现有一个圆心角为,半径为的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为( )A .B .C .D .7、如图,正方形ABCD 内接于⊙O ,点P 在劣弧AB 上,连接DP ,DP 交AC 于点Q .若QO=PQ ,则QA QC的值为( ) (A )132-(B )32(C )23+(D )23+8、已知锐角△ABC 的顶点A 到垂心H 的距离等于它的外接圆的半径,则∠A 的度数是( ) (A )30° (B )45° (C )60° (D )75°9、如图,已知平行四边形ABCD ,过A 、B 、C 三点的圆交AD 于E ,且与CD 相切。
与圆有关的位置关系
R与圆有关的位置关系一、知识梳理1、点和圆的位置关系.对于给定的圆,平面上的点与这个圆的位置关系有三种: 点在圆内;点在圆上;点在圆外.点P 在⊙O 内0d R ⇔≤<; 点Q 在⊙O 上d R ⇔=; 点R 在⊙O 外d R ⇔>. 2、直线与圆的位置关系.直线l 与O 相离d R ⇔>; 直线l 与O 相切d R ⇔=; 直线l 与O 相交0d R ⇔≤<.3、圆与圆的位置关系.圆与圆的位置关系可以分为三种情况: 若两圆没有公共点,则两圆相离; 若两圆有唯一公共点,则两圆相切;若两圆有两个公共点,则两圆相交.(1)相离⎧⎨⎩外离内含;(2)相交;(3)相切⎧⎨⎩外切内切.外离12d R R ⇔>+ 外切12d R R ⇔=+ 相交1212R R d R R ⇔-<<+内切12d R R ⇔=- 内含120d R R ⇔<-≤ 相交两圆连心线的性质定理:相交两圆的连心线垂直平分两圆的公共弦. 相切两圆连心线的性质定理:相切两圆的连心线经过切点.二、例题精讲例1、如图,在ABC △中,90C ∠=︒,43AC BC ==,,点P 是线段AC 上的一个动点,以点P 为圆心、P A 长为半径作⊙P ,B C 、两点分别在这个圆的外部和内部,试确定点P 的位置范围.A例2、如图,⊙1O 与⊙2O 内切于点P ,经过⊙1O 上点Q 的切线与⊙2O 相交于A 、B 两点,直线PQ 交⊙2O 于点R .求证: =RARB .例3、已知Rt ABC △中,90ABC ∠=︒,3AB =,4BC =,以点B 为圆心作⊙B . (1)如果⊙B 与斜边AC 相切,那么B 的半径长R 是多少?(2)如果⊙B 与斜边AC 只有唯一一个公共点,求⊙B 的半径长R 的取值范围. (3)⊙B 如果与斜边AC 有两个公共点,求⊙B 的半径长R 的取值范围. (4)如果⊙B 与斜边AC 没有公共点,求⊙B 的半径长R 的取值范围.1、已知矩形ABCD 中,3AB =,4BC =,如果分别以点A 、C 为圆心的两圆相切,点D 在C 内,点B 不在C 内,那么A 的半径长R 的取值范围是什么?PO 1 O 2QABR·· ABCD343DA2、已知Rt ABC △中,90ABC ∠=︒,3AB =,4BC =,点O 是AC 上一点,AO m =,O 的半径长为1,如果O 与直角边AB 没有公共点,求m 的取值范围.例4、已知两相交圆的半径是5和4,公共弦长为6,求这两圆的圆心距.例5、已知点()2 0A ,、()8 0B ,.(1)点P 在y 轴正半轴上,若过点P 、A 、B 的圆的面积最小,求点P 的坐标; (2)点P 在直线y x =上,若过点P 、A 、B 的圆的面积最小,求这个圆的圆心坐标.1、已知1O 与2O 相交于A 、B 两点,连心线12O O 交AB 于点C,1O A =,2O A =6AB =,求12O AO ∠的度数.2、已知:如图,两个半径长为r 的等圆1O 与2O 外切于点T ,点A 、点B 分别是1O 、2O 上的点,且AT BT ⊥,垂足为点T .试猜想线段AB 的长与半径r 的数量关系,并证明你的猜想.压轴题:已知一次函数m x y +-=21的图像经过点A (-2,3),并与x 轴相交于点B ,二次函数22-+=bx ax y 的图像经过点A 和点B .(1)分别求这两个函数的解析式;(2)如果将二次函数的图像沿y 轴的正方向平移,平移后的图像与一次函数的图像相交于点P ,与y 轴相交于点Q ,当PQ ∥x 轴时,试问二次函数的图像平移了几个单位.如图,已知AB ⊥MN ,垂足为点B ,P 是射线BN 上的一个动点,AC ⊥AP ,∠ACP =∠BAP ,AB =4,BP =x ,CP =y ,点C 到MN 的距离为线段CD 的长. (1)求y 关于x 的函数解析式,并写出它的定义域.(2)在点P 的运动过程中,点C 到MN 的距离是否会发生变化?如果发生变化,请用x 的代数式表示这段距离;如果不发生变化,请求出这段距离.(3)如果圆C 与直线MN 相切,且与以BP 为半径的圆P 也相切,求BP ∶PD 的值.AB P D CNM。
圆与圆的位置关系
练习
2、圆x2+y2-2x-5=0与圆x2+y2+2x-4y-4=0的交点 为A,B,则线段AB的垂直平分线的方程是( ). A、x+y-1=0 C、x-2y+1=0 B、 2x-y+1=0 D、 x-y+1=0
y 3、如果实数x,y满足(x-2)2+y2=3,试求 x 的 最大值,y-x的最小值.
△<0
△=0 △>0
n=0
两圆相切
两个圆相交
例3. 已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 : x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位 置关系.
练习
1、已知圆C1 : x2+y2+2x+3y+1=0和 圆C2 :x2+y2+4x+3y+2=0,试判断圆C1与圆C2 的位置关系.
; / 河源整形医院 河源整形美容 河源激光整形美容 河源医学整形整容 望都无法实现,冰凝真是对自己又恨又恼,但她更痛恨这受制于人的王府生活。望着跳跃的烛火,冰凝感慨万千:只壹年的时间,竟然早已物 是人非,沧海桑田,自己从壹各无忧无虑的小姑娘,变成壹各处处受气的小老婆。这么大的落差,实在是需要她用很长、很长的壹段时间来消 化,来适应。无论做啥啊、想啥啊,冰凝仍是无法让自己的心情好起来,于是她狠狠地甩甩头,企图把这些不愉快的事情都甩掉,因为她实在 不想再在这各问题上转圈圈。那就想点儿别的事情吧!可是,无论她怎么转念,这念想都要转到宝光寺上面。去年施粥的情景还历历在目,宝 光寺残垣断壁的样子时时地浮现眼前。她太惦记宝光寺咯:庙宇重建得好不好?僧人们的生活苦不苦?香客们去得多不多?越想,却越是觉得 不踏实。现在的她,无论有啥啊想法都是无济于事,被禁锢在王府中,既不能送去她的关心,也无法表达她的问候,她唯壹能做的,只是在这 京城里,遥遥地为宝光寺祈福而已。王爷是参惮礼佛之人,因此王府里建有专门的佛堂――万安堂。看看沙漏,三更天都快要过完咯,佛堂应 该没有人咯吧。于是冰凝唤来吟雪,两各人穿戴整齐,她要去佛堂给宝光寺烧几柱香。壹路走,她壹路怀念此前三各月独住府里的生活,只有 她壹各主子,不用担心遇见这各,碰见那各,不用小心翼翼地怕被人寻咯短处。哪像现在,即使去各佛堂还要小心翼翼,躲到深更半夜。自由 自在的日子真是越想越惬意,越想越令她怀念。顶着寒风,主仆两人深壹脚浅壹脚,相扶相伴地来到佛堂,果然不出冰凝所料,这各时辰,佛 堂里壹各人都没有。自从众人从园子里回来,也只有在深更半夜,冰凝才能自由自在地做壹回自己。虔诚地焚上香,冰凝跪拜在佛祖面前,真 诚地送上自己的祝福:祈求佛祖大慈大悲,祈求菩萨格外施恩,保佑寺院,保佑僧侣,保佑香客,保佑天底下所有的生灵……远远地见到佛堂 里有人影晃动,王爷很是诧异,这各时辰,居然还会有人?怀着万分诧异的心情,待走近之后仔细定睛壹看,门口站着的,居然是怡然居的大 丫环吟雪!他不是冰凝,作为政治嗅觉异常灵敏的他,在生活中也将这种物质发挥到咯极至,因此每壹各人他接触过的人,都会记得很清楚, 即使是各丫环,他都记得。只是这各结果实在是大大出乎他的意料:竟然会是年氏在里面!犹豫咯壹下,最终还是决定进来,他是爷,难道他 还需要怕啥啊人,还需要躲着谁吗?不过,他仍是先嗽咯壹下嗓子,算是提醒壹下她吧。他没有吓唬人的嗜好,而且,隐约地,他觉得像年氏 这么柔弱的人,似乎只是壹阵风就能将她吹倒,假如凭白地受咯惊吓,估计就会立即晕倒在他的眼前咯。她要是昏倒咯,就需要他去扶她,甚 至
与圆相关的位置关系
➢ 典型例题解析
【例3】如图,O是∠CAE平分线上的一点,以 点O为圆心的圆和∠CAE的两边分别交于点B、C 和D、E,连结BD、CE.
那么3这条弦所对的圆周角为 ( A.60° B.120°
)D
C.45° D.60°或120°
6.(江苏苏州市)如图,四边形ABCD内接于⊙O,若它的
一个外角∠DCE=70°,则∠BOD=(D
)
A.35° C.110°
B.70° D.140°
结束寄语
• 数学之所以诱人,就 在于它的奥妙无穷.
一、判断题
之间的距离是______cm.
5、⊙O的半径是6,弦AB的长是6,则弧AB的中点到AB的中点的距离是
______.CPOBAD
6、如图:⊙O的直径AB⊥CD于P,
C
AP=CD=4cm,则OP=______cm. A O P B
D
7、已知⊙O中,AB是弦,CD是直径,且CD⊥AB于M.⊙O的半径是 15cm,OM:OC=3:5,则AB=______.
( √) 7、经过圆O内一点的所有弦中,以与OP垂直的弦最短. (√) 8、弦的垂直平分线经过圆心. ( √ ) 9、⊙O的半径是5,弦AB∥CD,AB=6,CD=8,则两弦间的距
离是1. ( ×) 10.在半径是4的圆中,垂直平分半径的弦长是3.( × ) 11.任意一个三角形一定有一个外接圆且只有一个外接圆.
C GD B
F A EO
证明:过O作OG⊥CD ∵ OG⊥CD ∴ DG=CG
∵ CE⊥CD,DF⊥CD,OG⊥CD ∴CE∥OG ∥ DF
圆的位置关系
圆1.圆的定义和有关概念(1)圆的定义,有两种方式:①在一个平面内,线段OA绕它固定的一个端点O旋转一周,一个端点A随之旋转说形成的图形叫做圆。
固定端点O叫做圆心,以O为圆心的圆记作O,线段OA叫做半径;②圆是到定点的距离等于定长的点的集合。
注意:圆心确定圆的位置,半径决定圆的大小。
①(2)与圆有关的概念:①弦:连接圆上任意两点的线段叫做弦;如图1所示线段AB,BC,AC都是弦;②直径:经过圆心的弦叫做直径;如AC 是O的直径,直径是圆中最长的弦;③弧:圆上任意两点之间的部分叫做圆弧,简称弧,如曲线BC,BAC都是O中的弧,分别记作BC和BAC;④半圆:圆中任意一条直径的两个端点分圆成两条弧,每条弧都叫做半圆,如AC是半圆;⑤劣弧和优弧:像BC这样小于半圆周的圆弧叫做劣弧,像BAC这样大于半圆周的圆弧叫做优弧;⑥同心圆:圆心相同,半径不等的圆叫做同心圆;⑦弓形:由弦及其说对的弧所组成的图形叫做弓形;⑧等圆和等弧:能够重合的两个圆叫做等圆,在同圆或等圆中,能够重合的弧叫做等弧;⑨圆心角:定点在圆心的角叫做圆心角如图1中的∠AOB,∠BOC是圆心角,圆心角的度数:圆心角的读书等于它所对弧的度数;∠⑩圆周角:定点在圆上,两边都和圆相交的角叫做圆周角;如图1中的∠BAC,∠ACB都是圆周角。
(3)圆的有关性质①圆的对称性圆是轴对称图形,经过圆心的直线都是它的对称轴,有无数条。
圆是中心对称图形,圆心是对称中心,优势旋转对称图形,即旋转任意角度和自身重合。
②垂径定理A.垂直于弦的直径平分这条弦,且评分弦所对的两条弧;B.平分弦(不是直径)的直径垂直于弦,并且评分弦所对的两条弧。
如图2所示。
注意(1)直径CD,(2)CD AB,(3)AM=MB,(4)BD AC=BC,(5)AD=BD.若上述5个条件中有2个成立,则另外3个业成立。
因此,垂径定理业称五二三定理,即推二知三。
(以(1),(3)作条件时,应限制AB不能为直径)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2讲与圆有关的位置关系
一、【教学目标】
1. 熟悉点与圆、直线与圆以及圆与圆的位置关系,能够将半径与到圆心的距离与之对应.
2. 了解三角形的内心和外心及内切圆、外接圆、内接三角形、外切三角形的概念.
3. 了解切线相关的概念,掌握切线长及切线长定理.
二、【教学重难点】
1.教学重点:直线与圆的位置关系、圆与圆的位置关系、切线及切线长定理
2.教学难点:灵活应用切线及切线长定理,易错题中对位置关系的全面分析
三、【考点聚焦】
考点一. 点和直线与圆的位置关系
1.点与圆的位置关系
(1).点到圆心的距离(d)、圆的半径(r)
(2).两点确定无数个圆.(圆心在哪)
不在同一直线上的三个点确定一个圆.(圆心怎么找)
注意:经过三角形三个顶点可以画一个圆,并且只能画一个.
(3).经过三角形三个顶点的圆叫做三角形的外接圆.三角形外接圆的圆心叫做这个三角形的外心,这个三角形叫做这个圆的内接三角形(三角形三条边的垂直平分线的交点).
2.直线与圆的位置关系
(1) r为圆的半径,d为圆心到直线的距离:?
考点二. 切线及切线长定理
3.圆的切线
(1)定义:和圆有唯一公共点的直线叫做圆的切线,这个公共点叫切点.
(2)切线的性质定理:圆的切线垂直于经过切点的半径.
(3)切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
推论:①经过圆心且垂直于切线的直线必经过切点,②经过切点且垂直于切线的直线必经过圆心.
4.切线长定理
(1)切线长定义:圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.
(2)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角.
注意:切线是直线,不能度量;切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
5.三角形的内切圆:与三角形各边都相切的圆叫三角形的内切圆.
三角形内切圆的圆心叫做三角形的内心.这个三角形叫做圆的外切三角形.
注意:三角形的内心就是三角形三条内角平分线的交点.
6.三角形外心、内心有关知识比较
考点三. 圆与圆的位置关系
7.圆与圆的位置关系
(其中R 、r 为两圆的半径,d 为圆心距)
四、【典例分析】
题型1 点与圆的位置关系
【示例一】如图,已知等边△ABC 的边长为,下列以A 为圆心的各圆中,半径是3cm
的圆是( )
变式1 点P 到⊙0的最短距离为2 cm ,最长距离为6 cm ,则⊙0的半径是______.
题型2 切线(直线与圆的位置关系)
cm 32
【示例二】如图,AB为的⊙O直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,试说明:AC平分∠DAB.
变式1 如图,PA、PB是⊙O的切线,A、B为切点,∠APB=78°,点C是⊙O上异于A、B 的任意一点,那么∠ACB=__________.
变式4 如图,PA与PB分别切⊙O于A、B两点,C是上任意一点,过C作⊙O的切线交PA及PB于D、E两点,若PA=PB=5cm,则△PDE的周长为________cm.
变式2 已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.试说明DC是⊙O的切线.
变式3 如图,已知PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于C.如果PA=4cm,PD=2cm,求半径OA的长.
变式4 如图,D是⊙O直径AB延长线上一点,PD是⊙O的切线,P是切点,∠D=30°,线段PA与PD相等吗?为什么?
题型3圆与圆的位置关系
【示例四】如图,两圆同心,半径分别为9cm和5cm,另有一个圆与这两圆都相切,则此圆半径为___________
A.2cm B.7cm
C.2cm或7cm D.4cm
变式1 两圆半径长分别是R和r(R>r),圆心距为d,若关于x的方程有两相等的实数根,则两圆的位置关系是_________
)d
R(
rx
2
x2
2=
-
+
-
A.一定内切B.一定外切
C.相交D.内切或外切
变式2 如图,施工工地的水平面上,有三根直径都是1米的水泥管两两相切摞在一起,则其最高点到地面的距离是( )
A.2 B.
C.D.
变式3 点P在⊙0外,OP=13 cm,PA切⊙0于点A,PA=12 cm,以P为圆心作⊙P与⊙0相切,则⊙P的半径是______.
变式4 若⊙O1与⊙02相交,公共弦长为24 cm,⊙O1与⊙02的半径分别为13 cm和15 cm,则圆心距0102的长为______.
五、【课后习题】
1.如图,点O是△ABC的内心,AO的延长线交△ABC的外接圆于点D,下列结论:①BD=CD =DO;②∠ACO=∠ABO;③∠BOD=∠COD;④∠AOB=∠CBO;⑤DD2=DD?DD;⑥OA =OB=OC.其中正确的有( )
A.2个B.3个
C.4个D.5个
2.如图,AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC于点D,试判断△AED的形状.并说明理由.
3. 如图,要在一个直角三角形的铁片上裁剪下一个图片,已知AB=60cm,BC=80cm,为了充分地利用这块铁片,使剪裁下来的图片的直径尽量大一些,应该怎样裁剪?这个圆的最大直径是多少?。
