第三讲化学反应流体动力学模型
化学反应过程流体动力学模拟及优化研究
化学反应过程流体动力学模拟及优化研究在工业生产中，化学反应过程是极其关键和重要的一个环节。
在化学反应中，流体动力学是一个非常重要的问题。
流体动力学是研究流体在各种外力作用下运动行为的一门学科，在化学反应中，它可以用来模拟反应器中的流体运动。
通过对流体动力学的研究，我们可以更好地优化化学反应过程并提高生产效率。
化学反应过程中的流体动力学模拟是一个复杂的过程。
化学反应通常需要反应器来控制反应过程。
反应器中的流体性质会影响化学反应的速率和输出。
在这种情况下，流体动力学模拟可以用来研究反应器中流体的运动和混合情况，以确定反应的条件和优化反应器的设计。
为了模拟化学反应过程中的流体动力学，我们需要发展数学方法和计算机模拟技术。
近年来，随着计算机技术的发展和计算流体力学方法的成熟，我们可以计算出复杂反应过程中流体的动力学行为。
在化学反应中，流体动力学模拟可以被用来研究流体的动力学性质、输运过程、传质过程、反应过程等。
流体动力学模拟通常可以通过计算机模拟来实现。
在计算流体力学中，物理场被离散化成网格，而基于网格的方程组求解方法被使用来计算流体的运动。
在研究和实践中，我们发现计算流体力学模拟的精度和计算速度通常是此类问题的主要挑战之一，因此，研究如何提高计算流体力学模拟的精度和计算速度是非常关键的。
在计算流体力学中，更好的网格设计对于模拟精度非常重要。
高质量的网格可以提高计算模型的准确性和稳定性，同时，优化的网格设计可以加速计算流程并减小计算代价。
在模拟化学反应过程中的流体动力学时，流体中存在许多波动和涡旋。
如果计算模型的网格过于粗糙，它不能适当地捕捉流体中的小尺度信息，影响计算结果的准确性。
因此，在模拟流体动力学中，优化的网格设计显得十分重要。
尽管流体动力学模拟十分复杂，但进行流体动力学模拟并不一定要使用高档的计算机系统。
实际上，大多数计算流体力学程序可以在标准计算机上运行。
在开发流体动力学模拟程序时，高效并行计算和优化的算法设计对于提高计算效率非常重要。
化学反应动力学
计算例题
解：苯的单程转化率: 39/100＝0.39 苯的总转化率: 39/40=0.975 氯苯的选择性: 38/39= 0.974 氯苯的总收率 38/40= 0.95 或 0.975×0.974＝0.95
很低，但总转化率和总收率可以很高。 29
循环物料 原料 反 应 器
换热器 分 离 器 产品
7
转化率
转化率：转化率是用来表示化学 反应进行的程度一个参数。一般 指关键反应组分的转化量与其起 始量的比值。 XA = ( nA0 – nA )／ nA0 XA = ( NA0 – NA )／ NA0
8
单程与全程转化率
单程转化率：以 反应器入口组成 原料 及出口组成为基 准计算的转化率。 全程转化率：以 初始原料组成与 离开反应系统的 组成为基准计算 的转化率
4
复杂反应系统特点
复杂反应系统是指在反应器中同时进行这两个 复杂反应系统是指在反应器中同时进行这两个 或两个以上的反应。 或两个以上的反应。 主要讨论的两种复杂反应系统是：连串反应与 主要讨论的两种复杂反应系统是：连串反应与平 k2 行反应。 A k 1 → P → S
动力学方程： rA = k 1c A rS = k 2 c P rP = k 1 c A − k 2 c P
17
反应器中的Leabharlann 想流动平推流模型平推流模型： 平推流模型： （活塞流） 一般流动
无返混； 无返混； 所有物料在反应器中停留时间均相同； 所有物料在反应器中停留时间均相同； 物料组成随反应器位置变化。 物料组成随反应器位置变化。 符合平推流模型特点的反应器称为平推流反应器 推流反应器（ 符合平推流模型特点的反应器称为平推流反应器（活 塞流反应器简称 简称PFR） 塞流反应器简称 ）
化工学公式总结化工过程与反应动力学的模型
化工学公式总结化工过程与反应动力学的模型化工学公式总结化工过程与反应动力学的模型是化工学中重要的理论基础，它们描述了化学反应中物质转化的速率、平衡态以及反应机理等关键性质。
本文将对化工过程与反应动力学的模型进行总结，旨在帮助读者加深对这一领域的理解。
一、质量守恒与能量守恒方程化工过程中，质量守恒与能量守恒是最基本且必须满足的原理。
在进行化学反应的系统中，质量守恒方程可以描述物质的输入、输出与转化。
能量守恒方程则描述了能量的输入、输出与转化。
这两个方程对于理解化工过程的物质与能量变化十分重要，是建立其他模型的基础。
二、扩散模型在化工过程中，扩散现象普遍存在。
扩散模型通过描述物质在不同相间传递的速率，如气体到液体、固体到液体等。
扩散模型通常采用菲克第一定律和菲克第二定律进行描述。
菲克第一定律描述了扩散速率与浓度梯度之间的关系，菲克第二定律描述了扩散过程中浓度分布的变化。
三、反应动力学模型反应动力学模型描述了化学反应速率与反应物浓度之间的关系。
常见的反应动力学模型有速率方程、反应级数和反应速率常数等。
速率方程描述了反应速率与反应物浓度的关系，根据反应的类型可以采用零、一、二、三级反应等不同反应级数的模型。
反应速率常数表示了单位时间内单位体积反应物消失或生成的量。
四、平衡态模型平衡态模型用于描述化学反应达到平衡时反应物与生成物浓度的关系。
平衡态模型根据反应的类型可采用理想气体状态方程、溶液的溶解度平衡常数等。
由平衡常数与反应物浓度之间的关系，可以预测反应在不同条件下的平衡位置。
五、传热模型传热模型用于描述化工过程中的热传递现象，包括导热、对流和辐射等。
传热模型可以采用傅里叶传热定律、牛顿冷却定律和辐射传热方程等进行描述。
这些模型对于设计化工过程中的换热器、反应器等设备具有重要指导意义。
六、动态模型动态模型描述了化工过程与反应在时间上的变化。
动态模型一般采用微分方程进行描述，如质量守恒方程、能量守恒方程和动态反应动力学方程等。
化学反应动力学-3
d 故有 ( k f k r ) dt 积分后得： 0 exp{ (k f kr )t} 0 exp(t ) 1 1 k f kr ( k f k r )
：弛豫变量。 ：弛豫速率常数。 ：弛豫时间，标志了弛豫过程的平均时间。
I3- 在 = 352 nm 有很高的摩尔消光系数。
12
现代 UV 分光光度计的波长范围通常为 190 900 nm，人们很容易找到反应物或产物在此 范围内有吸收。 优点： （1）可利用的化学反应范围较宽，从快速反 应到慢反应均可。 （2）方法灵敏度高。（3）选择性好。 （4）可用于混合物中物质性质十分相近但吸 收光谱不同的化合物的同时测出。 （5）可用于高浓度与极低浓度物质的测定。
34
对平衡体系施加扰动的信号有脉冲式、阶 跃式、周期式等。 脉冲式信号：在短时间内施加一强大的扰 动，使体系产生弛豫变量 = 0，继之反应 体系回复原始的环境条件。 阶跃式信号：在短时间内突然改变外界条 件而不再回复到原来的环境条件。
10
5、分光光度法 动力学分光光度法是通过测定反应物或产物 中某指定物质的吸光度随时间的变化来测定反 应速率。 要求：反应物和产物有不同的吸收光谱，并且 吸收物质的吸收强度要足够大。 原理：Beer-lambert law
I0 lg cl A It
I0：入射光光强
It：透过光光强
：摩尔消光系数
fructose + glucose
-92.4
+52.7
9
3、电导法
RCO2Et + OHRCO 2- + EtOH
ci i
：比电导或电导率。 ci：离子 i 的浓度。 i：离子 i 的当量电导。
化学反应工程第三章反应器内的流体流动
物料的浓度变化。
如测定数据属于离散型， 则：
3.2.3 寻求停留时间分布的实验方法
在实验时，时间间隔可以取成等值，得：
平均停留时间和散度可按下式计算：
当 为定值时，
散度
3.2.3 寻求停留时间分布的实验方法
例3-2 在稳定操作的连续搅拌式反应器的进料中脉冲
m 50g
注入染料液（
）,测出出口液中示踪剂浓度随时
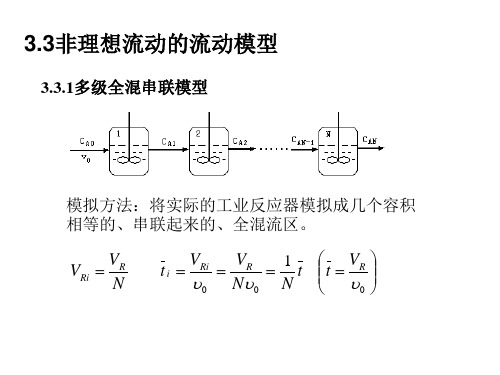
多级混合模型是由N个容积为V的全混釜串联组成，从一 个釜到下一个釜的管道内无返混且不发生化学反应，示 意如图3-8：
图3-8 多级混合模型
3.4.1 多级混合模型
经推导可得该多级混合模型的停留时间分布规律为：
F ( ) cN 1 1 1 1 1 exp( N )[1 ( N ) ( N ) 2 ( N ) 3 （N ) N 1 ] c0 1 ！ 2 ！ 3! （N 1 ）！
（t）；另一部分是阶跃输入前的物料量为Vc0－中时间
大于t的示踪剂，其量为Vc0－[1-F（t）] 。即：
即得：
（3-15）
如果阶跃输入前进口物料中不含示踪剂，即 ，则上 c F ( t ) 式可以改写成： （3-16） c0
3.2.3 寻求停留时间分布的实验方法
例3-1 测定某一反应器停留时间分布规律，采用阶跃输 入法，输入的示踪剂浓度 ，在出口处测定响应曲线得到 的数据如下表3-1所示：
占的分率。依此定义，E(t)和F(t)之间应具有如下关
系： 以及
3.2.1 停留时间分布的定量描述
在t=0时 F(0)=0和t=∞时 ，关于E(t)、F(t)曲线以及它 们之间的关系示于图3-2中。
图3—2 停留时间分布曲线
化学反应工程-11-第三章-均相非理想流动反应器
F (θ ) = F (t )
三、E (θ ) ~ θ 的特征
⑴存在一个最大值 E (θ )max
求最大值：
NN E (θ ) = θ N −1e − Nθ (N − 1)! dE (θ ) =0 dθ
NN dE (θ ) = θ N − 2 ⋅ (N − 1)e − Nθ − Nθ N −1e − Nθ dθ (N − 1)!
总结：
N =1 时
N =∞ 时
σ θ2 = 1
σ θ2 = 0
(CSTR )
(PFR )
例1有一管式反应装置经脉冲示踪法实验测得如下表所示的 数据： υ 0 = 0.8 m 3 / min , m = 80 kg
t (分)
CA kg / m3
0
2 6.5
4 12.5
6 12.5
8 10.0
10 5.0
示踪物作脉冲输入，根据以前知识，CA具有以下形式：
0 CA = ?
t < tP = t ≥ tP
(1 − f m )VR
v0
某时刻t时，对CSTR，对A作物料衡算
dn A dt dC A − υ 0 C A = f mVR dt M t = t P CA = f mV R v0 ⋅ 0 = v0 ⋅ C A +
t = tP t ≠ tP
对1、2、3三点作物料衡算 、 、 三点作物料衡算
I m v0 C Am + (1 − I m )v0 C AP = v0 C A
C A = I m C Am + (1 − I m )C AP
∞ E (t ) = 0
t =t = t≠t
f PV R v0
第三章 流体动力学基础
1、在水位恒定的情况下： （1）A®A¢不存在时变加速 度和位变加速度。 （2）B®B¢ 不存在时变加速 度，但存在位变加速度。 2、在水位变化的情况下： （1）A®A¢ 存在时变加速度， 但不存在位变加速度。 （2）B®B¢ 既存在时变加速 度，又存在位变加速度。
图3-19
第二节 流体质点运动特点和有旋流
图3-13
非均匀流——流线不是平行直线的流 动， 。 非均匀流中流场中相应点的流速大 小或方向或同时二者沿程改变，即沿流 程方向速度分布不均。例：流体在收缩 管、扩散管或弯管中的流动。（非均匀 流又可分为急变流和渐变流）
4.渐变流与急变流
非均匀流中如流动变化缓 慢，流线的曲率很小接近平行， 过流断面上的压力基本上是静 压分布者为渐变流(gradually varied flow)，否则为急变流。
图3-17
（3）三元流
三元流（threedimensional flow):流动 流体的运动要素是三 个空间坐标函数。例 如水在断面形状与大 小沿程变化的天然河 道中流动，水对船的 绕流等等，这种流动 属于三元流动。（图 3-18）
图3-18
三.描述流体运动的方法
1.拉格朗日法 拉格朗日方法（lagrangian method）是以 流场中每一流体质点作为描述流体运动 的方法，它以流体个别质点随时间的运 动为基础，通过综合足够多的质点（即 质点系）运动求得整个流动。——质点 系法
一、流体质点的运动 特点 刚体的运动是由 平移和绕某瞬时轴 的 转动两部分组成，如 图3-20(a)。
图3-20(a)
流体质点的运动， 一般除了平移、转 动外，还要发生变 形（角变形和线变 形），如图3-20(b)。
图3-20(b)
二、角速度的数学表达式 流体质点的旋转用角速度表征，习 惯上是把原来互相垂直的两邻边的角速 度平均值定义为该转轴的角速度。
流体力学ppt课件-流体动力学
g
g
2g
水头
，
z
p
g
v2
2g
总水头， hw 水头损失
第二节 热力学第一定律——能量方程
水头线的绘制
总水头线
hw
对于理想流体，总水
1
v12 2g
2
v22 2g
头线是沿程不变的，
测压管水头线
p2
为一水平直线，对于
g
实际流体，总水头沿 程降低，但测压管水
p1 g
头线沿程有可能降低、
z2
不变或者升高。
z1
v2 A2 e2
u22 2
gz2
p2
v1A1 e1
u12 2
gz1
p1
微元流管即为流线，如果不 可压缩理想流体与外界无热 交换，热力学能为常数，则
u2 gz p 常数
2
这个方程是伯努利于1738年首先提出来的，命名为伯努利 方程。伯努利方程的物理意义是沿流线机械能守恒。
第二节 热力学第一定律——能量方程
皮托在1773年用一根弯成直角的玻璃管，测量了法国塞纳河 的流速。原理如图所示，在液体管道某截面装一个测压管和 一个两端开口弯成直角的玻璃管（皮托管），皮托管一端正 对来流，一端垂直向上，此时皮托管内液柱比测压管内液柱 高h，这是因为流体流到皮托管入口A点受到阻滞，速度降为 零，流体的动能变化为压强势能，形成驻点A，A处的压强称 为总压，与A位于同一流线且在A上游的B点未受测压管的影 响，其压强与A点测压管测得的压强相等，称为静压。
第四章 流体动力学
基本内容
• 雷诺输运公式 • 能量方程 • 动量方程 • 流体力学方程应用
第一节 雷诺输运方程
• 前面解决了流体运动的表示方法,但要在流 体上应用物理定律还有困难.